Flavin Charge Transfer Transitions Assist DNA Photolyase Electron Transfer

Abstract

This contribution describes molecular dynamics, semi-empirical and ab-initio studies of the primary photo-induced electron transfer reaction in DNA photolyase. DNA photolyases are FADH⁻-containing proteins that repair UV-damaged DNA by photo-induced electron transfer. A DNA photolyase recognizes and binds to cyclobutatne pyrimidine dimer lesions of DNA. The protein repairs a bound lesion by transferring an electron to the lesion from FADH⁻, upon photo-excitation of FADH⁻ with 350–450 nm light. We compute the lowest singlet excited states of FADH⁻ in DNA photolyase using INDO/S configuration interaction, time-dependent density-functional, and time-dependent Hartree-Fock methods. The calculations identify the lowest singlet excited state of FADH⁻ that is populated after photo-excitation and that acts as the electron donor. For this donor state we compute conformationally-averaged tunneling matrix elements to empty electron- acceptor states of a thymine dimer bound to photolyase. The conformational averaging involves different FADH⁻ - thymine dimer confromations obtained from molecular dynamics simulations of the solvated protein with a thymine dimer docked in its active site. The tunneling matrix element computations use INDO/S-level Green’s function, energy splitting, and Generalized Mulliken-Hush methods. These calculations indicate that photo-excitation of FADH⁻ causes a π → π^* charge-transfer transition that shifts electron density to the side of the flavin isoalloxazine ring that is adjacent to the docked thymine dimer. This shift in electron density enhances the FADH⁻ - to - dimer electronic coupling, thus inducing rapid electron transfer.

INTRODUCTION

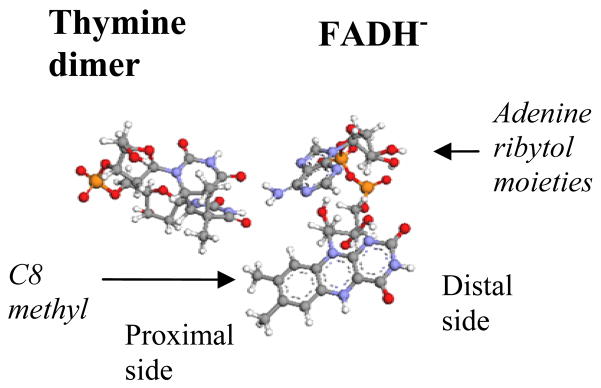
DNA photolyases repair UV-damaged DNA by photo-induced electron transfer [1]. The electron-cofactor of a photolyase is a two-electron reduced flavin adenine dinucleotide (FADH⁻). The protein also contains a chromophore that acts as an antenna molecule (either MTHF in folate class photolyases or 8-HDF in deazaflavin class photolyases). Cyclobutane pyrimidine dimer (CPD) photolyases recognize and bind to CPD lesions of DNA. Upon binding of a CPD lesion to the protein the lesion flips into the protein’s active site and docks next to FADH⁻ (figure 1). Absorption of light by the antenna chromophore (in the 350–450 nm region) induces energy transfer by dipole-dipole interactions to FADH⁻. The excited FADH⁻ transfers an electron to the docked CPD lesion. The transfer of an electron to the CPD initiates the conversion of the dimer to two pyrimidine monomers and the repair of the lesion.

FIGURE 1.

DNA photolyase FADH⁻ - thymine dimer geometry. The side of the flavin isoalloxazine ring that is further away from the dimer is denoted distal and the side that is closest to the dimer is denoted proximal.

The photo-induced electron transfer (ET) reaction that initiates pyrimidine dimer repair, ${}^1\text{F}{\text{ADH}}^{-}\ast +\text{Pyr}-\text{Pyr}\stackrel{e^{-}}{\to }{\text{FADH}}^{•}+{\text{Pyr}-\text{Pyr}}^{•-}$, occurs at a rate of 200⁻¹ psec⁻¹ [2]. We studied the mechanism of this ET reaction using molecular dynamics simulations of the solvated protein with a thymine dimer docked in its active site, coupled to electronic structure and electronic coupling calculations of the FADH⁻ - thymine dimer pair. Our purpose is to identify the electron-donating excited state of FADH⁻, its average electronic coupling to thymine dimer electron-accepting states, and the electron transfer pathways that mediate this coupling. The electron-donating state of FADH⁻* is identified by comparing the calculated absorption spectrum of FADH⁻ in DNA photolyase to the experimental spectrum. The computed average electronic coupling and the proposed electron transfer pathways between FADH⁻ and the dimer are tested by predicting the rate of the photo-induced ET reaction which is known from experiment. The calculations show that the directionality of the π → π^* charge-transfer transitions of the flavin isoalloxazine ring play a central role in determining the ET rate and the ET pathways [3]

COMPUTATIONAL METHODS

Molecular Dynamics Simulations

We performed MD simulations on E. Coli photolyase (PDB structure 1DNP [4]) with a thymine dimer docked in its active site, using the AMBER 8.0 program [5] and the AMBER force field [6]. Partial charges for the dimer and FADH⁻ were calculated at the Hartree-Fock 6-31G(d) level using Gaussian 98 [7], and were fitted with the RESP procedure [8]. The MD simulations involved a constant pressure (NpT) ensemble, Langevin thermostat, periodic boundary conditions, and full electrostatics particle mesh Ewald calculations. The protein was solvated with a 95×75×75A TIP3P water box, and Na⁺ ions were added to neutralize the system. The initial energy minimization used 5000 steps, with harmonic constraints imposed on the protein backbone and cofactor heavy atoms, and was followed by 300 psec MD using the same harmonic constraints. The system was equilibrated for 500 psec at 300K without constraints and then additional MD was performed for 100 psec. Conformational snapshots were saved every 1 psec.

Excited State Electronic Structure Calculations

The excited-state calculations used the time dependent density functional (TDDFT) [9], time dependent Hartree-Fock (TDHF) [10], and INDO/S configuration interaction singles (CIS) methods [11]. This was done in order to gauge the reliability of our calculations by seeking robust predictions. We performed the electronic structure calculations on FADH- for several molecular geometries derived from several protein-FADH⁻-dimer MD conformations (separated by 20–80 psec). For each conformation we performed both vacuum and solvated calculations. The FADH⁻ solvation shell included the active site residues 222, 234–239, 271, 338, 341, 344, 372, 374, and 378 of E. coli photolyase, the thymine dimer, 47 water molecules, and Na+ ions used for charge neutralization in MD (all represented by Amber force-field atomic charges). The Na+ ions were used to vary the total charge of the system so that FADH- is either fully neutralized (total charge 0), or it has an effective charge of −1 (total charge −1). For the INDO/S CIS calculations we used the program of ref [13], and for the ab initio calculations the program Gaussian03 [12].

Tunneling Matrix Element Calculations

The electronic-coupling calculations were performed at the INDO/S level with the the program of ref [13] and the Harlem program [14]. Three different computational methodologies were used: the “Green’s function” [15], the “energy splitting” [16], and “Generalized Mulliken Hush” (GMH [17]) methods. The three approaches give similar results, with Green’s function and GMH electronic-coupling values being nearly identical.

RESULTS AND DISCUSSION

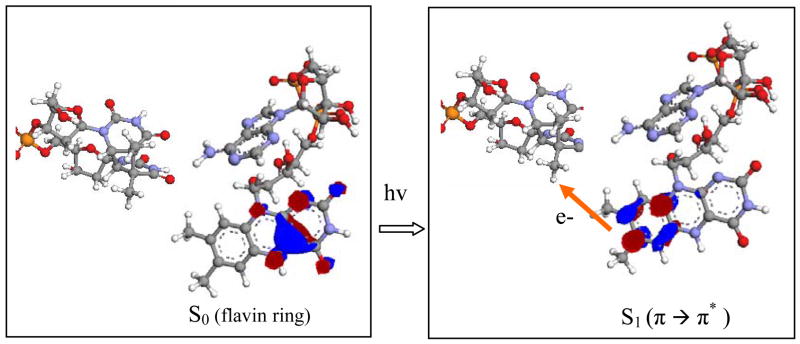
The observed absorption spectrum of E. coli photolyase (in the 300–500 nm range) with only the FADH- cofactor has a maximum of ε ≈ 3 × 10⁴ (M⁻¹cm⁻¹) at λ ≈ 300 nm, and a secondary maximum of ε ≈ 6–7 × 10³ (M⁻¹cm⁻¹) at λ ≈ 365 nm. The INDO/S calculations predict that the two lowest singlet excited states of FADH- (S1 and S2) are of π → π* character, and both involve the displacement of electron amplitude from the distal side to the proximal side of the flavin ring (figure 1). At much higher energies there is also a π → π* singlet excited state (S3) that retains the electron amplitude on the distal side of the flavin ring (figure 1), and also π → π* states where the π* is localized on the adenine ring. The INDO/S calculations identify the 365 nm maximum in the experimental absorption spectrum with the S2 excited state (predicted oscillator strength f = 2–3 × 10⁻¹ and λ =390–400 nm). S1 has much lower oscillator strength. The TDDFT/BH and HLYP calculations predict flavin-flavin π → π* excitations that are similar to the INDO/S S1 and S2 states, and also low-lying flavin-adenine π → π*excitations. The S1 and S2 TDDFT absorption wavelengths are slightly smaller (by 10–20 nm) than the INDO/S values. The TDDFT oscillator strength for S2 is of the order of 10⁻¹ (as in INDO/S), whereas the strengths for S1 and the flavin-adenine excitations are negligible. TDHF greatly underestimates the absorption wavelengths.

Upon photo-excitation of FADH⁻, the high-oscillator-strength S2 and S3 states will be populated. There is evidence from time-resolved absorption and fluorescence experiments on flavin componds [18] that the internal conversion rate in the π* singlet excited state manifold is a few hundred fsec to a psec (especially for high energy Sn states). Therefore, since ET takes place in 200 psec, we expect that prior to ET the FADH⁻ has relaxed to the S1 state that is localized on the proximal side of the flavin ring (figure 1). The possibility that the electron is localized on the adenine ring of FADH⁻ prior to ET is excluded by femtosecond time resolved experiments of the ET reaction which do not observe real adenine intermediates even for DNA photolyase without a CPD in the adtive site [2].

For the tunneling matrix element calculations the donor (D) molecular orbital (MO) was chosen to be the π* MO that is populated by the excited electron in S1 and is localized on the proximal side of the flavin ring (figure 2, right). The acceptor (A) MO’s were chosen to be the empty orbitals of the thymine dimer that are closest in energy to the D MO. We computed $T_{DA}^{(\mathit{rms})}=\sqrt{\langle T_{DA}^2\rangle }$ for several D-A MO pairs where the averages were taking over 100 MD snapshots separated by 1 psec time intervals. The calculations predicted $T_{DA}^{(\mathit{rms})}$ of the order of 5 × 10⁻⁴ eV. The predicted room-temperature ET rate is of the order of 200⁻¹ psec⁻¹, assuming activation less ET with a reorganization energy of approximately 1 eV[19]. This prediction compares well with experiment, although it should be noted that there is substantial solvent reorganization of the active site upon photo-excitation [2], making the estimation of the reorganization energy difficult.

FIGURE 2.

The mechanism of the photo-induced ET reaction that initiates CPD repair in DNA photlyase

To identify the tunneling pathways between FADH⁻ and the dimer we computed $T_{DA}^{(\mathit{rms})}$ for modified FADH⁻ donor cofactors. One type of FADH⁻ modification, involved the replacement of the ribytol and adenine moieties (figure 1) by a methyl group at the C1^/ position, thus eliminating adenine-mediated pathways. The second type of modification replaced the C8 methyl group on the proximal side of the flavin ring (figure 1) with a hydrogen. The removal of the C8 methyl group eliminates the strongest methyl-group-mediated pathways. The above modifications of FADH⁻ did not change the character and relative energies of the lowest π → π* singlet states of the flavin ring. Therefore, we used the same D MO as in the full FADH⁻ calculations (i.e., the π* MO of the lowest singlet π → π* state of the flavin ring, localized on its proximal side). The conformational averaging of the tunneling matrix elements for the modified FADH⁻ cofactors was performed using MD snapshots from the original protein-FADH⁻-dimer simulations. For each snapshot we performed the FADH⁻ atom deletions and replacement described above without perturbing the positions of the remaining FADH⁻ atoms and the conformation of the adjacent dimer. Our calculations showed that the deletion of the C8 methyl group reduced $T_{DA}^{(\mathit{rms})}$ by a factor of 4–5, whereas the delition of the adenine ane ribytol moieties did not significantly affect the $T_{DA}^{(\mathit{rms})}$ value. This is strong evidence that the C8 methyl group between the proximal side of the flavin ring and the thymine dimer provides the dominant tunneling pathways for the FADH⁻ to dimer electronic coupling (figure 2, right).

CONCLUSION

DNA photolyase uses the directionality of the intrinsic π → π* charge transfer transitions of the flavin isoalloxazine ring to enhance ET to the cyclobutane dimer. Photo-excitation of FADH⁻ causes the displacement of electron density from the side of the flavin ring that is further away from the dimer to the side adjacent to it. This displacement enhances the FADH⁻ - to - dimer electronic coupling because it permits short tunneling pathways to the dimer, with single through-space jumps. In DNA photolyase the ET pathways are photo-selected.