Methodology for patient-specific modeling of atrial fibrosis as a substrate for atrial fibrillation

Abstract

Personalized computational cardiac models are emerging as an important tool for studying cardiac arrhythmia mechanisms, and have the potential to become powerful instruments for guiding clinical anti-arrhythmia therapy. In this article, we present the methodology for constructing a patient-specific model of atrial fibrosis as a substrate for atrial fibrillation. The model is constructed from high-resolution late gadolinium-enhanced magnetic resonance imaging (LGE-MRI) images acquired in vivo from a patient suffering from persistent atrial fibrillation, accurately capturing both the patient’s atrial geometry and the distribution of the fibrotic regions in the atria. Atrial fiber orientation is estimated using a novel image-based method, and fibrosis is represented in the patient-specific fibrotic regions as incorporating collagenous septa, gap junction remodeling, and myofibroblast proliferation. A proof-of-concept simulation result of reentrant circuits underlying atrial fibrillation in the model of the patient’s fibrotic atrium is presented to demonstrate the completion of methodology development.

Introduction

Atrial fibrillation (AF) is a major cause of morbidity and mortality, contributing significantly to global health expenditure. Although catheter ablation has emerged as a promising treatment strategy for patients who suffer from AF, approximately 30% of procedures fail to terminate the arrhythmia. Clinical evidence demonstrates that the extent of left atrial (LA) fibrosis is correlated with the success of treatment outcomes in patients with AF^1,2, suggesting that information regarding the extent and morphology of fibrosis in the patient’s atrium may be a valuable tool in guiding catheter ablation techniques. Recent advances in in vivo imaging techniques allow for the visualization of fibrosis throughout the patient’s atria, providing impetus for image-based computational modeling to accurately represent both the geometry of the patient’s atria and the specific fibrosis distribution. The ability to develop such a customized atrial model has important implications for personalized AF treatment, a long-term goal of the clinical community, which could significantly improve the success rates of ablation procedures.

Personalized computational models of the heart allow for the integration of insight obtained from cutting-edge developments in various realms of cardiac research. The ability to replicate the exact geometry of a living patient’s heart, and the structural remodeling therein, capitalizes on recent advances in late gadolinium-enhanced magnetic resonance imaging (LGE-MRI) methodology, which uses gadolinium contrast to localize and quantify the degree of fibrosis and structural remodeling.³ Experimental findings obtained in cellular-, tissue-, and organ-level studies represent crucial inputs to the computational model. Clinical knowledge of the patient’s arrhythmia etiology, disease progression, and therapy outcome allows for the validation of patient-specific heart models. With the methodology for developing personalized computational models of the heart well underway, better understanding of the mechanisms underlying cardiac disease and arrhythmias will enable computational approaches to provide a powerful new tool in the clinic: a novel way to predict disease and guide treatments.

In this study, we use state-of-the-art techniques to develop the methodology for generation of patient-specific atrial models with accurate fibrotic lesion distribution. MR images were obtained from a patient suffering from persistent AF. Following image segmentation and interpolation, patient geometries were reconstructed. Atrial fiber orientation was estimated using a novel image-based method whereby the patient atrial geometry is registered with atlas atria whose geometry and fiber orientations are known. As one possible scenario of fibrotic remodeling, fibrotic lesions are modeled to contain non-conducting collagenous septa, connexin redistribution, and myofibroblast proliferation. Finally, we show a proof-of-concept simulation using a model of an AF patient’s atrium, whereby pulmonary vein ectopy, indeed, resulted in arrhythmia. This simulation demonstrates that the methodology is fully operational.

Model development and simulation proof-of-concept

Patient geometry reconstruction

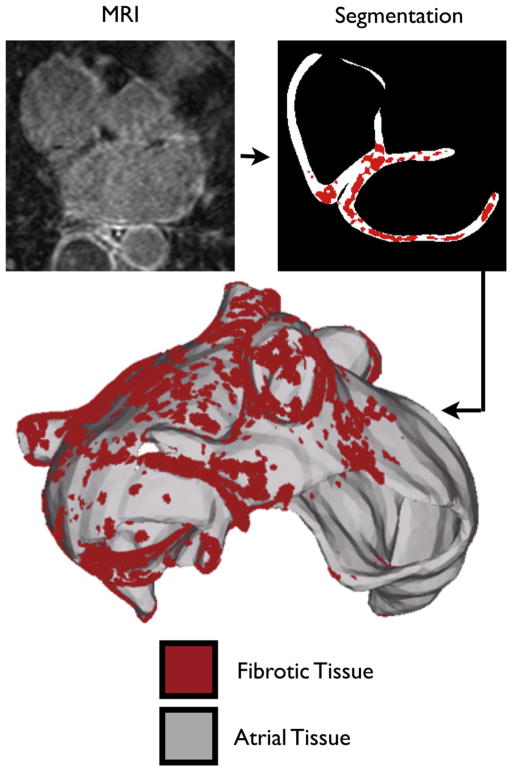
A patient with persistent AF presenting to the University of Utah for catheter ablation underwent pre-ablation LGE-MRI evaluation at a resolution of 1250×1250×1500 μm³, following the methodology of Akoum et al.⁴; a representative slice of the MR image stack is shown in Fig. 1. Epicardial and endocardial atrial borders were manually contoured using Corview (MARREK Inc., Salt Lake City, UT, USA), an image display and analysis software package. The relative extent of pre-ablation enhancement was quantified within the left atrial (LA) wall with a threshold-based algorithm utilizing pixel intensities from atrial tissue. The patient was classified as a Utah stage 4, indicating extensive fibrosis of the LA wall.⁴ Mean pixel intensity was obtained from the atrial tissue region, and fibrotic regions were segmented out based on pixel intensity of 0.5 standard deviations above the mean intensity level (Fig. 1). A shape-based interpolation technique⁵ was applied to the binary masks representing the endocardium, epicardium, and fibrotic regions at the acquired resolution, and the results were combined to generate a high-resolution segmented image of the atrial wall with fibrosis, with an isotropic voxel size of 400 μm³. From this image, the atrial surface was extracted, and the resolution of the surface was reduced using surface mesh coarsening software, ACVD (Creatis, Lyon, France). The meshing package TetGen (WIAS, Berlin, Germany) was used to construct a finite element tetrahedral mesh within the surface (Fig. 1). Each element of the 2.3 million node mesh was labeled as fibrotic or non-fibrotic based on the location of its centroid in the high-resolution segmented image.

Fig. 1.

Model generation. Representative MRI slice of the human heart, segmentation of atrial slice, and 3D atrial model.

Fiber orientation estimation

Due to the lack of imaging technology for obtaining myocardial fiber data in vivo, assigning realistic fiber orientations in the reconstructed models of the human atria is a challenging problem. We have recently developed an image-based method for predicting fiber orientations in a patient-specific ventricular geometry, by registering the geometry with an atlas heart whose geometry and fiber orientations are known.⁶ Validation tests have demonstrated that these predicted fiber orientations closely match acquired fiber orientations. For the first time, this methodology was extended to assign fiber orientation in a patient-specific atrial model. Briefly, an atrial model with accurate fiber data.⁷ was obtained for use as an atlas model, and >100 corresponding anatomical landmarks were manually identified on both the atlas and patient image stacks (Fig. 2A). The landmarks were then used for a combination of a 3D variant of the thin plate spline transformation (3DTPST).⁸ and large deformation diffeomorphic metric mapping (LDDMM)⁹, which morphed the atrial atlas geometry to closely match the patient atria. In the 3DTPST, each point x in the atlas image was mapped to a point y using the equation

Fig. 2.

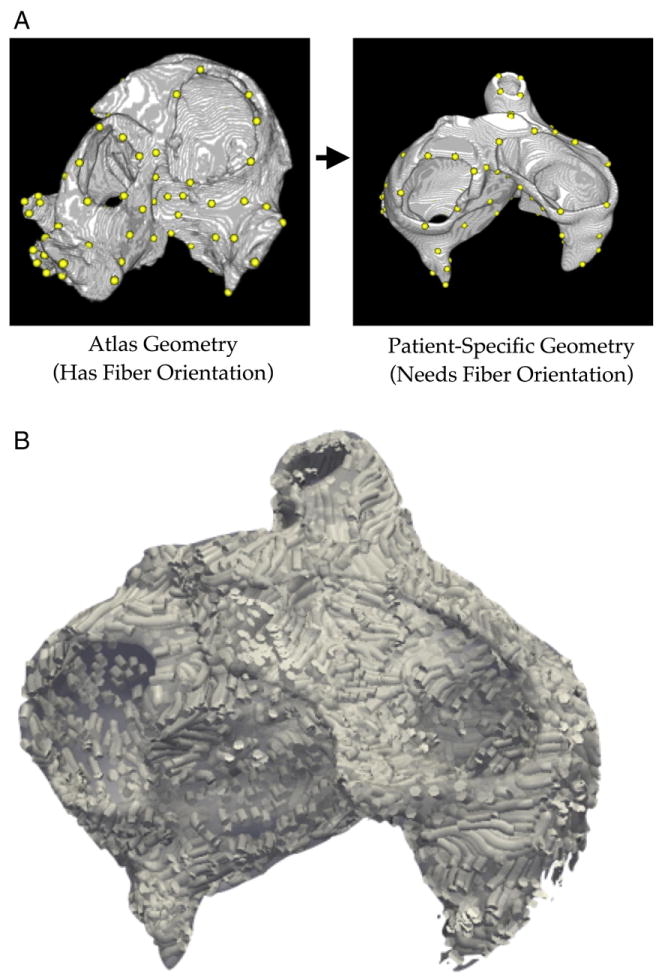
(A) Corresponding anatomical landmarks (yellow dots) on the atlas and patient image stacks. (B). Estimation of patient geometry fiber orientation.

$$y=\sum _{i=1}^n{c}_i{\left|\right|x-l_i\left|\right|}^2\mathit{log}({\left|\right|x-l_i\left|\right|}^2)+p(x),$$

where n is the number of landmark pairs, l_i is the location of the ith landmark in the atlas image, c_i is a scalar coefficient, and p is a first-degree polynomial in x. The values of c_i and the coefficients of p were determined by solving the system of n linear equations obtained from the above equation by substituting y with, for each l_i, the location of the corresponding landmark in the patient image. The atlas image morphed by the 3DTPST was further transformed using LDDMM to closely match the patient image. In the LDDMM, given the 3DTPST transformed atlas image I_a: Ω→R and the patient image I_p:Ω→R, a flow of diffeomorphisms ϕ_t: Ω→Ω was computed to transform I_a to match I_p, where Ω⊂R³ is the 3D cube in which the image data are defined and t∈[0,1]. The final diffeomorphism φ= φ₁ is calculated by means of a gradient descent search such that ||I_a = φ⁻¹ − I_p||, i.e., the difference between the transformed atlas image and the patient image is minimized. More details on 3DTPST and LDDMM can be found in previous publications.^8,9 The final deformation field resulting from the combination of 3DTPST and LDDMM was then applied to deform the atlas fiber orientations to obtain an estimate of the patient atrial fiber orientations (Fig. 2B). The fiber orientations deformation was achieved using the preservation of principal components method described previously.¹⁰

Atrial tissue electrophysiological representation

Atrial myocyte membrane kinetics was represented by the Courtemanche–Ramirez–Nattel model of the human atrial action potential under AF.¹¹ Additional parameters were adjusted to match clinical data from patients with chronic AF.¹² Conductivities were chosen such that conduction velocity fell within the range recorded in the human atrium.¹³

Fibrotic tissue representation

Connexin distribution

AF is associated with the down-regulation and lateralization of connexins, the gap junctional proteins, in atrial myocytes.^14,15 Therefore, myocardial conductivity values in the fibrotic regions of the model were reduced by 20% in the longitudinal direction and 50% in the transverse direction, compared to those in the remainder of atrial tissue, to account for both the overall reduction of Cx43 volume fraction observed during AF compared to sinus rhythm (~30% reduction¹⁴), as well as the documented Cx43 lateralization in AF compared to sinus rhythm.¹⁵

Inclusion of collagenous septa

Sustained AF is associated with an up-regulation of collagen volume in the atrium.¹⁶ Collagenous septa form sheets, separating myofibrils in the heart, and act as passive barriers to electrical propagation. However, there are significant challenges associated with representing such fine structural discontinuities in computational models, as the spatial resolution of the mesh must be very fine in order to account for these entities. Costa et al.¹⁷ have recently developed a novel numerical technique that accounts for the effects of microscopic conduction barriers without physically representing the structures in the computational mesh. The authors demonstrated that introducing infinitely thin layers of electrical isolation in a coarse 2D mesh, achieved via element decoupling, faithfully represents the propagation observed in a high-resolution mesh where the structural discontinuities are explicitly represented.

In this project, we further developed this technique and extended it to 3D. We used 3D element decoupling to account for the fine conduction barriers introduced by collagenous septa in atrial fibrosis. Insulating sheets were randomly seeded and grown along element faces parallel to fiber orientation in the fibrotic regions of the patient-specific atrial model. Adjacent elements on opposing sides of the insulating sheet were decoupled by duplicating nodes positioned along the insulating sheet. Element indices were then renumbered to use these duplicated nodes, ensuring that adjacent elements on opposing sides of the sheet did not share the same nodes. Due to the no-flux boundary conditions assumed along these insulating sheets, the propagation delay caused by node duplication was identical to the barrier effect caused by the presence of infinitesimally thin collagenous septa.

Myofibroblast infiltration

In order to populate the fibrotic region of the model with myofibroblasts, as observed experimentally, myofibroblast properties were assigned to 1% of the elements, at random distribution, within the patient-specific fibrotic regions. Myofibroblast model membrane kinetics in the fibrotic regions were represented by the model of MacCannell et al.¹⁸, which includes inwardly rectifying (K_ir) and time- and voltage-gated (K_v) K⁺ currents. Myofibroblasts were electrically coupled to adjacent myocytes, and were modeled as isotropic with reduced conductivity (75% of that of the atrial myocyte’s primary fiber direction), representing the reduction of single gap junction conductance measured in myofibroblast–myocyte pairs as compared to inter-myocyte junctions.¹⁹

Simulation protocol

Mathematical description of current flow in cardiac tissue in the human atrium was based on the monodomain representation. Simulations were executed using the simulation package, CARP (CardioSolv LLC).²⁰ The model was paced for five beats at a 365-ms basic cycle length, and an ectopic beat was stimulated from a left pulmonary vein.

Simulation of atrial fibrillation in the fibrotic atrium: a proof of concept

A simulation was performed with the patient-specific atrial model to illustrate the substrate’s susceptibility to reentry²¹, thus demonstrating that the methodology is fully operational.. Fig. 3 shows transmembrane potential maps of the patient’s LA at several time intervals after the ectopic beat; ectopy results in unidirectional block and reentry, initiating arrhythmia in the atrium that lasted >5s in duration. The formation of reentrant circuits in the fibrotic atrium following an ectopic beat in the pulmonary vein region suggests that personalized models could be used to predict the occurrence of arrhythmia in the patient atrium it was generated from.

Fig. 3.

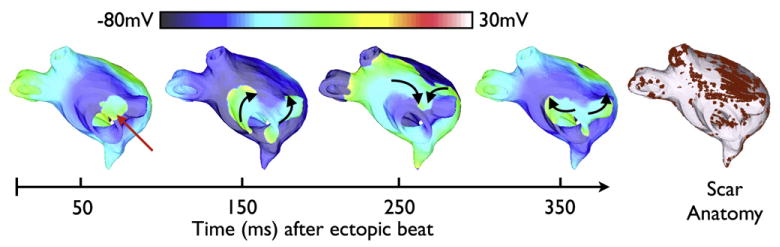
Transmembrane potential maps of arrhythmia at four time instants in the patient-specific LA model following pulmonary vein ectopy. Red arrow indicates the location of the ectopic beat. Conduction direction is indicated by the black arrows. Scar anatomy (red) is depicted at right.

Discussion

A body of research has suggested that spatial variations in fibrosis patterns differentially affect electrical propagation in the heart. In explanted human hearts, it was found that alterations in activation delays are imposed by different patterns of fibrosis.²² Recent work by Tanaka et al.²³ demonstrates that the spatial distribution of fibrosis regulates changes in AF activation frequency and dynamics in the posterior LA during heart failure. Computational modeling has shown that failure of electrical propagation is highly dependent on the spatial pattern of fibrosis.²⁴ This dependency of conduction failure on fibrosis has been demonstrated to be exacerbated under conditions of reduced sodium current, where conduction block occurred at lower fibrosis density. These findings provide impetus for the use of patient-specific fibrotic distributions during the investigation of AF initiation and maintenance dynamics. Further elucidation of how spatial variations in fibrosis affect AF will help in the guidance of AF treatment therapies. The goal of this study was to develop the methodology for generation of patient-specific atrial models with accurate fibrotic lesion distribution, providing a powerful new tool for the investigation of the mechanistic relationship between AF and fibrotic remodeling in the atria.

While biophysically detailed computational models representing generalized geometries and conditions are useful in providing mechanistic insight into cardiac patho-physiological function, they do not take into account the variations in disease states and heart geometries that are observed in a population. Therefore, patient-specific models, which take into account a patient’s unique disease presentation, are necessary for clinical applications. There has been a recent push toward the development and validation of such personalized models; Pop et al.²⁵ demonstrated in a recent study that MRI-based models of infarcted pig ventricles can accurately reproduce electrical data recorded during an experimental electrophysiological study. The models were reconstructed from ex vivo MRI and diffusion tensor MRI of pig hearts, and were able to successfully predict infarct-related ventricular tachycardia inducibility after programmed electrical stimulation. While this study demonstrates the ability of patient-specific models to be used as a predictive tool, its reliance on ex vivo imaging techniques limits its usability in the clinic. The methods presented herein, however, allow for patient-specific atrial modeling based on in vivo imaging techniques, providing a novel methodology that has strong potential for clinical translation.

Conclusion

This article presents the methodology by which patient-specific models of atrial fibrosis can be constructed from high-resolution LGE-MR images in vivo. An LA model was generated from images obtained from a patient suffering persistent AF. A proof-of-concept simulation shows the initiation of arrhythmia following pulmonary vein ectopy due to the presence of fibrotic lesions, demonstrating the completion of the methodology development and the feasibility of developing patient-specific atrial models. The modeling pipeline provides a novel tool whereby patient-specific fibrotic lesion distribution can be investigated in association with the initiation and maintenance of AF, and has the potential to become a powerful means to guide treatments of arrhythmia in the atria.