ELASTIC NET FOR COX’S PROPORTIONAL HAZARDS MODEL WITH A SOLUTION PATH ALGORITHM

Abstract

For least squares regression, Efron et al. (2004) proposed an efficient solution path algorithm, the least angle regression (LAR). They showed that a slight modification of the LAR leads to the whole LASSO solution path. Both the LAR and LASSO solution paths are piecewise linear. Recently Wu (2011) extended the LAR to generalized linear models and the quasi-likelihood method. In this work we extend the LAR further to handle Cox’s proportional hazards model. The goal is to develop a solution path algorithm for the elastic net penalty (Zou and Hastie (2005)) in Cox’s proportional hazards model. This goal is achieved in two steps. First we extend the LAR to optimizing the log partial likelihood plus a fixed small ridge term. Then we define a path modification, which leads to the solution path of the elastic net regularized log partial likelihood. Our solution path is exact and piecewise determined by ordinary differential equation systems.

1. Introduction

The main goal of survival analysis is to characterize the dependence of the survival time Y on a covariate vector X = (X₁, . . . , X_p)^T. Cox’s proportional hazards model (Cox (1972)) assumes that the hazard function h(y|x) of a subject with covariate vector x takes the form

$$h(y|\mathit{x})=h_0(y)\text{exp}({\mathit{x}}^T\mathit{\beta }),$$ (1.1)

where h₀(y) is a completely unspecified baseline hazard function and β = (β₁, . . ., β_p)^T. In practice, it is not necessary that all covariates contribute to predicting survival outcomes. Thus, another goal of survival analysis is to identify important risk factors and quantify their risk contributions. As survival data with many predictors prevail in clinical trial studies, risk factor identification becomes more important than ever for analyzing high-dimensional survival data. The problem is to select a submodel of (1.1) by providing a sparse estimate of β.

There are many model selection techniques in the literature and most of them have been successfully extended to survival analysis. They include such classical methods as the best-subset selection and stepwise selection. More recently, Tibshirani (1996) proposed to use the L₁ penalty to regularize least squares regression; sparse estimate of the regression parameter is made possible due to the L₁ penalty’s singularity at the origin. This technique was named the least absolute shrinkage and selection operator (LASSO), and later extended to the Cox proportional hazards model in Tibshirani (1997). However the LASSO penalty leads to biased estimates for true non-zero coefficients. To alleviate this bias issue, Fan and Li (2001) proposed the SCAD penalty, which is symmetric and piecewise quadratic. It is linear around the origin and flattens out near the two ends; in between, it is smoothly connected by two quadratic pieces. They showed that asymptotically the SCAD penalized estimate behaves like the oracle estimate were the true sparsity pattern known a priori. The oracle property of the SCAD was later extended to survival models in Fan and Li (2002). The adaptive-LASSO was proposed for least squares regression by Zou (2006), and for Cox’s proportional hazards model by Zhang and Lu (2007), and its oracle properties were established as well. There are many other techniques available for variable selection, including the elastic net (Zou and Hastie (2005)). See Fan and Lv (2010) and references therein for an overview of variable selection methods.

A novel least angle regression (LAR) solution path algorithm was proposed in Efron et al. (2004). The LAR produces a piecewise linear solution path for the least squares regression. They showed that slight modifications of the LAR lead to the LASSO and Forward Stagewise linear regression solution paths. Together they are called LARS. For data {(y_i, z_i), i = 1, . . . , n} with z_i = (z_i1, . . . , z_ip)^T ∈ ℝ^p, ordinary least squares (OLS) regression solves

$$\underset{\mathit{w}}{\text{min}}\frac{1}{2}{\displaystyle \sum _{i=1}^n{(y_i-{\mathit{z}}_i^T\mathit{w})}^2}$$ (1.2)

to estimate w = (w₁, . . . , w_p)^T. Applying location and scale transformations if necessary, we assume without loss of generality that ${\displaystyle {\sum }_{i=1}^n{z}_{ij}=0,{\displaystyle {\sum }_{i=1}^n{z}_{ij}^2=1}}$ for j = 1, . . . , p, and ${\displaystyle {\sum }_{i=1}^n{y}_i=0}$.

For OLS, the LAR provides a solution path w(t) indexed by t ∈ [0, ∞). It starts at the origin with w(0) = 0; for large enough t, w(t) is the same as the full solution to (1.2). The intermediate solution path is piecewise linear; over each piece, it moves along the direction that keeps the correlation between the current residuals and each active predictor equal in absolute value. Denote the jth predictor vector by z^(j) = (z_1j , . . . , z_nj)^T, and define the residual vector at t by e(w(t)) = (e₁(w(t)), . . . , e_n(w(t)))^T with $e_i(\mathit{w}(t))=y_i-{\mathit{z}}_i^T\mathit{w}(t)$ for i = 1, . . . , n. Then along the LAR solution path w(t), the current correlation e(w(t))^Tz^(j) has the same absolute value for each active predictor j. Note that

$$\mathit{e}{(\mathit{w}(t))}^T{\mathit{z}}^{(j)}=-\frac{1}{2}\left(\frac{\partial }{\partial w_j}{\displaystyle \sum _{i=1}^n{(y_i-{\mathit{z}}_i^T\mathit{w})}^2}\right){|}_{\mathit{w}(t)}.$$

This implies that the objective function has the same absolute value of the first-order partial derivatives for each active predictor along the LAR solution path. Mathematically,

$$\left|\left(\frac{\partial }{\partial w_j}{\displaystyle \sum _{i=1}^n{(y_i-{\mathit{z}}_i^T\mathit{w})}^2}\right){|}_{\mathit{w}(t)}|=|\left(\frac{\partial }{\partial w_{j\prime }}{\displaystyle \sum _{i=1}^n{(y_i-{\mathit{z}}_i^T\mathit{w})}^2}\right){|}_{\mathit{w}(t)}\right|$$ (1.3)

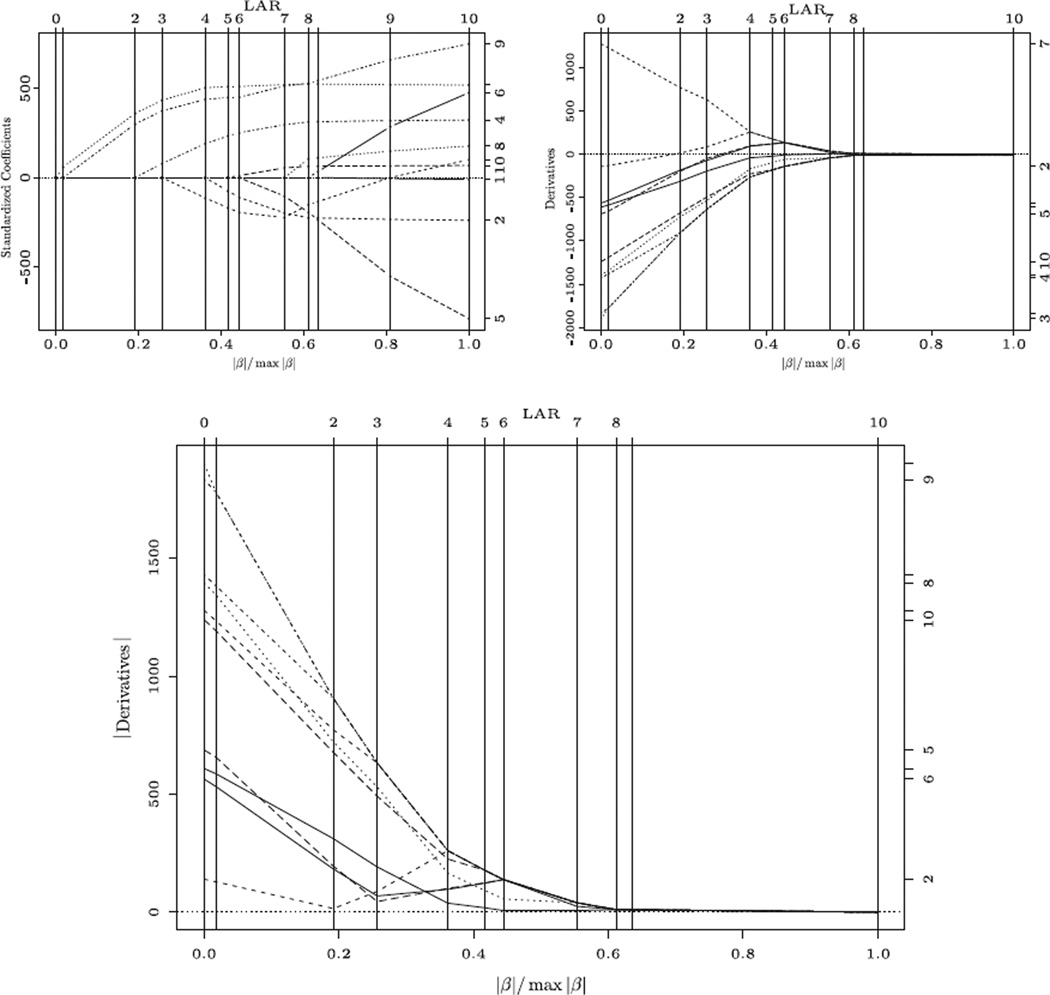
for any j and j′ among the active set at t. For the diabetes data in the R package LARS, we plot the LAR solution path in the top left panel of Figure 1. The first-order partial derivatives along the LAR solution path are shown in the top right panel of Figure 1. The derivatives in absolute value, namely $\left|\left(\frac{\partial }{\partial w_j}{\displaystyle {\sum }_{i=1}^n{(y_i-{\mathit{z}}_i^T\mathit{w})}^2}\right){|}_{\mathit{w}(t)}\right|$, are given in the bottom panel of Figure 1. One sees that, at the end of each LAR step, a new predictor joins the group of active predictors, sharing the honor of having the same largest absolute value of the first-order partial derivatives. The LAR algorithm terminates at the full OLS estimate of (1.2) when all the first-order partial derivatives are exactly zero. Based on this observation, Wu (2011) proposed an extension to handle generalized linear models and more generally the quasi-likelihood method.

Figure 1.

LAR path of diabetes data: the top left panel plots the LAR path w_j(t) against the relative one-norm |w(t)|/|w(∞)| for each predictor j = 1, 2, . . . , 10; the top right panel and the bottom panel plot the derivative $\left(\frac{\partial }{\partial w_j}{\displaystyle {\sum }_{i=1}^n{(y_i-{\mathit{z}}_i^T\mathit{w})}^2}\right){|}_{\mathit{w}(t)}$ and its absolute value $\left|\left(\frac{\partial }{\partial w_j}{\displaystyle {\sum }_{i=1}^n{(y_i-{\mathit{z}}_i^T\mathit{w})}^2}\right){|}_{\mathit{w}(t)}\right|$, respectively, along the LAR path, for different predictors.

In this work, we extend the LAR to the Cox’s proportional hazards model. With the elastic net penalty in mind, we add a fixed small ridge term to the log partial likelihood function and call this extension CoxLAR-ridge. When the ridge term is exactly zero, we have the original log partial likelihood and call the corresponding algorithm CoxLAR. As in Efron et al. (2004) and Wu (2011), we show that the CoxLAR-ridge can be slightly modified to get the corresponding whole solution path for the LASSO regularized counterpart; it is called CoxEN as the LASSO penalty with a small ridge term leads to the elastic net penalty. By setting the ridge term to be zero the CoxEN includes the CoxLASSO, the LASSO regularized log partial likelihood, as a special case. Together, we use CoxLARS in the same spirit as LARS in Efron et al. (2004). In addition to considering different models, another difference from Wu (2011) is that we include a ridge penalty term to consider the more general elastic net penalty. The elastic net penalty is highly desirable in that it is capable of selecting more predictors than the sample size, while it is known that the number of predictors selected by the LASSO can be at most equal to the sample size. See more discussion on this issue in Zou and Hastie (2005).

Previously Park and Hastie (2007) provided a solution path algorithm for L₁-regularized generalized linear models and Cox’s proportional hazards model. Their algorithm is based on the predictor-corrector method of convex optimization. In their R package “glmpath”, one may choose an extreme small bound for arc length (L₁ norm) of each step to obtain an exact solution path. In this case, it essentially uses a warm start each time to compute the exact solution at a fine grid of the tuning parameter and connects these exact solutions by straight lines. They still need to solve many optimization problems, one at each tuning parameter point. They did not address how the solution changes when the tuning parameter changes. Our new algorithms CoxLAR and CoxLASSO answer this question, the solution path propagates according to ordinary differential equation (ODE) systems. Thus the commonly used fourth-order Runge-Kutta method can be used to solve these ODE systems to obtain the whole CoxLARS solution paths. Other papers on solution path algorithms include Hastie et al. (2004), Rosset and Zhu (2007), Zou (2008), Friedman, Hastie, and Tibshirani (2008), Yuan and Zou (2009), and references therein. In particular, Zou (2008) proposed an efficient adaptive shrinkage method for the Cox’s proportional hazards model and adapted the LARS to provide a piecewise linear solution path.

The rest of the article is organized as follows. Section 2 presents our new algorithm CoxLARS. Properties of the CoxLARS are given in Section 3. Numerical examples in Section 4 illustrate how our new algorithm works with data sets. A summary is given in Section 5. The appendix gives all technical proofs.

2. Extension of LARS: CoxLARS

Consider a sample of n subjects. Let T_i and C_i be the failure time and censoring time, respectively, for subject i = 1, . . . , n. Write Y_i = min(T_i, C_i) and let the censoring indicator be δ_i = I(T_i ≤ C_i). Denote the covariate vector of the ith subject by x_i = (x_i1, . . . , x_ip)^T. Assume that T_i and C_i are conditionally independent given covariate vector x_i, and that the censoring mechanism is noninformative. Our data set is {(x_i, y_i, δ_i), i = 1, . . . , n}.

Assume the data come from model (1.1). For simplicity, we suppose there are no ties in the observed failure times, otherwise techniques in Breslow (1974) may be used. The log partial likelihood is given by

$$L_{pl}(\mathit{\beta })={\displaystyle \sum _{i=1}^n{\delta }_i{\mathit{x}}_i^T\mathit{\beta }}-{\displaystyle \sum _{i=1}^n{\delta }_i\text{log}\left({\displaystyle \sum _{j\in R_i}\text{exp}({\mathit{x}}_j^T\beta )}\right)},$$ (2.1)

where R_i = {j = 1, . . . , n : y_j ≥ y_i} denotes the risk set just before the time y_i.

Note that when the elastic net penalty (Zou and Hastie, 2005) is considered, we are solving

$$\underset{\mathit{\beta }}{\text{min}}{\displaystyle \sum _{i=1}^n{\delta }_i{\mathit{x}}_i^T\mathit{\beta }}-{\displaystyle \sum _{i=1}^n{\delta }_i\text{log}\left({\displaystyle \sum _{j\in R_i}\text{exp}({\mathit{x}}_j^T\mathit{\beta })}\right)}+\frac{\gamma }{2}{\displaystyle \sum _{j=1}^p{\beta }_j^2+\lambda }{\displaystyle \sum _{j=1}^p|{\beta }_j|,}$$ (2.2)

where γ ≥ 0 and λ ≥ 0 are two regularization parameters. In order to incorporate the elastic net into our consideration, we include a small ridge penalty term and set

$$L(\mathit{\beta })\equiv L_{\gamma }(\mathit{\beta })\triangleq {\displaystyle \sum _{i=1}^n{\delta }_i{\mathit{x}}_i^T\mathit{\beta }}-{\displaystyle \sum _{i=1}^n{\delta }_i\text{log}\left({\displaystyle \sum _{j\in R_i}\text{exp}({\mathit{x}}_j^T\mathit{\beta })}\right)+\frac{\gamma }{2}{\displaystyle \sum _{j=1}^p{\beta }_j^2}}$$ (2.3)

for some fixed small γ ≥ 0. Note that this reduces to the LASSO penalized counterpart when γ = 0. It is known that the LASSO penalty can select at most n predictors for the p > n case. However as long as γ > 0, we can select more than n predictors by solving (2.2) when p > n. Our consideration is similar to the LARS-EN algorithm proposed in Zou and Hastie (2005) in that the LARS-EN adapted the LARS algorithm to obtain elastic net solution path for each fixed ridge term.

We use t to index our solution path. As motivated by (1.3), our extension CoxLAR-ridge seeks a solution path β(t) of (2.3) that satisfies

$${\left|\frac{\partial }{\partial {\beta }_j}L(\mathit{\beta })\right|}_{\mathit{\beta }(t)}|={\left|\frac{\partial }{\partial {\beta }_{j\prime }}L(\mathit{\beta })\right|}_{\mathit{\beta }(t)}|$$ (2.4)

for any two predictors j and j′ that are active at t.

For L(β), denote its vector of first-order partial derivatives by b(β) = (b₁(β), . . . , b_p(β))^T and its matrix of second-order partial derivatives by M(β) = (m_jk(β))_1≤j,k≤p, where

$$b_j(\mathit{\beta })=\frac{\partial }{\partial {\beta }_j}L(\mathit{\beta })={\displaystyle \sum _{i=1}^n{\delta }_i{x}_{ij}}-{\displaystyle \sum _{i=1}^n{\delta }_i}\frac{{\sum }_{l\in R_i}\text{exp}({\mathit{x}}_l^T\mathit{\beta }){\mathit{x}}_{lj}}{{\sum }_{l\in R_i}\text{exp}({\mathit{x}}_l^T\mathit{\beta })}+\gamma {\beta }_j$$

and $m_{jk}(\mathit{\beta })=\frac{{\partial }^2}{\partial {\beta }_j\partial {\beta }_k}L(\mathit{\beta })$ is given by

$$-{\displaystyle \sum _{i=1}^n{\delta }_i[\frac{{\sum }_{l\in R_i}\text{exp}(x_l^T\mathit{\beta }){\mathit{x}}_{lj}{x}_{lk}}{{\sum }_{l\in R_i}\text{exp}(x_l^T\mathit{\beta })}-\frac{({\sum }_{l\in R_i}\text{exp}({\mathit{x}}_l^T\mathit{\beta }){\mathit{x}}_{lj})({\sum }_{l\in R_i}\text{exp}({\mathit{x}}_l^T\mathit{\beta }){\mathit{x}}_{lk})}{{({\sum }_{l\in R_i}\text{exp}({\mathit{x}}_l^T\mathit{\beta }))}^2}]+\gamma I_{\left\{j=k\right\}}}$$

for 1 ≤ j, k ≤ p, where I_{j=k} = 1 if j = k and 0 otherwise.

At t with solution β(t), denote the corresponding active index set by 𝒜(β(t)) and, interchangeably, by 𝒜_t. For any two index sets 𝒜 and ℬ, vector b, and matrix M, let b_𝒜 be the sub-vector of b consisting of those elements with index in 𝒜, and M_𝒜,ℬ be the sub-matrix of M consisting of those elements with row index in 𝒜 and column index in ℬ. When 𝒜 = {j} is a singleton, we write M_j,ℬ, similarly M_𝒜,k when ℬ = {k}. Denote the complement of 𝒜 by 𝒜^c = {1, . . . , p} \ 𝒜.

Note that, at any t with active predictor set 𝒜, the corresponding solution component is set to zero for any inactive predictor, namely β_j (t) = 0 for any j ∉ 𝒜. Thus it is enough to find how the solution coefficient components, corresponding to active predictors β_j(t) with j ∈ 𝒜, are updated. Recall that our desired solution path should be such that the active predictors have the same absolute value of the first-order partial derivatives as at (2.4). Thus, as t grows, |b_j(β(t))| decreases at the same speed for j ∈ 𝒜. Assume that in a small neighborhood of t, the active set 𝒜_t remains the same as 𝒜, say. Note that

$$\frac{d}{dt}{\mathit{b}}_{𝒜}(\mathit{\beta }(t))={\mathit{M}}_{𝒜,𝒜}(\mathit{\beta }(t))\frac{d}{dt}{\mathit{\beta }}_{𝒜}(t),$$ (2.5)

since the active set 𝒜_t remains the same as 𝒜 and thus β_𝒜^c (t) = 0 in a small neighborhood of t.

According to (2.4),

$$\frac{d}{dt}{\mathit{b}}_{𝒜}(\mathit{\beta }(t))=c(t)\left\{-\text{sign}({\mathit{b}}_{𝒜}(\mathit{\beta }(t)))\right\}$$ (2.6)

for some c(t) > 0. Here the negative sign on the right hand side ensures that |b_j(β(t))| is decreasing in t for each j ∈ 𝒜. Furthermore (2.6) guarantees that the |b_j(β(t))|, j ∈ 𝒜, decrease at the same speed. Note that we can think of t as a function of τ with the solution path indexed by τ. With an appropriate choice of t(τ), (2.6) holds with t replaced by τ and the c(t) term replaced a constant. Different c(t) lead to different indexing systems of the solution path. Thus, without loss of generality, we set c(t) ≡ 1 in (2.6) and write

$$\frac{d}{dt}{\mathit{b}}_{𝒜}(\mathit{\beta }(t))=-\text{sign}({\mathit{b}}_{𝒜}(\mathit{\beta }(t))).$$ (2.7)

In fact this turns out to be a good choice in that t here is simply related to the maximum absolute value of the first-order derivatives at t, as we shall see later.

Based on (2.5) and (2.7), the solution path should satisfy

$$\frac{d}{dt}{\mathit{\beta }}_{𝒜}(t)=-{({\mathit{M}}_{𝒜,𝒜}(\mathit{\beta }(t)))}^{-1}\text{sign}({\mathit{b}}_{𝒜}(\mathit{\beta }(t))).$$ (2.8)

Recall that β_𝒜^c (t) = 0. These completely define the path updating direction $\frac{d}{dt}\mathit{\beta }(t)$. Thus for any t* > t, we may take a tentative solution path piece

$${\tilde{\mathit{\beta }}}_{𝒜}(t^{*})={\mathit{\beta }}_{𝒜}(t)-{\displaystyle {\int }_t^{t^{*}}{({\mathit{M}}_{𝒜,𝒜}(\tilde{\mathit{\beta }}(\tau )))}^{-1}\text{sign}({\mathit{b}}_{𝒜}(\tilde{\mathit{\beta }}(\tau )))d\tau \text{and}{\tilde{\mathit{\beta }}}_{{𝒜}^c}(t^{*})}=\mathbf{0}.$$ (2.9)

With this tentative solution path piece, we implicitly assume that the active set remains the same between t and t*. Assume that, at the start with t, |b_j (β(t))| = |b_j′(β(t))| for any j, j′ ∈ 𝒜. Then (2.9) guarantees that |b_j(β̃(t*))| = |b_j′(β̃(t*))| for any j, j′ ∈ 𝒜 along the tentative solution path piece β̃(t*) for t* > t and, further, that |b_j(β̃ (t*))| is decreasing in t* for j ∈ 𝒜. Thus, as t* increases, some inactive predictor m ∉ 𝒜 may have |b_m(β̃ (t*))| ≥ |b_j(β̃ (t*))| for j ∈ 𝒜. Whenever this happens, the active predictor set has changed and we cannot use (2.9) any more. For any j ∉ 𝒜, define

$$T_j=\text{min}\left\{t^{*}>t:\left|b_j(\tilde{\mathit{\beta }}(t^{*}))\right|\ge \left|b_m(\tilde{\mathit{\beta }}(t^{*}))\right|\right\},$$ (2.10)

where m is any member of the active predictor set 𝒜. Then the active set changes at T = min_j∉𝒜 T_j from 𝒜 to 𝒜 ∪ {j*}, where j* = argmin_j∉𝒜 T_j.

2.1. Algorithm CoxLAR(-ridge)

The previous discussion leads us to our extension CoxLAR(-ridge) algorithm that is systematically presented next.

We initialize our solution path by identifying the predictor j so that the objective function L(β) changes fastest with respect to β_j beginning at β = 0; set

$$t_0=-\underset{j=1,\dots ,p}{\text{max}}|b_j(\mathbf{0})|.$$ (2.11)

This specially defined t₀ together with (2.7), leads to t = –max_j |b_j (β(t))| along our solution path. Our solution path begins with β(t₀) = 0; the corresponding initial active predictor set is ${𝒜}_{t_0}=\left\{\underset{1\le j\le p}{\text{argmax}}|b_j(\mathbf{0})|\right\}$.

Given t₀, β(t₀), and 𝒜_t0, we update our solution path using (2.9) until a new variable joins the active set at some t₁(> t₀) to be determined. We may temporarily update the solution using

$${\tilde{\mathit{\beta }}}_{{𝒜}_{t_0}}(t)={\mathit{\beta }}_{{𝒜}_{t_0}}(t_0)-{{\displaystyle {\int }_{t_0}^t({\mathit{M}}_{{𝒜}_{t_0},{𝒜}_{t_0}}(\tilde{\mathit{\beta }}(\tau )))}}^{-1}\text{sign}({\mathit{b}}_{{𝒜}_{t_0}}(\tilde{\mathit{\beta }}(\tau )))d\tau \text{ and }{\tilde{\mathit{\beta }}}_{{𝒜}_{t_0}^c}(t)=\mathbf{0}$$ (2.12)

for t > t₀. Here β̃(t) is a temporary solution path defined for any t > t₀. For any j ∉ 𝒜_t0, let

$$T_j=\text{min}\left\{t>t_0:\left|b_j(\tilde{\mathit{\beta }}(t))\right|\ge \left|b_m(\tilde{\mathit{\beta }}(t))\right|\right\},$$ (2.13)

where m ∈ 𝒜_t0. Then

$$t_1=\underset{j\notin {𝒜}_{t_0}}{\text{min}}{T}_j$$ (2.14)

is a transition point because the set of active predictor variables changes there.

The CoxLAR-ridge algorithm updates by setting

$${\mathit{\beta }}_{{𝒜}_{t_0}}(t)={\mathit{\beta }}_{{𝒜}_{t_0}}(t_0)-{{\displaystyle {\int }_{t_0}^t({\mathit{M}}_{{𝒜}_{t_0},{𝒜}_{t_0}}(\mathit{\beta }(\tau )))}}^{-1}\text{sign}({\mathit{b}}_{{𝒜}_{t_0}}(\mathit{\beta }(\tau )))d\tau \text{ and }{\mathit{\beta }}_{{𝒜}_{t_0}^c}(t)=\mathbf{0}$$ (2.15)

for all t ∈ [t₀, t₁]. The active predictor set stays the same for t ∈ [t₀, t₁), namely 𝒜_t = 𝒜_t0. At t₁, we update the active predictor set by setting 𝒜_t1 = 𝒜_t0 ∪ {j ∉ 𝒜t₀: T_j = t₁}.

At t = t₁, the number of active predictors is two. Due to (2.5), (2.8), (2.12), (2.13) and (2.14), solution β(t₁) satisfies |b_j(β(t₁))| = |b_j′(β(t₁))| > |b_k(β(t₁))| for any k ∉ 𝒜_t1 and any j, j′ ∈ 𝒜_t1.

The CoxLAR-ridge algorithm continues with the updated t₁, β(t₁), and 𝒜t₁, proceeding according to Algorithm 1. Note that at the end of the mth CoxLARridge step, the transition point t_m, solution β(t_m), and active predictor set 𝒜_tm satisfy t_m = −|b_j(β(t_m))| for any j ∈ 𝒜_tm, and |b_j(β(t_m)| = |b_j′(β(t_m)| > |b_k(β(t_m)| for any k ∉ 𝒜_tm and any j, j′ ∈ 𝒜_tm.

At the end of the (p – 1)th CoxLAR-ridge step in Step 2 of Algorithm 1, all predictors are active. Then, in Step 3, the CoxLAR solution path moves along a direction such that the absolute values of the first-order partial derivatives decrease at the same speed until all the first-order partial derivatives are exactly zero, which happens at t = 0. The solution at t = 0 exactly corresponds to the full solution argmin_β L(β), just as the LAR solution ends at the full OLS estimate. This completes our CoxLAR-ridge solution path. When the ridge term in L(β) is exactly zero by setting γ = 0, we are essentially working directly with the original log partial likelihood function and the CoxLAR-ridge is also the CoxLAR in this case.

Remark 1. Note that the instantaneous path updating direction is given by –(M_𝒜t,𝒜t(β(t)))⁻¹ sign(b_𝒜t(β(t))). For least squares regression, the objective function is exactly quadratic and thus M_𝒜t,𝒜t depends only on the active set 𝒜_t, but not on the current solution β_𝒜t (t). Note that sign(b_𝒜t(β(t))) does not change in a small neighborhood of t. This implies that, within a small neighborhood of t, the instantaneous path updating direction is the same for least squares regression. This leads to the piecewise linearity of the LAR path (Efron et al. (2004)) and in a more general setting (Rosset and Zhu (2007)).

Algorithm 1. CoxLAR(-ridge) for the Cox’s proportional hazards model.

1. Initialize by setting $t_0=-\underset{j=1,\dots ,p}{\text{max}}|b_j(\mathbf{0})|,\mathit{\beta }(t_0)=\mathbf{0},\text{ and }{𝒜}_{t_0}=\left\{{\text{argmax}}_{1\le j\le p}|b_j(\mathbf{0})|\right\}$.

2. For m = 0, 1, . . . , p − 2, take the tentative solution path using

   $${\tilde{\mathit{\beta }}}_{{𝒜}_{t_m}}(t)={\mathit{\beta }}_{{𝒜}_{t_m}}(t_m)-{{\displaystyle {\int }_{t_m}^t({\mathit{M}}_{{𝒜}_{t_m},{𝒜}_{t_m}}(\tilde{\mathit{\beta }}(\tau )))}}^{-1}\text{sign}({\mathit{b}}_{{𝒜}_{t_m}}(\tilde{\mathit{\beta }}(\tau )))d\tau \text{ and }{\tilde{\mathit{\beta }}}_{{𝒜}_{t_m}^c}(t)=\mathbf{0}$$

   for t ≥ t_m. Let t_m+1 = min_j∉𝒜tm T_j, where

   $$T_j=\text{min}\left\{t>t_m:\left|b_j(\tilde{\mathit{\beta }}(t))\right|\ge \left|b_k(\tilde{\mathit{\beta }}(t))\right|\text{ for some }k\in {𝒜}_{t_m}\right\}\text{ for }j\notin {𝒜}_{t_m}.$$

   Update the solution path with

   $${\mathit{\beta }}_{{𝒜}_{t_m}}(t)={\mathit{\beta }}_{{𝒜}_{t_m}}(t_m)-{{\displaystyle {\int }_{t_m}^t({\mathit{M}}_{{𝒜}_{t_m},{𝒜}_{t_m}}(\mathit{\beta }(\tau )))}}^{-1}\text{sign}({\mathit{b}}_{{𝒜}_{t_m}}(\mathit{\beta }(\tau )))d\tau \text{ and }{\mathit{\beta }}_{{𝒜}_{t_m}^c}(t)=\mathbf{0}$$

   for t ∈ [t_m, t_m+1]. Set 𝒜_t = 𝒜_tm for t ∈ [t_m, t_m+1) and 𝒜_tm+1 = 𝒜t_m ∪ [j ∉ 𝒜_tm : T_j = t_m+1}.
3. At the end of Step 2, 𝒜_tp−1 is {1, 2, . . . , p}. Next take

   $$\mathit{\beta }(t)=\mathit{\beta }(t_{p-1})-{{\displaystyle {\int }_{t_{p-1}}^t({\mathit{M}}_{{𝒜}_{t_{p-1}},{𝒜}_{t_{p-1}}}(\mathit{\beta }(\tau )))}}^{-1}\text{sign}({\mathit{b}}_{{𝒜}_{t_{p-1}}}(\mathit{\beta }(\tau )))d\tau ,$$

   and 𝒜_t = {1, 2, . . . , p} for t between t_p−1 and t_p = 0.

2.2. Cox-LASSO modification

Efron et al. (2004) showed that the whole LASSO regularized least squares regression solution path can be obtained by a slight modification of the LAR. This is confirmed by Wu (2011). Next we define our Cox-LASSO modification, and prove that the CoxLAR-ridge with the Cox-LASSO modification produces the whole elastic net regularized solution path for the Cox’s proportional hazards model by noting that adding another LASSO penalty into L(β) leads to the elastic net penalized log partial likelihood function in (2.2).

Consider the LASSO regularized counterpart of (2.3),

$$\underset{{\beta }_0,\mathit{\beta }}{\text{min}}L(\mathit{\beta })+\lambda {\displaystyle \sum _{j=1}^p|{\beta }_j|}$$ (2.16)

which is exactly the same as (2.2), and is equivalent

$$\underset{{\mathit{\beta }}_0,\mathit{\beta }}{\text{min}}L(\mathit{\beta })\text{subject to}{\displaystyle \sum _{j=1}^p|{\beta }_j|}\le s,$$ (2.17)

where two regularization parameters λ ≥ 0 and s ≥ 0 are in some one-to-one correspondence.

Let β̂ be a LASSO solution to (2.16). We can show that the sign of any nonzero component β̂_j must disagree with the sign of the current derivative b_j(β̂), see Lemma 2 in Section 3.

Suppose t = t* at the end of a CoxLAR-ridge step and that we have a new active set 𝒜*. At the next CoxLAR-ridge step with t ∈ [t*, T] for some T to be determined, our solution path moves along the tentative solution path

$${\tilde{\mathit{\beta }}}_{{𝒜}^{*}}(t)={\mathit{\beta }}_{{𝒜}^{*}}(t^{*})-{{\displaystyle {\int }_{t^{*}}^t({\mathit{M}}_{{𝒜}^{*},{𝒜}^{*}}(\tilde{\mathit{\beta }}(\tau )))}}^{-1}\text{sign}({\mathit{b}}_{{𝒜}^{*}}(\tilde{\mathit{\beta }}(\tau )))d\tau \text{and}{\tilde{\mathit{\beta }}}_{{({𝒜}^{*})}^c}(t)=\mathbf{0}$$ (2.18)

for t ≥ t*. The end point T is given by T = min_j∉𝒜* T_j, where

$$T_j=\text{min}\left\{t>t^{*}:\left|b_j(\tilde{\mathit{\beta }}(t))\right|\ge \left|b_k(\tilde{\mathit{\beta }}(t))\right|\text{ for some }k\in {𝒜}^{*}\right\}\text{ for }j\notin {𝒜}^{*}.$$

.

For some j ∈ 𝒜*, β̃_j(t) may have changed sign at some point between t* and T, in which case the sign restriction given in Lemma 2 must have been violated. We set S_j = min{t ∈ (t*, ∞) : β̃_j(t) = 0} for j ∈ 𝒜*, where β̃_j(t) is the jth component of β̃ (t) defined by (2.18). If S = min_j∈𝒜* S_j < T, β̃(T) defined by (2.18) cannot be a LASSO regularized solution to (2.16) since the sign restriction in Lemma 2 has already been violated. The Cox-LASSO modification can be applied to ensure that we can get the LASSO regularized solution to (2.16).

Cox-LASSO modification: If S < T, stop the ongoing CoxLAR-ridge step at S and remove j̃ from the active set 𝒜* by setting 𝒜_S = 𝒜_t* \ {j̃}, where j̃ is chosen such that S_j̃ = S. At the new transition point S, the new path updating direction $\frac{d}{dt}\mathit{\beta }(t)$ is calculated using (2.8) based on the new active predictor set 𝒜* \ {j̃}.

Theorem 1 guarantees that the Cox-LASSO modification leads to the LASSO regularized solution path to (2.16), which is the LASSO regularized log partial likelihood (CoxLASSO) when γ = 0, and the elastic net regularized log partial likelihood (CoxEN) when γ > 0. We use CoxLARS to refer to CoxLAR, CoxLARridge, CoxLASSO, and CoxEN.

Note that at each transition point of our CoxLARS solution path, two kinds of event can happen: either an inactive predictor joins the active predictor set or an active predictor is removed from the active predictor set. As in Efron et al. (2004), we assume a “one at a time” condition holds. With the “one at a time” condition, at each transition point t* only a single event can happen, namely, either one inactive predictor variable becomes active or one currently active predictor variable becomes inactive.

Theorem 1. Under the Cox-LASSO modification, and assuming the “one at a time” condition, the CoxLAR-ridge algorithm yields the LASSO regularized solution path to (2.16).

Remark 2. For simplicity we make the “one at a time” assumption. But, even when the “one at a time” condition does not hold, a CoxLASSO/CoxEN solution path is still available. The same discussion in Efron et al. (2004) applies. In applications, some slight jittering may be applied, if necessary, to ensure the “one at a time” condition holds.

2.3. Updating via ODE

Our CoxLARS algorithm involves an essential piecewise updating step

$${\tilde{\mathit{\beta }}}_{{𝒜}_{t^{*}}}(t)={\mathit{\beta }}_{{𝒜}_{t^{*}}}(t^{*})-{{\displaystyle {\int }_{t^{*}}^t({\mathit{M}}_{{𝒜}_{t^{*}},{𝒜}_{t^{*}}}(\tilde{\mathit{\beta }}(\tau )))}}^{-1}\text{sign}({\mathit{b}}_{{𝒜}_{t^{*}}}(\tilde{\mathit{\beta }}(\tau )))d\tau \text{ and }{\tilde{\mathit{\beta }}}_{{𝒜}_{t^{*}}^c}(t)=\mathbf{0}$$ (2.19)

beginning at a transition point t* with solution β(t*) and active predictor set 𝒜_t*.

Note that the piecewise solution path (2.19) can be easily obtained by setting β̃_j(t) = 0 for j ∉ 𝒜_t* and t > t*, and solving the following ordinary differential equation (ODE) system

$$\frac{d}{dt}{\tilde{\mathit{\beta }}}_{{𝒜}_{t^{*}}}(t)=-{({\mathit{M}}_{{𝒜}_{t^{*}},{𝒜}_{t^{*}}}(\tilde{\mathit{\beta }}(t)))}^{-1}\text{sign}({\mathit{b}}_{{𝒜}_{t^{*}}}(\tilde{\mathit{\beta }}(t)))$$

with initial value condition β̃_𝒜t* (t)|_t=t* = β_𝒜t* (t*). This is a standard initial-value ODE system and there are many efficient methods to solve it, for example Euler method, backward Euler method, midpoint method, and the family of Runge-Kutta methods, among many others. The commonly used member of the Runge-Kutta method family is the fourth-order Runge-Kutta method. See Atkinson, Han, and Stewart (2009) for a comprehensive introduction to the methods for solving ordinary differential equations. Our numerical examples employ the Matlab ODE solver “ODE45”, which exactly implements the fourth-order Runge-Kutta method.

3. Properties of CoxLARS

In this section, we establish some properties of our CoxLARS path, and prove Theorem 1.

With the “one at a time” condition, at each transition point t* either one inactive predictor becomes active or one active predictor becomes inactive. For the first type, the active set changes from 𝒜 to 𝒜* = 𝒜 ∪ {j*} for some j* ∉ 𝒜. We show in Lemma 1 that this new active predictor joins in a “correct” manner. Lemma 1 applies to CoxLARS.

Lemma 1. For any transition point t* during the CoxLARS solution path, if predictor j* is the only addition to the active set at t* with β (t*) and active set changing from 𝒜 to 𝒜* = 𝒜∪{j*}, then the path updating direction $\frac{d}{dt}{\mathit{\beta }}_{{𝒜}^{*}}(t)$ at t* has its j*th component disagreeing in sign with the current derivative b_j* (β(t*)).

Lemma 1 is a key property for showing that the Cox-LASSO modification leads to the LASSO or elastic net regularized log partial likelihood solution path in that Lemma 1 ensures that, at any transition point, the new predictor variable enters in a “correct” manner. This “correct” manner is required by the LASSO penalty as is seen in Lemma 2.

Next we extend Lemmas 7–10 of Efron et al. (2004) to the Cox’s proportional hazards model. Our Lemmas 2–5 concern properties of the LASSO regularized solution path for (2.16) or equivalently (2.17), and as a result they lead to the proof of Theorem 1. For any s ≥ 0, we denote the unique solution of (2.17) by β̂ = β̂(s), which is continuous in s; uniqueness is due to the convexity of ${\displaystyle {\sum }_{j=1}^p|{\beta }_j}|$ and the strict convexity of L(β). Throughout, we use the hat notation to designate a solution of (2.16), equivalently (2.17). For any s ≥ 0, let 𝒩_s ≡ 𝒩(β̂(s)) ≜ {j : β̂_j(s) ≠ 0} denote the index set of nonzero components of β̂(s). Our goal is to show that the nonzero set 𝒩_s is also the active predictor set that determines the CoxLARS path updating direction.

Let β̂ be a solution of (2.16). We show that any non-zero component β̂_j must disagree in sign with the current first-order derivative.

Lemma 2. A LASSO regularized solution β̂ to (2.16) satisfies sign(β̂_j) = −sign (b_j(β̂)) for any j ∈ 𝒩 (β̂).

Let 𝒮 be an open interval of the s axis, with infimum s, within which the nonzero set 𝒩_s of β̂(s) remains constant, 𝒩_s = 𝒩 for s ∈ 𝒮 and some 𝒩.

Lemma 3. For s ∈ {s} ∪ 𝒮, the LASSO regularized estimate β̂(s) of (2.17) updates along the CoxLARS path updating direction.

Lemma 4. For an open interval 𝒮 with a constant nonzero set 𝒩 during the LASSO regularized path β̂(s) of (2.17), let s = inf(𝒮). Then for s ∈ 𝒮 ∪ {s}, the first-order derivatives of L(β) at β̂(s) satisfy |b_j(β̂(s))| = max_l=1,2,...,p |b_l(β̂(s))| for j ∈ 𝒩 and |b_j(β̂(s))| ≤ max_l=1,2,...,p| b_l(β̂(s))| for j ∉ 𝒩.

Let s denote such a point, s = inf(𝒮) as in Lemma 4, with the LASSO regularized solution β̂ to (2.17), current derivatives b_j(β̂) for j = 1, 2, . . . , p, and maximum absolute derivative D̂ (β̂) = max_j=1,2,...,p |b_j(β̂)|. Let 𝒜₁ = {j : β̂ _j ≠ 0}, 𝒜₀ = {j : β̂_j = 0 and |b_j(β̂)| = D̂(β̂)}, and 𝒜₁₀ = 𝒜₁ ∪ 𝒜₀. Take β^(θ) = β̂ + θd for some vector d ∈ ℝ^p, T(θ) = L(β^(θ)), and $S(\theta )={\displaystyle {\sum }_{j=1}^p|{\beta }_j^{(\theta )}}|$. Let $\dot{S}(\theta )=\frac{d}{d\theta }S(\theta ),\dot{T}(\theta )=\frac{d}{d\theta }T(\theta ),\text{and}\ddot{T}(\theta )=\frac{d^2}{d{\theta }^2}T(\theta )$.

Lemma 5. At s, we have

$$R(\mathit{d})=-\frac{\dot{T}(0)}{\dot{S}(0)}\le \widehat{D}(\widehat{\mathit{\beta }}),$$ (3.1)

with equality only if d_j = 0 for $j\in {𝒜}_{10}^c$ and sign(d_j) = −sign(b_j(β̂)) for j ∈ 𝒜₀. If so,

$$\ddot{T}(0)={\mathit{d}}_{{𝒜}_{10}}^T{\mathit{M}}_{{𝒜}_{10},{𝒜}_{10}}(\widehat{\mathit{\beta }}){\mathit{d}}_{{𝒜}_{10}}.$$ (3.2)

Lemma 5 implies that, at any transition point, the active predictor set of the LASSO regularized solution to (2.17) is a subset of 𝒜₁₀. With the LASSO regularization, we are minimizing L(β) subject to a constraint on the one norm of β. In a small neighborhood β̂+θd around β̂, we are minimizing T(θ) subject to an upper bound on S(θ). The first part of Lemma 5 implies that the instantaneous relative changing rate of T(θ) and S(θ) is ≥ − D̂ (β̂). For β^(θ), its one-norm S (θ) is increasing in θ as long as − ${\displaystyle {\sum }_{j\in {𝒜}_1}\text{sign}}(b_j(\widehat{\mathit{\beta }}))d_j+{\displaystyle {\sum }_{j\in {𝒜}_0}|d_j|+{\displaystyle {\sum }_{j\in {𝒜}_{10}^c}|d_j|>0}}$ and the best instantaneous relative changing rate is achieved for moving along β̂ + θd as long as d_j = 0 for $j\in {𝒜}_{10}^c$ and sign(d_j) = −sign(b_j(β̂)) for j ∈ 𝒜₀. In particular, sign(d_j) = −sign(b_j(β̂) for j ∈ 𝒜₀ requires that the coefficient of any new active predictor variable should disagree in sign with the corresponding current first-order partial derivative. This is ensured by Lemma 1 and the “one at a time” condition.

The second part of Lemma 5 provides second-order information on the relative change of T(θ) with respect to S(θ). As we only care about direction, assume $\dot{S}(0)=-{\displaystyle {\sum }_{j\in {𝒜}_1}\text{sign}(b_j(\widehat{\mathit{\beta }}))d_j+{\displaystyle {\sum }_{j\in {𝒜}_0}\left|d_j\right|}}$ = Δ for some Δ > 0. Note that $T(\theta )\approx T(0)+\dot{T}(0)\theta +\frac{1}{2}\ddot{T}(0){\theta }^2+o({\theta }^2)$. Then we need to find the most efficient direction d to decrease T(θ) among all possible direction d satisfying ${\displaystyle {\sum }_{j\in {𝒜}_1}\text{sign}(b_j(\widehat{\mathit{\beta }}))d_j+{\displaystyle {\sum }_{j\in {𝒜}_0}\left|d_j\right|}}$ = Δ and sign(d_j) = −sign(b_j(β̂)) for j ∈ 𝒜₀. In terms of the second-order information, we need to solve

$$\text{min\hspace{1em}\hspace{1em}}{\mathit{d}}_{{𝒜}_{10}^T}^T{\mathit{M}}_{{𝒜}_{10},{𝒜}_{10}}(\widehat{\mathit{\beta }}){\mathit{d}}_{{𝒜}_{10}}$$ (3.3)

$$\text{subject to }-{\displaystyle \sum _{j\in {𝒜}_1}\text{sign}(b_j(\widehat{\mathit{\beta }}))}{d}_j+{\displaystyle \sum _{j\in {𝒜}_0}|d_j|=\mathrm{\Delta }},$$

$$\text{sign}(d_j)=-\text{sign}(b_j(\widehat{\mathit{\beta }}))\text{ for }j\in {𝒜}_0$$

with a fixed Δ > 0 to select the optimal solution updating direction d. It turns out that the optimal solution to (3.3) is exactly given by our CoxLARS path updating direction as proved next.

Lemma 6. Our CoxLARS path updating direction (2.8) solves (3.3).

4. Numerical Examples

In this section, we use numerical examples to demonstrate how the extension CoxLARS works. In our implementation we first calculate t₀, then set δ_t = −t₀/K, where K is some large positive number. In our examples we use K = 2,000. In addition to the transition points t_ks, we evaluate the solution over our solution path at a grid of size δ_t. More specifically, for each piece of our solution path over [t_k, t_k+1], we calculate our solution β(t) at t = t_k + mδ_t for m = 1, 2, . . . , ⌊(t_k+1 − t_k)/δ_t⌋, where ⌊a⌋ denotes the integer part of a, even though the CoxLARS solution paths are defined for any t ∈ [t₀, 0].

Example 1. We use a simulated dataset to demonstrate that the true LASSO regularized solution path is not piecewise linear. We set p = 3 and n = 40. The predictor covariates were generated as X ~ 𝒩 (0, Σ), where Σ is the variance-covariance matrix with (i, j)th element 1 if i = j, and 0.9 otherwise. Conditional on X = (x₁, x₂, x₃)^T, the lifetime was generated from model (1.1) with a constant baseline hazard function h₀(y) = 1 and true regression coefficient vector β = (2, −2, 2.5)^T. The censoring time was uniformly distributed over [0, 8] and the corresponding censoring rate is 32.3%. We applied the CoxLASSO (with a ridge term γ = 0).

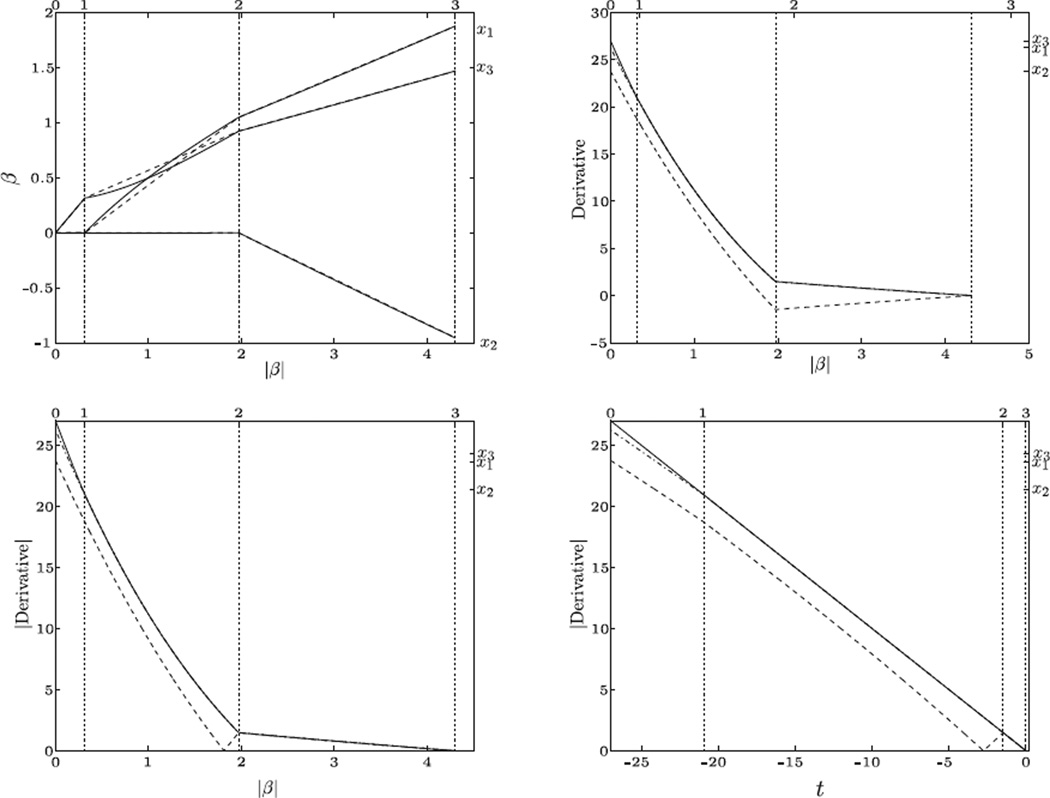
The CoxLASSO solution path is shown by the solid lines in the top left panel of Figure 2. The dashed straight lines are obtained by connecting the solutions at the transition points. The true LASSO regularized solution path is clearly not piecewise linear. The first-order partial derivatives along the CoxLASSO solution path are shown in the top right panel of Figure 2. The absolute value of the first-order partial derivatives along the CoxLASSO solution path are shown in the bottom two panels of Figure 2. with different horizontal axis scales. The bottom left panel is plotted with respect to the one-norm of β(t) while the right panel uses t. A straight diagonal line is observed in the bottom right panel since our CoxLARS ensures that t = −max_j=1,...,p|b_j(β(t))|.

Figure 2.

CoxLASSO path of Example 1: the top left panel plots the CoxLASSO path β(t) with respect to the one-norm |β(t)|; the top right panel plots the first-order derivatives b_j(β(t)) with respect to |β(t)|; the bottom left and right panels plot |b_j(β(t))| along the CoxLASSO path with respect to |β(t)| and t, respectively.

Example 2. Here we demonstrate how the Cox-LASSO modification leads to the CoxLASSO path when γ = 0 and the CoxEN path when γ > 0. We chose n = 200 and p = 12. The predictor covariates X were generated from N(0, Σ), with (i, j) element of Σ being 1 when i = j, 0.3 when 1 ≤ i, j ≤ 11 and |i–j| = 1, (−0.18)ⁱ⁺¹ when j = 12 and 1 ≤ i ≤ 11, and (−0.18)^j+1 when i = 12 and 1 ≤ j ≤ 11. Conditional on covariates, the lifetime was generated from model (1.1) with h₀(y) = 1 and true coefficient vector given by (−0.8, 1.6, −0.8, 1, 0, 1.5, −1.2, 3, 0, 0, 0, 0.5)^T. The censoring time was generated from Uniform[0, 10] leading to a censoring rate of 30.5%. In general, the Cox-LASSO modification may not have any effect and conseqently the CoxLAR and CoxLASSO paths are exactly the same. We designed Example 2 to show the effect of the Cox-LASSO modification.

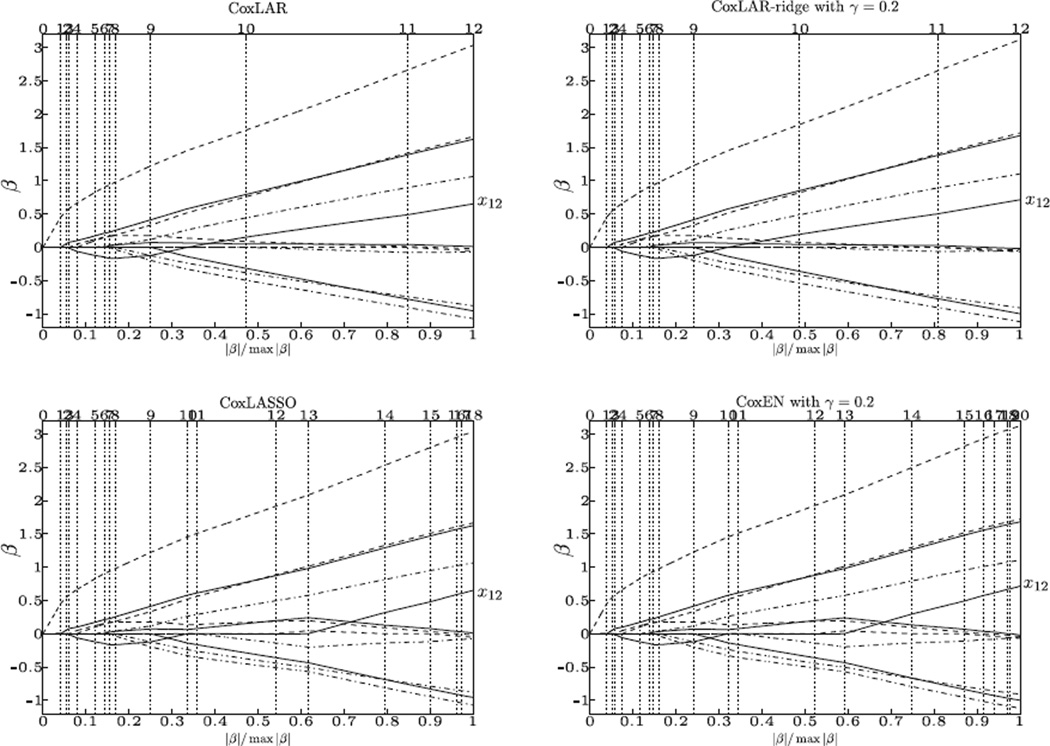
CoxLARS solution paths are shown in Figure 3. When γ = 0, solution paths of the CoxLAR and CoxLASSO are given in the top left and bottom left panels, respectively. The CoxLAR path shows that coefficient of variable X₁₂ switches sign between the 9th and 10th transition points. Thus a new transition point is added to the CoxLASSO solution path, in which the coefficient corresponding to X₁₂ is kept at zero between the 10th and 13th transition points. When we add a small ridge term by setting γ = 0.2, the corresponding paths are shown in the right panels of Figure 3. A similar phenomenon is observed.

Figure 3.

CoxLARS paths of Example 2.

Example 3. The primary biliary cirrhosis data were collected in the Mayo Clinic trial on primary biliary cirrhosis of liver conducted between 1974 and 1984, see Therneau and Grambsch (2001). This study included a total of 424 patients. Clinical, biochemical, serological, and histological parameters were collected for each patient. Before the end of the follow-up, 125 patients died. We study the dependency of the survival time on seventeen covariates: continuous variables are age (in years), albumin (albumin in g/dl), alk (alkaline phosphatase in units/litre), bili (serum bilirubin in mg/dl), chol (serum cholesterol in mg/dl), copper (urine copper in g/day), platelets (platelets per cubic ml/1,000), prothrombin (prothrombin time in seconds), sgot (liver enzyme in units/ml), and trig (triglycerides in mg/dl); categorical variables are ascites (0 denotes absence of ascites and 1 denotes presence of ascites), edema (0 denotes no oedema, 0.5 denotes untreated or successfully treated oedema, and 1 denotes unsuccessfully treated oedema), hepatom (0 denotes absence of hepatomegaly and 1 denotes presence of hepatomegaly), sex (0 denotes male and 1 denotes female), spiders (0 denotes absence of spiders and 1 denotes presence of spiders), stage (histological stage of disease, graded 1, 2, 3, or 4), and treatment (1 for control and 2 for treatment). See Dickson et al. (1989) for more detailed information.

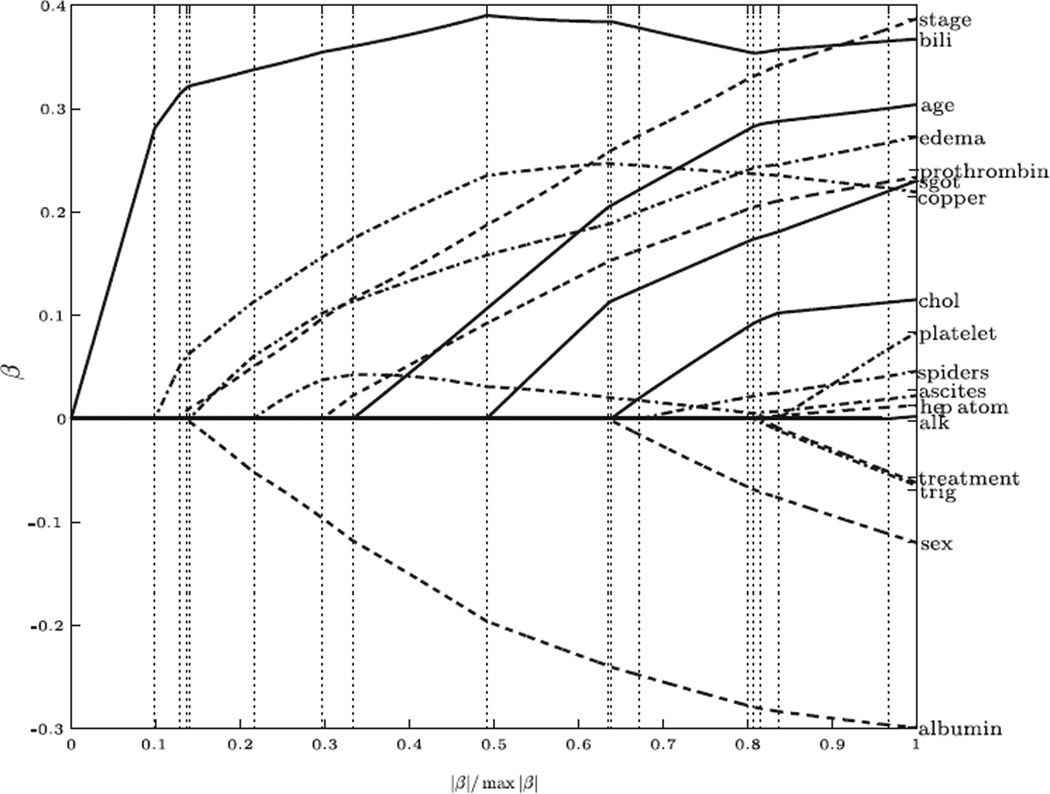
After excluding patients with any missing value, there are 276 patients. Out of these 276 patients, 111 died before the end of the follow-up. We standardized each predictor variable to have mean zero and variance one. CoxLARS was applied to the standardized data with all seventeen variables included. With ridge parameter γ = 0, the CoxLAR and CoxLASSO gave the same solution path, see Figure 4.

Figure 4.

CoxLARS path of the PBC data with γ = 0.

5. Discussion

In this work, we have proposed the extension CoxLAR(-ridge) of the LAR to handle Cox’s proportional hazards model. Our CoxLAR(-ridge) solution paths are based on ODE systems. Results show that a Cox-LASSO modification on CoxLAR(-ridge) leads to the exact solution of the corresponding LASSO regularized solution path. As the solution path propagates according to ODE systems, it allows us to develop a solution path package using efficient ODE solvers.

LARS is very attractive due to its speed that is possible because the corresponding path is piecewise linear. However when it comes to the Cox’s proportional hazards model, the solution path is not piecewise linear due to the nature of the log partial likelihood, as demonstrated by Example 1. This makes the implementation of the CoxLARS more difficult. Currently we have implemented the primitive version of our algorithm using the fourth-order Runge-Kutta method, which works fairly well. In addition, it is commonly assumed that the regression coefficients are sparse in the high dimension variable selection literature. Consequently there is not much need for us to compute the whole solution path. A BIC criterion may be combined as we progress along the solution path to identify an optimal solution and terminate our solution path algorithm thereafter, as done in Wu (2011).

Appendix

Proof of Lemma 1. The new path updating direction defined using the new active predictor set 𝒜* is given by $\frac{d}{dt}{\mathit{\beta }}_{{𝒜}^{*}}(t)=-{\mathit{M}}_{{𝒜}^{*},{𝒜}^{*}}{(\mathit{\beta }(t^{*}))}^1\text{sign}({\mathit{b}}_{{𝒜}^{*}}(\mathit{\beta }(t^{*})))$. Using the formula for inverting a block matrix, the j*th component of our path updating direction $\left(\frac{d}{dt}\mathit{\beta }(t)\right){|}_{t^{*}}$ is given by

$$\frac{1}{\eta }[{\mathit{M}}_{j*,𝒜}(\mathit{\beta }(t^{*}))-{\mathit{M}}_{𝒜,𝒜}{(\mathit{\beta }(t^{*}))}^{-1}\text{sign}({\mathit{b}}_{𝒜}(\mathit{\beta }(t^{*})))-\text{sign}(b_{j^{*}}(\mathit{\beta }(t^{*})))],$$ (A.1)

where η = M_j*,j*(β(t*)) −M_j*,𝒜(β(t*))M_𝒜,𝒜(β(t*))⁻¹ M_𝒜,j*(β(t*)) > 0 in that M(β) is positive definite when n > p, and x^(j), j = 1, 2, . . . , p are linearly independent. The first term in (A.1) involves M_𝒜,𝒜(β(t*))⁻¹sign(b_𝒜(β(t*))), which is exactly the opposite of the path updating direction calculated at t* using the old active set 𝒜 by ignoring the addition of predictor variable j*.

Consider ignoring the new active variable j* and updating path along the path updating direction evaluated by the old active predictor set 𝒜. This leads to another solution path piece β̄(t) defined by

$${\overline{\mathit{\beta }}}_{𝒜}(t)={\mathit{\beta }}_{𝒜}(t^{*})-{\displaystyle {\int }_{t^{*}}^t{\mathit{M}}_{𝒜,𝒜}{(\overline{\mathit{\beta }}(\tau ))}^{-1}\text{sign}({\mathit{b}}_{𝒜}(\overline{\mathit{\beta }}(\tau )))}d\tau \text{ and }{\overline{\mathit{\beta }}}_{{𝒜}^c}(t)=\mathbf{0}$$

when t is inside a small neighborhood [t* − Δ_t, t* + Δ_t]. The neighborhood is chosen such that both solution component β̄_j(t) and the first-order partial derivative b_j(β̄(t)) do not change sign for t ∈ [t* − Δ_t, t* + Δ_t] and j ∈ 𝒜. Consequently when t ∈ [t* − Δ_t, t* + Δ_t],

$$\frac{d}{dt}{b}_j(\overline{\mathit{\beta }}(t))=-\text{sign}(b_j(\overline{\mathit{\beta }}(t)))=-\text{sign}(b_j(\overline{\mathit{\beta }}(t^{*})))$$

for j ∈ 𝒜 due to (2.5) and (2.8). Note that, for t ∈ [t* − Δ_t, t* + Δ_t],

$$\frac{d}{dt}{b}_{j^{*}}(\overline{\mathit{\beta }}(t))={\displaystyle \sum _{j=1}^p{m}_{j*j}}(\overline{\mathit{\beta }}(t))\frac{d}{dt}{\overline{\beta }}_j(t)=-{\mathit{M}}_{j*,𝒜}(\overline{\mathit{\beta }}(t)){\mathit{M}}_{𝒜,𝒜}{(\overline{\mathit{\beta }}(t))}^{-1}\text{sign}({\mathit{b}}_{𝒜}(\overline{\mathit{\beta }}(t)))$$ (A.2)

due to the definition of β̄(t) (because β̄_j(t) = 0 for j ∉ 𝒜 and t ∈ [t* − Δ_t, t* + Δ_t]).

Recall that for t ∈ [t* − Δ_t, t*], β(t) = β̄(t), and our CoxLARS solution matches β̄(t) exactly. Note that our CoxLARS definition implies that

$$|b_{j^{*}}(\overline{\mathit{\beta }}(t))|<|b_j(\overline{\mathit{\beta }}(t))|$$ (A.3)

for any j ∈ 𝒜 and t ∈ [t* − Δ_t,t*). This means that the predictor variable j* has a smaller absolute value of the first-order partial derivative than active predictors in 𝒜 for t ∈ [t* − Δ_t, t*) and that it catches up with active predictors in 𝒜 at t*, noting the definition of j*.

Lemma 1 can be proved by contradiction. If our claim is wrong, then

$$[{\mathit{M}}_{j*,𝒜}(\mathit{\beta }(t^{*})){\mathit{M}}_{𝒜,𝒜}{(\mathit{\beta }(t^{*}))}^{-1}\text{sign}({\mathit{b}}_{𝒜}(\mathit{\beta }(t^{*})))-\text{sign}(b_{j^{*}}(\mathit{\beta }(t^{*})))]\text{ sign}(b_{j^{*}}(\mathit{\beta }(t^{*})))>0$$

due to (A.1) and the fact that η > 0. This means that

$${\mathit{M}}_{j*,𝒜}(\mathit{\beta }(t^{*})){\mathit{M}}_{𝒜,𝒜}{(\mathit{\beta }(t^{*}))}^{-1}\text{sign}({\mathit{b}}_{𝒜}(\mathit{\beta }(t^{*})))\text{sign}(b_{j^{*}}(\mathit{\beta }(t^{*})))>1.$$

. The fact that β̄(t) = β(t) for t ∈ [t* − Δ_t, t*] implies that there exists some 0 < ε < Δ_t such that

$${\mathit{M}}_{j*,𝒜}(\overline{\mathit{\beta }}(t)){\mathit{M}}_{𝒜,𝒜}{(\overline{\mathit{\beta }}(t))}^{-1}\text{sign}({\mathit{b}}_{𝒜}(\overline{\mathit{\beta }}(t)))\text{sign}(b_{j^{*}}(\overline{\mathit{\beta }}(t)))>1\text{ for }t\in (t^{*}-\epsilon ,t^{*})$$ (A.4)

due to continuity. By noting (A.2) and $\frac{d}{dt}{b}_j(\overline{\mathit{\beta }}(t))=-\text{sign}(b_j(\overline{\mathit{\beta }}(t)))$ for j ∈ 𝒜 and t ∈ (t* − ε, t*), (A.4) contradicts the conclusion that the predictor variable j* has a smaller absolute value of the first-order partial derivative than active predictors in 𝒜 for t ∈ [t* − Δ_t, t*) and that it catches up with active predictors in 𝒜 at t*. This completes our proof.

Proof of Lemma 2. For any j ∈ 𝒩 (β̂), taking differentiation of the objective function in (2.16) with respect β_j, we get

$$\frac{\partial }{\partial {\beta }_j}L(\mathit{\beta })+\lambda \text{sign}({\beta }_j)$$ (A.5)

which has to be equal to zero at β̂ because β̂ is the corresponding optimal solution. This completes the proof by noting that λ ≥ 0 and, when λ = 0, $\frac{\partial }{\partial {\beta }_j}L(\mathit{\beta })=0$ for all j.

Proof of Lemma 3. Note that β̂(s) is the optimal solution to (2.17) and has a nonzero set 𝒩_s that is constant for s ∈ 𝒮, say 𝒩. Then β̄_𝒩(s) also minimizes

$$L({\widehat{\mathit{\beta }}}_{𝒩})\triangleq {\displaystyle \sum _{i=1}^n{\delta }_i{\mathit{x}}_{i𝒩}^T{\widehat{\mathit{\beta }}}_{𝒩}-}{\displaystyle \sum _{i=1}^n{\delta }_i\text{log}\left({\displaystyle \sum _{m\in R_i}\text{exp}({\mathit{x}}_{m𝒩}^T{\widehat{\mathit{\beta }}}_{𝒩})}\right)+\frac{\gamma }{2}{\widehat{\mathit{\beta }}}_{𝒩}^T{\widehat{\mathit{\beta }}}_{𝒩}}$$ (A.6)

subject to

$$-s_{𝒩}^T{\widehat{\mathit{\beta }}}_{𝒩}=s\text{and sign}({\widehat{\beta }}_j)=-s_j\text{for}j\in 𝒩,$$ (A.7)

where s_j = sign(b_j(β̂(s)), j = 1, 2, . . . , p, denotes the sign of the current first-order partial derivatives, s = (s₁, s₂, . . . , s_p)^T, and the second sign constraint is due to Lemma 2. Here x_i𝒩 is the sub-vector of x_i with index in 𝒩. Note that the inequality constraint in (2.17) can be replaced by the constraint ${\displaystyle {\sum }_{j=1}^p\left|{\beta }_j\right|=s}$ as long as s is less than the one-norm of the full solution argmin_β L(β). This justifies (A.7). Note further that the optimal solution β̂_𝒩(s) is strictly inside the simplex (A.7) since β̂_j(s) ≠ 0 for j ∈ 𝒩 and s ∈ 𝒮. This, in combination with the strict convexity of the object function L(β̂_𝒩), implies that the condition sign(β̂_j) = −s_j for j ∈ 𝒩 can be dropped. Consequently β̂_𝒩 (s) solves

$$\text{min }L({\widehat{\mathit{\beta }}}_{𝒩})\text{ subject to }-{\mathit{s}}_{𝒩}^T{\widehat{\mathit{\beta }}}_{𝒩}=s\text{.}$$

By introducing a Lagrange multiplier λ, we get

$$\frac{\partial }{\partial {\widehat{\mathit{\beta }}}_{𝒩}}L({\widehat{\mathit{\beta }}}_{𝒩})-\lambda {\mathbf{s}}_{𝒩},$$ (A.8)

which is equal to 0 at β̂_𝒩 = β̂_𝒩(s) because β̂_𝒩(s) is the corresponding optimal solution.

Now consider two different values s⁽¹⁾ and s⁽²⁾ in 𝒮 with s < s⁽¹⁾ < s⁽²⁾. The corresponding Lagrange multiplier are denoted by λ⁽¹⁾ and λ⁽²⁾, and they satisfy λ⁽¹⁾ > λ⁽²⁾. Putting them into (A.8) and differencing, we get

$$\frac{\partial }{\partial {\widehat{\mathit{\beta }}}_{𝒩}}L({\widehat{\mathit{\beta }}}_{𝒩}){|}_{{\widehat{\mathit{\beta }}}_{𝒩}(s^{(2)})}-\frac{\partial }{\partial {\widehat{\mathit{\beta }}}_{𝒩}}L({\widehat{\mathit{\beta }}}_{𝒩}){|}_{{\widehat{\mathit{\beta }}}_{𝒩}(s^{(1)})}=({\lambda }^{(2)}-{\lambda }^{(1)}){\mathit{s}}_{𝒩}.$$ (A.9)

Note that β̂_𝒩^c (s) = 0 for any s ∈ 𝒮. Thus (A.9) is the same as

$${\mathit{b}}_{𝒩}(\widehat{\mathit{\beta }}(s^{(2)}))-{\mathit{b}}_{𝒩}(\widehat{\mathit{\beta }}(s^{(1)}))=({\lambda }^{(2)}-{\lambda }^{(1)}){\mathit{s}}_{𝒩}.$$ (A.10)

Dividing both sides of (A.10) by s⁽²⁾ − s⁽¹⁾ and letting s⁽²⁾ → s⁽¹⁾, we get

$$\frac{d}{ds}{\mathit{b}}_{𝒩}(\widehat{\mathit{\beta }}(s)){|}_{s^{(1)}}=\lambda \prime (s^{(1)}){\mathit{s}}_{𝒩},$$ (A.11)

where $\lambda \prime (s)=\frac{d}{ds}\lambda (s)<0$. Noting that $\frac{d}{ds}\mathit{b}(\widehat{\mathit{\beta }}(s))=\mathit{M}(\widehat{\mathit{\beta }}(s))\frac{d}{ds}\widehat{\mathit{\beta }}(s),{\widehat{\mathit{\beta }}}_{{𝒩}^c}(s)=\mathbf{0}$ for s ∈ 𝒮, (A.11) becomes ${\mathit{M}}_{𝒩,𝒩}(\widehat{\mathit{\beta }}(s^{(1)}))\frac{d}{ds}{\widehat{\mathit{\beta }}}_{𝒩}(s){|}_{s^{(1)}}=\lambda \prime (s^{(1)})s_{𝒩}$, which leads to $\frac{d}{ds}{\widehat{\mathit{\beta }}}_{𝒩}(s){|}_{s^{(1)}}=\lambda \prime (s^{(1)}){({\mathit{M}}_{𝒩,𝒩}(\widehat{\mathit{\beta }}(s^{(1)})))}^{-1}{\mathit{s}}_{𝒩}$. Noting that λ′(s) < 0, this shows that for any s ∈ 𝒮, the solution of (2.17) progresses along the CoxLARS path updating direction. It also holds for s due to continuity.

Proof of Lemma 4. Due to (A.5), |b_j(β̂(s))| = |b_j′(β̂(s))| for any j, j′ ∈ 𝒩. Thus it is enough to prove that |b_l(β̂(s))| ≤ |b_j(β̂(s))| for any l ∉ 𝒩, j ∈ 𝒩, s ∈ 𝒮 ∪ {s}. We this first for s ∈ 𝒮, by contradiction. Suppose there is some j* ∉ 𝒩 and some s* ∈ 𝒮 such that

$$|b_{j^{*}}(\widehat{\mathit{\beta }}(s^{*}))|>|b_j(\widehat{\mathit{\beta }}(s^{*}))|.$$ (A.12)

Let d = (d₁, d₂, . . . , d_p)^T with d_j = −sign(β̂_j(s*))(= sign(b_j(β̂(s*))), due to Lemma 2) for j ∈ 𝒩, d_j* = −n_𝒩sign(b_j*(β̂(s*))), and d_j′ = 0 for j ∈ (𝒩 ∪ {j*})^c, where n_𝒩 denote the size of 𝒩.

Consider L(β̂(s*) + ud) as a function of u. Its derivative is given by

$$\frac{d}{du}L(\widehat{\mathit{\beta }}(s^{*})+u\mathit{d})={\displaystyle \sum _{j=1}^p{b}_j}(\widehat{\mathit{\beta }}(s^{*})+u\mathit{d})d_j+O(u).$$ (A.13)

When u = 0, the right side of (A.13) becomes

$$n_{𝒩}|b_j(\widehat{\mathit{\beta }}(s^{*}))|-n_{𝒩}|b_{j^{*}}(\widehat{\mathit{\beta }}(s^{*}))|<0,$$ (A.14)

where j ∈ 𝒩, and negativity is due to (A.12). Note that min_j∈𝒩 |β̂_j(s*)| > 0 since s* ∈ 𝒮. When 0 < u < min_j∈𝒩 $|{\widehat{\beta }}_j(s^{*})|,{\displaystyle {\sum }_{j=1}^p|{\widehat{\beta }}_j(s^{*})|}={\displaystyle {\sum }_{j=1}^p|{\widehat{\beta }}_j(s^{*})+u{d}_j|}$, noting the above definition of d. However, (A.14) contradicts the fact that β̂(s*) is an optimal solution to (2.17). This proves our claim for s ∈ 𝒮. Our claim holds at s simply due to continuity.

Proof of Lemma 5. Note that $\dot{S}(0)=-{\displaystyle {\sum }_{j\in {𝒜}_1}\text{sign}(b_j(\widehat{\mathit{\beta }}))d_j+{\displaystyle {\sum }_{j\in {𝒜}_0}\left|d_j\right|+{\displaystyle {\sum }_{j\in {𝒜}_{10}^c}\left|d_j\right|}}}$ due to Lemma 2 and $\dot{T}(0)=-{\displaystyle {\sum }_{j\in {𝒜}_1}{b}_j(\widehat{\mathit{\beta }})d_j}+{\displaystyle {\sum }_{j\in {𝒜}_0}{b}_j(\widehat{\mathit{\beta }})d_j}+{\displaystyle {\sum }_{j\in {𝒜}_{10}^c}{b}_j(\widehat{\mathit{\beta }})d_j}$. Thus, due to Lemma 4 and the above definition of 𝒜₀, we have

$$R(\mathit{d})\triangleq -\frac{\dot{T}(0)}{\dot{S}(0)}=\widehat{D}(\widehat{\mathit{\beta }})\frac{-{\displaystyle {\sum }_{j\in {𝒜}_1}\text{sign}(b_j(\widehat{\mathit{\beta }}))d_j}-{\displaystyle {\sum }_{j\in {𝒜}_0}\text{sign}(b_j(\widehat{\mathit{\beta }}))d_j}-{\displaystyle {\sum }_{j\in {𝒜}_{10}^c}{d}_j{b}_j(\widehat{\mathit{\beta }})/\widehat{D}(\widehat{\mathit{\beta }})}}{-{\displaystyle {\sum }_{j\in {𝒜}_1}\text{sign}(b_j(\widehat{\mathit{\beta }}))d_j}+{\displaystyle {\sum }_{j\in {𝒜}_0}|d_j|}+{\displaystyle {\sum }_{j\in {𝒜}_{10}^c}|d_j|}},$$

which is analogous to Equation (5.40) of Efron et al. (2004). It is enough to consider all d satisfying − ${\displaystyle {\sum }_{j\in {𝒜}_1}\text{sign}(b_j(\widehat{\mathit{\beta }}))d_j+{\displaystyle {\sum }_{j\in {𝒜}_0}\left|d_j\right|+{\displaystyle {\sum }_{j\in {𝒜}_{10}^c}\left|d_j\right|>0}}}$, which corresponds to Ṡ(0) > 0. Thus we need $d_j\text{sign}(b_j(\widehat{\mathit{\beta }}))\le 0\text{ for }j\in {𝒜}_0\cup ({𝒜}_{10}^c)$ in order to maximize R(d). In this case we have

$$R(\mathit{d})=\widehat{D}(\widehat{\mathit{\beta }})\frac{-{\displaystyle {\sum }_{j\in {𝒜}_1}\text{sign}(b_j(\widehat{\mathit{\beta }}))d_j+{\displaystyle {\sum }_{j\in {𝒜}_0}|d_j|}+{\displaystyle {\sum }_{j\in {𝒜}_{10}^c}|d_j|\frac{|b_j(\widehat{\mathit{\beta }})|}{\widehat{D}(\widehat{\mathit{\beta }})}}}}{-{\displaystyle {\sum }_{j\in {𝒜}_1}\text{sign}(b_j(\widehat{\mathit{\beta }}))d_j+{\displaystyle {\sum }_{j\in {𝒜}_0}|d_j|}+{\displaystyle {\sum }_{j\in {𝒜}_{10}^c}|d_j|}}},$$ (A.15)

which is < D̂(β̂) unless d_j = 0 for $j\in {𝒜}_{10}^c$, since |b_j(β̂) | < D̂ (β̂) for $j\in {𝒜}_{10}^c$. This proves (3.1). In this case a second order Taylor expansion leads to (3.2).

Proof of Lemma 6. The positive definiteness of M_{𝒜10,𝒜10} implies that (3.3) is equivalent to

$$\text{min\hspace{1em}\hspace{1em}}{\mathit{d}}_{{𝒜}_{10}^T}^T{\mathit{M}}_{{𝒜}_{10},{𝒜}_{10}}(\widehat{\mathit{\beta }}){\mathit{d}}_{{𝒜}_{10}}$$ (A.16)

$$\text{subject to}-{\displaystyle \sum _{j\in {𝒜}_1}\text{sign}(b_j(\widehat{\mathit{\beta }}))d_j}+{\displaystyle \sum _{j\in {𝒜}_0}|d_j|}\ge \mathrm{\Delta }$$

$$\text{sign}(d_j)=-\text{sign}(b_j(\widehat{\mathit{\beta }}))\text{ for }j\in {𝒜}_0.$$

For (A.16), we combine the two constraints and solve the simpler version

$$\text{min }{\mathit{d}}_{{𝒜}_{10}^T}^T{\mathit{M}}_{{𝒜}_{10},{𝒜}_{10}}(\widehat{\mathit{\beta }}){\mathit{d}}_{{𝒜}_{10}}\text{subject to}-{\displaystyle \sum _{j\in {𝒜}_1}\text{sign}(b_j(\widehat{\mathit{\beta }}))d_j}-{\displaystyle \sum _{j\in {𝒜}_0}\text{sign}(b_j(\widehat{\mathit{\beta }}))d_j}\ge \mathrm{\Delta }.$$ (A.17)

Afterward, we show that the solution to (A.17) satisfies the sign constraint in (A.16). By introducing a Lagrange multiplier for (A.17), we solve

$$\text{min }{\mathit{d}}_{{𝒜}_{10}^T}^T{\mathit{M}}_{{𝒜}_{10},{𝒜}_{10}}(\widehat{\mathit{\beta }}){\mathit{d}}_{{𝒜}_{10}}+\lambda \left(-{\displaystyle \sum _{j\in {𝒜}_1}\text{sign}(b_j(\widehat{\mathit{\beta }}))d_j-}{\displaystyle \sum _{j\in {𝒜}_0}\text{sign}(b_j(\widehat{\mathit{\beta }}))d_j-\mathrm{\Delta }}\right).$$ (A.18)

Differentiating the objective function in (A.18) with respect to d_𝒜10 and solving for d_𝒜10, we get the optimal solution (λ/2)(M_{𝒜10,𝒜10}(β̂))⁻¹sign(b_𝒜10(β̂)), which is exactly the same as our CoxLARS path updating direction, noting that the Lagrange multiplier λ < 0. Note that the “one at a time” condition implies that 𝒜₀ is a singleton. Consequently, this optimal solution satisfies the sign constraint in (A.16) due to Lemma 1.

Proof of Theorem 1. Theorem 1 can be proved by induction as in Efron et al. (2004), by noting that Lemmas 2–5 are extensions of Lemmas 7–10 of Efron et al. (2004), which are the key results for establishing that the LASSO modification leads to the LASSO solutions, and parallel extensions of their Constraints 1–4 on page 437 are straightforward. We skip these details.