Exploring Resting-State Functional Connectivity with Total Interdependence

Abstract

Resting-state fMRI has become a powerful tool for studying network mechanisms of normal brain functioning and its impairments by neurological and psychiatric disorders. Analytically, independent component analysis and seed-based cross correlation are the main methods for assessing the connectivity of resting-state fMRI time series. A feature common to both methods is that they exploit the covariation structures of contemporaneously (zero-lag) measured data but ignore temporal relations that extend beyond the zero-lag. To examine whether data covariations across different lags can contribute to our understanding of functional brain networks, a measure that can uncover the overall temporal relationship between two resting-state BOLD signals is needed. In this paper we propose such a measure referred as total interdependence (TI). Comparing TI with zero-lag cross correlation (CC) we report three results. First, when combined with a random permutation procedure, TI can reveal the amount of temporal relationship between two resting-state BOLD time series that is not captured by CC. Second, comparing resting-state data with task-state data recorded in the same scanning session, we demonstrate that the resting-state functional networks constructed with TI match more precisely the networks activated by the task. Third, TI is shown to be more statistically sensitive than CC and provides better feature vectors for network clustering analysis.

Introduction

The brain is comprised of many anatomically and functionally distinct networks. These networks are spontaneously active even in the absence of sensory input or motor output (Biswal et al., 1995; Fox and Raichle 2007; Kenet et al. 2003; Raichle and Mintun 2006). Progress over the past 15 years has firmly established that functional magnetic resonance imaging (fMRI) data recorded during rest is an important tool to reveal the spatial organization and temporal dynamics of these networks (Lowe et al. 2000; Yan et al. 2009; van den Heuvel and Hulshoff Pol 2010). When two distinct brain regions are said to belong to the same functional network the main criterion is that the intrinsic blood oxygen level dependence (BOLD) fluctuations from the two regions significantly co-vary with one another (Dosenbach et al., 2007; Fox et al., 2006). Remarkably, functional networks identified in such a statistical manner match the brain networks activated by various cognitive tasks (Biswal et al., 1995; Fox, et al., 2006), correlate with behavior during development and aging (Beason-Held et al., 2009; Church et al., 2009; Jolles et al. 2011; Kelly et al., 2009), and predict brain pathology (He B.J. et al., 2007a; He Y. et al., 2007b; Lynall et al., 2010; Supekar et al., 2008).

There are two classes of methods for mapping resting-state functional brain networks: independent component analysis (ICA) (Beckmann et al., 2005; Damoiseaux et al., 2006) and seed-based correlation analysis (Biswal et al., 1995; Fox et al., 2005). Whereas ICA has the advantage of being model-free and entirely data-driven, seed-based correlation is more convenient for examining the connectivity between a given region of interest and the rest of the brain. Statistically, both methods exploit the contemporaneous covariation structures in the data. Among time series models, such characterization is only sufficient for the white noise process, which, by definition, may only exhibit contemporaneous correlations. It is well-established that resting-state fMRI are not white noise; they are time series exhibiting rich temporal patterns such as rhythmic activities in the low frequencies (Chang and Glover, 2010). Physiological factors that can contribute to temporal relations across scans include intrinsic temporal structures in neuronal signals such as local field potentials, neuronal transmission delays (Nishitani and Hari, 2002; Schmolesky et al., 1998; Van Essen et al., 1992), and variable latency in the hemodynamic response function (Handwerker et al., 2004). How much temporal dependence between BOLD signals was ignored by the prevailing statistical approaches? To what extent the ignored temporal structure may have contributed to our understanding of cognitive brain networks? These questions remain to be answered. In addition, the ignored temporal dependence may help explain the discrepancy between spatial structures identified by resting-state analysis and that by task activation.

In this paper we introduce a novel method called total interdependence (TI) to measure the overall temporal relationship between two resting-state fMRI time series. Although this measure has been considered in past neurophysiological (Rajagovindan and Ding 2008; de Pasquale et al., 2010) and task-state fMRI studies (Roebroeck et al., 2005), it has not been applied to resting-state fMRI data. The mathematical theory behind the method was first developed by Gelfand and Yaglom in the context of assessing mutual information between two Gaussian stochastic processes (Gelfand and Yaglom, 1959). Geweke (1982) further showed that for two time series this quantity is the sum of three possible contributors towards their overall temporal interdependence: the influence the first time series exerts upon the second, the influence the second time series exerts upon the first, and co-varying common input (Rajagovindan and Ding, 2008). This observation forms the basis of the term total interdependence. In this work, analyzing resting-state fMRI data, we compared the performance of TI to that of the conventional cross correlation (CC) method. In addition, task-state fMRI data recorded immediately following the resting-state period in the same scanning session were used to further validate the TI method, and to establish the functional significance of the resting-state networks identified by TI.

Methods

Experimental design and data acquisition

Twelve healthy subjects gave informed consent and participated in the study. The experimental protocol was approved by the Institutional Review Board of Beijing Normal University. Both resting-state data and task-state data were recorded in the same scanning session. During resting-state recording, the subject was instructed to relax with their eyes closed for 10 minutes. After a 5 minute break, the subject performed a trial-by-trial cued visual spatial attention task (Wen et al., in press). There were 12 attention blocks (A blocks) and 12 passive view blocks (B blocks). Each attention block lasted 1 minute. The passive view block was of the same duration in which the same stimuli as the attention block were presented but no attention was required. There were 15 trials in each attention block. Each trial started with a cue directing the subject’s covert attention to either the left or the right visual field. Imperative stimuli were presented following a delay period. The subjects were instructed to respond to the target stimuli in the attended hemifield (Rajagovindan and Ding, 2011; Wen et al., in press) by pushing a button with their right hand. Fixation was maintained toward the center of the presentation screen throughout the experiment. Attention blocks and passive view blocks were divided into 6 runs with each run containing 4 blocks organized in an ABBA and a BAAB fashion across runs. Brain activations and deactivations obtained by contrasting attention blocks against passive view blocks provide regions of interest to be used to initiate and validate the resting-state analysis.

Functional MRI data were recorded on a 3-Tesla Siemens whole-body MRI system at the Beijing Normal University MRI center using a T2*-weighed echoplanar imaging (EPI) sequence (echo time (TE), 30ms; repetition time (TR), 2000ms). Each whole-brain volume consisted of 33 axial slices (field of view, 200 mm; matrix, 64×64; slice thickness, 3.60mm, flip Angle=90°, voxel size=3.13×3.13×3.60mm). For high-resolution anatomic images a T1-weighted 128-slice MPRAGE sequence was used (TR, 2530 ms; TE, 3.39 ms; flip angle, 7°; inversion time, 1100 ms voxel size=1 ×1.33 ×1mm).

Definition of seed regions

Both cross correlation (CC) and total interdependence (TI) are seed-based methods. We combined task-state data and resting-state data to define seed regions. For task-state data, the first 5 time points (10 seconds) of each run were discarded to eliminate transient effects, and the remaining data were preprocessed using SPM2 (http://www.fil.ion.ucl.ac.uk/spm/). Preprocessing steps included slice timing, motion correction, coregistration to individual anatomical image, normalization to the Montreal Neurological Institute (MNI) template (Friston et al., 1995), and re-sampling of the functional images into a 3×3×3 mm³ per voxel resolution. Normalized images were spatial-smoothed using an 8mm FWHM (Full Width at Half Maximum) Gaussian core. Global scaling was then applied to remove the global signal before GLM analysis. We note that although the removal of global signal is a debated issue (Zarahn et al. 1997; Aguirre et a., 1998; Glover et al., 2000; Gavrilescu et al., 2002; Junghöfer et al., 2005; Macey et al. 2004; Wise et al., 2004; Birn et al. 2006; Lund et al., 2006; Fox et al., 2009), for our data, global scaling appeared to give more precisely defined regions of task activation, which was crucial for providing a template to compare with resting-state data. In the random-effects analysis, for each subject, from the fitted GLM model, the attend condition and the passive view condition were compared to produce the contrast image. These contrast images were fed into a GLM that implemented a one-sample t-test to yield group-level activation regions (t>5.20, FDR corrected, p<0.002) and deactivation regions (t<−5.20, FDR corrected, p<0.002). Among regions activated by the attention task, we selected bilateral intraparietal sulcus (IPS) and bilateral frontal eyefield (FEF) of the dorsal attention network (DAN) (Corbetta and Shulman 2002; Corbetta et al., 2008), and dorsal anterior cingulate cortex (dACC) and bilateral anterior insular cortex (AI) of the task control network (TCN) (Dosenbach et al., 2006), to aid and to validate the resting-state analysis. Voxels with local maximum t-values in these regions were chosen as the seed voxels. Their coordinates were given in Table 1.

Table 1.

Center coordinates of task-activated regions of interest

ROI			MNI coordinate (mm)
	t-value	p (FDR)	x	y	z
dACC	14.64	<0.0002	6	12	48
rAI	16.57	<0.0002	36	27	6
lAI	14.11	<0.0002	−30	21	0
rIPS	18.38	<0.0002	42	−48	51
lIPS	12.90	<0.0002	−30	−63	54
rFEF	10.68	<0.0002	30	0	57
lFEF	9.63	<0.0002	−30	−3	54

dACC: dorsal anterior cingulated cortex; AI: anterior insular; IPS: inferior parietal sulcus; FEF: frontal eyefield; p: significance level; MNI: Montreal Neurological Institute; r: right; l: left.

The resting-state time series was preprocessed using similar steps and filtered between 0.01–0.1Hz with a zero-phase bandpass FIR filter (Fox et al., 2006; Lowe et al. 2000). Because the regions deactivated by the attention task are rather diffuse, to more precisely define the default mode network, an ICA analysis was applied where the resting-state time series from all subjects were concatenated for each voxel. Twenty five aggregate independent components (ICs) were identified using the GIFT toolbox (http://icatb.sourceforge.net/) where the number of components was determined by the Minimum Description Length (MDL) criterion provided by the toolbox. All aggregate ICs were visually inspected, and the IC representing the default mode network (DMN) was selected (Buckner et al., 2008). Among the DMN regions, we selected the posterior cingulate cortex (PCC), the medial prefrontal cortex (mPFC), and the bilateral inferior parietal lobe (IPL) for the resting-state analysis. The seed voxel in each region was chosen to be the voxel that attained the local maximum t-value in the group ICA map (t>4.75, FDR corrected, p<0.005). The coordinates of these voxels were given in Table 2. Importantly, seed voxels identified in this manner also fell in the task-deactivated regions, and the DMN network identified with ICA exhibited substantial overlap with the task-deactivation map.

Table 2.

Center coordinates of regions of interest in DMN

ROI			MNI coordinate (mm)
	t-value	p (FDR)	x	y	z
PCC	10.51	<0.0002	3	−54	27
MPFC	27.35	<0.0002	−9	60	21
rIPL	9.63	<0.0002	48	−63	24
lIPL	13.78	<0.0002	−51	−69	27

PPC: posterior cingulate cortex; MPFC: medial prefrontal cortex; IPL: inferior parietal lobule; DMN: default mode network. Conventions are otherwise the same as Table 1.

Cross correlation and total interdependence

We compared two connectivity methods: cross correlation (CC) (Fox et al., 2005) and total interdependence (TI). For a pair of simultaneously acquired time series: (x₁,y₁), (x₂,y₂), (x₃,y₃),…(x_n,y_n), CC was computed according to

$${\mathit{\text{CC}}}_{x,y}=({\displaystyle {\sum }_{i=1}^n}{x}_i{y}_i)/\sqrt{({\displaystyle {\sum }_{i=1}^n}{x}_i{x}_i)}\sqrt{({\displaystyle {\sum }_{i=1}^n}{y}_i{y}_i)}.$$ (1)

From the definition, it is clear that CC only measures the contemporaneous (zero-lag) linear relationship between x time series and y time series, and does not account for the possible relations existing across different lags (e.g. between x_i and y_i+2). In contrast, TI, as defined by Gelfand and Yaglom (1959), was computed according to:

$${\mathit{\text{TI}}}_{x,y}=-\frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }}\text{ln}(1-{C_{\mathit{\text{xy}}}}^2(\lambda ))d\lambda ,$$ (2)

where C_xy(λ) is the coherence between the two random processes, x and y, at frequency f = λ/2π. For two Gaussian processes this formula was shown to measure the total amount of mutual information between them. Geweke (1982) further demonstrated that TI captures the total linear relationship between x and y time series. Numerically, for a given sampling frequency f_s, Eq. (2) can be recast into an implementable form:

$${\mathit{\text{TI}}}_{x,y}=-\frac{2}{f_s}{\displaystyle \sum _{i=1}^{N-1}}\text{ln}(1-{C_{\mathit{\text{xy}}}}^2(i\mathrm{\Delta }f))\mathrm{\Delta }f,$$ (3)

where $\mathrm{\Delta }f=\frac{f_s}{2(N-1)}$ is the frequency resolution and N is the number of desired frequency points in the interval between 0 and the Nyquist frequency f_s/2.

In this study CC was calculated directly from data using standard procedures. TI was estimated by fitting bivariate autoregressive (AR) models to pairs of BOLD signals (Bressler and Seth, 2011; Ding et al., 2000; 2006). Coherence was derived from the model coefficients and integrated over frequency according to Eq. (3). Applying Akaike information criterion (AIC) and Lagrange multiplier whiteness test (Lütkepohl, 2005) the optimal model order was determined to be 2.

Functional connectivity maps

For a given seed region X, the CC values with respect to the rest of the brain were normalized by Fisher’s transformation for each subject before group analysis. The TI values were z-transformed for each subject according to, t_i = (TI_i−mean({TI_i}))/std({TI_i})), where TI_i is the value of TI between the seed voxel and the ith voxel, and {TI_i} denotes the collection of such values from all voxels. For both CC and TI, group level one-sample t-test was applied to yield the X-seeded CC map and the X-seeded TI map.

Comparison of methods

Several tests were performed to compare the performance of TI and CC. First, for a pair of time series: (x₁,y₁), (x₂,y₂), (x₃,y₃),…(x_n,y_n), we randomly but synchronously shuffled the time indices to generate a pair of surrogate time series, (x_k1,y_k1), (x_k2,y_k2), (x_k3, y_k3),…(x_kn,y_kn), where (k1, k2, k3…, kn) were a random permutation of (1,2,3,…n). CC would remain the same for the shuffled time series according to Eq. (1). TI, however, would be reduced because the shuffling procedure destroyed the temporal relations across lags. By computing the percentage reduction of TI, we can demonstrate intuitively and quantitatively the degree of total interdependence between the two time series that is not captured by CC. For this test, time series from voxels in a spherical region of 5 mm in diameter surrounding the seed voxel of a region of interest were extracted to represent that region of interest. Between two regions of interest we considered all pairwise combinations of voxels within two similarly constructed spheres. For each pair of time series, random shuffling was carried out 50 times, and the 50 values of TI were averaged and compared with the TI from the original time series to calculate percentage reduction.

Second, the spatial patterns of CC and TI maps were compared. To assess the functional significance of these patterns, we further compared them with well-established network models. Two quantities were used for these comparisons: spatial correlation and spatial overlap. For a given brain, we generated a binary version of the map by assigning to its suprathreshold voxels the value of 1 and other voxels the value of 0, and treated the binary map as a vector in a space whose dimension equals to the total number of voxels. Spatial correlation between two maps is the normalized dot-product of the two corresponding vectors (Fox et al., 2006). Spatial overlap was used to compare the similarity between CC and TI maps in a given brain region. Letting {V_CC} denote the collection of the suprathreshold voxels (t>5.20) in the CC map and {V_TI} the collection of suprathreshold voxels (t>5.20) in the TI map, and letting |{x}| denote the number of elements in the set {x}, the spatial overlap between the two maps for the region is |{V_CC} ∩ {V_TI}|/|{V_CC} ∪ {V_TI}|×100% (Fox et al., 2006).

Third, for visualization purposes, brain maps were projected onto a 3-dimensional brain template from the MRIcroN software package (http://www.cabiatl.com/mricro), as well as onto a flattened 3-dimensional brain surface template from the CARET software packages (http://brainmap.wustl.edu/caret.html).

Fourth, receiver operator characteristic (ROC) curve was applied to compare the statistical sensitivity of CC and TI in deciding the network membership of predefined voxels. The ROC curve is a graphical plot of true positive rate (TPR) against false positive rate (FPR) of making a binary decision when the discrimination threshold is varied (Lasko et al., 2005). For the dACC-seeded map, suprathreshold voxels in AI, or {AI_t>thres}, known from prior work as part of TCN (Dosenbach et al., 2006; Seeley et al., 2007), were defined as true positive detections, whereas suprathreshold voxels in FEF, {FEF_t>thres}, known from prior work as part of DAN (Corbetta and Shulman, 2002; Corbetta et a al., 2008), were defined as false positive detections. TPR and FPR were computed according to TPR = |{AI_t>thres}|/|{AI}| and FPR = |{FEF_t>thres}|/|{FEF}|. Here {AI} and {FEF} were predefined according to the task activation map (t>5.20, FDR corrected, p<0.002). Similarly, for the rIPS-seeded maps, {FEF_t>thres} were defined as true positive detections, and {AI_t>thres} as false positive detections. The ROC curve was constructed by plotting TPR = |{FEF_t>thres}|/|{FEF}| = versus FPR = |{AI_t>thres}|/|{AI}| as threshold was varied. Between CC and TI, if the ROC curve for one measure is more biased toward the TPR axis, this measure is said to perform better in discriminating between the true and false populations. The diagonal line on the TPR-FPR plane is equivalent to random guesses.

Fifth, a clustering analysis was applied to maps generated from 7 seed regions, including dACC, bilateral AIs, bilateral FEF, and bilateral IPS. The purpose was to examine whether TCN and DAN, two functional networks known to be comprised of these regions, could be correctly segregated by CC and TI. Each map, generated by either CC or TI, was treated as a vector in a high dimensional feature space (Cohen et al., 2008). The Euclidean distance between two feature vectors was calculated to determine the similarity of the two spatial maps. If two regions belonged to the same functional network, the connectivity maps seeded in these two regions should be more similar (shorter Euclidean distance) than the connectivity maps generated by two seed regions belonging to different functional networks (longer Euclidean distance). K-means algorithm (k=2) (MacQueen, 1967) was used to segregate feature vectors. Similar approach has been applied in previous functional mapping studies (Fox et al., 2006).

Results

Random permutation and total interdependence

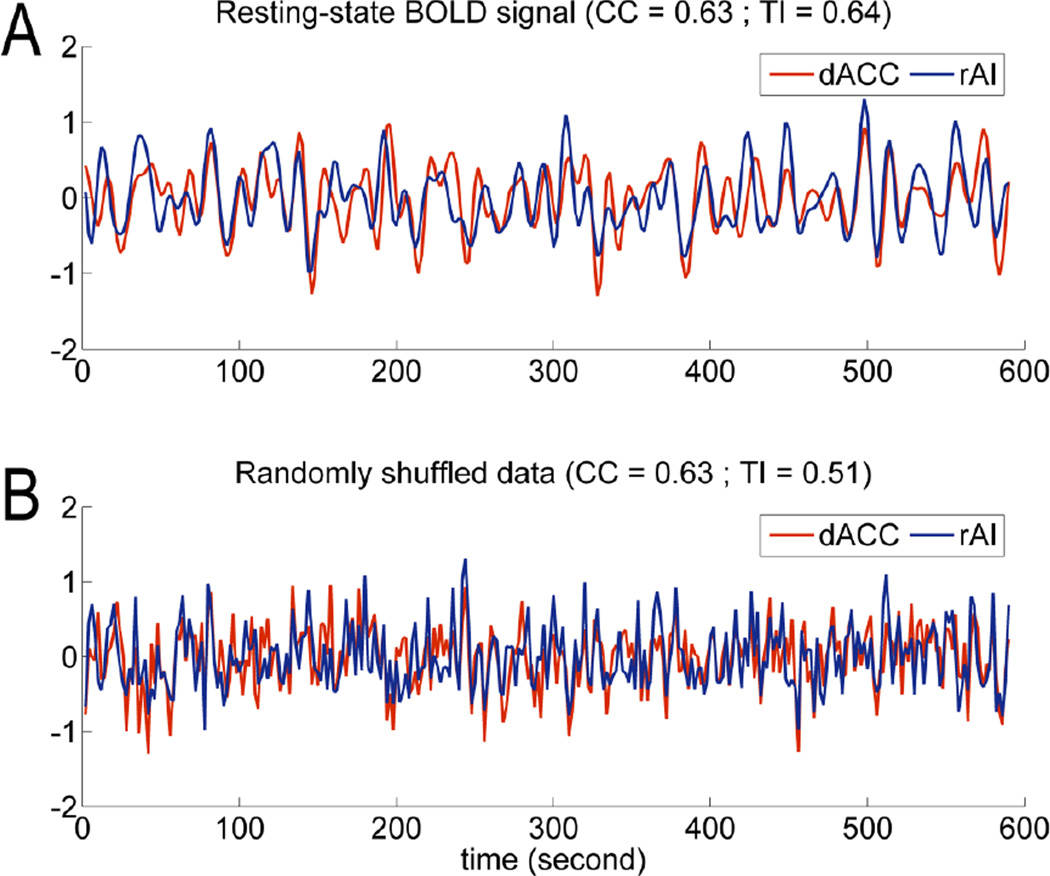
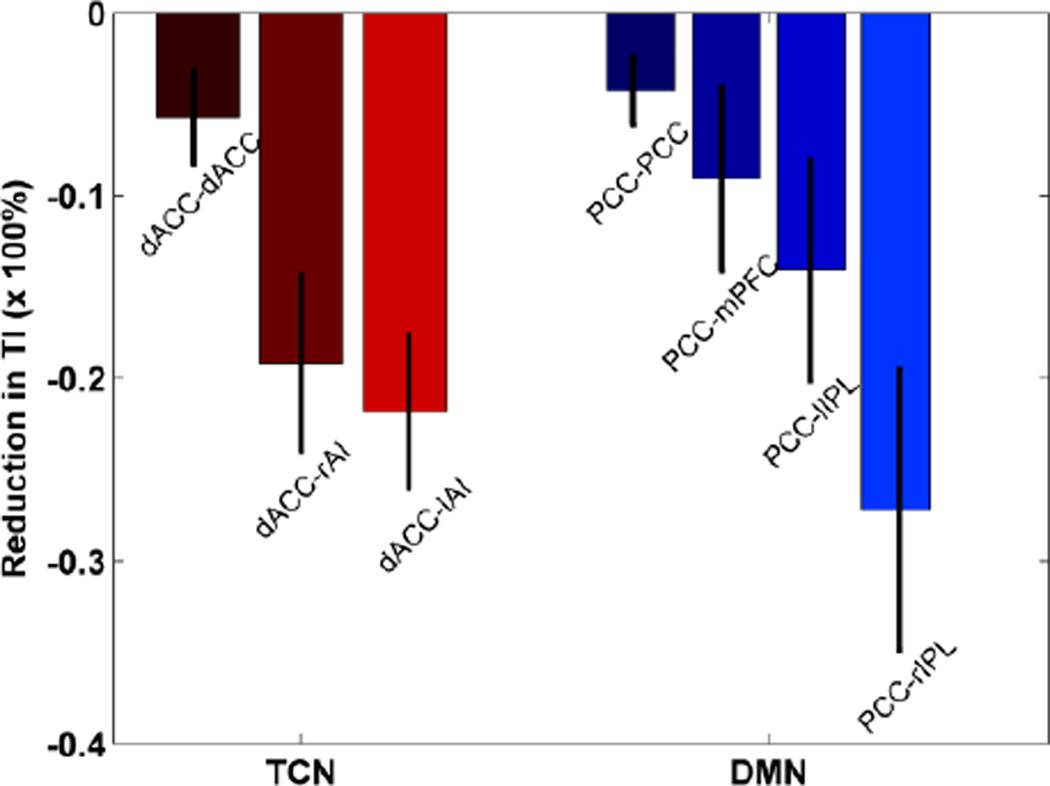
We start by assessing the degree of temporal relationship between two BOLD signals that is not captured by cross correlation (CC). Resting-state recordings from a typical voxel in the dorsal anterior cingulate cortex (dACC) and a typical voxel in the right anterior insula (rAI) were displayed in Figure 1A. Surrogate data, created by randomly but synchronously shuffling the time indices of both time series, were shown in Figure 1B. Despite the qualitative difference in appearance between the original data and the shuffled data, CC was not changed (see Eq. (1)), equaling to r=0.63 for both cases. However, total interdependence (TI) was reduced from 0.64 (Figure 1A) to 0.51 (Figure 1B), a reduction of (0.51–0.64)/0.64=−20%. This percentage change reflected the amount of temporal relationship occurring across non-zero lags that were unaccounted for by CC. In Figure 2, for the default mode network (DMN), the percentage change in TI averaged across subjects was −4% for PCC-PCC (posterior cingulate cortex), −9% for PCC-mPFC (medial prefrontal cortex), −14% for PCC-lIPL (left inferior parietal lobe), and −28% for PCC-rIPL (right inferior parietal lobe). For the task control network (TCN), the percentage change averaged across subjects was −6% for dACC-dACC, −19% for dACC-rAI, and −22% for dACC-lAI (left anterior insula).

Figure 1.

Original and randomly shuffled BOLD signals. A: Resting-state fMRI data from dorsal anterior cingulate cortex (dACC) and right anterior insula cortex (rAI). Bandpass filtering between 0.01 and 0.1 Hz was applied. B: Surrogate data where the time indices for the two BOLD signals in Figure 1A were randomly but synchronously shuffled. Cross correlation (CC) remained the same for both Figure 1A and 1B. The reduction in total interdependence (TI) was indicative of the amount of temporal relationship between the two signals in Figure 1A not captured by CC.

Figure 2.

Reduction in total interdependence (TI) after temporal randomization. dACC and posterior cingulate cortex (PCC) were chosen as seed regions for the task control network (TCN) and the default mode network (DMN), respectively. mPFC: medial prefrontal cortex; lIPL: left inferior parietal lobe; rIPL: right inferior parietal lobe; rAI: right anterior insular; lAI: left anterior insular.

Default mode network

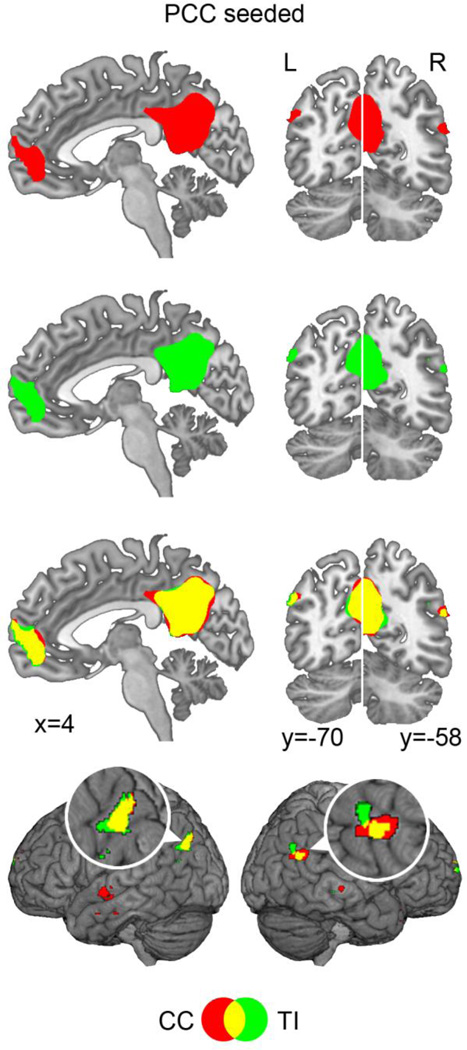
The connectivity between the seed voxel in PCC and all other voxels in the brain was evaluated using CC and TI. Figure 3 showed the resultant maps after taking t>5.20 (FDR corrected, p<0.002) as the threshold for both measures; voxels that were in anti-phase relationship with the seed voxel were excluded. Both CC and TI maps resembled the known spatial structure of the DMN, and the spatial correlation between the two maps was 0.83, indicating that they were similar. Closer examination of Figure 3 revealed that CC and TI maps overlapped differently in different DMN regions. For PCC, mPFC, and lIPL, where the two maps were more similar, the spatial overlap between the two maps, which was the ratio between the number of overlapping voxels and the number of voxels in the union of CC and TI maps (see method), was 77% for PCC, 65% for mPFC, and 35% for lIPL. For rIPL, where the two maps were least similar, the spatial overlap was 20%. These findings were in agreement with Figure 2, which showed that for PCC-PCC, PCC-mPFC, and PCC-lIPL, the temporal relationship that was not captured by CC was relatively small, at −4%, −9%, and −14%, respectively, whereas for PCC-rIPL, the amount of temporal relationship missed by CC was larger, at −28%.

Figure 3.

PCC-seeded connectivity maps. Both the CC map (red) and the TI (green) map contained the major nodes in the default note network (DMN) (t=5.20, p<0.002, FDR corrected for both CC and TI). The overlap (yellow) between the two maps was higher in mPFC, lIPL, and PCC than in rIPL. rIPL and lIPL regions were magnified to facilitate visual comparison.

Task control network

The connectivity between the seed voxel in dACC and all other voxels in the brain was evaluated using CC and TI. The CC map in Figure 4 (t>5.20, FDR corrected, p<0.002) included dACC and bilateral AIs, the three established regions of TCN (Dosenbach et al., 2006), as well as right frontal eyefield (rFEF) and right middle frontal gyrus (rMFG), two areas of the frontal-parietal attention system (Corbetta and Shulman, 2002; Corbetta et al., 2008). In contrast, using the same threshold, the TI map included only dACC and bilateral AIs, suggesting that TI was able to identify TCN more precisely, without having to contend with the intrusion from areas belonging to other networks. The spatial correlation between the CC map and the TI map was 0.48, suggesting that relative to DMN where the spatial correlation between CC and TI maps was 0.83, the two maps for TCN were more discrepant.

Figure 4.

dACC-seeded connectivity maps. Although both the CC map (red) and the TI map (green) contained dACC, rAI, and lAI, the three nodes in TCN (t=5.20, p<0.002, FDR corrected for both CC and TI), the CC map also contained regions beyond TCN, including frontal eyefield (FEF), middle frontal gyrus (MFG), and middle cingulate gyrus (MCG).

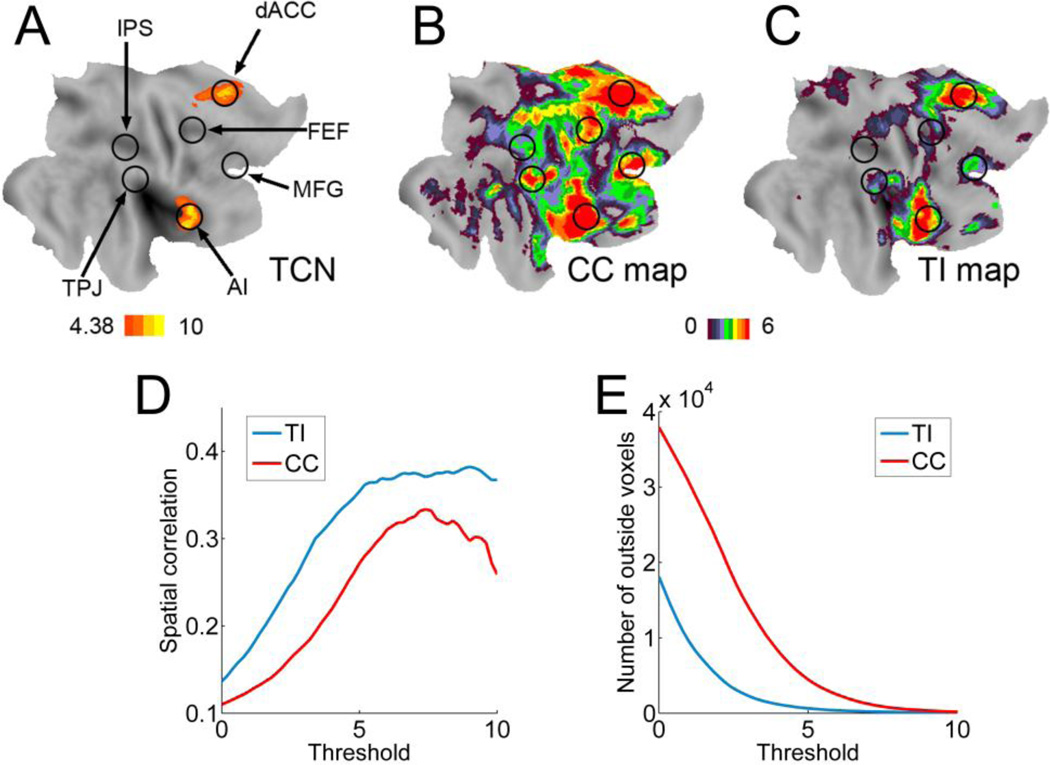
The dACC-seeded CC and TI maps were examined further by comparing them with the task-defined TCN (Figure 5A). By not selecting an a priori threshold, dACC-seeded maps in the right hemisphere were represented as color-coded t-values (t>0) in Figures 5B and 5C. For TI (Figure 5C), the three regions of the TCN network were clearly delineated with sharp and clearly defined boundaries, whereas for CC (Figure 5B), dACC and AI clusters were more diffuse and the map included other regions not belonging to TCN, including FEF, MFG, intraparietal sulcus (IPS), and temporal parietal junction (TPJ). Similar effects were found in the left hemisphere. In Figure 5D, the spatial correlation between the task-defined TCN and the dACC-seeded TI and CC maps revealed that over a broad range of threshold values, the TI map has larger overlap with the task-defined TCN than the CC map. The number of suprathreshold voxels in TI and CC maps that did not belong to the task-defined TCN, plotted as a function of threshold in Figure 5E, demonstrated that the TI contained fewer false-positive detections than CC.

Figure 5.

Comparison between task-state and resting-state data. A: Regions activated by the attention task were marked by circles. TCN was highlighted. B: dACC-seeded CC map from resting-state data. C: dACC-seeded TI map from resting-state data. Group level t-values were color-coded and projected on a flattened brain surface template of the right hemisphere. The CC map (B) was more diffuse and contained many regions not belonging to TCN. In contrast, the TI map (C) was more localized and matched more precisely the TCN activated by the attention task. D: Spatial correlation between the task-activated TCN and suprathreshold resting-state CC and TI maps. E: Number of voxels in suprathreshold TI and CC maps that do not belong to the task-activated TCN. IPS: intraparietal sulcus; TPJ: temporoparietal junction.

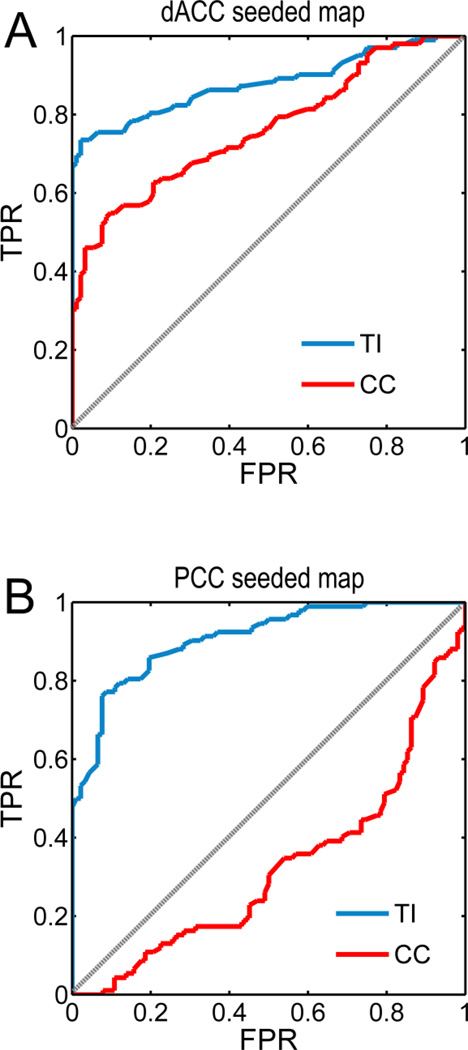
ROC analysis of statistical sensitivity

The statistical sensitivity of TI and CC was tested using the receiver operator characteristic (ROC) curve method. Between two measures, the measure whose ROC curve is more biased toward the true positive rate (TPR) axis is said to perform better in discriminating between a true and a false population. For dACC-seeded maps, voxels in task-activated AI formed the true population, and voxels in task-activated FEF formed the false population. In contrast, for rIPS-seeded maps, true and false populations were reversed. The ROC curves obtained from TI for both cases indicated that it exhibited superior statistical sensitivity in correctly deciding the network membership of predefined voxels.

Clustering analysis

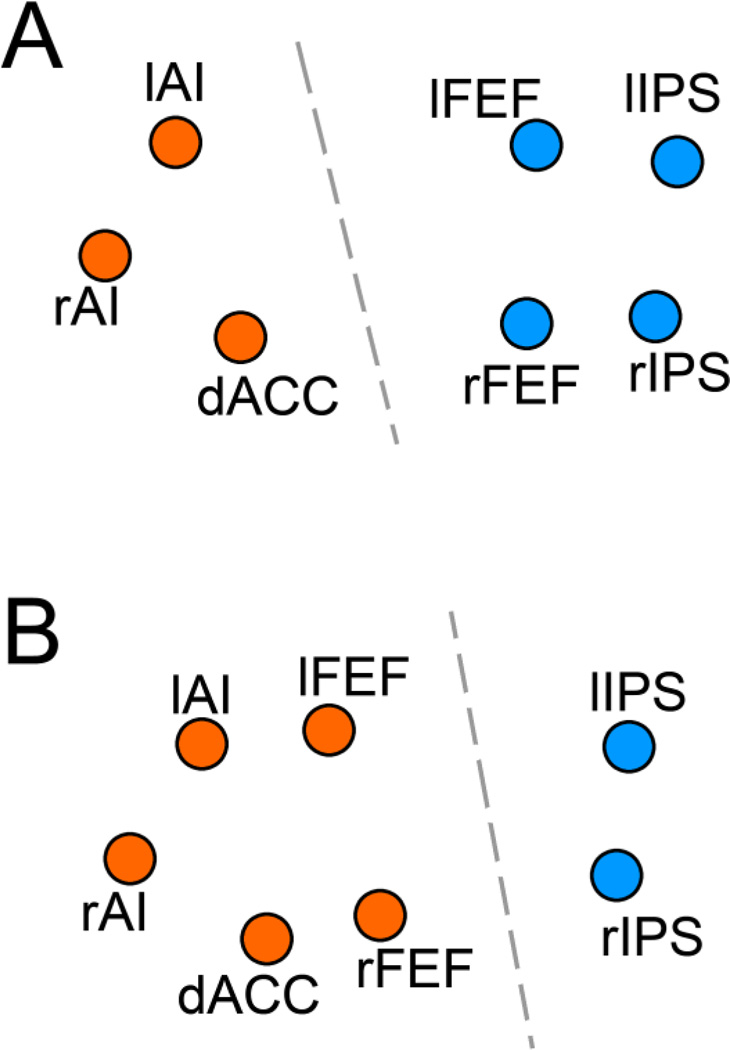
Past work has used resting-state connectivity maps as feature vectors to divide brain regions into distinct functional networks through clustering analysis (Church et al., 2009; Hlinka et al., 2011). As shown in Figure 7A, for TI, the dACC-seeded spatial map and bilateral AI-seeded spatial maps were clustered together to form one network, in agreement with prior knowledge that these areas belong to TCN (Dosenbach et al., 2006; Seeley et al., 2007). Bilateral FEF-seeded and bilateral IPS-seeded maps, on the other hand, were clustered together to form another network, again in agreement with prior knowledge that these areas belong to DAN (Corbetta and Shulman 2002; Seeley et al., 2007). In contrast, for CC (Figure 7B), bilateral FEF-seeded, dACC-seeded and bilateral AI-seeded maps were incorrectly clustered together to form one network, and the bilateral IPS-seeded maps were clustered together to form another.

Figure 7.

K-means clustering analysis. A: TI maps, treated as feature vectors, allowed the correct grouping of brain regions into the two known function networks: TCN (orange) and DAN (blue). B: CC maps, treated as feature vectors, made the incorrect assignment of rFEF and lFEF to TCN.

Discussion

Prevailing methods for resting-state functional connectivity analysis do not take into account the time series structure in resting-state fMRI data. We propose to address this problem by introducing a method called total interdependence (TI). It was shown that, when combined with a random permutation approach, TI can reveal the degree of temporal dependence between BOLD signals that were not captured by the traditional zero-lag cross correlation (CC) method. Functionally, TI was able to more precisely identify the three constituent regions of the task control network, which were further validated by the task-state data recorded during the same experiment. Finally, we showed that TI performed better in a clustering analysis of network segregation and exhibited superior statistical sensitivity.

Measures of temporal relationship

Seed-based connectivity analysis can reveal brain regions whose activities co-vary with that of the seed region. Such covariations indicate shared functionality and are the basis for defining functional networks (Biswal et al., 1995; Buckner et al., 2008; Fox et al., 2006; Vincent et al., 2007). Which statistical measure is chosen to perform functional connectivity mapping, however, could significantly influence the outcome. Zero-lag cross correlation coefficient, by far the most widely practiced, is a linear method and does not take into account the temporal dependence beyond the contemporaneously acquired data points. Past work has pointed out its weaknesses (Garofalo et al., 2009). A recent study by Hlinka et al. (2011) adopted mutual information to measure both linear and nonlinear portions of the interaction between fMRI time series. They found that the nonlinear portion is negligible for the reason that fMRI time series are well-approximated by Gaussian stationary processes. Recognizing the presence of temporal relationship across different scans, Curtis et al. (2005) introduced spectral coherence to measure functional connectivity between different brain regions, disclosing modulated frontal-parietal interactions in a working memory task. To what extent the temporal relationship across different scans may impact resting-state connectivity analysis remains to be clarified. This is the main objective of the present study.

Our starting point is the introduction of total interdependence in Eq. (2). Although TI is defined in terms of spectral coherence, the formula in Eq. (2) allows it to be interpreted as the total amount of mutual information between two Gaussian stationary processes (Gelfand and Yaglom 1959). Geweke (1982) further demonstrated that the quantity in Eq. (2) can be decomposed into 3 components, namely,

$${\mathit{\text{TI}}}_{x,y}=F_{x\to y}+F_{y\to x}+F_{\mathit{\text{xy}}},$$ (3)

where F_x→y is the causal influence from x to y, F_y→x is the causal influence from y to x, and F_xyis the instantaneous causality between x and y, reflecting possible common input (Brovelli et al., 2004; Ding et al., 2006; Goebel et al., 2003; Granger, 1967; Jiao et al., 2011; Rajagovindan and Ding, 2011; Roebrock et al., 2005). In light of the fact that these three components represent the all possible ways two time series can interact with one another, we thus term the quantity in Eq. (2) total interdependence.

Temporal structures in resting-state fMRI data

A bivariate white noise process, whose power spectra are flat, exhibits only contemporaneous correlation. CC captures the entire temporal dependence for such processes. However, neurobiological time series, including BOLD signals, are usually not white noise processes. Being able to assess the amount of temporal relationship missed by CC is thus a key step towards understanding its limitations. We proposed to accomplish this by randomly but synchronously shuffling the time indices of two fMRI time series and comparing TI before and after this randomization. The result showed that CC stayed unchanged while TI was reduced after temporal order randomization. Because for white noise there should be no reduction in TI, the percentage of the reduction following the temporal randomization procedure can thus be viewed as the amount of temporal relationship not captured by CC.

For the voxel pairs in the default mode network (DMN), the amount of uncaptured temporal relationship varied from quite substantial (PCC-rIPL at 28%) to less substantial (PCC-PCC at 4%, PCC-lIPL at 9%, and PCC-mPFC at 14%); see Figure 2. In agreement with this, the PCC-seeded CC map and TI map were more overlapped in PCC, mPFC, and lIPL, but less overlapped around rIPL; see Figure 3. Past work has shown that DMN is functionally more lateralized to the left hemisphere (Buckner et al., 2008, 2009). This means that PCC-rIPL may not be as strongly coupled as PCC-lIPL. The CC approach, measuring only part of the total interdependence, may work even less effectively in this case when connectivity is relatively weak to begin with. For the voxel pairs in the task control network (TCN), similar patterns of TI reduction were observed, as seen in Figure 2.

Physiologically, besides temporal correlations inherent in various rhythmic neural activities, neural transmission and processing delays (Nishitani and Hari, 2002; Schmolesky et al. 1998; Van Essen et al., 1992) between different nodes of a large-scale network, and variations in the hemodynamic response functions (Aguirre et al., 1998; Handwerker et al., 2004; Kruggel and von Cramon, 1999) are other contributing factors to the presence of temporal dependence beyond the zero-lag. Our observation that uncaptured temporal dependence by CC is more substantial for voxel pairs between far-separated regions than for voxel pairs within a region can be seen as a manifestation of these factors. On the other hand, while TI is reduced for dACC-dACC and PCC-PCC following random shuffling, the reduction is much less severe relative to that of interregional TI, indicating that the temporal relationship between functionally similar voxels in the same brain region is dominated by contemporaneous dependence.

Functional significance of TI

As shown in Figure 2, the degree of temporal relationship not captured by CC can vary from ROI pair to ROI pair, and from network to network, causing differences in spatial maps established by CC and TI. How to evaluate the functional significance of these differences? We addressed this by combining task-state data with resting-state data and by focusing on the three core regions in the task control network. Temporal randomization test revealed that for dACC-rAI and dACC-lAI, about 20% of the temporal relationship was not captured by CC. The dACC-seeded CC map included FEF, an area of the dorsal attention network, in addition to more diffusely defined dACC and bilateral AIs, members of the task control network. In contrast, the dACC-seeded TI map was free from the confounding influences from other networks and contained sharply-defined dACC and bilateral AIs, which were further shown to be highly consistent with the three core regions defined by our attention task; see Figures 4 and 5.

Functional imaging studies have firmly established the role of dACC and bilateral AI in exerting control over behavioral performance at the task level in a variety of experimental contexts (Botvinick et al., 2004; Dosenbach et al., 2006; Kerns et al., 2004; Nelson et al., 2010; Sridharan et al., 2008). Resting-state connectivity analysis based on cross correlation, however, has to date often not been able to unequivocally establish dACC and bilateral AI as forming a distinct resting-state functional network (Seeley et al., 2007). The consistent inclusion of areas such as FEF and lateral prefrontal regions in CC maps has led to the debate of whether these additional areas should be considered part of the task control network (Church et al., 2009; Dosenbach et al., 2006; Fox et al., 2005; 2006; Mennes et al., 2010; MacDonald et al., 2000). Whereas independent component analysis (ICA) can sometimes identify the three core regions of TCN, it is often the case that the ICA components containing this network often contain additional regions such as dorsal lateral prefrontal cortex, anterior frontal lobe, supplementary motor areas, or temporal lobe (Beckmann et al., 2005; De Luca et al. 2006). There were even reports where dACC is missing from the ICA component (Damoiseaux et al. 2006; 2008). In light of the foregoing, TI, with its ability to clearly establish dACC and bilateral AI as forming a distinct functional network at rest, provides results more in line with task-based imaging studies, and thus represents an improvement over previous methods.

Analogous to the task control network, the FEF-seeded map constructed with CC (not shown) always includes dACC and AI regions (Fox et al., 2006), in addition to the other dorsal attention network areas. This is again inconsistent with the task-based imaging studies where the different functional roles played by the two networks have been carefully delineated. The application of connectivity measures such as TI, which takes into consideration of the overall temporal interdependence between BOLD signals, can help resolve these inconsistencies. Although by applying a more stringent threshold CC can generate maps that better resemble the TCN activation map the match remains not as precise as the TI map. Figures 5D and 5E address this point. Over a broad range of threshold values the spatial correlation between the CC map and the task-defined TCN is lower than that between the TI map and the task-defined TCN. As the threshold increases, the regions included in the CC map begin to shrink rapidly, whereas the regions included in the TI map stay relatively constant. The ROC curve analysis and the clustering analysis (Figures 6 and 7) further demonstrate TI as exhibiting better statistical characteristics than CC.

Figure 6.

ROC analysis of statistical sensitivity. A: True positive rate (TPR) versus false positive rate (FPR) as function of discrimination threshold when deciding whether a predefined voxel belonged to TCN in the dACC-seeded resting-state maps. Task-activated voxels in rAI and rFEF were defined as the true and false populations respectively. B: TPR versus FPR when deciding whether a predefined voxel belonged to DAN in the rIPS-seeded resting-state maps. Task-activated voxels in rFEF and rAI were defined as the true and false populations respectively. In both cases TI achieved superior statistical sensitivity over CC.

Estimation of TI

TI is defined in terms of spectral coherence (Eq. (2)). There are two ways to compute spectral coherence from time series data: nonparametric Fourier-based methods and parametric AR-based methods. For long and relatively noise-free time series, Fourier based spectral analysis and AR-based spectral analysis produce similar results (Dhamala et al., 2008). Functional fMRI data, whether recorded during resting-state or during task-state, are often short and noisy. Nonparametric spectral analysis is not optimal for this type of data. Parametric spectral analysis based on AR model fitting is known to be more robust and can provide smooth and accurate spectral estimates (Ding et al., 2000; Jiao et al., 2011; Wen et al., in press). This is the reason behind our adoption of the parametric AR method to assess the performance of TI. It should be note that filtering can impact the value of TI. In this study resting-state fMRI data were band-pass filtered between 0.01–0.1 Hz (Lowe et al., 2000; Fox et al., 2005, 2006). This commonly applied filter allowed us to compare our results with the results of other resting-state studies.

Highlights.

• >New measure called total interdependence (TI) is introduced to analyze resting-state connectivity.
• >TI captures overall temporal relationship between BOLD signals.
• >The amount of temporal relationship not captured by CC was revealed.
• >TI networks match more precisely the functional networks established by task activation.
• >TI is more statistically sensitive than CC in disassociating functional networks.