Abstract
A critical element in theoretical characterization of the mechanism of proton-coupled electron transfer (PCET) reactions, including hydrogen atom transfer (HAT), is the formulation of the electron and proton localized diabatic states, based on which a More O’Ferrall-Jencks diagram can be represented to determine the step-wise and concerted nature of the reaction. Although the More O’Ferrall-Jencks diabatic states have often been used empirically to develop theoretical models for PCET reactions, the potential energy surfaces for these states have never been determined directly based on first principles calculations using electronic structure theory. The difficulty is due to a lack of practical method to constrain electron and proton localized diabatic states in wave function or density functional theory calculations. Employing a multistate density functional theory (MSDFT), in which the electron and proton localized diabatic configurations are constructed through block-localization of Kohn-Sham orbitals, we show that distinction between concerted proton-electron transfer (CPET) and HAT, which are not distinguishable experimentally from phenomenological kinetic data, can be made by examining the third dimension of a More O’Ferrall-Jencks diagram that includes both the ground and excited state potential surfaces. In addition, we formulate a pair of effective two-state valence bond models to represent the CPET and HAT mechanisms. We found that the lower energy of the CPET and HAT effective diabatic states at the intersection point can be used as an energetic criterion to distinguish the two mechanisms. In the isoelectronic series of hydrogen exchange reaction in (PhX)2H•, where X = O, NH, and CH2, there is a continuous transition from a CPET mechanism for the phenoxy radical-phenol pair to a HAT process for benzyl radical and toluene, while the reaction between PhNH2 and PhNH• has a mechanism intermediate of CPET and HAT. The electronically nonadiabatic nature of the CPET mechanism in the phenol system can be attributed to the overlap interactions between the ground and excited state surfaces, resulting in roughly orthogonal minimum energy paths on the adiabatic ground and excited state potential energy surfaces. On the other hand, the minimum energy path on the adiabatic ground state for the HAT mechanism coincides with that on the excited state, producing a large electronic coupling that separates the two surfaces by more than 120 kcal/mol.
1. Introduction
Proton-coupled electron transfer (PCET) reactions are central to a variety of chemical and biological processes, including solar energy conversion, enzymatic catalysis and electrochemistry.1–6 PCET reactions can occur sequentially through an initial electron transfer followed by proton transfer (ET/PT) or proton transfer followed by electron transfer (PT/ET). In the other extreme of the mechanistic spectrum, PCET can take place simultaneously as concerted proton-electron transfer (CPET), and the electron and proton can start from and end in, respectively, the same or different donor and accept sites.7–8 Formally, the transfer of one electron and one proton to and from a single site is equivalent to a net hydrogen atom transfer (HAT), and the distinction between CPET and HAT has been particularly ambiguous and sometimes controversial, despite PCET has been extensively studied both experimentally and theoretically.9–11 (The term PCET is used to broadly describe any reaction involving the transfer of electrons and protons, whereas CPET is used for a specific, a concerted PCET mechanism).3,6 In this article, we use multistate density functional theory (MSDFT)12–13 to examine the hydrogen exchange reactions in the isoelectronic series of (C6H5)2H, X = O, NH, and CH2, and show that the HAT and CPET reactivity is blended, and both pathways involve the same valence bond (VB) structures, albeit, to variable extents. Importantly, the difference between CPET and HAT mechanisms can be revealed in the third dimension of a More O’Ferrall-Jencks diagram, which illustrates how the 4-VB state mixing leads to almost a conical intersection (seam) in the PCET pathway vs. a very large energy separation between the ground and excited state in PhCh2 •/PhCh3.
To begin, is there a distinction, and if so, is there a need to distinguish the difference between HAT and CPET where both the electron and proton start and end on the same donor and acceptor? First, the differentiation is important because the two processes can have very different solvent effects with CPET more prone to changing reaction mechanism,14–19 and they can exhibit different chemical reactivity, including kinetic isotope effects.20–21 For example, the rate of hydrogen abstraction from a C-H donor by a free radical typically shows little solvent effects, whereas that from a O-H bond by an alkoxy or an aryloxy radical can vary as much as 102-fold and the mechanism may change from a concerted process into a sequential PT/ET.3,15,18,22–23 Mayer emphasized that the HAT mechanism is characterized by a single kinetic step, and HAT is viewed as a type of CPET.11,19,24 Under this definition, many hydrogen abstraction reactions by transition metal complexes, in which an oxidizing metal center accepts the electron while a proton is translocated to a basic site, often recognized as CPET, are categorized as HAT. This view provided an important insight in understanding the reactivity for a broad range of reactions involving concerted transfer of an electron and a proton. Nevertheless, phenomenological kinetic parameters are not sufficient to provide the detailed mechanisms for these processes as illustrated by the isoelectronic hydrogen exchange reactions between phenol and phenoxy radical and between toluene and benzyl radical; the former follows a CPET mechanism, whereas the latter is a HAT.25–26
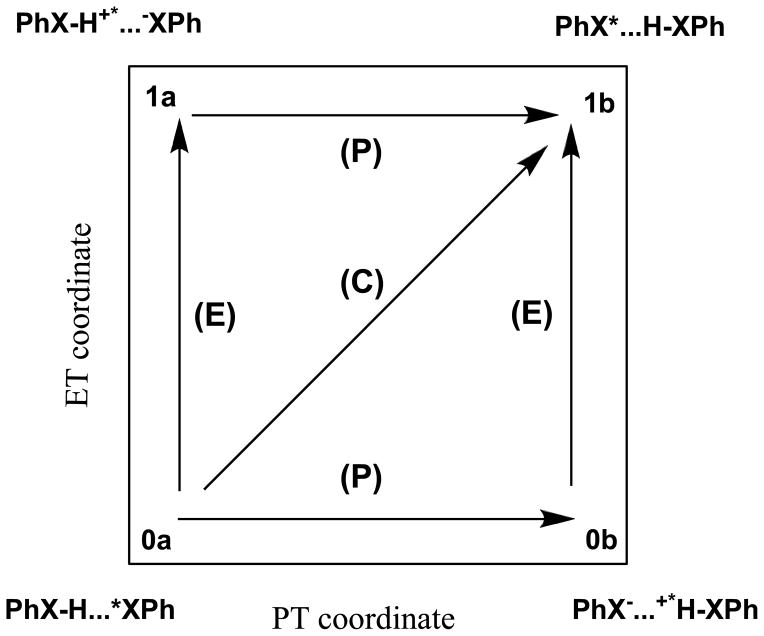
There have been extensive theoretical and computational studies of PCET reactions, including the pioneering works of Cukier, Hammes-Schiffer, Stuchebrukhov and others.2,6–7,9,11,24,27–34 The general approach is based on Marcus theory of electron transfer35 and a generalized More O’Ferrall-Jencks plot36–37 to represent the continuous variation of PT and ET reaction mechanisms.7,38 This is illustrated in Scheme 1 for the hydrogen exchange reaction between PhXH and PhX• radical, where X = O, NH, and CH2. The four corners of the More O’Ferrall-Jencks plot in Scheme 1 specify the effective VB states, called diabatic states, corresponding to the electron and proton localized on the donor and acceptor sites, respectively. Consequently, each point in this diagram represents an admixture of the four diabatic configurations,39 whose structural weights correspond to the contributions of a particular electronic state and can be used as an ET reaction coordinate. In Scheme 1, pathways (E) and (P) represent the step-wise mechanisms of either ET followed by PT (ET/PT) or PT followed by ET (PT/ET), while the diagonal route (C) corresponds to concerted proton and electron transfer, encompassing both CPET and HAT. Deviations from the diagonal path reflect the degree of nonsynchronicity. In such a 2-D representation in Scheme 1, the concerted processes are characterized by a single kinetic step and there is no distinction between CPET and HAT.
Scheme 1.
Schematic representation of the mechanism for the coupled transfer of proton and electron as a function of electron transfer and proton transfer coordinates.
The reactions between phenol and phenoxy radical and its isoelectronic analog toluene and benzyl radical have been studied computationally by a number of authors.25–26,33,40–43 Mayer, Borden and coworkers first showed that the hydrogen exchange between phenol and benzyl radical follows a concerted CPET mechanism, whereas the hydrogen atom abstraction of toluene by benzyl radical is a HAT.25 Mayer et al. examined the alignment of frontier molecular orbitals of the PhO• ··· HOPh complex and found that the orbital occupied by the unpaired electron is symmetrically orthogonal to that of the donor-proton bond in the direction of proton migration. In this arrangement, there is strong hydrogen bonding interaction, making the phenyl units essentially co-planar in the transition structure.25 Consequently, five electrons are critically involved in the coupled proton and electron transfer, and the singly occupied molecular orbital (SOMO) is highly delocalized at the transition state. On the other hand, in the pair where hydrogen bonding is absent, the orbital occupied by the unpaired electron is nearly perpendicular to the two phenyl rings, but it coincides with that of the proton transfer coordinate at the transition state. In this case, a classical three-electron/three-center process is depicted, and the SOMO is localized in the C…H…C region.25,43 This vivid orbital interaction picture is intuitive and has created a major impression in the interpretation of HAT and CPET reactions, but it is not clear on situations where there is significant mixing of orbitals in the transition states.15,18,26,33,41–43 Subsequently, Hammes-Schiffer and coworkers,26 who also used orbital symmetry to describe the two reactions, pointed out that the concerted proton and electron transfer in the phenol system is electronically nonadiabatic, whereas the reaction of benzyl radical and toluene takes place on the adiabatic potential energy surface. It was suggested that electronic adiabaticity can be used to differentiate CPET and HAT reactions.26 Tishchenko et al. highlighted the involvement of both the ground and excited potential energy surfaces in CPET and emphasized competition between adiabatic barrier crossing and nonadiabatic transition through conical intersection.33 These concepts probed the mechanistic features of CPET and HAT from different perspectives, although a common theme in these studies is that they are based on calculations using delocalized wave functions.
Alternatively, the origin of the reaction barriers can be understood using valence bond (VB) theory, in which localized configurations are used.44 One approach for rationalizing the origin of reaction barriers is the valence bond state correlation diagram (VBSCD) introduced by Shaik,44–47 and it has been recently applied to a range of hydrogen atom transfer reactions.48–49 In the latter work, the difference between HAT and CPET mechanisms was described in terms of the extent of HAT and charge transfer character in VB configuration mixing.
In this study, we also adopt a valence bond-based approach to examine the origins of the CPET and HAT mechanisms in the hydrogen atom exchange reactions of (PhX)2H•, where X = O, NH, and CH2. To begin our study, we use a block-localized density functional theory (BLDFT)12,50 to define non-orthogonal PT and ET diabatic (localized) configurations first.12,39,51–52 Then, these electronic configuration state functions (CSFs) are used in configuration interaction to yield the adiabatic (delocalized) ground and excited state.12,50 In such a multistate DFT (MSDFT), the overlap between different diabatic states is explicitly determined using non-orthogonal CSFs. In contrast, our approach differs from diabatization procedures through orthogonal transformation of the delocalized MCSCF or CASSCF wave functions to extract diabatic states.53 A critical assumption in such procedures is that the overlap integral between diabatic states is zero since there is no way to determine it in these approaches. However, the overlap interactions contain key information in the understanding of the mechanistic difference between CPET and HAT.
In the following, we first summarize the method used to define diabatic states for the three hydrogen exchange reactions through block-localization of Kohn-Sham orbitals. Then, we construct the characteristic state functions corresponding to the CPET and HAT reaction pathways. This is followed by results and discussion on the qualitative and quantitative features of the potential energy surfaces (PES) for the CPET and HAT mechanisms. The paper is concluded with a summary of the main findings of this study.
2. Method
2.1. Diabatic and Adiabatic States
The mechanisms of the concerted and sequential ET and PT processes can be characterized by the four VB states illustrated in Scheme 1.7,38 If we use, respectively, 0 and 1 to indicate the localized electronic configurations, and a and b to denote the transferring proton localized on the donor (initial) and acceptor (final) sites (Scheme 1), each diabatic state of the corresponding Lewis configuration can be represented by a single determinant of block-localized Kohn-Sham (BLKS) orbitals in density functional theory (DFT):12,39,51
| (1) |
| (2) |
| (3) |
| (4) |
In eqs 1–4, X = O, NH, or CH2, Â is the antisymmetrizer, and denotes a product of the occupied BLKS orbitals for the kth (k =1,2) fragment specified in parentheses in diabatic state γ (γ = 0a, 0b, 1a, and 1b). The resonance (mixing) of the VB-like CSFs defined by eqs 1–4 yields the adiabatic ground and excited states for the coupled ET and PT reaction, which are determined by configuration interaction in multistate density functional theory (MSDFT).12
The VB-like wave function for the coupled proton and electron transfer reaction is written as a linear combination of the four CSFs:12,39
| (5) |
where cγ is the coefficient for state γ. The BLKS determinants are used to yield constrained electron densities in DFT calculations to determine the energies of the diabatic states and the off-diagonal coupling elements, required for determining the rate constant.12,39 Importantly, the function ΦMSDFT itself is not used to generate the ground state density as in multiconfiguration density functional methods.54–56 Instead, the ground and excited state energies are obtained as the lowest and higher roots of the corresponding generalized secular equation.12 Thus, ΦMSDFT is only used as an auxiliary function to define the Hamiltonian matrix. MSDFT has the advantage that both the electronically localized diabatic and the resonance delocalized adiabatic states can be determined to study energy transfer and PCET reactions.
Note that by construction, the Kohn-Sham orbitals are block-localized in the molecular fragments in eqs 1–4 to represent the specific Lewis resonance structure, or diabatic configurations.39,51,57 BLDFT12,52 is a strictly constrained density functional theory58 in that the total electron density can be partitioned into the sum of fragment densities at the basis set level:
| (6) |
where the integration of the fragmental density for fragment k (k=1,2) satisfies the charge constraint, ∫ ρk (r)dr = nk, where nk is the number of electrons in block k. BLDFT differs from the constrained DFT approach used by Van Voorhis and coworkers,59 in which the electron density is constrained in a finite spatial region with the use of delocalized Kohn-Sham orbitals over the entire molecular system.60–63 In BLDFT, the BLKS orbitals are orthogonal within each block as in standard DFT, which is computationally efficient, but orbitals between different blocks are nonorthogonal.12,39,44,51
2.2. Effective CPET and HAT States
It is useful to combine two of the diabatic configurations defined in eqs 1–4 (see Scheme 1) to reduce the four-state theory into a pair of two-state models,39,44,51,57 to describe, respectively, the CPET and HAT mechanisms.7 In hydrogen atom transfer, by definition, the electronic configuration is adiabatic with respect to the hydrogen nuclear position (otherwise, it would involve separate ET, hence not a HAT).7,64 Thus, the electronically localized VB configurations for a given proton (nucleus) configuration in eqs 1–4 must be combined to yield a lower energy state, i.e., the corresponding diabatic state for HAT. Specifically, at a given localized proton position on the donor a (acceptor b) site, the effective diabatic states for the HAT reactant and product are generated from the resonance of the initial (0) and final (1) electronic configurations:
| (7) |
| (8) |
where cγ are the configurational coefficients. The resonance of the HAT reactant (R) and product (P) VB diabatic states produces the adiabatic ground state potential surface for HAT, on which nuclear tunneling occurs (although the treatment of nuclear tunneling in rate calculation is not the subject of the present study).65–67
In the CPET mechanism, electron transfer is nonadiabatic by definition (otherwise it would have been a HAT), and each PCET diabatic state (not necessarily concerted) is stabilized by the accompanying proton tunneling, thus, a proton-coupled electron transfer. Consequently, the effective diabatic configuration for the CPET process is a combination of the two localized proton configurations at a given electronic localization, in the reactant (0) and product (1) well, respectively:
| (9) |
| (10) |
where the prime over the mixing coefficients distinguishes them from those in eqs 7 and 8. Here, electron tunneling can be treated by Marcus theory for electron transfer using eqs 9 and 10 as the initial and final electron transfer diabatic states. The electronic diabatic coupling at the diabatic state crossing point is given as follows:
| (11) |
where is the overlap integral. The exchange and diagonal matrix elements, defined in terms of CSFs by and , are computed using block-localized density functional theory in the present study.12,52
2.3. Reaction Coordinates
The concertedness of the CPET mechanism in the (PhX)2H• systems is characterized by the More O’Ferrall-Jencks diagram in the ET and PT transfer coordinates (Scheme 1). The proton reaction coordinate is conveniently defined by the nuclear positions as follows:
| (12) |
where and are, respectively, the distance of the migrating hydrogen from the donor atom X (reactant state) and from the acceptor atom X′ (product state). For the electron transfer process, we use the configuration weight χ, corresponding to the initial electronic diabatic state (χ = 0) and the final electronic diabatic state (χ = 1) to monitor the effect of electronic mixing on the protonic configurations. Thus, for a given χ value at the protonic coordinate ΔRp, we define the following admixture of electronic configurations:
| (13) |
| (14) |
to determine the potential energy E(χ, ΔRp) as a function of the proton transfer (ΔRp) and electronic mixing (χ) coordinate.12,39 We note that the coordinate χ can be converted to the Chirgwin-Coulson VB structural weight (both values have a range of 0 to 1 and are identical for the initial and final states),68–69 which is a more rigorous representation of the contributions of each VB-like electronic state (eq 9 and 10); here, we have simply used χ in the representation.
3. Computational Details
The transition state structures and the minimum energy complexes for the hydrogen atom exchange reaction in (PhX)2 H•, X = O, NH, and CH2, were optimized using the hybrid density functional B3LYP70–71 with the 6-31G(d) basis set. Similar calculations have been described in the work of Mayer et al. on the phenol and toluene systems.25 Therefore, these structures are similar to those reported in that work (Scheme 2). Because of strong hydrogen bonding interactions, the transition structure of (PhO)2H• is close to planar with the transferring hydrogen lying in the molecular plane. For (PhCH2)2H•, on the other hand, the transferring hydrogen is perpendicular to the two aromatic rings (Scheme 2), which are parallel to one another. The transition structure for (PhNH)2H• has a geometry intermediate of the arrangements of the other two systems. The computed barriers for hydrogen atom transfer are about 9, 13, and 17 kcal/mol relative to the hydrogen bonding complexes for (PhO)2H• and (PhNH)2 H•, and to the separated species for (PhCH2)2H•, respectively, which are again similar to those by Mayer et al.25 Following approaches used in other studies of proton-coupled electron transfer reactions,26,29,43 a series of BLDFT calculations, also at the B3LYP/6-31G(d) level, were performed along the proton transfer coordinate ΔRp at the transition structure for each system ranging from 0.0 to 0.75 Å. The rational is that heavy atom reorganization is slower than hydrogen transfer. This yields the potential energy surfaces for the four diabatic states in each case. For a given proton coordinate, ΔRp, the adiabatic ground and excited states were determined using these diabatic CSFs. Furthermore, two of the four diabatic CSFs are combined and optimized via configuration interaction to yield the CPET (eqs 9 and 10) and HAT (eqs 7 and 8) effective diabatic states.
Scheme 2.
Illustration of the optimized transition structures for the hydrogen atom transfer reaction of PhX-H···• X – Ph, where X = O, NH, and CH2, using B3LYP/6-31G(d).
Note that the use of B3LYP in the present MSDFT calculations for PCET reactions is different from standard (delocalized) DFT calculations with the B3LYP functional. It is well-known that B3LYP severely underestimates reaction barriers for hydrogen abstraction reactions,72 partially due to the self-interaction error,73 which is greater at the transition state since the reactant and product diabatic states are degenerate. In MSDFT, static correlation effects are partially incorporated in the multiconfigurational approach with VB-like configurations (eqs 1–4). Importantly, dynamic correlation effects are retained in the block-localized DFT treatment of these diabatic states.13 Thus, the use of MSDFT with B3LYP avoids some of the self-interaction errors in that model, but still maintains its excellent treatment of dynamic correlation. Borden and coworkers found that the MPW1K model performs “much better” than B3LYP on PCET reactions.72 Inagaki et al. showed that the enhanced performance correlates with the extent of Hartree-Fock (HF) exchange included in the hybrid functional.43 B3LYP contains 20% HF exchange, whereas 43% HF exchange is included in MPW1K; the latter was specifically optimized to better reproduce hydrogen atom transfer barriers.74 Inagaki et al. further examined the performance of long-range corrected BLYP (LC-BLYP) and a LC plus Coulomb-attenuating method (rCAM-B3LYP). The computed barrier for (PhO)2H• progressively increases with increasing percentage of HF exchange from about 9 (B3LYP) to 16 (MPW1K), and finally to 24 kcal/mol in rCAM-B3LYP calculations. For comparison, CASSCF, which was also used in the work of Hammes-Schiffer and coworkers,26 and MRMP/CASSCF barriers are, respectively, about 40 and 12.5 kcal/mol from the hydrogen-bonded complex.43 The MSDFT barrier is expected to be similar to that from rCAM-B3LYP calculations. Indeed, the computed value is 19.2 kcal/mol from MSDFT/B3LYP calculations.
All calculations are performed using a locally modified version of the GAMESS program.75
4. Results and Discussion
4.1. Diabatic and Adiabatic Potential Energy Profiles
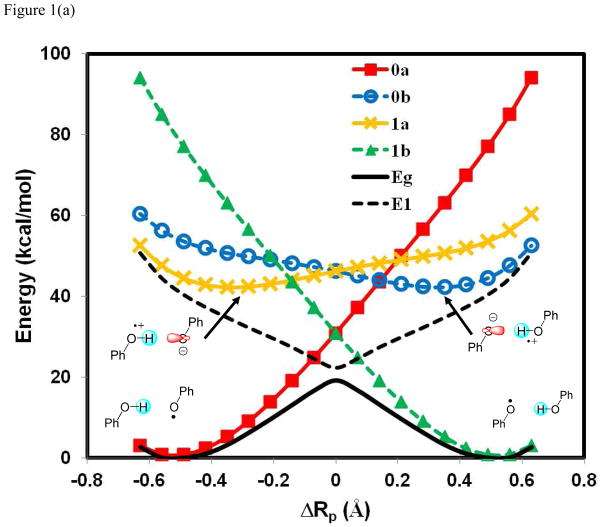
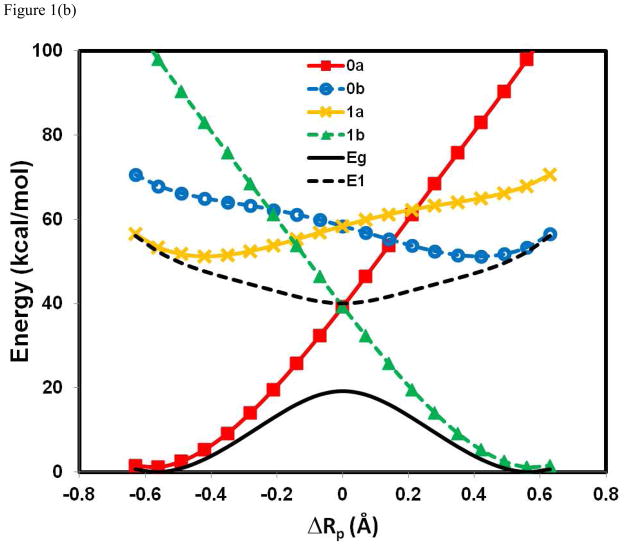
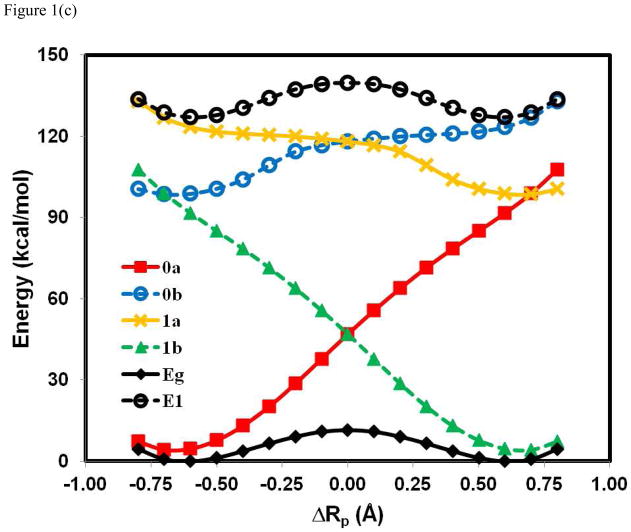
Figure 1 shows the computed potential energy profiles of the four diabatic states as well as the adiabatic ground and the first excited state for the three hydrogen atom exchange reactions in (PhX)2H•, X = O, NH, and CH2, using BLDFT with B3LYP/6-31G(d). It is no exaggeration to say that the present calculations provided the first potential energy surfaces of these diabatic states for a PCET process from first principles using an explicit electronic structure theory (of course, these states have often been described in theoretical works and have been modeled empirically). More seriously, Figure 1 reveals that there is significant electronic coupling among the four diabatic states, resulting in an avoided crossing and stabilization of the adiabatic potential energy surface. The energies of the reactant ( ) and product ( ) diabatic states show similar behaviors with a rapid increase in energy away from the corresponding equilibrium geometries. The main difference is found in the electron transfer states, and , which exhibit greater variations among the three systems. In particular, the energy for is lower than that for at the reactant state configuration in the (PhO)2H• system, but the order is reversed in (PhCH2)2H•. This reversal is mainly due to the difference in electron affinity of the free radical species, which are 52, 39, and 21 kcal/mol for X = O, NH, and CH2, respectively. In all cases, it is clear that a simple two-state model involving only the initial reactant and final product states, and , is not sufficient to model the present coupled transfer of an electron and a proton because the diabatic crossing energy is even above the excited state surface in two of the three systems.
Figure 1.
Computed potential energy profiles for the diabatic states corresponding to the four corners in a More O’Ferrall-Jencks diagram (Scheme 1) for the hydrogen atom transfer reactions in (PhX)2H•), where X = O, NH, and CH2. The proton coordinate, ΔRp, is defined as the relative distance of the transferring hydrogen from the donor and acceptor atoms. The corresponding wave functions for the individual Lewis structures are specified by Ψ0a[Ph – XH··· • X – Ph] (0a) in red, Ψ1a[Ph – XH+• ··· − X – Ph] (1a) in brown, Ψ0b [Ph – X− ··· +• HX – Ph] (0b) in blue, and Ψ1b[Ph – X• ··· HX – Ph] (1b) in green. In addition, the adiabatic ground state (Eg) and the first excited state (E1), which are obtained through configuration interaction using the four valence bond configurations, are given in black as solid and dashed curves, respectively. The reaction between phenoxy radical and phenol is shown in (a), between PhNH• and aniline in (b), and between benzyl radical and toluene in (c). All valence bond configurations are determined using block-localized density functional theory with the B3LYP functionals and 6-31G(d) basis set.
The most striking finding in Figure 1 is the variation of the energy gap between the adiabatic ground and excited states at the crossing point of the diabatic states (ΔRp = 0 Å), changing from a value of 3.0 kcal/mol for PhOH···• OPh, to 20 kcal/mo for PhNH2···• NHPh, and finally to 128 kcal/mol for PhCH3···• CH2Ph. For comparison, the energy gap for PhOH···• OPh from a recent SA-CASSCF(11,10) (MCQDPT) calculation is 4.4 (3.8) kcal/mol, the original study of Mayer et al. reported a value of 3.7 kcal/mo from CASPT2(15,14), in reasonable agreement with the present result. Qualitatively, one may conclude that the hydrogen migration in the phenoxy-phenol system follows an electronically nonadiabatic path, whereas the very large avoided crossing energy at the transition state of the benzyl radical-toluene reaction ensures that the reaction takes place entirely on the adiabatic ground state. This is consistent with the conclusions on the basis of orbital symmetry15,25 and on adiabaticity parameters from analyses of CASSCF(3,6)/6-31G results involving three active electrons.26
The symmetric aniline system in Figure 1b, PhNH2···• NHPh, has not been theoretically investigated. Based on the qualitative trends in Figure 1b, however, it is not straightforward to draw conclusions on its adiabatic or nonadiabatic character, nor the nature of orbital alignments, except that it is a concerted PCET. Thus, additional analysis of the diabatic and adiabatic states are necessary to shed light on its mechanistic character.
4.2. Diagnostic Features of CPET and HAT Mechanisms
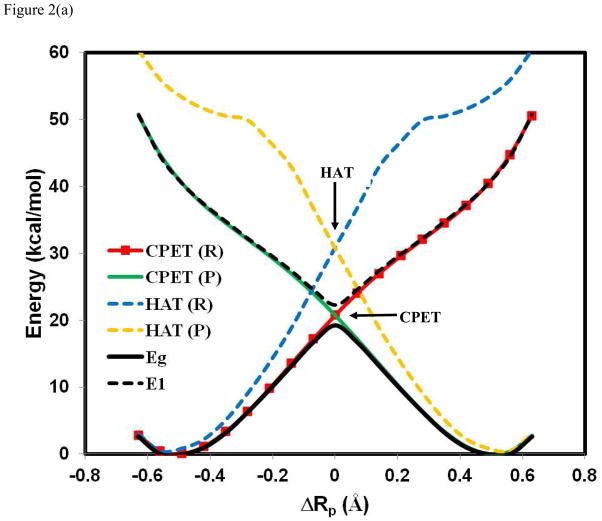
Figure 2 depicts the energy curves of the HAT (eqs 7 and 8) and the CPET (eqs 9 and 10) diabatic states for the three hydrogen exchange reactions, along with the adiabatic ground and excited states already depicted in Figure 1. First, in the reaction of PhOH···• OPh(Figure 2a), the diabatic crossing energy for the CPET reactant and product states is lower than that of the HAT configurations by 10.2 kcal/mol. In fact, the diabatic crossing point for the HAT configurations is above the energy of the adiabatic excited state, suggesting that the coupled transfer of a proton and an electron in the phenoxy radical-phenol system cannot be adequately described by the mixing and avoided crossing of HAT diabatic states because the resonance of the two diabatic configurations will necessarily yield two adiabatic states, one above (out-phase combination) and one below (in-phase combination) the crossing point.44–47 Comparison of the features of the CPET diabatic states and the adiabatic potential energy surfaces in Figure 2a shows that the diabatic and adiabatic surfaces essentially overlap, except near the critical region where nonadiabatic coupling is promoted by an intersection of the CPET diabatic configurations.7,31,44,48–49,76 This demonstrates that the CPET reactions of phenoxy radical and phenol involve both ground and excited state potential energy surfaces, which can be modeled by using the CPET diabatic states.
Figure 2.
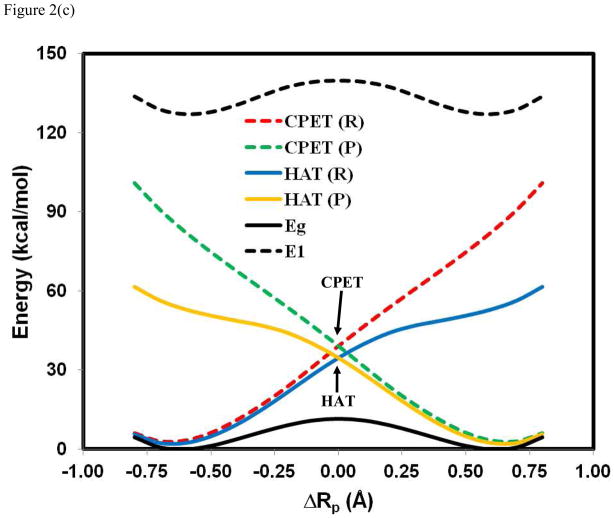
Potential energy surfaces for the effective reactant (R) and product (P) diabatic states corresponding to the hydrogen atom transfer (HAT) and to the proton-coupled electron transfer (PCET) mechanisms. For HAT, the electronic states are adiabatic to the localized proton configurations by definition. Thus, the HAT reactant state, HAT(R) in blue, is a combination of the electronically localized states in Figure 1 with the proton configuration on the donor site, , and the HAT product state, HAT(P) in brown, is given by . For CPET, electron transfer is nonadiabatic, and is assisted by proton transfer. Hence, the CPET reactant state, CPET(R) in read, is a combination of the proton configurations with the donor electronic configuration (see Figure 1), , and the CPET product state, CPET(P) in green, is defined by . The interactions either between the HAT reactant and product diabatic states, or between the CPET reactant and product diabatic states, result in an avoided crossing, and the interaction (either HAT or CPET) that produces curves that matche the adiabatic potential energy surfaces (in black, which is the same as that in Figure 1) for the overall reaction is classified as the reaction mechanism. This often coincides with the mechanism with a lower relative energy at the diabatic crossing points. The reaction between phenoxy radical and phenol is illustrated in (a), between PhNH• and aniline in (b), and the hydrogen abstraction of toluene by benzyl radical in (c).
The effective two-state diabatic and adiabatic potential surfaces for the reaction between toluene and benzyl radical15,25 are displayed in Figure 2c, which exhibits very large coupling to promote a strongly avoided crossing along the entire proton coordinate. The energy gap is 128 kcal/mol at the crossing point, similar to that found for hydrogen transfer reactions involving only σ bonds.33,77 In this case, the hydrogen transfer occurs entirely on the electronically adiabatic potential surface, consistent with previous conclusions.15,25–26,33 Notably, the diabatic crossing energy for the HAT mechanism is lower than that of the PCET process, which loses meaning in such a fully electronically delocalized, adiabatic resonant system. Nevertheless, it indicates that the HAT diabatic states are the lower energy configurations than CPET states for the hydrogen abstraction of toluene by benzyl radical.
The trend in the diabatic and adiabatic potential energy profiles for the reaction of PhNH2 ···• NHPh is intermediate of that of the phenol and toluene systems. In this case, the preference for CPET or HAT mechanisms is not straightforward simply by inspecting the “adiabaticity” or the energy gap of the potential energy surfaces. Figure 2b shows that the energy at the crossing point between the CPET diabatic states (eqs 9 and 10) is lower than that of the HAT states (eqs 7 and 8) by 6.2 kcal/mol, suggesting that the hydrogen atom exchange in PhNH2 ···• NHPh is best described as a CPET process. Clearly, unlike the case of PhOH···• OPh, it is expected that there is significant competition with the over-barrier process in the HAT mechanism (see discussion below).
The electronic coupling energies, VCPET, for the three hydrogen exchange reactions are 1.5, 10, and 23 kcal/mol for (PhX)2H• (X = O, NH, CH2), respectively, which may be compared with the corresponding values of 2.0 and 40.9 kcal/mol for X = O and CH2 determined by Skone et al. using CASSCF(3,6)/6-31G.26 The magnitude of electronic coupling for the aniline system in Figure 1b, PhNH2 ···• NHPh, is on the borderline between an adiabatic and a nonadiabatic process.
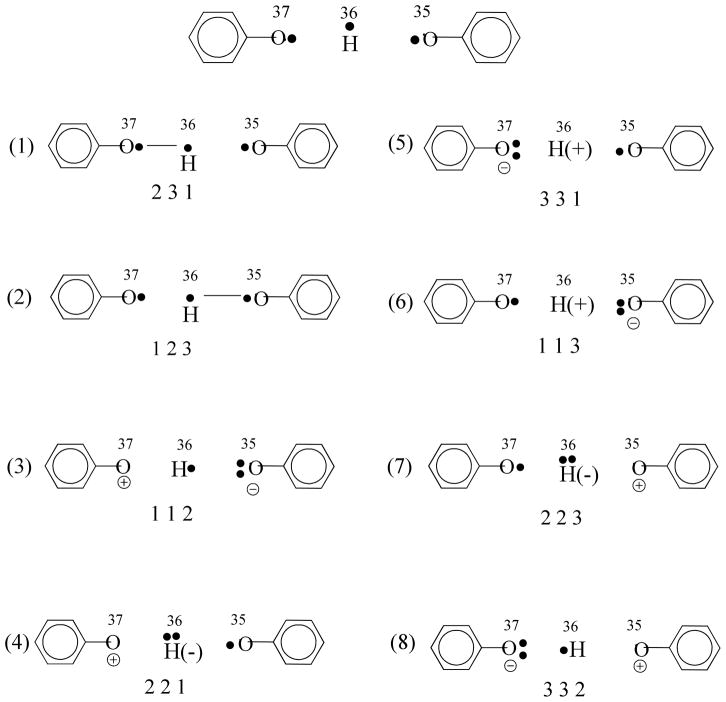
To provide further insight on the nature of VB orbital interactions, we have performed ab initio valence bond self-consistent field (VBSCF) calculations for the PhOH···• OPh system at the transition state.78–80 The main purpose here is to illustrate the connection and difference between MSDFT and ab initio VB theory. The VB space for the coupled proton and electron transfer includes three orbitals and three electrons, which result in a total of eight CSFs depicted in Figure 3. The equivalence between VB configurations and the diabatic states defined in eqs 1–4 can be readily established.39 For example, the BLDFT determinant for the state in which both electron and proton are localized in the donor fragment (eq 1), , corresponds to a linear combination of VB configurations 1,4, and 5 in Figure 3. The product state, (eq 4), results from combination of VB configurations 2, 6, and 7. These are the corresponding Lewis structures. In both cases, four determinants are needed to construct the VB wave function, whereas a single determinant is used in the BLDFT representation. In VBSCF, an electronic coupling of 0.01 kcal/mol (3.7 cm−1) was obtained, much smaller than MSDFT and CASSCF results (the origin of this difference is not clear).
Figure 3.
Illustration of the valence bond configuration state functions used in ab initio VBSCF calculations. The top structure illustrates the three valence bond orbitals (orbital numbers 35, 36 and 37); for convenience, they are labeled as VB orbitals 1, 2 and 3, respectively. The optimized VB orbitals are depicted in Figure 4. The sequence of three numbers under each VB configuration specifies the orbital occupied by an electron. The dash (bond) line between two atoms specifies spin coupling between two electrons, which are listed first in the sequence. For example, in VB configuration (1), the sequence, 231, denotes the determinant wave function of α(2)β(3)α(1)-β(2)α(3)α(1), involving VB orbitals 2, 3 and 1.
Figure 4 illustrates the optimized VB orbitals in the VB wave function both for HAT (Figure 4a) and CPET (Figure 4b) mechanisms. Note that for the HAT state, the optimized orbital on the migrating hydrogen atom is aligned along the vector from the donor to the acceptor atom. On the other hand, in the CPET state, the hydrogen orbital is of π-symmetry as that of the donor and acceptor fragmental orbitals. The qualitative features from VBSCF are in excellent agreement with the analyses of Mayer et al.,25 which were performed on two transition structures for two different reactions. The orbital features associated with the two mechanisms are naturally produced on the same structure for the same reaction – an analysis that can be performed using a localized VB theory, but not possible using delocalized MO or KS-DFT approaches. This is precisely the reason why VB theory can provide insights in understanding PCET reactivity. More importantly, the illustration in Figure 4 demonstrates that the determining factor of a HAT or a CPET mechanism is not simply an orbital alignment of molecular or KS orbitals – they are important and relevant, but not sufficient. The HAT and CPET reactivity is blended, involving the same valence bond (VB) structures, albeit, to different extents, and HAT and CPET compete kinetically to contribute to the overall rate.
Figure 4.
Optimized valence bond orbitals (a) for the HAT diabatic state, and (b) for the PCET diabatic state at the transition state for the hydrogen exchange reaction between phenoxy radical and phenol. Although the same basis orbitals are used, the resulting VB orbitals are different for different mechanisms because of the constraint of selecting different VB configurations (Figure 3) to define HAT or CPET mechanisms (see text for the corresponding definition). Here, we establish that these constraints in VBSCF are equivalent to the definition in MSDFT by eqs 7–10, although the former utilizes multi-determinants for each diabatic state, and the latter makes use of a computationally more efficient, single-determinant approximation. In both mechanisms, orbitals 1 and 3 are dominantly localized on the two phenoxy fragments, respectively, whereas for the HAT mechanism (a), orbital 2 for the migrating hydrogen is aligned along the vector between the donor and acceptor oxygen atoms, and for the CPET mechanism (b), the hydrogen orbital is perpendicular to that vector. Note that the local VB orbitals cannot be directly compared with the delocalized molecular orbitals. It is also interesting to point out that one can specifically define HAT or CPET orbitals by making different combinations of the VB configurations in Figure3 in VBSCF, as also done in MSDFT by eqs 7–10. This is not possible in delocalized molecular orbital or density functional calculations.
4.3. Comparison with Shaik’s VBSCD Approach
It has brought to our attention that two articles on a valence-bond view of hydrogen transfer reactions have been published at about the time when this article was submitted to this journal. Those studies provided an informative perspective on HAT and CPET reactions using valence bond state correlation diagram (VBSCD) that was introduced by Shaik45–46 and has been extensively used on a broad range of chemical and biological reactions.46,81–83 Consequently, we make a comparison of the key features between that work and the present MSDFT study.
The VBSCD approach as applied to HAT and CPET reactions is summarized in Figure 5, following closely the nomenclature and discussion of the original figures in refs 48 and 49. Figure 5 contains two sets of VB-state curves, corresponding to the “normal HAT” process in solid curves, and to a proton transfer (by mixing the two PT curves) in dashed curves.48–49 The four low-energy structures, two on the reactant (R) side (ΨHAT,R and ΨPT,R) and two on the product (P) side (ΨHAT,P and ΨPT,P), are formally the same VB diabatic configurations depicted in the More O’Ferral-Jencks diagram (Scheme 1), and the VB-state curves shown in Figure 1. The VB energy curves presented in refs 48 and 49 were drawn qualitatively based on the energies at the extreme (R and P) points. The common connection to Scheme 1 suggests that MSDFT in this work can be used to quantify the state energies in VBSCD.
Figure 5.
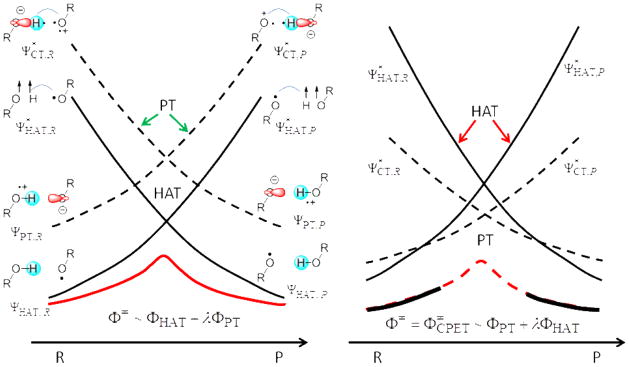
VBSCDs describing the dichotomy of HAT and PCET processes by mixing normal HAT valence bond states (solid curves) and proton transfer (PT) curves (dashed curves) along the reaction coordinate. (a) represents a case where the PT states lie higher than the HAT state. The wave function of the transition state (Φ≠) has a dominant HAT character with a secondary PT component (λ <1). The wave function for HAT is generated by mixing the two HAT diabatic configurations (ΦHAT =aRΨHAT,R + aPΨHAT,P), and that for PT by mixing the PT states (ΦPT = bRΨPT,R + bPΨPT,P). (b) illustrates a case where the PT curves are low-lying and descend below the HAT crossing point. The transition state is now a PCET-type with a predominant PT character and a secondary HAT contribution (λ <1). This figure was redrawn to match the present discussion based on figure 6 of ref 49.
In VBSCD, the HAT product VB-configuration at the reactant geometry is called the promoted state, labeled as (also called image state, excited state, or prepared state), of the HAT reactant, which features triplet decoupling of the O-H bond electrons and repairing of the electron on H• with the electron on the acceptor oxygen atom; a similar product promoted state is denoted. The relative energies of the promoted states can be related to bond dissociation energies and radical structural reorganization energies, etc.44,48–49 The promoted states for the PT curves are called charge transfer (CT) states, so labeled in Figure 5 as in the original papers.48–49 For example, the promoted state of the PT curve for the R state (ΨPT,R) is denoted by , which is equivalent to the P diabatic state of the PT curve (ΨPT,P) at the R geometry in MSDFT. We simply call these VB states diabatic and adiabatic states with an aim for rate calculations using Marcus theory approach.51,57 Note that the PT process of the “CT” states from ΨPT,R to ΨPT,P (Figure 5) is in fact accompanied by an electron transfer in the opposite direction; thereby, the overall process may be called an anti-PCET process.
The conceptual advance in understanding HAT and CPET mechanisms from VBSCD analyses is depicted in Figure 5. Figure 5a presents a case where the CT states lie higher than the HAT states, thereby, “the wave function of the transition state has a dominant HAT character with a secondary PT character”.48–49 On the other hand, Figure 5b shows a scenario where the CT curves descend below the crossing point of the HAT curves. Consequently, the transition state is now a CPET-type with a predominant PT character and a secondary HAT contribution.48–49 Since the ground states at the reactant and product geometries are still dominated by the HAT states, the result of VB mixing is a CPET transition state for a net HAT reaction. Therefore, according to VBSCD theory of refs 48 and 49, the relative heights of the HAT and PT crossing points determines the transition state character.
In principle, the VB characterization of proton-coupled electron transfer is conceptually the same from VBSCD and MSDFT theories,44–46 but there are also important differences. In MSDFT, each of the diabatic HAT state curves is electronically adiabatic, where the proton is associated with either the donor or the acceptor Lewis structures. Therefore, the HAT states are admixtures of the ET states (eqs 7 and 8, red and green curves in Figure 2). We do not invoke the type of PT process described in refs 48 and 49 (see Figure 5), although such a PT reaction can be studied with MSDFT with these four basic VB states. In MSDFT, the PCET state curves (not necessarily CPET) are represented as ET diabatic configurations assisted by PT (eqs 9 and 10, brown and blue curves in Figure 2). The mixing and avoided crossing of the two HAT states, and of the two PCET states, although both include the contributions from all four basic diabatic configurations in Figure 1, generate the adiabatic ground state for the HAT, and for the CPET pathway, respectively. The adiabatic ground state surface from one of the two mechanisms that matches the adiabatic ground state obtained from all four independent states (Figure 1) is recognized as the mechanism with a greater contribution to the net hydrogen atom transfer, and thus, simply characterized as the reaction mechanism. Often, a simple, straightforward indicator is the relative energies at the crossing points of the HAT and CPET state curves, with the lower curve best representing the reaction mechanism from a VB state interaction perspective.
For the phenoxy-phenol system, the rule of diabatic crossing (RDC) predicts that the mechanism follows predominantly a CPET processes since the energy of the CPET crossing point is lower than that of the HAT one. However, when the MSDFT energies are used, the corresponding PT curves in VBSCD analysis are above the HAT curves (Figure 2). Thus, it would have been a HAT according to that analysis. For benzyl-toluene, both methods correctly predict that the net hydrogen atom abstraction is a HAT.
Clearly, there is no strict division between HAT and CPET and they are not kinetically distinguishable; the overall rate is a sum of the two processes, where some reactions may have greater HAT contribution while others less. As pointed out by Shaik and coworkers, since ET states are the basis configurations for the PCET process, “unlike HAT, the PCET reaction is expected to be sensitive to solvation”.48 MSDFT provides a procedure to estimate the reaction rates both for HAT and for CPET processes,51,57 the sum of which can be compared with experimental kinetic data.
The VBSCD and MSDFT approaches to PCET reactions have many similarities, both making use of diabatic crossing energies as a simple rule-of-thumb, RDC, criterion to understand the mechanistic character for these processes. The VB state curves from MSDFT can be considered as a VBSCD diagram.
4.4. Origin of CPET and HAT Mechanisms
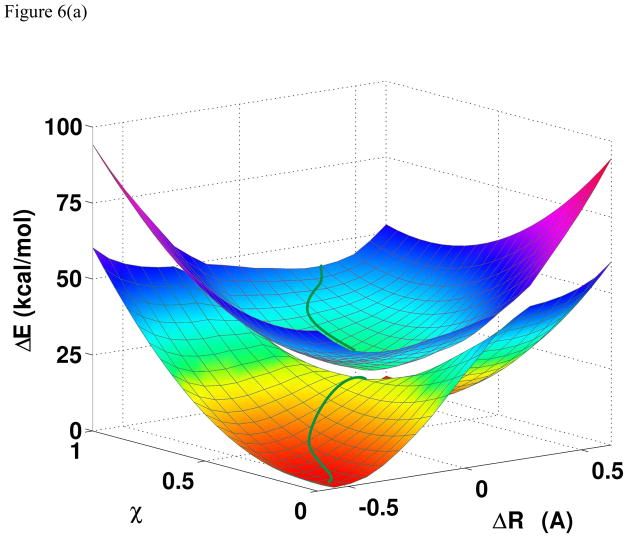
The origin of the nonadibatic CPET mechanism and the adiabatic HAT reaction are revealed in Figures 6–8, in which the two-dimensional More O’Ferrall-Jencks plots have been extended to three dimensions, including both the ground and excited state PES. This is significant because the extension highlights the difference between the two concerted mechanisms, both following the diagonal path in Scheme 1. Figure 6a illustrates the PES for the adiabatic ground and excited states of the PhOH···• OPh reaction, and PT and ET processes are fully concerted in the ground state potential surface with a net hydrogen atom transfer. A striking finding is that the separation between the ground and excited state surfaces are close in energy along a seam in the direction nearly orthogonal to the minimum energy path on the adiabatic ground state. The topographical features of the adiabatic ground and excited state surfaces in Figure 5a suggest a conical intersection seam can be located by a slight distortion in the molecular geometry. The involvement of both the adiabatic ground and excited state PES, through conical intersection seam, provides an important insight on the CPET mechanism as also described by Tishchenko et al.33 Interestingly, there is significant mixing between the proton-localized diabatic states for each electronic configuration (eqs 9 and 10), but the interaction between the two electronic configurations is small. As a result, the CPET diabatic states defined in eqs 9 and 10 are more stabilized (lower in energy) than the HAT diabatic states (eqs 7 and 8).
Figure 6.
(a). Computed two-dimensional potential energy surfaces for the adiabatic ground state and the first excited state as a function of the proton transfer (ΔRp) and the electron transfer (χ) coordinates for the proton and electron transfer between phenol and phenoxy radical. (b). Minimum energy paths of the adiabatic ground state (green) and the excited state (red) overlaid on the isoenergy contours for the ground state. Multistate density functional theory is used in all calculations with the B3LYP functional along with the 6-31G(d) basis set.
Figure 8.
Computed two-dimensional potential energy surfaces for the adiabatic ground state and the first excited state as a function of the proton transfer (ΔRp) and the electron transfer (χ) coordinates for the hydrogen abstraction of toluene by benzyl radical. Multistate density functional theory is used in all calculations with the B3LYP functional along with the 6-31G(d) basis set.
We found that the minimum energy paths on the ground and the first excited state surfaces are roughly orthogonal in the critical region for the reaction in the PhOH···• OPh system (Figure 6b). As a result, the minimum energy path on the excited state surface and the ridge separating the reactant and product states of the ground state follow the same coordinates, resulting in a low energy conical interaction seam accessible through thermal motions. The implication is that although vibronic overlap can be an important factor in rate computation, the availability of thermally accessible conical intersections provides an alternative prediction for the rate of CPET reactions. In contrast, the hydrogen abstraction reaction between toluene and benzyl radical has significant overlay among the VB diabatic states, in which electronic configuration mixing dominates the entire process (Figure 8). Thus, the large electronic resonance between the electronic diabatic states promotes a strongly avoided intersection, resulting in a large energy gap between the adiabatic ground and excited states. For the HAT reaction of PhCH2H···• CH2Ph, the minimum energy path on the adiabatic ground surface essentially coincides with that on the excited state. In such a fully adiabatic process, separation of the electron transfer coordinate from the proton transfer coordinate loses meaning. Consequently, a single reaction coordinate is sufficient to represent the HAT reaction.
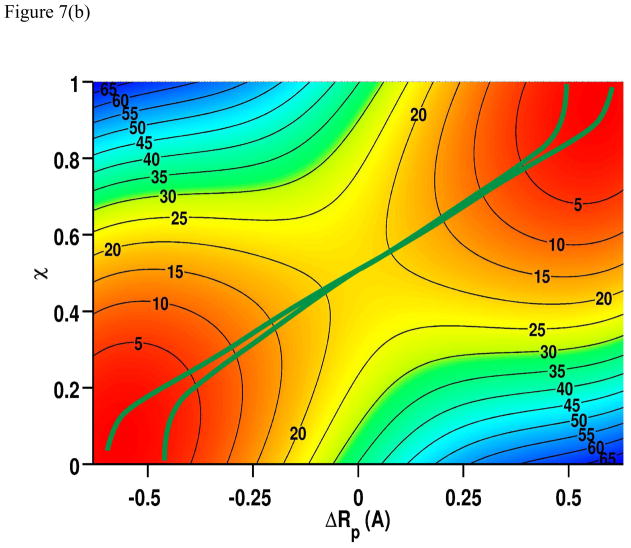
The topographic features of the adiabatic ground and excited state surfaces for the PhNHH···• NHPh reaction are intermediate of CPET in PhOH···• OPh and HAT in PhCH2H···•CH2Ph. There is clear separation between the adiabatic ground and excited state surfaces along the ET and PT coordinates (Figure 7a), yet the energy gap is far smaller than that for the hydrogen abstraction of toluene by benzyl radical. The minimum energy paths on the adiabatic ground and excited states are now oriented with significant overlap (Figure 7b). Thus, PhNH2 and •NHPh represents a reaction that is on the borderline of CPET and HAT mechanisms.
Figure 7.
(a). Computed two-dimensional potential energy surfaces for the adiabatic ground state and the first excited state as a function of the proton transfer (ΔRp) and the electron transfer (χ) coordinates for the proton and electron transfer between aniline and PhNH• radical. (b). Minimum energy paths of the adiabatic ground state (green) and the excited state (red) overlaid on the isoenergy contours for the ground state. Multistate density functional theory is used in all calculations with the B3LYP functional along with the 6-31G(d) basis set.
5. Summary
We have described a constrained density functional theory through block-localization of Kohn-Sham orbitals to determine the electron- and proton-localized diabatic states associated with the coupled proton and electron transfer or hydrogen atom transfer reactions in the isoelectronic series of (PhX)2H•, where X = O, NH, and CH2. Then, these valence bond-like diabatic states are used in configuration interaction to yield the potential energy surfaces for the adiabatic ground and excited states. To distinguish the mechanistic difference between concerted proton-electron transfer (CPET) and hydrogen atom transfer (HAT), we formulated a pair of effective two-state VB models, respectively, by combining the proton-localized configurations at fixed electronic diabatic states, or by combining the electronic diabatic states for given proton configurations.
Using multistate density functional theory, we found that the relative energies at the intersection of the CPET and HAT diabatic states, i.e., the rule of diabatic crossing (RDC), can be used as an energetic criterion to classify the two reaction mechanisms. Thus, if the energy at the crossing point for the CPET diabatic states is lower than that for the HAT diabatic states, the reaction mechanism is considered to have a greater concerted proton-electron transfer character. Conversely, if the energy at the crossing point of the HAT diabatic states is lower than that of CPET states, the HAT mechanism is a preferred process. A similar analysis has been reported by Shaik and coworkers based on valence bond state correlation diagrams, although different criteria are used. For the extreme cases, the results from VB-based approaches are consistent with proposals using electronic adiabaticity. It is emphasized that there is no strict division of the HAT and CPET mechanisms for a given reaction and they are not distinguishable based solely on phenomenological kinetic parameters; both contribute and the overall rate is the sum of that of the individual processes. The diabatic states and potential energy surfaces defined for HAT and PCET processes from first principles calculations can be used to determine these rate constants.
The origin of relatively small electronic coupling in the CPET-dominated mechanism of the phenolic system is revealed in a More O’Ferrall-Jencks diagram extended to the third dimension that includes both the ground and excited potential energy surfaces. Although electron transfer and proton transfer are concerted both for CPET and HAT (thus, not distinguishable with the classical picture of a 2-D More O’Ferrall-Jencks plot), the mechanistic difference is distinguished by the presence of a low-energy conical intersection seam in the direction perpendicular to the minimum energy path on the adiabatic ground state. This results in minimal overlap interaction between the electronic diabatic states and weak electronic coupling. On the other hand, the minimum energy path of the adiabatic ground state for the HAT mechanism in the benzyl-toluene system coincides with that on the excited state resulting in a large electronic coupling that separates the two surfaces by more than 5 eV (~130 kcal/mol). The topographic features for the PhNHH···• NHPh system are found between those for the CPET reaction of phenoxy radical and phenol and for the HAT mechanism of benzyl radical and toluene. The minimum energy paths on the adiabatic ground and excited states are oriented with significant overlap. In this case, it is predicted that both HAT and CPET processes compete and the dominating contribution may be tuned with varying solvent polarity and hydrogen bonding abilities since HAT and CPET have different ionic characters and different sensitivities to solvent effects.
Acknowledgments
This work has been partially supported by the National Science Foundation (CHE09-57162) and the National Institutes of Health (GM46736).
Contributor Information
Wei Wu, Email: weiwu@xmu.edu.cn.
Jiali Gao, Email: gao@jialigao.org.
References
- 1.Stubbe J, Nocera DG, Yee CS, Chang MCY. Chem Rev. 2003;103:2167. doi: 10.1021/cr020421u. [DOI] [PubMed] [Google Scholar]
- 2.Mayer JM. Ann Rev Phys Chem. 2004;55:363. doi: 10.1146/annurev.physchem.55.091602.094446. [DOI] [PubMed] [Google Scholar]
- 3.Warren JJ, Tronic TA, Mayer JM. Chem Rev. 2010;110:6961. doi: 10.1021/cr100085k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Magnuson A, Anderlund M, Johansson O, Lindblad P, Lomoth R, Polivka T, Ott S, Stensjo K, Styring S, Sundstrom V, Hammarstrom L. Acc Chem Res. 2009;42:1899. doi: 10.1021/ar900127h. [DOI] [PubMed] [Google Scholar]
- 5.Hammarstrom L, Styring S. Energy Envir Sci. 2011;4:2379. [Google Scholar]
- 6.Costentin C, Robert M, Saveant JM. Acc Chem Res. 2010;43:1019. doi: 10.1021/ar9002812. [DOI] [PubMed] [Google Scholar]
- 7.Cukier RI, Nocera DG. Ann Rev Phys Chem. 1998;49:337. doi: 10.1146/annurev.physchem.49.1.337. [DOI] [PubMed] [Google Scholar]
- 8.Reece SY, Nocera DG. Ann Rev Biochem. 2009;78:673. doi: 10.1146/annurev.biochem.78.080207.092132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hammes-Schiffer S. Acc Chem Res. 2009;42:1881. doi: 10.1021/ar9001284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Siegbahn PEM, Blomberg MRA. Chem Rev. 2010;110:7040. doi: 10.1021/cr100070p. [DOI] [PubMed] [Google Scholar]
- 11.Mayer JM. Acc Chem Res. 2011;44:36. doi: 10.1021/ar100093z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cembran A, Song L, Mo Y, Gao J. J Chem Theory Comput. 2009;5:2702. doi: 10.1021/ct9002898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mo YR, Bao P, Gao JL. Phys Chem Chem Phys. 2011;13:6760. doi: 10.1039/c0cp02206c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Litwinienko G, Ingold KU. J Org Chem. 2004;69:5888. doi: 10.1021/jo049254j. [DOI] [PubMed] [Google Scholar]
- 15.Litwinienko G, Ingold KU. Acc Chem Res. 2007;40:222. doi: 10.1021/ar0682029. [DOI] [PubMed] [Google Scholar]
- 16.MacLean PD, Chapman EE, Dobrowolski SL, Thompson A, Barclay LRC. J Org Chem. 2008;73:6623. doi: 10.1021/jo8005073. [DOI] [PubMed] [Google Scholar]
- 17.Horner G, Lewandowska A, Hug GL, Marciniak B. J Phys Chem C. 2009;113:11695. [Google Scholar]
- 18.Foti MC. Int J Chem Kinet. 2012;44:524. [Google Scholar]
- 19.Warren JJ, Mayer JM. In: Proton-Coupled Electron Transfer: A Carrefour of Chemical Reactivity Traditions. Formosinho S, Barroso M, editors. The Royal Society of Chemistry; Cambridge: 2012. p. 1. [Google Scholar]
- 20.Sajenko I, Pilepic V, Brala CJ, Ursic S. J Phys Chem A. 2010;114:3423. doi: 10.1021/jp911086n. [DOI] [PubMed] [Google Scholar]
- 21.Warren JJ, Mayer JM. J Am Chem Soc. 2010;132:7784. doi: 10.1021/ja102337n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Warren JJ, Mayer JM. Proc Nat Acad Sci. 2010;107:5282. doi: 10.1073/pnas.0910347107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mayer JM. Acc Chem Res. 2011;44:36. doi: 10.1021/ar100093z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mayer JM. J Phys Chem Lett. 2011;2:1481. doi: 10.1021/jz200021y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mayer JM, Hrovat DA, Thomas JL, Borden WT. J Am Chem Soc. 2002;124:11142. doi: 10.1021/ja012732c. [DOI] [PubMed] [Google Scholar]
- 26.Skone JH, Soudackov AV, Hammes-Schiffer S. J Am Chem Soc. 2006;128:16655. doi: 10.1021/ja0656548. [DOI] [PubMed] [Google Scholar]
- 27.Cukier RI. J Phys Chem. 1994;98:2377. [Google Scholar]
- 28.Cukier RI. J Phys Chem. 1996;100:15428. [Google Scholar]
- 29.Hammes-Schiffer S, Stuchebrukhov AA. Chem Rev. 2010;110:6939. doi: 10.1021/cr1001436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hammes-Schiffer S. J Phys Chem Lett. 2011;2:1410. doi: 10.1021/jz101532g. [DOI] [PubMed] [Google Scholar]
- 31.Soudackov A, Hammes-Schiffer S. J Am Chem Soc. 1999;121:10598. [Google Scholar]
- 32.Stuchebrukhov A. J Theor Comput Chem. 2003;2:91. [Google Scholar]
- 33.Tishchenko O, Truhlar DG, Ceulemans A, Nguyen MT. J Am Chem Soc. 2008;130:7000. doi: 10.1021/ja7102907. [DOI] [PubMed] [Google Scholar]
- 34.Costentin C, Robert M, Saveant JM. Phys Chem Chem Phys. 2010;12:11179. doi: 10.1039/c0cp00063a. [DOI] [PubMed] [Google Scholar]
- 35.Marcus RA. J Phys Chem B. 2007;111:6643. doi: 10.1021/jp071589s. [DOI] [PubMed] [Google Scholar]
- 36.More O’Ferrall RA. J Chem Soc B. 1970:274. [Google Scholar]
- 37.Jencks WP. Chem Rev. 1972;72:705. [Google Scholar]
- 38.Hammes-Schiffer S. Acc Chem Res. 2001;34:273. doi: 10.1021/ar9901117. [DOI] [PubMed] [Google Scholar]
- 39.Song L, Gao J. J Phys Chem A. 2008;112:12925. doi: 10.1021/jp803050e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Markle TF, Tenderholt AL, Mayer JM. J Phys Chem B. 2012;116:571. doi: 10.1021/jp2091736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.DiLabio GA, Johnson ER. J Am Chem Soc. 2007;129:6199. doi: 10.1021/ja068090g. [DOI] [PubMed] [Google Scholar]
- 42.Costentin C, Robert M, Saveant JM. J Am Chem Soc. 2010;132:2845. doi: 10.1021/ja103421f. [DOI] [PubMed] [Google Scholar]
- 43.Inagaki T, Yamamoto T, Kato S. J Comput Chem. 2011;32:3081. doi: 10.1002/jcc.21892. [DOI] [PubMed] [Google Scholar]
- 44.Shaik S, Hiberty PC. A Chemist’s Guide to Valence Bond Theory. John Wiley & Sons, Inc; Hoboken, New Jersey: 2008. [Google Scholar]
- 45.Shaik SS. J Am Chem Soc. 1981;103:3692. [Google Scholar]
- 46.Shaik S, Shurki A. Angew Chem, Int Ed. 1999;38:587. doi: 10.1002/(SICI)1521-3773(19990301)38:5<586::AID-ANIE586>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- 47.Shaik S, Hiberty PC. Rev Comput Chem. 2004;20:1. [Google Scholar]
- 48.Li CS, Danovich D, Shaik S. Chem Sci. 2012;3:1903. [Google Scholar]
- 49.Lai WZ, Li CS, Chen H, Shaik S. Angew Chem Int Ed. 2012;51:5556. doi: 10.1002/anie.201108398. [DOI] [PubMed] [Google Scholar]
- 50.Gao J, Cembran A, Mo Y. J Chem Theory Comput. 2010;6:2402. doi: 10.1021/ct100292g. [DOI] [PubMed] [Google Scholar]
- 51.Mo Y, Gao J. J Comput Chem. 2000;21:1458. [Google Scholar]
- 52.Mo Y, Song L, Lin Y. J Phys Chem A. 2007;111:8291. doi: 10.1021/jp0724065. [DOI] [PubMed] [Google Scholar]
- 53.Valero R, Song L, Gao J, Truhlar DG. J Chem Theory Comput. 2008;4 doi: 10.1021/ct9002459. ASAP. [DOI] [PubMed] [Google Scholar]
- 54.Leininger T, Stoll H, Werner HJ, Savin A. Chem Phys Lett. 1997;275:151. [Google Scholar]
- 55.Ukai T, Nakata K, Yamanaka S, Takada T, Yamaguchi K. Mol Phys. 2007;105:2667. [Google Scholar]
- 56.Kurzweil Y, Lawler KV, Head-Gordon M. Mol Phys. 2009;107:2103. [Google Scholar]
- 57.Mo Y, Gao J. J Phys Chem A. 2000;104:3012. [Google Scholar]
- 58.Dederichs PH, Bluegel S, Zeller R, Akai H. Phys Rev Lett. 1984;53:2512. doi: 10.1103/PhysRevLett.56.2407. [DOI] [PubMed] [Google Scholar]
- 59.Kaduk B, Kowalczyk T, Van Voorhis T. Chem Rev. 2012;112:321. doi: 10.1021/cr200148b. [DOI] [PubMed] [Google Scholar]
- 60.Wu Q, Van Voorhis T. J Chem Phys. 2006;125:164105. doi: 10.1063/1.2360263. [DOI] [PubMed] [Google Scholar]
- 61.Wu Q, Cheng CL, Van Voorhis T. J Chem Phys. 2007;127:164119. doi: 10.1063/1.2800022. [DOI] [PubMed] [Google Scholar]
- 62.Wu Q, Kaduk B, Van Voorhis T. J Chem Phys. 2009;130:034109. doi: 10.1063/1.3059784. [DOI] [PubMed] [Google Scholar]
- 63.Difley S, Van Voorhis T. J Chem Theory Comput. 2011;7:594. doi: 10.1021/ct100508y. [DOI] [PubMed] [Google Scholar]
- 64.Cukier RI. J Phys Chem B. 2002;106:1746. [Google Scholar]
- 65.Gao J, Truhlar DG. Ann Rev Phys Chem. 2002;53:467. doi: 10.1146/annurev.physchem.53.091301.150114. [DOI] [PubMed] [Google Scholar]
- 66.Pu J, Gao J, Truhlar DG. Chem Rev. 2006;106:3140. doi: 10.1021/cr050308e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Major DT, Gao J. J Chem Theory Comput. 2007;3:949. doi: 10.1021/ct600371k. [DOI] [PubMed] [Google Scholar]
- 68.Chirgwin HB, Coulson CA. Proc R Soc London Ser A. 1950;2:196. [Google Scholar]
- 69.Coulson CA, Danielson U. Arkiv Fysik. 1954;8:245. [Google Scholar]
- 70.Becke AD. J Chem Phys. 1993;98:5648. [Google Scholar]
- 71.Lee C, Yang W, Parr RG. Phys Rev B. 1988;37:785. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 72.Lingwood M, Hammond JR, Hrovat DA, Mayer JM, Borden WT. J Chem Theory Comput. 2006;2:740. doi: 10.1021/ct050282z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Cohen AJ, Mori-Sanchez P, Yang W. Science. 2008;321:792. doi: 10.1126/science.1158722. [DOI] [PubMed] [Google Scholar]
- 74.Lynch BJ, Fast PL, Harris M, Truhlar DG. J Phys Chem A. 2000;104:4811. [Google Scholar]
- 75.Schmidt MW, Baldridge KK, Boatz JA, Elbert ST, Gordon MS, Jensen JH, Koseki S, Matsunaga N, Nguyen KA, Su SJ, Windus TL, Dupuis M, Montgomery JS. J Comput Chem. 1993;14:1347. [Google Scholar]
- 76.Kirby JP, Roberts JA, Nocera DG. J Am Chem Soc. 1997;119:9230. [Google Scholar]
- 77.Porter RN, Stevens RM, Karplus M. J Chem Phys. 1968;49:5163. [Google Scholar]
- 78.Shaik S, Wu W, Dong K, Song L, Hiberty PC. J Phys Chem A. 2001;105:8226. [Google Scholar]
- 79.Song L, Mo Y, Zhang Q, Wu W. J Comput Chem. 2005;26:514. doi: 10.1002/jcc.20187. [DOI] [PubMed] [Google Scholar]
- 80.Song L, Song J, Mo Y, Wu W. J Comput Chem. 2009;30:399. doi: 10.1002/jcc.21065. [DOI] [PubMed] [Google Scholar]
- 81.Shaik SS, Schlegel HB, Wolfe S. Theoretical Aspects of Physical Organic Chemsitry: The SN2 Mechanism. Wiley; New York: 1992. [Google Scholar]
- 82.Shaik S, Kumar D, de Visser SP, Altun A, Thiel W. Chem Rev. 2005;105:2279. doi: 10.1021/cr030722j. [DOI] [PubMed] [Google Scholar]
- 83.Wu W, Su PF, Shaik S, Hiberty PC. Chem Rev. 2011;111:7557. doi: 10.1021/cr100228r. [DOI] [PubMed] [Google Scholar]