Simultaneous evaluation of the harms and benefits of treatments in randomized clinical trials: demonstration of a new approach

Abstract

Background

One aim of personalized medicine is to determine which treatment is to be preferred for an individual patient, given all patient information available. Particularly in mental health, however, there is a lack of a single objective, reliable measure of outcome that is sensitive to crucial individual differences among patients.

Method

We examined the feasibility of quantifying the total clinical value provided by a treatment (measured by both harms and benefits) in a single metric. An expert panel was asked to compare 100 pairs of patients, one from each treatment group, who had participated in a randomized clinical trial (RCT) involving interpersonal psychotherapy (IPT) and escitalopram, selecting the patient with the preferred outcome considering both benefits and harms.

Results

From these results, an integrated preference score (IPS) was derived, such that the differences between any two patients’ IPSs would predict the clinicians’ preferences. This IPS was then computed for all patients in the RCT. A second set of 100 pairs was rated by the panel. Their preferences were highly correlated with the IPS differences (r=0.84). Finally, the IPS was used as the outcome measure comparing IPT and escitalopram. The 95% confidence interval (CI) for the effect size comparing treatments indicated clinical equivalence of the treatments.

Conclusions

A metric that combines benefits and harms of treatments could increase the value of RCTs by making clearer which treatments are preferable and, ultimately, for whom. Such methods result in more precise estimation of effect sizes, without increasing the required sample size.

Introduction

The concept of personalized medicine has two separate but related interpretations: to the basic scientist, it means identification of the biomarkers associated with differential responses to treatments so as to better understand the etiology of the disorder or to develop new drugs to target those biomarkers. To the clinician and patient, it means identifying the best treatment for individual patients using the patient’s characteristics, the focus of this report. Despite the enthusiasm for the concept of personalized treatment, its implementation represents a substantial challenge, particularly in the area of mental health treatment. A major part of the difficulty stems from the absence of a single direct, objective, reliable measure of outcome (such as survival time in cancer) sensitive to the crucial individual differences among patients that mental health treatments target. Instead, multiples outcomes (e.g. symptom reduction, relapse protection, change in underlying mechanisms, side-effect burden, quality of life, functional status, patient satisfaction) are evaluated separately.

Despite recent advances in the design and conduct of clinical trials, statistical significance (p values) is still overemphasized and effect sizes not consistently reported. Moreover, when effect sizes are presented, the current standard practice is to evaluate outcomes on multiple measures, each considered separately. In approaching outcomes in this manner, as multiple testing proliferates false-positive results, researchers are required to adjust the p value for multiple testing, which, in turn, reduces the power to detect treatment differences, thus proliferating false negatives. When researchers adjust for multiple testing and increase the sample size to control both types of errors, multiple different answers to the question of interest result, increasing the confusion regarding which treatment is preferable. Thus, to begin, we emphasize measures of clinical significance over measures of statistical significance (Kraemer & Kupfer, 2006; Kraemer & Frank, 2010; Kraemer et al. 2011).

We have also argued (Kraemer & Frank, 2010) that to move the pursuit of personalized medicine forward, it is important that treatment evaluation is based not on the examination of the statistical effects of treatments on scores from multiple separate response measures but rather on the clinical effect of treatments for individual patients who experience the joint impact of those multiple measures. If some method could be found to capture the totality of a treatment’s clinical impact on patients, it would significantly advance the ability of clinicians to recommend a specific treatment to a particular individual, considering all of a patient’s relevant facts (Kraemer & Frank, 2010). There are several possible methodological approaches (Kraemer et al. 2011), but here we demonstrate one such method, implemented by creating a metric that reflects clinicians’ decision making when considering both harms and benefits, and demonstrate its use and value by a re-evaluation of the outcomes of a clinical trial for the treatment of depression.

We used data gathered from a randomized clinical trial (RCT) examining two treatment strategies for unipolar depression, one beginning with interpersonal psychotherapy (IPT) and the other with escitalopram (MH065376, E. Frank, PI). Our first aim was to generate a metric that combines benefits and harms of each treatment for each participant. We then demonstrate how this metric can be used as an outcome measure directly relevant to clinical decision making. Finally, we evaluate the response to the treatments using this new metric to show the advantages of using such a metric in RCTs.

Method

The RCT

The data used in this study came from a completed RCT, the methods of which have been described elsewhere (Frank et al. 2011). In brief, the sample consisted of 291 out-patients in a DSM-IV-defined episode of unipolar major depression as determined by the SCID (APA, 2000), with a minimum score of 15 on the 17-item Hamilton Depression Rating Scale (HAMD-17; Hamilton, 1960). In the study, patients were randomly allocated to one of two treatment strategies, one beginning with IPT (Klerman et al. 1984) and the other with pharmacotherapy (escitalopram). Study participants who had not responded by 6 weeks or remitted by 12 weeks were given the combination of IPT and escitalopram. A total of 142 participants were allocated to initial pharmacotherapy, and 149 to initial psychotherapy. The crucial value of the effect size used in power computations for the RCT corresponded to a success rate difference (SRD) (Kraemer & Kupfer, 2006) of 0.28 [a standardized mean difference of 0.5 or the number needed to treat (NNT) equal to 4]. Thus, it was stipulated a priori (Kraemer & Thiemann, 1987; Cohen, 1988) that effect sizes corresponding to SRD >0.28 would be considered of clinical significance; effect sizes corresponding to SRD<0.28 would be indicative of clinical equivalence of treatments.

Patient summaries

We developed a clinical summary profile for each participant from the original RCT. Pairs of such profiles, one from each treatment group, were presented to each member of a panel of expert judges, ‘blinded’ to participants’ treatment assignments, and each judge was asked (independently) to select which of each pair had, in his or her view, a clinically preferable response, with ties permitted.

Expert panel participants

The expert panel consisted of three males and four females with varied experiences related to the treatment of depression, and representative of the various types of clinical viewpoints. The panel included two psychiatrists, a social worker, a psychiatric nurse, an individual with lived experience of depression, a patient advocate, and a health economist. The study was conducted at the University of Pittsburgh Medical Center’s Depression and Manic Depression Prevention Program, part of the Western Psychiatric Institute and Clinic (WPIC). The protocol was approved by the Institutional Review Board of the University of Pittsburgh.

Exploratory phase

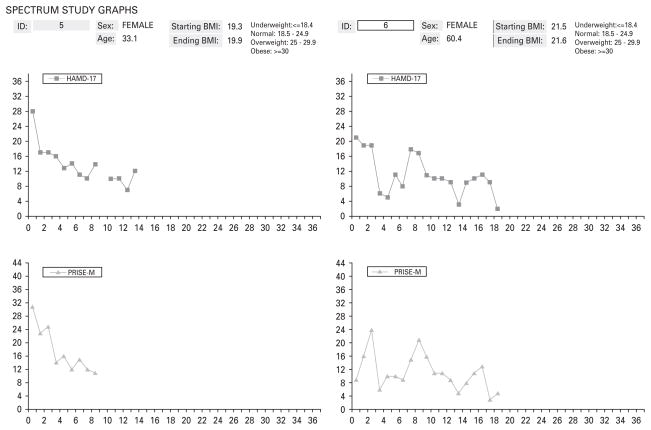
In the exploratory phase, each panel member was asked to consider 100 pairs of patient profiles, incorporating a graph of the patient’s symptom scores (the total score on the HAMD; Hamilton, 1960) and another graph representing the side-effects scores on the Patient Rated Inventory of Side Effects – Modified Version (PRISE-M; Rush & O’Neal, 1999) reported each week by the patient, along with information about the participant’s age, gender, time of occurrence of remission (if any), protocol discontinuation (if any), and baseline and ending body mass index (BMI), all printed on a single page (see Fig. 1 for two such examples). These 100 pairs of profiles were randomly selected from the 142×149=21 158 possible pairs of participants in the trial, one from each treatment group, and were ‘blinded’ as to group membership. Panel members were instructed to examine each pair and decide which patient in each pair had the better outcome, or whether the two patients’ outcomes were equivalent (a tie). The variables depicted in the graphs were explained to the panel members. Panel members were supplied with copies of the instruments used to measure benefit (HAMD) and harm (PRISE-M). No specific instructions were given regarding how to make their ratings. They were given roughly 3 weeks to complete the ratings.

Fig. 1.

Sample clinical information graphs for one escitalopram and one interpersonal psychotherapy (IPT) study participant. HAMD-17, 17-item Hamilton Depression Rating Scale; PRISE-M, Patient Rated Inventory of Side Effects – Modified Version.

We were aware that crucial to the success of this approach would be the selection of items presented to the panel. It is important that each construct considered is measured reliably, is valid, and is relatively non-overlapping with other variables to be included. If a measure of, for example, psychological well-being were included, and it was not measured reliably or it measured facility in the English language rather than well-being, the expert clinicians would still treat that measure as if it were psychological well-being. This will undermine the quality of any metric resulting from the panel’s process. In any case, the more information experts are asked to consider, the more difficult the choice, and again, the quality of the resulting metric will suffer.

Variable reduction

After excluding unreliable and questionably valid measures, highly correlated measures are considered. When there are multiple measures of a single construct, the challenge is to select the best such measure. This may simply be the most reliable single measure, or a combination of such measures, or the one most highly correlated with panel choices in the exploratory phase.

Statistical analysis

There are many possible mathematical models; here we assumed that each patient, i, has a true integrated preference score (IPS) that balances the effects of multiple benefits and harms (i.e. observed variables X_i1, X_i2, …, X_iK) using a series of weights (b₁, b₂, …, b_K) as described in the following linear equation:

$${\text{IPS}}_i=b_{\mathbf{0}}+b_{\mathbf{1}}{X}_{i\mathbf{1}}+b_{\mathbf{2}}{X}_{i\mathbf{2}}+\dots +b_K{X}_{iK}.$$

It is assumed that the probability that the response of patient i from the IPT treatment group is considered preferable to that of patient j from the escitalopram treatment group (p_ij) is determined by the difference in their IPS scores, IPS_i – IPS_j, specifically that:

$$ln\left(\frac{p_{ij}}{1-p_{ij}}\right)=a_{\mathbf{0}}+b_{\mathbf{1}}{DX}_{\mathbf{1}ij}+b_{\mathbf{2}}{DX}_{\mathbf{2}ij}+\dots +b_K{DX}_{\mathit{Kij}},$$

where DX_1ij =X_i1 − X_j1, DX_2ij =X_i2 − X_j2, etc.

The observed paired preferences proportions (estimating p_ij) are fitted to the observed variable differences to estimate b₁, b₂, …, b_K. These weights are then applied to the observed variables for each individual patient in the RCT, to obtain an estimated IPS for each individual patient.

Validation phase

In the validation phase, a second, independent sample of 100 pairings, one from the IPT-assigned group and one from the escitalopram group, was randomly chosen and these pairs were again rated by our expert panel, as described earlier. We then compared the actual preferences expressed by the panel in this second round with the paired differences in the IPS derived in the initial round. This is a necessary step because fitting a mathematical model to data often shows excellent fit to the data from which it is derived, but poor fit to an independent sample from the same population, a consequence of capitalization on chance in the first sample. If the score does not validate, it is necessary to adjust the variable selection or the mathematical model and begin again.

Application phase

Following validation, in the application phase the IPS for all patients in the RCT was used as the outcome measure to compare the IPT and escitalopram groups in the trial, to derive the effect size and its confidence interval (CI).

The between-treatment group difference was tested using the Mann–Whitney U test. The SRD can be calculated from the Mann–Whitney U statistic, using the formula 2U/(n₁×n₂)−1, where n₁ and n₂ are the sample sizes of the two treatment groups respectively. The SRD is the difference between the probability that a patient assigned to IPT has a higher IPS than a patient assigned to escitalopram and the probability that a patient assigned to escitalopram has a higher IPS than a patient assigned to IPT. A more user-friendly measure of the relative value of treatments is the NNT, which can be easily derived from the SRD (NNT=1/ SRD). The NNT is the number of patients who would have to be treated with IPT to expect one more ‘success’ (in this case, a higher IPS score) than if the same number had been treated with escitalopram (Kraemer & Kupfer, 2006). CIs for the SRD were calculated using Efron’s (1988) percentile method, based on B=10 000 bootstrap samples.

Results

Exploratory phase

We then needed to decide which of the multiple measures that could be derived from the information in the patient profiles (Table 1) would be considered in the derivation of the IPS. The three variables selected for inclusion from among the many considered were the 12-week HAMD slope, H_i (lower H is clinically preferable), the 12-week PRISE mean, P_i (lower P is clinically preferable), and their product, H_iP_i (an interaction term). By combining the HAMD slope and the PRISE mean scores over time, the problem of correlated outcomes was avoided and reliability was increased. In the case of the HAMD, the slope over time was used to focus on the response trajectory; in the case of the PRISE, the mean over time was used because the mean was more highly correlated with rater choices in the exploratory study compared with the slope. Other possible measures that we considered (time to remission, change scores, maximal PRISE) were correlated with one or the other of the chosen scores, and were less correlated with rater choices. Finally, the interaction term was included because it was thought that if benefit were low (high H), side-effects might be weighted more heavily, and that with very serious side-effects (high P), clinical benefits might be weighted less. Of the 700 ratings (100 pairs of profiles × 7 raters) made in the exploratory phase, 19% were ties; in the remaining 81%, raters were able to identify a preferred outcome.

Table 1.

Summary variables available for assessing benefits and harms

HAMD-17 variables
1.	Symptom level at 12 weeks (with LOCF if week 12 not completed)
2.	Pre–post decrease in symptoms (LOCF if 12 weeks not completed)
3.	Slope of symptom on ln(t+1)
4.	Was there a response in the 12-week period? Yes/No
5.	Time to response (used 12 weeks if no response)
6.	Was there a remission in the 12-week period? Yes/No
7.	Time to remission (used 12 weeks if no response)
8.	Average symptom level observed
9.	Maximum symptom level observed
10.	Was there any time (after 6 weeks) symptom level was greater than 15? Yes/No
11.	Was there any time response followed by 50% increase in the score at response? Yes/No
PRISE variables
12.	PRISE score at 12 weeks (with LOCF if week 12 not completed)
13.	Pre–post decrease in PRISE score (LOCF if 12 weeks not completed)
14.	Slope of symptom on ln(t+1)
15.	Average symptom level observed
16.	Maximum symptom level observed
17.	Was there any time symptom level was greater than the 75th percentile?
18.	Was there any time symptom level was greater than the 90th percentile?
19.	Was there a 50% increase from baseline at any point?
20.	Was there any time a 10-point increase between adjacent weeks?

HAMD-17, 17-item Hamilton Depression Rating Scale; LOCF, last observation carried forward; PRISE, Patient Rated Inventory of Side Effects.

The resulting IPS from fitting the model to these data was:

$${\text{IPS}}_i=0.332-0.66H_i-0.11P_i+0.014H_i{P}_i.$$

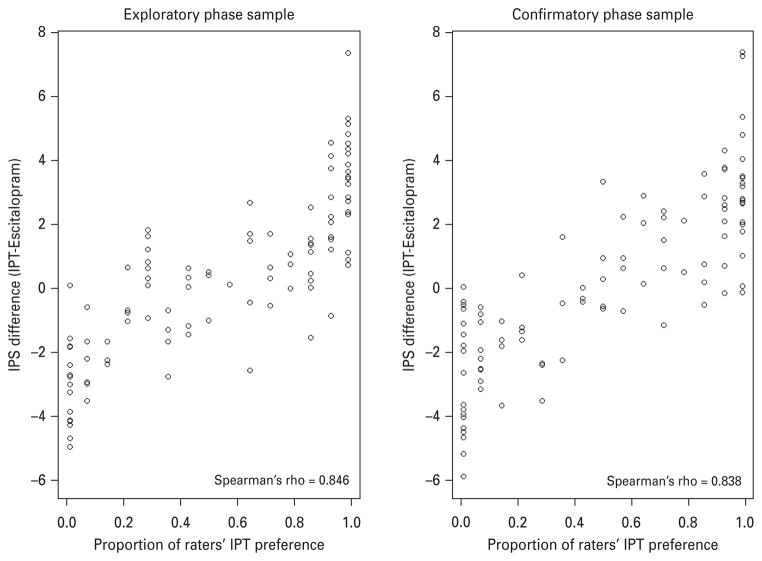
The paired IPS differences were compared to the proportion of raters’ preferring IPT over escitalopram (see Fig. 2). Spearman’s r (=0.846) indicated a very strong relationship between the predicted differences and the rater preferences.

Fig. 2.

Paired integrated preference score (IPS) differences versus raters’ preference, 100 pairs in each phase. (a) Exploratory phase sample. (b) Confirmatory phase sample. IPT, interpersonal psychotherapy.

We also used the exploratory sample to assess the inter-rater reliability of the raters’ preferences. The overall κ of 0.49 indicated that there was moderate agreement among the seven raters. (For comparison, the inter-rater κ for coronary angiograms is about 0.5; Detre et al. 1975.) Pairwise inter-rater κ coefficients are displayed in Table 2. The level of agreement between specific pairs of raters ranged from a minimum of κ =0.35 (‘fair’) to a maximum of κ= 0.62 (‘substantial’). There was no obvious pattern of agreement explained by either profession or gender, although this study was not specifically designed to detect such patterns.

Table 2.

Pairwise inter-rater reliability κ coeffcients, each based on 100 pairs

Profession	Gender	Rater	Rater
			1	2	3	4	5	6	7
1. Health economist	Male	1	–
2. Psychiatrist no. 1	Male	2	0.531	–
3. Psychiatrist no. 2	Male	3	0.511	0.38	–
4. Patient advocate	Female	4	0.516	0.394	0.504	–
5. Social worker	Female	5	0.553	0.565	0.51	0.635	–
6. Patient	Female	6	0.458	0.504	0.548	0.352	0.503	–
7. Psychiatric nurse	Female	7	0.546	0.625	0.448	0.364	0.517	0.473	–

Validation phase

Of the 700 ratings (100 pairs of profiles × 7 raters) made in the validation phase, 16.43% were ties, with the remaining 83.57% being rated definitively. The Spearman rank r between predicted choices based on the IPS difference and the actual choices of the experts in the validation phase (r=0.84) showed only a very slight decrease from that in the exploratory phase (r=0.85), as shown in Fig. 2, indicating that the raters were highly consistent in their judgments from the first to the second phase, and that the IPS derived in the exploratory phase predicts panel choices very well.

Application phase

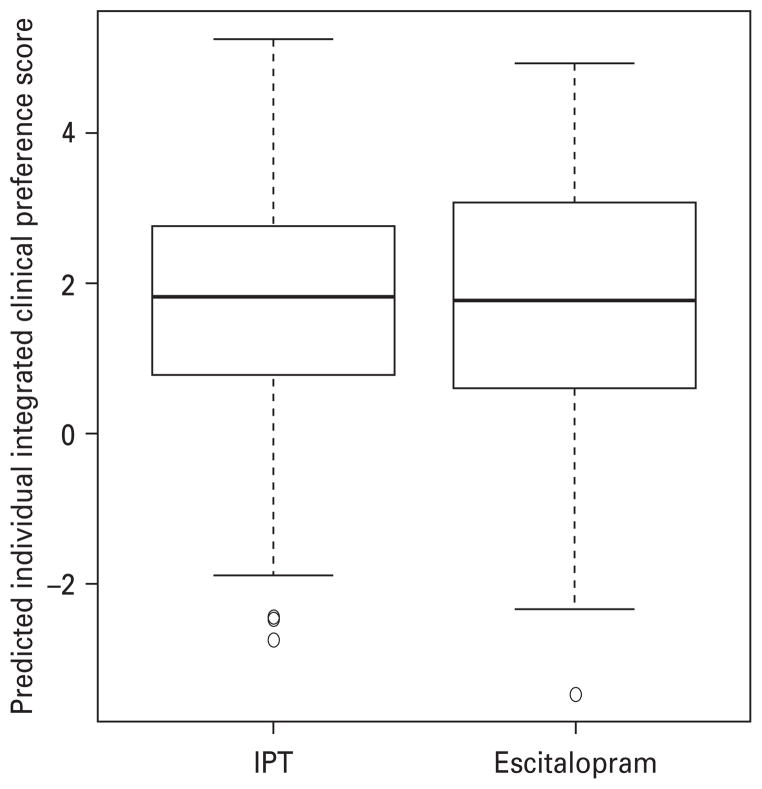
Boxplots of the individual IPSs, for the IPT and escitalopram groups, are shown in Fig. 3. There was no statistically significant difference between the IPSs in the two groups (Mann–Whitney test, p=0.63). The estimated SRD was −0.033 (95% CI −0.168 to 0.103), slightly favoring escitalopram, which can be expressed as an NNT of +30.1. The fact that the 95% CIs for SRD lie completely within the SRD range from −0.28 to +0.28, where 0.28 was established a priori as the threshold of clinical significance, indicates that these are clinically equivalent treatment strategies, a determination that typically requires a much larger sample size than showing a statistically significant differential effect between two treatments.

Fig. 3.

Individual predicted clinical preference scores (IPSs) for patients in interpersonal psychotherapy (IPT) (149 patients) and escitalopram (142 patients) groups.

Discussion

In this study we have shown that we can use a simple description of patient response in an RCT to form a metric (IPS) that combines and weights information about individual benefits and harms, and that can then be used to evaluate treatment outcomes in a way which comes closer to the goal of clinical evaluation at the individual patient level. Specifically, we used a small panel of experts who compared pairs of patients using a range of clinical information about patient response to derive an IPS. This score could then be used in statistical analyses to evaluate the treatments under study.

Could the same objective be achieved using a purely statistical method to combine and weight the benefits and harms without involving an expert panel, such as factor analysis or latent class analysis?

This is unlikely because it misses the crucial point of assessing the clinical significance of the harm–benefit profile. Such mathematical models focus on the inter-correlations between the variables considered, with no reference to the impact on patient well-being of what is represented in those variables.

Does the process of developing an IPS have to be repeated for each RCT?

Once it is agreed that the information provided in the ‘report card’ suffices to describe the range of variables that should influence clinical decision making, and an IPS is derived and validated in one RCT, the same IPS could then be applied in future studies in the same patient population, regardless of which treatments are being compared. Because such a metric uses multiple sources of information, it is likely to be more reliably measured than any single component measure is, thus leading to greater power to detect treatment differences without an increase in sample size. Moreover, such a metric is likely to be highly sensitive to individual differences between subjects. Thus, if certain patients in a treatment experience one benefit and other patients experience others, but every patient experiences one or another, analysis of each individual benefit separately might find no difference between treatment groups, but a metric that recognized all benefits simultaneously might find otherwise.

Were the variables in Fig. 1 sufficient to describe the entire range of variables that might influence clinical decision making?

The aim of this study was to test the concept, to find whether an expert panel would be willing and able to perform the task, whether a sample of 100 pairs sufficed to generate a score that could be independently validated, and so on. Thus, we presented a great deal of information to the panel, but in the form of trajectories only on two composite measures, one assessing harm and the other assessing benefit, plus information on gender, age, beginning and ending BMI. The decision to limit the task in this way was taken so as to demonstrate the approach in its least complicated form. The more information and the more complex the information presented to the experts, the more difficult will be the task of making decisions. Although selection of non-overlapping, high-quality responses presented in the clearest and most simple form is important, nevertheless in future applications of this method it will be important to consider more evaluations. In the case of major depression, for example, some possible benefits (e.g. eliminating suicidal thinking) are likely to be given greater weight than others (e.g. improving difficulty with concentration), whereas certain harms (e.g. persistent sexual dys-function) are likely to be viewed as more ‘harmful’ than others (e.g. transient nausea). It may well be useful to consider certain benefits and harms separately from others for panel evaluation. Similarly, some raters may value increases in functional ability more than a decrease in symptoms or even increases in certain areas of functional ability or certain types of symptoms more than others. This study represents an introductory step towards determining how best to make use of the multiple pieces of quantitative information generated in clinical trials.

Were the selection criteria for the expert panel or the number on the expert panel adequate?

The expert panel in this study was selected to represent a broad range of views on assessing the clinical impact of treatments on patients. If the panel had included, for example, only patients or only clinicians, the results might have been different, although there is no indication from comparing individual rater responses that there would be any major differences (Table 2). When the inter-rater reliability is 0.49, as in this case, the reliability of the consensus of seven raters, by the Spearman–Brown formula (Brown, 1910; Spearman, 1910; Kraemer, 1979), is approximately 0.87. Thus, in this case, the sample size of seven seems adequate for excellent reliability of the consensus judgment that is used to develop the IPS (p_ij). However, whether the consensus judgment of this panel would adequately represent the consensus judgment of panels similarly constituted at other sites cannot be guaranteed. What we learn here is that panelists can and will do the task of comparing complex reports of patients’ responses and achieve reliability. Moreover, experts can and do simultaneously consider harms and benefits in making these comparisons, as indicated in the weights derived for the IPS. Future work might attempt to model individual judges’ profiles to calculate even more fine-grained, personalized metrics.

What have we gained from developing the IPS over simply having clinicians make the call?

The correlation between the actual judgments and the IPS score differences in the validation sample was high, not perfect, but much higher than the inter-rater reliability. Previous studies of the clinical judgment process have repeatedly shown that models of expert judges’ decision-making processes are better than the judges themselves at predicting clinical outcomes (Goldberg, 1970; Grove & Meehl, 1996; Karelaia & Hogarth, 2008). This highly replicated finding seems to be a result of the fact that expert judges are not totally consistent in the application of the decision rules they individually set, and different expert judges are not totally consistent with each others’ decision rules. Modeling the judgment process over a sample of experts discloses the commonalities, and the resulting metric can be applied with perfect consistency across an entire sample.

If we are to take advantage of the well-stated goals of the National Institute of Mental Health (NIMH) Strategic Plan and move mental health treatments toward truly personalized medicine, we must do a better job of evaluating the degree to which a given treatment can be expected to meet the totality of the goals of a particular patient in a specific context. It is confusing for clinicians and medical consumers to read reports on RCTs in which treatment A is preferable to treatment B on some outcomes, treatment B is preferable to treatment A on others, and no significant differences are found on yet others. In that case, what is the recommendation to clinicians ? Moreover, it is disappointing to clinical researchers to make the effort to undertake well-designed and well-executed RCTs only to have many non-statistically significant results, and even when statistically significant, with clinically unimpressive effect sizes.

In general, to have adequate power to detect moderators of treatment on outcome requires much larger sample sizes than are needed to detect differences in treatment outcomes. When such a metric is applied in an analysis that includes potential moderators of treatment outcome, such as genetic, pharmacogenetic or other biomarker information, and alternative classification methods such as those we have proposed (Cassano et al. 1997; Frank et al. 1998) or those being developed by the NIMH (Insel et al. 2010), the added power and sensitivity to individual differences can bring us closer to the goal of individualizing care or truly personalized medicine.

Here, we have taken only an initial step by developing methods for creating a single outcome metric that contains information derived from comprehensive profiles of treatment outcome and one that simultaneously captures multiple aspects of outcome, including both benefits and harms for one specific disorder (unipolar depression), and have demonstrated that such a goal can be achieved, at least in principal. We believe that once the methods are fully developed, such methods can be applied to evaluations of treatments for any psychiatric disorder and, indeed, for any disorder in medicine. The application of such methods would increase the value of RCTs to clinicians, making much clearer which treatments are preferable, and for whom. Finally, because the application of such methods tends to increase power to detect treatment differences, and results in increased precision in estimation of effect sizes without an increase in sample size, this method might enable clinical researchers to design more cost-effective and successful RCTs.