Quantitative assessment of gestational sac shape: the gestational sac shape score

Abstract

Objective

To develop a quantitative method for characterizing gestational sac shape.

Methods

Twenty first-trimester gestational sacs in normal pregnancies were studied with three-dimensional (3D) ultrasonography. The 3D coordinates of surface-point sets were obtained for each sac using 30-, 15- and six-slice sampling. Cubic spline interpolation was used with the 15- and six-slice surface-point samples to generate coordinates for those 30-slice surface points not measured. Interpolated and measured values, the latter from the 30-slice sample, were compared and the percent error calculated. Cubic spline interpolation was used to determine the coordinates of a standard surface-point sample (3660) for each sac in each slice sample. These coordinate data were used to give each sac a standard configuration by moving its center of gravity to the origin, aligning its inertial axes along the coordinate axes and converting its volume to 1.0 mL. In this form, a volume shape descriptor could be generated for each sac that was then transformed into a vector containing only shape information. The 20 shape vectors of each slice sample were subjected to principal components analysis, and principal component scores (PCSs) calculated. The first four PCSs were used to define a gestational sac shape score (GSSS-30, GSSS-15 or GSSS-6) for each sac in a given slice sample. The characteristics of each set of GSSSs were determined and those for the GSSS-15 and GSSS-6 were compared with the GSSS-30 characteristics.

Results

Cubic spline interpolations were very accurate in most cases, with means close to 0%, and approximately 95% of the errors being less than 10%. GSSS-30 accounted for 67.6% of the shape variance, had a mean of zero and an SD of 1.1, was normally distributed and was not related to menstrual age (R = −0.16, P = 0.51). GSSS-15 and GSSS-6 had essentially the same characteristics. No significant differences between individual GSSS-30 values and those for GSSS-15 or GSSS-6 were found, indicating the absence of a slice sample effect.

Conclusion

Using sophisticated mathematical methods, the gestational sac shape, initially represented by the 3D coordinates of 3660 surface points, was converted to a single number, the GSSS. This score had the appropriate properties for quantitatively characterizing normal, first-trimester gestational sac shapes. As it can be obtained from as few as six slices, it should be useful in many clinical situations. This novel approach has the potential for providing quantitative shape information about a variety of biological shapes and how they change over time.

INTRODUCTION

As is well known in embryology and pathology, the normal development of various anatomical structures and their response to pathological processes are associated with changes in shape. 0 Evaluation of shapes is a routine part of ultrasound examinations and is used to determine whether a given structure appears ‘normal’ or ‘abnormal’. In serial examinations, changes in shape over time (‘shape trajectories’) are followed to assess the normalcy of development or the progression of a detected abnormality. Because these shape evaluations are usually subjective, impressions are recorded in statement such as ‘The fetal heart appears normal’ or ‘The obstruction of the urinary tract appears more severe’.

The development of three-dimensional ultrasonography (3DUS) has added major new capabilities to the assessment of anatomical structures. One of the most important is the ability to capture the entire volume of objects if they fit within the sweep volume of the scanner. This includes the gestational sac¹, early placentas², several fetal organs^3-6 and various parts of the fetal body^7,8. However, access to this volume information requires location of the object’s surface so that its volume can be defined. This is usually done by manually tracing the boundaries of object profiles in images of the entire sweep volume, a procedure that has been greatly facilitated by the development of sophisticated software, such as VOCAL and EchoPAC-30, for handling volume data. At the present time, object contouring is sued for volume determination and generation of 3D images⁹. However, this procedure also provides the x, y and z coordinates of points located on the surface of the object, the necessary information required for quantitative shape analysis¹⁰.

The most general definition of an object’s ‘shape’ is the location of its surface in 3D space. If the x, y and z coordinates of all points on an object’s surface are known, its ‘shape’ is completely define. However, for most objects there are regions where very little shape change occurs so the surface can be well approximated by a plane define by the coordinates of a representative sample of surface points¹⁰. This means that the ‘shape’ of an object can be specified to any degree of accuracy by selection of an appropriate sample of surface points.

However, coordinate data for surface points contain more information about the object than just its shape. Its location, orientation and volume also contribute to the measured coordinates of surface points. In order to use surface-point coordinates in a quantitative shape analysis, difference in these variables must be eliminated. This can be accomplished by placing the center of gravity of all objects at the origin, aligning the objects’ inertial axes along the axes of the external coordinate system, and converting all objects’ volumes to a standard volume. Mathematical procedures for transforming measured coordinate data to coordinate data from an object with these properties have been developed¹⁰. When these procedures have been carried out, differences in transformed surface-point coordinates between objects are due only to differences in shape.

This study presents a novel procedure for deriving a single number, the ‘shape score’, from the surface-point coordinates of standardized gestational sacs. This number, which characterizes the shape of the gestational sac quantitatively, is called the gestational sac shape score (GSSS).

PATIENTS AND METHODS

Patient Sample

The study population consisted of 20 pregnant women of mean maternal age 29.0 ± 5.3 years. Scans were performed in the Division of Fetal Imaging at William Beaumont Hospital> Subjects were invited to participate under informed consistent from both Institutional Review Boards at William Beaumont Hospital and the National Institutes of Child Health and Human Development. The protocol included first-trimester pregnancies with cardiac activity. Pregnancies with known sonographic abnormalities were excluded from the study. All the pregnancies had normal outcomes. Fetal age was based on the first day of the last menstrual period and menstrual age was confirmed by first-trimester crown-rump length measurements¹¹. These patients were scanned at a mean menstrual age of 9.3 ± 0.9 weeks. The morphological appearance of these gestational sacs, obtained using the VOCAL technique, has been described in a previous publication¹.

Acquisition of gestational sac surface-point coordinate data

Ultrasound volume acquisitions were performed using 3D transabdominal sonography (Voluson 730 Expert™, RAB 4-8L transducer, GE Healthcare, Milwaukee, WI, USA). Each sweep took approximately 10 s to complete. This information was archived on CD-ROM media.

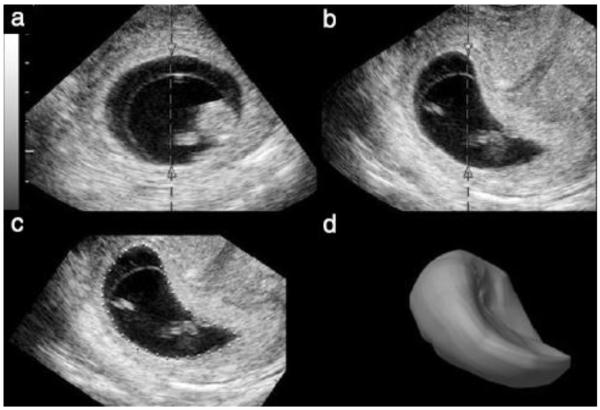
A single volume data set was arbitrarily chosen for analysis from each subject, with the exception of one case where 3D data were collected from two visits at 8.4 and 10.3 weeks’ menstrual age. Multiplanar views of each gestational sac were obtained using a customized research version of four-dimensional) 4D View software, Version 5.0 (GE Healthcare). Electronic markers were first placed on the anterior and posterior sac walls. Gestational sac profiles were then generated and their contours manually traced using a graphics pen and tablet (Intuos™, WACOM Technology, Vancouver, WA, USA) at 30-, 15-, or 6-degree intervals until completion of a 180-degree rotational sweep. A surface rendered model of the gestational sac was created by VOCAL, its geometric surfaces resulting from the user-defined rotational steps¹² (Figure 1). This research software was also used to export surface-point coordinates (x,y,z) of the surface model to a text file for additional analysis.

Figure 1.

Gestational sac contouring, illustrating the steps used to obtain sac contours. (a) The sac-sectioning axis is chosen (arrowheads). (b) A section made at right angle to the sectioning axis in (a). (c) The small white dots outline the sac contour of the sac surface. (d) The data obtained by contouring are in the form of a three-dimensional image of the sac or the x, y and z coordinates of surface points.

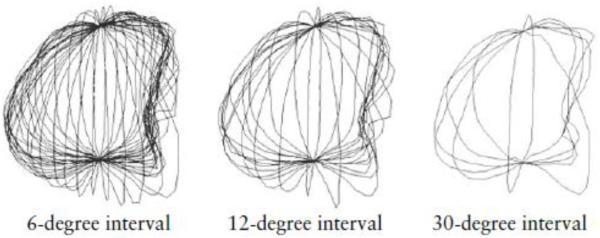
The traced contours, saved in the form of Cartesian coordinates of the surface points, provided data on 122 surface points per sampling slice. Contour sampling using 6-degree, 12-degree, and 30-degree steps is shown in Figure 2. For the 6-degree sampling, 30 sampling slices were generated and the 3D Cartesian coordinates of 3660 sampling points recorded. Data for the 12-degree sampling were from 15 slices and 1830 sampling points while for the 30-degree sampling they were from six slices and 732 sampling points. The coordinates of surface points can be in Cartesian form (x_i, y_i, z_i) or converted onto spherical coordinates (r_i, θ_i, φ_i), using the following functions:

$$r_i=\sqrt{x_i^2+y_i^2+z_i^2}$$

$${\theta }_i={\tan }^{-1}\left(\frac{y_i}{x_i}\right)$$

$${\varphi }_i={\cos }^{-1}\left(\frac{z_i}{r_i}\right)$$

where r_i is the radial value, θ the angle between the plane of the slice and the vertical axis and φ the location of the surface point along the contour (Figure S1).

Figure 2.

Gestational sac slice sampling, depicting the three slice samples used in this investigation. Slices of each gestational sac are generated at 6-degree intervals using VOCAL and their contours determined manually (30-slice set). To obtain a 15-slice set, every other contour is selected (slices at 12-degree intervals). If every fifth slice is selected (six-slice set), the slice interval is 30 degrees.

Standardization of surface-point samples

As utilizing manual tracing of contours to generate surface-point samples does not produce a consistent set of surface points, a means for determining the coordinates of a standard set of surface points was required. Also, additional surface detail can be retained by using smaller sampling steps since more sampling points can be included in the data set. To determine the appropriate value for the sampling step, we compared the sampling efficiency of different sampling steps. For this purpose, we needed to obtain the radial values at a standard set of sampling directions. A cubic-spline interpolation procedure¹³ was used in this experiment to estimate the radial values at standard locations (6-degree intervals for θ and 3-degree interval for φ). Splines are piece-wise defined smooth and continuous polynomials whose individual curves and their first and second derivatives meet at the endpoints of intervals. Cubic splines require the degree of polynomials to be three or less. The interpolation can be done by solving a symmetric system of linear equations to find the coefficients of the polynomials (Mathworld)¹⁴. This procedure was implemented using MATLAB function interp1¹⁵.

The cubic spline interpolation procedure was used with the coordinate data obtained from the 12-degree and 30-degree sampling steps to evaluate how well these two samples could retain surface details. The actual radial values r(θ, φ) obtained using the 6-degree sample were compared to the interpolation results at the same locations and the differences expressed as percents of the values for the 6-degree sample. In the 12-degree sample, the r-values for 30 sampling slices, a total of 1830 surface points, were approximated and compared to those measured in the 6-deree sample. In the 30-degree sample, the r-values for 48 sampling slices, a total of 2928 surface points, were approximated and compared to those measured in the 6-degree sample (Table S1).

As the accuracy of the spline interpolation method was quite good, this procedure was used with all 12-degree and 30-degree samples to generate the coordinates of a standard set of surface points, which has a sampling density equivalent to the 6-degree samples (i.e. 30 sampling slices (θ interval = 6 degrees) along the longitude with 122 sampling points φ interval = 3 degrees) on each slice contour (total number of surface points = 3660)) (Figure S2).

Sac standardization

To make valid shape comparisons, the effect of differences in location, orientation and size must be removed from the surface-point data. We first generated a triangular surface mesh from the surface-point coordinate data, then applied a voxelization algorithm¹⁶. To the mesh to generate volumetric data, and computed the location, orientation and size information from the volumetric data. The voxelization algorithm uses a uniform three-dimensional grid to sample the space defined by the contours. The resolution of the 3D grid was 0.4 × 0.4 × 0.4 mm (6.4 × 10⁻⁵ mL) and the volume enclosed by this elementary component of the grid is referred to as a voxel. The smaller the voxel, the better the descriptor can detect fine surface detail.

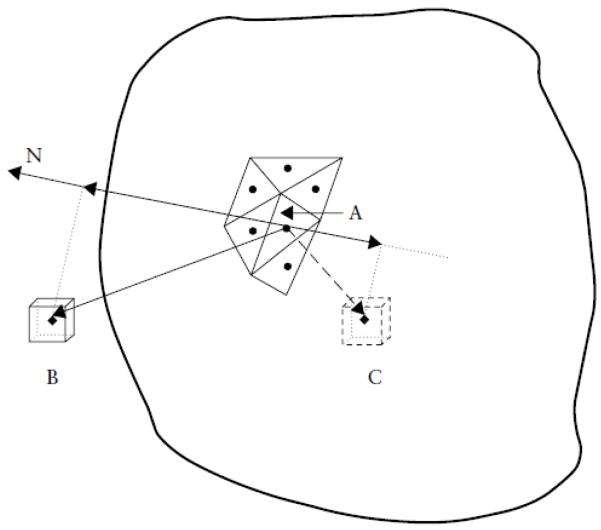
Voxels were assigned a value of 1 or 0 depending on whether they were inside the space defined by the contours (1) or outside this space (0). This is done by determining the vector between the center of the voxel and the center of the nearest surface triangle (Figure 3). This vector was projected on to the triangle’s normal unit vector (originating from the triangle’s center and projecting outward) by calculating the vector dot product. Vector dot products greater than zero indicated locations outside the sac while those less than zero indicated locations inside the sac.

Figure 3.

Location of voxels inside or outside of the gestational sac, showing the procedure for identifying the position of voxels. The nearest surface triangle (A) to a voxel (B or C) is identified (size of voxels magnified for illustration). From the center of the triangle, the normal unit vector (N), perpendicular to the sac surface, and vectors to the centers of the voxels are determined. The voxel vectors are projected onto the unit vector N and their dot products calculated. Dot product values are positive if the voxels are outside the sac and negative if they are inside the sac.

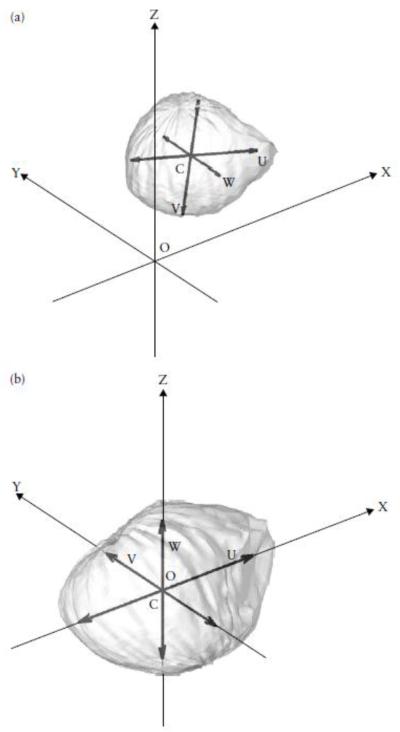
The volume of each sac was computed from this volumetric descriptor by counting the total number of 1′s in the 3D grid and multiplying it by the voxel volume. Assuming the density of a sac is homogenous, the center Where N is the total number of voxels inside the space defined by the contours. Using these data, the surface-point coordinates of each sac were transformed to that of a sac with its center of gravity at the origin of the external coordinate system (Figure 4), as described previously¹⁰. Similarly, the inertial tensor of this space (a matrix containing the moments and products of inertia associated with the three Cartesian axes) can be computed from the coordinates of all the voxels inside of the contours:

$$I_{xx}=\sum _i(y_i^2+z_i^2),I_{yy}=\sum _i(x_i^2+z_i^2),I_{zz}=\sum _i(y_i^2+x_i^2),$$

$$I_{xy}=I_{yx}=\sum _i{x}_i{y}_i,I_{yz}=I_{zy}=\sum _i{y}_i{z}_i,I_{xz}=I_{zx}=\sum _i{x}_i{z}_i$$

where I_xx, I_yy and I_zz are the moments of inertia and I_xy, I_yz and I_xz are the products of inertia.

Figure 4.

Standardization of gestational sac location and orientation, illustrating the procedures used to eliminate the effects of location and orientation on coordinate data. (a) The locations of the center of gravity (C) and the inertial axes (U, V and W) of a gestational sac are determined with respect to the external coordinate system. (b) The sac center of gravity is then moved to the origin (O) of this coordinate system and its inertial axes aligned with the X, Y and Z axes.

A mathematical procedure called diagonalization¹⁷ was applied to these inertial tensors to extract the cosines of the angles between the principal axes of inertia and the axes of the external coordinate system. These data were used to transform the surface-point coordinates of each sac to that of a sac with its principal axes of inertia aligned along the axes of the external coordinate system (Figure 4), as described previously¹⁰. The volumes of these sacs were standardized to 1mL by dividing all the surface coordinates by the cube root of the sac volume. The size of the standard voxel was changed to 0.01 × 0.01 × 0.01 cm (1 × 10⁻⁶ mL). Since all sacs have the same volume, there are about 10⁶ voxels inside each sac.

Volume descriptor

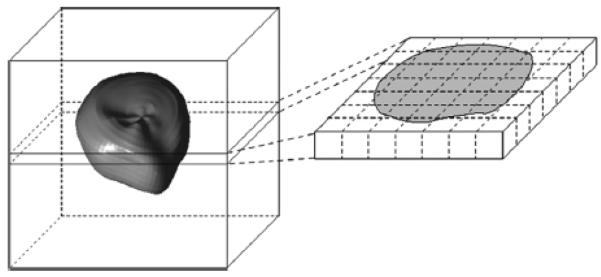
As indicated previously, standard voxels inside the sac are assigned a value of 1 and those outside the sac a value of 0. However, the number of standard voxels is so high (10⁶) that a lower resolution 3D grid must be used to generate a more reasonable volumetric shape descriptor. This is achieved by placing a 3 × 3 × 3 –cm (27 mL) box, centered at the origin, around each sac. The volume of this box is divided into 21 × 21 × 21 standard cubes (total number = 9261) having equal volumes of 0.0029 mL (Figure 5).

Figure 5.

Volume shape descriptor, illustrating the box (left side) into which each standardized gestational sac is placed, their centers of gravity coinciding. The box is subdivided into cubes, some completely inside or outside the sac and some partially inside/outside the sac (right side). The locations of the cubes with respect to the sac are determined only by sac shape.

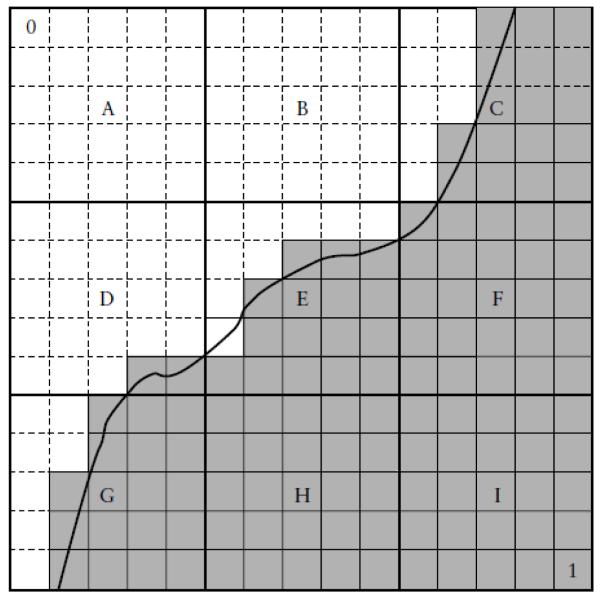
The value assigned to each cube is determined by summing the number of voxels of value 1 inside the cube and dividing this sum by the total number of voxels within the cube. Figure 6 illustrates this cube score assignment procedure. In this example, each cube contains 25 voxels (actual number of voxels per cube = 2915). Cubes A and B are completely outside the sac so are assigned cube scores of 0. Cubes H and I are completely inside the sac, so are assigned cube scores of 1. Cubes C, D, E, F and G are partially outside and partially inside of the contour and their scores are 17/25 (0.68), 2/25 (0.08), 17/25 (0.68), 1.00 and 18/25 (0.72), respectively.

Figure 6.

The procedure used to calculate cube scores. Cubes are composed of voxels that are assigned a score of 0 (upper left corner) or 1 (lower right corner), depending on whether they are outside or inside the sac. Cube scores are averages of their voxel scores. If all voxels are outside the sac (A, B) the cube scores are 0. If all voxels are inside the sac (H, I), the cube scores are 1.0. If some voxels are inside and some are outside (C, D, E, F, G), the cube scores are between 0 and 1.0. Such cube scores indicate the location of the sac surface and are determined only by shape.

Conversion of volume descriptor to shape vector

The shape vector used in the principal components analysis (PCA) was obtained by reshaping the 21 × 21 × 21 3D matrix of cube scores into a one-dimensional (1D) vector of size 9261; i.e. the 3D cube scores were sequentially placed in a single row, the shape information being retained by the score’s position in the row. The shape vectors of the 20 sacs were stored in the two-dimensional (2D) matrix of size 20 × 9261. If the 20 entries of a column vector in the 2D matrix were all zeros or ones, it indicated that the corresponding cubes were either outside or inside of all the sacs. Such columns can be removed from the 2D matrix because they do not provide shape variation information. Only the column vectors that are a matrix of different values in the range of 0 and 1 need be retained for PCA. In these studies there were 810 such column vectors. To explore how the PCA results might be affected by different types of sampling, we have generated the shape vectors of all 20 sacs from the data obtained in 30-slice, 15-slice and six-slice sampling procedures.

Principal components analysis

30-slice data set

1. Initially, PCA¹⁸ was carried out on the set of 20 shape vectors derived from the coordinate data obtained from the 30 slices made on each gestational sac. Since there were 810 column vectors containing shape information, 810 principal components (PCs) were defined. The shape variance accounted for and the set of weighting factors were calculated for each PC from the data for each sac. As approximately 90% of the shape variance was accounted for by the first 10 PCs, subsequent analysis was limited to these PCs.

2. Using the set of 810 weighting factors for each PC and the corresponding cube scores, PC_i scores (PC_iSs) were calculated for the first 10 PCs for each of the 20 sacs. A series of seven ‘shape scores’ (SSs) were calculated by adding PC_iSs serially (e.g. SS-1: PC₁; SS-2: PC₁ + PC₂S; …SS-7: sum of PC₁S to PC₇S). In these linear combinations, each PC_iS was weighted (w_i) by the fraction of shape variance accounted for by the PC (e.g. SS-4 = w₁PC₁S + w₂PC₂S + w₃PC₃S + w₄PC₄S).

3. Evaluation of the seven SSs was carried out with the following tests and the results obtained used to select the GSSS.

1. Assessment of changes in individual SSs as the number of included PC_iSs increased by calculation of the percentage change:

   $$\text{percent change}=\left\{({\mathrm{SS}}_{\mathrm{j}}-{\mathrm{SS}}_{\mathrm{i}})\right]\times 100$$

   where SS_i and SS_j are the SSs that include a specified number of PC_iSs and that number plus one, respectively.

2. Evaluation of the normalcy of the SS distributions using the Anderson-Darling test of normality¹⁹.

3. Calculation of mean and standard deviation of SSs.

4. Comparison of individual SSs using the paired t-test.

5. Examination of SS histograms.

6. Relationship of GSSS to menstrual age at the time of the scan using linear regression analysis²⁰.

15-slice and six-slice data sets

1. PCA was carried out on the shape vectors derived from the 15-slice and six-slice surface-point coordinate data sets as described for those derived from the 30-slice data set. The relationships of the two sets of PC_iSs obtained to the 30-slice PC_iS set were evaluated by linear correlation. All correlations were positive except for the PC₂S derived from both the 15-slice and six-slice data sets, which were negative (r = −0.84 and −0.98, respectively). To maintain consistency in the relationship between the PC_iSs of the 30-slice set and those of the 15- and six-slice sets, all PC₂Ss for these two sets were multiplied by −1 before their use in obtaining SS values.

2. GSSS values for individual sacs were determined as described for the 30-slice data set using coordinate data derived from the 15- and six-slice data sets, except for calculation of percent change values.

3. Individual GSSS values for the 15- and six-slice data sets were compared with those for the 30-slice data set using the paired t-test and linear regression analysis.

RESULTS

Cubic spline interpolations

The interpolated values derived from the six-slice and 15-slice sets were compared with actual measured values derived from the 30-slice set (Table S1). The mean percent differences for all sacs from both samples were very close to 0%, indicating no systematic errors. More than 90% of the errors were within± 10%, except for sacs 8 and 9 in the 15-slice sets and sacs 7, 8 and 9 of the six-slice sets, each of which had more than 85% of the errors within ± 10%. Further study of these exceptions (not reported here) indicated that the increase in error size for some r-values was due to the fact that multiple r-values were obtained in certain directions. This occurs when a sac is not convex in a given region and the surface is intersected more than once. In such situations, r-values cannot be used to define sac shape quantitatively.

Principle components analysis

30-slice sets

As the 30-slice sets provide measurements of gestational sac surface-point coordinates at 6-degree intervals, they represent the most detailed characterization of sac shapes and utilize no interpolated surface points in the standard surface-point sample. Therefore these data sets were taken as the best representatives of the gestational sac shapes.

Given in Table S2 are the SSs derived from the first seven of the 810 PC_iSs. The first seven PCs accounted for 28.1%, 18.4%, 11.0%, 7.4%, 6.3%, 4.7% and 4.0% of the cube score variance/covariance (total for first seven PCs = 80.5%; total for first 10 PCs = 89.3%). As seen in Table 1, the mean percent change between SS-4 and SS-5 (6.3%) was considerably less than that between SS-3 and SS-4 (35.3%) and the SDs associated with these mean percent changes (40.0% vs. 101.8%) were quite different. The difference in percent change was not significant by t-test (P = 0.25), probably owing to the small sample size (20) and high random variability. However, the mean SS-4 to SS-5 percent change was similar to those seen between SSs containing more PC_iSs. These results suggest relative stability in individual SS values beginning with SS-4. SS-4 accounted for 67.6% of the shape variance/covariance (Table S2). Based on these findings, subsequent analysis was limited to the first four SSs.

Table 1.

Changes in individual shape scores associated with inclusion of an increasing number of principal component scores in shape score (n = 20)

Change	Mean (%)	Median (%)	SD	Change >25%
SS-1 to SS-2	23.2	9.8	102.7	15/20
SS-2 to SS-3	−114.5	−4.5	−328.9	9/20
SS-3 to SS-4	35.3	5.0	101.8	5/20
SS-4 to SS-5	6.3	1.9	40.0	5/20
SS-5 to SS-6	7.3	0.2	16.9	3/20
SS-6 to SS-7	−4.9	−0.9	12.0	3/20

The distribution of the first four SSs did not show significant deviations from a normal distribution by the Anderson-Darling normality test (Table S3). Their means and standard deviations were essentially the same. The means did not differ from zero and the standard deviations were around one. Paired t-tests showed no significant differences in comparisons of individual SS values. Based on these findings and those presented in Table 1, SS-4 was chosen as the GSSS (GSSS-30). The distribution of the GSSS-30 is given in Figure S3. The relationship of GSSS-30 to the menstrual age at the time of scan is given in Figure S4. No relationship between GSSS-30 and menstrual age was seen for the 8-12 week time period (r = −0.16, P = 051).

15-slice and six-slice data sets

Given in Table S4 are the first four SSs derived from the 15-slice and six-slice data sets. The first four PCs obtained from the 15-slice data set accounted for 27.0%, 19.7%, 13.5% and 7.1% of the cube score variance/covariance, respectively (total for first four PCs = 69.3%; total for first 10 PCs = 88.8%). For the six-slice data set, the comparable results were 28.7%, 18.4%, 11.0% and 7.4% (total for first 4 PCs = 65.5%; total for first 10 PCs = 89.3%).

There were no significant differences between the first 4 SSs derived from either data set (Table S5). The means did not differ from zero and the standard deviations were around one in all cases. Paired tests indicated no significant differences between individual SS values for either data set. All four SSs had distributions that were not significantly different from a normal distribution by the Anderson-Darling normality test in both slice samples. TO be consistent with the decisions made for the 30-slice data set, SS-4 was chosen as the GSSS for both the 15-slice and six-slice samples (GSSS-15, GSSS-6).

Comparisons of GSSS-15 and GSSS-6 with GSSS-30

Table 2 gives the characteristics of GSSS-30, GSSS-15 and GSSS-6. Paired tests showed no significant differences in an individual GSSS values between GSSS-30 and GSSS-15 or GSSS-30 and GSSS-6. Linear regression analysis using GSSS-15 as the dependent variable and GSSS-30 as the independent variable gave an R² of 95.1% with an intercept of 0.00001 and a slope of 0.982. A similar analysis using GSSS-6 as the dependent variable gave an R² of 97.8% with an intercept of 0.0000 and a slope of 1.005. These results indicate no effect of slice sample size on the GSSS. Therefore the more practical six-slice sample can be used without significant loss of shape information in quantitative studies of gestational sac shape.

Table 2.

Characteristics of gestational sac shape scores (GSSS) derived from 30-slice (GSSS-30), 15-slice (GSSS-15) and six-slice (GSSS-6) data sets (n = 20)

			Normality test* P	Paired t-test
GSSS	Mean	SD		Comparison	P
−30	0.00	1.11	0.11	GSSS-30 vs. GSSS-15	1.00
−15	0.00	1.12	0.19	GSSS-30 vs. GSSS-6	1.00
−6	0.00	1.13	0.07	Gsss-15 vs. GSSS-6	1.00

^*Anderson-Darling normality test used.

DISCUSSION

Quantitative shape analysis

In addition to a robust definition of shape and surface-point coordinate data containing only shape information, quantitative shape analysis also requires a standard surface-point sample, an appropriate shape descriptor and analytical methods for converting shape data into numeric values. The procedures described above satisfy all these criteria.

As it is not possible to measure the coordinates of all surface-point coordinates, each set of measurements must be considered a sample of the complete coordinate data set. This means that the surface points with measured coordinates vary from object to object. Shape comparisons based on surface-point coordinates must use the same set of surface points if the comparisons are to be valid. This requires the ability to determine the coordinates of a standard surface-point sample even when they are not measured. Cubic spline estimates of r (the unknown coordinate in spherical coordinates) are biased and agree well with measured values when the latter are known (Table S1). The validity of using interpolated surface-point coordinate values is also demonstrated by the very similar GSSS values obtained using 30-slice (0% interpolated values), 15-slice (50% interpolated values and six-slice (80% interpolated values) samples. Thus, for gestational sacs, reasonable coordinate values for a standard surface-point sample can be obtained, whether they are measured or not. The general usefulness of cubic splines for this purpose can only be known by carrying out similar studies on other objects of obstetrical interest. However, in different fields, cubic splines have been shown to be very effective in mapping object surfaces²¹.

The volume shape descriptor used in this study was adapted from that described by Kaufman et al.²² and is widely used in computer graphics. Since it involves only assigning numbers to voxels within (1) and outside (0) the object, the problem of multiple r-values in a given direction is eliminated. This permits its use with complex object shapes including those with concavities such as gestational sacs¹. As the voxel volume is very small relative to the standard volume of the sac (1 ×10⁻⁶ mL vs. 1.0 mL), the mapping of the sac surface is quite precise. Since within the box placed around the sac, the cubes are still quite small relative to the sac volume (2.9 × 10⁻³ mL vs. 1.0 mL) and the number of voxels in each cube (2915) is very large, little information about the location of the sac surface is likely to be lost by converting the cube scores. However, the number of data points related to shape is significantly reduced (9261 vs. 1 × 10⁶), a number that is reduced further by eliminating column vectors that are all 0 or all 1.0 (810 vs. 9261). It should be pointed out that the volume of the box around the sacs (27 mL) is arbitrary and depends on the maximal dimensions of the objects being studied. Its volume must simply be sufficient to completely enclose all objects in a given sample. If a box size is changed, this should be done by changing the number of cubes rather than the cube size so shape resolution will not be altered.

PCA is a standard multivariate procedure frequently used to reduce the number of explanatory variables by defining a set of PCs. In evaluation of the gestational sac shape, we found that only four of the PCs needed to be considered (out of 810 determined by PCA) because they accounted for approximately 68% of the shape variability found in the cube scores and produced GSSS values that were relatively stable with the inclusion of more PC scores (Tables S2 and S4). Weighting the PC scores by the amount of shape variance/covariance accounted for by their PCs in the calculation of GSSS values, a frequently used procedure, gives more importance to the PCs that account for more of the shape variability. The properties of the GSSS values obtained (zero mean, SD of approximately 1.0, normal distribution, no relation to menstrual age, not significantly affected by slice sample size) are those of an ideal score for gestational sac shapes from normal pregnancies.

Previous studies of shape in the first trimester of pregnancy

Organic shape changes are technically difficult to characterize in an accurate and reproducible manner. Shape assessment, however, may offer some prognostic significance. For example, a study of 486 consecutive first-trimester pregnancies evaluated the size and shape of the secondary yolk sac²³. Of seven patients with abnormally shaped yolk sac, three had abnormal outcome. Kucuk et al.²⁴ reported that an abnormal appearing yolk sac allowed prediction of an abnormal pregnancy outcome with a sensitivity of 29%, a specificity of 95%, a positive predictive value of 47% and negative predictive value of 90%. Rempen²⁵ also described the use of 3DUS for the assessment of endometrial shape from a coronal plane as an additional predictor of extrauterine pregnancy during the first trimester. Toward this end, we have recently described both quantitative and morphological assessment of early normal gestational sacs using 3DUS and the VOCAL technique¹. This longitudinal study found that early gestational sacs variably appeared as ellipsoid or discoid structures with a concave indentation from the placenta. Many sacs also had additional surface features (e.g. concave, irregular, or smooth) that made discrete shape classification quite difficult. More sophisticated methods are clearly needed for the objective characterization of changing biological shapes during pregnancy.

Future developments

The availability of a quantitative measure of gestational sac shape makes possible a number of potentially important applications. As this study was carried out on gestational sacs in uncomplicated pregnancies, it provides an initial quantitative description of normal gestational sac shape. An expanded study of this kind would provide a definitive definition of GSSS in normal pregnancies.

Having a normal standard defined, studies of sac shapes in abnormal pregnancies and their quantitative comparison to sac shapes in normal pregnancies may resolve the question of whether or not sac shape is an indicator of abnormal development. This type of study could be made at different time points and evaluated cross-sectionally or longitudinally. If serial measurement were made on the same sac, ‘shape trajectories’ could be defined by fitting time-dependent functions to sets of GSSS values. ‘Shape-trajectory’ comparisons might reveal pathologic processes not detected at single time points.

As the methods described here are quite general, it is likely that they could be applied to other obstetrical problems where change in shape is important (e.g. normal organ development, development and progression of structural anomalies). Studies of more complex systems could be considerably enhanced if fluid-filled cavities or different tissue characteristics are present. Techniques such as power Doppler, color Doppler B-flow imaging or 3D inversion mode could be used to enhance the differences between the structures of interest and their backgrounds, allowing the use of surface-detecting algorithms and automatic contouring procedures. These techniques, combined with VOCAL, could greatly simplify the acquisition of surface-point coordinate data. Such automation may expand the use of quantitative shape analysis in the evaluation of common obstetrical problems

CONCLUSIONS

The paradigm for scientific studies in all disciplines is essentially the same: observation, measurement, quantitative comparison, predictive model development. For many decades, the evaluation of shape in obstetrical ultrasonography has been limited to observation and subjective assessment. The methods presented here, only possible with 3DUS, provide the means for measuring and quantitatively comparing shapes in both mother and fetus. The usefulness of these methods in clinical situations and the development of predictive models based on shape still need to be investigated. However, past experience indicates that full realization of the scientific paradigm usually improves diagnostic accuracy and may lead to unexpected therapeutic benefits. One would also expect this to be the case for clinical entities where shape change is an important part of the process.

Supplementary Material

Figure S1

Spherical coordinates of surface points, showing how the spherical coordinates of surface points that were used in evaluating the cubic spline interpolation procedure were defined. The location of a surface point (SP) on the slice contour is determined by distance from the origin (r), the angle θ between the plane of the slice and the z-axis and the angle φ between the projection of r on the x–y plane and the x-axis. If θ and φ are specified, values of r can be determined by measurement or interpolation and then compared.

Figure S2

Surface points defined by cubic splines, showing a magnified segment of a gestational sac surface showing segments of traced contours (thick black line) and surface points with measured coordinates (dots). The three broken lines going through these surface points are the cubic splines derived from the measured coordinate data. These spline functions are used to calculate estimates of the coordinates of additional surface points (indicated by the x’s), which can be used to specify estimated contours (thin black lines).

Figure S3

Distribution of the 20 GSSS-30 values obtained in this study. Because of the small sample size, the shape of the distribution must be considered only an approximation. However, it was not found to be statistically different from a normal distribution (P = 0.11).

Figures S4

Relationship of GSSS-30 to menstrual age, showing GSSS-30 values as a function of menstrual age at the time of scan. No statistically significant correlation between GSSS-30 and menstrual age was found (P = 0.51).