Improved Heritability Estimation from Genome-wide SNPs

Abstract

Estimation of narrow-sense heritability, h², from genome-wide SNPs genotyped in unrelated individuals has recently attracted interest and offers several advantages over traditional pedigree-based methods. With the use of this approach, it has been estimated that over half the heritability of human height can be attributed to the ∼300,000 SNPs on a genome-wide genotyping array. In comparison, only 5%–10% can be explained by SNPs reaching genome-wide significance. We investigated via simulation the validity of several key assumptions underpinning the mixed-model analysis used in SNP-based h² estimation. Although we found that the method is reasonably robust to violations of four key assumptions, it can be highly sensitive to uneven linkage disequilibrium (LD) between SNPs: contributions to h² are overestimated from causal variants in regions of high LD and are underestimated in regions of low LD. The overall direction of the bias can be up or down depending on the genetic architecture of the trait, but it can be substantial in realistic scenarios. We propose a modified kinship matrix in which SNPs are weighted according to local LD. We show that this correction greatly reduces the bias and increases the precision of h² estimates. We demonstrate the impact of our method on the first seven diseases studied by the Wellcome Trust Case Control Consortium. Our LD adjustment revises downward the h² estimate for immune-related diseases, as expected because of high LD in the major-histocompatibility region, but increases it for some nonimmune diseases. To calculate our revised kinship matrix, we developed LDAK, software for computing LD-adjusted kinships.

Introduction

The linear mixed model, long a mainstay of heritability estimation,^1–3 fits a covariance structure specified by a matrix of kinship coefficients to a vector of measured phenotypes. The term “mixed” refers to the presence of both an unobserved random effect, usually interpreted in terms of a polygenic contribution to the trait, and one or more fixed effects corresponding to individual SNPs or other covariates. For association analysis, the SNP effects are of interest and the random effect is used for overcoming confounding due to population structure and cryptic relatedness.⁴ In plant and animal breeding, estimation of the random effects (“breeding values”) is of primary importance because these values reflect a “true” phenotype adjusted for environmental effects or measurement error. Narrow-sense-heritability estimates $\left({\hat{h}}^2\right)$ are based on the squared regression coefficient of the random effect.

Mixed-model analysis in quantitative genetics was developed by animal breeders decades ago, but the advent of dense genome-wide SNP data has radically enhanced its applicability, for example, to the use of apparently unrelated individuals. This might seem counterintuitive given that relatedness is central to heritability, but the key insight made by Yang et al.⁵ is that dense genotype data permit the exploitation of small differences in the proportions of genome shared among apparently unrelated individuals, and this has advantages over the traditional pedigree-based approaches. Specifically, it is the short genomic regions passed down to unrelated individuals from their remote common ancestors that generate linkage disequilibrium (LD). So, h² estimated from unrelated individuals corresponds only to the causal-variant heritability that is tagged by the genotyped SNPs (this is sometimes referred to as the “chip heritability”). Investigating the genetic architecture of complex traits thus becomes possible through the estimation of h² components tagged by different SNP sets, which one can obtain, for example, by imposing minor-allele-frequency (MAF) thresholds or restricting attention to specific pathways or genomic regions (termed “genomic partitioning”).⁶

The usual mixed models in quantitative genetics assume independent Gaussian effect sizes. The “thin tails” property of the Gaussian distribution makes it unrealistic for individual SNP effect sizes, but we illustrate by simulating from distributions with thicker tails that ${\hat{h}}^2$ is reasonably robust to this assumption. Further, the standardization made by Yang et al.⁵ and other authors when they computed SNP-based kinship coefficients implies a specific relationship between MAF and the variance of effect sizes such that rarer SNPs tend to have larger effect sizes. We show that ${\hat{h}}^2$ is somewhat robust to the relationship between MAF and effect size. A polygenic assumption, one of many small phenotypic effects distributed genome-wide, is often employed for justifying a mixed-model analysis. This assumption proves to be unnecessary because ${\hat{h}}^2$ remains unbiased (although precision is eroded) as the number of causal variants is reduced, even down to a monogenic model.

Although these results support the use of SNP-based mixed-model analysis for estimating h² from unrelated individuals, we did uncover serious cause for concern: linkage disequilibrium (LD) can generate large biases. Contributions to h² from causal variants tend to be overestimated in regions of strong LD and underestimated in regions of low LD. Of course, SNP-based ${\hat{h}}^2$ cannot capture any causal-variation component that is not tagged by a genotyped SNP, but we show that even when all causal variants are genotyped and hence fully tagged, SNP-based ${\hat{h}}^2$ reflects patterns of LD, in addition to causal variation. Likewise, the contributions to ${\hat{h}}^2$ from untyped causal variants can be overestimated or underestimated according to their LD with genotyped SNPs.

Patterns of LD are strongly linked to MAF: on average, the signals from low-frequency variants are less replicated than those from high-frequency variants. Therefore, ${\hat{h}}^2$ will be too low for traits with predominantly low-frequency causal variants and will be too high for those with predominantly high-frequency causal variants. This has consequences when one performs genomic partitioning to investigate the frequency spectrum of causal variants for complex traits. Yang et al.⁵ suggested a transformation that involves uniformly scaling the usual SNP-based kinship coefficients; this transformation counteracts the average bias caused by LD but requires prior knowledge of the MAF spectrum of causal variants. We propose a different adjustment in which SNPs are weighted according to how well they are tagged by their neighbors. Using simulated data, we demonstrate that our adjustment both greatly reduces bias and increases the precision of SNP-based ${\hat{h}}^2$.

When we reanalyzed the height data⁵ with our LD-adjusted kinship matrix, ${\hat{h}}^2$ changed only slightly, suggesting that any underestimation of contributions to h² in low-LD regions is balanced by overestimation elsewhere. We also analyzed seven traits studied by the Wellcome Trust Case Control Consortium (WTCCC).⁷ For both hypertension and type 2 diabetes, ${\hat{h}}^2$ increased by nearly a quarter when we used our LD-adjusted kinships instead of a standard kinship matrix, suggesting that these traits’ causal variants tend to be poorly tagged and thus have a lower-than-average MAF. By contrast, for rheumatoid arthritis, ${\hat{h}}^2$ was reduced by one-tenth when we used LD-adjusted kinships. This disease, along with type 1 diabetes, has major-histocompatibility-complex (MHC) risk variants that tend to be well tagged; the estimated heritability attributed to chromosome 6 was substantially reduced for both these diseases.

Material and Methods

The Linear Mixed Model

The essence of mixed-model analysis in quantitative genetics is partitioning the phenotypic variance-covariance matrix between two (or more) specified matrices. Given phenotypic values $\mathbf{Y}=\left(Y_1,\dots ,Y_n\right)$, a typical form is

$$\text{Var}\left(\mathbf{Y}\right)={\sigma }_g^2\mathbf{G}+{\sigma }_e^2\mathbf{I},$$ (Equation 1)

where G is a matrix of kinship coefficients and I is the n × n identity matrix, which implicitly assumes independence across individuals of environmental effects and measurement error. Estimates ${\hat{\sigma }}_g^2$ and ${\hat{\sigma }}_e^2$ are typically obtained via restricted maximum likelihood (REML).⁸ Then, h², the $\text{Var}\left(\mathbf{Y}\right)$ proportion explained by additive genetic effects, is estimated by

$${\hat{h}}^2=\frac{{\hat{\sigma }}_g^2}{{\hat{\sigma }}_g^2+{\hat{\sigma }}_e^2}.$$ (Equation 2)

We can derive Equation 1 by assuming

$$Y_i=\mu +\sum _{j=1}^m{Z}_{ij}{u}_j+e_i,$$ (Equation 3)

in which $Z_{ij}$ is the genotype of individual i at the j^th of m diallelic causal loci given an additive coding of genotypes standardized to have zero mean and unit variance for each j and in which $e_i$ and $u_j$ are independently Gaussian with zero mean and variances ${\sigma }_e^2$ and ${\sigma }_g^2/m$, respectively. Then, Y is multivariate Gaussian with $\text{E}\left(Y_i\right)=\mu$ and

$$\text{Var}\left(\text{Y}\right)=\frac{{\sigma }_g^2}{m}{\text{ZZ}}^T+{\sigma }_e^2\text{I},$$

where Z denotes the matrix of $Z_{ij}$ values. We thus have Equation 1 with $\mathbf{Z}{\mathbf{Z}}^T/m$ in place of G. If Z were not column standardized, Equation 2 might not hold; a more general form is given in Appendix B.

With Z column standardized, ${\mathbf{Z}}^T\mathbf{Z}/n$ is a sample correlation matrix of causal variants. It follows that each $Z_{ij}{Z}_{i^{\prime }j}$ can be regarded as an estimator of the population correlation coefficient at locus j on the basis of just one pair of individuals, i and i′. Therefore, the ii′ entry of $\mathbf{Z}{\mathbf{Z}}^T/m$ is an average over loci of allelic correlation estimates for i and i′. This average can be interpreted as a measure of the excess sharing of causal alleles by i and i′ relative to independent allele assignments. Equation 3 specifies an additive model, and so ${\hat{h}}^2$ in Equation 2 is an estimate of h².

For binary outcomes, the same analysis can be applied, but the resulting ${\hat{h}}^2$ depends on the case-control ratio, which can be chosen arbitrarily. One solution is to implement this analysis with a subsequent transformation of the estimate to an underlying liability scale adjusted for ascertainment effects.^9,10

Pedigree- and SNP-Based Kinship Matrices

Because $\mathbf{Z}{\mathbf{Z}}^T/m$ is unknown, it has traditionally been replaced by the kinship matrix G, whose ii′ entry is the probability that homologous alleles from i and i′ are identical by descent from common ancestors within a specified pedigree. Assuming that pedigree founders are completely unrelated, then G reflects genome-wide average allelic correlation, which might be a reasonable proxy for allelic correlation at the causal loci, for example, if little is known about the genetic architecture of the phenotype. However, the identity-by-descent (IBD) approach is unsatisfactory because IBD values depend on the available pedigree, which is always incomplete. In any case, the phenomenon of interest is genome sharing, for which pedigrees only give expected and not realized values.

Nowadays, the proxy for G can be kinship coefficients computed from genome-wide SNP genotypes rather than from a known pedigree. There are at least two popular coefficients for measuring the relatedness of two individuals from genome-wide SNPs:⁴ their average allelic correlation and their proportion of shared alleles. These are sometimes labeled as IBD and IBS (identity by state) methods, but we avoid this terminology; in the absence of an explicit pedigree, meaningfully defining IBD is difficult. If we assume Equation 3, a natural choice is the average allelic correlation matrix $\mathbf{A}=\mathbf{X}{\mathbf{X}}^T/m^{\prime }$, where X is defined in the same way as Z except that SNP genotypes replace causal-locus genotypes and m′ is the number of genotyped SNPs. A slight modification of A was adopted by Yang et al.⁵ Although A is computed from data, in practice it is treated as known in Equation 1, as was the case for pedigree-based G.

Simulation Study

We implemented a simulation study to check four key assumptions underlying ${\hat{h}}^2$ obtained via mixed-model analysis in which G was replaced by $\mathbf{A}=\mathbf{X}{\mathbf{X}}^T/m^{\prime }$, as well as to check its sensitivity to LD. We merged the 2,699 and 2,501 individuals who passed quality control (QC) from the UK 1958 Birth Cohort samples and National Blood Service samples, respectively.⁷ Following Yang et al.,⁵ we removed individuals so that $\left|{\text{A}}_{i{i}^{\prime }}\right|$ < 0.024 for all pairs ii′, leaving n = 5,127. Unless otherwise stated, results were obtained with only the m′ = 81,327 SNPs (on chromosomes 1 and 2) that passed QC, which included requiring a MAF > 0.01.

We generated 50 replicate phenotype vectors Y for each scenario. Except where specified otherwise, we chose for each scenario 100 causal variants and simulated Gaussian effect sizes to achieve h² equal to either 0.5 or 0.8. Because SNP-based ${\hat{h}}^2$ only measures the h² proportion that is tagged by the SNPs, the true value of h² is usually unknown. To allow us to assess the bias and precision of ${\hat{h}}^2$, for the simulations reported here, we chose causal variants from among the genotyped SNPs so that h² was known. Given Y and the kinship matrix, estimates ${\hat{\sigma }}_g^2$ and ${\hat{\sigma }}_e^2$, as well as estimates of their SDs, were obtained with the REML algorithm incorporated in the software GCTA (Genome-wide Complex Trait Analysis).¹¹

SNP-Based ${\hat{h}}^2$: Implicit Assumptions

First, using $\mathbf{A}=\mathbf{X}{\mathbf{X}}^T/m^{\prime }$ in place of G in Equation 1 supposes a polygenic model in which all SNPs contribute to Y. We investigated this assumption by varying the numbers of causal SNPs for fixed h².

Second, assigning a common variance to the standardized effect sizes u_j in Equation 3 implies an equal contribution to h² from each causal locus. Under the assumption of Hardy-Weinberg equilibrium, this implies that v_j, the per-allele effect size at the j^th causal locus, has variance

$$\text{Var}\left(v_j\right)\mathrm{\propto }\frac{1}{p_j\left(1-p_j\right)},$$ (Equation 4)

where p_j is the population MAF. A corresponding relationship applies to the SNP effect sizes when $\mathbf{Z}{\mathbf{Z}}^T/m$ is replaced with A. A similar assumption is implicit in many tests of genetic association,¹² and a tendency for alleles of greater effect to have lower MAF is expected under a range of evolutionary models.¹³ Using known susceptibility loci, Park et al.^14,15 found empirical evidence for this trend in all eight traits that they studied, even after adjusting for power to detect, and this relationship was significant for three of the traits. To investigate the impact of assuming Equation 4, we considered four relationships of the form

$$\text{Var}\left(v_j\right)\propto {\left[p_j\left(1-p_j\right)\right]}^{\alpha },$$ (Equation 5)

which can be implemented in the computation of A by appropriate scaling of the column-centered genotypes (the standard scaling, dividing each column by the square root of its variance, corresponds to α = −1). When α < 0, per-allele effect sizes increase as the MAF decreases, whereas they decrease when α > 0. We simulated Y by assuming α = −2, −1, 0, and 1, and for each Y, we calculated ${\hat{h}}^2$ by assuming each of the four effect-size models when calculating A. Here, it was important to use the full equation for calculating ${\hat{h}}^2$ (Appendix B) because Equation 2 only applies when A is computed with α₂ = −1.

The third implicit assumption that we checked is that of a Gaussian distribution for genetic effect sizes. This can be criticized because the “thin tails” of the Gaussian means that larger-than-usual effect sizes are strongly penalized. The normal exponential gamma (NEG) has been proposed as more realistic for SNP effects¹⁶ in that it has thicker tails than both the Gaussian and (when the shape parameter is small) the Laplace (double exponential) distributions. It can be modeled as a Laplace distribution with a gamma-distributed rate. Decreasing the gamma shape parameter leads to thicker tails, whereas increasing it recovers the Laplace distribution. We simulated Y by assuming NEG effect sizes with shape parameters of 10, 2, and 1, and we adjusted the scale parameter in each case to obtain the desired h².

In a similar vein, our fourth test was to investigate the Gaussian assumption for the noise term e_i in Equation 3. We did this by estimating h² when e_i was simulated from five other distributions, including both heavier-tailed and skewed distributions (see Figure S4A, available online).

The Effect of LD on ${\hat{h}}^2$

If a causal variant is tagged by multiple genotyped SNPs, then some or all of its signal can be replicated, and this can lead to overestimation of its contribution to h². For the dense SNP sets used in current genome-wide association studies, LD induces strong correlations between SNPs, and SNP-based ${\hat{h}}^2$ reflects patterns of LD, in addition to the architecture of causal variants. This problem does not depend on the total amount of tagging: if all SNPs were duplicated exactly once, the amount of tagging would double, yet A, and hence ${\hat{h}}^2$, would remain unchanged. Instead, the problem concerns relative amounts of tagging: some of the causal variants are tagged more than others, distorting their estimated contributions to h².

Pruning (or “thinning”) the columns of X is a common approach to reducing correlation among SNPs.¹⁷ Pruning has limited consequences for identifying relatedness because genomic segments shared from a recent common ancestor will usually extend well beyond the usual range of LD. However, it is not a satisfactory solution for the problem of uneven tagging in obtaining ${\hat{h}}^2$ from unrelated individuals because these share short genomic segments and so tagging of causal variation will be lost. Instead, we propose to overcome the problem by scaling SNP genotypes according to local patterns of LD. The goal of the scaling is that the signal from each SNP is downweighted so that replication of its signal by neighboring SNPs can be compensated for. We denote by A^∗ the weighted allelic correlation matrix, which is defined the same as A except that each column X_j of X is replaced by $\sqrt{w_j}{\text{X}}_j$ and the denominator m′ is replaced by $\sum _j{w}_j$. The w_j’s are chosen so that

$$w_j+\sum _{j^{\prime }}{w}_{j^{\prime }}{r}_{j{j}^{\prime }}^2{e}^{-\lambda d_{j{j}^{\prime }}}$$ (Equation 6)

is constant over j. Here,$r_{j{j}^{\prime }}^2$ denotes the squared correlation between SNPs j and j′, a standard measure of LD, and the summation is over SNPs j′ such that $e^{-\lambda d_{j{j}^{\prime }}}$ > 0.125, where λ is a constant and d_jj′ denotes the base-pair distance between SNPs j and j′. The motivation for requiring constancy of Equation 6 is that it (almost) represents the total replication of the signal from SNP j (after weighting). Identifying w_j’s satisfying this requirement is a linear programming problem (see Appendix A, where we also discuss appropriate values for λ). For example, a set of k SNPs all in perfect LD but in linkage equilibrium (LE) with all other SNPs would each be assigned (approximately) w_j = 1/k, so the signal from a causal variant tagged by these SNPs would be counted once overall. Zou et al.,¹⁸ when considering a similar problem, suggested weights satisfying

$$\frac{1}{w_j}=1+\sum r_{j{j}^{\prime }}^2,$$ (Equation7)

which also reduces to 1/k in this simple setting but provides a less satisfactory solution for incomplete LD (see Figure S1D). The value of ${\sum }_{j^{\prime }}{r}_{j{j}^{\prime }}^2{e}^{-\lambda d_{j{j}^{\prime }}}$ can be viewed as a measure of the tagging of SNP j; for the simulations of Figure 3, weakly and very weakly tagged causal variants were those in the bottom 40% and 20%, respectively, of values for this sum, whereas strongly and very strongly tagged causal variants were those in the top 40% and 20%, respectively.

Figure 3.

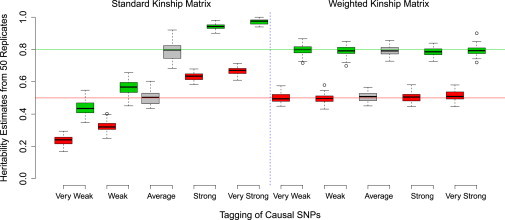
Distributions of ${\hat{h}}^2$ with and without Adjustment for LD

The x axis indicates the relative levels of tagging of the causal variants. The boxes indicate interquartile ranges of ${\hat{h}}^2$ under SNP-based mixed-model analysis using A (left) or A^∗ (right). Colors correspond to simulated h² (red, 0.5; green, 0.8), and gray boxes indicate that causal variants were chosen at random without regard to tagging.

Results

Polygenic Assumption

Figure 1A shows that ${\hat{h}}^2$ remained approximately unbiased in our simulations as the number of causal variants m decreased down to one. A polygenic assumption is thus not required for ${\hat{h}}^2$ to be useful, and even a large ${\hat{h}}^2$ does not, taken alone, indicate a polygenic component to the genetic architecture of a trait. Intuitively, it seems reasonable that A remains a good proxy for $\mathbf{Z}{\mathbf{Z}}^T/m$ even for a single, randomly placed locus. As expected, the precision of ${\hat{h}}^2$ reduced as m declined; this effect was largely eliminated when A was replaced with A^∗.

Figure 1.

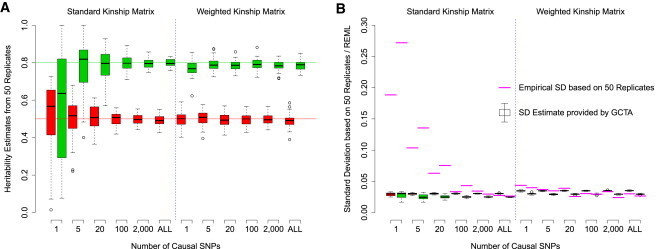
Investigation of the Robustness of ${\hat{h}}^2$ to Assumptions of Polygeneity

(A) The distribution of ${\hat{h}}^2$ for different numbers of causal variants, from one up to “ALL” (all 81,327 SNPs), with the use of the standard kinship matrix A (left) and the weighted kinship matrix A^∗ (right). Boxes indicate interquartile ranges, colors correspond to simulated h² (red, 0.5; green, 0.8), and whiskers span the full range except for outliers, indicated with circles.

(B) The layout matches that of (A), but now the boxes correspond to the REML SD estimates calculated by GCTA, and the purple lines mark the empirical SD estimates based on the 50 replicates.

Figure 1B compares the REML estimates of SD provided by GCTA with the empirical SD based on the 50 replicates for each scenario. GCTA never reported SD > 0.04, which greatly exaggerated the precision of ${\hat{h}}^2$ when m was small. In contrast, when using our LD-adjusted kinship matrix, GCTA always gave an SD within 0.01 of the empirical estimate, even for small m.

When m is small, many SNPs do not tag any causal variant, so estimation could be improved by the removal of redundant SNPs from X.¹⁹ As an illustration of the potential gain, in a further simulation (Figure S2), we found that when m′ included five times as many redundant SNPs as SNPs tagging causal variants, the empirical standard deviation of ${\hat{h}}^2$ was approximately twice as much as when only the nonredundant SNPs were used. In practice, it would be challenging to identify SNPs that do not tag any causal variation. However, these results would suggest that inclusion of the redundant SNPs has limited consequence.

Relationship between Effect-Size Variance and MAF

Considering relationships between MAF and causal effect-size variance of the form of Equation 5, Figure 2 shows that, as expected, ${\hat{h}}^2$ was most accurate when the analysis assumption (α₂) matched that of the simulation (α₁). However, the standard choice of α₂ = −1 (the second block of eight boxes) appeared to give the most stable ${\hat{h}}^2$ among the models considered here and would therefore seem the most prudent choice when the correct relationship is uncertain. A similar pattern was observed when A^∗ was used instead of A (results not shown).

Figure 2.

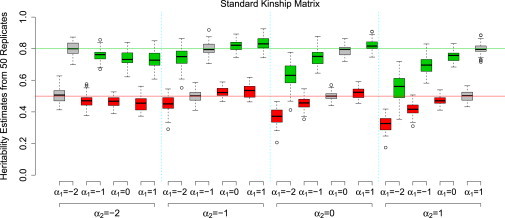
Investigation of the Robustness of ${\hat{h}}^2$ to Assumptions of the Relationship between Effect-Size Variance and MAF

Phenotypes were simulated with each of four models (indexed by α₁) for the relationship between effect-size variance and MAF (Equation 5). Analysis was performed with each of the same four models (indexed by α₂) when allele counts were standardized. Boxes indicate interquartile ranges of ${\hat{h}}^2$. Colors correspond to simulated h² (red, 0.5; green, 0.8), and gray boxes indicate that the analysis model matches the simulation model (α₁ = α₂).

The Assumption of Gaussian Effect Sizes and Noise Terms

The four panels of Figure S3A show the densities of the Gaussian and the three NEG distributions. Despite the important differences in the tails, the distribution of ${\hat{h}}^2$ was only modestly affected by the choice of effect-size distribution (Figure S3B): some precision was lost by a wrong Gaussian assumption, but little bias appeared to be introduced. These findings are consistent with the robustness to violations of the polygeneity assumption discussed above because when effect sizes are sampled from the NEG with low shape parameter, h² is dominated by a few large effects. Once again, A^∗ outperformed A by showing lower variance and little, if any, bias.

Similarly, when we generated phenotypes by using five alternative distributions for $e_i$ in Equation 3, we observed little effect on ${\hat{h}}^2$ (Figure S4).

The Effect of LD on ${\hat{h}}^2$

The effects of uneven tagging are visible in the left half of Figure 3. In the underlying simulation, the causal variants were chosen only from areas of either high LD or low LD (see Material and Methods for definitions). When the causal variants were in regions of high LD and were therefore tagged better than average by neighboring SNPs, their contributions to the phenotype tended to be overestimated: ${\hat{h}}^2$ > h². Conversely, in regions of low LD, we typically found ${\hat{h}}^2$ < h². The degree of tagging is strongly correlated with MAF, and so we observed that the contribution to h² of low-MAF causal variants tended to be underestimated, whereas that of high-MAF causal variants was overestimated (Figure S5).

The right half of Figure 3 illustrates the reduction in bias and increase in precision of ${\hat{h}}^2$ when it is based on A^∗ rather than A. When A^∗ was used, the median ${\hat{h}}^2$ in each scenario was within 2% of h², whereas for A, it ranged from 50% to 133% of h². Using the weights defined by Equation 7 instead gave results intermediate between those based on A and A^∗ (results not shown, but follow from Figure S1D). Even if causal variants are drawn at random so that ${\hat{h}}^2$ is approximately unbiased for h² (as for the gray boxes in Figure 3), individual causal variants can still be affected by uneven tagging, and this can reduce the precision of $\widehat{h^2}$. This effect is particularly evident in Figure 1 when there are few causal variants; in this case, $\widehat{h^2}$ based on A^∗ is much more precise than when it is based on A.

The w_j’s are constructed to equalize the tagging of genotyped SNPs, but the tagging of untyped variants will not necessarily be equalized. However, in a simulation study in which only alternate SNPs were considered to be genotyped, we found that w_j’s also greatly reduced the variation in the tagging of untyped SNPs (Figure S1C).

Comparison with the Approach of Yang et al.

The impact of LD and MAF on ${\hat{h}}^2$ was considered by Yang et al.⁵ They proposed a transformation that can be used for negating the average bias caused by variable LD and also for estimating $h_C^2$, the total heritability due to common variation. They examined the accuracy of using the sharing of genotyped SNPs to estimate the sharing of causal variants by regressing $\mathbf{Z}{\mathbf{Z}}^T/m-\mathbf{I}$ on A − I. A slope coefficient β < 1 indicates that kinships are being overestimated by A (which typically leads to ${\hat{h}}^2<h_C^2$), and the opposite occurs when β > 1. By observing the results of simulations, they obtained for β an empirical formula that takes into account the MAF spectrum of the causal variants and the total number of genotyped SNPs, and they proposed replacing A in the mixed-model analysis with β (A − I) + I. Although this approach can reduce the bias due to variable LD in ${\hat{h}}^2$, the fact that it requires knowledge of the MAF spectrum of causal variants is not usually feasible. In any case, the bias is caused by levels of LD at the causal variants, and MAF is an imperfect indicator of such levels.

On can also use the proposal of Yang et al.⁵ to estimate ${\hat{h}}^2/h_C^2$ by taking into account the expected overestimation of kinship values caused by incomplete tagging of causal alleles. When our weighted kinship matrix A^∗ is used, this fraction can be estimated more directly by the calculation of the average proportion of untyped variation captured by the genotyped SNPs (Figure S6).

A Test for Inflation Due to Population Structure

A criticism of SNP-based ${\hat{h}}^2$ is its potential sensitivity to population structure. The danger was highlighted by Browning and Browning,²⁰ who constructed a pseudo case-control association study by using the UK controls of the original WTCCC;⁷ when treating 90% of English individuals as controls and 90% of Scottish and Welsh individuals as cases, they obtained a highly significant value of ${\hat{h}}^2$ (7 SDs above 0). The inflation due to population structure for ${\hat{h}}^2$ can be estimated by the difference between the sum of ${\hat{h}}^2$ obtained from disjoint halves of the genome (say, chromosomes 1–8 and 9–22) and ${\hat{h}}^2$ calculated from the whole genome.⁶ In Figure S7, we apply this approach to a replicate of the study of Browning and Browning and show that it is effective in overcoming the problem they highlighted.

Guarding against Genotyping Errors

Our simulation study avoided any problem arising from genotyping errors by using called SNP genotypes as causal variants. For real case-control studies, ${\hat{h}}^2$ can be sensitive to different genotyping error rates in cases and controls; careful QC can reduce, but not eliminate, the problem. Replacing A with A^∗ could exacerbate the problem because poorly genotyped SNPs tend to have lower LD with neighboring SNPs, and this leads them to receive a relatively high weighting. To overcome this danger, we suggest calculating $r_{j{j}^{\prime }}^2$ separately in cases and controls and then using the larger of the two values during computation of w_j. Then, if a SNP is, say, poorly genotyped in cases, its w_j will not artificially be increased provided that it is correctly genotyped in controls. We show in Figure S8 that ${\hat{h}}^2$ remains approximately unbiased under this approach. An even more cautious approach would be to compute weightings from a completely independent (but ethnically matched) data set, which would not be affected by genotyping anomalies in the analysis data set.

Application to Height and WTCCC Data Sets

We repeated the analysis of human height (MIM 606255) by using the post-QC data of Yang et al.⁵ Using A as the kinship matrix, we obtained ${\hat{h}}^2$ = 0.44 (0.09 SD), which was almost unchanged (${\hat{h}}^2$ = 0.45, 0.10 SD) when we replaced A with the LD-adjusted A^∗. The lack of change in ${\hat{h}}^2$ suggests that, when A is used, any underestimation of heritability from poorly tagged variants is compensated for by an overestimation of heritability from well-tagged variants. Yang et al.⁵ suggested that the difference between their ${\hat{h}}^2$ and the accepted value of h² ≈ 0.8 could be explained by a model in which all causal variants have a MAF in the range [0.01, 0.1]. However, given that our LD-adjusted kinships better appreciate the contribution of low-MAF variants, explaining the gap between ${\hat{h}}^2$ and h² in terms of common (MAF > 0.01) causal variants would require them to have an even narrower range of MAF.

Next, we applied our method to the seven traits of the original WTCCC study:⁷ bipolar disorder (BD [MIM 125480]), coronary artery disease (CAD [MIM 608320]), Crohn disease (CD [MIM 266600]), hypertension (HT [MIM 145500]), rheumatoid arthritis (RA [MIM 180300]), type 1 diabetes (T1D [MIM 222100]), and type 2 diabetes (T2D [MIM 125853]). For each study, approximately 2,000 patients were combined with a set of 3,004 common controls sourced from the 1958 Birth Cohort (58BC; 1,504 individuals) and the National Blood Service (NBS; 1,500 individuals). Three of these traits (BD, CD, and T1D) have been previously studied with the same WTCCC data by Lee et al.,¹⁰ whereas RA and T1D have been examined with different data.²¹ We also followed Lee et al.¹⁰ in contrasting the 58BC and NBS samples in a pseudo case-control study, for which we expect h² = 0. Although these studies involve binary outcomes, for the purpose of comparing the standard and weighted kinship matrices, it suffices to estimate h² on the observed scale rather than convert to the liability scale.

Because of the potential inflation caused by population structure and genotyping errors for ${\hat{h}}^2$, Lee et al.¹⁰ employed stricter QC criteria than did the WTCCC,⁷ and we applied similarly strict QC. Specifically, we first filtered out individuals with >2.5% missing genotypes or with heterozygosity (calculated across a pruned set of high-quality SNPs) not within [0.295, 0.345]. Next, for each of the seven case and two control data sets, we removed SNPs that had either a MAF < 0.01 or call rate < 0.99 or that were significant at 5% for Hardy-Weinberg equilibrium. Then, for each study, we rejected SNPs significant at 5% for differential missingness between cases and controls. Finally, for each study, we computed (unweighted) allelic-correlation kinship coefficients by using a set of about 50,000 SNPs in approximate LE. Apparent population outliers were removed on the basis of the first two principal components. Following Yang et al.,⁵ we selectively removed individuals so that no pair remained with kinship greater than the absolute value of the smallest observed value (between 2.5% and 3.6%) for that data set. For the pseudo case-control study, 2,834 individuals and 297,894 SNPs remained; for each of the other studies, between 4,415 and 4,690 individuals and between 278,772 and 285,989 SNPs remained. For each study, we included the top 20 axes from principal-component analysis of the kinship matrix used above for identifying related individuals. We also assessed the inflation caused by population structure, and because cases and controls were genotyped separately, we implemented the procedure described above in “Guarding against Genotyping Errors.”

For the seven traits and the pseudo case-control study, Table 1 presents ${\hat{h}}^2$ (calculated with both the standard and the LD-adjusted kinship matrices) for each case, evaluated either across all SNPs or across just those on chromosome 6 (Table S1 provides additional details, including implementation of the above test for inflation due to population structure and an assessment of the impact of genotyping errors). The largest differences in ${\hat{h}}^2$ when A was used instead of A^∗ occurred for BD (+1.6 SDs), HT (+1.6 SDs), RA (−0.9 SD), and T2D (+1.5 SDs). Note that these are differences between statistics computed with the same data and which estimate the same quantity, so it does not make sense to test for significance of these differences. An increased ${\hat{h}}^2$ provides evidence that BD, HT, and T2D are predominantly affected by variants of lower MAF, and this causes the standard analysis to underestimate their SNP-based heritability. RA and T1D both have their strongest (marginal) associations in a region of high LD in HLA-DRB1 (MIM 142857) at 6p21 in the MHC region and have estimated odds ratios of 2.36 and 5.49, respectively (see Figures S9–S16 for the results of marginal analyses). Unsurprisingly, the contribution to ${\hat{h}}^2$ from chromosome 6 is reduced for these two conditions when A^∗ is used in place of A.

Table 1.

Analysis of WTCCC Traits

Trait or Study	Total Heritability${\hat{\mathit{h}}}^{\mathbf{2}}$(SD)			Chromosome 6 Heritability${\hat{\mathit{h}}}_{\mathbf{6}}^{\mathbf{2}}$(SD)
	Standard	Weighted	Difference	Standard	Weighted	Difference
Bipolar disease	59 (6)	69 (8)	+10	4 (2)	5 (2)	0
Coronary artery disease	39 (6)	41 (8)	+3	2 (2)	1 (2)	−1
Crohn disease	54 (6)	58 (8)	+5	5 (2)	6 (2)	+1
Hypertension	42 (6)	52 (8)	+10	5 (2)	8 (2)	+4
Rheumatoid arthritis	57 (6)	52 (8)	−6	19 (2)	17 (2)	−2
Type 1 diabetes	73 (6)	74 (8)	0	37 (2)	35 (2)	−2
Type 2 diabetes	35 (6)	44 (8)	+9	4 (2)	5 (2)	+1
Pseudo case-control study	11 (10)	7 (14)	−4	0 (2)	1 (3)	+1

The variance explained by all SNPs and by just those on chromosome 6 with the use of both the standard and the weighted kinship matrix for the seven traits and the pseudo case-control study. The SD is the value given by the GCTA software.

Discussion

The two leading explanations for the “missing heritability” of complex phenotypes have been (1) many rare variants of small or modest effect size and (2) many common variants of weak effect.²² SNP-based mixed-model analysis of unrelated individuals has been used for providing support for the latter explanation,^{5,6,21,23–25} thus pointing researchers in the direction of, for example, pathway analyses for assisting in the identification of common variants with small effect sizes. SNP-based mixed-model analyses can help further by estimating h² components attributable to pathways, genomic regions, or MAF classes.⁶

We have examined the assumptions that underlie the use of SNP-based mixed-model analysis for estimating h², and we have illustrated through simulation that the resulting ${\hat{h}}^2$ is reasonably robust to four underpinning assumptions but is vulnerable to uneven LD. Use of the standard allelic-correlation kinship coefficients overestimates the contribution to h² from causal variants that are well tagged and underestimates that from poorly tagged variants. This observation is particularly pertinent for traits where many of the causal variants have an intermediate MAF (say, between 0.01 and 0.1). For example, in a simulation with causal variants restricted to SNPs with a MAF in this range, (unadjusted) ${\hat{h}}^2$ was typically 25% smaller than h². When variants were selected from the 20% of SNPs with the lowest LD with neighboring SNPs, we observed ${\hat{h}}^2$/ h² as small as 0.5.

We have proposed estimating h² instead with the use of A^∗, a kinship matrix adjusted for local patterns of LD. This largely eliminates the biases based on the standard kinship matrix A in ${\hat{h}}^2$ and increases its precision. This adjustment improves current methods for investigating the architecture of complex traits with the use of SNP-based genomic partitioning, and we expect that using A^∗ will provide benefits for other applications of the mixed model in quantitative genetics, such as association analysis and prediction of phenotype.

Computational demands

Solving Equation 6 is computationally demanding for reasonably sized problems, but in Appendix A, we describe a good approximation obtained by a partitioning of the genome into regions. With this approximation, the time needed for computing the weightings is similar to that required for computing the standard kinship matrix A. Once the w_j’s are available, calculating the weighted kinship matrix A^∗ can be significantly faster than calculating A because in a dense SNP set, many SNPs are assigned w_j = 0 and can be ignored. Our LDAK software, which calculates both the w_j’s and A^∗, is freely available (see Web Resources below).

Appendix A: Calculating Weights for the LD-Adjusted Kinship Matrix

To explain the problems caused by LD, suppose that SNP 1 and SNP 2 are perfectly correlated. Use of the standard kinship matrix A in mixed-model analysis implicitly assumes the same effect-size distributions for all SNPs, so the analysis would be unchanged by the removal of SNP 1 but would double the prior effect-size variance for SNP 2. A similar effect arises if the two SNPs are correlated less than perfectly. As such, the effect of any causal allele, and its contribution to ${\hat{h}}^2$, can be exaggerated by multiple tagging SNPs. Conversely, the contribution will be understated if the causal allele is tagged by relatively few SNPs.

To offset this effect of LD, we propose introduction of w_j’s > 0 and the replacement of $\mathbf{A}=\mathbf{X}{\mathbf{X}}^T/m^{\prime }$ with a weighted kinship matrix A^∗, computed in the same way except that X_j (the allele counts for SNP j, scaled and centered) is replaced with

$${\text{X}}_j^{\text{∗}}=\sqrt{w_j^{\text{∗}}}{X}_j\text{where}{w}_j^{\text{∗}}=w_j\frac{m^{\prime }}{\sum _j{w}_j}.$$

Therefore, a $\mathbb{N}\left(0,{\sigma }_g^2/m^{\prime }\right)$ prior distribution for the effect size for X_j is equivalent to a $\mathbb{N}\left(0,w_j^{\text{∗}}{\sigma }_g^2/m^{\prime }\right)$ prior for the effect size of $X_j^{\text{∗}}$. We seek w_j’s that equalize the implied prior effect-size distributions of causal variants, irrespective of their tagging by SNPs. With genotypes standardized to have variance 1, the amount of a causal signal tagged by both X₁ and X₂ is r₁₂, the correlation between SNPs 1 and 2. In a similar fashion, r₁₃ will represent the extent to which a causal signal tagged by X₁ is replicated by X₃. Under the linear model, the combined phenotypic effect of X₁, X₂, and X₃ is X₁u₁ + X₂u₂ + X₃u₃. Therefore, the contribution in the direction of X₁ is u₁ + r₁₂u₂ + r₁₃u₃, which has prior variance

$$\left(w_1^{\text{∗}}+r_{12}^2{w}_2^{\text{∗}}+r_{13}^2{w}_3^{\text{∗}}\right)\frac{{\sigma }_g^2}{m^{\prime }}.$$

We can obtain similar expressions for the signals represented by X₂ and X₃ and similarly extend this to consider all m′ genotyped signals. Our aim is that the variance terms for all these prior distributions are equal, which we can achieve by solving a matrix equation of the form Cw = 1:

$$\left[\begin{array}{cccccc}1& \text{C}{\left(1,2\right)}^2& \text{C}{\left(1,3\right)}^2& \cdots & \text{C}{\left(1,m^{\text{'}}-1\right)}^2& \text{C}{\left(1,m^{\text{'}}\right)}^2\\ \text{C}{\left(2,1\right)}^2& 1& \text{C}{\left(2,3\right)}^2& \cdots & \text{C}{\left(2,m^{\text{'}}-1\right)}^2& \text{C}{\left(2,m^{\text{'}}\right)}^2\\ \text{C}{\left(3,1\right)}^2& \text{C}{\left(3,2\right)}^2& 1& \cdots & \text{C}{\left(3,m^{\prime }-1\right)}^2& \text{C}{\left(3,m^{\prime }\right)}^2\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ \text{C}{\left(m^{\prime }-1,1\right)}^2& \text{C}{\left(m^{\prime }-1,2\right)}^2& \text{C}{\left(m^{\prime }-1,3\right)}^2& \cdots & 1& \text{C}{\left(m^{\prime }-1,m^{\prime }\right)}^2\\ \text{C}{\left(m^{\prime },1\right)}^2& \text{C}{\left(m^{\prime },2\right)}^2& \text{C}{\left(m^{\prime },3\right)}^2& \cdots & \text{C}{\left(m^{\prime },m^{\prime }-1\right)}^2& 1\end{array}\right]\left[\begin{array}{c}{w}_1\\ w_2\\ w_3\\ ⋮\\ w_{m^{\prime }-1}\\ w_{m^{\prime }}\end{array}\right]=\left[\begin{array}{c}1\\ 1\\ 1\\ ⋮\\ 1\\ 1\end{array}\right],$$

where for the moment, $\text{C}{\left(j,j^{\prime }\right)}^2$ represents the correlation squared between variants j and j′. Requiring w_j > 0 means that there is usually no (exact) solution to this equation, and we instead seek the best achievable approximate solution in the sense of least absolute error. That is, we seek to minimize

$$\sum _j\left|1-{\text{C}}_{j}w\right|,$$

where C_j denotes the j^th row of C. Equivalently, we minimize ${\sum }_j{a}_j$, subject to

$$-a_j\le 1-{\text{C}}_{j}w\le a_j\text{and}{a}_j\ge 0\text{for all}j,$$

which is a linear programming problem that could, in theory, be solved with the simplex algorithm.

The approach above considers global correlations and could, if solvable, be used for addressing the effects of both short- and long-range LD. However, if we assume that long-range LD due, for example, to population structure has been addressed with other measures, we can restrict attention to local LD. Let d_jj′ represent the distance in base pairs between variants j and j′ and be set to $\mathrm{\infty }$ if the two SNPs are on different chromosomes. We define the elements of matrix C as

$$\text{C}{\left(j,j^{\prime }\right)}^2=\{\begin{array}{ll}{e}^{-\lambda d_{j{j}^{\prime }}}{r}_{j{j}^{\prime }}^2\hfill & \text{if}{e}^{-\lambda d_{j{j}^{\prime }}}>0.125\text{and}{r}_{j{j}^{\prime }}^2>0.01\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$

The exponential term attempts to model the scope of LD, and λ reflects its rate of decay. We fix λ so that $\text{exp}\left(-\lambda d_{j{j}^{\prime }}\right)$ = 0.125 when d_jj equals 3 Mbp. The requirement that $r_{j{j}^{\prime }}^2$ > 0.01 corresponds loosely to requiring that $r_{j{j}^{\prime }}^2$ be significantly above zero for typical sample sizes. We experimented with varying λ to achieve window sizes between 1 Mbp and 10 Mbp, as well as with setting the $r_{j{j}^{\prime }}^2$ threshold to 0 and 0.05, and observed little change in ${\hat{h}}^2$, except when we used the minimum window size of 1 Mbp, which seemed insufficient to account for the full effects of LD.

Now that matrix C is sparse (typically with only tens of nonzero elements in each row), solving the linear-programming problem becomes more manageable. In particular, solving for w_j decomposes into independent solutions for each chromosome. Even with this shortcut, for our simulation study data, the largest C matrix, which contained about 40,000 rows for chromosome 2, and the corresponding optimization problem could still require a few days to be solved on a standard processor. Therefore, we further subdivided the C matrices to include at most 3,000 SNPs at a time and allowed a buffer of 500 SNPs at each boundary to minimize the effect of the subdivision. We checked the weights for the 1,000 SNPs in common between a pair of adjacent windows and found that the concordance between the central 500 of these SNPs was almost perfect. Typically, disruption was noticeable only for the last few tens of SNPs of each window, indicating that a buffer of 500 SNPs was sufficient.

When we used windows of size 3,000 SNPs (plus buffers of 500 SNPs), calculating the weights for the entire genome took approximately 40 computer hours for the simulation sample size of 5,127 (this process can be spread across multiple processors if desired). A potential future improvement of the method could allow for data-dependent λ that reduces window sizes in regions of low LD to reduce computing time but that expands them for high LD; this might improve h² estimation, for example, in the MHC.

Appendix B: Calculating Heritability from Estimates of ${\sigma }_g^2$ and ${\sigma }_e^2$

Let V_T denote the total phenotypic variance, and let V_R denote the residual variance (which equals the phenotypic variance when all genetic effects are correctly included in the model). Assuming that the phenotype has been centered to have mean of zero, we can write

$$V_T=\frac{\sum _i\left(y_i^2\right)}{n}-{\left(\frac{\sum _i{y}_i}{n}\right)}^2\text{and}{V}_R=\frac{\sum _i{\left(e_i\right)}^2}{n}-{\left(\frac{\sum _i{e}_i}{n}\right)}^2.$$

To calculate the expected values of V_T and V_R, consider that

$$\begin{array}{c}\mathbb{E}\left(u_j{u}_{j^{\prime }}\right)=0\text{for}j\ne j^{\prime },\mathbb{E}\left(u_j^2\right)={\sigma }_g^2\text{for}j=1,2,\dots ,m,\\ \mathbb{E}\left(e_i{e}_{i^{\prime }}\right)=0\text{for}i\ne i^{\prime },\mathbb{E}\left(e_i^2\right)={\sigma }_e^2\text{for}i=1,2,\dots ,n,\\ \text{and}\mathbb{E}\left(u_j{e}_i\right)=0,\forall j,i.\end{array}$$

Considering the expectation of the terms in the first summation in V_T, we obtain

$$\begin{array}{c}\mathbb{E}\left(y_i^2\right)=\mathbb{E}\left[{\left(z_{i1}{u}_1+z_{i2}{u}_2+\dots +z_{im}{u}_m+e_i\right)}^2\right]\\ =\mathbb{E}\left[z_{i1}^2{u}_1^2+z_{i2}^2{u}_2^2+\dots +z_{im}^2{u}_m^2+e_i^2\right]\\ =\left(z_{i1}^2+z_{i2}^2+\dots +z_{im}^2\right){\sigma }_g^2+{\sigma }_e^2,\end{array}$$

whereas the expected value required for the second summation is

$$\begin{array}{l}\mathbb{E}\left[{\left(y_1+y_2+\dots +y_n\right)}^2\right]=\mathbb{E}\left[{\left(Z_{11}{u}_1+\dots +Z_{1m}{u}_m+e_1+\dots +Z_{n1}{u}_1+\dots +Z_{nm}{u}_m+e_n\right)}^2\right]=\mathbb{E}\left[\sum _{i{i}^{\prime }}{Z}_{i1}{Z}_{i^{\prime }1}{u}_1+\dots +\sum _{i{i}^{\prime }}{Z}_{im}{Z}_{i^{\prime }m}{u}_m+e_1^2+e_2^2+\dots +e_n^2\right]=\left(\sum _j\sum _{i{i}^{\prime }}{Z}_{ij}{Z}_{i^{\prime }j}\right){\sigma }_g^2+n{\sigma }_e^2.\hfill \\ \therefore \mathbb{E}\left(V_T\right)=\frac{\text{trace}\left(\mathbf{Z}{\mathbf{Z}}^T\right)}{n}{\sigma }_g^2+{\sigma }_e^2-\frac{\text{sum}\left(\mathbf{Z}{\mathbf{Z}}^T\right)}{n^2}{\sigma }_g^2-\frac{1}{n}{\sigma }_e^2.\end{array}$$

For the residual variance, calculation of the expectation is more straightforward:

$$\mathbb{E}\left(V_R\right)=\frac{\mathbb{E}\left[e_1^2+e_2^2+\dots +e_n^2\right]}{n}-\frac{\mathbb{E}\left[{\left(e_1+e_2+\dots +e_n\right)}^2\right]}{n^2}={\sigma }_e^2-\frac{1}{n}{\sigma }_e^2.$$

Although the expected heritability is 1 − $\mathbb{E}\left(V_R/V_T\right)$, because the fraction is bottom heavy, it should be reasonable to approximate this value with 1 − $\mathbb{E}\left(V_R\right)/\mathbb{E}\left(V_T\right)$, from which we obtain

$$\mathbb{E}\left(h^2\right)\approx 1-\frac{\mathbb{E}\left(V_R\right)}{\mathbb{E}\left(V_T\right)}=\frac{1-\left(1-\frac{1}{n}\right){\sigma }_e^2}{\left(\frac{\text{trace}\left(\mathbf{Z}{\mathbf{Z}}^T\right)}{n}{\sigma }_g^2-\frac{\text{sum}\left(\mathbf{Z}{\mathbf{Z}}^T\right)}{n^2}{\sigma }_g^2+\left(1-\frac{1}{n}\right){\sigma }_e^2\right)}.$$ (Equation B1)

With the usual column standardization, the genotype matrix has trace n and sum 0. Therefore, the heritability estimate will take the simpler form

$${\hat{h}}^2=1-\frac{\left(1-\frac{1}{n}\right){\hat{\sigma }}_e^2}{\left({\hat{\sigma }}_g+\left(1-\frac{1}{n}\right){\hat{\sigma }}_e^2\right)}=\frac{{\hat{\sigma }}_g^2}{{\hat{\sigma }}_g^2+\left(1-\frac{1}{n}\right){\hat{\sigma }}_e^2},$$

which, for large n, tends to the form provided in the main text. However, for all other transformations, it is important to use the complete form, Equation B1. In particular, dividing the kinship matrix by a constant will lead to an estimate of ${\sigma }_g^2$ multiplied by that constant. When the full form is used, ${\hat{h}}^2$ will be invariant to any such scaling (or, indeed, shifting) of the kinship matrix; however, with the simple form, the heritability estimate would be unjustifiably affected.

Web Resources

The URLs for data presented herein are as follows:

• Linkage-Disequilibrium Adjusted Kinships (LDAK), http://www.ldak.org

• Online Mendelian Inheritance in Man (OMIM), http://www.omim.org

• Wellcome Trust Case Control Consortium, https://www.wtccc.org.uk