An Exponential Combination Procedure for Set-Based Association Tests in Sequencing Studies

Abstract

State-of-the-art next-generation-sequencing technologies can facilitate in-depth explorations of the human genome by investigating both common and rare variants. For the identification of genetic factors that are associated with disease risk or other complex phenotypes, methods have been proposed for jointly analyzing variants in a set (e.g., all coding SNPs in a gene). Variants in a properly defined set could be associated with risk or phenotype in a concerted fashion, and by accumulating information from them, one can improve power to detect genetic risk factors. Many set-based methods in the literature are based on statistics that can be written as the summation of variant statistics. Here, we propose taking the summation of the exponential of variant statistics as the set summary for association testing. From both Bayesian and frequentist perspectives, we provide theoretical justification for taking the sum of the exponential of variant statistics because it is particularly powerful for sparse alternatives—that is, compared with the large number of variants being tested in a set, only relatively few variants are associated with disease risk—a distinctive feature of genetic data. We applied the exponential combination gene-based test to a sequencing study in anticancer pharmacogenomics and uncovered mechanistic insights into genes and pathways related to chemotherapeutic susceptibility for an important class of oncologic drugs.

Introduction

Advances in high-throughput arrays have made feasible the genotyping of hundreds of thousands to millions of SNPs for a large number of subjects.¹ As a result, genome-wide association studies (GWASs) have flourished in the past decade, and thousands of SNPs have been successfully associated with complex disease traits.² Despite the success of GWASs, a large proportion of genetic variation underlying disease risk remains unidentified.³ One possibility is that many of the causal variants are rare in the population and are therefore poorly captured by GWASs. As state-of-the-art technology, next-generation sequencing provides a more accurate and comprehensive measurement of genetic variation, especially for the rare part of the frequency spectrum.⁴ Rare variants appear infrequently in the sampled subjects, making them less likely (unless the sample size is very large) to be detected with single-SNP inference. Moreover, as millions of variants are tested for association, one needs to apply a stringent multiple-testing adjustment. Therefore, in current sequencing studies, power for detecting risk-associated rare variants is a major concern.

For improving the power for detecting genetic risk factors, a natural approach in sequencing studies is to analyze sets of genetic variants.^5–11 The rationale is that by accumulating information on functionally related variants, one can gain power to detect associations. In addition, the number of tests is greatly reduced, and the significance criterion is relaxed. In the set-based analysis, a set is often defined by functional “units,” for example, a gene⁵ or a pathway.¹² To illustrate the concepts, we mainly focus on gene-based analysis, although similar arguments could be applied to other genetic units.

Various methods have been proposed for jointly analyzing multiple variants in a gene. In the cohort allelic sums test,⁵ the combined-multivariate-and-collapsing method,⁶ and the weighted sum test by Madsen and Browning (designated here as the burden test),⁷ rare-allele counts of individual variants are collapsed (with weights) in a gene for cases and are contrasted with those for controls for the formation of an association statistic. The C-alpha test¹⁰ is based on the sum of variant statistics, each of which compares the observed and the expected variance of minor allele frequencies (MAFs) in cases for a variant in the gene. The C-alpha test is robust to the direction of association effects. Wu et al. (2011)¹¹ proposed a weighted kernel regression approach (sequence kernel association test [SKAT]) that upweighs rare variants. Under certain conditions, such as assigning equal weights to variants regardless of MAF and with no covariates, SKAT and some other regression-based tests^8,9 are almost equivalent to the C-alpha test. We mainly discuss the burden test and the C-alpha test in this work as examples of set-based tests. In large samples, the burden test can be approximated by a linear combination of normal statistics, whereas the C-alpha test can be approximated by a linear combination of chi-square statistics. They represent two classes of set-based tests.

Set-based methods can be viewed as ways of combining individual statistics, i.e., of determining whether an effect is present in at least one of the variants in the set. Many set-based test statistics can, in fact, be represented as the linear combination of variant statistics. Linear combination has been widely used because it is not only simple but is also the most powerful test for testing against simple alternative hypotheses.¹³ In the context of case-control sequencing studies, linear combination is powerful if the goal is to test whether odds ratios are equal to 1 for all variants in a gene, as opposed to whether odds ratios are equal to some given value, say 1.2. However, linear combination is no longer the most powerful test if the alternative is composite, for example, not all odds ratios are equal to one. In addition to linear-combination procedures, other methods for combining individual test statistics in a set-based test are also proposed and discussed. Fisher’s and Tippett’s methods are widely used as combination tests.¹⁴ Fisher’s method rejects large values of $-2\sum \log \left({\text{p}}_i\right),$ where ${\text{p}}_i$ is the p value corresponding to the individual statistic $Z_i$.¹⁵ Tippett’s method rejects low values of the minimum of p values, $\text{min}\left({\text{p}}_i\right)$.¹⁴ These two combination procedures are nonparametric in the sense that they are based on individual p values in a set regardless of the distributional form of the test statistics.

Some other nonparametric set-based methods have been proposed in the context of genetics or expression studies. For example, Zaykin et al. (2002)¹⁶ proposed a truncated product method for combining p values in a set. Zaykin et al. (2007)¹⁷ proposed a soft-threshold method with a test statistic as the sum of inverse gamma transformation of p values in a set. Yu et al. (2009)¹⁸ and Biernacka et al. (2012)¹⁹ extended the p value combination methods to gene-set or pathway analysis in association studies. These methods share a similar idea to our proposed method: when only a small number of statistics in a set are from the alternative, linear combination or Fisher’s method might not be powerful, and when more than one statistic in a set is from the alternative, Tippett’s method is also not optimal. In contrast to our proposed method, these methods^16–19 are based on combining individual p values instead of test statistics in a set. In sequencing studies that involve a lot of rare variants, individual p values for rare variants might be unreliable, and set-based tests based on individual p values can result in loss of power, especially when rare variants are more strongly associated with disease risk than common variants.

For combining multiple one-sided normal statistics, van Zwet and Oosterhoff (1967)²⁰ proposed the statistic $\sum \exp \left(w_i{Z}_i\right)$, where $w_i$ is the weight and $Z_i$ is normally distributed. Koziol and Perlman (1978)²¹ proposed the statistic $\sum \exp \left(w_i{Z}_i\right)$ for combining independent chi-square statistics. Both take the sum of the exponential of individual statistics as set statistics. In contrast with Fisher’s, Tippett’s, and other nonparametric methods, linear combination and the sum of exponential of statistics are parametric because they are derived from the density functions of statistics from exponential families.

In this work, we propose an exponential-combination (EC) framework for set-based association tests in sequencing studies. EC is not just one test statistic but is, rather, a general procedure that can be used for combining individual variant statistics for performing set-based analysis. The proposed EC procedure improves power under a natural class of alternatives for set-based tests in sequencing studies. Genetic data, particularly sequencing data, have distinctive features that can guide us in finding powerful combination procedures. Specifically, among tens of millions of known variants, only a very small proportion is related to disease risk for any particular disease. If a gene harbors k variants and $k^{\prime }$ of them are truly associated with disease risk, it is likely that $k^{\prime }\ll k$, particularly if k is large. Thus, instead of testing against a generic alternative (e.g., when at least one SNP is associated), a more realistic composite alternative hypothesis is to test whether only a small number among all variants have nonzero effects while all the other variants have zero effects. We term this kind of alternative a sparse alternative.

EC accounts for these distinctive features of sequencing studies. In the following sections, we derive the EC statistic against a sparse alternative from both Bayesian and frequentist perspectives. With simulated examples and an application to sequencing-based data in pharmacogenomics, we show that EC is more powerful than other combination methods for set-based tests when only a small number of variant statistics are truly from the alternative.

Material and Methods

We denote with k the number of variants in a set under investigation. Many commonly used set-based test statistics can be written as a linear combination of variant statistics, i.e., $Z={\sum }_{i=1}^k{\pi }_i{Z}_i$, where ${\pi }_i$ $\left({\pi }_i\ge 0\right)$ is the weight and $Z_i$ is the statistic of the i^th variant. When only a small number of variant statistics are from the alternative, a more powerful combination procedure exists. This powerful combination is to take the sum of the exponential of squared variant statistics, $Z={\sum }_{i=1}^k{\pi }_i\text{exp}\left(w_i{Z}_i^2\right)$ if $Z_i$ is (approximately) normally distributed, or the sum of the exponential of variant statistics, $Z={\sum }_{i=1}^k{\pi }_i\text{exp}\left(w_i{Z}_i\right)$ if $Z_i$ is (approximately) chi-square distributed. Here, $w_i$ $\left(w_i\ge 0\right)$ is the weight on the exponential scale, and ${\pi }_i$ is the weight on the linear scale for the individual variant statistic $Z_i$. We suggest the use of $w_i=1/2$ and ${\pi }_i=1$ as the default.

The Bayesian Interpretation of EC

The distinctive feature of genetic data—sparse association—could be modeled in the prior of Bayesian inference. Suppose that the variant statistics $Z_1,\dots ,Z_k$ are independently distributed and that each has the density function $f\left(z_i;{\theta }_i\right),i=1,\dots ,k$, where ${\theta }_i$ is the parameter of interest. To test the null hypothesis, $H_0:{\theta }_i\le 0$ $\forall$ i, against the alternative hypothesis, H₁: at least one ${\theta }_i>0$, the Bayes test has the rejection region

$$\left\{\left(z_1,\dots ,z_k\right):\int \prod _{i=1}^k\left[\frac{f\left(z_i;{\theta }_i\right)}{f\left(z_i;0\right)}\right]d\varphi \left({\theta }_1,\dots ,{\theta }_k\right)\text{>}c\right\},$$ (Equation 1)

where ϕ represents the prior probability distribution of $\left({\theta }_1,\dots ,{\theta }_k\right)$ over the alternative space $\Omega$ and c is chosen for achieving the overall significance level α. The Bayes test minimizes the Bayes risk and is most powerful if the prior is correctly specified.

Different priors yield different Bayes tests, and we consider here two classes of prior distributions. Under the alternative with a “class I prior,” ${\theta }_i$’s vary independently over the alternative space $\Omega$, and each ${\theta }_i$ has marginal prior ${\varphi }_i\left({\theta }_i\right)$. When $Z_i$’s are normally or chi-square distributed and have marginal conjugate priors for the ${\theta }_i$’s, the integral in Equation 1 reduces to rejecting large ${\sum }_{i=1}^k{\pi }_i{Z}_i$, where ${\pi }_i$’s are the weights and are functions of ${\varphi }_i$’s.²¹ Therefore, the linear-combination test is the Bayes test under the class I prior. For example, when each variant in a gene is independently associated with disease risk with a nonzero log odds ratio, the linear combination of variant statistics is powerful.

Now consider another type of prior, “class II prior,” where only one ${\theta }_i\ne 0$ and all other ${\theta }_j$’s $=0\left(i\ne j\right)$. The prior puts positive probability ${\eta }_i$ at the coordinate axis $\left(0,\dots ,{\theta }_i,\dots ,0\right)$ in the alternative space, where ${\sum }_i{\eta }_i=1$. With class II prior, we only consider each coordinate axis to decide the rejection rule for the Bayes test. The Bayes test in Equation 1 rejects when the following is large:

$$\sum {\eta }_i\underset{-\infty }{\overset{\infty }{\int }}\frac{f\left(z_i;{\theta }_i\right)}{f\left(z_i;0\right)}{\varphi }_i\left({\theta }_i\right)d{\theta }_i.$$ (Equation 2)

Suppose that each $Z_i$ independently follows a normal distribution with mean ${\theta }_i$ and unit variance $Z_i\sim N\left({\theta }_i,1\right)$. With class II prior, we have $\theta =\left(0,\dots ,0,{\theta }_i,0,\dots ,0\right)$ with probability ${\eta }_i$ under the alternative, where ${\theta }_i\sim {\varphi }_i\left({\theta }_i\right)=N\left(0,{\tau }_i^2\right)$. Here, we choose $N\left(0,{\tau }_i^2\right)$ as the prior for ${\theta }_i$ because it is the conjugate prior for the normal distribution and gives an explicit analytic form. This test can be viewed as a union-intersection test of two one-sided tests: one is for testing $H_0:{\theta }_i\le 0$ for all i against H₁: only one ${\theta }_i>0$; the other is for testing $H_0:{\theta }_i\ge 0$ for all i against H₁: only one ${\theta }_i<0$. The rejection rule in Equation 2 for testing the first one-sided test is rejecting large values of

$$\sum {\pi }_i\text{exp}\left(w_i{Z}_i^2\right),$$ (Equation 3)

where ${\pi }_i\propto {\eta }_i$ and $w_i=1/2\left(1+1/{\tau }_i^2\right)$. It is natural to use ${\eta }_i=1/k$. As the hyperparameter ${\tau }_i$ becomes large, $w_i$ converges to 1/2. On the basis of a similar derivation, this is also the rejection rule for the second one-sided test $H_0:{\theta }_i\ge 0$ for all i versus H₁: only one ${\theta }_i<0$. Therefore, to combine multiple normal statistics and to test whether one of them has a nonzero mean, the Bayes test rejects a large value of the EC of squared normal statistics, $\sum \text{exp}\left(1/2Z_i^2\right)$.

Consider the sparse alternative that at least one and at most $k^{\prime }$ out of k statistics have ${\theta }_i>0$, for which $k^{\prime }\ll k$. Under this sparse alternative, the Bayes test is not easily derived and does not have a simple form. However, this sparse alternative is much closer to class II priors than to class I priors. Even though EC is not necessarily the Bayes test under general sparse alternatives, it remains more powerful than linear combination for combining normal or chi-square statistics.

From a Frequentist Perspective: EC as a Score Test

Interestingly, the same EC procedure can also be derived as the score test for testing $H_0:p=0$ against $H_1:p>0$ on the basis of the profile likelihood $f\left(z_i,\dots ,z_k|{\theta }_1,\dots ,{\theta }_k,p\right)$, where p is the probability of ${\theta }_i$ being nonzero. Let X be the number of ${\theta }_i$’s that are nonzero and let $X\sim B\left(k,p\right)$. The full likelihood is

$$\begin{array}{l}L=f\left(z_1,\dots ,z_k|p\right)=\int f\left(z_1,\dots ,z_k|x\right)f\left(x|p\right)dx\\ \propto \sum _{x=0}^k\sum _{\left(1\right),\dots ,\left(k\right)\in \Lambda }{e}^{-\frac{1}{2}\sum _{i=1}^x{\left(z_{\left(i\right)}-{\theta }_{\left(i\right)}\right)}^2}{e}^{-\frac{1}{2}\sum _{i=x+1}^k{z}_{\left(i\right)}^2}\left(\begin{array}{c}k\\ x\end{array}\right)p^x{\left(1-p\right)}^{k-x},\end{array}$$

where $\Lambda$ is composed of all permutations $\left\{\left(1\right),\dots ,\left(k\right)\right\}$ of the labels for the k variant statistics. For $x=0$, we define ${\sum }_{i=1}^0{\left(z_{\left(i\right)}-{\theta }_{\left(i\right)}\right)}^2=0$. For $x=k$, we define ${\sum }_{i=k+1}^k{z}_{\left(i\right)}^2=0$.

Consider the score test for testing $H_0:p=0$ against $H_1:p>0$. Specifically, at each $X=0,\dots ,k$, one can maximize the likelihood for the nonzero means ${\hat{\theta }}_{\left(i\right)}^{MLE}=z_{\left(i\right)}$. The resulting profile likelihood is given by

$$\tilde{L}\propto e^{-\frac{1}{2}\sum _{i=1}^k{z}_i^2}\sum _{x=0}^k\sum _{\left(1\right),\dots ,\left(k\right)\in \Lambda }{e}^{\frac{1}{2}\sum _{i=1}^x{z}_{\left(i\right)}^2}\left(\begin{array}{c}k\\ x\end{array}\right)p^x{\left(1-p\right)}^{k-x}.$$

If we take the derivative of the log profile likelihood with respect to p, we obtain the following score function:

$$\frac{d\text{log}\tilde{L}}{dp}=\frac{\sum _{x=0}^k\sum _{\left(1\right),\dots ,\left(k\right)\in \Lambda }{e}^{\frac{1}{2}\sum _{i=1}^x{z}_{\left(i\right)}^2}\left(\begin{array}{c}k\\ x\end{array}\right)p^x{\left(1-p\right)}^{k-x}\left(\frac{x}{p}-\frac{k-x}{1-p}\right)}{\sum _{x=0}^k\sum _{\left(1\right),\dots ,\left(k\right)\in \Lambda }{e}^{\frac{1}{2}\sum _{i=1}^x{z}_{\left(i\right)}^2}\left(\begin{array}{c}k\\ x\end{array}\right)p^x{\left(1-p\right)}^{k-x}}.$$

As $p\to 0$, only $X=0$ and $X=1$ contribute to the numerator and only $X=0$ contributes to the denominator, giving the score evaluated at null:

$$\underset{p\to 0}{\text{lim}}\frac{d\text{log}\tilde{L}}{dp}=-k+k\sum _{i=1}^k{e}^{\frac{1}{2}{z}_i^2}.$$

Hence, the score test for testing $H_0:p=0$ rejects large values of ${\sum }_{i=1}^k\text{exp}\left(1/2Z_i^2\right)$, which is the same as the Bayesian test derived under the class II prior.

EC of Chi-Square Statistics

In a related work, Koziol and Perlman (1978)²¹ discussed the combination procedures for combining independent chi-square statistics. In brief, let $Z_i$ be chi-square distributed with degrees of freedom (df) $d{f}_i$ and noncentrality parameter ${\theta }_i$. For testing $H_0:\theta =0$ against $H_1:\sum {\theta }_i>0$ with class II priors, the prior distribution is that with probability ${\eta }_i$, ${\theta }_i$ is distributed according to the conjugate prior gamma distribution ${\varphi }_i\left({\theta }_i\right)=\left({\alpha }_i^{d{f}_i/2}/\Gamma \left(d{f}_i/2\right)\right){\theta }_i^{d{f}_i/2-1}\text{exp}\left(-{\alpha }_i{\theta }_i\right),$ where ${\alpha }_i$ is a hyperparameter and all other ${\varphi }_j\left({\theta }_j\right)=0$ $\left(j\ne i\right)$. Under this alternative, the Bayes test in Equation 2 can be reduced to rejecting large

$$\sum _{i=1}^k{\pi }_i\text{exp}\left(w_i{Z}_i\right),$$ (Equation 4)

where ${\pi }_i\propto {\eta }_i$ and $w_i=1/\left(2\left(2{\alpha }_i+1\right)\right)$. We use ${\eta }_i=1/k$. When ${\alpha }_i$ is small, the exponential weight $w_i$ also approaches 1/2. The Bayes test in Equation 4 rejects large ${\sum }_{i=1}^k\text{exp}\left(\left(1/2\right)Z_i\right)$ when each $Z_i$ is 1 df chi-square distributed.

Weights

Although the idea of EC is to “boost” the large individual statistics in a set when only very few are expected to be from the alternative, how much we should boost is not an arbitrary decision. Large exponential weights could yield huge combined statistics under both the null and the alternative, resulting in low power for distinguishing the alternative from the null. On the basis of mathematical derivations, we obtained the exponential weight $w_i=1/2$ when combining k normal or chi-square statistics for testing against the most sparse alternative—only one out of k is from the alternative. When the alternative is less sparse, $w_i<1/2$ might be slightly more powerful because it puts more weights on statistics other than the largest ones. In general, when multiple standardized statistics are combined, exponential weights around or less than 1/2 are appropriate. In Appendix A, we derive the EC statistics for the burden and the C-alpha tests on the basis of their respective standardized variant statistics. By standardization, we implicitly impose the exponential weights that are inversely proportional to the SD of variant statistics under the null. Because rare variants have smaller SDs, they are weighted more heavily than common variants in the EC analyses.

Sequential Precision-Improvement Permutation for Calculating p Values

As a result of low rare-allele counts in the sample, the individual variant statistics, $Z_i$’s, do not often follow the standard normal or chi-square distribution. Even when they do, the EC statistic, ${\sum }_{i=1}^k\text{exp}\left(\left(1/2\right)Z_i^2\right)$ for combining normal or ${\sum }_{i=1}^k\text{exp}\left(\left(1/2\right)Z_i\right)$ for combining 1 df chi-square statistics, does not have a trivial distribution. Moreover, the parametric form of the EC statistic might become intractable when the linkage disequilibrium (LD) structure among variants is unknown and not easily estimated.

To accurately assess the significance, we permuted phenotypes to calculate the p values. To alleviate the computational burden, we used a sequential precision-improvement permutation algorithm to calculate set-based p values. Specifically, we first permuted phenotypes B = 100 times and estimated the p value for each set. For sets with p values less than 10/B = 0.1, we recalculated their p values with ten times more permutations (B = 1,000) to improve precision. If any genes still had p values less than 10/B = 0.01, we recalculated their p values with ten times more permutations (B = 10⁴). We repeated this procedure until no gene had a p value with low precision (<10/B) or until the number of permutations was greater than a certain fixed number, for example, 10⁶.

Results

Simulations: Power Comparison with Other Combination Procedures Combining Two Chi-square Statistics

Consider a simple scenario: a gene with only two variants. We first calculated the test statistic for each variant, $Z_i\left(i=1,2\right)$. Under the null, i.e., if the variant is not risk associated, $Z_i$ follows a chi-square distribution with 1 df and noncentrality parameter ${\theta }_i=0$. Under the alternative, ${\theta }_i>0$. To test whether the gene is associated with disease risk is to test whether either statistic Z_i is from the alternative. We compared the acceptance boundaries (at size α = 0.01) of four combination procedures for combining two chi-square statistics (see Figure 1). The four combination procedures are: the EC method with gene statistic ${\sum }_{i=1}^2\text{exp}\left(Z_i/2\right)$, Tippett’s method with gene statistic ${\text{min}}_{i=1,2}\left({\text{p}}_i\right)$, where ${\text{p}}_i$ is the p value for $Z_i$ $\left(i=1,2\right)$, Fisher’s method with statistic $-2{\sum }_{i=1}^2\text{log}{\text{p}}_i$, and the linear-combination method with gene statistic ${\sum }_{i=1}^2{Z}_i$. The linear combination and Fisher’s combination have smaller acceptance regions near the symmetric line $z_1=z_2$ (Figure 1) and are thus more powerful when both variant statistics are from the alternative. Exponential and Tippett’s combinations are more powerful near the lines when $z_1=0$ or $z_2=0$. They are more powerful when only one variant statistic is from the alternative. Tippett’s method, however, has the least power when $z_1=z_2$, whereas EC remains competitive when $z_1=z_2$.

Figure 1.

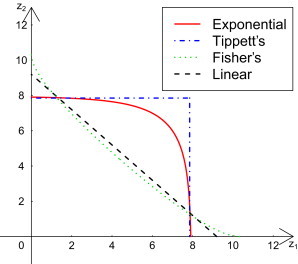
Boundary of Acceptance Regions of the Four Combination Procedures

For testing the noncentrality parameters for $Z_1,Z_2\sim {\chi }_1^2$, $H_0:{\theta }_1={\theta }_2=0$ versus $H_1:{\theta }_1\ge 0$ and ${\theta }_2\ge 0$ with ${\theta }_1+{\theta }_2>0$, the boundaries of acceptance regions of exponential (red solid), Tippett’s (blue dot-dash), Fisher’s (green dotted), and linear (black dashed) combination procedures are compared. The size of each combined test is α = 0.01.

Comparing the Four Combination Procedures on Two Commonly Used Set-Based Methods in Sequencing Studies

We simulated data sets with 10,000 variants not associated with disease risk and 5,000 variants associated with disease risk. For all 5,000 risk-associated variants, we simulated the rare-allele counts to be positively associated with disease risk (i.e., deleterious) with odds ratios uniformly distributed from 1.2 to 1.8. Because all risk-associated variants are associated with risk in the same direction, the simulation is in favor of the burden test. Our EC statistic is based on the sum of the exponential of squared normal (or chi-square) statistics and it is not affected by the direction of association. The simulated data consists of 500 cases and 500 controls. The MAFs of these simulated variants were sampled uniformly from 0.1% to ∼10%. We also repeated the simulations with MAFs from 0.1% to ∼1%, i.e., those involving only rare and very rare variants. The conclusions are the same (see Figure S1, available online).

We compared the power of different combination procedures on the basis of two commonly used set-based tests, the burden test⁷ and the C-alpha test,¹⁰ in three different scenarios: small genes with ten variants in each gene, moderately-sized genes with 100 variants, and large genes with 300 variants. For each scenario, we simulated 1,000 genes. We calculated the gene-level statistics of the burden test and the C-alpha test, and both were based on the linear combination of variant statistics. We derived the EC of these statistics (see Appendix A). We also compared the original linear combination and the proposed EC with Tippett’s and Fisher’s combinations on the burden and the C-alpha statistics. Fisher’s and Tippet’s methods combine variant-level p values in a gene. In sequencing studies, the parametric p values for individual variants can be unreliable as a result of low minor-allele counts for rare variants. To make a fair comparison, we calculated the permutation-based p values for individual variants and then calculated the gene-level statistics for Fisher’s and Tippet’s methods. Even when based on permutation, variant-level p values for very rare variants can still be unreliable, and Fisher’s and Tippet’s methods can suffer from power losses, especially if rarer variants are more strongly associated with disease risk. To assess the significance of the four combination methods, we calculated the gene-level p values for each with up to 10⁴ permutations of phenotypes by using the proposed sequential precision-improvement permutation method.

Figure 2 shows the power comparison of the four combination procedures for different gene sizes as the number of risk-associated variants in each simulated gene increases from 0 to 10. The p value cutoff is 0.001 (other thresholds yield similar conclusions). EC is always more powerful than Tippet’s method, especially when the number of risk-associated variants in a gene is less sparse, e.g., in small genes. Linear combination and Fisher’s method are more powerful than EC in detecting small genes when most variants (≥5 out of 10) are associated with disease risks. To detect moderately sized or large genes, the linear combination of burden statistics is not powerful if only a small number of variants are associated with disease risk (Figure 2A). This is because a few risk-associated variants are combined linearly with a large number of nonassociated variants, and the overall signal strength is diluted. The linear combination of C-alpha statistics still has some power (Figure 2B) but is much less powerful than the EC of C-alpha statistics, especially for large genes with 300 variants. For large genes, EC is always more powerful than competing methods. In practice, with the availability of whole-genome sequencing, the number of variants in a gene can be larger than 300, and the EC procedure can be quite useful.

Figure 2.

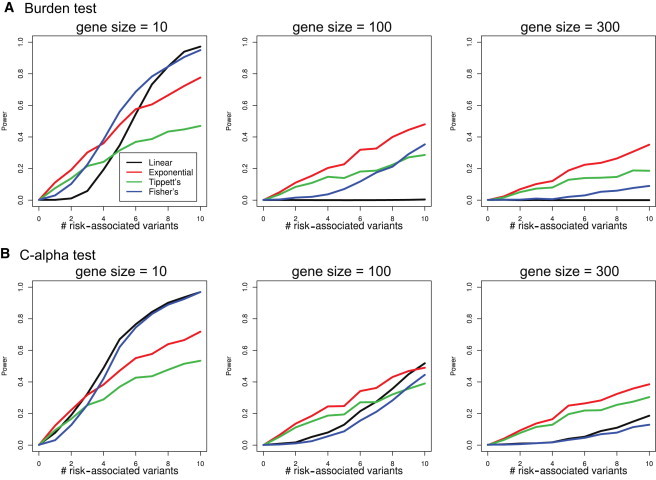
Power Comparison of the Four Combination Procedures on the Burden Test and the C-alpha Test at the p Value Cutoff of 0.001

We compared the power of different combination procedures for different gene sizes as the number of risk-associated variants in each simulated gene increased from 0 to 10. The MAFs of the variants in the simulation range from 0.1% to 10%.

The burden test and the C-alpha test are chosen as examples because in large samples, they can be approximated by a linear combination of normal and chi-square statistics, respectively. In this simulation, as a result of limited sample size and low MAFs of some variants, many variant statistics might not be normal or chi-square distributed. Nevertheless, we still see power improvement from EC when the number (or proportion) of risk-associated variants is relatively small. This indicates that violation of normal or chi-square distribution assumptions does not invalidate our claim—EC is powerful against a sparse alternative.

Comparing the Four Combination Procedures on Simulations Based on Genotype Data from the 1000 Genomes Project

To evaluate the performance of different combination procedures for dependent variants, we conducted simulations based on the whole-genome sequencing data of the 60 HapMap CEU (Utah residents with ancestry from northern and western Europe from the CEPH collection) samples from the 1000 Genomes Project.²² In our simulations and the data analyses that followed, we assigned variants within the start and end coordinates of a gene as the variants of the gene. There were 9,390 genes with at least two variants. The median, mean, and maximum gene sizes were 61, 168.4, and 19,817 variants, respectively. We compared the four combination procedures for combining variant score statistics (or p values of variant score tests) in the genes. The score statistic for variant i is calculated as $q_i={\left({\sum }_j{g}_{ij}{y}_j\right)}^2$, where $g_{ij}$ is the rare-allele count for variant i in individual j and $y_j$ is the standardized phenotype for individual j. Linear combination of variant score statistics in a gene is formed as ${\sum }_j{c}_i{q}_i$, where $c_i$ is the weight for $q_i$ and is inversely proportional to the SD of the score statistic for variant i under the null. Except for the weighting scheme, the linear combination of score statistics is equivalent to SKAT with a weighted linear kernel.¹¹ The EC of score statistics is ${\sum }_i\text{exp}\left(\left(1/2\right)c_i{q}_i\right)$. Because the SDs of score statistics for rare variants are smaller than those for common variants, rarer variants are weighted more. Singletons within a gene are collapsed. Fisher’s and Tippett’s statistics are calculated on the basis of permutation-based variant-level p values in the genes. We first simulated a continuous phenotype under the null, i.e., no gene or variant is associated with the simulated phenotype. For each method, we calculated the gene-level p values for the 9,390 genes with 1,000 permutations. The p values for all methods were uniformly distributed under the null (see Figure S2).

To compare the power under sparse alternatives with dependence, we simulated one continuous phenotype for each gene in the data and simulated the phenotypes to be associated with one to four independent variants in a gene (larger genes were more likely to harbor more causal variants). The log odds ratios were simulated to be proportional to $1/\sqrt{\text{MAF}}$ of the variants. Although only up to four independent causal variants were simulated for each gene, the actual number of phenotype-associated variants could be much larger than four, especially for larger genes, as a result of strong LD among variants in a gene. Table 1 shows the power comparison of the four procedures at different p value cutoffs. EC is 20%–30% more powerful than Tippett’s method. This is possibly because dependence among variants reduces the level of sparsity in the alternative, and by considering statistics other than the maximum (or p values other than the minimum), EC can gain additional power. An alternative explanation is that we simulated rarer variants to be more strongly associated with phenotype and that the p values for very rare variants are less reliable, and as such, Tippett’s method based on individual variant p values can suffer from loss of power. Even with LD among variants, the alternative is still sparse, and EC can be 30%–50% more powerful than either Fisher’s or the linear method.

Table 1.

Power Comparison of the Four Combination Procedures at Different p Value Cutoffs

p Value Cutoff	Linear Combination	EC	Tippett’s Method	Fisher’s Method
0.001	0.186	0.266	0.191	0.169
0.005	0.270	0.381	0.286	0.252
0.010	0.326	0.450	0.349	0.306
0.050	0.496	0.636	0.538	0.484

The results are based on a simulation with genotype data from 60 CEU samples from the 1000 Genomes Project and simulated continuous phenotypes. The following abbreviation is used: EC, exponential combination.

Application to Cell-Based Pharmacogenomics

In previously reported cell-based pharmacogenomics studies, cell lines that had been derived from HapMap CEU samples were treated with platinating agents and assayed for cellular susceptibility phenotypes.²³ In our study, we focused on two platinating agents: carboplatin and cisplatin. The platinating agents are some of the most commonly used chemotherapeutic drugs and are often used clinically against a wide variety of cancers, including head-and-neck cancer (MIM 275355), ovarian cancer (MIM 167000), lung cancer (MIM 211980), and colorectal cancer (MIM 114500).²⁴ Platinum-based treatment can be accompanied by intrinsic and acquired resistance, but the molecular mechanism of resistance is not well understood. Translationally, there is an urgent need for a reliable approach to identifying patients at risk for significant toxicities.²⁵ Cell-based studies have shown that pharmacologic phenotypes in the platinating agents are heritable traits.²⁶ With extensive genotypic (from the HapMap Project) and whole-genome sequence (from the 1000 Genomes Project) data,^1,22 pharmacogenomic studies of lymphoblastoid cell lines have facilitated the investigation of potential genetic etiologies. Investigators have sought to characterize the role of genetic variation in conferring platinum-induced cytotoxicity and in the development of platinum resistance.²⁷

In this study, the half-maximal inhibitory concentration (IC₅₀) was used for measuring the growth-inhibition effect of two anticancer drugs, carboplatin and cisplatin. Specifically, IC₅₀ of carboplatin (or cisplatin) measures the dose of carboplatin (or cisplatin) needed for inhibiting the cells by 50%. Out of the 60 CEU samples (from the 1000 Genomes Project) from which genotype data are available, 58 of them have available (from previous studies^23,28,29) the log2-transformed IC₅₀ of both carboplatin and cisplatin, and the two cytotoxicity phenotypes are significantly correlated (correlation = 0.487).

To identify genes associated with the log2 IC₅₀ of carboplatin, and separately with the log2 IC₅₀ of cisplatin, we formed gene statistics by the linear combination and the EC of score statistics of variants within a gene. We calculated p values by permuting the phenotypes by using the proposed computationally efficient permutation algorithm (see Material and Methods). Because the sample size in this study was limited and because ∼30% of the variants had five or fewer rare-allele counts in this data, the individual variant p values could be unreliable even when they were calculated on the basis of permutation. Results from Fisher’s and Tippett’s methods based on combining variant-level p values are therefore not presented in this analysis.

Figures 3A and 3B show the scatter plots of the p values by linear-combination tests and the p values by EC in the analyses of the two drugs, carboplatin and cisplatin, respectively. Genes with small p values by linear-combination tests always have small EC p values. In contrast, genes with small EC p values might not be identified by linear-combination tests. These plots show that EC is more powerful than linear-combination tests in both carboplatin and cisplatin analyses. At different p value cutoffs, EC often yields more significant findings than do linear-combination tests (see Table S1).

Figure 3.

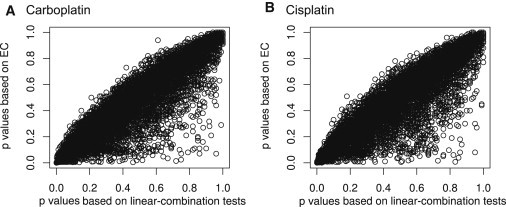
Scatter Plots of p Values Based on Linear Combination Tests and p Values Based on EC in the Analyses of Carboplatin and Cisplatin

(A) Carboplatin.

(B) Cisplatin.

To facilitate further insights into the underlying mechanism of resistance, we conducted DAVID (Database for Annotation, Visualization and Integrated Discovery) functional enrichment analyses³⁰ on the top 100 EC-identified genes associated with carboplatin and cisplatin. The top 100 genes associated with carboplatin showed a highly significant enrichment: 29 genes were involved in acetylation and had a Benjamini-Hochberg-adjusted p value of 0.0076. It has been reported that acetylation might interfere with resistance mechanisms of chemotherapeutic agents such as carboplatin and might elevate the activity of the drug.^31,32 Some other pathways, such as blood-group antigens, phosphoproteins, and transmembrane proteins, are also significantly enriched with the top genes from EC in the DAVID functional analyses. In contrast, only the blood-group-antigen pathway is significantly enriched with the top genes from linear combination in the DAVID functional analyses.

Identified Susceptibility Loci Enable Hypotheses on Mechanism of Toxicities

Two claudin-family genes, namely CLDN9 and the adjacent CLDN6, show suggestive evidence of association with both carboplatin and cisplatin log2 IC₅₀. Claudins are integral membrane proteins that are components of tight junction strands. Given that potentially permanent hearing loss is one of the devastating toxicities associated with the platinum compounds, both the role of the claudin-9 gene as essential for hearing in mice studies and the high sequence conservation of the gene between mice and humans³³ are noteworthy. On the basis of the EC analysis, the p values for CLDN9 are 0.00085 in cisplatin (ranked fourth among 9,390 genes) and 0.0015 in carboplatin (ranked 16th); the p values for CLDN6 are 0.00072 (ranked third) and 0.0012 (ranked tenth) for cisplatin and carboplatin, respectively. Ototoxicity is much more frequent in cisplatin than in carboplatin,³⁴ consistent with our finding that both genes are slightly more significant in cisplatin than in carboplatin. On the basis of the linear-combination analysis, the p values of the two genes are very close to those of EC but have slightly worse rankings. These two adjacent genes harbor 14 variants, mostly with MAFs ≥ 5%, and rare-allele counts of most variants are negatively correlated with log2 IC₅₀ of both cisplatin and carboplatin. This suggests that rare alleles or mutations in claudins might confer sensitivity to the two platinating agents, consistent with the previous finding that wild-type claudin-9 is required for the preservation of sensory cells in the hearing organ.³³ Figure 4A displays the association and LD plot³⁵ of the 14 variants in the two genes. Although none of the variants has an individual variant p value that reaches genome-wide significance, several variants (whether in LD or not) are suggestively associated with carboplatin and cisplatin. These results potentially implicate CLDN9 as a platinum biomarker.

Figure 4.

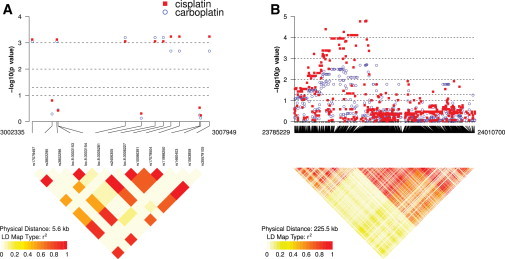
Individual Variant Association to Platinating Agents and LD Plots

(A) The 14 SNPs in CLDN9 and CLDN6 on chromosome 8. From left to right, the first five SNPs are in CLDN9 and the other nine are in CLDN6.

(B) The 585 SNPs in CDH2 on chromosome 10.

Another gene, cadherin-2 (CDH2 [MIM 114020]), is highly significant with a p value of 0.0007 (ranked second) for cisplatin and a p value of 0.038 for carboplatin by EC. CDH2 is also known as neural cadherin (NCAD) and is a calcium-dependent cell-cell adhesion glycoprotein. The protein is commonly present in cancer cells and has an important function in transendothelial migration. Remarkably, in a genome-wide transcriptional study of genes with significantly altered expression between carboplatin-sensitive (S) and carboplatin-resistant (R) cells, CDH2 was found to have nearly 14× lower expression in R cells than in S cells.^36,37 Figure 4B displays the association and LD plot³⁵ of all variants in the genes. Among the 585 variants, rare-allele counts of 461 and 419 variants are negatively correlated with log2 IC₅₀ of cisplatin and carboplatin, respectively. Except for a few variants with individual SNP p values below 10⁻⁴, most are not significantly associated with either drug. In contrast, this gene is not significant by linear-combination analysis.

Discussion

We propose an EC procedure that sums the exponential of variant statistics in a gene- or set-based test. We provide theoretical support for the proposed procedure from both Bayesian and frequentist perspectives, as well as empirical evidence via simulated and real application examples, showing that EC is powerful for detecting sparse alternatives. EC is a general and flexible framework that can be used for improving power for many existing methods for set-based analysis of sequencing data. Furthermore, the proposed procedure is applicable not only to sequencing data but also to GWAS data or other settings where risk-associated genetic factors are sparse.

EC is presented here as a gene- or set-based method. In principle, it is applicable to analyses of pathways, gene-gene or gene-environment interactions, or other much larger sets of genomic features. The extensions of EC to the latter settings might require additional development. For example, in a pathway, there are specific correlation structures among variants in a gene and variants between genes. By treating a pathway as a larger set of variants, one can lose the advantage of pathway analysis. Furthermore, when a pathway becomes too large (say, with more than 10,000 variants) and the risk-associated variants in a pathway are too sparse, even EC might not be powerful in detecting them. For pathway analysis in association studies, Yu et al. (2009)¹⁸ and Biernacka et al. (2012)¹⁹ applied combination methods to gene-level p values. Alternatively, a mixture of EC and other methods at the gene and SNP levels might be useful.

Application of the proposed approach to the pharmacogenomics of platinum compounds (specifically, carboplatin and cisplatin), widely used for the treatment of various cancers, has revealed mechanistic insights underlying resistance and toxicity. The EC analysis identifies more significance than does linear combination at most p value thresholds and implicates shared genetic mechanisms influencing the drug effects of the two chemotherapeutic agents, which are often interchangeably used. In addition, results based on EC recapitulate earlier findings that found potential connections between cell adhesion and the development of chemoresistance.³⁷ Our study identified platinum-associated genes previously shown to be important for hearing loss (a devastating toxicity associated with these compounds) in animal studies.

There might be other situations in which multiple very rare variants in a set are associated with disease risk and in which each of them is only weakly associated with risk. If more than half of the variants in a set are risk associated, the alternative hypothesis is different from the sparse alternative discussed in this work. EC with the proposed form might not be most powerful in those situations. On the basis of preliminary exploration, other forms of EC statistics might offer good power for combining multiple very rare variants. For example, the EC statistic of the form $\sum \text{exp}\left(w_i{Z}_i\right)$, when $Z_i$ is normally distributed, was proposed by van Zwet and Oosterhoff (1967)²⁰ for the combination of multiple one-sided tests. This form of EC of burden statistics is very powerful when one combines multiple very rare variants with the same direction of association with disease risk (e.g., multiple singletons, doubletons, or tripletons with deleterious rare alleles). However, for combining only a small number of risk-associated rare and common variants, the power of $\sum \text{exp}\left(w_i{Z}_i\right)$ is slightly lower than the power of the proposed EC statistic, $\sum \text{exp}\left(w_i{Z}_i^2\right)$, where $Z_i$ is normally distributed.

One caveat of the current EC procedure is that it does not directly incorporate the potential dependence structure among variant statistics, which could have complicated effects on the combined statistic. To circumvent the need to estimate the dependence structure for rare variants and properly control the type-I-error rate, we proposed a sequential precision-improvement permutation algorithm to obtain p values. Although permutation-based strategies are often computationally demanding, the proposed algorithm permutes as few as 100 times for the majority of the genes (or sets). This algorithm is not only computationally efficient but also accounts for the potential effect of the different number of variants in different sets.

With rapid advances in next-generation-sequencing technologies, many studies are conducting association analyses between disease risk and whole-exome or whole-genome sequencing data. Set-based methods have become more and more widely utilized for identifying genetic risk factors associated with various disease traits. The identified genetic factors, especially the rare ones, could be used for improving our understanding of disease etiology and for developing personalized approaches to disease prevention and treatment.

Appendix A

EC for the Burden Test

The burden statistic by Madsen and Browning (2008) collapses genetic burdens (weighted rare-allele counts) in cases. The burden test contrasts the burden statistics in cases versus controls and can be shown to be nearly equivalent to rejection for extreme $S={\sum }_{i=1}^k{s}_i/\sqrt{n{f}_i\left(1-f_i\right)},$ where $f_i$ is the MAF in controls and $s_i$ is the rare-allele count for the i^th variant in cases. The burden test is also equivalent to rejecting large normalized statistic $S^{\prime }={\sum }_{i=1}^k{s}_i^{\prime }={\sum }_{i=1}^k(s_i-2n{f}_i)/\sqrt{2n{f}_i\left(1-f_i\right)}$, where $s_i^{\prime }$ is the standardized variant statistic and 2n is the total number of alleles in cases. We propose the EC of the burden statistic as

$$\tilde{S}=\sum _{i=1}^k\text{exp}\left(\frac{1}{2}{s}_i^{\prime 2}\right).$$

EC for the C-alpha Test

The C-alpha test statistic is defined as $T={\sum }_{i=1}^k{t}_i$ and $t_i={\left(s_i-v_i\gamma \right)}^2-v_i\gamma \left(1-\gamma \right)$, where $s_i$ is the rare-allele count for variant i in cases, $v_i$ is the total rare-allele count for variant i in all samples, and γ is the proportion of cases among all samples; each variant statistic t_i contrasts the variance of observed rare-allele counts in cases with expected variance and tests for overdispersion of variant i. It can be seen that the original C-alpha statistic linearly combines the test statistic from each variant. We propose the EC of the C-alpha statistic as

$$\tilde{T}=\sum _{i=1}^k\text{exp}\left(\frac{1}{2}{t}_i^{\prime }\right),$$

where $t_i^{\prime }$ is a weighted variant statistic, $t_i^{\prime }=c_i{t}_i$. We propose the weight $c_i$ to be inversely proportional to the SD of $t_i$ under the null, where the SD can be estimated by permutation. Because statistics of rarer variants have smaller SDs, rarer variants are weighted more in the combination test.

Web Resources

The URL for data presented herein is as follows:

• Online Mendelian Inheritance in Man (OMIM), http://www.omim.org