A Benchmark Test Suite for Proton Transfer Energies and its Use to Test Electronic Structure Model Chemistries

Abstract

We present benchmark calculations of nine selected points on potential energy surfaces describing proton transfer process in three model systems, H₅O₂⁺, CH₃OH…H⁺…OH₂, and CH₃COOH…OH₂. The calculated relative energies of these geometries are compared to those calculated by various wave function and density functional methods, including the polarized molecular orbital (PMO) model recently developed in our research group and other semiempirical molecular orbital methods. We found that the SCC-DFTB and PMO methods (the latter available so far only for molecules consisting of only O and H and therefore only for the first of the three model systems) give results that are, on average, within 2 kcal/mol of the benchmark results. Other semiempirical molecular orbital methods have mean unsigned errors (MUEs) of 3 to 8 kcal/mol, local density functionals have MUEs in the range 0.7 to 3.7 kcal/mol, and hybrid density functionals have MUEs of only 0.3 to 1.0 kcal/mol, with the best density functional performance obtained by hybrid meta-GGAs, especially M06 and PW6B95.

1. INTRODUCTION

Proton transfer is of central importance to almost every branch of chemistry, and it has been the subject of intense research during recent years. The current literature has many experimental and theoretical investigations [1-9] dealing with the proton transfer process. Modeling proton transfer reactions is often challenging because of the complexity of processes involving H-bond network rearrangement. Hence, it is important that theoretical chemists develop and validate methods that effectively model this category of reactions even in complex systems. High-level ab initio methods are reliable for small molecules but computationally expensive for complex systems, and there are system sizes for which the scaling of ab initio methods like coupled cluster theory, Møller-Plesset perturbation theory, and even density functional theory (DFT) makes them too expensive. Semiempirical molecular orbital theory then becomes the method of choice. In semiempirical molecular orbital methods some of the missing basis set and correlation effects have been included through parameterization.

The purpose of this letter is to present benchmark coupled cluster results for selected distinguished points on potential energy surfaces for proton transfer reactions and use them to assess presently available semiempirical methods for predicting the proton transfer energies; and the results are also compared with density functional results and other high-level wave function calculations. We are particularly interested in checking the accuracy of our newly developed neglect-of-diatomic-differential-overlap semiempirical molecular orbital method called the polarized molecular orbital (PMO) model [10]. The accuracy of the PMO method has been previously tested [10] for properties including polarizability, atomization energy, ionization potential, and complexation energy of water clusters, and the PMO method gives more accurate values for the above properties than the other NDDO methods. Also, several previous NDDO methods yield qualitatively incorrect geometries for water dimer, whereas PMO not only gives the qualitatively correct structure but also gives reasonably accurate geometrical parameters.

2. COMPUTATIONAL DETAILS

The geometries of H₅O₂⁺, CH₃COOH..H₂O, and CH₃OH..H⁺..H₂O are optimized with the density functional methods M08-SO [11], M08-HX [11], M06-2X [12,13], M06-L [13,14], M06 [13,15], M05-2X [13,16], M05 [17], BLYP [18,19], B3LYP[19-21], PBE [22,23], PBE0 [22-24], PW6B95 [25], PWB6K [25], SOGGA11 [26], and VSXC [27] and the wave function methods CCSD [28-31] (coupled cluster theory with single and double excitations), MP2 (second-order Møller perturbation theory), and HF theory (Hartree–Fock). Note that BLYP, PBE, and SOGGA11 are local density functionals of the generalized gradient approximation (GGA) type, M06-L and VSXC are meta-GGAs, B3LYP and PBE0 are hybrid GGAs, and the other functionals tested are hybrid meta-GGAs. Hybrid density functionals include a portion of nonlocal exchange calculated by the HF formula and another portion calculated by local functions of the density and density gradient, and—for hybrid meta-GGAs—the local kinetic energy density.

Ab initio single-point CCSD(T) [32] calculations (CCSD with a quasiperturbative treatment of connected triple excitations) have been performed to compute the electronic energies based on geometries optimized at the M06-2X and CCSD levels of theory; the single-point calculations based on the M06-2X and CCSD geometries will be labeled as //M and //C, respectively. The MG3S [33] basis set has been used for all the above calculations. In addition, the inexpensive HF/STO-3G method was also used to optimize the geometries. All the DFT, MP2, and conventional CCSD(T) calculations were performed using the Gaussian09 program [34], and the MN-GFM module [35] that contains additional Minnesota density functionals.

Single-point energy calculations by the explicitly correlated coupled-cluster CCSD(T)-F12a method [36] in combination with the jun-cc-pVTZ [37] basis set have been performed by using the Molpro program [38] and M06-2X/MG3S optimized geometries. These calculations should be very accurate (M06-2X/MG3S usually gives adequate geometries for coupled cluster calculations, and CCSD(T)-F12a/jun-cc-pVTZ should be close to the complete-basis-set limit of CCSD(T)), and these serve as our benchmarks.

We also tested several semiempirical molecular orbital methods. The performance of the SCC-DFTB method is especially interesting because of recent studies of whether it correctly predicts the sign of energy difference between Zundel and Eigen forms of the hydrated proton [39]. The MNDO, AM1, and PM3 methods are interesting because of their very widespread use; the PDDG/PM3, RM1, and PM6 methods are improved versions of PM3, and the PDDG/MNDO method is an improved version of MNDO. The AM1 [39], MNDO [40], PM3 [41], PM6 [42], RM1 [43], PDDG/PM3 [44], PDDG/MNDO [45,46] calculations and calculations by our recent PMO model [10] were performed using the MOPAC program, version 5.018mn [47]. Self-consistent charge density functional tight binding (SCC-DFTB) [48] calculations were performed using the CHARMM [49-52] program. These semiempirical molecular orbital calculations were all carried out at consistently optimized geometries, in some cases with the constraints stated. The reason we use constraints is to examine points on the potential surfaces that are not stationary points but are liable to be important in the dynamics of certain proton transfer processes.

3. RESULTS AND DISCUSSION

3.1. Proton Transfer in H₅O₂⁺

The protonated water dimer, H₅O₂⁺ has attracted considerable interest during recent years because of its importance in chemistry and biology [53-56]. In water, the proton occurs mainly in two hydration structures, the H₉O₄⁺ [57] and the H₅O₂⁺ [58-60] structures, known respectively as Eigen and Zundel structures. Recently, Johnson and coworkers [56] examined the change in vibrational frequency of the proton upon systematic changes in its immediate environment. Scuseria et.al [55] calculated the proton transfer barrier height of H₅O₂⁺ with various O-O distances using a variety of DFT functionals. In this work, we perform similar calculations to check the accuracy of semiempirical methods. For this, three H₅O₂⁺ structures are optimized; two of these involve O-O distances greater than the equilibrium one; at such distances there is a barrier to transferring the proton.

The first H₅O₂⁺ structure, called structure (a), is freely optimized; the second structure, (b), is optimized at fixed O-O distance (2.7 Å) [the central H atom is allowed to find its equilibrium position]; and structure (c) is optimized at a fixed O-O distance (2.7 Å) with the central H atom equidistant between the two O atoms. In both second and third structures, the four outer H atoms were relaxed to their equilibrium positions.

The optimized structures calculated by the M06-2X/MG3S level of theory are shown in Figure 1. Table 1 shows the calculated energy difference between the three structures of H₅O₂⁺ as calculated by various methods. The proton transfer barrier height for an external O-O separation of 2.7 Å has been calculated by subtracting the energy of structure (b) from that of structure (c). The calculated values of barrier heights by different methods are compared with the value obtained by the more accurate CCSD(T)-F12a method.

Figure 1.

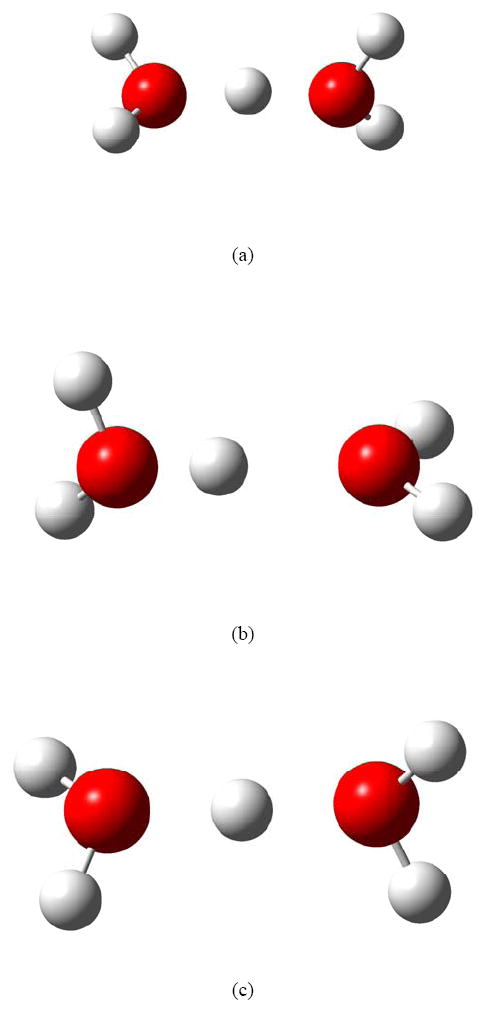
The structures of H₅O₂⁺ optimized by M06-2X/MG3S.

Table 1.

The calculated relative energies (in kcal/mol) between the optimized and partially optimized structures of H₅O₂⁺, CH₃OH…H⁺…OH₂ and CH₃COOH…OH₂ and mean unsigned errors (in kcal/mol).

Methods	H5O2+			CH3OH…H+…OH2			CH3COOH…OH2		MUE(3)a	MUE(8)b
	(Ec − Eb)	(Ec − Ea)	(Eb − Ea)	(EC − EB)	(EC − EA)	(EB − EA)	ΔE1	ΔE2
Wave function theory
CCSD(T)-F12a/jun-cc-pVTZ//M	5.27	9.99	4.72	9.85	11.93	2.09	183.43	-10.61	0.00	0.00
MP2/MG3S	5.15	9.97	4.82	9.48	11.82	2.34	182.87	-10.68	0.08	0.20
CCSD(T)/MG3S//M	5.59	10.12	4.53	10.25	12.12	1.87	184.50	-10.70	0.21	0.33
CCSD(T)/MG3S//C	5.61	10.12	4.51	10.23	12.32	2.09	186.47	-10.68	0.23	0.83
CCSD/MG3S	6.42	10.60	4.17	11.28	13.18	1.89	185.48	-9.99	0.77	0.91
HF/MG3S	10.43	13.20	2.78	16.41	17.40	0.99	187.19	-7.61	3.44	3.77
HF/STO-3G	3.18	24.22	21.05	6.64	24.06	17.42	249.33	-10.86	10.89	16.18
Hybrid density functional theory
M06/MG3S	5.07	10.21	5.14	9.37	11.32	1.95	182.85	-11.10	0.28	0.29
PW6B95/MG3S	4.78	9.79	5.01	9.35	11.64	2.30	183.60	-10.09	0.33	0.33
M08-HX/MG3S	5.42	9.73	4.31	9.81	12.03	2.22	181.93	-11.57	0.27	0.44
M08-SO/MG3S	5.25	9.75	4.49	9.75	11.56	1.81	181.92	-11.73	0.16	0.48
M05/MG3S	4.37	9.75	5.38	9.13	10.80	1.67	183.21	-10.47	0.60	0.49
PBE0/MG3S	4.03	9.99	5.96	8.29	11.35	3.06	183.15	-10.73	0.83	0.75
M06-2X/MG3S	3.94	10.25	6.31	8.30	11.73	3.43	183.73	-11.29	1.06	0.91
B3LYP/MG3S	3.82	8.94	5.12	8.33	10.67	2.34	183.06	-9.59	0.97	0.92
PWB6K/MG3S	6.38	11.55	5.17	11.15	13.65	2.50	184.62	-10.81	1.04	0.99
M05-2X/MG3S	3.41	9.75	6.34	8.05	11.35	3.30	183.65	-11.19	1.24	1.02
Density functional theory without HF exchange
M06-L/MG3S	4.06	8.80	4.75	8.31	10.32	2.01	184.80	-10.83	0.81	0.72
VSXC/MG3S	4.18	7.67	3.49	9.82	10.92	1.10	182.90	-12.32	1.55	1.11
SOGGA11/MG3S	3.17	9.43	6.26	7.19	10.27	3.08	179.84	-6.49	1.40	2.15
PBE/MG3S	1.96	7.56	5.60	5.67	8.43	2.76	181.24	-11.04	2.21	2.20
BLYP/MG3S	2.14	6.82	4.68	6.24	8.27	2.03	169.35	-8.87	2.11	3.68
Semiempirical molecular orbital theory including overlap
SCC-DFTB	4.07	9.26	5.19	6.22	8.96	2.74	185.36	-7.97	0.80	1.78
NDDO Methods
PMO	4.32	8.40	4.07	…	…	…	…	…	1.06	…
PDDG/PM3	8.28	9.90	1.62	8.93	10.17	1.24	192.07	-5.01	2.06	3.00
RM1	2.44	10.69	8.25	2.51	9.34	6.83	185.39	-3.85	2.36	3.81
AM1	9.60	7.43	-2.18	12.97	10.13	-2.84	190.29	-7.44	4.60	4.21
PM3	12.67	8.84	-3.84	13.81	14.13	0.32	194.85	-5.97	5.70	5.14
PM6	0.00	3.41	3.41	0.89	3.34	2.45	166.44	-8.90	4.38	6.22
PDDG/MNDO	13.15	14.53	1.38	14.98	14.51	-0.47	166.38	-1.17	5.25	6.56
MNDO	20.63	21.45	0.82	21.64	23.40	1.76	186.19	-0.88	10.24	8.35

^aMUE(3) is the unsigned error averaged over the three energy differences of H₅O₂⁺.

^bMUE(8) is the unsigned error averaged over all eight relative energies.

Table 1 shows that hybrid density functionals are usually more accurate (MUE of 0.3 to 1.0 kcal/mol) than local density functionals (MUE of 0.7 to 3.7 kcal/mol). Semiempirical molecular orbital theory is less accurate than most density functionals with most MUEs in the range 3.0 to 8.4 kcal/mol. The most accurate semiempirical molecular orbital method, on average, is SCC-DFTB, followed by PDDG/PM3.

The PMO method is so far parameterized only for the compounds containing H and O (there are no carbon parameters yet). The table shows excellent performance for the three cases on which it can be tested. At the time that this paper was being prepared we and our coworkers (H. Leverentz, L. Fiedler, Y. Wang, P. Zhang, J. Han, and the present authors) already had a preliminary parametrization of PMO for carbon-containing molecules, without the present data in the training set. Testing this version of PMO for the remaining six data (see next two sections) showed better overall accuracy [MUE(3) = 1.4 kcal/mol; MUE(8) = 2.7 kcal/mol] than the previous NDDO results; however, we do not present the detailed results here because PMO for carbon-containing compounds is being further optimized against a broader training set that includes the data presented here and other new data. We anticipate that the data presented here may also be useful for other parametrization and validation studies. For example, it would be useful to use them to test two other semiempirical methods: OMx [61] and the third-order extension of SCC-DFTB, called DFTB3 [2,63].

3.2. Proton Transfer in CH₃OH…H⁺…OH₂

Methanol is one of the smallest molecules that contains both hydrophilic and hydrophobic groups; it is mixable with water in all proportions and forms multiple hydrogen bonds [64]. It can be protonated to form CH₃OH₂⁺ in the presence of strong acids. The methyloxonium ion (CH₃OH₂⁺) plays a significant role in many organic and biological reactions [65]. Experimental [56,66,67] and theoretical [68] studies have been carried out to study the proton transfer in CH₃OH…H⁺…OH₂. Johnson and coworkers [56] suggested that methanol can better accept the excess charge of protonation than can H₂O. Here, we test the accuracy of various electronic structure methods to predict the proton transfer energy in the model CH₃OH…H⁺…OH₂. For this, three CH₃OH…H⁺…OH₂ structures were optimized. The first structure, called A, is freely optimized; the second structure, called B, is optimized at fixed O-O distance (2.7 Å) and the central H atom was allowed to find its equilibrium position, and the third structure, called C, is optimized at fixed O-O distance (2.7 Å) but fixing the position of the central H atom to be equidistant between the two O atoms. The structures of CH₃OH…H⁺…OH₂ optimized by M06-2X/MG3S method are shown in Figure 2. The calculated energy differences between these three structures are summarized in Table 1.

Figure 2.

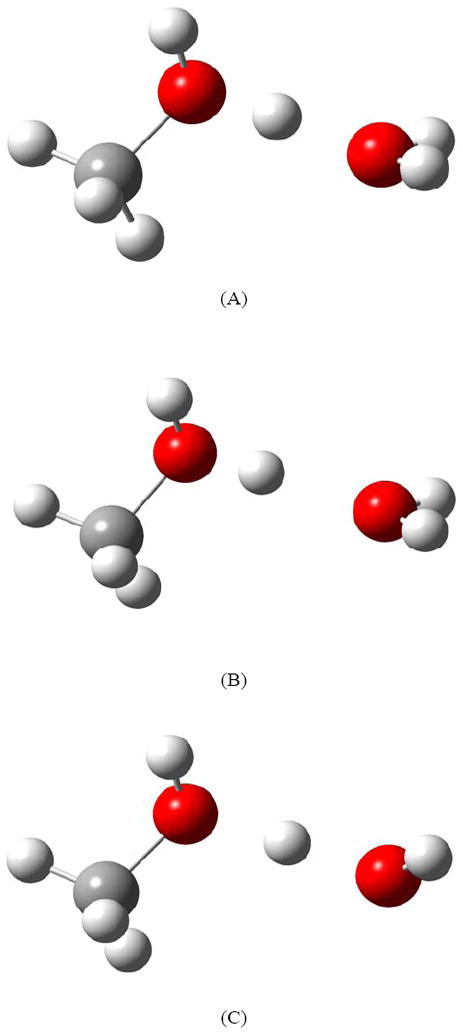
The structures of CH₃OH…H⁺…OH₂ optimized by M06-2X/MG3S.

Table 1 shows that only four of the density functionals (M06, PW6B95, M08-HX, and M08-SO) predict all three energy differences correctly to within 1 kcal/mol. None of the semiempirical molecular methods is that accurate, but PDDG/PM3 predicts all three energy differences within 1.8 kcal/mol.

3.3. Proton Transfer in CH₃COOH…OH₂

Acetic acid is one of the simplest carboxylic acids. It has received attention from both experimental [69,70] and theoretical [71] points of view. In the present study, the structures CH₃COO⁻, H₃O⁺, CH₃COOH, H₂O and CH₃COOH…H₂O are optimized with various ab initio, density functional, and semiempirical molecular orbital methods; see Fig 3. The relative energies of CH₃COO⁻ + H₃O⁺ (ΔE₁) and CH₃COOH…H₂O (ΔE₂) with respect to CH₃COOH + H₂O have been calculated and are summarized in the Table 1. For each method, the two calculated relative energies are compared with the CCSD(T)-F12a method and the mean unsigned error (MUE) has been calculated by taking the average absolute errors calculated for all the structures with respect to the more accurate CCSD(T)-F12a method.

Figure 3.

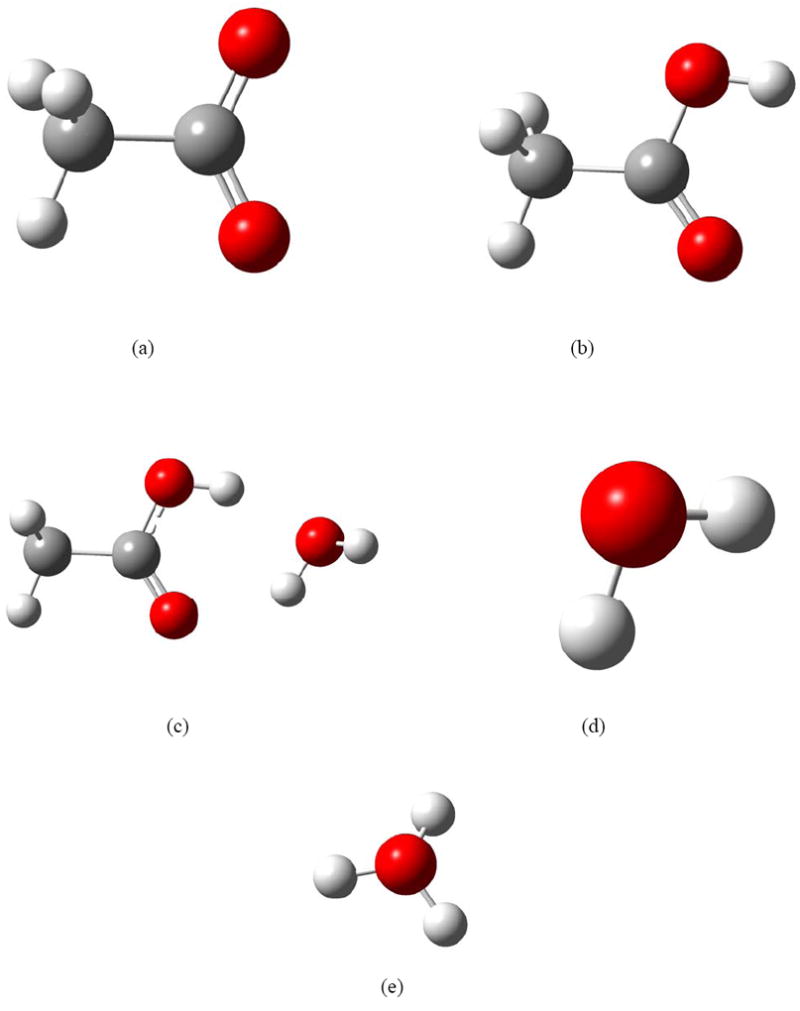
The structures of (a) CH₃COO⁻. (b) CH₃COOH, (c) CH₃COOH…H₂O, (d) H₂O and (e) H₃O⁺ optimized by M06-2X/MG3S.

In this case six of the density functionals (M06, PW6B95, M05, PBE0, M06-2X, and M05-2X) predict both energy differences to within 1 kcal/mol. None of the semiempirical methods predicts both of them within 2 kcal/mol, but SCC-DFTB predicts them both within 2.64 kcal/mol.

4. CONCLUSIONS

In the present study, we have performed benchmark calculations for assessing density functionals and semiempirical molecular orbital methods. We tested six wave function methods, 15 density functional methods, and nine semiempirical molecular orbital methods. The mean unsigned error, averaged over the eight cases studied, is given in the last column of the table. Among the tested NDDO methods, PMO is the best performing method and it gives an MUE of only 1.06 kcal/mol for H₅O₂⁺, which is less than the HF method and some of the DFT methods without HF exchange. We recommend that the PMO method may be an efficient and accurate alternative to computationally expensive methods for these types of proton transfer calculations. The SCC-DFTB method is also recommended for this purpose, and it has a mean unsigned error of only 1.8 kcal/mol for all eight cases. The other semiempirical orbital methods have mean unsigned errors of 3–8 kcal/mol, which is remarkably good when one recalls that these methods are formally simplified and parameterized versions of minimal-basis set Hartree-Fock theory, represented here by the HF/STO-3G method, which has mean unsigned error of 16 kcal/mol. Five of the hybrid meta-GGA density functionals (M06, PW6B95, M08-HX, M08-SO, and M05) show remarkably good accuracy when averaged over the eight tests, with the first two having mean unsigned errors of 0.3 kcal/mol, the next having a mean unsigned error of 0.4 kcal/mol, and the next two having a mean unsigned error of 0.5 kcal/mol. PW6B95 is noteworthy for having only six semiempirical parameters.

Highlights.

We present benchmark calculations of energies, barriers for proton transfer to water.

Methods include hybrid meta-GGAs, M06-L, PW6B95, SOGGA11, MP2, SCC-DFTB, PMO, NDDO