Silicon as an Unconventional Detector in Positron Emission Tomography

Abstract

Positron emission tomography (PET) is a widely used technique in medical imaging and in studying small animal models of human disease. In the conventional approach, the 511 keV annihilation photons emitted from a patient or small animal are detected by a ring of scintillators such as LYSO read out by arrays of photodetectors. Although this has been a successful in achieving ~5mm FWHM spatial resolution in human studies and ~1mm resolution in dedicated small animal instruments, there is interest in significantly improving these figures. Silicon, although its stopping power is modest for 511 keV photons, offers a number of potential advantages over more conventional approaches. Foremost is its high spatial resolution in 3D: our past studies show that there is little diffculty in localizing 511 keV photon interactions to ~0.3mm. Since spatial resolution and reconstructed image noise trade off in a highly non-linear manner that depends on the PET instrument response, if high spatial resolution is the goal, silicon may outperform standard PET detectors even though it has lower sensitivity to 511 keV photons. To evaluate silicon in a variety of PET “magnifying glass” configurations, an instrument has been constructed that consists of an outer partial-ring of PET scintillation detectors into which various arrangements of silicon detectors can be inserted to emulate dual-ring or imaging probe geometries. Recent results have demonstrated 0.7 mm FWHM resolution using pad detectors having 16×32 arrays of 1.4mm square pads and setups have shown promising results in both small animal and PET imaging probe configurations. Although many challenges remain, silicon has potential to become the PET detector of choice when spatial resolution is the primary consideration.

1. Introduction

As use of positron emission tomography increases in medicine, there is increasing demand for higher spatial resolution for imaging mouse and rat models of human disease as well as for improved detection of small tumors in many cancers. The conventional approach to achieving higher resolution is to scale down crystal dimensions in scintillation detector configurations currently used in PET instruments. Although this has been successful in improving spatial resolution to 1–1.5mm FWHM for small animal imaging, and arrays of new silicon photomultipliers have recently buoyed this effort, it remains challenging to achieve spatial resolution in the deep submillimeter regime at high detection effciencies.

We have been investigating an alternative approach to achieving high spatial resolution: use of silicon as a detector for 511 keV annihilation photons rather than a high-Z scintillator such as LYSO [1]. In a separate effort, silicon has been considered for PET by Di Domenico, et al. [2]. Although detection effciency is significantly less than for dense scintillators (attenuation length 1.1 cm for LYSO vs. 5.0 cm for Si) and the photoelectric interaction effciency is well below 1% at 511 keV, Compton interactions can be localized to high precision, which can result in instruments whose resolution is limited only by the range of the positron in tissue before annihilation [3]. Moreover, it appears possible to achieve reasonable system effciencies using a combined silicon/scintillator PET scanner [4]. In the past, we have applied this technology to single-slice demonstrators and devices compatible with nuclear magnetic resonance imaging (MRI) to evaluate the effect of strong magnetic fields on positron-range [5]. In the present study, we examine the use of silicon as the inner detector in a dual-ring, magnifying PET geometry. We focus here on the ability to achieve high spatial resolution in a field-of-view (FOV) appropriate for imaging small animals such as mice and rats; nevertheless, the basic ideas can be extended to other magnifying geometries such as PET imaging probes that can be used to obtain high-resolution images in pre-specified regions-of-interest in human subjects [6].

2. High Resolution PET

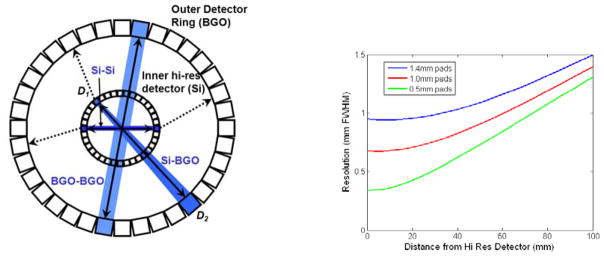
Shown at left in Fig. 1 is the dual-ring, magnifying geometry. An inner detector ring, in this case comprising high-resolution silicon detectors, surrounds a small FOV and is in turn surrounded by a conventional position-sensitive scintillation detector used in PET. Note that three significant coincidence events can occur, which we denote as Si-Si, Si-BGO, and BGO-BGO. Si-Si and BGO-BGO events clearly support the highest and lowest spatial resolution, respectively. Resolution for mixed Si-BGO coincidences, however, varies with the fractional position along the line-of-response (LOR) connecting the two detectors.

Figure 1.

Left: drawing of magnifying PET geometry showing three major coincidence types. Right: plot of resolution vs. distance from the silicon detector for Si-BGO coincidences for Si detectors having 0.5 mm, 1.0 mm, and 1.4 mm square pads in coincidence with a detector at distance 570 mm having 6 mm FWHM resolution.

For two PET detectors D₁ and D₂ separated by distance D (millimeters), the resolution R_D transverse to a line-of-response (LOR) at distance α×D from D₁ is given by

$$R_D\approx \sqrt{{(1-\alpha )}^2(r_{C1}^2{cos}^2{\theta }_1+r_{D1}^2{sin}^2{\theta }_1)+{\alpha }^2(r_{C2}^2{cos}^2{\theta }_2+r_{D2}^2{sin}^2{\theta }_2)+{(\alpha (1-\alpha )D\delta )}^2}$$ (1)

where 0 ≤ α ≤ 1 is the fractional distance along the LOR starting at D₁,θ_i is the angle-of-incidence of the LOR on each detector, and δ = 0.0088 radians is the FWHM angular uncertainty due to acolinearity of the annihilation radiation in water. Intrinsic resolution (FWHM) for each detector in the tranverse (circumferential) and depth directions is denoted as r_Ci and r_Di, respectively.

Eq. (1) shows that resolution along the LOR is dominated by the detector closest to the source. Detectors having high resolution, such as achievable with silicon, can thus provide excellent resolution in the magnifying geometry of Fig. 1. Although beyond the scope of this presentation, resolution recovery can be done to an extent with PET systems having poorer intrinsic resolution but incurs the significant penalty of increased noise in reconstructed images (see Figs. 7–8 in [7]). Because of this, silicon may be preferable when high resolution in PET is a primary goal. At right in Fig. 1 is the intrinsic resolution plotted against distance from the silicon detector for three pad sizes (0.5 mm, 1.0 mm, and 1.4 mm square) in coincidence with detector located at distance 570 mm having 6 mm FWHM intrinsic resolution. Even though the external detector has relatively poor resolution and no depth-of-interaction resolution, spatial resolution within a FOV appropriate for pre-clinical imaging of small animals can be significantly better than 1 mm FWHM.

3. Demonstration Instrument

To demonstrate the principles of the magnifying geometry and the use of silicon for PET, the device shown in Fig. 2 was constructed atop a 1.2 m ×1.8 m optical table. A partial ring of conventional PET BGO block detectors at 500 mm radius surrounds a partial “ring” consisting of four silicon-pad detectors located at a nominal radius of 70 mm from the center of the 45 mm diameter field-of-view. In order to acquire PET data over the angular range of 180° required for reconstruction, objects are typically rotated in 6° increments during data collection. To reduce the single-event rates in both silicon and BGO detectors (high rates lead to a large random coincidence rate and increase deadtime), sources are shielded with lead and collimated to a 1 mm thick slice using tungsten (which is removed for volume PET data collection as described below). Trigger and position information from each detector in the setup is routed to a VME based data acquisition system that includes a programmable FPGA module (CAEN v1495) that controls types of coincidence events accepted as well as readout of position and energy information from all detectors. All information for each coincidence is stored in an event list, which is then post-processed (e.g. energy and timing windows can be altered post-acquisition) to generate data for image reconstruction.

Figure 2.

Left: full test-bed showing partial-ring of BGO block detectors at 500mm radius, inner “ring” of silicon detectors, slice collimation and object turntable. Right: closeup view of silicon detectors set up for the single-slice arrangement. Detectors are easily rearranged to emulate other geometries such as volume PET and imaging probes.

3.1. Silicon detectors

The silicon detector technology used in this instrument is described by Meier, et al. [8]. In the configuration shown in Fig. 2, a stack of two 512-pad, 1 mm thick silicon detectors flank each side of the field-of-view. The 1.4 mm × 1.4 mm pads are arranged in a 32×16 array and each is read out by 4 128-channel VATA GP7 ASICs (Gamma-Medica Ideas, Northridge, CA USA). Each channel of the ASIC has a fast (150 ns) shaper and leading-edge threshold trigger for coincidence timing and a slow (500 ns) shaper for pulse-height. Detectors are controlled and read out using a VME-bus based system of custom boards.

Although not important for this application, energy resolution is nominally 2.4 keV FWHM for the 59.5 keV peak of ²⁴¹Am and position resolution is outstanding being primarily determined by the pad size rather than by the range of the Compton recoil electron [3]. Timing resolution, which is important for PET, is relatively modest. There are two issues: time-walk and jitter. The large range of pulse-heights associated with Compton interactions when combined with the leading-edge trigger and shaped signal (150 ns peaking time) leads to a large time-walk (up to 150 ns). Jitter results from electronic noise and from the fact that the shape of the detector signal used for timing can vary considerably depending on the random 3D interaction position of photons as well as the direction of the Compton recoil electron in the detector [9].

3.2. Scintillation detectors

The conventional PET ring consists of 24 BGO block detectors scavenged from a CTI 931 clincal PET scanner (vintage 1985). Each block has an 8 (circumferential) × 4 (axial) array of 6 mm ×12 mm ×30 mm BGO crystals. Interaction locations of annihilation photons are estimated by light-sharing among a 2×2 array of photomultipliers. Original PET electronics were replaced with simpler setup consisting of a fast channel and constant-fraction discriminator for coincidence timing and individual RC-CR shaping amplifiers for each PMT. Shaped signals for all blocks are routed to peak-sensing ADCs (CAEN v785) for position and energy estimation while timing signals are routed to the FPGA-based coincidence unit.

Performance of these older detector modules is far from the current state-of-the-art in PET. Position resolution is somewhat worse than 6 mm FWHM in the circumferential direction and 12 mm FWHM in the axial direction, energy resolution is ~20% FWHM, and timing resolution 12–20 ns FWHM at 511 keV. Nevertheless, as shown in the next section, these detectors provide a compelling demonstration of the resolution insensitivity predicted by eq. (1) when detectors having poor resolution are located far from the field-of-view in a magnifying geometry.

4. PET Imaging Results

4.1. Single slice configuration

Reconstructed images from a resolution phantom for the single-slice setup are shown in Fig. 3. To collect approximately 10⁷ Si-Si events in this low-effciency configuration, the resolution phantom was repeatedly filled with 185 MBq of ¹⁸F and imaged in 5 hour sessions (2.7 half-lives). Rod diameters are 4.8 mm, 4.0 mm, 3.2 mm, 2.4 mm, 1.6 mm and 1.2 mm. Data collected in list-mode were processed into sinograms having 0.2 mm bins in radius and 0.9° steps in angle over 180° for all event classes. Images were reconstructed using a maximum likelihood expectation-maximization (ML-EM) algorithm that incorporated a system model accounting for the measurement resolution of each event class [7].

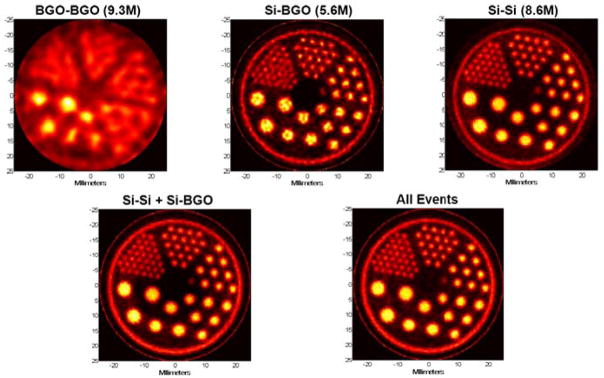
Figure 3.

Single-slice reconstructions. Top row: reconstructions from BGO-BGO, Si-BGO, and Si-Si coincidences alone (reconstructed using 1000, 400, and 100 iterations, respectively, using the ML-EM method noted in the text). Bottom row: reconstructions from combined Si-Si and Si-BGO events (left, 400 iterations) and all events (right, 1000 iterations).

As expected, reconstructions using only BGO-BGO events exhibit the poorest spatial resolution–somewhat worse than 3 mm FWHM due to mispositioning errors in the first-generation PET block detectors. Reconstructions from the Si-BGO events, on the other hand, are significantly better and demonstrate the magnifying PET concept. Even the 1.2 mm rods can be resolved in this reconstruction. The Si-Si reconstructions show the best resolution and also lower noise than images reconstructed using only Si-BGO events.

An appropriate reconstruction method can combine all classes of events to obtain a single reconstruction (a maximum likelihood method was described by Clinthorne, et al. in [7]). Correctly done, using all events can improve the quality of the reconstruction over that obtainable from the highest resolution data alone and at worst will not result in a poorer quality image. In the present situation, where the Si-Si data comprise a large fraction of the total, we might not expect to see significant benefits from adding the lower resolution events. The left and right images in the bottom row of Fig. 3 are reconstructions that combine the Si-Si and Si-BGO events and all events, respectively. As predicted, there is little to be gained by adding the lower resolution events in this case; however, when there are many fewer Si-Si events or when the desired reconstructed point spread function is broader, the lower resolution data may significantly reduce image noise.

4.2. Volume PET configuration

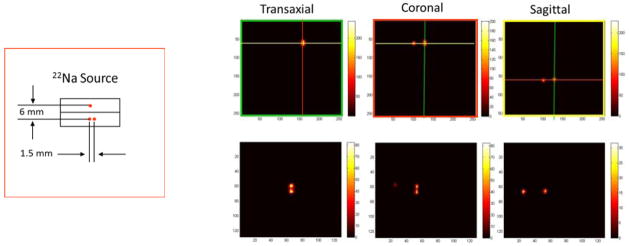
One of the advantages of the PET demonstrator is that it can be easily reconfigured to emulate different geometries. For the reconstructed images shown in Fig. 4, a volume PET imaging configuration was used in which the slice collimation was removed and the silicon detectors were rotated 90° such that the plane of each detector was perpendicular to optical table creating a 45 mm diameter × 22 mm axial field-of-view. For initial studies, three ²²Na point sources were combined as shown at left in Fig. 4. Data were again collected in list-mode over a 5 hour acquisition and the image volume was reconstructed directly from this data using a 3D list-mode maximum likelihood reconstruction. The top row of images in Fig. 4 show three orthogonal planes through reconstructions of the Si-BGO events (the colored lines corresponding to the plane of each image outlined by the same color). While the sources separated by 6 mm are easily distinguished, those separated by 1.5 mm are not. Reconstructions from the Si-Si events for a similar set of orthogonal planes are shown in the bottom row. All three points are clearly separated.

Figure 4.

Left: drawing of ²²Na source used for images at right. Right, top row: transaxial, coronal and sagittal planes from volume reconstruction of Si-BGO events. Sources separated by 6 mm are clearly resolved while those separated by 1.5 mm are not. Bottom row: reconstructions in similar orthogonal planes from Si-Si events. As expected, all sources are resolved.

5. Discussion and Conclusion

Although silicon has a lower detection effciency for a given volume than LYSO, it is a promising PET detector where high spatial resolution is a primary goal. In this context, it may find use in high-resolution preclinical PET for studying mechanisms of human disease with small animal models or in high-resolution imaging probes that can be used to augment conventional PET for human subjects. To test these concepts, we developed a reconfigurable “dual-ring” instrument consisting of a partial outer ring of conventional PET detectors at large radius supplemented by an partial inner ring of silicon. Both single-slice and volume PET geometries were evaluated as well as the ability of the image reconstruction to combine the three classes of “interesting” coincidences.

While silicon is an interesting detector material for high resolution PET, there are numerous challenges. The most significant at this point appear to be (1) dense packaging, (2) reading out high granularity detectors, and (3) coincidence timing. As an example, a tomograph with good effciency can be constructed by locating ~150 cm³ of silicon around a 4 cm diameter ×4 cm long FOV. Reading out the silicon at a granularity of 1 mm³ requires 150K separate positions (each associated with one channel of electronics in the current configuration). Moreover, at typical PET event rates, the desired timing resolution should be on the order of 10 ns FWHM or less to keep random coincidences low; however, present implementations are far from that figure. It is likely that these issues can be eventually resolved but significant work remains.

Research Highlights.

• We examine the use of position-sensitive silicon detectors in magnifying PET geometries

• A demonstrator using silicon detectors and BGO scintillation detectors was constructed

• Both single-slice and volume PET configurations were tested

• For a 4.5 cm field-of-view, resolutions <1mm were achievable

• Resolution will improve further with higher resolution silicon detectors