Active Detergent-solubilized H⁺,K⁺-ATPase Is a Monomer

Background: The proton pump H⁺,K⁺-ATPase is responsible for the acidification of the gastric fluid. The minimum organization required for its activity is not established.

Results: We defined a solubilization protocol allowing us to obtain pig gastric H⁺,K⁺-ATPase as an active species.

Conclusion: Active detergent solubilized H⁺,K⁺-ATPase is unambiguously an α,β monomeric protomer.

Significance: The H⁺,K⁺-ATPase functioning is most probably similar to other P-ATPases.

Abstract

The H⁺,K⁺-ATPase pumps protons or hydronium ions and is responsible for the acidification of the gastric fluid. It is made up of an α-catalytic and a β-glycosylated subunit. The relation between cation translocation and the organization of the protein in the membrane are not well understood. We describe here how pure and functionally active pig gastric H⁺,K⁺-ATPase with an apparent Stokes radius of 6.3 nm can be obtained after solubilization with the non-ionic detergent C₁₂E₈, followed by exchange of C₁₂E₈ with Tween 20 on a Superose 6 column. Mass spectroscopy indicates that the β-subunit bears an excess mass of 9 kDa attributable to glycosylation. From chemical analysis, there are 0.25 g of phospholipids and around 0.024 g of cholesterol bound per g of protein. Analytical ultracentrifugation shows one main complex, sedimenting at s_20,w = 7.2 ± 0.1 S, together with minor amounts of irreversibly aggregated material. From these data, a buoyant molecular mass is calculated, corresponding to an H⁺,K⁺-ATPase α,β-protomer of 147.3 kDa. Complementary sedimentation velocity with deuterated water gives a picture of an α,β-protomer with 0.9–1.4 g/g of bound detergent and lipids and a reasonable frictional ratio of 1.5, corresponding to a Stokes radius of 7.1 nm. An α₂,β₂ dimer is rejected by the data. Light scattering coupled to gel filtration confirms the monomeric state of solubilized H⁺,K⁺-ATPase. Thus, α,β H⁺,K⁺-ATPase is active at least in detergent and may plausibly function as a monomer, as has been established for other P-type ATPases, Ca²⁺-ATPase and Na⁺,K⁺-ATPase.

Introduction

The H⁺,K⁺-ATPase present in gastric mucosa is a P-type ATPase (1) capable of pumping protons or hydronium ions against very high concentration gradients (∼10⁶:1) by an electroneutral K⁺ exchange mechanism (2, 3). Like Na⁺,K⁺-ATPase, with which it shares high sequence similarity, H⁺,K⁺-ATPase is made up of an α-catalytic and a β-glycosylated subunit. It is responsible for the acidification of the gastric fluid, with important pathophysiological consequences in cases of gastric hypersecretion. Extensive investigations on H⁺,K⁺-ATPase have led to the successful development of drugs of the omeprazole type and of K⁺ competitive blockers like the Schering compound SCH28080 to inhibit H⁺,K⁺-ATPase in vivo (4–6). However, despite previous efforts, some fundamental aspects of the structure and function of H⁺,K⁺-ATPase are still not well understood, especially in relation to those of other P-type ATPases. This includes the relation between cation translocation and the organization of the protein in the membrane. Although analysis of ordered two-dimensional crystals indicates overall structural features of H⁺,K⁺-ATPase similar to those of Na⁺,K⁺-ATPase and sarcoplasmic reticulum Ca²⁺-ATPase (7–9), other studies on H⁺,K⁺-ATPase have indicated that retention of enzyme activity in the detergent-solubilized state depends on the enzyme being present in a α₂,β₂ dimer or higher oligomeric state of the α,β-protomer (10–18). The role of an obligate oligomeric organization of functional importance is underscored by functional evidence for half-of-the-sites reactivity and other observations in the membranous state (18, 19). Altogether, these findings are in marked contrast to those emerging earlier on sarcoplasmic reticulum Ca²⁺-ATPase, in particular from studies on detergent solubilization (20–22) and on reconstitution in a surplus of phospholipids (23) and detailed studies of the kinetics and ligand stoichiometry (21, 24). Despite the probable presence of protein-protein interactions in the native membrane, which may affect enzyme activity (25, 26), they all indicate monomeric Ca²⁺-ATPase as the fundamental Ca²⁺-transporting unit. For Na⁺,K⁺-ATPase, the evidence is more equivocal in that both monomeric and dimeric forms with retention of enzyme activity have been detected by analytical ultracentrifugation (27–30) and by HPLC (31–33). The requirement of an oligomeric structure as a sine qua non to preserve transport and enzyme activity, as claimed for H⁺,K⁺-ATPase and reported in a recent review (34), is not indicated by either the detergent data or by the available three-dimensional x-ray diffraction structures of Ca²⁺-ATPase (35, 36), Na⁺,K⁺-ATPase (37–39), and H⁺-ATPase (40, 41).

As a preliminary to attempts to crystallize H⁺,K⁺-ATPase for three-dimensional structural analysis, we have therefore felt the need to clarify the situation specifically for this transport protein. Could there be differences in the way in which H⁺,K⁺-ATPase is organized and works in the membrane compared with that of other P-type ATPases? One possibility is that such differences could reflect relatively strong interactions between H⁺,K⁺-ATPase α,β-protomers that are retained after detergent solubilization. Furthermore, differences could be related to differences in transport mechanism due to the particular status of protons as the transported species. A dimeric state, for instance, might facilitate transfer through the membrane, either as the hydronium ion, H₃O⁺, by the Grothuiss effect, or as H⁺ by a protein wire mechanism (42). In order to address these questions, we have in the present work attempted to apply our experience on the use of surfactants for solubilization of functionally active membrane proteins to H⁺,K⁺-ATPase in conjunction with structural studies by analytical ultracentrifugation and other advanced biophysical techniques (43). This has enabled us to provide a stringent analysis of the aggregational state of H⁺,K⁺-ATPase required to sustain activity.

EXPERIMENTAL PROCEDURES

H⁺,K⁺-ATPase Preparation

Tubulovesicular preparations of gastric H⁺,K⁺-ATPase were prepared by differential centrifugation of gastric mucosa of actively secreting (pink) specimens of pig stomachs, with slight modifications of the method described by Skrabanja et al. (44). The pig stomachs were obtained from a local slaughterhouse (Danish Crown, Horsens) and kept cold after slaughtering and in all subsequent steps. After transfer to the laboratory, gastric mucosa was scraped off from the stomach with a filet knife, minced twice with a garlic press, and homogenized at 1000 rpm with a homemade motorized and Teflon piston-based homogenizer in a buffer containing 0.25 m sucrose and 20 mm Tris-HCl (pH 7.4). The homogenate was centrifuged at 27,000 × g (15,000 rpm) for 20 min in a Sorvall SS-34 rotor and, after removal of the pellet, recentrifuged at 205,000 × g (46,000 rpm) in a Beckman Ti-45 angle rotor. The resulting pellet was resuspended with the buffer used for homogenization and layered on a two-step gradient consisting of 37% sucrose (w/v) and 20 mm Tris-HCl (pH 7.4) at the bottom with 7% Ficoll at the top (GE Healthcare), 0.25 m sucrose, and 20 mm Tris-HCl (pH 7.4). After centrifugation for 60 min at 217,000 × g (46,000 rpm) in a Beckman Ti-70 swing-out rotor, H⁺,K⁺-ATPase-containing vesicles were collected from the top of the Ficoll layer. As the last step, the vesicles were diluted with 20 mm Tris buffer (pH 7.4) and pelleted at 217,000 × g, followed by resuspension in the homogenization buffer at a final concentration of ∼5–7 mg of protein/ml and kept frozen in small aliquots at −20 °C.

Chromatographic Preparation of Active, Solubilized H⁺,K⁺-ATPase

An aliquot of the vesicular H⁺,K⁺-ATPase membranes was spun down by centrifugation at 50,000 rpm for 35 min, and the pellet (∼0.7 mg of protein) was resuspended with 0.7 ml of 40 mm KCl, 40 mm MES buffer (pH 6.0), 3 mm Mg²⁺, 1 mm EDTA, and 0.25 m sucrose. The membranes were solubilized by the addition of C₁₂E₈ at a 5:1 detergent/protein weight ratio. After removal of insoluble residues by centrifugation at 50,000 rpm for 35 min, the supernatant, which had a content of 1.1 mg of phospholipid/mg of protein, was applied to a Superose 6 10 × 300-mm column, pre-equilibrated with the same buffer except for the presence of Tween 20 (2 mg/ml) instead of C₁₂E₈. The sample was eluted at a rate of 0.25 ml/min with continuous monitoring of light absorption at 280 nm and refractive index.

Biochemical Analyses

Protein concentrations were determined by the method of Lowry (45) as modified by Hartree (46), and phospholipid concentrations were determined by the method of Bartlett (47). ATPase activities of the vesicular membranes were measured at 23 °C by enzymatic spectrophotometry with an ATP-regenerating system (48) in a 30 mm imidazole (pH 7.0) buffer, containing 5 mm Mg²⁺, 0.1 mm EDTA, and 1 mm ATP, to which had been added 0.42 μg of alameticin/μg of protein to make the vesicles leaky to the substrates. Detergent-solubilized ATPase activity was assayed in the column chromatographic solvent including the detergent.

Mass Spectroscopy (MS) Experiments

Membrane solubilization and purification of H⁺,K⁺-ATPase were performed as described above but in the presence of n-dodecyl-β-d-maltopyranoside (DDM)⁵ at 1 mg/ml. Three 500-μl fractions at 0.24, 0.27, and 0.35 mg/ml, eluting in the first part of the H⁺,K⁺-ATPase peak after the size exclusion chromatography, were concentrated to 15–20 μl, and the DDM concentration was reduced by two cycles of dilution and concentration by ultrafiltration (Centricon cut-off 100 kDa, Amicon) in 40 mm Tris, 40 mm KCl, 0.2 mg/ml DDM. Previously, Lenoir et al. (49) and Cardi et al. (50) indeed have indicated that low salt and low DDM are appropriate for MALDI experiments. MALDI-TOF MS spectra were measured on an Autoflex mass spectrometer (Bruker Daltonics) operated in linear positive ion mode. External calibration of the instrument was done using protein standard mixture II from Bruker Daltonics (BSA (66.5 kDa), protein A (44.6 kDa), and trypsinogen (23.9 kDa)), providing usual mass accuracy of ≤1000 ppm in this mass range. The samples were mixed in a ratio of 1:2 (v/v) with sinapinic acid matrix (Sigma; 10 mg/ml in acetonitrile/water, 0.1% TFA (50:50)), and 2 μl were deposited on the target. LC/ESI-TOF-MS analysis was carried out on a 6210 mass spectrometer interfaced with a binary pump liquid chromatography system (Agilent Technologies). The instrument was calibrated in the 300–3000 m/z range using ESI tuning mix from Agilent Technologies, allowing a mass accuracy of about 50 ppm. All solvents were HPLC grade. Solvent A was 0.03% TFA in water, and solvent B was 95% acetonitrile, 0.03% TFA. Samples were desalted on-line on a reverse phase cartridge (C4, Michrom Bioresources) with solvent A (2 min) and with 50% solvent B (10 min) at a flow rate of 0.3 ml/min. The sample was then separated and analyzed on a reverse phase column (Jupiter-C4; 5 μm, 300 Å, 50 × 1.0 mm; Phenomenex) with a linear gradient from 5 to 95% B in 15 min.

Analytical Ultracentrifugation Sedimentation Velocity (SV) Experiments

Sedimentation velocity experiments were done on an analytical ultracentrifuge XLI (Beckman Coulter, Palo Alto, CA) with a rotor speed of 42,000 rpm at 7 °C, using a rotor Anti-50 and double-sector cells (in Ti, Alu, or Epon) of optical path length 12 mm with sapphire windows. Cells were typically filled with 420 μl of sample and reference solvent. The reference solvent was without detergent. In some of the experiments, we used artificial boundary cells, allowing the equilibration at 3000 rpm of the levels of the two compartments prior to stopping the ultracentrifuge and rehomogenization of the sample prior to the SV experiments; initial volumes of the channels were 430/420 μl for reference solvent –here with detergent– and sample. Acquisitions were made using absorbance at 280 nm and interference optics. Sedimentation velocity analyses were performed by employing the Sedfit program, version 12.1 (available on the World Wide Web) in terms of continuous distributions c(s) of sedimentation coefficients (s) (51). The solvent density and viscosity were measured at 20 °C with a DMA 5000 density meter and AMVn viscosity meter (Paar, Graz, Austria), and extrapolated at 7 °C using tabulated data for water. For experiments in deuterated buffer, three fractions of 0.9 or 1.3 ml of H⁺,K⁺-ATPase from size exclusion chromatography in Tween 20 were recovered and solvent-exchanged to deuterated buffer (92.6% D₂O) of the same composition using desalting columns of 5 ml (PD10, Amersham Biosciences). The theoretical background has been detailed previously (43, 52, 53) (also see “Results”). For the analysis of the sedimentation in deuterated solvent, hydrogen/deuterium exchange of exchangeable hydrogens in the protein by deuterium leads to a reformulation of the buoyant molar mass,

where the summation represents the decomposition of the particle in terms of its components, with M and v̄ being defined for the fully hydrogenated components.

Size Exclusion Chromatography Coupled to Light Scattering Experiments

H⁺,K⁺-ATPase (30 μl) was injected into a high pressure liquid chromatography system LC20 AD (Shimadzu) in a KW 804 column (8 × 300 mm) preceded by a guard column (Shodex) and equilibrated at 4 °C, with a flow rate of 0.5 ml/min, with 40 mm KCl, 40 mm MES, pH 6, 0.25 m sucrose, 3 mm MgCl₂, 1 mm EDTA, 2 mg/ml Tween 20, the solvent being filtered at 0.1 μm. The elution profile was followed on-line by refractive index (Δn) measurements with an Optilab rEX refractometer (Wyatt Technology Corp.), absorbance at 280 nm (A₂₈₀) with a Shimadzu SPD-M20A detector, and light scattering intensity (I) with a miniDAWN TREOS detector (Wyatt Technology) using a laser emitting at λ = 658 nm. Data were analyzed using the ASTRA software (Wyatt Technology Corp.).

The basic equation for light scattering, restricted to diluted solutions (corresponding to negligible interparticle interactions between particles) of small particles (Stokes radius (R_S) < 20 nm) reduces to the following,

where I is the excess intensity of scattered light, K is an optical parameter = 4π²n²/(λ⁴N_A), and n is the refractive index. For a solute with known (∂n/∂c), the concentration c is estimated from the refractive index measurements, Δn = kc(∂n/∂c), where k is an instrumental constant.

For a complex described as a two-component system (with indexes labeled 1 and 2 for the components), the concentrations of the component within the complex (and thus its composition) are estimated from the combination of the absorbance, A_{1 cm, complex}, and refractive index, Δn_complex, using as inputs the extinction coefficients E_0.1% and (∂n/∂c) for the two components.

The derived refractive index increment and concentration of the complex are combined with scattered light intensity for the calculation of its molecular mass in Equation 2, where c, M, and (∂n/∂c) represent the complex: c = c₁ + c₂; M = M₁ + M₂; (∂n/∂c) = (∂n/∂c₁)c₁/(c₁ + c₂) + (∂n/∂c₂)c₂/(c₁ + c₂).

Numerical Values Used for the Analysis of SV and Size Exclusion Chromatography Coupled to Light Scattering Experiments

We extrapolate to 7 °C, from measurements done at 20 °C, solvent densities for 40 mm KCl, 40 mm MES, pH 6, 0.25 m sucrose, 3 mm MgCl₂, 1 mm EDTA in H₂O and D₂O, of 1.035 and 1.126 g/ml, respectively, and solvent viscosities of 1.83 and 2.24 cP, respectively. The numerical values for the components of the H⁺,K⁺-ATPase complex are reported in Table 1. Corrected s_20,w values were calculated considering v̄ = 0.83 ml/g for the H⁺,K⁺-ATPase complex and 0.87 ml/g for the Tween 20 or (Tween 20 + lipid) micelles.

TABLE 1.

Values characterizing the components of the solubilized and chromatographed H⁺,K⁺-ATPase complex

	M	δ	ν̄	∂n/∂c	MD/MD	E0.1%, 280 nm
	kDa	g/g protein	ml/g	ml/g		ml/(mg cm)
α,β H+,K+-ATPase	147.346a		0.734a	0.187b	1.011a	1.035a
Carbohydrate	9c	0.061c	0.63d	0.15e	1.019a	0f
Glycosylated protomerg	156.346		0.728	0.185	1.011	0.975
Tween 20	See “Results”	See “Results”	0.869h; 0.87c	0.082c	1.016a	0.0115c
Phospholipid	36.8c	0.25c	0.975i	0.12j	1.016f	0f
Cholesterol	3.5c	0.024c	0.975i

^a Calculated from amino acid sequence or estimated from chemical composition, α- and β-subunits have molecular masses of 114.288 and 33.058 kDa, respectively; ν̄ calculated using the Sednterp program is given at 7 °C (ν̄ = 0.739 ml/g at 20 °C); M_D/M_H values are derived considering 80% of maximum hydrogen/deuterium exchange for the protein and full exchange for the other components.

^b Data from Ref. 84.

^c This work; results concerning Tween 20 are described in supplemental Fig. S2 and used in this paper.

^d Data from Ref. 85.

^e Value for dextran from Ref. 86.

^f Considered values.

^g Derived from the values given in the two lines above.

^h Data from Ref. 75.

ⁱ Calculated according to the lipid composition of the membrane (supplemental Table S1) and the partial specific volumes given for individual lipids by Ref. 87); ν̄ for cholesterol is ill defined (see Ref. 87).

^j Given for dimyristoyl phosphatidylglycerol by Ref. 88.

RESULTS

Surfactant Solubilization of Tubular Vesicular Membranes and Preparation of Enzymatically Active H⁺,K⁺-ATPase

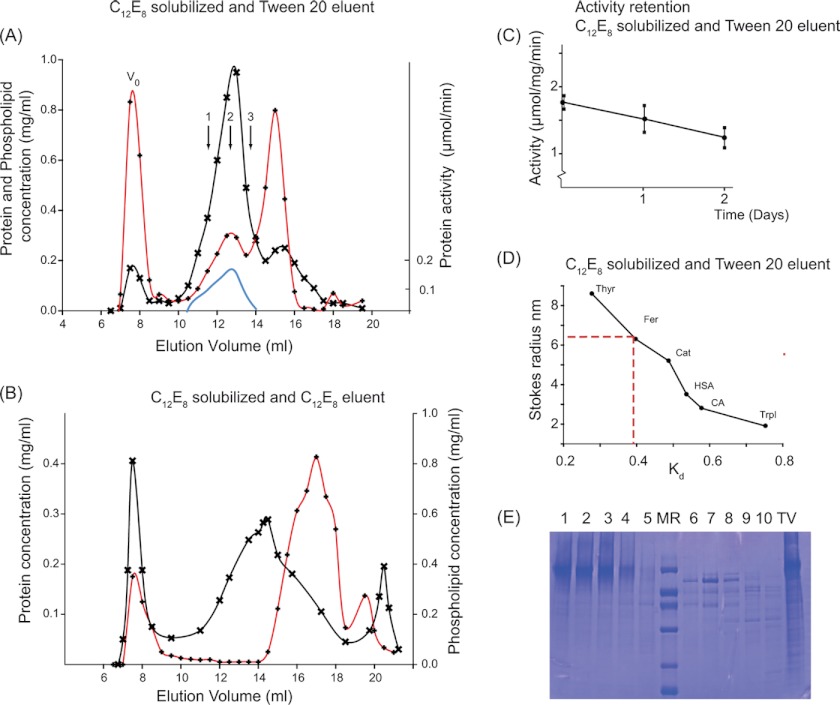
We prepared, as described under “Experimental Procedures,” tubulovesicular fractions with a high H⁺,K⁺-ATPase content by differential centrifugation of mucosal scrapings from actively acid-secreting mucosas of pig stomachs. The use of surfactants to extract and solubilize membrane proteins in their molecular entities from the membrane matrix is indispensable for studying in detail structural aspects, such as the role of monomeric/oligomeric organization and protein-protein interactions, for the functional properties of the membrane protein. In this way, indeed, it was established that sarcoplasmic reticulum Ca²⁺-ATPase, solubilized as a monomer by C₁₂E₈, retains all of the basic features required to function as a Ca²⁺-transporting unit, regardless of the tendency of this Ca²⁺ pump to undergo reversible and irreversible self-association (20). For Na⁺,K⁺-ATPase, this also appears to be the case (28–30), although dimerization of the α,β-protomer is a more pronounced feature of this ATPase than it is for Ca²⁺-ATPase (27, 31–33). Application of the same surfactant strategy to H⁺,K⁺-ATPase is fraught with the problem that it is difficult to avoid either irreversible or reversible inhibition of enzyme activity in the detergent-solubilized state. Nevertheless, it has been found that for H⁺,K⁺-ATPase, inactivation can be reduced by partial solubilization with mild non-ionic surfactant under conditions that include cryoprotection with sucrose or glycerol and a low (4 °C) temperature (e.g. see Ref. 15). A key point for our study was the need to provide efficient solubilization by a potentially abrasive surfactant, to ensure formation of the minimal size of the H⁺,K⁺-ATPase complex with retention of function. After a number of preliminary trials with various non-ionic detergents (see supplemental Fig. S1), we found that these requirements were best met by the combined use of C₁₂E₈ to initially solubilize the H⁺,K⁺-ATPase membranes, followed by exchange with the mild detergent Tween 20 to preserve activity in a following chromatographic separation. As can be seen from Fig. 1A, chromatography on Superose 6 resulted in the elution of three main peaks. In the first peak eluting at the void volume (V₀), there is some highly aggregated H⁺,K⁺-ATPase. There was also non-solubilized phospholipid eluted at this position because of its reduced solubility in Tween 20 when compared with C₁₂E₈ (54). This conclusion can be drawn from the evidently smaller concentration of phospholipid present in the void volume for the sample shown in Fig. 1B, where phospholipid was kept solubilized by C₁₂E₈ in the column eluant. With Tween 20 present in the eluant (Fig. 1A), the peak following the void volume has a high content of enzymatically active and essentially pure H⁺,K⁺-ATPase that elutes partially delipidated, with 0.25 mg of phospholipids/mg of protein. The third peak is mainly constituted by phospholipids that elute as mixed micelles with C₁₂E₈ (and probably also with some Tween 20) together with protein components of lower molecular mass present in the tubulovesicular preparation (Fig. 1E). Cholesterol was mainly detected in the third peak. However, there was also cholesterol in the protein peak, amounting to around 0.024 mg/mg of protein (data not shown). The H⁺,K⁺-ATPase present in the second peak (Fig. 1A) exhibited ATPase activity at a level similar to that of the membranous preparation (see supplemental Fig. S1C). The activity only slowly deteriorated over a period of 2 days when the column collected fractions were stored in the cold (4 °C) in the presence of 0.3 m sucrose (Fig. 1C). In contrast to these findings, when C₁₂E₈ was used instead of Tween 20 as the column eluant after initial solubilization with C₁₂E₈ (Fig. 1B), there was a large increase of protein in the void volume, and the H⁺,K⁺-ATPase in the second peak was inactive and delipidated and possessed an elution profile clearly revealing size heterogeneity. From column calibration data with water-soluble standard proteins (Fig. 1D), we could deduce an apparent value for the Stokes radius of 6.3 nm for the enzymatically active H⁺,K⁺-ATPase in the second peak in Fig. 1A.

FIGURE 1.

Preparation of H⁺,K⁺-ATPase, solubilized by C₁₂E₈ and purified by size exclusion chromatography with Tween 20. 2.4 mg of the tubulovesicular preparation of H⁺,K⁺-ATPase, suspended in 0.7 ml in a buffer containing 40 mm MES (pH 6.0), 40 mm KCl, 0.25 m sucrose, 3 mm Mg²⁺, and 1 mm EDTA, was solubilized with 14 mg of C₁₂E₈, and non-solubilized residues were removed by centrifugation for 35 min at 100,000 × g at 4 °C. 0.5 ml of the supernatant was loaded onto a 10 × 300-mm Superose 6 column, equilibrated, and eluted at a rate of 0.25 ml/min at 4 °C in the above buffer, not containing C₁₂E₈ but with Tween 20 at 2 mg/ml (A) or with C₁₂E₈ at 2 mg/ml but without Tween 20 (B). Protein concentration (crosses), phospholipid concentration (red lines with diamonds), and activity (continuous blue line) were measured at 23 °C as described under “Experimental Procedures.” The three arrows numbered 1, 2, and 3 correspond to regions of the peak analyzed in sedimentation velocity and shown in Fig. 3. V₀, void volume of the column. C, activities in top fraction kept at 4 °C measured as a function of time after column elution. D, column calibration with the following water-soluble globular proteins: thyroglobulin (Thyr), ferritin (Fer), catalase (Cat), human serum albumin (HSA), carbonic anhydrase (CA), and trypsin inhibitor (TrpI). E, SDS-PAGE (11% Tricine gels) prepared from fractions collected from an HPLC experiment similar to that shown in A. Lanes 1–5 are from fractions eluting at 12–14.5 ml, corresponding to the peak of enzymatically active H⁺,K⁺-ATPase. Lane MR contains the protein standard (phosphorylase b (92 kDa), BSA (67 kDa), ovalbumin (42 kDa), carbonic anhydrase (32 kDa), trypsin inhibitor (22 kDa), and α-lactalbumin (12 kDa)). Lanes 6–10 are from the third protein peak, corresponding to elution at 15–17 ml. The lane labeled TV represents the C₁₂E₈-solubilized tubulovesicular membranes.

The present protocol is similar to those previously used for preparation of C₁₂E₈-solubilized Ca²⁺-ATPase, followed by exchange with a milder detergent like Tween 80 (22) or an amphipol polymer (55). In all of these cases, C₁₂E₈ has been used to break up the native membrane structure by partially solubilizing the membrane lipid, followed by exchange with a milder and less abrasive detergent of the Tween series (22) or by amphipol treatment (55) to keep the ATPase soluble in an active form.

Molecular Mass Determination of the Two Subunits by MS

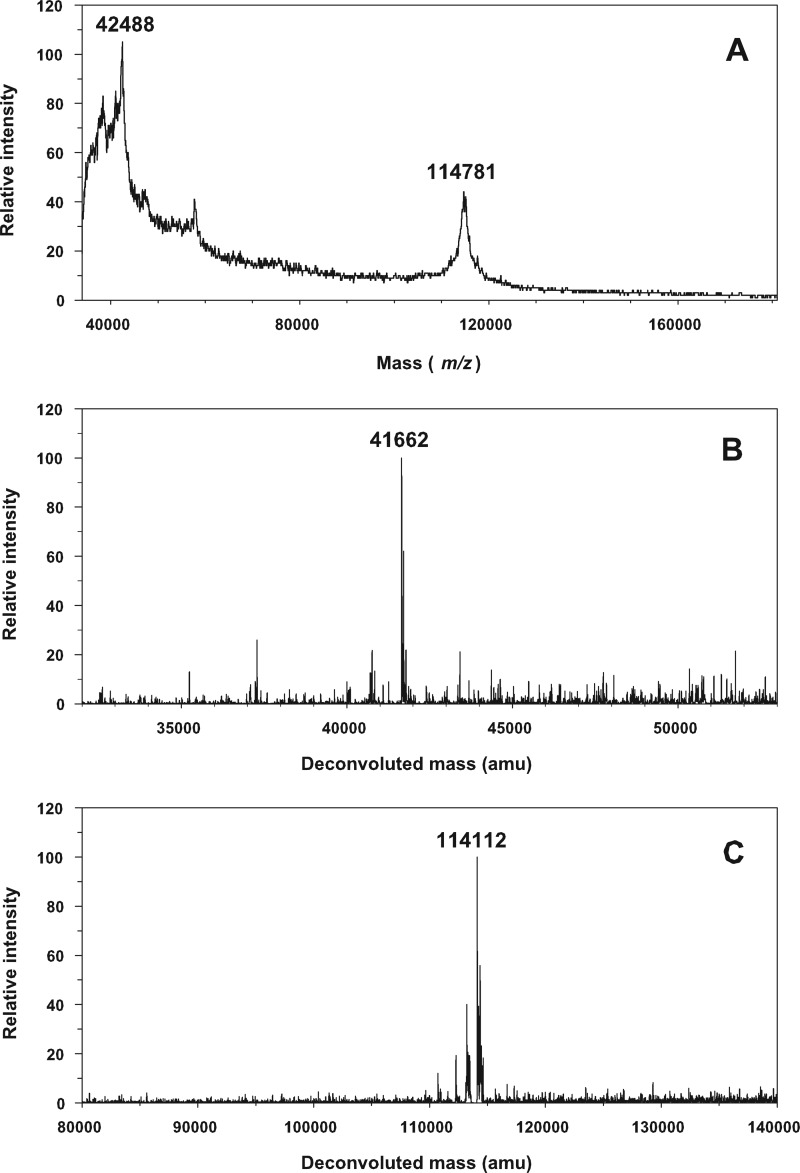
By MS, we have sought to evaluate the effect of post-translational modifications, in particular on the carbohydrate content of our H⁺,K⁺-ATPase preparations. The theoretical protein molecular masses deduced from the amino acid sequences are 114,287 Da for the α-subunit and 33,076 Da for the β-subunit. These values are listed in Table 1 together with numerical values of the other components present in the solubilized H⁺,K⁺-ATPase complex. Analysis by MS of H⁺,K⁺-ATPase in Tween 20 at 2 mg/ml did not allow identification of the H⁺,K⁺-ATPase polypeptide peaks; no protein peaks were detected due to the presence of this detergent. However, as shown in Fig. 2, it was possible to obtain clearly resolved mass spectra, albeit with low signal/noise ratios, for H⁺,K⁺-ATPase prepared by solubilization in DDM and then chromatographed at a column concentration of DDM of 0.2 mg/ml before concentration on Centricon 100 (Amicon). Analysis performed on two different samples by MALDI-TOF resulted in registration of molecular masses up to 42,488 Da attributable to the β-subunit and 114,781 Da for the α-subunit. For the α-subunit, the molecular mass exceeds the theoretical value by 494 Da; we cannot exclude the possibility that at least part of this slight difference can be related to instrument inaccuracy, arising because the calibration was done with protein standards of lower mass in the 20–70 kDa range. Thus, LC-ESI-TOF analysis gave slightly lower values (viz. 41,662 Da for the β-subunit and 114,112 Da for the α-subunit). Later in the LC elution, other contributions at 38,349 and 39,255 Da were detected. The origin of the latter two minor contributions is uncertain. We presume that they either represent protein unrelated to the β-subunit or correspond to β-subunits with different glycosylation levels or perhaps to derivatives formed by partial proteolysis of the β-subunit during the preparation.

FIGURE 2.

Mass spectroscopy of H⁺,K⁺-ATPase. A, MALDI-TOF spectrum providing molecular masses of 42,488 Da and 114,781 Da, corresponding to the glycosylated β-subunit and to the α-subunit. B and C, LC/ESI-TOF-MS spectra providing molecular masses of 41,662 Da, corresponding to the glycosylated β-subunit (B), and of 114,112 Da, corresponding to the α-subunit (C). m/z, mass/charge ratio. amu, atomic mass units.

For the α-subunit, the molecular mass obtained from LC-ESI-TOF is lower by 175 Da when compared with the theoretical mass value, and in this case a lower molecular mass is in accordance with known post-translational modifications, resulting in the removal of the N-terminal methionine (56), and with oxidation of some of the cysteine residues. Thus, we can conclude that the molecular masses measured by MALDI-TOF and LC-ESI-TOF for the α-subunit closely agree with that computed from the amino acid sequence. On the other hand, the molecular masses of the β-subunit as measured by the two ionization techniques are substantially higher than that calculated from the deduced amino acid sequence (by 9346 Da in MALDI TOF and by 8586 Da in LC-ESI-TOF). Therefore, this subunit, according to our MS data on pig stomach H⁺,K⁺-ATPase, includes a contribution from the glycosylated side chains that, based on a calculated protein molecular mass of 33,076, is about 9 kDa, corresponding to 0.06 g/g of protein. This value is, in fact, lower than the value of 20 kDa glycosylation that we have been able to calculate from the model put forward by Tyargarajan et al. (57) for rabbit gastric H⁺,K⁺-ATPase (see “Discussion”).

Sedimentation Velocity Experiments after Size Exclusion Chromatography

To study the size of the H⁺,K⁺-ATPase, solubilized by Tween 20 in an enzymatically active form (Fig. 1A), we used analytical ultracentrifugation, which is a versatile and powerful method by which to assess sample homogeneity and to characterize the monomeric/oligomeric states of proteins and their association equilibria (58). Previous experience has indicated that SV is to be preferred to sedimentation equilibrium in the study of the often inherently unstable detergent-solubilized membrane proteins (43). With SV it is possible to follow in detail the evolution of sedimentation profiles by repeating the scans with short time intervals. This obviates the long time periods required for concluding the sedimentation equilibrium experiments (43, 53). Thus, secondary aggregation of the detergent-solubilized membrane protein can be avoided, or at least checked, because the development of size heterogeneity is very easily revealed by repeated sedimentation velocity scans. SV can be used in conjunction with continuous size distribution analysis for accurate determination of sedimentation coefficients, s, for the different species present in a complex sample (51). The s values are related to the molecular mass (M), R_S, and the buoyancy term, (1 − ρv̄), of the sedimenting species by the Svedberg relation, which for the present purpose can be formulated in the following way.

In this equation, N_A is Avogadro's number, r and η are the solvent density and viscosity, and v̄ is the partial specific volume of the sedimenting species, which in our case includes bound lipid and detergent by the glycosylated protein. Because M and v̄ cannot be deconvoluted from SV measured at only one solvent density, we instead used the buoyant molar mass defined in Equation 1 as the experimentally relevant parameter (see “Results” and Equations 7–9). The frictional ratio f/f_min that relates R_S to the radius, R_min, of the anhydrous volume is determined by its shape and hydration.

In the c(s) analysis, reasonable hypotheses on the values of v̄, f/f_min, ρ and η are defined (f/f_min is fitted), allowing a plausible relationship between the buoyant mass and size of the particles. Furthermore, as will be shown, it is possible, by combining SV data obtained with different optics (absorbance and interference optics) or by recording the sedimentation in solvents with different densities, to determine all of the molecular parameters accessible to analytical ultracentrifugation. We have therefore based our study on the use of SV rather than on sedimentation equilibrium measurements, although the latter theoretically is more directly related to the determination of molecular mass.

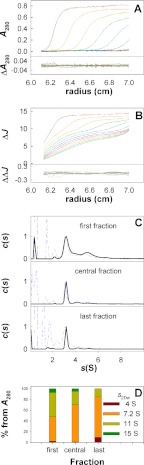
In our experiments, SV analysis was performed at 7 °C on samples prepared as in Fig. 1A by solubilization of H⁺,K⁺-ATPase in C₁₂E₈, followed by size exclusion chromatography on a Superose 6 column in the presence of Tween 20 and sucrose in the cold room. Three fractions, eluting from the column at different positions of the enzymatically active protein peak, as indicated by the 1, 2, and 3 in Fig. 1A were examined. Fig. 3A shows the UV absorption sedimentation profiles of the central top fraction 2, whereas Fig. 3B shows interference data obtained in the same experiment. The sedimentation profiles of Fig. 3A indicate the presence of one major boundary of the protein, whereas Fig. 3B obtained by interference optics shows the presence of one additional and slower moving component, which is attributable to the sedimentation of the detergent micelles. Global analysis of the entire SV scans as outlined above was done by subjecting the data to computer simulation to provide a continuous c(s) distribution of sedimentation coefficients (51). Fig. 3C compares the properties of the three studied fractions. When investigated at 280 nm, they all show one main complex sedimenting at 3.23 ± 0.03 S (corresponding to s_20,w = 7.2 ± 0.1 S). Other ill defined and larger species are present and sediment at 5 ± 0.2 S (s_20,w = 11.1 ± 0.4 S) and further up to 7 S (s_20w = 15.5 S). We found that the presence of the larger species was most prominent in samples collected from the first eluted fractions of the protein peak. These larger species appear as irreversibly aggregated material, because the s values and proportions of the different species were not modified when the samples were diluted twice (data not shown). Thus, there is no evidence for the existence of any reversible equilibrium between the differently sized species. Furthermore, we noted in introductory SV experiments, which we had performed at the more commonly used rotor temperature of 20 °C, that the proportion of the main s_20,w = 7.2 S species was drastically reduced (more than 50%) and was replaced by a predominant third species sedimenting at s_20,w = 15 S. A higher proportion of the larger species at s_20,w = 11.1 and 15 S was also observed in SV experiments of samples that had been stored for 18 h at 7 °C after chromatography or for samples of H⁺,K⁺-ATPase obtained after two size exclusion chromatographies (Superose 6 plus a silica column KW 804 as described under “Size Exclusion Chromatography Coupled to Light Scattering Experiments”). Accordingly, the larger species most likely represent a time- and temperature-dependent deterioration of the sample that is paralleled by the decline of enzyme activity as a function of time (Fig. 1). The ratios of the sedimentation coefficients of the larger species to that of the main species are 1.5 and 1.9 for species sedimenting at s_20,w = 11.1 and 15 S, respectively. This is close to the theoretical values of 1.59 and 2.08 expected for sedimentation of dimers and trimers of the same density and shape as the main species. The increased trend for aggregated ATPase to elute early from the column is apparent from Fig. 3D. In conclusion, the larger species probably correspond to irreversibly aggregated oligomeric forms (dimers, trimers, and larger multimers) of the main species related to aging, a process that occurs more rapidly at 20 °C than at 7 °C.

FIGURE 3.

Sedimentation velocity of H⁺,K⁺-ATPase. Experiments were done at 42,000 rpm and 7 °C for different fractions of the main H⁺,K⁺-ATPase peak from gel filtration. The solvent was 40 mm KCl, 40 mm MES buffer (pH 6.0), 3 mm Mg²⁺, 1 mm EDTA, 0.25 m sucrose, 2 mg/ml Tween 20. A and B, superposition, for the central fraction, of selected experimental and fitted profiles (top panels) and of their differences (bottom panels) obtained at 280 nm (A) and using interference optics (B). The last profiles correspond to 14 h of sedimentation. C, superposition of the c(s) distributions obtained in the range of 0.1–10 S from the two optics for (from top to bottom) the first, central, and last fractions of the main peak. D, evolution of the content of the fractions from gel filtration along the main peak of H⁺,K⁺-ATPase, evaluated from the area under the c(s) curve from the data at 280 nm. In this last panel, the sedimentation coefficients are given as s_20,w.

The profiles obtained by interference optics (Fig. 3B) were analyzed as depicted by the broken lines in Fig. 3C. They showed, in addition to the protein species detected at 280 nm, significant contributions of a boundary, sedimenting at 0.55 ± 0.1 S (s_20,w = 1.3 ± 0.2 S), attributable to Tween micelles (see the physical chemical characterization of Tween 20 in supplemental Fig. S2). The contributions seen at lower s values (s < 0.3 S) in Fig. 3C may be artifactual and were not analyzed further (they may be solvent components or result from improper deconvolution of systematic noises). In addition, there were ill defined contributions sedimenting between 1 and 2.7 S (Fig. 3C) with a mean value of 1.7 ± 0.1 S (s_20,w = 4.1 ± 0.2 S), which we consider represents the presence of the mixed lipid/detergent micelles that are observed to elute at the trailing edge of the enzymatically active peak of H⁺,K⁺-ATPase (see Fig. 1A). In accordance with this view, the concentration of these species was larger in the protein fractions eluted late in the size exclusion chromatography (Fig. 3C). Furthermore, the J/A₂₈₀ ratio (i.e. the ratio of the fringe shift to absorbance of these components at 280 nm) was very large (>50), indicative of a predominant detergent and lipid composition, not compatible with a pure protein-detergent complex.

Information on the composition of the ATPase complex could also be gained from the interference data by comparison of the values for the absorbance at 280 nm (A₂₈₀) and fringe shift (J) signals (see “Experimental Procedures”). As deduced from the c(s) analysis, the J/A₂₈₀ ratio for the main H⁺,K⁺-ATPase complex was 5.4 ± 0.6, and the ratio was 6.3 ± 2.2 for the dimer species. These values are much larger than the values of 2.68 for the deglycosylated protein and 2.81 for the glycosylated protein, which can be calculated for the detergent and lipid-free H⁺,K⁺-ATPase based on the values for refractive index increment (∂n/∂c) and E_0.1% extinction coefficient at 280 nm given in Table 1. The excess of fringe shift observed for the solubilized complex is obviously related to the binding of appreciable amounts of detergent and lipid, which on this basis can be estimated to be present in a total amount of about 1.6 g/g of protein, considering 0.274 g/g of bound lipid.

Hydrodynamic Characterization Based on Combining the s and R_S Values

By the preceding analysis, we have demonstrated that the main component of a Tween 20-solubilized and enzymatically active H⁺,K⁺-ATPase is present as a slowly moving species, sedimenting at s_20,w = 7.2 S. This is a low value when compared with previously reported values for sedimentation of related P-type ATPases (e.g. s_20,w = 10.6 S for the DDM-solubilized monomer of α,β Na⁺,K⁺-ATPase (30) and s_20,w = 7.5 S for the sarcoplasmic reticulum Ca²⁺-ATPase, which has no β-subunit (43)). We checked the consistency of our H⁺,K⁺-ATPase data by estimating the buoyant molecular mass of the enzymatically active peak by combining the measured sedimentation coefficient obtained in the sucrose-containing solvent (3.23 S) with R_S = 6.3 nm, as determined from calibrated size exclusion chromatography. This can be done by use of the following equation (36),

which, with a solvent viscosity η = 1.83 cP, results in an estimate of the buoyant molar mass (M_b) of the main species of 42.3 kDa. M_b is related to the molecular mass (M) and partial specific volume (v̄) of the sedimenting species by Equation 8,

where ρ is the solvent density, which is 1.035 g/ml in our experimental conditions. For the H⁺,K⁺-ATPase complex, M_b in the above expression is related to the molecular mass of the protein component, M_P, and the sum of the buoyancies of the protein (P)-, glycosyl (G)-, lipid (L)-, and detergent (D)-bound components by the following relation,

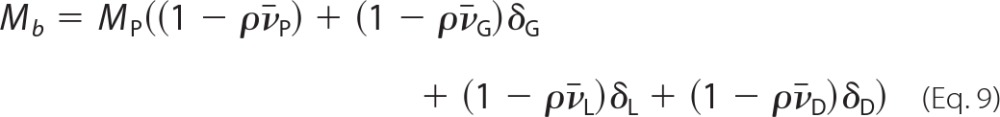where δ_G is the mass of the glycosyl-associated, δ_L of the lipid-associated, and δ_D of the detergent-associated components of the H⁺,K⁺-ATPase protein, expressed on a g/g basis. From these equations and using the numerical values given in Table 1, we calculate that, for a H⁺,K⁺-ATPase α,β-protomer, the protein content (with a molar mass of 147.3 kDa) contributes with 35.3 kDa and glycosylation (9 kDa) with 3.5 kDa to M_b. Bound phospholipid and cholesterol (with a global molar mass of 40.3 kDa) makes essentially no contribution (−0.1 kDa), because 1/v̄_L is close to ρ. The sum of these contributions in terms of buoyant mass, 38.7 kDa, for a H⁺,K⁺-ATPase α,β-protomer thus approaches that estimated according to Equation 7 experimentally for the buoyancy of the solubilized H⁺,K⁺-ATPase (42.3 kDa), except for a small residual (3.6 kDa) that may be attributed to bound Tween 20. The data are thus consistent with the elution of the Tween 20-solubilized H⁺,K⁺-ATPase as an unaggregated α,β-protomer with a moderate amount of bound detergent (on the order of 0.2–0.3 g of detergent/g of protein). This is a lower value for detergent binding than suggested from the J/A₂₈₀ analysis given above. However, it should be noted that the calculation of detergent binding from the buoyancy terms in Equation 9 is subject to uncertainty, being based on the difference between two large numbers (42.3 kDa − 38.7 kDa). In particular, the calculation is critically dependent on the correctness of the value for the column-based determination of Stokes radius, where it is known that the R_S values of membrane proteins, as compared with those of the water-soluble standard proteins used for column calibrations, can be influenced by the type of membrane protein and by the detergent in the column eluent (see Ref. 43).

Sedimentation Velocity Experiments in Deuterated Solvent

In order to proceed with the hydrodynamic analysis and arrive at a firm conclusion as to the aggregational state and other hydrodynamic parameters of the solubilized H⁺,K⁺-ATPase, we have made supplementary determinations of the sedimentation coefficients after exchange of the solvent in our samples with deuterated water. Previously, introducing density variation by exchange with heavy water has been established in sedimentation equilibrium experiments as a useful method to estimate the contribution that the partial specific volumes makes to M_b, the buoyant molar mass of the solubilized complex (59). In appropriate cases, this method can be used, by detergent density matching, to blank out the effect of detergent from the buoyancy term in sedimentation equilibrium experiments of membrane proteins (60). Recently, D₂O exchange has also been used to extend the scope for c(s) sedimentation velocity analysis, as a means to unravel the hydrodynamic properties of samples that are not homogeneous or stable (61, 62), and to account for the complexity of solubilized membrane proteins (63).

In our experiments, H⁺,K⁺-ATPase exchange with deuterated solvent was done by subjecting different fractions of the enzymatically active H⁺,K⁺-ATPase to solvent exchange on a PD10 column. The c(s) analysis shows that for three D₂O/H₂O-exchanged fractions, there is, as in hydrogenated solvent, one main peak and some aggregates, mainly dimers of the main complex, that as expected are less prominent in the later eluted fractions (shown in supplemental Fig. S3). The s values were logically reduced when compared with those obtained in hydrogenated solvent, due to the increase in density of the deuterated solvent (rising from 1.035 to 1.124 g/ml) and in the viscosity (rising from 1.83 cP to 2.24 cP). For the main peak, we determined s = 1.6 ± 0.1 S, whereas the sedimentation rates for the larger particles were in the range of 2.3–5 S. The analysis by interference could not be performed here in a satisfactory way, because the modeling was made difficult by the presence of Tween 20, which floats at −0.005 S under these conditions. Analysis of the sedimentation of the protein was done according to Equation 10,

where subscripts H and D refer to the relevant values in hydrogenated and deuterated solvents for the sedimentation coefficients, viscosities, densities, and molecular masses. Note that the denominator on the right-hand side incorporates a correction for the increase in molecular mass of the protein complex as a result of the deuterium/hydrogen exchange. With these data and considering the increase in molecular mass, M_D/M_H, caused by deuterium/hydrogen exchange in the H⁺,K⁺-ATPase complex, to be 1.014 (intermediate between that of the protein and the Tween 20/lipid component; see Table 1), we calculate from Equation 10 a value for the partial specific volume of the complex of 0.818 ± 0.015 ml/g (errors being evaluated from the imprecision on s_H and s_D). For a α,β-protomer of H⁺,K⁺-ATPase binding the amounts of carbohydrate, phospholipid, and cholesterol shown in Table 1, we calculate for this ensemble a molecular mass of 196.7 kDa and a partial specific volume of 0.779 ml/g. By the use of Equation 9, this can be used to derive an estimate of the amount of bound Tween 20 of 1.0 ± 0.7 g/g. The minimum radius (R_min) that can be calculated from this particle composition is 4.8 ± 0.4 nm, which also by the use of Equation 5 leads to a revised value for R_S of 7.9 ± 1.3 nm (f/f_min = 1.6 ± 0.2).

From the above analysis in D₂O/H₂O, we have thus obtained a set of solutions for all of the hydrodynamic parameters of the detergent-solubilized H⁺,K⁺-ATPase. This includes an estimate of the amount of bound Tween 20, arising as a side gain from the determination of the buoyancy of the whole complex. In order to explore further the range of values consistent with our data, we have followed a procedure described by Nury et al. (63). According to this, the detergent-solubilized complex is considered to be composed of two pseudocomponents: (i) the glycosylated protein and (ii) the detergent + lipid component. In this approach, the lipid and detergent are thus lumped together, and the analysis considers all possible solutions for δ_D+L, for different hypotheses of association states of the protein (monomer, dimer, etc.), and frictional ratios. The frictional ratio (f/f_min = R_S/R_min) is a shape factor that includes a contribution from hydration, whereas R_min is defined as the minimum radius of the anhydrous volume (defined by the product Mv̄). For proteins, the magnitude of f/f_min is restricted to a rather limited range. Values of 1.15–1.25 define globular and compact proteins (64). Coil-like disordered proteins have f/f_min in the range 1.5–3 depending on their masses (64). Typical values for glycolysated proteins are 1.5–1.8. From the Svedberg equation (Equation 1), and incorporating a correction for the slight increase of mass of the components due to hydrogen/deuterium exchange in deuterated solvents, the following equation is derived.

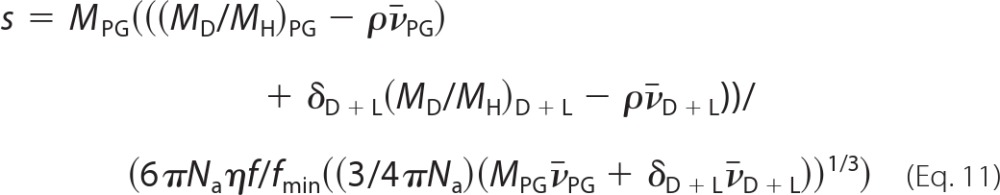The equation should be satisfied in different solvents (with defined values of s, (M_D/M_H)s, ρ, and η). If the oligomeric state (M_PG) and shape factor (f/f_min) are appropriately chosen, a unique pair of (δ_D+L, v̄_D+L) values must account for sedimentation in H₂O and D₂O buffers. We used the commercial computer algebra system Maple to draw the implicit function δ_D+L = f(v̄_D+L), based on different assumptions as to the magnitude of f/f_min and aggregational state. We considered at the outset that H⁺,K⁺-ATPase is a monomer or a dimer and assume different values of the frictional ratio. Fig. 4 shows the results for four hypotheses: H⁺,K⁺-ATPase as a monomer with f/f_min = 1.3 (Fig. 4A) or as a monomer with f/f_min = 1.5 (Fig. 4B) or f/f_min = 1.8 (Fig. 4C) and H⁺,K⁺-ATPase as a dimer with f/f_min = 1.5 (Fig. 4D). In each panel, four curves δ_D+L = f(v̄_D+L) are superimposed, representing the limiting values of the experimental sedimentation coefficients (s ± Δs) in the hydrogenated and deuterated solvents, thus a total of four s values. The areas delimited by the four curves (colored in gray in Fig. 4, A–C) define all possible mathematical solutions for δ_D+L = f(v̄_D+L) that are compatible with the experimental data. Among them, we exclude some irrelevant ones, because v̄_D+L has to be within the range defined by pure Tween 20 (0.87 ml/g) and lipid (0.98 ml/g). Real solutions for our ATPase will be further restricted to v̄_D+L within an even narrower range, because we know that both components will be present in the actual complex. We find that with these constraints, the s_H/s_D data are definitively not compatible with a globular compact monomer (f/f_min = 1.25; not shown). Fig. 4A therefore presents the analysis for the minimal f/f_min = 1.3 value compatible with our data, which includes v̄_D+L values that are just above 0.96 ml/g (i.e. mainly lipids), with δ_D+L being in the range of 0.55–0.85 g/g and R_S = 5.7 nm. The largest (mathematically found) anisotropy of f/f_min = 1.8 (Fig. 4C) would correspond to 1.7 ± 0.3 g/g of bound detergent + lipids (with v̄_D+L = 0.878 ± 0.005 ml/g (i.e. essentially pure detergent). Pure lipid or pure detergent are, of course, unlikely; these fractional ratios (1.3 and 1.8) are therefore excluded. Additionally, f/f_min = 1.8 corresponds to a large and unrealistic value of the Stokes radius (R_S = 9.2 nm). The analysis presented in Fig. 4B for f/f_min = 1.5 leads to v̄_D+L = 0.915 ± 0.005 ml/g, with δ_D+L in the range 0.9–1.4 g/g, and R_S = 7.1 nm. The v̄ and δ correspond closely to the composition determined above (see Table 2), and the Stokes radius is also in the range of that determined by calibrated size exclusion (6.3 nm). Furthermore, this frictional ratio is usual for glycosylated proteins. Finally, the graphical representation of the s_H/s_D analysis excludes definitively the possibility of a dimer (e.g. see Fig. 4D) and, by including possible errors in the analysis arising from imprecision in the measurements of the data and in related parameters (v̄ of the components), justifies the conclusion of the nature of the solubilized H⁺,K⁺-ATPase as an α,β-protomer with f/f_min values in the range of 1.4–1.6.

FIGURE 4.

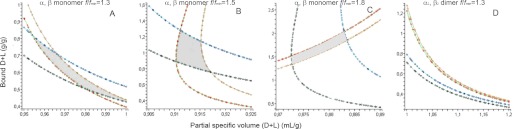
Graphical analysis of the sedimentation velocity of H⁺,K⁺-ATPase in hydrogenated and deuterated solvents. The analysis is made in terms of a complex composed of two pseudocomponents: the glycosylated protein and bound (detergent + lipid). Common input values are as follows: v̄_PG = 0.728 ml/g; η_H = 1.834 cP; ρ_H = 1.0354 g/ml; η_D = 2.2383 cP; ρ_D = 1.1257 g/ml; (M_D/M_H)_PG = 1.011; (M_D/M_H)_D+L = 1.016. In each panel, the four drawn curves give the ensemble of solutions (δ_D+L; v̄_D+L), with δ_D+L the amount in g/g of glycosylated protein and v̄_D+L the partial specific volume for bound detergent plus lipid. Lines are drawn for the limiting experimental values of the sedimentation coefficients determined from the c(s) analysis: s_H − Δs_H = 3.2 S (khaki line, gold point); s_H + Δs_H = 3.26 S (green line, red point); s_D − Δs_D = 1.5 S (cyan line, navy point); s_D + Δs_D = 1.65 S (aquamarine line, black point). PG, D+L, H, and D, glycosylated protein, detergent and lipid, hydrogenated solvent, and deuterated solvent, respectively. For each panel, the f/f_min and assembly state hypothesis are shown. Mathematical solutions are defined by the area encircled by the four curves.

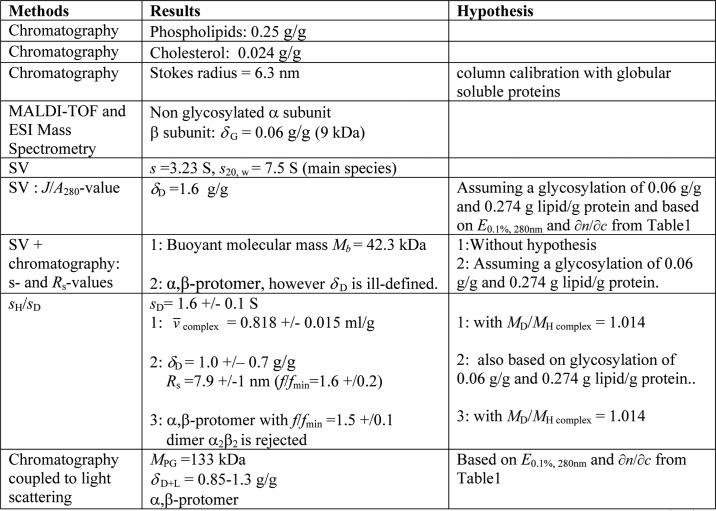
TABLE 2.

Summary of the composition and hydrodynamic data of the Tween 20-solubilized H⁺,K⁺-ATPase obtained by various procedures in the present study

Values in g/g are given in g per non-glycosylated protein.

Size Exclusion Chromatography Coupled to Light Scattering Experiments

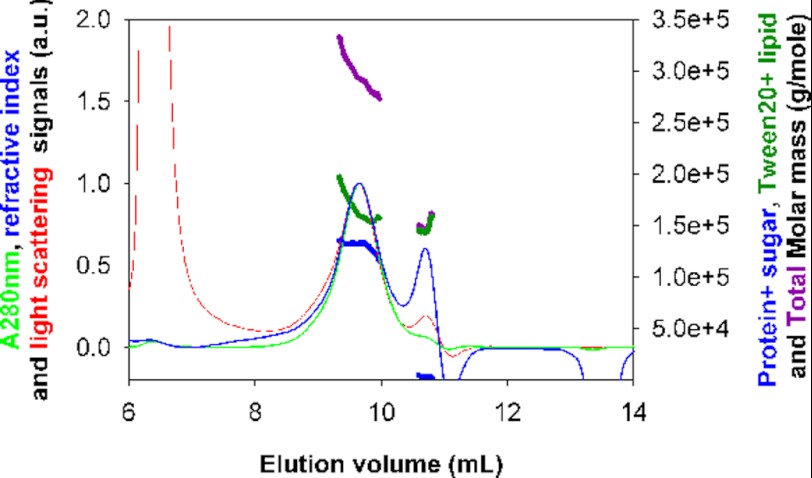
Light scattering coupled to size exclusion chromatography is a complementary and powerful method for investigation of the molar masses and interactions of solubilized membrane proteins in solution (43, 62). Aliquots of fractions of H⁺,K⁺-ATPase, eluted from the enzymatically active H⁺,K⁺-ATPase peak of a Superose 6 column by the usual procedure, were injected and gel-filtered in the presence of Tween 20 on a silica gel column. Changes in light absorption of the eluate were followed at 280 nm and simultaneously analyzed in terms of changes in refractive index and light scattered at three angles (Fig. 5). In our study, the combination of the signals was analyzed in terms of two components. The first one (PG) is the glycosylated protein. The second (D+L) consists of Tween 20 and lipid. The extinction coefficients E_{0.1%, 280} and refractive index increments (∂n/∂c) are given in Table 1. They were used in conjunction with the measurements of light absorption and refractive index as inputs for calculation of the absolute concentration and composition of the two-component complex. Simultaneously, the measurement of the scattered light intensity, I, allowed the determination of the molecular mass from Equation 2. By this procedure, we derive, at the maximum of the main peak, a molar mass of 133 kDa for the glycosylated protein (i.e. 124 kDa for the non-glycosylated protein). This is close to the expected value for a monomer (147 kDa); the difference can be accounted for by the imprecision in the inputs of the extinction coefficients and refractive index increments used for calculation of the molecular mass of the protein and the other components. The amount of bound (detergent + lipid) is in the range 0.85–1.3 g/g of the delipidated and detergent-free protein, depending on the choice of the increment of refractive index (0.082 or 0.12 ml/g) attributed to the (detergent + lipid) component. The peak at an elution volume of 10.7 ml is composed of detergent and lipids, with a low content of protein (2%) and an estimated molar mass of 140 or 97 kDa, depending on the choice of the increment of refractive index (0.082 or 0.12 ml/g). In an additional experiment with a fraction of H⁺,K⁺-ATPase eluted later from the Superose 6 column, we derive for the main peak very similar results (a molar mass of 149 ± 5 kDa for the nude protein with 0.8–0.9 g/g of bound Tween 20 + lipid) (data not shown).

FIGURE 5.

Molar protein mass of Tween 20-solubilized H⁺,K⁺-ATPase after size exclusion chromatography with registration of light absorbance at 280 nm, refractive index, and light scattering. Shown is a superposition of A₂₈₀ (green, thin), differential refractive index (blue, thin), and light scattering (red) signals, in arbitrary units (left axis), and molar masses for the glycosylated protein (blue, thick), detergent + lipid (green, thick), and complex (i.e. their sum (purple) (right axis)). The calculation considers (∂n/∂c) for the glycosylated protein to be 0.185 ml/g (with 9 kDa of carbohydrate for a monomeric α,β protein) and (∂n/∂c) for detergent + lipid to be 0.082 ml/g, with extinction coefficients of 0.975 and 0.0115 ml/(mg cm), respectively. H⁺,K⁺-ATPase after solubilization was subjected to size exclusion chromatography on a Superose 6 column; fractions corresponding to the central part of the main protein peak were pooled, and 30 μl were injected onto a KW 804 column equilibrated at 4 °C, with a flow rate of 0.5 ml/min, with an eluent filtered at 0.1 μm and containing 40 mm KCl, 40 mm MES (pH 6), 0.25 m sucrose, 3 mm MgCl₂, 1 mm EDTA, 2 mg/ml Tween 20.

DISCUSSION

In the present work, we provide the first conclusive evidence for the preparation of an enzymatically fully active α,β-protomer of H⁺,K⁺-ATPase, prepared by detergent solubilization from gastric mucosa membranes. The retention of activity in a monomeric state is similar to what has been observed for other P-type ATPases like the sarcoplasmic reticulum Ca²⁺-ATPase (22) and Na⁺,K⁺-ATPase (27–30). A plausible model presented in Fig. 6 was thus built based on the structure of the pig kidney Na⁺,K⁺-ATPase α1β1 complex. As noted in the Introduction, in previous studies on H⁺,K⁺-ATPase, retention of enzyme activity after treatment with non-ionic detergents has always been associated with solubilization of the ATPase in dimeric or higher oligomeric states. Combined with other functional and structural evidence, this has led to the view that for H⁺,K⁺-ATPase, obligatory protein-protein interactions are required for activating the ATP-dependent phosphorylation and dephosphorylation reactions and their coupling to H+/K⁺ translocation. In contrast to this, the present data offer evidence for the view that the detergent-solubilized H⁺,K⁺-ATPase α,β-protomer is the fundamental unit for H⁺,K⁺-ATPase function. In addition to the strong homology to Na⁺,K⁺-ATPase and Ca²⁺-ATPase, combined with much functional data, this is a suggestion that is supported by recent progress on the structure of H⁺,K⁺-ATPase, obtained on two-dimensional crystals of this protein with a resolution of 6.5 Å (8, 9, 65). These structural data suggest that the H⁺,K⁺-ATPase α,β-protomer with a few structural adaptations operates on the same general structural principles as Ca²⁺-ATPase (35, 36) and Na⁺,K⁺-ATPase (37–39). The differences include an intraprotomeric protein-protein interaction of the β-unit with the phosphorylation domain of the α-subunit for H⁺,K⁺-ATPase. It would account for the “ratchet” mechanism, proposed as a special mechanism that prevents reversal of the proton transport mechanism (9). Such a mechanism, by preventing the E2P conformation from becoming reversibly dephosphorylated by backward reaction with ADP via E1P (65), is considered necessary to explain the very high proton membrane gradients (∼10⁶:1) achievable by ATP phosphorylation with H⁺,K⁺-ATPase (66), E1P and E2P being the two main conformations of phosphorylated P-ATPases (e.g. see Ref. 36). Unique features of H⁺,K⁺-ATPase also comprise a modified E1P conformation, approaching that of E2P, and lack of evidence for wide opening of the intramembranous helices toward the extracytosolic side in E2P ground state in the BeF-stabilized crystals (65), in contrast to the luminal opening observed for the same kind of crystals in Ca²⁺-ATPase (67). These differences can probably be attributed to the particular status of the proton, which leaves this ion with more possibilities for a facile traverse through the H⁺,K⁺-ATPase membrane by hydronium ion and/or proton wiring mechanisms (37).

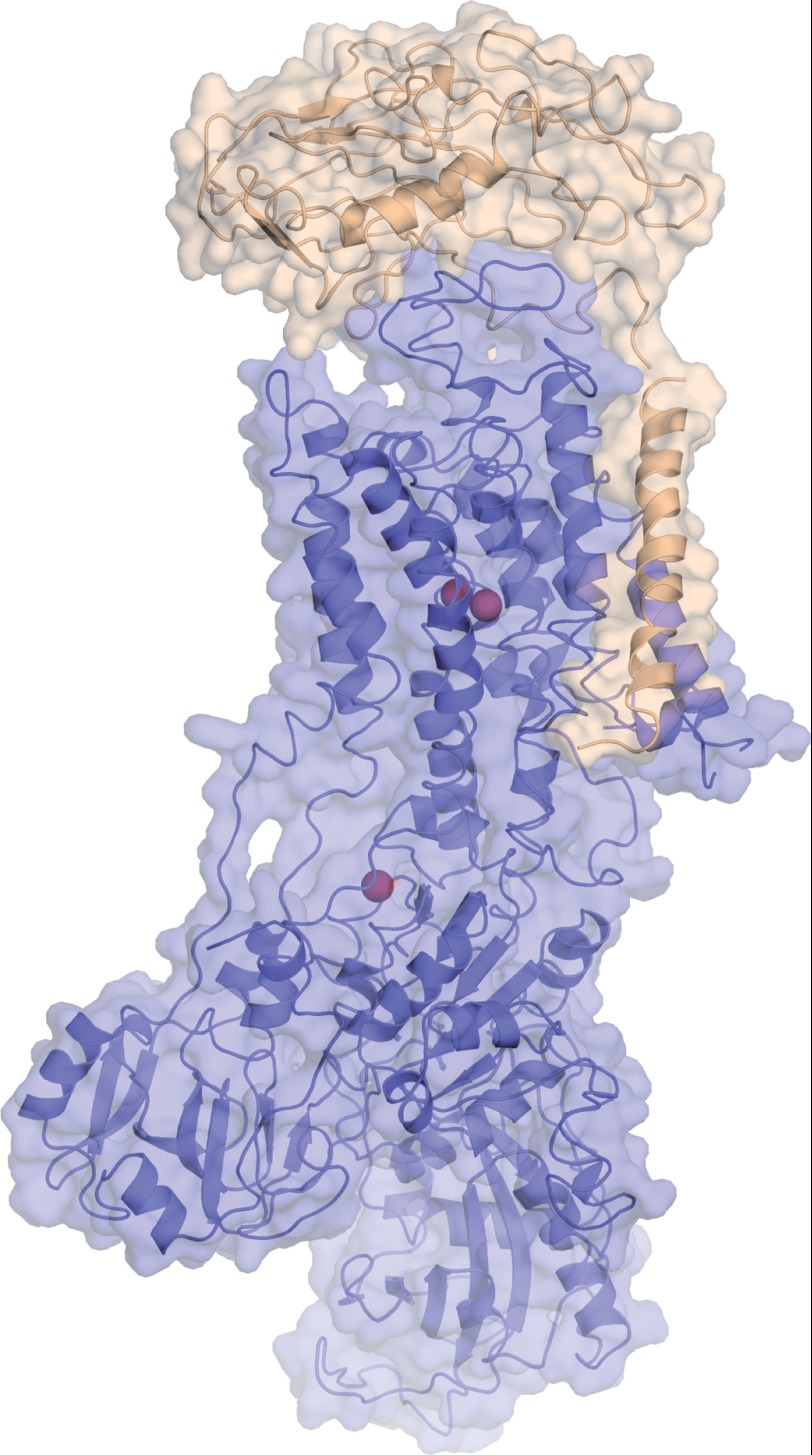
FIGURE 6.

Model of the α,β monomer H⁺,K⁺-ATPase. Shown is a model of the H⁺,K⁺-ATPase α,β monomer complex as represented by the structure of the pig kidney Na⁺,K⁺-ATPase α1β1 complex in the potassium-occluded state trapped with MgF₄²⁻ (Protein Data Bank entry 3KDP (37)). The α-subunit is shown in blue, and the β-subunit is shown in wheat. Potassium ions (two at membraneous transport sites, one at a cytoplasmic, regulatory site) are shown in brown spheres. The structure spans ∼160 Å in the long dimension, excluding glycosylations on the β-subunit.

However, it should be noted that, because the new data do not tell us much about the actual state of self-association of H⁺,K⁺-ATPase in the native membrane, they do not exclude the possibility that quaternary organization could be of regulatory importance for H⁺ transport through membranes, as has been inferred from kinetic experiments suggesting half-of-the-sites reactivity (18, 19). The main argument for half-of-the-sites reactivity of a membranous H⁺,K⁺-ATPase revolves around the issue of the maximal amount that can be obtained by phosphorylation with ATP in K⁺-free and hence dephosphorylation-blocked medium. The value obtained is around 2.5 nmol of phosphorylated enzyme/mg of protein (e.g. see Ref. 18). Does this value represent 50% of that which would be possible for a monoprotomeric and fully active protein (i.e. ∼5 nmol/mg for H⁺,K⁺-ATPase)? An affirmative answer to this question presupposes the availability of fully purified and active preparations of the enzyme. However, it is a common experience within the P-type ATPase field that even the best “pure” preparations of, for example, Ca²⁺-ATPase and Na⁺,K⁺-ATPase contain considerable amounts of inactive ATPase (e.g. see Refs. 36 and 68, 69). For these two enzymes, the level of inactive ATPase is close to 50% in the native membranes. Reliable stoichiometries are also made difficult by other methodological uncertainties, such as the determination of absolutely correct protein concentrations and upper values for ligand binding with low affinity. For instance, the error in protein determination using BSA as a standard for P-ATPase or other membrane proteins is on the order of 20% (e.g. see Refs. 70 and 71). The incompletely active proteins and methodological difficulties are the two factors that may explain the extremely large variability of results for stoichiometries obtained by different authors for describing the properties of ATPases (e.g. Na⁺,K⁺-ATPase) (72).

So far, the use of detergents to study the properties of the gastric acid pump has been hampered by the fact that H⁺,K⁺-ATPase, in comparison with other P-type ATPase cation pumps, is exquisitely sensitive to deterioration by exposure to detergents. This prevented us from employing detergents ordinarily used for this purpose to prepare solubilized H⁺,K⁺-ATPase in a structurally defined and functional state. We here introduced Tween 20 as a new detergent for keeping the ATPase in a solubilized and functionally active state. This was also the case for DDM (14), which could have been the only viable alternative for performing these experiments, but the enzyme was prepared with much less ATPase activity after HPLC (see supplemental Fig. S1C). Tween 20 is a sorbitol-based polyoxyethylene glycol detergent that is chemically heterogeneous (73). It is being used extensively as a membrane-transferring and surface-blocking agent in, for example, Western blot and ELISA experiments, but so far is rather inefficient as a solubilizer of biological membranes (54). This is probably due to the presence of a long and branched hydrophilic chain leading to a high hydrophilic-lipophilic balance number. Despite this, we had noticed in previous experiments that Ca²⁺-ATPase could be slowly solubilized as monomers from sarcoplasmic reticulum membranes by prolonged (overnight) treatment with Tween 20.⁶ However, proper solubilization of gastric H⁺,K⁺-ATPase membrane vesicles could not be done by treatment with Tween 20 alone (supplemental Fig. S1A). In order to achieve solubilization, we used an initial treatment with C₁₂E₈ to break up the membrane structure and partially delipidate the H⁺,K⁺-ATPase and combined this step with a quick exchange of C₁₂E₈ by Tween 20 to avoid inactivation of the enzyme. The fractionated separation on a Superose column indeed allowed us to maintain the H⁺,K⁺-ATPase in a solubilized and enzymatically active state (Fig. 1). This two-stage strategy is similar to that previously employed to keep Ca²⁺-ATPase in a solubilized and enzymatically active state with Tween 80 (22) and amphipol (74) after pretreatment with C₁₂E₈.

With this preparation, we determined by chemical analysis that lipids with our procedure were retained at a level of 0.25 g/g for phospholipids, and 0.024 g/g for cholesterol. Analysis of the phospholipid content of the tubulovesicular membranes indicated a usual overall fatty acid distribution but with a high content of phosphatidylethanolamine (53%) (supplemental Table S1). We also determined a rather low cholesterol content (7.5% (w/w) of total phospholipids). We consider that all lipid eluting together with H⁺,K⁺-ATPase by gel filtration is actually bound by the protein. To retain some lipid on the ATPase is important for the preservation of protein activity after solubilization, although too much will be expected to favor oligomerization (75). In addition, it is known that a suitable amount of lipid will be required to facilitate membrane protein crystallization (e.g. see Refs. 76 and 77).

As a second important point, we determined the glycosylation of the pig H⁺,K⁺-ATPase β-subunit to contribute with 9 kDa to the mass of the H⁺,K⁺-ATPase β-subunit, as determined by MS of the complete protein (Fig. 2). This value is significantly lower than the glycosylation level that we could estimate from the model for the β-subunit by Tyagarajan et al. (57) based on rabbit gastric H⁺,K⁺-ATPase. From this model, we calculate a glycosylation mass of 20 kDa, considering the masses of the main glycopeptides analyzed by MS analysis. Glycosylation heterogeneity was observed in the rabbit on all of the N-glycosylation sites (an additional O-glycosylation site is also mentioned but not characterized). The probable presence of microheterogeneity in the glycosylation pattern for pig gastric H⁺,K⁺-ATPase studied here is suggested from the smear observed on SDS-PAGE, whereas an inordinately high apparent molecular mass, resulting in an electrophoretic migration close to that of the α-subunit, could suggest that the β-subunit is only slowly released from the α,β complex during the SDS-PAGE procedure (Fig. 1E). The large difference in the glycosylation level estimated between pig and rabbit gastric H⁺,K⁺-ATPase could also arise for a number of other reasons. First, it is known that protein glycosylation is a highly regulated process that strongly depends on species, tissue localization, and cell metabolism (e.g. see Refs. 78 and 79 and references therein). In addition, we estimate a reduced number of potential glycosylation sites in the pig: six sites, including a marginal one, from the NetNGlyc 1.0 Server program as compared with seven N-glycosylation sites in H⁺,K⁺-ATPase from the rabbit. Furthermore, we cannot exclude either the possibility that partial deglycosylation has occurred during purification or that there has been incomplete glycosylation during the transit from the endoplasmic reticulum to the plasma membrane. It is interesting to note that, although glycosylation of H⁺,K⁺-ATPase and Na⁺,K⁺-ATPase is important for targeting of these proteins in polarized cells, their exact role in folding, stabilization, and transport function is still a debated issue (see Ref. 80 and references therein).

The determination of the association state of membrane proteins by hydrodynamic methods is not a simple procedure, because solubilized membrane proteins usually are multicomponent complexes (43, 53). This may explain part of the controversy concerning different proteins (e.g. see Refs. 63 and 81), including H⁺,K⁺-ATPase, whose association state was inferred from a variety of techniques (reviewed in Ref. 16) (e.g. native gel electrophoresis (14, 15), gel filtration (e.g see Ref. 16), or cross-linking (13)). To these difficulties is added sample instability in the detergent-solubilized state. It may explain the structural heterogeneity noticed for H⁺,K⁺-ATPase by chromatography or in single-molecule detection using total internal reflection fluorescence microscopy (16, 17), which has given rise to extreme difficulty in assigning which association state is the functional one. Our choice of sedimentation velocity allowed us to conduct the experiments within a time frame sufficiently short not to significantly perturb aggregation and other molecular properties as well as enzyme activity. A main species was identified, together with minor amounts of aggregates that clearly were attributable to sample aging. Our solubilized H⁺,K⁺-ATPase in addition to glycosylation and lipid contains bound Tween 20, for which we had no specific analytical procedure. Tween 20 bound to H⁺,K⁺-ATPase was first inferred from refractive index and UV absorption measurements, with suitable deductions for the changes of these parameters caused by the lipid and protein content (Table 1). This resulted in an estimate of 1.6 g/g, the precision of which, however, is strongly dependent on the exactness of the extinction coefficients (Table 1). Combining the values of the sedimentation coefficient and of the Stokes radius (estimated with undefined uncertainty to be 6.3 nm by the elution from calibrated Superose columns) did not allow us to define the detergent content but strongly suggested the sedimenting H⁺,K⁺-ATPase species to be in a monomeric α,β state. Furthermore, we were able to estimate the partial specific volume of the solubilized complex from the decrease in s_20,w following H₂O/D₂O solvent exchange. From the determined value of 0.813 ml/g and integrating this with our knowledge of the carbohydrate and lipid content, we can estimate the binding of Tween 20 to be 1.0 ± 0.7 g/g. In view of its sedimentation, a particle with this composition would correspond to a molecular dimension slightly larger than estimated from gel filtration. Analysis of the sedimentation in H₂O and D₂O, in the absence of any hypothesis on the lipid content, allowed us to confirm the description of the solubilized H⁺,K⁺-ATPase as a compact α,β-glycosylated monomer, with a frictional ratio of 1.5 ± 0.1 and 0.9–1.4 g/g of bound detergent plus lipids. Finally, independent measurements, employing gel filtration coupled to light scattering, absorbance, and refractive index detections, supported the view of an α,β monomer solvated with 1.1 ± 0.2 g/g of bound detergent plus lipids, based on the extinction coefficients calculated from sequence.

In conclusion, by our combined approach, a consistent picture is emerging from these measurements. In fact, we consider the present work as a showcase for how biophysical methods can be developed and adapted to answer specific questions of both structural and functional importance for membrane proteins. By these means, we have defined a solubilization protocol allowing us to obtain solubilized pig gastric H⁺,K⁺-ATPase as an active species over days, which was unambiguously present as an α,β monomeric protomer. We would like to point out that, by using similar experimental approaches, dimers were observed in solution for membrane proteins described to function as dimers in the membrane (e.g. cytochrome c oxidase (81) or ABC transporters (82, 83)). We conclude that the general functioning of H⁺,K⁺-ATPase is most probably similar to that of the Ca²⁺-ATPase and Na⁺,K⁺-ATPase.