Chiral micellar electrokinetic chromatography (CMEKC)-atmospheric pressure photoionization of benzoin derivatives using mixed molecular micelles

Abstract

In the present work we report, for the first time, the successful on-line coupling of chiral micellar electrokinetic chromatography (CMEKC) to atmospheric pressure photo-ionization mass spectrometry (APPI-MS). Four structurally similar neutral test solutes (e.g., benzoin derivatives) were successfully ionized by APPI-MS. The mass spectra in the positive ion mode showed that the protonated molecular ions of benzoins are not the most abundant fragment ions. Simultaneous enantioseparation by CMEKC and on-line APPI-MS detection of four photoinitiators: hydrobenzoin (HBNZ), benzoin (BNZ), benzoin methyl ether (BME), benzoin ethyl ether (BEE), were achieved using an optimized molar ratio of mixed molecular micelle of two polymeric chiral surfactants (polysodium N-undecenoxy carbonyl-L-leucinate and polysodium N-undecenoyl-L,L-leucylvalinate). The CMEKC conditions, such as voltage, chiral polymeric surfactant concentration, buffer pH, and BGE concentration, were optimized using a multivariate central composite design (CCD). The sheath liquid composition (involving % v/v methanol, dopant concentration, electrolyte additive concentration, and flow rate) and spray chamber parameters (drying gas flow rate, drying gas temperature, and vaporizer temperature) were also optimized with CCD. Models built based on the CCD results and response surface method was used to analyze the interactions between factors and their effects on the responses. The final overall optimum conditions for CMEKC-APPI-MS were also predicted and found in agreement with the experimentally optimized parameters.

1 Introduction

Enantiomeric separation and detection of chiral compounds with electrokinetic chromatography (EKC)-mass spectrometry (MS) is one of the challenging areas in the use of hyphenated technology for chiral analysis. Although a wide array of low molecular weight chiral selector(s) (e.g., cyclodextrins, macrocyclic antibiotics, unpolymerized chiral micelles), are available, the use of the aforementioned chiral selectors is very difficult when UV detection is replaced with electrospray ionization (ESI)-MS. This is mainly due to the use of charged chiral selector, which when present in the running buffer at concentrations ≥10 mM often interferes with the ionization of the analytes. Moreover, the conventional charged surfactant also coats on the surface of the ionization source, and suppresses the MS signal in a few runs. To overcome this problem, polymeric chiral surfactant (also known as chiral molecular micelle) was introduced for the first time by our research group in 2001 for micellar electrokinetic chromatography (MEKC)-ESI-MS [1]. The molecular micelles are typically in the high molecular mass range (15,000–20,000 Daltons), and are very hard to ionize in the ESI spray chamber, hence providing a much more stable baseline and cleaner electropherograms with significantly lower background noise. Other advantages of the molecular micelle include zero critical micelle concentration and compatibility of organic solvents [1–3]. Hence, several reports have identified the use of polymeric chiral surfactants in chiral MEKC-ESI-MS applications over the last decade [1–5]. Recently, both MEKC [6] and microemulsion electrokinetic chromatography (MEEKC) [7] were coupled to atmospheric pressure photoionization APPI-MS using conventional SDS micelles for achiral separations of neutral compounds. However, the aforementioned papers did not address MEKC-APPI-MS and MEEKC-APPPI-MS for the separation and detection of chiral hydrophobic and neutral compounds. In addition, to the best of our knowledge, no studies describing the separation of neutral or even charged chiral compounds using any chiral selector in EKC or MEKC equipped with APPI-MS can be found in the literature. This is surprising in light of the obvious benefits of APPI-MS over atmospheric pressure chemical ionization (APCI-MS) or ESI-MS for several classes of non-polar chiral compounds.

The APPI is one of the latest “soft ionization” modes of mass spectrometry. As mentioned earlier, APPI-MS is especially suitable for the analysis of highly non-polar or neutral compounds, which cannot be ionized by ESI or less efficiently by APCI. It is reported to be a more universal, rugged and sensitive ionization technique than APCI due to its higher tolerance to non-polar (e.g., hexane-based) mobile phase and low flow rates in HPLC-MS applications [8–10].

The feasibility of coupling CE to APPI-MS was first reported by Nilsson et al. [11]. In a short time, several works involving CE-APPI-MS have been reported [6, 12–16]. Mol and coworkers studied the setup and performance of CE-APPI-MS using non-volatile background electrolyte and an ion-trap mass spectrometer [6]. In the same work [6], this research group also reported a MEKC-APPI-MS of two neutral compounds using a running buffer of 20 mM SDS, 10 mM sodium phosphate and 20% acetonitrile. Zheng et al. [12] separated positional isomers of methylated benzo [α] pyrene (MBAP) with capillary electrochromatography using C-18 column followed by APPI-MS. The detection limits of three most carcinogenic MBAP isomers were reported in the range of 2.5–5.0 μg/mL. Schappler and coworkers successfully separated three basic compounds with CE-APPI-MS and optimized the APPI conditions with multivariate experimental designs [13]. The same research group also separated a series of pharmaceutical drugs (β-blockers, central stimulants, and diuretics) with MEEKC-APPI-MS using a microemulsion system containing SDS, butanol, and n-octane [14]. Hommerson et al. compared ESI and APPI for coupling to MEKC using SDS running buffer and APPI was found to provide better LOD [15]. They also tested drug impurity with different ionization sources (including ESI, APCI, APPI and dopant assisted APPI) for CE-MS [16]. However, as mentioned earlier, despite all the recent CE-APPI-MS applications of achiral compounds, no chiral selectors or chiral pseudostationary phases for MEKC-APPI-MS analysis is reported in the literature.

In this work, four chiral photoinitiators, hydrobenzoin (HBNZ), benzoin (BNZ), benzoin methyl ether (BME), and benzoin ethyl ether (BEE), were simultaneously enantioseparated with MEKC using a mixture of two chiral molecular micelles polysodium N-undecenoxy carbonyl-L-leucinate (poly-L-SUCL) and poly-sodium N-undecenoyl-L,L-leucylvalinate (poly-L,L-SULV). Chiral benzoins are important structural units of many useful biological compounds. These compounds are considered as versatile building blocks in many asymmetric synthesis. For example, enzymatic synthesis of chiral benzoins in high enantiomeric excess from racemic benzoyl benzene is reported [17]. One real life application of benzoin suggests that benzoin is a drug intermediate used in cancer treatment [18]. Hence, they are often used as model compounds to test the selectivity of the enantioselective analysis method in separation science [19–21]. The use of the two molecular micelles has provided good chiral resolutions and selectivities for the benzoin derivatives in previous MEKC-UV studies [3,19]. However, when MEKC is coupled to APPI-MS, the MEKC-UV conditions need to be reoptimized to compensate the use of volatile background electrolyte and the suction effect of nebulizing gas on the separation performance. These two are very important factors, which can have significant influence on the choice of buffer pH, surfactant concentration, as well as the separation voltage. Therefore, a series of factors that involved in the MEKC enantioseparation were first examined by sequential optimization experiments, using a univariate approach. Next, to guarantee an overall optimum condition and to understand the interactions between the various separation factors and the APPI-MS parameters, multivariate optimization or design of experiment (DOE) needs to be performed.

Central composite design (CCD) as one of the effective secondary DOE method was chosen because CCD allows the deduction of quadratic models and the resulting response surface method (RSM) analysis can be used to analyze the interactions between related factors [4, 22]. Besides MEKC conditions, sheath liquid composition and spray chamber conditions were also optimized using the same method.

2 Material and methods

2.1 Chemicals

The analytes R, R and S, S (±) hydrobenzoin (HBNZ), R,S benzoin (±) (BNZ), benzoin methyl ether (±) BME, as well as benzoin ethyl ether (±) BEE were purchased from Sigma-Aldrich (St. Louis, MO). Acetonitrile (ACN, HPLC grade) was purchased from Fisher Scientific (Fair Lawn, NJ). Acetic acid, methanol (Meow, HPLC grade) and aqueous solution of 7.5 M ammonium acetate (NH₄OAc) were purchased from Sigma-Aldrich (St. Louis, MO). Ammonium hydroxide (NH₄OH, 28%–30% ammonia solution) was purchased from EM Science (Gibbstown, NJ). Deionized water (18 MΩcm) was purified by a Barnstead Nanopure II Water System (Dubuque, IA). Chemicals (N-hydroxysuccinimide, N,N′-dicyclohexylcarbodiimide, undecylenic acid, isopropanol, ethyl acetate, and sodium bicarbonate) used to synthesize dipeptide surfactants were obtained from Sigma-Aldrich (St. Louis, MO). Sodium hydroxide (50%, w/w) was obtained from Fisher Scientific (Fair Lawn, NJ). Hydrochloric acid and tetrahydrofuran were purchased from Caledon Laboratories Ltd (Georgetown, Ont., Canada). Chemicals such as ω-undecylenyl alcohol, pyridine, dichloromethane, and L-leucine used to synthesize the surfactant monomer were purchased from Sigma-Aldrich (St. Louis, MO). Triphosgene was purchased from TCI-America (Portland, OR). Leucine-valine dipeptide was obtained from Bachem California Inc (Torrance, CA). Sodium sulfate anhydrous was purchased from EMD Chemicals (Gibbstown, NJ). All the chemicals have the purity of 98% or higher and were used as received without further purification unless specifically noted. The surfactant monomers of sodium N-undecenoyl-L, L-leucylvalinate (L, L-SULV) and sodium N-undecenoyl–, L-leucinate (L-SUCL) were synthesized following the procedures described in references [23–25]. The monomers were polymerized by Phoenix Memorial Laboratory (University of Michigan, Ann Arbor, MI) using a total dose of 20 M red of ⁶⁰Co γ-radiation.

2.2 Sample and running buffer preparation

Stock solutions of the analytes R, R and S, S (±) HBNZ, R, S (±) BNZ, (±) BME, and (±) BEE were prepared at the concentration of 8.0 mg/mL in ACN. Working standard of the analyte solution was prepared by mixing 20 all of each stock solution and then diluting the mixture with 80 all of H₂O to obtain the desired final concentration of 1.0 mg/mL for each benzoin derivative. The CE running buffer was prepared by diluting the 7.5 M NH₄OAc solution to the desired concentration. The pH of the NH₄OAc BGE was adjusted as needed with 1 M NH₄OH. Next, poly-L, L-SUCL and poly-SULV were dissolved in the NH₄OAc buffer to obtain the desired equivalent molar concentration, which is defined as the concentration of the polymeric surfactant that has the same weight as the monomer. The surfactant containing buffer was then vortexed, filtered by 0.45 μm PTFE syringe filter (Fisher Scientific, Pittsburgh, PA), and ultrasonicated for 15–20 min before use.

2.3 MEKC-APPI-MS instrumentation

All MEKC-APPI-MS experiments were performed on an Agilent CE (Agilent Technologies, Palo Alto, CA) interfaced to an Agilent 1100 series single quadrupole mass spectrometer (Agilent Technologies, Palo Alto, CA). The Agilent 3D-CE/MSD ChemStation software (Rev. A.10.02) was used for instrument control and data analysis. Sheath liquid was delivered by an Agilent 1100 series isocratic HPLC pump equipped with a 1:100 splitter. The MEKC separation was performed on a 120 cm long fused silica capillary (50 μm i.d., 360 μm o.d., Polymicro Technologies, Phoenix, AZ). At 60 cm from the injection end of the capillary, a 3 mm section of polyimide coating was burned off with a home-made electronic burner to create a UV detection window. New capillary was sequentially flushed with 1 M NH₄OH and triply deionized water for 40 minutes and 20 minutes, respectively before use. The capillary was flushed with the running buffer for 5 minutes using a pre-conditioning step before each run. After each run, the capillary was flushed with water for 2 minutes, 1 M NH₄OH for 2 minutes, and water for another 2 minutes as post-conditioning. The capillary temperature was set at 20 °C; positive voltage (anode at the inlet end and cathode at the MS end) was applied for all the experiments. Analytes were kept at 15 °C in the auto sampler and injected hydrodynamically at the pressure of 10 mbar for 10 sec.

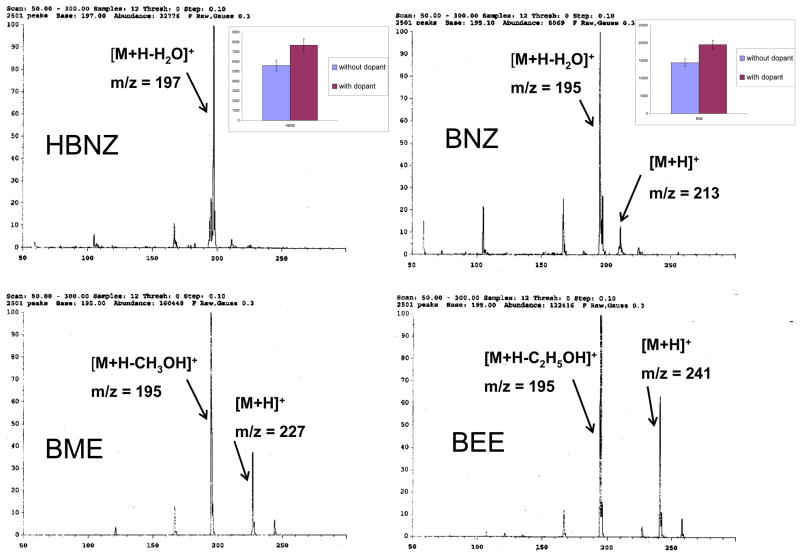
The nebulizer was mounted on a 36 mm plastic spacer, which was placed between the nebulizer and the APPI spray chamber. The nebulizer was grounded by a wire to maintain the steady current. The APPI lamp was a krypton UV lamp (emits photons at 10.0 and 10.6 eV) developed by Syagen Technology, Inc. (Tustin, CA). The following conditions were used for preliminary APPI-MS detection: nebulizer pressure, 5 psi; capillary voltage + 2000 V; fragmentor voltage, 90V; gain setting, 3. Other APPI-MS conditions were varied according to the experimental design. The positive ion mode was selected in which the ions were group SIM at m/z = 197 for HBNZ for its detection as [M+H-H₂O]⁺, whereas the most abundant ion [M+H–H₂O]⁺, [M+H-CH₃OH]⁺, and [M+H-C₂H₅OH]⁺ were observed for BNZ, BME, and BEE, respectively at m/z 195.

2.4 Experimental design and data processing

Experimental design and data analysis for the optimization of MEKC as well as APPI-MS parameters were performed on Design-Expert (version 7.0.3, Stat-Ease, Inc. Minneapolis, MN) software. Four factors (separation voltage, pH, surfactant concentration and NH₄OAC concentration) were chosen for MEKC optimization using CCD. All CCDs were generated using default settings. Experiments were carried out. The results of the experiments were then input into the software and the fitted models generated. The models were validated by analysis of variance (ANOVA), and the response surface plots were created by the software.

3 Results and discussion

3.1 Preliminary experiments

The preliminary experiments on the APPI-MS conditions (including both direct infusion experiments and on-line CMEKC-MS experiments) were carried out to determine the fragmentation pathway, most abundant ions and APPI-MS spray chamber parameters, which are most significant for better detectability of all four benzoins. These experiments were followed by a set of univariate experiments to determine the optimum mixed molecular micelle ratio, range and significance of CMEKC factors of all four benzoin derivatives. Because the parameter of sheath liquids (flow rate and composition) needs careful optimization in APPI-MS, the working range was carefully determine to promote efficient ionization of the benzoin derivatives.

3.1.1 Direct Infusion spectra and fragmentation pathway

Direct infusion experiments for the benzoins in both positive and negative ion modes showed that positive ion mode is more sensitive than negative mode. The full scan positive ion MS spectra for all four benzoin derivatives are shown in Fig. 1 at variable fragmentor voltages by direct infusion without dopant. However, with or without dopant, the fragmentation pattern in the mass spectrum remained the same for all four benzoins. The main ions (in water/-methanol/5mM ammonium acetate sheath liquid) for HBNZ and BNZ were the [M+H-H₂O]⁺ ions at m/z 197 and 195, but the protonated molecular ion [M+H]⁺ at m/z 213 is only observed for BNZ. Similarly, for BME and BEE, the highest abundant ion is observed at m/z 195, which corresponds to [M+H-CH₃OH]⁺ and [M+H-C₂H₅OH]⁺, respectively. In addition, [M+H]⁺is observed for both BME and BEE. Direct infusion experiments with and without dopant (i.e., acetone) were also conducted. Adding acetone in the sheath liquid increased the APPI-MS intensity of HBNZ and BNZ (insets of Fig. 1). In contrast, sensitivity of BME and BEE was not affected significantly (data not shown). This suggests that the proton affinity (PA) for HBNZ and BNZ is greater than that of the solvent (MeOH) as well as the dopant (acetone). Thus, proton transfer reaction could have been facilitated by both the solvent clusters (Sn) as well as the dopant. On the other hand, the PA of the benzoin ethers (i.e., BME and BEE) must be lower than dopant, but higher than solvent. Thus, the proton transfer to BME and BEE can be still be obtained by the proton transfer reaction between Sn (i.e., the use of 50/50% methanol/water) present in the sheath liquid and the benzoin ethers (M) [S_nH⁺ + M → MH⁺ + nS] [24].

Figure 1.

APPI-MS spectra of the four benzoin compounds. The inset plots of HBNZ and BNZ shows the signal intensity with and without 0.5% acetone. The error bar in each plot represents 3(σ) standard deviations.

The chemical structure the four benzoin derivatives are provided in Fig. 2. Note that HBZN is a diol with two chiral centers. Among its three possible isomers, only (1R, 2R) and (1S, 2S) forms are enantiomers, which are available commercially, whereas the (1R, 2S) form is the meso isomer and is excluded from the experiment. The BZN is a hydroxy ketone with two phenyl groups. BME and BEE are the methyl and ethyl ether of benzoin, respectively. Consistent with Fig. 1, the fragmentation pathway proposed in Figure 2 consists of protonated molecular ions of HBZN and BZ, which are significantly less stable and eventually lose water molecules to form fragment ions [M+H-H₂0]⁺ at m/z 195 and 197, respectively. Similarly, BME and BEE, after forming relatively low abundance [M+H]⁺ ions, losses CH₃OH and C₂H₅OH, respectively to form [M+H-CH₃OH] and [M+H-C₂H₅OH] species at m/z =195. Eventually, only two ions at m/z 195 and 197 were chosen in group SIM for the on-line MEKC-APPI-MS for the four benzoin compounds.

Figure 2.

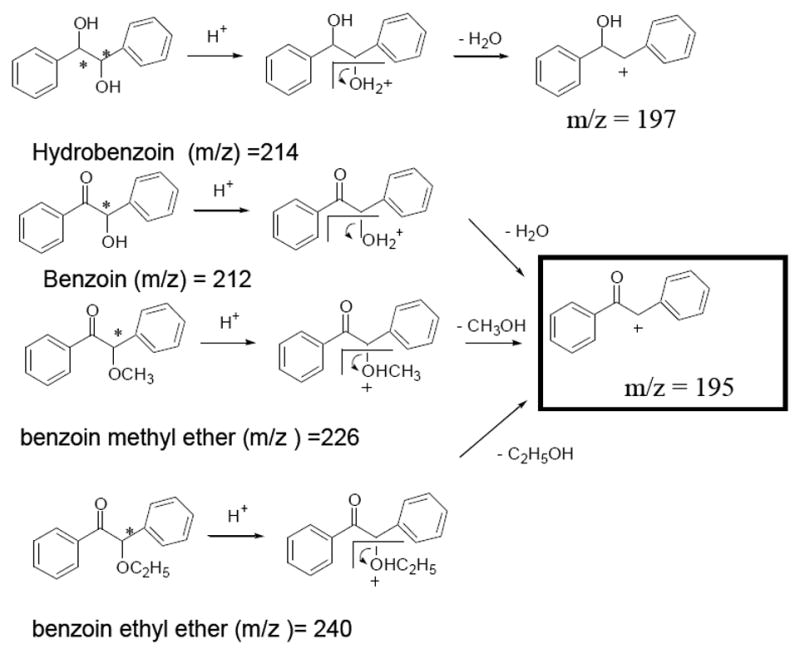
Proposed ionization and fragmentation mechanism of four benzoin derivatives in APPI-MS.

3.1.2 Determination of the APPI-MS conditions

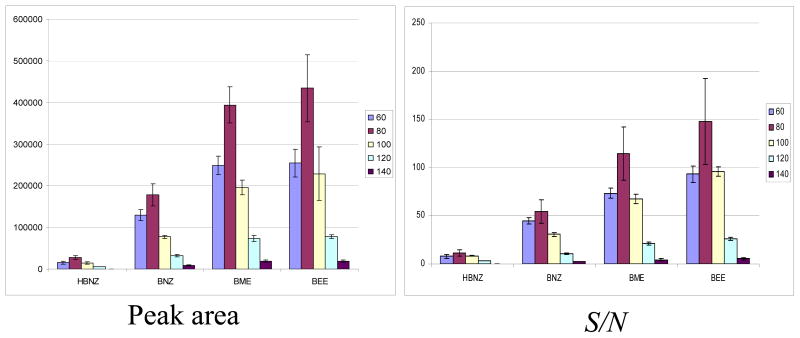
An online MEKC-APPI-MS study was carried out to determine the optimum fragmentor voltage for all four benzoins. The results shown in Fig. 3 illustrates that for all four derivatives, 80 V is the best fragmentor voltage in terms of peak area and S/N. MS capillary voltage and nebulizer pressure were also explored; 2000 V and 5 psi were determined respectively to be the best to provide the optimum S/N (data not shown). Other importance factors such as vaporizer temperature, drying gas flow rate, and drying gas temperature were investigated in the multivariate optimization. The DOE levels for these factors and their ranges determined by univariate experiments are listed in [supplementary section, Table S1].

Figure 3.

The bar plots showing the results of the online MEKC-APPI-MS fragmentor study. The error bar in each plot represents 3(σ) standard deviations. Experimental conditions: 120 cm ×50 μm i.d. fused silica capillary; 40 mM NH₄OAc, pH 10.0, with 70 mM mixed micelle of (poly-SULV and mM poly-SUCL 85:15, molar ratio); +25 kV, 20 °C; analyte: 1 mg/mL benzoin derivatives in 50/50 MeOH/H₂O, injected at 5 mbar, 10 sec; spray chamber parameters: drying gas flow rate 5 L/min; nebulizer pressure 5 psi; drying gas temperature 150 °C; vaporizer temperature 150 °C; capillary voltage 2000V; fragmentor voltage varied from 60–140 V, gain 3; SIM at m/z = 195, 197; sheath liquid: 5 mM NH₄OAc in 50/50 MeOH/H₂O, 0.5% Acetone; flow rate 7.5 μL/min.

3.1.3 CMEKC parameters

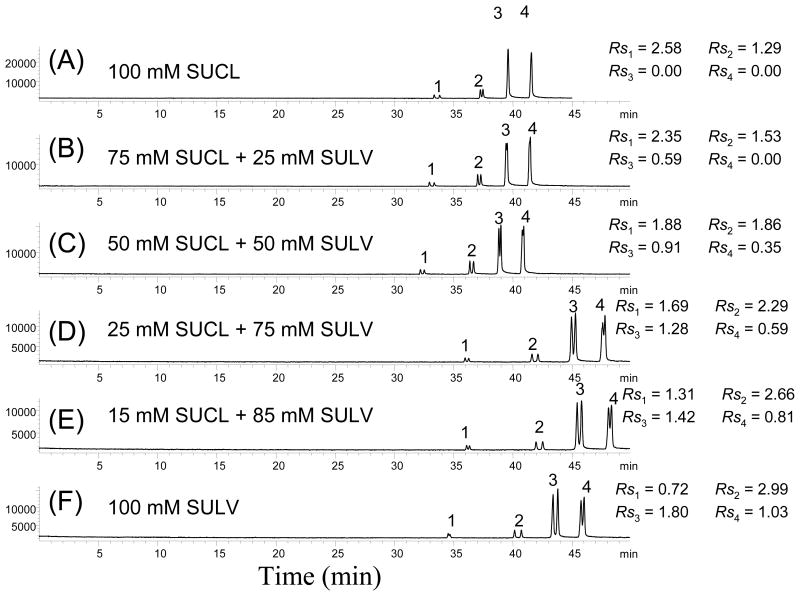
A series of sequential online CMEKC-APPI-MS experiments were performed to obtain the reasonable ranges for all the CMEKC parameters for multivariate studies. The first factor explored is the type of polymeric surfactant. Two most commonly versatile polymeric surfactants [i.e., alkenoxy-based single amino acid (poly-SUCL) and acyl-based dipeptide (poly-L, L-SULV)], were mixed in various proportions to test the synergistic effect for the simultaneous enantioseparation of all four benzoins. Using poly-L-SUCL alone was only very effective for the chiral separation of (±) HBNZ and to some extent (+) BNZ (Figure 4A). However, using poly-L,L-SULV, (±) BNZ, (±) BME, and (±) BEE, provided significantly higher chiral resolution (Figure 4F) compared to poly-L-SUCL. We hypothesize that the difference in chiral selectivity between the two molecular micelles might be due to the presence of carbamate group in poly-SUCL, which tends to form hydrogen bond with the hydroxyl group in HBNZ assisting chiral recognition. On the other hand, the amide bond in poly-SULV does not have this structural effect. To achieve a simultaneous enantioseparation of all four benzoins, a mixture of poly-SUCL and poly-L,L-SULV was investigated at different ratios via an online CMEKC-APPI-MS experiment (Figure 4B-E). The resulting electropherograms shows that with the increasing molar concentrations of poly-L,L-SULV, the chiral resolution for HBNZ decreases, while the chiral resolution for BNZ, BME, and BEE increases. As a compromise, a ratio of 15:85 (poly-SUCL: poly-L,L-SULV molar ratio) was chosen as the optimum mixed molecular micelle ratio.

Figure 4.

The CMEKC-APPI-MS electropherograms showing the effect of the mixed-micelle (poly-SUCL and poly-SULV) A-F ratio on the simultaneous enantioseparation of benzoin derivatives. Separation condition: 120 cm ×50 μm i.d. fused silica capillary; 25 mM NH₄OAc, pH 8.0, with 100 mM poly-SULV and poly-SUCL at different ratio; +25 kV, 20 °C; analyte: 1 mg/mL benzoin derivatives in 50/50 ACN/H₂O, injected at 5 mbar, 10 sec; spray chamber parameters: drying gas flow rate 5 L/min; nebulizer pressure 5 psi; drying gas temperature 150 °C; vaporizer temperature 150 °C; capillary voltage 2000V; fragmentor 80, gain 3; SIM at m/z = 195, 197; sheath liquid: 5 mM NH₄OAc in 50/50 MeOH/H₂O, 0.5% Acetone; flow rate 7.5 μL/min.

The levels and ranges of other CMEKC factors (NH₄OAc concentration, buffer pH, voltage, and polymeric surfactant concentration, Table S2) determined by univariate experiments were further explored in multivariate experimental design.

3.1.4 Determination of the sheath liquid conditions

Sheath liquid helps to ground the outlet end of the capillary and provide enhanced liquid flow to form a steady sprayer cone [1, 12, 28]. In CE-APPI-MS, sheath liquid is even more important due to the requirement of adding dopant to the analytes to obtain enhanced signal [9, 13]. A series of sequential experiments were performed to determine the ranges for the following parameter: sheath liquid composition, dopant type, dopant concentration, sheath liquid flow rate, pH of the sheath liquid, and electrolyte concentration in the sheath liquid. After the preliminary experiments (data not shown), the dopant type was determined to be acetone. Levels of other sheath liquid parameters explored in multivariate DOE are listed in Table S3.

3.2 Multivariate optimization experiments

Three sets of CCD experiments were performed to determine the optimum conditions for MEKC parameters, sheath liquid composition, and spray chamber parameters. Full factorial CCD was chosen as the design method due to its ability to evaluate the interactions between all factors with fairly less experiments [20, 27]. The factors used in these CCD experiments (Table S1, S2 and S3) as well as their levels were chosen based on the preliminary experiments aforementioned. The factors and their levels were input into the Design-Expert software and a series of runs at different level combinations were generated in random order. According to the rule of CCD, these runs include the combination of all factors at their + and − levels and several repetitive runs at their mean value (0 level, also called center point in CCD). Each factor was also tested at the value outside the +/− levels when other factors were held at 0 level. These runs are called axial or star points in CCD [20]. All the runs generated by CCD were performed and the results were input into the software as responses. Models that represent the relations between factors and responses were then fitted by least squares. These models were then evaluated by ANOVA, and RSM plots generated from the models were used to examine the interactions between factors and their effects to responses. Detailed description on CCD method can be found in literature [13, 20] and our earlier work [5, 27].

3.2.1 Optimization of MEKC parameters

Four factors (voltage, buffer pH, total surfactant concentration, and NH₄OAc concentration) were evaluated for the optimization of MEKC parameters. Their levels are listed in Table S1 (Supplementary Information). A total of 30 runs were generated by CCD. Detailed conditions for all the runs and their responses (ratio of chiral resolution/elution time of the last eluting enantiomer and total migration time) are shown in Table S4 (Supplemental Information). Rs/t_R is chosen as the response because it represents the best resolution in the least analysis time and has better repeatability in the CCD experiments. Run # 4, 11, 14, 17, 23, and 24 are repetitive runs. The %RSD for the four responses (Rs/t_R) of the four compounds of these repetitive runs are 10% for HBNZ, 5.0% for BNZ, 9.3% for BME, 6.1% for BEE), and 1.1% for total run time (i.e.,t_R), respectively. Thus, the RSD for Rs/tr in the range of 5–10% is acceptable, and t_R seems relatively small illustrating overall good to excellent repeatability for the CCD experiments.

Once the responses were input into the Design-Expert software, they were fit into different models (mean, linear, 2FI, quadratic, and cubic). These models were then compared by F-test. The most non-aliased model was eventually selected. The regression coefficients for all the factors in the eventually fitted models are shown in Table 1. The Prob>F values is the probability of corresponding factors having no effect on the response) are also listed. The factor is considered as significant effect on the response if the Prob>F value is smaller than 0.05. As indicated in Table 1, linear models were chosen for Rs/t_R of HBNZ, BME, and BEE; whereas quadratic models were chosen for Rs/t_R and t_R of BNZ.

Table 1.

Regression coefficient of the coded factors and analysis of variance for the response surface models of Rs/t_R and analysis time for the optimization of MEKC factors

Term	Rs/tR-HBNZ		Rs/tR-BNZ		Rs/tR-BME		Rs/tR-BEE		tRa
	Coefficient	Prob>F b	Coefficient	Prob>F	Coefficient	Prob>F	Coefficient	Prob>F	Coefficient	Prob>F
Intercept	0.018		0.049		0.033		0.017		44
F1 Voltage	0.0036	< 0.01	0.011	< 0.01	0.0082	< 0.01	0.0044	< 0.01	−14	< 0.01
F2 pH	0.0013	0.010	0.0016	0.053	0.00026	0.70	0.00044	0.37	2.1	< 0.01
F3 [Surf.]	0.0010	0.036	−0.00076	0.32	−0.00055	0.42	0.000095	0.84	3.9	< 0.01
F4 [NH4OAc]	0.00032	0.50	0.00063	0.41	0.000055	0.94	−0.00037	0.44	4.2	< 0.01
F1 F2			0.0012	0.21					−0.65	0.36
F1 F3			0.0012	0.22					−1.4	0.064
F1 F4			0.0022	0.029					−1.5	0.043
F2 F3			0.0010	0.28					0.98	0.18
F2 F4			−0.0018	0.071					0.12	0.87
F3 F4			0.0011	0.25					1.8	0.023
F12			−0.0015	0.042					3.9	< 0.01
F22			0.0012	0.12					1.7	< 0.01
F32			−0.0012	0.12					−0.065	0.90
F42			−0.00068	0.34					0.69	0.21
R2	0.75		0.94		0.85		0.77		0.98
Adjusted R2 c	0.71		0.89		0.83		0.74		0.97
Predicted R2 d	0.63		0.71		0.79		0.65		0.90

^aMigration time of the last peak.

^bProbability of the null hypothesis being true (the factor has no significant effect on the response) based on the F-test for comparing model variance with residual variance. Any term with P < 0.05 is considered significant, and call for rejection of null hypothesis.

^cCoefficient of determination adjusted for the number of terms in the model.

^dA measure of the amount of variation around the mean explained by the model, coefficient of determination is based on the predicted residuals from the model.

According to Table 1, three factors (voltage, buffer pH, and surfactant concentration) and two factors (voltage and and buffer pH) were found significant for Rs/t_R of HBNZ and BNZ, respectively. Their coefficients are all positive, meaning that they are all positively correlated to the response. As expected, voltage has a positive effect on the Rs/t_R value because higher voltage usually produces higher peak efficiency and thus improves the chiral resolution. The buffer pH also shows a positive effect. This is because higher pH causes higher ionization of the surfactant. The effect of pH is significant, since its Prob>F value is very close to or less than 0.05. Surprisingly, the concentration of polymeric surfactant is only significant to the Rs/t_R for HBZ but not for the remaining three benzoin derivatives. Perhaps, the more polymeric chiral surfactant in the running buffer, the better chiral separation is for the analyte with low retention (e.g., HBZ), but not for highly retained benzoin compounds (BME and BEE). For BNZ, another significant term is the product of voltage and NH₄OAc concentration (i.e.,F1×F4). This means that the interaction of these two terms is also significant. The square of the voltage (i.e., F1²) value for BNZ is significant as well, which means the effect of voltage on the Rs/t_R is not linear (i.e., not directly proportional). However, the products of other factors are not significant for the remaining three benzoin compounds.

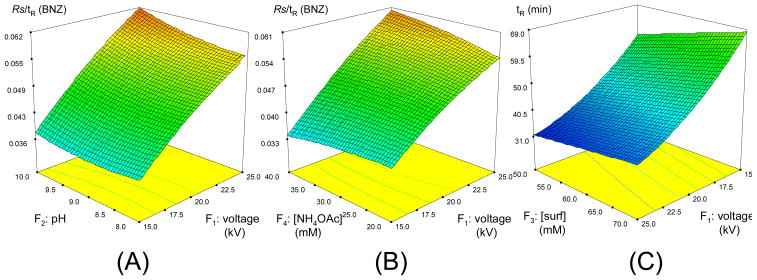
Figure 5(A) illustrates the RSM plots for the interaction between voltage and pH and their combined effect on the Rs/t_R of BNZ. It can be observed in this plot that voltage has a much bigger effect than pH since the slope is much steeper along the voltage axis. The Rs/t_R value is lower at a voltage 15 kV than 25 kV indicating a positive correlation between voltage and response. The plot along pH axis is almost flat when voltage is held at 15 kV. However, at 25 kV, it shows a positive trend, which makes the combination of 25 kV and pH 10.0 the highest point on the plot. Similar trend of RSM plots between voltage and [NH₄OAc] is shown in Fig. 5(B). The highest Rs/t_R value in this plot is when voltage is at 25 kV and [NH₄OAc] is 40 mM. The models for Rs/t_R of BME and BEE are very similar to BNZ. Both models are linear model but in both models, the only significant factor is voltage. It is also positively related to the response as the case of HBNZ.

Figure 5.

Response surface plots for the Rs/t_R of benzoin (A and B) and total retention time (C) in MEKC separation optimization using CCD experiment. Factors which are not analyzed in the plots are held at their mean values (i.e. level 0 in Table S1).

A quadratic model was selected for the total MEKC analysis time (t_R) by F-test. All of the first order terms are found significant in this model as indicated in Table 1, last column. The coefficient for voltage is negative. This means that higher voltage produces shorter run time. The coefficients for all the other three factors are positive, which suggests a positive correlation between these factors and the total run time. For pH, as mentioned above, increasing the buffer pH from 8.0–10.0 requires titration of NH₄OAC with NH₄OH increasing ionic strength. This is in agreement with the theory that higher BGE causes thinner electric double layer and lower the ζ potential, which consequently causes lower EOF and longer migration time [28–30]. Similarly, surfactant at higher concentration will retain the analytes more because the molecular micelle is a negatively charged and is moving in direction opposite to EOF causing longer elution time. Higher [NH₄OAc] also causes longer t_R due to increase in ionic strength as discussed above. In addition, note that the absolute value of the coefficient for voltage is the most positive among all the factors (see Table 1 row2 vs. rows 3–5). This means that voltage has the biggest influence on migration time.

Fig. 5C shows the RSM interaction plots of the two most significant factors (e.g., voltage and polymeric surfactant concentration with higher coefficients) on the t_R. The patterns of the other interaction factors (Table. S1) are similar to the one shown in Fig. 5(C). Note that the surface plot is strongly tilted along the voltage axis. This indicates a significant influence of voltage on t_R. In addition, note that t_R increases when voltage decreases. This suggests an inverse correlation between voltage and migration time as mentioned above. The slope of the plot increases slowly along the surfactant concentration axis form 50–70 mM suggesting a positive correlation between total mixed micelle concentration and total run time. The highest point on this plot is at the combination of voltage 15 kV and a total polymeric surfactant concentration of 70 mM (poly-SUCL:poly-L,L-SULV molar ratio 85:15). The R², adjusted R², predicted R² values for each model are tabulated in last few rows of Table 1. These values are all close to 1, suggesting a good fit for all models. Table S5 shows the ANOVA results for all the models. In this table, the Prob>F values for all the models are smaller than 0.05. This means that all models are significant, i.e., at least one factor in the model has significant effect on the response. Detailed explanation on how ANOVA are performed can be found in the literature and our earlier work [5, 20, 27].

After the models were validated by ANOVA, a criterion of highest Rs/t_R values for all analytes was input into the DOE software to obtain the optimum values for all factors. The final optimum condition for MEKC was determined to be: voltage 25 kV, buffer pH 10.0, total concentration of polymeric surfactants: 70 mM, concentration of NH₄OAc: 40 mM. Using the aforementioned optimized CMEKC conditions, the following online optimizations were performed for sheath liquid composition and spray chamber parameters.

3.2.2 Optimization of sheath liquid compositions

Four factors (percentage of MeOH, NH₄OAc concentration, percentage of acetone, and sheath liquid flow rate) were chosen in the CCD optimization of sheath liquid composition (Table S3, Supporting Information). A total of 30 runs were generated by CCD and response are tabulated in Table S6 (Supporting Information). Peak area of each analyte was chosen as the response instead of S/N. This is because that peak area was less sensitive to the change of retention time and thus introduces less error than S/N.

The regression coefficients for all the sheath liquid parameters are shown in Table 2. The models for the peak areas of HBNZ and BNZ are linear; while the models for BME and BEE are constant. For the peak area of HBNZ, two factors, % volume fraction of MeOH and sheath liquid flow rate are found significant (i.e., Prob>F value < 0.05). For example, judging from their coefficients %MeOH is positively correlated to the peak area, while flow rate is inversely related. For the peak area of BNZ, %MeOH and sheath liquid flow rate are also the only two significant factors, and they are also positively and negatively related to the response, respectively. For the peak areas of BME and BEE, the model is a constant. This means in the factor range we explored for the sheath liquid, the peak areas of the two analytes remains unchanged. Therefore, none of the factors are significant for these two compounds.

Table 2.

Regression coefficient of the coded factors and analysis of variance for the response surface models of peak area for the optimization of sheath liquid factors

Term	Peak area-HBNZ		Peak area-BNZ		Peak area-BME		Peak area-BEE
	Coeff	Prob>F	Coeff	Prob>F	Coeff	Prob>F	Coeff	Prob>F
Intercept	2.9×104		1.7×105		5.4×105		5.7×105
F1(MeOH)%(v/v)	5.2×103	0.016	2.9×104	0.015
F2 [NH4OAc]	1.0×103	0.57	1.3×104	0.12
F3 Acetone%	−1.7×103	0.35	−1.4×104	0.19
F4 Flow rate	−3.8×103	0.045	−2.3×104	0.035
R2	0.34		0.40		0.00		0.00
Adjusted R2	0.23		0.30		0.00		0.00
Predicted R2	0.022		0.09		−0.073		−0.073

Table S7 shows the ANOVA results of the four models for the optimization of the sheath liquid parameters. The models for the peak area of HBNZ and BNZ are found to be significant. Because the model for BME and BEE is constant, there are no Prob>F values for them. The final optimum sheath liquid composition was eventually determined to get the highest peak area for all analytes as follows: 50% MeOH, 5 mM NH₄OAc concentration, 0.5% acetone, sheath liquid flow rate 10 μL/min.

3.2.3 Optimization of spray chamber parameters

After optimizing the MEKC and sheath liquid conditions, the optimization of spray chamber parameters were performed. Three parameters, drying gas flow rate (DGF), drying gas temperature (DGT), and vaporizer temperature (VT), were chosen for the CCD. Their levels are listed in Table S1 (Supporting Information). Detailed experimental conditions and responses are shown in Table S8 (Supporting Information). Peak area is again chosen as the response for this experiment. Among the 20 experiments carried out, experiment # 13 was not successful due to current break down. This may be because high vaporizer temperature in this experiment causes significant drying at the capillary outlet resulting in poor grounding.

The regression coefficients for all the peak areas of the four analytes for the optimization of spray chamber parameters are listed in Table 3. All four models for the benzoin derivatives are quadratic. For the peak area of HBNZ, all the factors (except DGF) are found to be significant (i.e., Prob>F value < 0.05). On the other hand, in case of BNZ and BME two factors and one factor, respectively, whereas for BEE none of the factors were significant. Their R² values are all in acceptable range as shown in the bottom row of this table.

Table 3.

Regression coefficient of the coded factors and analysis of variance for the response surface models of peak area for the optimization of spray chamber factors

Term	Peak area-HBNZ		Peak area-BNZ		Peak area-BME		Peak area-BEE
	Coeff	Prob>F	Coeff	Prob>F	Coeff	Prob>F	Coeff	Prob>F
Intercept	4.2×104		2.3×105		5.1×105		5.7×105
F1 DGF	3.6×103	0.23	−8.9×103	0.60	−7.0×104	0.073	−7.7×104	0.056
F2 DGT	−7.5×103	0.025	−2.1×104	0.24	−5.1×104	0.18	−5.4×104	0.16
F3 VT	2.2×104	0.0001	−3.4×104	0.14	−5.7×103	0.90	−3.0×104	0.51
F1 F2	−8.3×103	0.048	−7.6×103	0.73	−1.3×104	0.79	−2.9×103	0.95
F1 F3	1.1×104	0.011	9.2×103	0.68	5.2×104	0.28	7.4×104	0.14
F2 F3	−9.8×103	0.024	−1.1×104	0.62	−2.3×104	0.62	−2.8×104	0.55
F12	−1.0×104	0.0056	−5.2×104	0.012	−5.6×104	0.14	−6.5×104	0.098
F22	2.2×103	0.45	5.7×103	0.74	1.2×104	0.73	1.7×104	0.65
F32	3.8×103	0.31	−5.2×104	0.037	−1.2×105	0.24	−1.1×105	0.040
R2	0.91		0.74		0.68		0.69
Adjusted R2	0.81		0.49		0.37		0.39
Predicted R2	0.24		−0.41		−0.63		−0.56

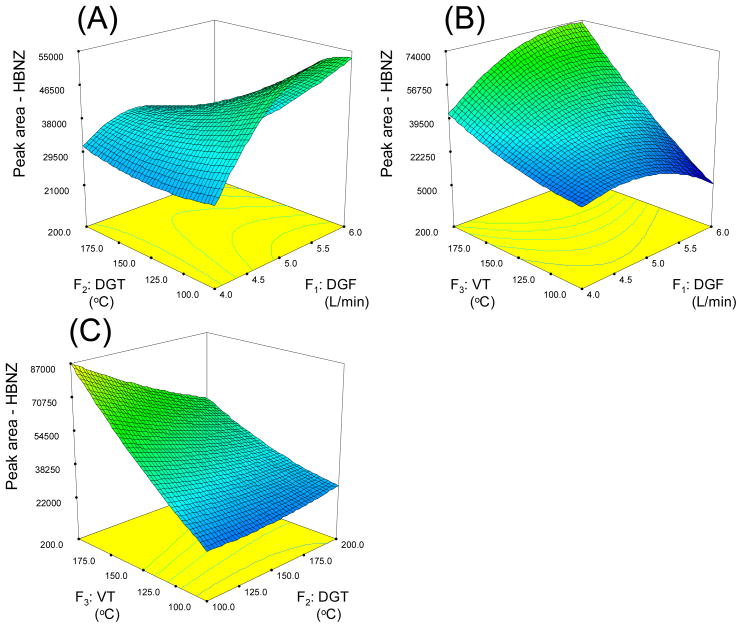
Fig. 6 illustrates the interactions of all three factors and their combined effect on the peak area of HBNZ. Fig. 6(A) is a saddle shaped surface. Along the DGF axis, the peak area grows higher when DGF increases from 4.0 to 6.0 L/min with a convex curvature. Along the DGT axis, on the other hand, the peak area gets higher when DGT decreases form 200 to 100 °C with a concave curvature. The maximum peak area found in this plot is at DGF at 5.5 L/min and DGT at 100 °C. Fig. 6(B) shows the relation between DGF and VT. The surface plot shows that peak area gets higher with an increasing DGF and VT. This provided the highest point at DGF of 6.0 L/min and VT at 200 °C. Fig. 6(C) illustrates the interaction between DGT and VT. Along the VT axis, the peak area is continuously increased when VT increases from 100 to 200 °C. This shows a positive correlation between VT and peak area. Along the DGT axis, the surface plot is almost flat at VT 100 °C, but shows strong negative correlation at VT 200 °C. Therefore, the maximum value of peak area in this plot can be found at VT 200 °C and DGT 100 °C.

Figure 6.

Response surface graphs for hydrobenzoin in spray chamber condition optimization using CCD experiment. Factors which are not analyzed in the plots are held at their mean values (i.e. level 0 in Table S7).

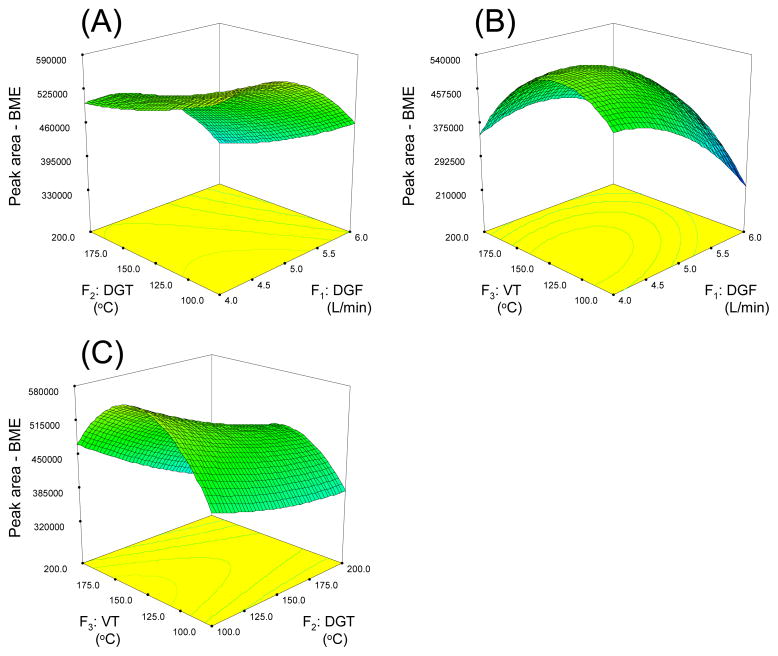
Fig. 7A shows the RSM plots for the peak area of BME. Note that the shapes of the RSM plots for the interaction factors for BME shows a different shape than the one observed for HBNZ in Fig. 6A. The highest point of this plot is at DGF 4.5 L/min and DGT 100 °C. Fig. 7(B) shows a dome shaped surface plot with a highest point at DGF 4.5 L/min and VT 145 °C, which is again significantly different from HBNZ. Another saddle shaped surface plot is shown in Fig. 7(C). A convex curvature can be observed along the VT axis with a highest point at 155 °C. A slight concave but upward trend can be found along the DGT axis when DGT is decreasing from 200 to 100 °C. Therefore, the overall highest point in this plot is at DGT 100 °C and VT 155 °C. The RSM plots for BNZ and BEE are very similar to those of BME (data not shown).

Figure 7.

Response surface graphs for benzoin methyl ether in spray chamber condition optimization using CCD experiment. Factors which are not analyzed in the plots are held at their mean values (i.e. level 0 in Table S7).

ANOVA data for models used in the optimization of spray chamber parameters is shown in Table S9 (Supplementary Information). It can be found that the model for the peak area of HBNZ is significant. For BNZ, it is almost significant. On the other hand, for BME and BEE, the models are not significant. The overall optimum spray chamber parameters determined for the simultaneous analysis of all four benzoin derivative by the models are: DGF at 5.0 L/min, DGT at 100 °C, and VT at 176 °C.

3.2.4 Overall optimum condition for MEKC-APPI-MS

The final overall optimum conditions for the chiral MEKC-APPI-MS of benzoin derivatives are the combinations of the optimized conditions aforementioned. The best conditions are: For MEKC: voltage 25 kV, buffer pH 10.0, total concentration of polymeric surfactant: 70 mM (poly-SUCL:poly-L,L-SULV molar ratio 85:15), concentration of NH₄OAc: 40 mM. For sheath liquid: MeOH%: 50%, NH₄OAc concentration: 5.0 mM, acetone 0.5 %:(v/v), flow rate: 10μL/min. For spray chamber: DGF: 5.1 L/min, DGT: 100 °C, and VT: 176 °C. Experiment at the aforementioned optimized conditions was performed and the results were compared with the values predicted by the model. The comparison is listed in Table 4. As shown in this table, the % errors between experimental and predicted values for all the responses for Rs/tr for HBNZ and BNZ are all reasonably small, whereas for the peak area of BME and BEE have significantly high error. This shows an overall good fit for all the models, and thus an acceptable predictability for shorter retained benzoin compounds but not for longer retained benzoin compounds.

Table 4.

Comparison of the model predicted values vs. the experimental values

	HBNZ		BNZ		BME		BEE		tR (min)
	Rs/tR	Peak area	Rs/tR	Peak area	Rs/tR	Peak area	Rs/tR	Peak area
Predicted	0.025	70514	0.064	267999	0.041	546381	0.021	603177	46.0
Experimental	0.024	53170	0.052	347734	0.036	902995	0.023	1193080	47.5
% error	4.0	25	19	30	12	65	9.5	98	3.3

Compared to the typical APPI-MS conditions used in ref. [6] (VT: 300 °C, DGT: 150 °C, DGF: 3 L/min, nebulizer pressure: 25 psi, sheath liquid flow rate: 15 μL/min) and ref [13] (VT: 330 °C, DGT: 250 °C, DGF: 1 L/min, nebulizer pressure: 10 psi, sheath liquid flow rate: 50 μL/min, capillary voltage: +800 V), the conditions we used are mild with lower temperatures (for both VT and DGT) due to the thermal instability of our analytes. In addition, the nebulizer pressure reported in this work is also significantly lower due to nature of chiral MEKC runs, which requires lower nebulizer pressure to separate two closely eluting optical isomers of each benzoin. Hence, the APPI-MS ionization conditions are both analytes dependent and CE modes used for separation.

3.2.5 Comparison of MEKC-UV-MS and MEKC-APPI-MS

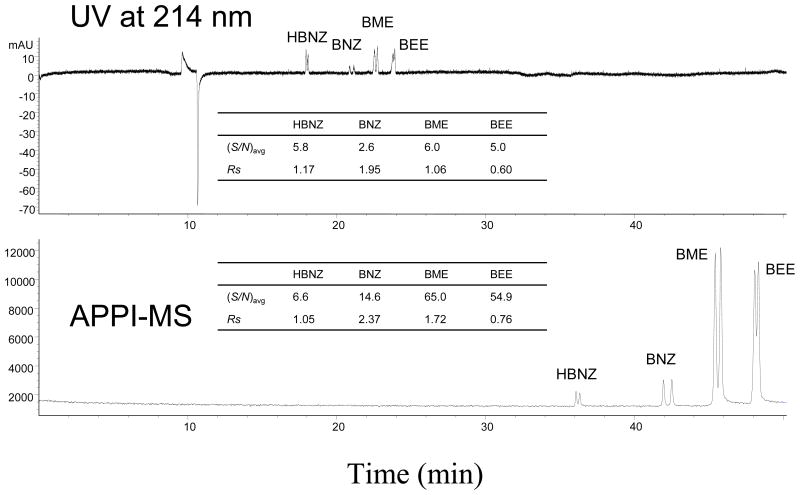
Because all the experiments in this study were all tandem UV-MS runs, the resolution and S/N between UV and MS were also compared. As shown in Figure 8, MEKC-APPI-MS gives much higher sensitivities (1.2–11.0 folds) than MEKC-UV for the analysis of all four benzoin derivatives. In addition, the chiral resolution of the last three benzoin derivatives were also higher for BNZ, BME and BEE but not for HBNZ. However, this high resolution in MEKC-APPI-MS was obtained at the expense of longer retention time.

Figure 8.

Representative electropherograms showing the comparison of CMEKC-UV vs. CMEKC-APPI-MS. Experimental conditions: 120 cm ×50 μm i.d. fused silica capillary; 55 mM NH₄OAc, pH 8.0, with 50 mM poly-SULV, 15 mM poly-SUCL; +25 kV, 20 °C; analyte: 1 mg/mL benzoin derivatives in 50/50 MeOH/H₂O, injected at 5 mbar, 10 sec; spray chamber parameters: drying gas flow rate 5 L/min; nebulizer pressure 5 psi; drying gas temperature 150 °C; vaporizer temperature 150 °C; capillary voltage 2000V; fragmentor 80 V, gain 3; SIM at m/z = 195, 197; UV absorbance at 214 nm; sheath liquid: 5 mM NH₄OAc in 50/50 MeOH/H₂O, 0.5% Acetone; flow rate 7.5 μL/min.

4 Concluding remarks

A mixed molecular micelle of poly-SUCL and poly-SULV was useful as the chiral pseudostationary phase for the simultaneous separation and high throughput optimization of all four benzoin compounds in MEKC-APPI-MS. A univariate approach was used to optimize the MEKC conditions, the sheath liquid composition, and the spray chamber parameters. Next, three set of full factorial CCD experiments were carried out separately after obtaining information on the optimization range from the univariate experiments. From the multivariate experiments, models were generated and RSM plots were created to evaluate the relationship between the MEKC-APPI-MS parameters and their effects on the responses. The final optimum conditions were also calculated from the models and runs were performed under these conditions. By comparing the experimental and theoretical data from these runs, a good fitness of the models can be seen for shorter retained benzoin compounds. In addition, significantly higher S/N and higher resolution can be obtained with MEKC-APPI-MS compared to MEKC-UV method.

Therefore, in this study we successfully demonstrated that molecular micelles can be used in APPI-MS and has potential to produce excellent sensitivity for select chiral molecules. In particular, when trying to separate non-polar, non-ionic chiral compounds the use of molecular micelles open up the possibility of performing APPI-MS with high sensitivity compared to APCI-MS or ESI-MS.