Varying Impacts of Alcohol Outlet Densities on Violent Assaults: Explaining Differences Across Neighborhoods

Abstract

Objective:

Groups of potentially violent drinkers may frequent areas of communities with large numbers of alcohol outlets, especially bars, leading to greater rates of alcohol-related assaults. This study assessed direct and moderating effects of bar densities on assaults across neighborhoods.

Method:

We analyzed longitudinal population data relating alcohol outlet densities (total outlet density, proportion bars/pubs, proportion off-premise outlets) to hospitalizations for assault injuries in California across residential ZIP code areas from 1995 through 2008 (23,213 space-time units). Because few ZIP codes were consistently defined over 14 years and these units are not independent, corrections for unit misalignment and spatial autocorrelation were implemented using Bayesian space-time conditional autoregressive models.

Results:

Assaults were related to outlet densities in local and surrounding areas, the mix of outlet types, and neighborhood characteristics. The addition of one outlet per square mile was related to a small 0.23% increase in assaults. A 10% greater proportion of bars in a ZIP code was related to 7.5% greater assaults, whereas a 10% greater proportion of bars in surrounding areas was related to 6.2% greater assaults. The impacts of bars were much greater in areas with low incomes and dense populations.

Conclusions:

The effect of bar density on assault injuries was well supported and positive, and the magnitude of the effect varied by neighborhood characteristics. Posterior distributions from these models enabled the identification of locations most vulnerable to problems related to alcohol outlets.

Greater densities of alcohol outlets, including bars/pubs, off-premise liquor outlets, and restaurants, have been linked to higher levels of both crime and violent assault (Gruenewald, 2008; Livingston et al., 2007). Several theories explain these associations (Roman et al., 2008). Alcohol outlets may increase access to and use of alcohol; outlets may be located in socially disorganized neighborhoods prone to crime; and greater densities of alcohol outlets, especially bars, may lead to the formation of core groups of problem drinkers prone to violence (Gruenewald, 2007; Gruenewald et al., 2006). The mechanisms underlying these social processes may not operate uniformly across all neighborhood environments. The influence of alcohol outlet density on assaultive violence may have an inordinately large effect in disorganized neighborhoods with populations at risk for violence.

A substantial body of empirical literature has examined relationships between alcohol outlets and assaults (Franklin et al., 2010; Gorman et al., 2005; Grubesic and Pridemore, 2011; Gruenewald et al., 2006; Lipton and Gruenewald, 2002; Livingston, 2008a; Pridemore and Grubesic, 2011; Scribner et al., 1995; Yu et al., 2008). Generally, these articles find positive associations between on- and off-premise outlets and assaults. Assaultive violence is typically measured using police reports and arrest records (Pridemore and Grubesic, 2011; Toomey et al., 2012), which encompass more and less severe violence, or hospitalizations for violent assaults (Lipton and Gruenewald, 2002)—cases severe enough to result in overnight hospitalization. Many recent studies have split apart the associations between bars, off-premise outlets, and restaurants (or off- vs. on-premise establishments). Several of these studies found the strongest associations between assaults and off-premise outlets (Gruenewald et al., 2006; Pridemore and Grubesic, 2011), whereas others had mixed findings regarding bars versus offpremise outlets (Franklin et al., 2010). Most have focused on one city or small geographic regions, such as Washington, DC (Franklin et al., 2010), Cincinnati, OH (Pridemore and Grubesic, 2012), and Los Angeles, CA (Scribner et al., 1995). The vast majority of these studies examined crosssectional data and did not address the spatial dependence of contiguous geographic units, which can lead to substantive bias in statistical tests. One prior study (Gruenewald and Remer, 2006) used a panel containing the roughly one third of California ZIP codes that were geographically stable over a short 5-year period and corrected for failures of unit independence. However, biases that may have arisen from selection of this subset of ZIP code areas are unknown.

Beyond these limitations of previous empirical studies, there are two reasons to further examine space-time data relating outlets to violence. First, the spatial scale of outlet effects is unknown. The degree to which bar densities in nearby neighborhood areas affect violence among residents of local areas has not been adequately considered. Because alcohol outlets within an area may serve both local residents and customers from nearby areas, the spatial scale of outlet effects may be larger than any single unit. Models that measure impacts only within local areas will therefore miss effects on violence in neighboring areas, understating outlet effects. Although the effects of alcohol outlet densities in adjacent areas have been examined in relation to both traffic crashes (Gruenewald et al., 1996; Treno et al., 2007) and violent assaults (Gruenewald et al., 2006) using the limited data sets noted above, a comprehensive assessment of these effects is unavailable in the literature.

Second, very few studies have explored the heterogeneity of effects between alcohol outlets and assaultive violence across neighborhood contexts (Gruenewald et al., 2006; Pridemore and Grubesic, 2012). Gruenewald et al. (2006) found that the association between bar density and assaults was only present in poor, minority neighborhoods. In the broader literature on neighborhood effects on health, the impacts of factors such as social cohesion and disorder differ by other neighborhood characteristics such as poverty and racial/ethnic composition (Diez Roux and Mair, 2010). The cumulative impacts of neighborhood characteristics are often more than the sum of their parts. Exploration of potential interactions between alcohol outlet densities and other environmental characteristics is essential to identify specific neighborhoods where outlet densities interact with other neighborhood conditions to create a disproportionate burden of assaults.

The goals of this analysis were to (a) determine whether serious assaults increase with greater outlet densities and the size of these effects, (b) assess the spatial scale of these effects by introducing spatial lags of outlet densities, and (c) determine if the impact of greater outlet densities is stronger in areas with larger populations at risk for violence (poor, minority populations in dense urban areas). Using ZIP code–level data for the entire state of California from 1995 through 2008 (Claritas, 2002; ESRI, 2002–2009), we examined the associations between hospitalizations for violent assault and alcohol outlet densities, proportion of bars/pubs, and proportion of off-premise alcohol outlets. Because ZIP code areas are redefined over time, these analyses required the use of statistical corrections for these unit misalignments. This allowed us to examine relationships between outlets and violence across the entire state of California over a full 14 years. We used results from our models to identify areas with greater expected rates of assault hospitalization and to assess the relative magnitudes of effects of outlet densities on violent assaults in these areas.

Method

Data sources and variables

Annual data, including hospital discharges, alcohol retail licenses, and Census-based registries, were aggregated over a 14-year period (1995 through 2008) across more than 1,600 ZIP code areas of California, for a total of 23,213 space-time units. These data were used to conduct a population-level Bayesian space-time analysis of associations between assault hospitalizations and alcohol outlet densities.

Assault hospitalizations.

The primary outcome measure was injuries from assaults resulting in hospitalization, obtained from the California Office of Statewide Health Planning and Development (1995–2008) hospital discharge data. There were approximately 15,000–17,000 assault injuries per year that required hospitalization with at least one overnight stay. Assaults were measured by annual counts of hospital discharge assault injuries (E-codes 960–969) located by residential ZIP code. These codes identified serious injuries that result from interpersonal violence of all sorts (Gruenewald and Remer, 2006).

Alcohol outlet density.

Alcohol outlet license data were obtained from the California Department of Alcohol Beverage Control (1995–2008). Three types of retail alcohol outlets were identified: off-premise establishments (license types 20 and 21), restaurants (license types 41 and 47), and bars/pubs (license types 23, 40, 42, 48, 61, and 75). Each outlet was geocoded to the premise address and spatially joined to year-specific ZIP code polygons. The overall outlet density estimates used in the models were calculated as the number of outlets per square mile within each ZIP code in each year, re-scaled to 10 outlets per square mile for ease of presentation. Outlet densities in adjacent areas were represented by the unweighted averages of densities across “spatially lagged” ZIP codes (those immediately adjacent to each ZIP code). Geographic adjacencies were defined as sharing a boundary or touching at a single point, allowing for a 0.5-meter tolerance to compensate for imprecision in boundary maps. The mean number of neighboring ZIP codes was 5.5 (SD = 2.4). To minimize collinearity and examine the direction and strength of associations between outlet types and assaults, measures of the proportion of outlets that were off-premise establishments and bars/pubs were calculated for each ZIP code and its spatial lags.

Demographic and environmental covariates.

Estimates of annual ZIP code–level demographic data, including percentage White, percentage Hispanic, percentage African American, median household income (per $10,000, adjusted to 2008 values), age distribution categories (percentage age 19 or younger, 20–24 years, 25–44 years, 45–64 years), and population density (10,000/mile2), were collected from the America Sourcebook (CACI Marketing Systems, 1996, 1997, 1998, 1999, 2000; ESRI Business Information Solutions, 2002–2008). Racial/ethnic densities were re-scaled to represent a 10% increase. County-level measures of the unemployment rate were collected from the State of California Employment Development Department (n.d.).

Other ZIP code characteristics were the overall hospitalization rate, presence of highway systems, and the density of overall retail establishments. The overall hospitalization rate, calculated as the number of discharges per 100,000 persons, was included as a covariate to control for differences in access to inpatient care. A binary variable indicating the presence of a Category 1 or 2 highway was calculated using the ESRI 2008 major roads shapefile to account for ZIP codes’ connectedness to regional transportation networks. Yearspecific ZIP code maps were overlaid onto the 2008 road shapefile to determine whether a highway was contained within the ZIP in a given year. There is very little variation in major roadways from year to year, making it reasonable to use the 2008 file for all years. A measure of the density of overall retail establishments was derived from County Business Patterns data (U.S. Department of Commerce, U.S. Census Bureau, n.d.). Using North American Industry Classification System codes, counts of all “retail trade” (Sectors 44, 45) and “accommodations and food service” (Sector 72) establishments were tallied. Density was calculated as the number of retail establishments per 10 square miles of ZIP code area.

Not all data were available for all units in all years. Roughly 3% of ZIP codes lacked values for total population, and these were assigned a minimal population of 5 to allow for nonzero population risks in all areas. Census-based rate variables (e.g., percentage African American) were undefined in those ZIP codes and were thus assigned the California state average for the year. These missing Census values typically occurred in unpopulated areas, such as national forests. Interactions between proportion bars and median household income, population density, percentage African American, percentage Hispanic, and percentage White were calculated for use in final models.

Unit misalignment.

Statistical corrections for the possible biasing effects of changes in the number and shape of ZIP codes from one year to the next were essential for conduct of these analyses. We assumed that the most substantial source of bias would be related to changes in population estimates for ZIP codes that were redefined from one year to the next. Identical ZIP codes were defined as those having identical shapes and locations (even though sometimes assigned different numerical values). Misaligned ZIP codes were those that did not share common boundaries from one year to the next. We included a measure of the geographic instability of a ZIP code’s population between consecutive years, calculated as the percentage of year-2000 Census block populations within a given year’s ZIP code definition that would not have fallen within the boundaries of the best-matched ZIP code in the prior year (range: 0%–63.3%). Large values of this measure indicated substantial changes in population covered by a misaligned ZIP code. The instability measure allowed us to test the assumption that ZIP code boundary shifts did not substantively bias other effects estimates.

Data analysis

We used a Bayesian Space-Time Misalignment Poisson model developed by Zhu and co-authors (2011) to perform panel analyses using all ZIP codes in California over a period of 14 years despite frequent changes in the size and shape of these geographic units. This misalignment approach introduces a separate conditional autoregressive (CAR) random effect for each year-specific map of spatial adjacencies to account for spatial autocorrelation. These CAR random effects are assumed to have mean zero and share a common standard deviation. The model also allows for a second, separate, random effect that is not spatially autocorrelated. Because ZIP codes were nested within counties, a third, county-level, random effect was included to provide an additional control for these nested effects.

The outcome measure in all models is the annual count of violent assaults by ZIP code. Poisson models were used, as assault hospitalizations are a count:

where Y_i,t represents the count of assault hospitalizations in ZIP code i during year t and E_i,t denotes the expected number of assault hospitalization visits under the assumption that statewide assault hospitalizations are distributed among ZIP codes in direct proportion to population. Therefore, exp(μ_i,t) is interpreted as the relative risk of residing in spatial unit i at time point t: regions with exp(μ_i,t) > 1 will have greater counts than expected, and regions with exp(μ_i,t) < 1 will have fewer than expected. Following standard generalized linear models, the log-relative risk, μ_i,t, is modeled linearly as:

This is a linear combination of fixed covariate effects and random effects that may take account of spatial and/or temporal correlation. Vector α_t is a set of year-specific intercepts that control for statewide changes in assault hospitalization risks that are not explained by other covariates. Matrix 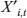contains space- and time-specific covariates and β is a vector of fixed-effects estimates of the impacts of those covariates. θ_i,t and ϕ_i,t denote the pair of random effects capturing spatially unstructured heterogeneity and CAR spatial dependence, respectively. ζ_i denotes a third random effect allowing for nesting of ZIP codes within counties. Models included fixed effects for neighborhood demographics, alcohol outlet densities, overall hospitalization rates, population density, retail clutter, presence of highways, and ZIP code instability (misalignment). Additional models were introduced to explore the effects of spatial lags and bar interactions. Three main models were run: Model 1 included all covariates but no interactions or spatial lags; Model 2 added spatial lag effects for density of alcohol outlets, proportion off-premise, and proportion bars; and Model 3 included bar spatial lags and added interactions between proportion bars and other neighborhood characteristics. For each model, we calculated the ratio of variance explained by the CAR random effect (ϕ_i,t) to the total ZIP-level random-effect variance (attributable to θ_i,t and ϕ_i,t).

Models were estimated using WinBUGS 1.4.3 software (Lunn et al., 2000). Uninformed priors were specified for all fixed and random effects. Models were allowed to burn-in for 50,000 Markov Chain Monte Carlo (MCMC) iterations, a sufficient number of iterations for all parameter estimates to stabilize and converge between two chains with different initial values. Posterior estimates were sampled for an additional 50,000 MCMC iterations to provide model results. Traces of MCMC iterations demonstrated good convergence for all parameters.

Results

Table 1 presents descriptive statistics for ZIP codes in California from 1995 to 2008 (23,213 ZIP codes). The unweighted mean density of alcohol outlets across ZIP codes was 8.3 per square mile (re-scaled for the analyses to tens of outlets per square mile to ease presentation of regression results). There is great variability in outlet densities, ranging from 0 to 63.5 per square mile. On average, 42.0% of these were off-premise outlets, 8.8% were bars, and the remaining 49.1% were restaurants. The racial/ethnic distributions in average ZIP codes were 4.9% African American, 26.1% Hispanic, and 69.4% White. The ranges of both population and square miles per ZIP code were large, with the resulting population density measure (re-scaled to 10,000 population per square mile) mean of 0.32 (range: 0.00–5.46).

Table 1.

Descriptive statistics, ZIP codes in California, 1995–2008 (n = 23,213 ZIP code years)

Variable	M	SD	Minimum	Maximum
Population	20,867.970	20,864.04	1.000	110,374.000
Area (mile2)	94.996	254.225	0.010	3,870.944
Population density (10,000/mile2)	0.324	0.537	0.001	5.461
Alcohol outlets/mile2 (×10)	0.832	3.014	0.000	63.514
Proportion bars/pubs	0.088	0.112	0.000	1.000
Proportion off-premise outlets	0.420	0.227	0.000	1.000
Lagged alcohol outlets/mile2 (×10)	0.793	2.547	0.000	43.991
Lagged proportion bars	0.095	0.041	0.000	0.400
Lagged proportion off-premise outlets	0.437	0.110	0.000	1.000
Percentage African American (10%)	0.491	0.894	0.000	8.720
Percentage Hispanic (10%)	2.608	2.123	0.000	9.800
Percentage White (10%)	6.938	2.084	0.000	10.000
Percentage age 0–19 years	27.851	7.734	0.000	92.700
Percentage age 20–24 years	6.832	5.322	0.000	100.000
Percentage age 25–44 years	29.146	7.578	0.000	100.000
Percentage age 45–64 years	23.486	7.672	0.000	100.000
Household income ($10,000)	5.665	2.711	0.010	60.203
Overall hospitalization rate (/100,000)	266,678.400	3,225,306.000	0.000	317,400,000.000
Presence of a highway (proportion yes)	0.642	0.480	0.000	1.000
ZIP code instability	0.705	3.918	0.000	63.325
Retail clutter/mile2 (×10)	2.448	9.870	0.000	226.388
Unemployment (%) (county level)	6.881	2.982	2.000	29.900
Number of assault hospitalizations	9.616	17.424	0.000	356.000

Table 2 shows results from the three Bayesian Space-Time Misalignment Poisson models and presents posterior estimates of the effects of each fixed-effect variable, expressed as a relative rate (calculated as Exp[raw coefficient]). The relative rate is for the median estimate from the sampled posterior distribution and is followed in parentheses by the 95% credible interval from that distribution. Credible intervals are defined as the 2.5th and 97.5th percentiles of the posterior distribution for each variable in the model and are interpreted in a similar manner to a 95% confidence interval from a standard regression model. Year-specific intercepts were included in all models, but because all years overlapped the mean and there was no indication of a trend, these have been suppressed in the table. Model 1 includes all the main effects of outlet density (Table 2). Proportion of bars and overall outlet density were both associated with greater assault hospitalizations, whereas proportion of off-premise outlets was associated with fewer assault hospitalizations. A higher percentage African American and percentage Hispanic, lower percentage White, lower median household income, presence of a highway, higher retail clutter density, and lower population density were all associated with greater assault injuries.

Table 2.

Relative rates (RRs) [95% credible intervals] and Ln(RR), assault hospitalizations, Bayesian spatial misalignment models (n = 23,213 ZIP codes)

	Model 1		Model 2		Model 3
Variable	RR [95% credible interval]	Ln(RR)	RR [95% credible interval]	Ln(RR)	RR [95% credible interval]	Ln(RR)
Alcohol outlet effects
Alcohol outlets/mile2 (×10)	1.023 [1.017, 1.030]a	0.023	1.020 [1.012, 1.027]a	0.020	1.018 [1.011, 1.025]a	0.018
Proportion bars/pubs	2.114 [1.817, 2.421]a	0.749	2.100 [1.829, 2.413]a	0.742	1.433 [0.638, 3.028]	0.360
Proportion off-premise outlets	0.910 [0.850, 0.983]a	-0.095	0.902 [0.838, 0.968]a	-0.103	0.909 [0.843, 0.984]a	-0.096
Lagged alcohol outlets/mile2 (×10)	1.007 [1.000, 1.015]	0.007	1.005 [0.998, 1.013]	0.005
Lagged proportion bars	1.863 [1.318, 2.591]a	0.622	1.834 [1.272, 2.602]a	0.607
Lagged proportion off-premise outlets	1.039 [0.899, 1.183]	0.038	1.045 [0.923, 1.203]	0.044
Bar outlet interactions
Bar × Percentage African American (10%)					1.144 [1.006, 1.305]a	0.266
Bar × Percentage Hispanic (10%)					0.943 [0.877, 1.016]	0.016
Bar × Percentage White (10%)					1.134 [1.048, 1.222]a	0.201
Bar × Household Income ($10,000)					0.882 [0.825, 0.944]a	-0.125
Bar × Population Density (10,000/mile2)					2.206 [1.680, 2.951]a	0.791
Demographic characteristics
Percentage African American (10%)	1.308 [1.291, 1.326]a	0.269	1.306 [1.290, 1.323]a	0.267	1.286 [1.265, 1.314]a	0.252
Percentage Hispanic (10%)	1.140 [1.129, 1.149]a	0.131	1.136 [1.126, 1.148]a	0.128	1.144 [1.130, 1.157]a	0.134
Percentage White (10%)	0.990 [0.980, 0.999]a	-0.010	0.990 [0.982, 1.000]a	-0.010	0.978 [0.968, 0.992]a	-0.022
Unemployment (%) (county level)	0.988 [0.973, 1.002]	-0.012	0.991 [0.978, 1.003]	-0.009	0.988 [0.968, 1.001]	-0.012
Household income ($10,000)	0.836 [0.830, 0.843]a	-0.179	0.837 [0.831, 0.844]a	-0.178	0.844 [0.834, 0.852]a	-0.170
Presence of a highway	1.042 [1.021, 1.065]a	0.041	1.041 [1.018, 1.063]a	0.040	1.033 [1.010, 1.057]	0.033
Overall hospitalization rate (/100,000)	1.029 [1.026, 1.033]a	0.029	1.030 [1.026, 1.033]a	0.029	1.029 [1.026, 1.033]a	0.029
Retail clutter/mile2 (×10)	1.003 [1.001, 1.005]a	0.003	1.003 [1.002, 1.005]a	0.003	1.004 [1.002, 1.006]a	0.004
Population density (10,000/mile2)	0.920 [0.893, 0.942]a	-0.084	0.920 [0.896, 0.944]a	-0.083	0.836 [0.801, 0.872]a	-0.179
Percentage age 0–19 years	0.998 [0.996, 1.001]	-0.002	1.000 [0.997, 1.002]	0.000	0.999 [0.997, 1.002]	-0.001
Percentage age 20–24 years	0.981 [0.977, 0.985]a	-0.019	0.981 [0.977, 0.985]a	-0.019	0.982 [0.978, 0.985]a	-0.019
Percentage age 25–44 years	1.007 [1.004, 1.009]a	0.007	1.008 [1.005, 1.009]a	0.008	1.007 [1.005, 1.009]a	0.007
Percentage age 45–64 years	1.012 [1.008, 1.017]a	0.012	1.012 [1.008, 1.016]a	0.012	1.012 [1.008, 1.016]a	0.012
Misalignment effects
ZIP code instability	0.999 [0.995, 1.003]	-0.001	0.999 [0.995, 1.003]	-0.001	0.999 [0.995, 1.003]	-0.001
	Mdn [95% credible interval]		Mdn [95% credible interval]		Mdn [95% credible interval]
Random effects
County-level random effects (s.d.)	0.341 [0.304, 0.386]		0.342 [0.305, 0.386]		0.342 [0.304, 0.388]
Spatial random effects (s.d. CAR process)	0.353 [0.336, 0.371]		0.354 [0.335, 0.371]		0.350 [0.336, 0.367]
ZIP code–level random effects (s.d.)	0.286 [0.272, 0.299]		0.286 [0.273, 0.303]		0.288 [0.273, 0.301]
Spatial to total random variability ratiob	0.604 [0.563, 0.645]		0.604 [0.552, 0.646]		0.595 [0.558, 0.638]

Notes: Ln(RR) = natural log of median relative rate; CAR = conditional autoregressive.

^aIndicates findings that are well supported by the data as evidenced by credible intervals that exclude one for relative risks;

^bcalculated as the variance ratio of spatial to spatial and nonspatial random effects.

Model 2 (Table 2) adds spatial lag terms for outlet density, proportion bars, and proportion off-premise outlets. None of the main effects changed substantively between Models 1 and 2. The association between the spatial lag bar effect and assaults was well supported and positive and of a similar magnitude to the main bar effect. Model 3 added interaction terms between proportion bars and percentage Hispanic, percentage White, percentage African American, median household income, and population density. The main effect for population density was negative and well supported, whereas the interaction term between population density and bars was positive and well supported. This can be interpreted to mean that as population density increases, the positive association between bar density and assaults increases. There was a negative and well-supported interaction between household income and bars, meaning that the strength of the positive bar effect becomes weaker as median household income increases. The positive, well-supported association between percentage African American and bar density indicates that the positive bar association becomes stronger as the proportion of African Americans residing in a ZIP code increases. Taken together, these interaction effects indicate that dense, minority, low-income neighborhoods are particularly vulnerable to the effect of bar density on assault hospitalizations.

The CAR spatial random effect explained 60% of the overall error variance in each of the three models, indicating that there is substantial spatial autocorrelation in these models. Posterior spatial random effects from the model were used to calculate Moran coefficients providing a standardized assessment of spatial autocorrelation (approximately bounded by -1.0 and 1.0); these ranged between 0.475 and 0.502 (p < .001) (data not shown), indicating further the substantial degree to which assaults are autocorrelated across adjacent ZIP code areas. Without proper correction for these CAR effects, the likelihood of Type I errors is quite high.

Discussion

The results of these analyses demonstrate that local rates of assault hospitalizations are related to densities of alcohol outlets, proportional number of bars, local ZIP code characteristics, and the availability of alcohol through alcohol outlets in nearby areas (spatial lag effects). Bar/pub densities interacted with measures of at-risk populations (low median household income, high population density) to account for greater proportions of assaults across ZIP codes, apparently accelerating risks for violence in these areas. Importantly, the results suggest that bar densities, in both local and adjacent ZIP codes, are associated with greater assault injuries. The scale of outlet effects is, on average, larger than an average ZIP code.

Our results are also generally consistent with a social ecologic framework, which predicts increased violence in areas with a high density of alcohol outlet access, particularly in crowded urban neighborhoods with high minority population concentrations (Gruenewald, 2007). The strong interactions indicate that individuals who live in areas with high population density, a high percentage of African Americans, and low median household income are particularly vulnerable to the effects of local bar density. This variation may be attributable to other environmental neighborhood characteristics, such as social disorganization and low social control. It may also reflect the heterogeneity in the type of bars in a ZIP code, or that the presence of a bar does not have the same impact in every neighborhood environment. The strong bar density effect in neighborhoods characterized by low mean household income, a high percentage of African Americans, and high population density demonstrates the importance of examining the heterogeneity of the bar density effect across ZIP codes.

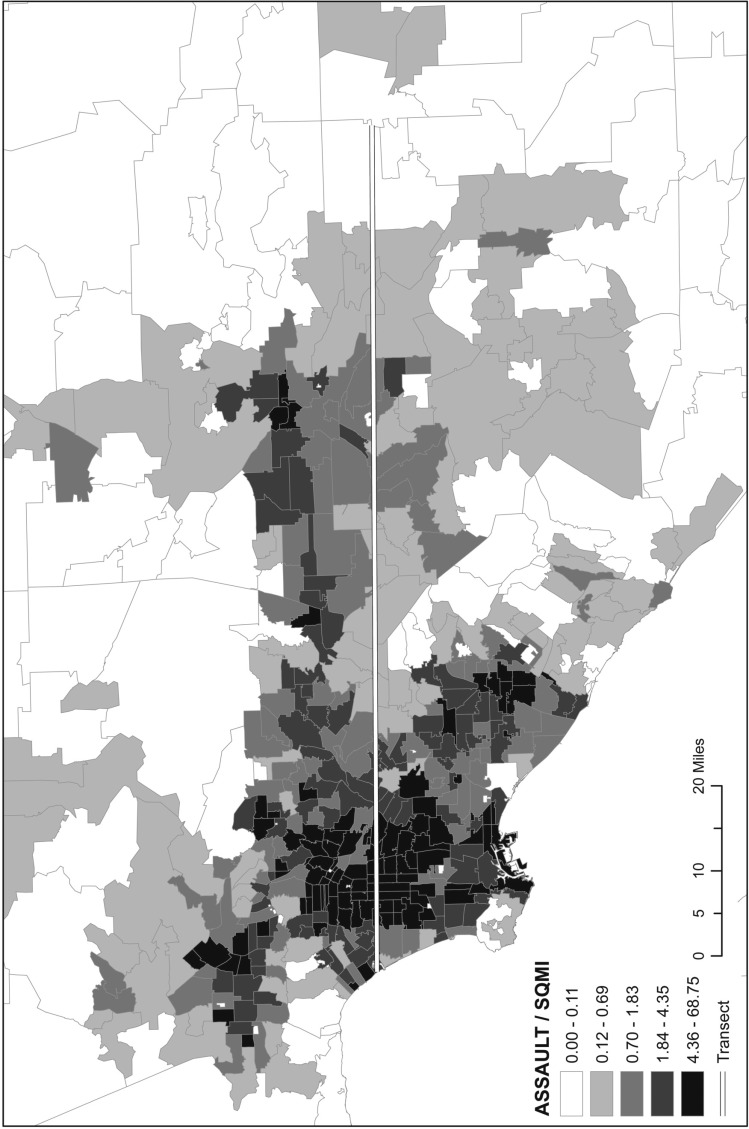
Geographic assessments of the impacts of alcohol markets on violent assaults are essential to the identification of heterogeneous risks related to outlets across neighborhood areas. To display these varying impacts of alcohol outlets on assault injuries, we created a transect map running east to west in the Los Angeles region. As shown in Figure 1, the transect runs from Marina Del Rey in the west through poor areas south of downtown Los Angeles and out to Banning, in the desert approximately 90 miles away; the transect is overlaid on a thematic map of rates of assault hospitalizations across ZIP codes in the region from 2008. Figure 2 displays the quantitative impacts of alcohol outlets and environmental and demographic covariates on assaults across ZIP codes along the transect (posteriors from Model 3). Each vertical band represents a single ZIP code, and within each ZIP code are shown the effects of covariates that either raise risks (above the zero-risk line) or lower risks (below that horizontal line) for assault. The top transect presents posterior risks of violent assault associated with (a) alcohol outlet density, (b) proportion off-premise outlets, (c) proportion bars, (d) spatial lag of proportion bars, and (e) moderated bar effects. The bottom figure illustrates the posterior risks related to (a) population density, (b) mean household income, (c) percentage African American, (d) percentage Hispanic, and (e) percentage white. The transects are useful visualizations of the relative contribution of different outlet, population, and demographic characteristics to assaults across areas and illustrate the varying impacts of outlet densities across areas of the region. As shown, bar effects are sometimes large (e.g., in poor, minority areas with large populations) and sometimes much smaller (e.g., in wealthy suburban areas). The proportion of bars in a ZIP code has much larger positive effect in several areas along the transect. Average income has a large, negative association in many ZIP codes. Percentage African American has a larger effect closer to Marina Del Rey, which decreases eastward along the transect. Thus, the transects in Figure 2 demonstrate the heterogeneous impacts of these covariates across areas of the region, suggesting locations where the addition or elimination of outlets may have greater or lesser effects on violence. Information provided by analyses of this type can be used to ask, and answer, the question of where we should put resources to try to minimize or reduce the number of alcohol outlets for the largest effect.

Figure 1.

Assault hospitalizations per square mile, Los Angeles Basin, with transect (2008)

Figure 2.

Transect through Los Angeles area, full model (Model 3)

Limitations

Population models such as those presented here have the virtue that they can comprehensively identify aggregate outlet effects across diverse populations living in many different neighborhood conditions. It is possible to identify risks associated with alcohol outlets and relate exposures to these outlets to a variety of problem outcomes. As an aggregate population analysis, however, it is not possible to illuminate the connecting theory that leads from a global assessment of exposures to alcohol outlets to the individual behaviors that are affected by these exposures. For this purpose, multilevel contextual data and analysis models are required. Thus, the individual behavioral mechanisms that underlie the observed effects remain to be explored further. Other limitations of the current analyses include our reliance on binary measures of ZIP code adjacencies (a more sophisticated measure using road network connectivity might be considered) and an exclusive focus on relatively severe injuries related to assaults. Given the severity of the outcome, the results of these analyses are not directly comparable to analyses of assault incidents or police arrests because those are likely to include both less and more severe assault injuries. Our results are similar to studies looking at police records, however, which often find bar density to be associated with increased arrests for violent and nonviolent assaults (Alaniz et al., 1998; Livingston, 2008b; Pridemore and Grubesic, 2012). The large spatial autocorrelations observed in these analyses demonstrate that spatial analytical methods are necessary for unbiased analyses of assaults and alcohol outlets at this level of geographic resolution. Future research using smaller spatial scales (more highly resolved spatial data) will help determine the true size of the spatial effects. Furthermore, dynamic models of outlet effects as they evolve can help lead to greater understanding of these processes over shortand long-term periods.