Abstract
We report simulations of X-ray absorption near edge structure (XANES), resonant inelastic X-ray scattering (RIXS) and 1D stimulated X-ray Raman spectroscopy (SXRS) signals of cysteine at the oxygen, nitrogen, and sulfur K and edges. Comparison of the simulated XANES signals with experiment shows that the restricted window time-dependent density functional theory is more accurate and computationally less expensive than the static exchange method. Simulated RIXS and 1D SXRS signals give some insights into the correlation of different excitations in the molecule.
INTRODUCTION
New, high intensity X-ray sources1, 2 have triggered current interest in nonlinear spectroscopy with X-rays.3, 4, 5 The pump-probe experiment is the simplest time-resolved X-ray measurement. It was performed in atoms. Impulsive 1D-stimulated X-ray Raman spectroscopy (SXRS)6 and 2D-SXRS signals7 were simulated for trans-N-methylacetamide (tNMA) at the N and O K-edges. These signals pose considerable theoretical and experimental challenges. These studies used the static exchange (STEX) approximation for the core-excited states, an approach whose limitations will be discussed in Sec. 2A. The simulation of resonant X-ray spectroscopy signals requires calculation of core excited states. A major difficulty in these calculations is that every high energy core-excited state is embedded in a continuum of excited states which have very weak X-ray transition dipole moments to the ground state. For K shell spectra we have the low lying L, M, etc., core excitations as well as numerous valence excitations. Conventional numerical methods that calculate the eigenvalues from the bottom-up then become very tedious. Other complications, such as self-interaction for localized core orbitals and relativistic effects for heavy atoms make the calculation of core-excited states very challenging. The easiest way to represent a core hole on an atom is to increase the nuclear charge by one. This is known as the equivalent core approximation (ECA) or Z + 1 approximation.8, 9 ECA was very easily used to simulate the X-ray nonlinear signals.10, 11, 12, 13, 14 It is also very easy to apply to singly or doubly core excited states. However, ECA is a crude representation of the charge near the excited atom, and only applies to deep core holes. In addition, it does not represent the correct spin of the system. STEX15, 16, 17 provides a higher level approximation: a core hole is explicitly created in the electron configuration and the occupied orbitals of the core excited N-electron system are represented by the occupied orbitals of an ionic N-1-electron system. One goal of this paper is to compare and contrast the STEX and restricted window time-dependent density functional theory (REW-TDDFT) methods. We found that REW-TDDFT gives better relative peak positions and better peak intensities, compared to STEX. The latter is sometimes qualitatively incorrect in some cases.
First, we briefly discuss some other methods which have been used to calculate core-excited state properties. In the 1970s Slater proposed the transition state method,18, 19 in which the excitation energies are calculated from the energy difference of the two orbitals involved in the transition with both orbitals occupied by a half electron. The orbital binding energy may be also calculated using the transition potential method,20, 21 as the derivative of the total energy with respect to the occupation number when the occupation number is 0.5. Both transition state and transition potential methods introduce electronic relaxation but are very expensive for large systems since a separate self-consistent field (SCF) calculation is needed for each transition. These approaches have some additional disadvantages. The calculated excited states are not orthogonal, and a half electron in an orbital does not represent a real physical spin. The transition potential method usually underestimates core excitation energies by about 1.5∼2 eV and has been used in simulations of surface adsorbates X-ray absorption near edge structure (XANES) spectra.21
The multiple scattering Xα method has been extensively used in the past 30 years22, 23, 24 to model core-excitations.18 In solid state systems, pseudopotentials are usually used to represent the core hole. Several other models exist, e.g., the full core hole (FCH), half core hole (HCH) and excited state core hole (XCH). FCH is similar to STEX and HCH is equivalent to the transition potential method.25 XCH is FCH with a self-consistent inclusion of the excited electron.26 For simple solid systems such as diamond and α-quartz, pseudopotential calculations give very accurate X-ray absorption spectra.27 Even though the core hole pseudopotential approach has been effective, it is not easy to transfer pseudopotentials between different computational packages and those pseudopotentials must be tested extensively in different chemical environments.
Many-body methods account for a large part of electron correlation and are highly accurate, but computationally expensive. They have only been applied to highly symmetric (e.g., diamond28, 29) or very small systems (e.g., a neon chain of three atoms30). A quasiparticle theory has been used to study core excited states31 by solving a Dyson equation with the photoelectron self-energy term. The Bethe-Salpeter approach has also been successfully applied to XANES calculations.28, 29 The dynamics of core holes and particles can also be obtained by means of Green's function techniques,30, 32 using the algebraic diagrammatic construction approach.33
The complex resonant propagator method34, 35, 36 developed by Norman and co-workers is unique since it directly calculates the X-ray absorption cross section at a particular frequency without explicitly addressing the excited states. The polarizability is obtained by solving a response equation. The accuracy of the results depends on the level of electronic structure theory used. Restricted open-shell Kohn-Sham orbitals have been used to construct the polarization propagator and give very good XANES spectra of a large molecule, copper phthalocyanine.37 Since the excited states are not explicitly addressed, many response calculations are needed in order to cover a broad frequency range.
Other high level ab initio methods such as the equation of motion coupled cluster (EOM-CC) method,38 the symmetry-adapted-cluster configuration interaction (SAC-CI) method,39, 40, 41, 42, 43 and multireference coupled cluster approaches44 have also been applied to study core excited states. They are very accurate (error less than 0.1 eV) but their computational scaling is not favorable. They are, therefore, usually used to produce benchmark results for very small molecules such as CO or N2O.39, 43 Another interesting idea related to excited state calculation is the correlated orbital theory (COT).45 Effective one-particle equations, whose eigenvalues correspond to the exact principal ionization potentials (IPs) and electron affinities (EAs), are constructed. With the exchange-correlation potential obtained from ab initio DFT,46, 47 COT produces principal IPs and EAs comparable to the very accurate IP-EOM-CCSD results.45 Applying COT to core excited state calculations is an interesting future possibility.
Time-dependent density functional theory48 has become the method of choice for calculating valence excited states49, 50 because of its good balance between accuracy and computational expense. Core excited state calculations using conventional TDDFT bottom-up implementations are difficult since there are many valence excited states below the core excited states. New algorithms are needed. In this paper, we describe the REW approach51 that can circumvent this problem.
We compare the REW-TDDFT method with the STEX approach and apply them to calculating the linear absorption, frequency, and stimulated time-domain X-ray Raman spectra of cysteine. This small sulfur-containing amino acid provides an important structural function by connecting different regions of proteins through disulfide bonds and has been implicated in biological charge transfer in the respiratory complex I.52 We first describe the STEX and REW-TDDFT methods in detail, comparing both formalisms. XANES, resonant inelastic X-ray scattering (RIXS), and 1D-SXRS simulations are then presented for cysteine at the K edges of nitrogen and oxygen, and the K and edges of sulfur. We show that REW-TDDFT offers a substantial improvement on STEX, in both accuracy and computational expense. By comparing the two-color SXRS signals taken with positive and negative time delays, we can see interference between the resonant X-ray polarizabilities for different atomic sites in a molecule.
METHODS
The STEX method
According to Hunt and Goddard's analysis,15 the virtual orbitals of a (N-1)-electron system are good approximations for the excited state orbitals of the N-electron system at the Hartree Fock level of theory (N-1 approximation). STEX uses the occupied orbitals of the (N-1)-electron ionic system to represent the occupied orbitals of the core-excited system. First, a core electron is removed and a SCF calculation is performed on the N-1 ionic system. This is not straightforward since the core hole collapses easily during the SCF process. Suitable constraints are necessary to avoid this collapse. One approach, the maximum overlap method,53 chooses the new occupied orbitals to be those have a maximum overlap with the old occupied orbitals during the SCF process. We have used a carefully chosen level shift54, 55 parameter in the STEX calculations reported here to guarantee that we target the right core-excited state. Upon exciting a core electron to a virtual orbital, we obtain an open-shell singlet state
| (1) |
where are spin states, j is the core orbital index, l is the virtual orbital index, and is the N-electron reference state. With this wave function, the eigenvalue equations for the excited orbitals in the N-1 approximation are
| (2) |
The STEX Fock operator is constructed using the orbitals of the N-1 ionic system
| (3) |
Here, is the single-particle Hamiltonian (kinetic plus nuclear attraction part), and are the Coulomb and exchange operators for the core orbital j, respectively,
| (4) |
Since is different from the Fock operator of the (N-1)-electron system, its eigenvectors are not orthogonal to the occupied molecular orbitals (MOs) of the (N-1)-electron system. The projection operator projects out all occupied orbitals of the (N-1)-electron system from the basis set
| (5) |
The eigenvectors of the projected STEX Fock operator provide a good representation for the excited orbitals. The STEX orbitals are the occupied orbitals of the (N-1)-electron system and the eigenvectors of the projected STEX Hamiltonian. The core excitation energy within the orbital approximation is finally given by
| (6) |
where IPj is the ionization potential of the core electron j (got from the energy differences of the (N-1)-electron system and the N-electron system). A more accurate excitation manifold can be obtained by running configuration interaction singles (CIS) calculations using the STEX orbitals as a reference.
Restricted excitation window TDDFT
The response equation of TDDFT and its implementation in NWChem code have been described in Refs. 56, 57, 58. Formally, equivalent expressions were derived for the time-dependent Hartree-Fock (TDHF) theory.59 We briefly outline the formalism here. The TDDFT response equation can be written as an eigenvalue problem (Casida equation)
| (7) |
where
| (8) |
and ωi are the excitation frequencies. Here, the indices i, j, and a, b indicate occupied and virtual Kohn-Sham orbitals, respectively, and τ, σ are spin variables; ɛi, j, a, b are Kohn-Sham orbital energies. The coupling matrix K is given by
| (9) |
where ψiσ, ψaσ, ψjτ, and ψbτ are Kohn-Sham orbitals and the exchange-correlation kernel is the second derivative of the exchange-correlation functional. After solving Eq. 7, the eigenvalues are given by the square of the excitation energies, and the oscillator strengths can be extracted from the eigenvectors Fi with standard methods.56 Equation 7 is usually solved by the Davidson iterative algorithm.60 Conventional TDDFT implementations have difficulties in dealing with core excitations, since there could be hundreds or even thousands of valence excitations below the target core excitation in a large molecule. Any bottom-up algorithm for computing the eigenvalue spectrum thus becomes prohibitively expensive. This numerical difficulty can be circumvented by only allowing electrons to be excited from a certain set of relevant core orbitals, thereby creating a restricted excitation window. This method was proposed by Stener and co-workers51 and followed by other authors.61, 62 Two schemes have been used to define the restricted excitation window: (i) directly select the core orbitals of interest (e.g., all MOs dominated by nitrogen 1s atomic orbitals); and (ii) use some orbital energy or energy difference cutoff to filter out all orbitals or orbitals pairs which lie above or below the cutoff. (i) is intuitive but becomes inconvenient if there are many atoms of interest of the same type in a large molecule. Orbital localization schemes have been developed for equivalent atoms in a molecule.62, 63, 64 (ii) is more convenient for specifying all relevant core orbitals of the same type of atoms. REW-TDDFT has been implemented in a development version of NWChem code.65, 66 An orbital energy cutoff is set in the program input to restrict the excitation window: any orbital with energy higher than the cutoff is excluded. Trial excitation vectors are prepared in this REW before the Davidson iterative solver is invoked to find the relevant eigenvectors. Very recently, Schmidt and co-workers proposed that core excited states can be accessed by standard TDDFT eigensolver by shifting the orbital energy differences.67 This is very similar to Stener and co-workers' implementation in the ADF package.68, 69 Li et al. also suggested to project the TDDFT response equation into a subspace, in which the trial vectors correspond to energies in a specific range.70 Conventional density functionals used in TDDFT calculations often underestimate core excitation energies, which is due to the self-interaction error.61, 71, 72, 73, 74 Core-valence hybrid71, 75, 76 and short-range corrected hybrid functionals77, 78 were proposed to improve the accuracy of TDDFT for core excitations.
In the present study, we use the adiabatic approximation for the exchange-correlation kernel , i.e., we neglect the frequency-dependence of the kernel. The frequency-dependence becomes important when the excitation studied has a significant double or multiple excitation character.79 However, in this study we only discuss core excitations which are dominated by single excitations. The adiabatic approximation is adequate for these single core excitations. This conclusion is based on several successful applications of the REW-TDDFT approach in conjunction with using non-local hybrid density functionals on molecular systems.62, 66, 70, 78, 80 Frequency-dependent exchange-correlation kernels have been proposed recently and tested on model systems.81, 82
Comparison of STEX and REW-TDDFT
STEX is a simple single Slater determinant theory that can be applied to deep as well as shallow core holes. The independent channel approximation is used and orbital relaxation is included, but electron correlations are neglected. In addition, the influence of the excited electron on the other N-1 inner electrons is neglected. Running a SCF calculation with a core-hole configuration is not trivial and often leads to convergence problems. In addition, calculating the transition dipole moments between states in the two excitation manifolds is not straightforward, as the STEX orbitals are not orthogonal to the MOs of the N-electron system. After applying Löwdin's rule83 for calculating one-particle operator expectation value between nonorthogonal states on the same basis set, the transition dipole between two states reads
| (10) |
where ΨA, B are two nonorthogonal excited states, is the transition dipole operator, am and bn are CI coefficients for different single excitation configurations (m and n) of state A and B, respectively,
| (11) |
is the transition dipole matrix between single excitation configurations m and n, cip, m, A and cjq, n, B are MO coefficients for the configurations m and n of state A and B, respectively, and
| (12) |
is the overlap matrix between the MOs of the configurations m and n of state A and B, respectively. ϕi, j in Eqs. 11, 12 are basis functions and i, j, p, q, k, l are indices for these basis functions. Minor(Smn)ij denotes the (i, j) minor of the matrix Smn. Calculations based on Eq. 10 becomes very tedious if the size of the basis set is large.
REW-TDDFT is simple to use and can be readily applied to various types of core holes. With the energy cutoff, near-degenerate MOs can be included in the REW so that core hole mixing can be observed, which is not possible in STEX calculations. Electron correlation is partially accounted for in the exchange-correlation kernel but MO relaxation is ignored. Since REW-TDDFT is a response approach based on the ground state, no SCF core excited state orbitals, which may cause convergence problems, are needed. Moreover, all MOs are orthogonal and Eq. 10 reduces to transition dipoles between different MOs, which drastically reduces the computational effort.
In both STEX and REW-TDDFT core excited state calculations, a constant energy shift must be added to the calculated excitation energies to agree with experiment. This reflects the absence of electron correlation in STEX, the lack of self-interaction in the density functionals, and also accounts for basis set error and relativistic effects.
RESULTS
Computational details
The geometry of cysteine was optimized using the quantum chemistry package GAUSSIAN84 at the B3LYP/6-311G** level. The STEX model used to calculate the core-excited states was implemented in a modified version of the quantum chemistry package Psi3.85 All STEX transition frequencies and dipoles moments were calculated using the orbital approximation at the HF/6-311G** level. Implementation details are given in Appendix C of Ref. 6. All TDDFT calculations were performed with a development version of NWChem code65, 66 at the CAM-B3LYP86/6-311G** level of theory with the Tamm-Dancoff approximation .87 In REW-TDDFT calculations, the energy cutoffs were chosen a little bit higher than the energies of the interested orbitals. Since the core orbital energies are well separated, these settings would only keep the relevant orbitals in the REW.
Absorption spectra
The cysteine XANES was calculated at the nitrogen K-, oxygen K-, and sulfur K-, L-edges with STEX and REW-TDDFT for comparison. All calculations are compared with experiment (adapted from Refs. 88 and 89) in Fig. 1. In order to match experiment, the transitions energies were shifted. The energy shifts for different edges and theories are listed in Table 1. In order to match experiment, where above the K-edge the spectra become very broad due to coupling with a continuum of photoelectron states, we have used an energy-dependent core-excited state linewidth Γe, which is shown in the dashed lines overlaying the XANES plots in Fig. 1. The phenomenological linewidths used in XANES curve fitting are also shown on Fig. 1. A more detailed analysis of core excitations above the molecular ionization potential is needed to describe these effects. A static core-hole linewidth, corresponding to the core-hole lifetime,90 was used in calculating the RIXS and SXRS spectra. The static linewidths for the N1s, O1s, S1s, and S2p core holes were 0.09 eV, 0.13 eV, 0.59 eV, and 0.054 eV, respectively.
Figure 1.
Calculated XANES spectra of cysteine taken at the nitrogen, oxygen, and sulfur K-edges (solid red traces), from either the REW-TDDFT (top) or STEX (bottom) level of theory, compared with experimental spectra (solid blue traces) adapted from Refs. 88 and 89. In plotting the calculated absorption, the stick spectrum (black lines) is convoluted with a Lorentzian function with an energy-dependent linewidth, Γe, whose value is given by the dashed green trace (the same Γe is used for both REW-TDDFT and STEX).
Table 1.
Shifts (in eV) for excitation energies calculated at different edges and level of theories.
| Nitrogen K | Oxygen K | Sulfur K | Sulfur L | |
|---|---|---|---|---|
| STEX | 3.6 | −5.0 | 4.5 | −46.5 |
| TDDFT | 16.0 | 14.5 | 57.7 | 5.3 |
For the high energy range in Fig. 1 (e.g., with energy 10 eV or more higher than the rising edge), the core excited states strongly couple with the ionized continuum states to form resonances, which we do not consider in our calculations. Our comparison is based on the peaks around the pre- and near-edge (XANES). Many peaks around the nitrogen K-edge absorption edge are missing in STEX, which cannot reproduce the broad peak in experiment. The REW-TDDFT results show such peaks. STEX requires individual calculations for each of the two oxygen atoms in cysteine. Unfortunately, the double-bonded oxygen suffers from a serious convergence problem in the ΔSCF step6 of the STEX calculation. According to our experience, this kind of SCF convergence problem is not rare in STEX calculations. STEX predicts a too strong peak around 538.6 eV for the other hydroxyl oxygen, so that the shoulder peak around 535.0 eV is covered. We can clearly see this shoulder peak in REW-TDDFT spectrum. STEX gives too weak peaks for the sulfur K-edge around 2479.0 eV, making the broad peak shown in experiments less obvious. At the L-edge spin-orbit interaction splits the core excited states into two edges (2p1/2 and 2p3/2), which makes the situation more complicated. However, ligand field multiplet studies have found that spin-orbit interaction does not affect L-edges too much,91 and other spin-free DFT studies have also given good L-edge results.92, 93 Very recently, it has been shown that the Ru L3 edge including scalar relativistic corrections via the zeroth order regular approximation can be modeled reliably with REW-TDDFT.66 So spin-orbit interaction is neglected in this study. STEX and REW-TDDFT results for sulfur L-edge are similar. In all, the simulated XANES results for different edges from the two theories support that REW-TDDFT is more accurate and computationally less expensive than STEX.
In Secs. 3C, 3D, we use the REW-TDDFT results to simulate frequency- and time-domain spectroscopic signals that depend on the coupling between valence- and core-excited states. Dipoles between the ground and valence-excited states can be directly probed via UV absorption. The UV absorption spectrum for cysteine calculated with REW-TDDFT, plotted according to Eq. (17) of Ref. 7, is shown in Fig. 2. In this calculation, as well as the Raman simulations presented in Secs. 3C, 3D, we set the valence excited state linewidth to eV for the sake of visualizing the results. A theory of the relaxation dynamics which governs the actual lineshape, e.g., nuclear motion, interaction with a thermal bath, etc., is beyond the scope of the present study.
Figure 2.
Calculated UV absorption spectrum of cysteine from TDDFT. The same active valence excitations contribute to the Raman signals shown below.
RIXS
Frequency-domain spontaneous Raman (RIXS) is the simplest technique that can probe the correlation between valence and core excitations. In RIXS, a monochromatic X-ray beam (ω1) interacts with the sample, and the spontaneous emission (ω2) is frequency-resolved, with peaks recorded at . We take the incident beam ω1 to be polarized, and the scattered light ω2 is also sent through a polarization filter detected at the magic angle (54.7°) with respect to the excitation beam polarization. The Kramers-Heisenberg formula for Raman scattering is given by Eq. (19) of Ref. 7.
In Fig. 3, we show the RIXS spectra taken at the nitrogen, oxygen, and sulfur K-edges, and the sulfur L-edge. The vertical axis represents the core-excitation frequency (with the first K-edge transition set to zero), and the horizontal axis represents valence excitation frequencies. The nitrogen RIXS spectrum shows that each core excited state is primarily coupled to a single valence excitation. The nitrogen peaks are mainly along a diagonal line, indicating that a single particle picture is appropriate for nitrogen excitations, where a core electron is promoted to an unoccupied valence orbital and then an electron from the highest occupied molecular orbital (HOMO), or an orbital nearly degenerate in energy to the HOMO, is demoted to fill the core hole. In this case, ω2 is approximately independent of ω1.
Figure 3.
Calculated RIXS signal at the nitrogen K-edge, oxygen K-edge, sulfur K-edge, and sulfur L-edge from cysteine. The excitation frequency ω1 is given with respect to the K-edge frequency.
The oxygen RIXS reveal that the first core-excited state is coupled to many different valence excitations, and therefore the single-particle picture whereby the oxygen 1s electron is promoted to a single unoccupied valence orbital is not appropriate here. We also see that the valence excited states present in the oxygen RIXS are coupled to multiple core-excited states. The same is true for the sulfur 1s RIXS spectrum. The sulfur 2p RIXS spectrum is uniquely sparse; only a handful of states with energy within 2 eV of the L-edge are coupled to valence states of moderate energy.
Time-domain SXRS
Stimulated X-ray Raman spectra were introduced in earlier works.6, 7, 11 Two ultrashort pulses, the pump and probe, separated by a controllable time delay impinge upon the sample. The signal is defined as the change in the integrated transmission of the probe due to the presence of the probe. The first pulse interacts twice with the molecule, transiently promoting a core electron to the valence band and then de-exciting the system and filling the previously created core-hole by stimulated emission. In the presence of the core-hole, the system is in a non-stationary state, and the final state will be a linear superposition of valence electron-hole pairs. Thus, the states accessed by a SXRS experiment are the same states that contribute to a UV/Vis absorption spectrum, but at different intensities, since the selection rules for optical and X-ray Raman excitation are different.
In analogy with optical spectroscopy, the 1D-SXRS signal is essentially the ground-state bleach (GSB) component of a pump-probe signal. The other two contributions, the stimulated emission and excited-state absorption components, both involve the creation of an excited state population by the first pulse, i.e., the two interactions with the first pulse occur on different sides of the density matrix. In order for this population to influence the subsequent absorption of the probe pulse, it must still be present after the interpulse delay τ. Here we take advantage of the short lifetimes of core-excited state, typically smaller than 10 fs for the atoms under consideration here, and assume that the interpulse delay is longer than the lifetime. We thus need only consider the GSB contribution. Just as in traditional (vibrational) resonance Raman, where only those modes whose potential surfaces are distorted by the electronic excitation contribute to the signal, in SXRS only those valence excitations which are perturbed by a core-hole local to the atom in question show up prominently.
Assuming that the pump and probe pulses are polarized at the magic angle with respect to each other, we can write the 1D-SXRS signal as
| (13) |
where
| (14) |
is the effective isotropic polarizability averaged over the spectral envelope of the jth ultrashort pulse, . The polarizability is a rank-2 tensor, however, by using a magic angle polarization scheme we are able to focus only on the isotropic component The effective polarizability is complex and symmetric, i.e., it is non-Hermitian. It is useful to define Hermitian and anti-Hermitian components of the polarizability as
| (15) |
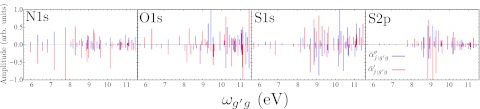
Expressions for the matrix elements of these operators, evaluated for Gaussian pulse envelopes, can be found in Ref. 7. The linear portion of the effective polarizabilities for pulses tuned to the four core-transitions considered here are shown in Fig. 4.
Figure 4.
Hermitian and anti-Hermitian parts of the effective isotropic polarizabilities (Eq. 14) for the four pulses used in our simulations, in arbitrary units. The Hermitian part is purely real, while the anti-Hermitian part is purely imaginary.
The 1D-SXRS signal is collected in the time-domain and Fourier transformed (FT), giving
| (16) |
In Eq. 16, we only include the Ω > 0 component. Since SXRS is a pump-probe signal its Fourier transform obeys S(−Ω) = S*(Ω). When the pump pulse is on resonance, the anti-Hermitian part of the polarizability is finite, and the signal does not separate into dispersive and absorptive lineshapes. In Fig. 5, we show the calculated modulus 1D-SXRS signals for cysteine using Gaussian pulses (FWHM 128 as), with the excitation pulse central frequency tuned to the core-edge transition energy for the four core-excitations considered here, and the pulses polarized at the magic angle relative to each other.
Figure 5.
1D SXRS spectra from cysteine with the two pulses polarized at the magic angle. The pulses are Gaussian, with bandwidth 14 eV, FWHM. The center frequency of the pulses is set to the core edge frequency for a given atom. Spectra in the same row share a common pump pulse, while spectra in the same column share a common probe pulse.
Signals in the same row have the same pump pulse, while signals in the same column share a common probe pulse. The one color signals, with identical pump and probe pulses, are along the diagonal. The one-color signals give essentially the same information as the RIXS, integrated along ω1 gated by the pulse bandwidth, with the exception of polarization effects. In SXRS, it is possible to obtain a signal that is proportional to the isotropic polarizability by using magic angle polarization, but in RIXS it is not. Note that the strong S1 and S4 resonances in the sulfur K-edge RIXS () in Fig. 3 are nearly absent from the S1s/S1s SXRS signal in Fig. 5. This is indicative of the fact that the upward and downward transition dipoles which comprise the Raman transition are perpendicular, or nearly so, to each other.94
Two-color SXRS signals provide a window into the interaction between localized core orbitals and delocalized valence excitations for which there is no frequency-domain analog. These signals can be interpreted as the time-dependent overlap between a doorway valence wavepacket created at time zero by pulse 1, and a window valence wavepacket created at time τ by pulse 2. We can see from Eq. 16 that only the anti-Hermitian part of the probe polarizability contributes to the signal, whereas both Hermitian and anti-Hermitian parts of the pump polarizability are relevant. The two-color signals have no time-reversal symmetry, i.e., the signal is different for negative τ than for positive τ. Thus the spectra are not symmetric with respect to the interchange of the center frequencies of the pump and probe pulses, though and examination of the modulus signals shown in Fig. 5 shows that they are similar.
To examine the difference between two-color 1D-SXRS signals taken with time-reversed pulses, we define the difference signal as
| (17) |
The Fourier transform of Eq. 17 is
| (18) |
Unlike Eq. 16, and Eq. 18 does separate into purely dispersive and purely absorptive components. The difference spectrum gives amplitude level information regarding the interference between valence wavepackets created at different atomic sites within the molecule.
Figure 6 shows the N1s/O1s O1s/N1s, and N1s/O1s difference spectra. We note that the modulus spectra for the two two-color signals are nearly identical to each other, with some minor differences in signal amplitude. However, many of the peaks have different phases as can be seen by looking at the real and imaginary parts of the FT spectra, such that the difference spectrum is of the same order of magnitude as either of two-color spectra. In the bottom right panel, we show both the modulus of the difference spectrum (solid trace) and the difference between the moduli of the two-color spectra (dashed trace). This is instructive as it shows which peaks differ only in phase between the two signals (where the solid trace is large but the dashed trace is small), and which peaks differ in amplitude between the two signals (where the solid and dashed traces have the same magnitude).
Figure 6.
(Top row) The N1s/O1s (solid traces) and O1s/N1s (dashed traces) signals, shown as the real (left), imaginary (middle), and modulus (right) of the Fourier transform signal. As shown in the text, differences between these signals are related to the complex valued polarizability when the pulses are near resonance with multiple core transitions. The real and imaginary FT signals are both mixtures of dispersive and Lorentzian lineshapes. (Bottom row) The left and middle panels show the imaginary and real parts of the FT difference spectra. Unlike the top row, here the imaginary part is purely absorptive and the real part purely dispersive. The right panel shows both the modulus of the difference signal (solid trace), and the difference of the modulus signals (dashed trace). Peaks for which the solid trace is large in value, but the dashed trace is not, indicate that the two signals have similar magnitude for a given peak but have a large phase difference. Peaks for which the two traces are similar in magnitude indicate that the phase and amplitude for that peak are different for the two pulse configurations.
In Fig. 7, we show the modulus of the difference and the difference of the moduli signals for all six two-color configurations considered here (the upper left panel of Fig. 7 is thus a repeat of the lower right panel of Fig. 6). We see that in the N1s/O1s case, the peaks below 9 eV show mainly differences in phase between the two signals. Alternatively, in the N1s/S1s case, the difference appears to be mostly at the amplitude level, with the S1s/N1s two-color signal being uniformly larger than the N1s/Sls signal. The S1s/S2p difference signal is another case where the difference is in amplitude rather than phase.
Figure 7.
Difference 1D-SXRS spectra for the six possible two-color combinations considered here. The top middle panel, for example, shows the modulus of the difference between the N1s/S1s and S1s/N1s signals as the solid trace, and the difference between the moduli of the N1s/S1s and S1s/N1s signals as the dashed trace.
CONCLUSIONS
REW-TDDFT is a simple and efficient method for calculating core-excited states. Its major advantage over STEX is that both core- and valence-excited states can be represented as linear combinations of electron-hole pairs in the same molecular orbital basis, which greatly simplifies the transition dipole calculations. This also makes it a good tool for X-ray spectroscopy simulations on large molecular systems. However, because of the adiabatic approximation,79 most modern implementations of TDDFT cannot handle doubly excited states, which are necessary in many types of nonlinear spectroscopy simulations. This problem will be addressed in our future study.
We have presented calculated frequency-domain and time-domain X-ray Raman signals, RIXS and SXRS, respectively, for the amino acid cysteine. The RIXS signal can reveal coupling between core and valence degrees of freedom, by showing which valence-excitations are perturbed by which core excitations. It is important to emphasize that SXRS is not merely the Fourier transform of RIXS. SXRS probes different tensor elements of the polarizability than RIXS does, allowing the isolation of the isotropic signal through magic angle detection. Further, two-color SXRS probes cross correlations between valence excitations created at different atomic centers in the molecule. By looking at the difference between two-color pump/probe signals taken with positive and negative time delays, we gain amplitude-level information regarding the valence wavepackets created at the different sites.
ACKNOWLEDGMENTS
The support of the Chemical Sciences, Geosciences and Biosciences Division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy is gratefully acknowledged. We also gratefully acknowledge the support of the National Science Foundation (Grant No. CHE-1058791), and the National Institutes of Health (Grant No. GM-59230). A portion of the research and REW-TDDFT development (N.G.) was performed at EMSL, a national scientific user facility sponsored by the U.S. Department of Energys Office of Biological and Environmental Research and located at Pacific Northwest National Laboratory (PNNL). PNNL is operated for the Department of Energy by the Battelle Memorial Institute under Contract No. DE-AC06-76RLO-1830.
References
- Ullrich J., Rudenko A., and Moshammer R., Annu. Rev. Phys. Chem. 63, 635 (2012). 10.1146/annurev-physchem-032511-143720 [DOI] [PubMed] [Google Scholar]
- Gallmann L., Cirelli C., and Keller U., Annu. Rev. Phys. Chem. 63, 447 (2012). 10.1146/annurev-physchem-032511-143702 [DOI] [PubMed] [Google Scholar]
- Doumy G., Roedig C., Son S.-K., Blaga C. I., DiChiara A. D., Santra R., Berrah N., Bostedt C., Bozek J. D., Bucksbaum P. H., Cryan J. P., Fang L., Ghimire S., Glownia J. M., Hoener M., Kanter E. P., Krässig B., Kuebel M., Messerschmidt M., Paulus G. G., Reis D. A., Rohringer N., Young L., Agostini P., and DiMauro L. F., Phys. Rev. Lett. 106, 083002 (2011). 10.1103/PhysRevLett.106.083002 [DOI] [PubMed] [Google Scholar]
- Marangos J., Contemp. Phys. 52, 551 (2011). 10.1080/00107514.2011.607290 [DOI] [Google Scholar]
- Hoener M., Fang L., Kornilov O., Gessner O., Pratt S. T., Ghr M., Kanter E. P., Blaga C., Bostedt C., Bozek J. D., Bucksbaum P. H., Buth C., Chen M., Coffee R., Cryan J., DiMauro L., Glownia M., Hosler E., Kukk E., Leone S. R., McFarland B., Messerschmidt M., Murphy B., Petrovic V., Rolles D., and Berrah N., Phys. Rev. Lett. 104, 253002 (2010). 10.1103/PhysRevLett.104.253002 [DOI] [PubMed] [Google Scholar]
- Healion D., Wang H., and Mukamel S., J. Chem. Phys. 134, 124101 (2011). 10.1063/1.3557057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biggs J. D., Zhang Y., Healion D., and Mukamel S., J. Chem. Phys. 136, 174117 (2012). 10.1063/1.4706899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nozières P. and De Dominicis C. T., Phys. Rev. 178, 1097 (1969). 10.1103/PhysRev.178.1097 [DOI] [Google Scholar]
- Schwarz W. H. E. and Buenker R. J., Chem. Phys. 13, 153 (1976). 10.1016/0301-0104(76)80019-5 [DOI] [Google Scholar]
- Schweigert I. V. and Mukamel S., Phys. Rev. Lett. 99, 163001 (2007). 10.1103/PhysRevLett.99.163001 [DOI] [PubMed] [Google Scholar]
- Schweigert I. V. and Mukamel S., Phys. Rev. A 76, 012504 (2007). 10.1103/PhysRevA.76.012504 [DOI] [Google Scholar]
- Schweigert I. V. and Mukamel S., J. Chem. Phys. 128, 184307 (2008). 10.1063/1.2839859 [DOI] [PubMed] [Google Scholar]
- Schweigert I. V. and Mukamel S., Phys. Rev. A 78, 052509 (2008). 10.1103/PhysRevA.78.052509 [DOI] [Google Scholar]
- Healion D. M., Schweigert I. V., and Mukamel S., J. Phys. Chem. A 112, 11449 (2008). 10.1021/jp803824a [DOI] [PubMed] [Google Scholar]
- Hunt W. J. and W. A.GoddardIII, Chem. Phys. Lett. 3, 414 (1969). 10.1016/0009-2614(69)80154-5 [DOI] [Google Scholar]
- Ågren H., Carravetta V., Vahtras O., and Pettersson L. G. M., Chem. Phys. Lett. 222, 75 (1994). 10.1016/0009-2614(94)00318-1 [DOI] [Google Scholar]
- Ågren H., Carravetta V., Vahtras O., and Pettersson L. G. M., Theor. Chem. Acta 97, 14 (1997). 10.1007/s002140050234 [DOI] [Google Scholar]
- Slater J. C., Adv. Quantum Chem. 6, 1 (1972). 10.1016/S0065-3276(08)60541-9 [DOI] [Google Scholar]
- Slater J. C. and Johnsson K. H., Phys. Rev. B 5, 844 (1972). 10.1103/PhysRevB.5.844 [DOI] [Google Scholar]
- Stener A., Lisini M., and Decleva P., Chem. Phys. 191, 141 (1995). 10.1016/0301-0104(94)00347-D [DOI] [Google Scholar]
- Triguero L., Pettersson L. G. M., and Ågren H., Phys. Rev. B 58, 8097 (1998). 10.1103/PhysRevB.58.8097 [DOI] [Google Scholar]
- Natoli C. R., Misemer D. K., Doniach S., and Kutzler F. W., Phys. Rev. A 22, 1104 (1980). 10.1103/PhysRevA.22.1104 [DOI] [Google Scholar]
- Fonda L., J. Phys.: Condens. Matter 4, 8269 (1992). 10.1088/0953-8984/4/43/004 [DOI] [Google Scholar]
- Ankudinov A. L., Ravel B., Rehr J. J., and Conradson S. D., Phys. Rev. B 58, 7565 (1998). 10.1103/PhysRevB.58.7565 [DOI] [Google Scholar]
- Hetényi B., Angelis F. D., Giannozzi P., and Car R., J. Chem. Phys. 120, 8632 (2004). 10.1063/1.1703526 [DOI] [PubMed] [Google Scholar]
- Prendergast D. and Galli G., Phys. Rev. Lett. 96, 215502 (2006). 10.1103/PhysRevLett.96.215502 [DOI] [PubMed] [Google Scholar]
- Taillefumier M., Cabaret D., Flank A.-M., and Mauri F., Phys. Rev. B 66, 195107 (2002). 10.1103/PhysRevB.66.195107 [DOI] [Google Scholar]
- Shirley E. L., Phys. Rev. Lett. 80, 794 (1998). 10.1103/PhysRevLett.80.794 [DOI] [Google Scholar]
- Soininen J. A. and Shirley E. L., Phys. Rev. B 54, 165112 (2001). 10.1103/PhysRevB.64.165112 [DOI] [Google Scholar]
- Dutoi A. D., Cederbaum L. S., Wormit M., Starcke J. H., and Dreuw A., J. Chem. Phys. 132, 144302 (2010). 10.1063/1.3353161 [DOI] [PubMed] [Google Scholar]
- Rehr J. J. and Ankudinov A. L., Coord. Chem. Rev. 249, 131 (2005). 10.1016/j.ccr.2004.02.014 [DOI] [Google Scholar]
- Kuleff A. I. and Cederbaum L. S., Phys. Rev. Lett. 98, 083201 (2007). 10.1103/PhysRevLett.98.083201 [DOI] [PubMed] [Google Scholar]
- Schirmer J., Trofimov A. B., and Stelter G., J. Chem. Phys. 109, 4734 (1998). 10.1063/1.477085 [DOI] [Google Scholar]
- Ekström U., Norman P., Carravetta V., and Ågren H., Phys. Rev. Lett. 97, 143001 (2006). 10.1103/PhysRevLett.97.143001 [DOI] [PubMed] [Google Scholar]
- Norman P., Bishop D. M., Jensen H. J. A., and Oddershede J., J. Chem. Phys. 115, 10323 (2001). 10.1063/1.1415081 [DOI] [Google Scholar]
- Norman P., Bishop D. M., Jensen H. J. A., and Oddershede J., J. Chem. Phys. 123, 194103 (2005). 10.1063/1.2107627 [DOI] [PubMed] [Google Scholar]
- Linares M., Stafström S., Rinkevicius Z., and Norman H. Å. P., J. Phys. Chem. B 115, 5096 (2011). 10.1021/jp103506g [DOI] [PubMed] [Google Scholar]
- Nooijen M. and Bartlett R. J., J. Chem. Phys. 102, 6735 (1995). 10.1063/1.469147 [DOI] [Google Scholar]
- Ueda K., Hoshino M., Tanaka T., Kitajima M., Tanaka H., Fanis A. D., Tamenori Y., Ehara M., Oyagi F., Kuramoto K., and Nakatsuji H., Phys. Rev. Lett. 94, 243004 (2005). 10.1103/PhysRevLett.94.243004 [DOI] [Google Scholar]
- Kuramoto K., Ehara M., and Nakatsuji H., J. Chem. Phys. 122, 014304 (2005). 10.1063/1.1824899 [DOI] [PubMed] [Google Scholar]
- Kuramoto K., Ehara M., Nakatsuji H., Kitajima M., Tanaka H., Fanis A. De, Tamenori Y., and Ueda K., J. Electron Spectrosc. Relat. Phenom. 142, 253 (2005). 10.1016/j.elspec.2004.09.011 [DOI] [Google Scholar]
- Ehara M., Nakatsuji H., Matsumoto M., Hatamoto T., Liu X. J., Lischke T., Prümper G., Tanaka T., Makochekanwa C., Hoshino M., Tanaka H., Harries J. R., Tamenori Y., and Ueda K., J. Chem. Phys. 124, 124311 (2006). 10.1063/1.2181144 [DOI] [PubMed] [Google Scholar]
- Tanaka T., Ueda K., Feifel R., Karlsson L., Tanaka H., Hoshino M., Kitajima M., Ehara M., Fukuda R., Tamaki R., and Nakatsuji H., Chem. Phys. Lett. 435, 182 (2007). 10.1016/j.cplett.2006.12.071 [DOI] [Google Scholar]
- Brabec J., Bhaskaran-Nair K., Govind N., Pittner J., and Kowalski K., “Applications of the state-specific multireference coupled cluster methods to core-level excitations,” J. Chem. Phys. (in press). [DOI] [PubMed]
- Bartlett R. J., Chem. Phys. Lett. 484, 1 (2009). 10.1016/j.cplett.2009.10.053 [DOI] [Google Scholar]
- Schweigert I. V., Lotrich V. F., and Bartlett R. J., J. Chem. Phys. 125, 104108 (2006). 10.1063/1.2212936 [DOI] [PubMed] [Google Scholar]
- Schweigert I. V. and Bartlett R. J., J. Chem. Phys. 129, 124109 (2008). 10.1063/1.2978171 [DOI] [PubMed] [Google Scholar]
- Runge E. and Gross E. K. U., Phys. Rev. Lett. 52, 997 (1984). 10.1103/PhysRevLett.52.997 [DOI] [Google Scholar]
- Dreuw A. and Head-Gordon M., Chem. Rev. 105, 4009 (2005). 10.1021/cr0505627 [DOI] [PubMed] [Google Scholar]
- Jacquemin D., Mennucci B., and Adamo C., Phys. Chem. Chem. Phys. 13, 16987 (2011). 10.1039/c1cp22144b [DOI] [PubMed] [Google Scholar]
- Stener M., Fronzoni G., and de Simone M., Chem. Phys. Lett. 373, 115 (2003). 10.1016/S0009-2614(03)00543-8 [DOI] [Google Scholar]
- Hayashi T. and Stuchebrukhov A. A., Proc. Natl. Acad. Sci. U.S.A. 107, 19157 (2010). 10.1073/pnas.1009181107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert A. T. B., Besley N. A., and Gill P. M. W., J. Phys. Chem. A 112, 13164 (2008). 10.1021/jp801738f [DOI] [PubMed] [Google Scholar]
- Saunders V. R. and Hiller I. H., Int. J. Quantum Chem. 7, 699 (1973). 10.1002/qua.560070407 [DOI] [Google Scholar]
- Guest M. F. and Saunders V. R., Mol. Phys. 28, 819 (1974). 10.1080/00268977400102171 [DOI] [Google Scholar]
- Casida M. E., Recent Advances in Density Functional Methods, Part I (World Scientific, Singapore, 1995). [Google Scholar]
- Bauernschmitt R. and Ahlrichs R., Chem. Phys. Lett. 256, 454 (1996). 10.1016/0009-2614(96)00440-X [DOI] [Google Scholar]
- Hirata S. and Head-Gordon M., Chem. Phys. Lett. 302, 375 (1999). 10.1016/S0009-2614(99)00137-2 [DOI] [Google Scholar]
- Tretiak S. and Mukamel S., Chem. Rev. 102, 3171 (2002). 10.1021/cr0101252 [DOI] [PubMed] [Google Scholar]
- Davidson E. R., J. Comput. Phys. 17, 84 (1975). 10.1016/0021-9991(75)90065-0 [DOI] [Google Scholar]
- Besley N. A. and Noble A., J. Phys. Chem. C 111, 3333 (2007). 10.1021/jp065160x [DOI] [Google Scholar]
- DeBeer-George S., Petrenko T., and Neese F., Inorg. Chim. Acta 361, 965 (2008). 10.1016/j.ica.2007.05.046 [DOI] [Google Scholar]
- Ray K., George S. D., Solomon E. I., Wieghardt K., and Neese F., Chem. Eur. J. 13, 2783 (2007). 10.1002/chem.200601425 [DOI] [PubMed] [Google Scholar]
- DeBeer-George S., Petrenko T., and Neese F., J. Phys. Chem. A 112, 12936 (2008). 10.1021/jp803174m [DOI] [PubMed] [Google Scholar]
- Valiev M., Bylaska E., Govind N., Kowalski K., Straatsma T., van Dam H., Wang D., Nieplocha J., Apra E., Windus T., and de Jong W., Comput. Phys. Commun. 181, 1477 (2010). 10.1016/j.cpc.2010.04.018 [DOI] [Google Scholar]
- Lopata K., Kuiken B. E. V., Khalil M., and Govind N., J. Chem. Theory Comput. 8, 3284 (2012). 10.1021/ct3005613 [DOI] [PubMed] [Google Scholar]
- Schmidt N., Fink R., and Hieringer W., J. Chem. Phys. 133, 054703 (2010). 10.1063/1.3435349 [DOI] [PubMed] [Google Scholar]
- Baerends E. J., Ellis D. E., and Ros P., Chem. Phys. 2, 41 (1973). 10.1016/0301-0104(73)80059-X [DOI] [Google Scholar]
- Fonseca-Guerra C., Snijders J. G., te Velde G., and Baerends E. J., Theor. Chem. Acta 99, 391 (1998). 10.1007/s002149800m26 [DOI] [Google Scholar]
- Liang W., Fischer S. A., Frisch M. J., and Li X., J. Chem. Theory Comput. 7(11), 3540 (2011). 10.1021/ct200485x [DOI] [PubMed] [Google Scholar]
- Nakata A., Imamura Y., and Nakai H., J. Chem. Phys. 125, 064109 (2006). 10.1063/1.2227379 [DOI] [PubMed] [Google Scholar]
- Imamura Y. and Nakai H., Int. J. Quantum Chem. 107, 23 (2007). 10.1002/qua.21025 [DOI] [Google Scholar]
- Song J. W., Watson M. A., Nakata A., and Hirao K., J. Chem. Phys. 129, 184113 (2008). 10.1063/1.3010372 [DOI] [PubMed] [Google Scholar]
- Tu G., Rinkevicius Z., Vahtras O., Ågren H., Ekström U., Norman P., and Carravetta V., Phys. Rev. A 76, 022506 (2007). 10.1103/PhysRevA.76.022506 [DOI] [Google Scholar]
- Nakata A., Imamura Y., Ostuka T., and Nakai H., J. Chem. Phys. 124, 194105 (2006). 10.1063/1.2173987 [DOI] [PubMed] [Google Scholar]
- Imamura Y., Kobayashi R., and Nakai H., J. Chem. Phys. 134, 124113 (2011). 10.1063/1.3569030 [DOI] [PubMed] [Google Scholar]
- Besley N. A., Peach M. J. G., and Tozer D. J., Phys. Chem. Chem. Phys. 11, 10350 (2009). 10.1039/b912718f [DOI] [PubMed] [Google Scholar]
- Besley N. A. and Asmuruf F. A., Phys. Chem. Chem. Phys. 12, 12024 (2010). 10.1039/c002207a [DOI] [PubMed] [Google Scholar]
- Maitra N. T., Zhang F., Cave R. J., and Burke K., J. Chem. Phys. 120, 5932 (2004). 10.1063/1.1651060 [DOI] [PubMed] [Google Scholar]
- Nardelli A., Fronzoni G., and Stener M., Phys. Chem. Chem. Phys. 13, 480 (2011). 10.1039/c0cp00708k [DOI] [PubMed] [Google Scholar]
- Romaniello P., Sangalli D., Berger J. A., Sottile F., Molinari L. G., Reining L., and Onida G., J. Chem. Phys. 130, 044108 (2009). 10.1063/1.3065669 [DOI] [PubMed] [Google Scholar]
- Sangalli D., Romaniello P., Onida G., and Marini A., J. Chem. Phys. 134, 034115 (2011). 10.1063/1.3518705 [DOI] [PubMed] [Google Scholar]
- Löwdin P.-O., Phys. Rev. 97, 1474 (1955). 10.1103/PhysRev.97.1474 [DOI] [Google Scholar]
- Frisch M. J., Trucks G. W., Schlegel H. B.et al. , GAUSSIAN 09, C01 Gaussian Inc., Wallingford, CT, 2009.
- Crawford T. D., Sherrill C. D., Valeev E., Fermann J., King R., Leininger M., Brown S., Janssen C., Seidl E., Kenny J., and Allen W., J. Comput. Chem. 28, 1610 (2007). 10.1002/jcc.20573 [DOI] [PubMed] [Google Scholar]
- Yanai T., Tew D., and Handy N., Chem. Phys. Lett. 393, 51 (2004). 10.1016/j.cplett.2004.06.011 [DOI] [Google Scholar]
- Hirata S. and Head-Gordon M., Chem. Phys. Lett. 314, 291 (1999). 10.1016/S0009-2614(99)01149-5 [DOI] [Google Scholar]
- Zubavichus Y., Shaporenko A., Grunze M., and Zharnikov M., J. Phys. Chem. A 109, 6998 (2005). 10.1021/jp0535846 [DOI] [PubMed] [Google Scholar]
- Jalilehvand F., Chem. Soc. Rev. 35, 1256 (2006). 10.1039/b417595f [DOI] [PubMed] [Google Scholar]
- Zschornack G., Handbook of X-Ray Data (Springer-Verlag, Berlin, 2007). [Google Scholar]
- de Groot F. M. F., Hu Z. W., Lopez M. F., Kaindl G., Guillot F., and Tronc M., J. Chem. Phys. 101, 6570 (1994). 10.1063/1.468351 [DOI] [Google Scholar]
- Campbell L. and Mukamel S., J. Chem. Phys. 121, 12323 (2004). 10.1063/1.1814101 [DOI] [PubMed] [Google Scholar]
- Van Kuiken B. E., Huse N., Cho H., Strader M. L., Lynch M. S., Schoenlein R. W., and Khalil M., J. Phys. Chem. Lett. 3, 1695 (2012). 10.1021/jz300671e [DOI] [PubMed] [Google Scholar]
- Healion D., Biggs J. D., and Mukamel S., Phys. Rev. A 86, 033429 (2012). 10.1103/PhysRevA.86.033429 [DOI] [Google Scholar]