Abstract
Background
Using a bifurcated Y-graft as the Fontan baffle is hypothesized to be a means to streamline and improve flow dynamics through the total cavopulmonary connection (TCPC). This study conducted numerical simulations to evaluate this hypothesis using post-operative data from five patients.
Methods
Patients were imaged with cardiac magnetic resonance or computed tomography after receiving a bifurcated aorto-iliac Y-graft as their Fontan conduit. Numerical simulations were performed using in vivo flow rates, as well as two levels of simulated exercise. Two TCPC models were virtually created for each patient to serve as the basis for hemodynamic comparison. Comparative metrics included connection flow resistance and inferior vena caval flow distribution.
Results
Results demonstrate good hemodynamic outcomes for the Y-graft options. The consistency of inferior vena caval flow distribution was improved over TCPC controls, while the connection resistances were generally no different from the TCPC values, except for one case in which there was a marked improvement under both resting and exercise conditions. Examination of the connection hemodynamics as they relate to surgical Y-graft implementation identified critical strategies and modifications that are needed to potentially realize the theoretical efficiency of such bifurcated connection designs.
Conclusions
Five consecutive patients received a Y-graft connection to complete their Fontan procedure with positive hemodynamic results. Refining the surgical technique for implementation should result in further energetic improvements that may help improve long-term outcomes.
Keywords: hemodynamics; Fontan procedure; blood flow; heart defects, congenital
INTRODUCTION
Surgical palliation (the “Fontan procedure”) is needed to correct the class of congenital heart defects that result in the presence of a single functional ventricle. The predominant repair of these defects is the total cavopulmonary connection (TCPC), in which the superior vena cava (SVC) and inferior vena cava (IVC) are connected to the pulmonary arteries (PA)[1]. While representing an energetic improvement over previous designs, the TCPC creates an adverse hemodynamic environment due to the collision of the caval flows[2–4]. The idea of using a flow bifurcation in the Fontan connection was first proposed by Soerensen et al.[5] (“Optiflo”; U.S. Patent #7811244). The motivating concept was that by dividing and rerouting one or both of the vena caval flows, the inefficient collision and mixing at the PA junction can be avoided.
Subsequent studies have analyzed and sought to optimize the design of the Fontan Y-graft (half of the Optiflo) using virtually rendered models[6, 7]. However, the recent work of Kanter et al.[8] represents the first clinical report of Y-graft usage in a consecutive series of Fontan patients. Post-operative imaging data from these patients provide the unique opportunity to evaluate the hemodynamic outcomes of this series and compare them to what could have been realized with possible surgical alternatives. This objective is achieved in this study by numerically evaluating the connections under resting and simulated exercise flow conditions, and comparing these performance characteristics to extracardiac TCPC models virtually created for the same patients.
METHODS
This analysis of clinically collected patient imaging and/or catheterization data was approved by the institutional review boards of Emory University and Georgia Tech in conjunction with an established data sharing agreement between the institutions. Informed consent for the use of image data for research purposes was obtained in each case.
Patients and Data Acquisition
Five consecutive patients at Children's Healthcare of Atlanta received a commercially available bifurcated aorto-iliac polytetrafluoroethylene (PTFE) graft (Gore-Tex; Flagstaff, AZ) as their Fontan baffle. For the purposes of this study, such connections will be referred to as YCPCs. Patient characteristics are provided in Table 1. Cardiovascular Magnetic Resonance (CMR) images were acquired for three patients prior to hospital discharge to assess Fontan anatomy and through-plane velocities for selected slices in the IVC, SVC, LPA, RPA and aorta (via phase contrast). In two cases (1,5), computed tomography (CT) was instead acquired to provide anatomic information. Pre-operative phase contrast CMR data were available for patient 5 to provide flow information, while cardiac catheterization was used to dictate vessel flow rates for patient 1 (see footnote in Table 2). Patient anatomies and (CMR) velocities were reconstructed based on previously published methods[9, 10]. The resulting flow conditions imposed in the numerical simulations are summarized in Table 2.
Table 1.
Patient Characteristics
| Patient | Age (yrs) | BSA (m2) | Y-graft Size (mm) |
|---|---|---|---|
| Pt. 1 | 5.4 | 0.72 | 20×10 |
| Pt. 2 | 2.1 | 0.53 | 18×9 |
| Pt. 3 | 3.7 | 0.73 | 20×10 |
| Pt. 4 | 2.3 | 0.47 | 20×10 |
| Pt. 5 | 11.0 | 1.09 | 20×10 |
Table 2.
Relevant Post-operative Vessel Flow Conditions
| Percentage Distribution | ||||||
|---|---|---|---|---|---|---|
| Patient | CI (L/min/m2) | ReIVC | IVC | SVC (/LSVC) | LPA | RPA |
| Pt. 1 * | 3.8 | 564.0 | 55 | 45 | 48 | 52 |
| Pt. 2 | 3.8 | 110.4 | 32 | 68 | 33 | 67 |
| Pt. 3 | 3.4 | 178.5 | 45 | 55 | 34 | 66 |
| Pt. 4 | 3.0 | 118.2 | 44 | 56 | 74 | 26 |
| Pt. 5 | 3.5 | 136.0 | 24 | 55/21 | 68 | 32 |
CI – Cardiac Index; ReIVC− Reynolds number at IVC inlet (resting conditions)
Flow data taken from cardiac catheterization (CMR-measured flows used for all others); pulmonary flow taken as QSVC, difference between pulmonary, systemic flows taken as QIVC. PA split set as ratio of outlet cross-sectional areas.
To provide a basis for hemodynamic comparison to these YCPCs, two virtual extracardiac TCPC models were made for each patient representing the alternative connections they may have received instead of a Y-graft[11]. The two designs varied slightly in caval offset, and are thus designated as the `t-junction' and `offset' models. Baffle diameters matched the diameter at the base of the Y-graft. Figure 1 shows the anatomical comparison of all connections.
Figure 1.
Patient YCPCs (top row; with photo of bifurcated PTFE graft) and virtually modeled t-junction (middle row) and offset (bottom row) TCPC controls for all 5 patients.
Computational Fluid Dynamics Analysis
A fully validated, in-house computational solver (based on the sharp-interface immersed boundary method with a fractional step implementation [12, 13]) was used for all hemodynamic analyses. Cartesian grid spacing was set at 2% of IVC diameter, which is sufficient for mesh independent results[13]. The governing equations were solved in their complete unsteady formulation. Time-varying flow conditions (measured from CMR) were imposed in three of the patients (2–4) for whom such data were available, while time-averaged conditions were used for the remaining two patients. In addition to baseline (resting) flows, simulated exercise conditions were also investigated. Exercise limitations are a known chronic issue with Fontan patients[14, 15] and previous studies have shown that the non-linear increases in TCPC power loss with increased flow rates may be an important contributor[16, 17]. Further, since small inefficiencies under resting conditions may be amplified and exacerbated with higher flows, these simulations are a means to assess the hemodynamic characteristics and robustness for a given connection geometry. Per standard practice, simulated exercise conditions of two and three times baseline (`2×' and `3×') were numerically imposed by respectively doubling and tripling the measured cardiac output and imposing that difference as additional (time-averaged) IVC flow (approximating lower limb exercise)[7, 16]. The pulmonary flow splits were maintained constant across these varied conditions as suggested by previous studies[18].
The primary basis for comparison was the hemodynamic resistance (R) across the connection (; where ΔP is pressure drop, QVC is the sum of caval inflows, and BSA is the body surface area)[17]. Additionally, the IVC flow distribution to the PAs, believed to be an important consideration to avoid pulmonary arteriovenous malformations (PAVM)[19], was quantified[20]. These values are reported as “hepatic flow distribution” (HFD). Further, to facilitate qualitative hemodynamic comparisons, the magnitude of viscous dissipation (i.e., μ|▽2V|; is viscosity, V is velocity) and 3D vortex core visualization (via iso-surfaces of the second invariant of the deformation matrix, Q)[21] were also used, where appropriate.
RESULTS
The resistance and HFD results are detailed in Tables 3 and 4, respectively, and summarized in Figure 2. For resistance, the YCPC group had the lowest average value. However, this trend was skewed by a single case (pt. 1) for whom there was a significant improvement in efficiency with the YCPC. For the remaining patients, there were only minor differences. The non-linear response to simulated exercise was consistent among the connections (Figure 2A).
Table 3.
Connection Resistance Summary [mmHg*min/L] at Rest and Exercise
| Rest | 2× | 3× | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Patient | YCPC | t-junction | Offset | YCPC | t-junction | Offset | YCPC | t-junction | Offset |
| Pt. 1 | 0.33 | 1.26 | 1.21 | 0.74 | 2.57 | 2.29 | 1.22 | 3.95 | 3.43 |
| Pt. 2 | 1.6 | 1.6 | 1.5 | 2.63 | 2.42 | 2.60 | 3.93 | 3.83 | 3.83 |
| Pt. 3 | 0.17 | 0.15 | 0.23 | 0.40 | 0.32 | 0.46 | 0.68 | 0.51 | 0.62 |
| Pt. 4 | 0.2 | 0.19 | 0.19 | 0.57 | 0.55 | 0.67 | 0.89 | 0.90 | 1.08 |
| Pt. 5 | 0.33 | 0.33 | 0.32 | 1.80 | 1.50 | 1.62 | 3.56 | 2.54 | 2.81 |
| Mean | 0.53 | 0.71 | 0.69 | 1.23 | 1.47 | 1.53 | 2.06 | 2.35 | 2.35 |
Table 4.
HFD Results [%LPA]
| Rest | 2× | 3× | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Patient | YCPC | t-junction | Offset | YCPC | t-junction | Offset | YCPC | t-junction | Offset |
| Pt. 1 | 70 | 65 | 42 | 51 | 56 | 38 | 47 | 52 | 42 |
| Pt. 2 | 32 | 16 | 4 | 30 | 14 | 9 | 30 | 24 | 20 |
| Pt. 3 | 49 | 57 | 28 | 45 | 47 | 42 | 44 | 43 | 41 |
| Pt. 4 | 52 | 46 | 35 | 58 | 56 | 60 | 66 | 65 | 69 |
| Pt. 5 | 49 | 31 | 100 | 58 | 56 | 82 | 62 | 60 | 76 |
| Mean | 51 | 43 | 42 | 49 | 46 | 46 | 50 | 49 | 49 |
| Standard Deviation | 14 | 20 | 36 | 12 | 18 | 27 | 15 | 16 | 23 |
Figure 2.
Mean, maximum, and minimum values of connection resistance (A) and flow distribution (B) for each connection (YCPC, TCPC, Offset) and flow condition (1×, 2×, 3×) investigated.
With respect to HFD under baseline conditions, the Y-grafts had the smallest range and standard deviation among all patients (Figure 2B). By comparison, the TCPC offset models had a range of almost 100%, denoting significant patient-to-patient variation. Additionally, while there is no accepted `optimal' value for HFD, the mean YCPC value (rest conditions) was closest to 50%, denoting desirable left/right balance.
Detailed Hemodynamic Analyses
As seen in Table 3 and Fig. 2A, the resistance values varied considerably among patients. Thus, rather than focusing on the absolute magnitude of power loss, we seek to identify the factor(s) that mediated energy dissipation differences for a given patient across connection types, to then identify possible means for improvement. Two trends were discernable: dissipation through local vessel constrictions (Figure 3), and dissipation resulting from complex mixing and recirculation (Figure 5).
Figure 3.
Comparison of YCPC and TCPC hemodynamics for patients 1 (A), 2 (B; representative image), and 5 (C). The resting velocity streamlines (top row), 3× velocity streamlines (middle row), and viscous dissipation contours (bottom row) are shown in each case.
Figure 5.
Velocity streamlines (a,d), vortex core isosurfaces (Q=800 (top), 13000 (bottom)) (b,e), and viscous dissipation contours localized to the vortex isosurfaces (c,f) for Patients 3 (top, rest) and 4 (bottom, 3×).
Figure 3 shows the resting (top) and 3× (middle) velocity streamlines, as well as resting viscous dissipation contours (bottom) for the YCPC and one TCPC option for Patients 1, 2, and 5. For Patient 1, there was a section of the LPA that was mildly stenotic, which resulted in significant convective acceleration and dissipation of LPA flow for both connections, even under resting conditions. However, the position of the left branch of the Y-graft helped to augment the size of the vessel, bypass the throat of the constriction, and reduce flow separation in the distal LPA (particularly with exercise), as compared to the t-junction results. These characteristics resulted in a significant reduction of the viscous losses (bottom row).
For patient 2 (Figure 3B), an acute stenosis in the LPA was again observed, except in this case it was distal to the Y-graft anastomosis. As a result, this patient consistently had among the highest resistance values in the study, irrespective of IVC baffle design (Figure 3, bottom row).
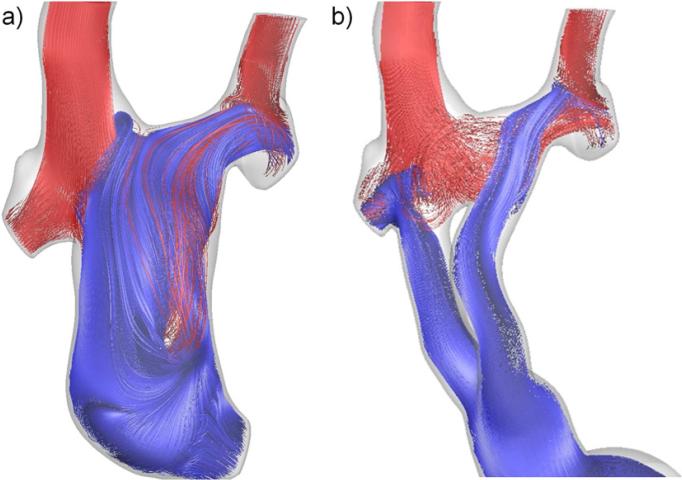
Patient 5 was unique in this series based on the presence of bilateral SVCs, and the use of numerical modeling to pre-operatively plan the procedure [22] and suggest surgical revision to a Y-graft. As seen in Figure 4a, the previous TCPC exhibited severely unbalanced HFD (blue) to the PAs (and thus right lung PAVMs developed) because of the unequal distribution of RSVC/LSVC flows (55% Qs vs. 21% Qs, respectively). In contrast, Figure 4b shows that the Y-graft delivers IVC flow to both PAs. With respect to energy efficiency, however, the extended length of the Y-graft conduit (Figure 1) caused significant acceleration and flow separation through the branches (Figure 3C) that increased energy losses.
Figure 4.
Streamlines color coded by vessel of origin (red-SVC, blue- IVC) for a) the Patient 5 offset TCPC (i.e., the failed connection prior to surgical revision) and b) the post-revision YCPC.
For the remaining two patients (3- top; 4- bottom), Figure 5 shows velocity streamlines (a) and coherent vortex cores (b; to facilitate appreciation of the complex flow recirculation). In these patients, both branches of the Y-graft were connected nearly perpendicularly to the PAs, resulting in significant flow recirculation at the anastomoses (arrow, Figure 5a). The vortex cores (fig. 5b) provide improved visualization of these rotational flow structures and show their expansive size. Rather than being local, contained phenomena, these vortices bilaterally originated in the high shear wake region distal to the IVC bifurcation and extended downstream into the PAs. As a result, figure 5c shows that local regions of relatively high energy dissipation (from the color contours) were created at multiple downstream locations adjacent to these cores because of the complex fluid motion.
DISCUSSION
This study, in conjunction with the clinical report of Kanter, et al.[8], clearly demonstrates that the surgical implementation of the Fontan Y-graft is feasible. The additional contribution of this work is the identification and elucidation of the hemodynamic implications associated with the characteristics of the surgical design. In other words, the use of a Y-graft does not necessarily imply that it is as optimally efficient as in idealized studies[5, 7]_ENREF_12. The following sections will analyze the numerically-derived 3D velocity fields in the context of the causative geometric design characteristics.
Hemodynamic Efficiency
The theoretical benefits of flow bifurcation in the cavopulmonary pathway originated with the experimental and numerical work of Soerensen et al.[5], in which the multiple bifurcations of the Optiflo were shown to outperform an idealized TCPC model. Rather than requiring a collision and 90° redirection of caval flows, the Optiflo eff iciently redirected flow, ensuring a smooth and streamlined transition to the PAs. Marsden et al. followed with a numerical investigation in patient-specific models, focusing only on the bifurcation of the IVC[7], demonstrating again the potential for energetic improvements.
These hypothetical gains were not realized in the present in vivo implementations. In four of the five cases, Y-graft resistance was approximately equal to the resistances of the virtual TCPC controls. Clearly, since this is the first attempt at systematic, Y-graft use for the Fontan procedure, a learning curve to optimize the surgical implementation should be anticipated. In that regard, it is promising that there is no evidence in this series of diminished early outcome. These results suggest that the YCPC may be `forgiving' enough to still be energetically equivalent to the TCPC when the design is theoretically sub-optimal. Yet, there is also clear evidence from at least one case, that the energetics can be better than the TCPC.
In that case (patient 1), the decreased resistance is attributable to the fact that the Y-graft position augmented and bypassed an acute stenosis in the LPA that was otherwise a significant resistive element. Given the recent report showing the prevalence of sub-aortic PA stenosis[23] in single ventricle patients (particularly those with hypoplastic left heart syndrome), this potential strength of the Y-graft is something to consider for targeted use. However, this specific application does not tap into the fundamental characteristics of the Y-graft that make it efficient.
One possible reason for the efficiency differences is the size selected for the Y-graft branches. Larger branches allow for lower fluid velocities and shear stresses[7]; however, they also impose increased spatial constraints, and are not available “off the shelf,” as the current grafts are. Without a pre-fabricated graft, the bifurcation must be constructed ad hoc, which creates an additional set of design variables and possible failure modes (e.g., thrombosis formation along additional suture lines). As such, a more pragmatic question to ask is, can the efficiency results be improved with the existing graft design to remove the need for pursuing size and construction alternatives?
A recent study by Yang et al. sought to parametrically optimize the Y-graft design (e.g., branch placement, angle, size, etc.)[6]. While, in theory, such an analysis would be helpful in directing surgical decision-making, insufficient mathematical constraint of the design variables limits the ability to translate those results into quantitative guidelines for surgical implementation. However, the demonstrated importance of tangential alignment of the bifurcation branches with the PA axis is a relevant message that was implicit in the original Optiflo design concept and provides an interesting perspective for the present results.
In this light, there were two primary shortcomings in these patient connections that limited hemodynamic efficiency and should be surgically addressed in future cases. The first was the near perpendicular angle of approach in most of the connections. This perpendicular connection creates a scenario in which the IVC flow enters the PA, impinges on the opposite (e.g., superior) vessel wall, and must undergo significant secondary recirculation to align with the PA axis of flow. As shown in Figure 5, this recirculation may create dissipative secondary flow structures that can extend to significant lengths downstream and decrease overall connection efficiency. Introducing an anterior curvature to the baffle may facilitate better angulation than a straight t-junction approach would allow. Beveling the distal ends of the graft is also suggested to achieve the efficiency benefits of a flared connection [24].
The second shortcoming was the close proximity or even medial (to the SVC) placement of the Y-graft branches, which allows for continued interaction and mixing between the caval flows. In the extreme case where one branch was positioned exactly opposite the SVC (as in patients 1 (fig 3A) and 4 (fig 5, bottom)), there is direct caval flow competition and the associated energy dissipation that a bifurcated design was intended to avoid. Placing the right branch distal to the right pulmonary upper lobe and the left branch immediately posterior to the ascending aorta provides the best means to avoid that scenario. Furthermore, positioning of the SVC at the Glenn stage could be adjusted in future Y-graft candidates to provide additional lateral space for the branches.
Importantly, these design factors are independent of graft size and, in fact, smaller branches would facilitate placement according to these guidelines. This provides additional support for the present choice in Y-graft design, and indicates that future studies should pursue these design optimization modifications before ultimately answering the Y-graft sizing question.
With regard to the originally posed hypothesis, this work shows that the Fontan Y-graft can be effectively used in certain scenarios. Yet, this fact neither proves nor disproves the hypothesis with respect to energy efficiency because the question remains: can the suggested modifications ensure that the `optimal' Fontan Y-graft is consistently realized under anatomic size constraints? The answer is likely to be patient-specific in that the position and size of the PA, pulmonary veins, SVC, and aorta are sure to be the critical determinants of whether or not the desired shape and position of the Y-graft is achievable. Herein lies a potential application for patient-specific simulation-based surgical planning techniques for Fontan surgery[22, 25], which could be used to both select candidates for favorable YCPC implementation and visually provide the target landmarks for branch placement.
Caval Flow Distribution
Balanced HFD is an important consideration to prevent the formation of PAVM[19]. There is a lack of evidence to indicate the minimum thresholds to prevent PAVM formation; however, a split at or around 50/50 is a desirable target. In considering the HFD values of the various connections evaluated in this series, there was no clinical significance in the mean differences (YCPC vs. t-junction vs. Offset), as 40% vs. 50% HFD would not impact the patient outcomes. However, the smaller variance across the YCPC results is noteworthy because it demonstrates improved consistency and stability of that design. By comparison, there were three instances with TCPCs that exhibited severely unbalanced HFD. So while, on average, the Y-graft may not significantly improve IVC flow distributions, these data suggest it could reduce the occurrence of outliers with poor streaming performance. Such outliers are far more prevalent in specific groups, such as cases of interrupted IVC[26], suggesting that these are additional patients who may benefit from targeted Y-graft use over extracardiac baffles [22, 25].
LIMITATIONS
The primary limitations of this study are the assumption of rigid walls, and the use of time-averaged boundary conditions for many of the simulations. Although such assumptions have a slight effect on the quantitative output of the simulations, they would have affected the various geometries similarly and are therefore unlikely to alter the comparative conclusions drawn. In addition, there is obviously a lack of long term clinical follow-up for this patient series to determine the implications of the simulated hemodynamics, yet the results are sufficiently encouraging to motivate such long-term follow-up. This is the first hemodynamic evaluation of the in vivo Fontan Y-graft and therefore, despite these limitations, there is still significant clinical value to be gained from the results presented.
CONCLUSIONS
In summary, the detailed hemodynamics of the Fontan Y-graft in an in vivo setting have been investigated for the first time under a variety of relevant flow conditions and with direct comparison to patient-specific TCPC controls. Desirable IVC-PA flow distribution characteristics were found; however, the flow efficiency performance fell short of the outcomes predicted by previous models. A beneficial comparison was found when the Y-graft was able to offset the effects of acute PA stenosis, making such situations a potential for targeted usage. Further, detailed analysis of the surgical Y-graft implementation with respect to the resulting flow fields was used to identify strategies for improving performance on a broader scale. Future studies will model these hypothesized improvements and characterize the performance gains to assess surgical feasibility of the `optimal' Y-graft design.
Acknowledgements
This study was supported by the National Heart, Lung, and Blood Institute Grants HL67622 and R01HL098252, and a Pre-Doctoral Fellowship Award (10PRE3720002) from the American Heart Association.
ABBREVIATIONS LIST
- TCPC
Total Cavopulmonary Connection
- IVC
Inferior Vena Cava
- SVC
Superior Vena Cava
- PA
Pulmonary Artery
- LPA
Left Pulmonary Artery
- RPA
Right Pulmonary Artery
- CMR
Cardiac Magnetic Resonance
- YCPC
Y-graft Cavopulmonary Connection
- HFD
Hepatic Flow Distribution
- PAVM
Pulmonary Arteriovenous Malformations
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].de Leval MR, Kilner P, Gewillig M, Bull C. Total cavopulmonary connection: A logical alternative to atriopulmonary connection for complex Fontan operations. Journal of Thoracic and Cardiovascular Surgery. 1988;96:682–95. [PubMed] [Google Scholar]
- [2].Sharma S, Goudy S, Walker P, Panchal S, Ensley A, Kanter K, et al. In Vitro Flow Experiments for Determination of Optimal Geometry of Total Cavopulmonary Connection for Surgical Repair of Children with Functional Single Ventricle. Journal of the American College of Cardiology. 1996;27:1264–1269. doi: 10.1016/0735-1097(95)00598-6. [DOI] [PubMed] [Google Scholar]
- [3].Marsden AL, Vignon-Clementel IE, Chan FP, Feinstein JA, Taylor CA. Effects of Exercise and Respiration on Hemodynamic Efficiency in CFD Simulations of the Total Cavopulmonary Connection. Annals of Biomedical Engineering. 2007;35:250–263. doi: 10.1007/s10439-006-9224-3. [DOI] [PubMed] [Google Scholar]
- [4].de Leval MR, Dubini G, Migliavacca F, Jalali H, Camporini G, Redington A, et al. Use of computational fluid dynamics in the design of surgical procedures: Application to the study of competitive flows in cavopulmonary connections. The Journal of Thoracic and Cardiovascular Surgery. 1996;111:502–513. doi: 10.1016/s0022-5223(96)70302-1. [DOI] [PubMed] [Google Scholar]
- [5].Soerensen DD, Pekkan K, de Zelicourt D, Sharma S, Kanter K, Fogel M, et al. Introduction of a New Optimized Total Cavopulmonary Connection. Annals of Thoracic Surgery. 2007;83:2182–2190. doi: 10.1016/j.athoracsur.2006.12.079. [DOI] [PubMed] [Google Scholar]
- [6].Yang W, Feinstein JA, Marsden AL. Constrained optimization of an idealized Y-shaped baffle for the Fontan surgery at rest and exercise. Computer Methods in Applied Mechanics and Engineering. 2010;199:2135–2149. [Google Scholar]
- [7].Marsden AL, Bernstein AJ, Reddy VM, Shadden SC, Spilker RL, Chan FP, et al. Evaluation of a novel Y-shaped extracardiac Fontan baffle using computational fluid dynamics. Journal of Thoracic and Cardiovascular Surgery. 2009;137:394–403. doi: 10.1016/j.jtcvs.2008.06.043. [DOI] [PubMed] [Google Scholar]
- [8].Kanter KR, Haggerty CM, Restrepo M, de Zelicourt D, Rossignac J, Parks WJ, et al. Preliminary Clinical Experience with a Bifurcated Y-Graft Fontan Procedure (ABSTRACT). Western Thoracic Surgical Association 37th Annual Meeting; 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Frakes DH, Conrad CP, Healy TM, Monaco JW, Fogel M, Sharma S, et al. Application of an adaptive control grid interpolation technique to morphological vascular reconstruction. IEEE Trans Biomed Eng. 2003;50:197–206. doi: 10.1109/TBME.2002.807651. [DOI] [PubMed] [Google Scholar]
- [10].Sundareswaran K, Frakes D, Fogel M, Soerensen D, Oshinski JN, Yoganathan A. Optimum fuzzy filters for phase-contrast magnetic resonance imaging segmentation. Journal of Magnetic Resonance Imaging. 2009;29:155–165. doi: 10.1002/jmri.21579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Pekkan K, Whited B, Kanter K, Sharma S, de Zelicourt D, Sundareswaran K, et al. Patient-specific surgical planning and hemodynamic computational fluid dynamics optimization through free-form haptic anatomy editing tool (SURGEM) Med Biol Eng Comput. 2008;46:1139–52. doi: 10.1007/s11517-008-0377-0. [DOI] [PubMed] [Google Scholar]
- [12].Ge L, Sotiropoulos F. A numerical method for solving the 3d unsteady incompressible navier-stokes equations in curvilinear domains with complex immersed boundaries. Journal of Computational Physics. 2007;225:1782–1809. doi: 10.1016/j.jcp.2007.02.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].de Zélicourt D, Ge L, Wang C, Sotiropoulos F, Gilmanov A, Yoganathan AP. Flow Simulations in Arbitrarily Complex Cardiovascular Anatomies - an Unstructured Cartesian Grid Approach. Computers & Fluids. 2009;38:1749–1762. [Google Scholar]
- [14].Rosenthal M, Bush A, Deanfield J, Redington A. Comparison of Cardiopulmonary Adaptation During Exercise in Children After the Atriopulmonary and Total Cavopulmonary Connection Fontan Procedures. Circulation. 1995;91:372–378. doi: 10.1161/01.cir.91.2.372. [DOI] [PubMed] [Google Scholar]
- [15].Shachar G, Fuhrman B, Wang Y, Lucas RJ, Lock J. Rest and exercise hemodynamics after the Fontan procedure. Circulation. 1982;65:1043–1048. doi: 10.1161/01.cir.65.6.1043. [DOI] [PubMed] [Google Scholar]
- [16].Whitehead KK, Pekkan K, Kitajima HD, Paridon SM, Yoganathan AP, Fogel MA. Nonlinear power loss during exercise in single-ventricle patients after the Fontan: insights from computational fluid dynamics. Circulation. 2007;116:I165–71. doi: 10.1161/CIRCULATIONAHA.106.680827. [DOI] [PubMed] [Google Scholar]
- [17].Sundareswaran KS, Pekkan K, Dasi LP, Whitehead K, Sharma S, Kanter K, et al. The total cavopulmonary connection resistance: a significant impact on single ventricle hemodynamics at rest and exercise. American Journal of Physiology Heart and Circulatory Physiology. 2008;295:H2427–H2435. doi: 10.1152/ajpheart.00628.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Pedersen EM, Stenbog EV, Frund T, Houlind K, Kromann O, Sorensen KE, et al. Flow during exercise in the total cavopulmonary connection measured by magnetic resonance velocity mapping. Heart. 2002;87:554–8. doi: 10.1136/heart.87.6.554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Duncan B, Desai S. Pulmonary arteriovenous malformations after cavopulmonary anastomosis. Annals of Thoracic Surgery. 2003;76:1759–1766. doi: 10.1016/s0003-4975(03)00450-8. [DOI] [PubMed] [Google Scholar]
- [20].Dasi LP, Whitehead K, Pekkan K, de Zelicourt D, Sundareswaran K, Kanter K, et al. Pulmonary hepatic flow distribution in total cavopulmonary connections: Extracardiac versus intracardiac. The Journal of thoracic and cardiovascular surgery. 2011;141:207–214. doi: 10.1016/j.jtcvs.2010.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Hunt JCR, Wray AA, Moin P. Eddies, stream, and convergence zones in turbulent flows. Center for Turbulence Research Report CTR-S88. 1988;193 [Google Scholar]
- [22].De Zelicourt D, Haggerty CM, Sundareswaran KS, Whited B, Rossignac J, Kanter K, et al. Individualized Computer-Based Surgical Planning to Address Pulmonary Ateriovenous Malformations in Patients with a Single Ventricle with an Interrupted Inferior Vena Cava and Azygous Continuation. Journal of Thoracic and Cardiovascular Surgery. 2011;141:1170–1177. doi: 10.1016/j.jtcvs.2010.11.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Dasi LP, Sundareswaran KS, Sherwin C, de Zelicourt D, Kanter KR, Fogel MA, et al. Larger aortic reconstruction corresponds to diminished left pulmonary artery size in patients with single ventricle phyisology. Journal of Thoracic and Cardiovascular Surgery. 2010;139:557–561. doi: 10.1016/j.jtcvs.2009.08.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Ensley A, Lynch P, Chatzimavroudis GP, Lucas CL, Sharma S, Yoganathan AP. Toward Designing the Optimal Total Cavopulmonary Connection: An In Vitro Study. Annals of Thoracic Surgery. 1999;68:1384–1390. doi: 10.1016/s0003-4975(99)00560-3. [DOI] [PubMed] [Google Scholar]
- [25].Sundareswaran K, de Zélicourt D, Sharma S, Kanter K, Spray T, Rossignac JR, et al. Correction of pulmonary arteriovenous malformation using image based surgical planning. JACC Imaging. 2009;2:1024–1030. doi: 10.1016/j.jcmg.2009.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].McElhinney DB, Marx GR, Marshall AC, Mayer JEJ, del Nido P. Cavopulmonary pathway modification in patients with heterotaxy and newly diagnosed or persistent pulmonary arteriovenous malformations after a modified Fontan operation. Journal of Thoracic and Cardiovascular Surgery. 2011;131:1362–1370. doi: 10.1016/j.jtcvs.2010.08.088. [DOI] [PubMed] [Google Scholar]