Sensory motor remapping of space in human–machine interfaces

Abstract

Studies of adaptation to patterns of deterministic forces have revealed the ability of the motor control system to form and use predictive representations of the environment. These studies have also pointed out that adaptation to novel dynamics is aimed at preserving the trajectories of a controlled endpoint, either the hand of a subject or a transported object. We review some of these experiments and present more recent studies aimed at understanding how the motor system forms representations of the physical space in which actions take place. An extensive line of investigations in visual information processing has dealt with the issue of how the Euclidean properties of space are recovered from visual signals that do not appear to possess these properties. The same question is addressed here in the context of motor behavior and motor learning by observing how people remap hand gestures and body motions that control the state of an external device. We present some theoretical considerations and experimental evidence about the ability of the nervous system to create novel patterns of coordination that are consistent with the representation of extrapersonal space. We also discuss the perspective of endowing human–machine interfaces with learning algorithms that, combined with human learning, may facilitate the control of powered wheelchairs and other assistive devices.

Introduction

Human–machine interfaces (HMIs) come in several different forms. Sensory interfaces transform sounds into cochlear stimuli (Loeb, 1990), images into phosphenene-inducing stimuli to the visual cortex (Zrenner, 2002), or into electrical stimuli to the tongue (Bach-y-Rita, 1999). Various attempts, old and recent, have aimed at the artificial generation of proprioceptive sensation by stimulating the somatosensory cortex (Houweling and Brecht, 2007; Libet et al., 1964; Romo et al., 2000). Motor interfaces may transform electromyographic (EMG) signals into commands for a prosthetic limb (Kuiken et al., 2009), electroencephalogram (EEG) signals into characters on a computer screen, multi-unit recordings from cortical areas into a moving cursor (Wolpaw and McFarland, 2004), or upper body movements into commands for a wheelchair (Casadio et al., 2010).

Sensory and motor interfaces both implement novel transformations between the external physical world and internal neural representations. In a sensory interface, neural representations result in perceptions. In a motor interface, the neural representations reflect movement goals, plans, and commands. In a motor HMI, the problem of forming a functional map between neural signals and external environment is similar to remapping problems studied in earlier works, focused on the adaptation to force fields (Lackner and Dizio, 1994; Shadmehr and Mussa-Ivaldi, 1994) and dynamical loads. There, the environment imposed a transformation upon the relationship between the state of motion of the arm and forces experienced at the hand. The neural representation that formed through learning was an image in the brain of this new external relation in the environment. This image allows the brain to recover a desired movement of the hand by counteracting the disturbing force. Here, we take a step toward a more fundamental understanding of how space, “ordinary” space, is remapped through motor learning.

Motor learning

Recently, a simple and powerful idea has changed our view of motor learning. Motor learning is not only a process in which one improves performance in a particular act. Rather, it is a process through which the brain acquires knowledge about the environment. However, this is not the ordinary kind of knowledge (explicit knowledge) such as when we learn an equation or a historical fact. It is implicit knowledge that may not reach our consciousness, and yet it informs and influences our behaviors, especially those expressed in the presence of a novel situation. The current focus of most motor learning studies is on “generalization”; that is, on how experience determines behavior beyond what one has been exposed to. The mathematical framework for the concept of generalization comes from statistical theory (Poggio and Smale, 2003), where data points and some a priori knowledge determine the value of a function at new locations. If the new location is within the domain of the data, we have the problem of interpolation, whose solutions are generally more reliable than those of extrapolation problems, that is, when the predictions are made outside the domain of the data.

In the early 1980s, Morasso (1981) and Soechting and Lacquaniti (1981) independently made the deceivingly simple observation that when we reach to a target, our hands tend to move along quasi-rectilinear pathways, following bell-shaped speed profiles. This simplicity or “regularity” of movement is evident only when one considers motion of the hand: In contrast, the shoulder and elbow joints engage in coordinated patterns of rotations that may or may not include reversals in the sign of angular velocities depending on the direction of movement. These observations gave rise to an intense debate between two views. One view suggested that the brain deliberately plans the shape of hand trajectories and coordinates muscle activities and joint motions accordingly (Flash and Hogan, 1985; Morasso, 1981). The opposing view suggested that the shape of the observed kinematics is a side effect of dynamic optimization (Uno et al., 1989), such as the minimization of the rate of change of torque.

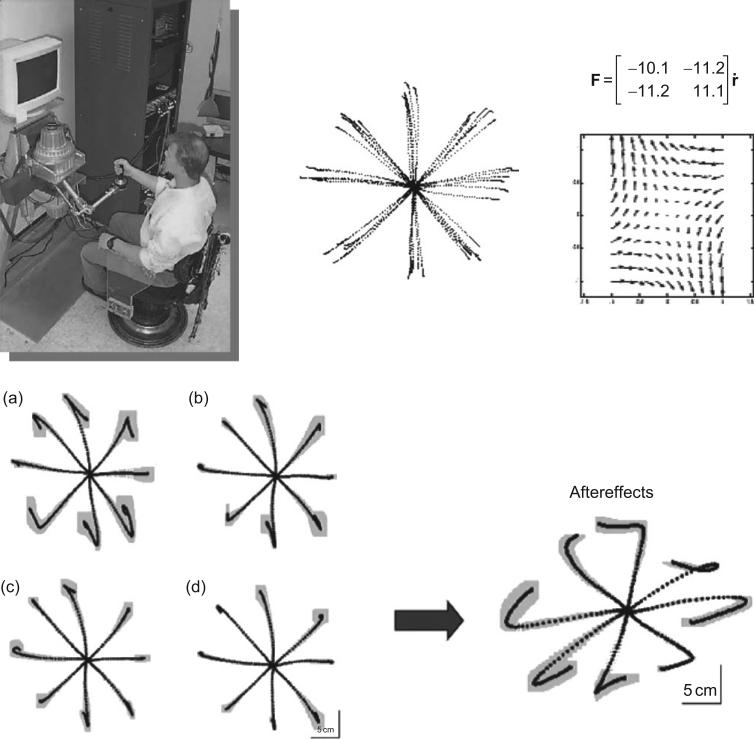
By considering how the brain learns to perform reaching movements in the presence of perturbing forces (Lackner and Dizio, 1994; Shadmehr and Mussa-Ivaldi, 1994), studies of motor adaptation to force fields provided a means to address, if not completely resolve, this debate. Such studies have two key features in common. First, perturbing forces were not applied randomly but instead followed some strict deterministic rule. This rule established a force field wherein the amount and direction of the external force depended upon the state of motion of the hand (i.e., its position and velocity). The second important element is that subjects were typically instructed to move their hand to some target locations but were not instructed on what path the hand should have followed. If the trajectory followed by the hand to reach a target were the side effect of a process that seeks to optimize a dynamic quantity such as the muscle force or the change in joint torque rate, then moving against a force field would lead to systematically different trajectories than if hand path kinematics were deliberately planned. Contrary to the dynamic optimization prediction, many force-field adaptation experiments have shown that after an initial disturbance to the trajectory, the hand returns to its original straight motion (Fig. 1). Moreover, if the field is suddenly removed, an aftereffect is transiently observed demonstrating that at least a portion of the response is a preplanned (feedforward) compensatory response.

Fig. 1.

Adaptation of arm movements to an external force field. Top-left: Experimental apparatus. The subject holds the handle of a two-joint robot manipulandum. Targets are presented on a computer monitor, together with a cursor representing the position of the hand. Top-middle: unperturbed trajectories, observed at the beginning of the experiment, with the motors turned off. Top-right: velocity-dependent force field. The perturbing force is a linear function of the instantaneous hand velocity. In this case, the transfer matrix has a negative (stable) and a positive (unstable) eigenvalue. The force pattern in the space of hand velocity is shown under the equation. At the center (zero velocity) the force is zero. Bottom-left panels (A–D): evolution of hand trajectories in four successive epochs, while the subject practiced moving against the force field. The trajectories are averaged over repeated trials. The gray shadow is the standard deviation. In the final set, the trajectories are similar to those executed before the perturbation was turned on. Bottom-right: Aftereffects observed when the field was unexpectedly turned off at the end of training (modified from Shadmehr and Mussa-Ivaldi, 1994).

Importantly, Dingwell et al. (2002, 2004) observed similar adaptations when subjects controlled the movement of a virtual mass connected to the hand via a simulated spring. In this case, adaptation led to rectilinear motions of the virtual mass and more complex movements of the hand. These findings demonstrate that the trajectory of the controlled “endpoint”—whether the hand or a hand-held object—is not a side effect of some dynamic optimization. Instead, endpoint trajectories reflect explicit kinematic goals. As we discuss next, these goals reflect the geometrical properties of the space in which we move.

What is “ordinary space”?

We form an intuitive understanding of the environment in which we move through our sensory and motor experiences. But what does it mean to have knowledge of something as fundamental as space itself? Scientists and engineers have developed general mathematical notions of space. They refer to “signal space” or “configuration space.” These are all generalizations of the more ordinary concept of space. If we have three signals, for example, the surface EMG activities measured over three muscles, we can form a three-dimensional (3D) Cartesian space with three axes, each representing the magnitude of EMG activity measured over one muscle. Together, the measured EMG signals map onto a single point moving in time along a trajectory through this 3D space. While this mapping provides us with an intuitive data visualization technique, signal spaces are not typically equivalent to the physical space around us, the so-called ordinary space. In particular, ordinary space has a special property not shared by all signal spaces. In the ordinary space, the rules of Euclidean geometry and, among these Pythagoras’ theorem, support a rigorous and meaningful definition of both the minimum distance between two points (the definition of vector length) and the angle between two such vectors. Although we can draw a line joining two points in the EMG space described above, the distance between EMG points will carry little meaning. Moreover, what it means to “rotate” EMG signals by a given angle in this space is even less clear.¹

Euclidean properties of ordinary space

The ordinary space within which we move is Euclidean (a special kind of inner product space). The defining feature of a Euclidean space is that basic operations performed on vectors in one region of space (e.g., addition, multiplication by a scalar) yield identical results in all other regions of space. That is, Euclidean space is flat, not curved like Riemannian spaces: if a stick measures 1 m in one region of Euclidean space, then it measures 1 m in all other regions of space. Although length and distance can be calculated in many ways, there is only one distance measure—the “Euclidean norm”—that satisfies Pythagoras’ theorem (a necessary condition for the norm to arise from the application of an inner product). The Euclidean norm is the distance measure we obtain by adding the squares of the projections of the line joining the two points over orthogonal axes. So, if we represent a point A in an N-dimensional space as a vector a=[a₁, a₂,. . .,a_N]^T and a point B as a vector b=[b₁, b₂,. . .,b_N]^T, then the Euclidean distance between a and b is

$$\text{dist}(\mathbf{a},\mathbf{b})=\sqrt{{(\mathbf{a}-\mathbf{b})}^{\mathrm{T}}\cdot (\mathbf{a}-\mathbf{b})}=\sqrt{{(a_1-b_1)}^2+{(a_2-b_2)}^2+\cdots +{(a_N-b_N)}^2}$$ (1)

We are familiar with this distance in 2D and 3D space. But the definition of Euclidean distance is readily extended to N dimensions. The crucial feature of this metric, and this metric only, is that distances are conserved when the points in space are subject to any transformation of the Euclidean group, including rotations, reflections, and translations. The invariance by translations of the origin is immediately seen. Rotations and reflections are represented by orthogonal matrices that satisfy the condition

$${\mathbf{R}}^{\mathrm{T}}\cdot \mathbf{R}=I$$ (2)

(i.e., the inverse of an orthogonal matrix is its transpose). For example, if we rotate a line segment by R, the new distance in Euclidean space is equal to the old distance, since

$$\begin{array}{cc}\hfill \sqrt{{[\mathbf{R}\cdot (\mathbf{a}-\mathbf{b})]}^{\mathbf{T}}\cdot \mathbf{R}(\mathbf{a}-\mathbf{b})}& =\sqrt{{(\mathbf{a}-\mathbf{b})}^{\mathbf{T}}\cdot {\mathbf{R}}^{\mathbf{T}}\cdot \mathbf{R}(\mathbf{a}-\mathbf{b})}\hfill \\ \hfill & =\sqrt{{(\mathbf{a}-\mathbf{b})}^{\mathbf{T}}\cdot (\mathbf{a}-\mathbf{b})}\hfill \end{array}$$ (3)

In summary, in the ordinary Euclidean space:

1. Distances between points obey Pythagoras’ theorem and are calculated by a sum of squares.

2. Distances (and therefore the size of objects) do not change with translations, rotations, and reflections. Or, stated otherwise, vector direction and magnitude are mutually independent entities.

Intrinsic geometry of sensorimotor signals in the central nervous system

Sensory and motor signals in the nervous system appear to be endowed with neither of the above two properties with respect to the space within which we move. For example, the EMG activities giving rise to movement of our hand would generally change if we execute another movement in the same direction and with the same amplitude starting from a new location. Likewise, the firing rates of limb proprioceptors undoubtedly change if we make a movement with the same amplitude from the same starting location, but now oriented in a different direction. Nevertheless, we easily move our hand any desired distance along any desired direction from any starting point inside the reachable workspace. It therefore seems safe to conclude that our brains are competent to understand and represent the Euclidean properties of space and that our motor systems are able to organize coordination according to these properties. From this perspective, the observation of rectilinear and smooth hand trajectories has a simple interpretation. Straight segments are natural geometrical primitives of Euclidean spaces: they are geodesics (i.e., paths of minimum length). The essential hypothesis, then, is that the brain constructs and preserves patterns of coordination that are consistent with the geometrical features of the environment in which it operates.

Encoding the metric properties of Euclidean space

Early studies of adaptation of reaching movements to force fields demonstrated the stability of planned kinematics in the face of dynamical perturbations (Shadmehr and Mussa-Ivaldi, 1994), suggesting that the brain develops an internal representation of the dynamics of the limb and its environment, which it uses to plan upcoming movements. The observation that subjects preferentially generate straight-line endpoint motions (Dingwell et al., 2002, 2004) further suggests that the nervous system also develops an internal representation of the environment within which movement occurs. Both representations are necessary to support the kind of learning involved in the operation of HMIs: Different HMIs require their users to learn the geometrical transformation from a set of internal signals endowed with specific metric properties (EEGs, multiunit activities, residual body motions, etc.) into control variables that drive a physical system with potentially significant dynamics (the orientation of a robotic arm, the position of a cursor, the speed and direction of a wheelchair, etc.). We next describe experiments that sought to test whether the brain constructs and preserves patterns of coordination consistent with the geometrical features of the environment using a noninvasive experimental approach with immediate relevance to the application of adaptive control in HMIs.

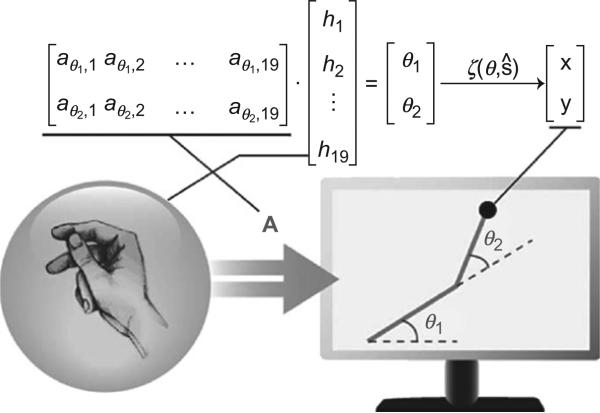
Mosier et al. (2005) and colleagues (Liu and Scheidt, 2008; Liu et al., 2011) studied how subjects learn to remap hand gestures for controlling the motion of a cursor on a computer screen. In their experiments, subjects wore a data glove and sat in front of a computer monitor. A linear transformation A mapped 19 sensor signals from the data glove into two coordinates of a cursor on a computer screen:

$$\mathbf{P}=\left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right]=\left[\begin{array}{ccccc}\hfill a_{x,1}\hfill & \hfill a_{x,2}\hfill & \hfill \dots \hfill & \hfill a_{x,19}\hfill & \hfill x_0\hfill \\ \hfill a_{y,1}\hfill & \hfill a_{y,2}\hfill & \hfill \dots \hfill & \hfill a_{y,19}\hfill & \hfill y_0\hfill \end{array}\right]\cdot {\left[h_1{h}_2\dots h_{19}1\right]}^{\mathbf{T}}=\mathbf{A}\cdot \mathbf{H}$$ (4)

Subjects were required to smoothly transition between hand gestures so as to reach a set of targets on the monitor. This task had some relevant features, namely:

1. It was an unusual task. It was practically impossible that a subject had previous exposure to the transformation from hand gestures to cursor positions.

2. The hand and the cursor were physically uncoupled. Vision was therefore the only source of feedback information about the movement of the cursor available to the subjects.

3. There was a dimensional imbalance between the degrees of freedom of the controlled cursor (2) and the degrees of freedom of the hand gestures measured by the data glove (19).

4. Most importantly, there was a mismatch between the metric properties of the space in which the cursor moves and the space of the hand gestures. Specifically, the computer monitor defines a 2D Euclidean space with a well-defined concept of distance between points, whereas there is no clear metric structure for hand gestures.

These features are shared by brain–machine interfaces that map neural signals into the screen coordinates of a computer cursor or the 3D position of a robotic arm. The hand-shaping task provides a simple noninvasive paradigm wherein one can understand and address the computational and learning challenges of brain–machine interfaces.

Learning an inverse geometrical model of space

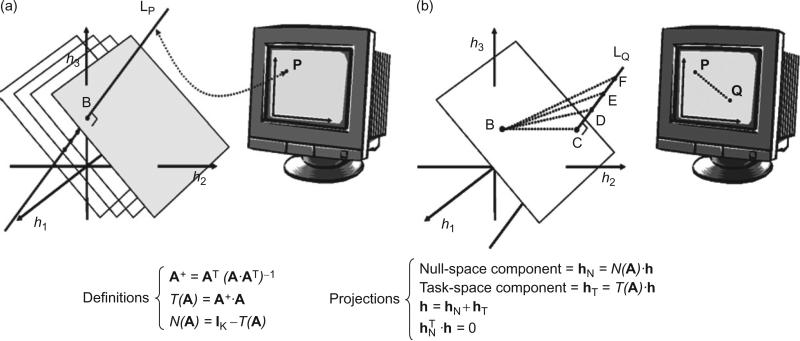
A linear mapping A from data-glove “control” signals to the two coordinates of the cursor creates a natural partition of the glove-signal space into two complementary subspaces. One is the 2D (x, y) task-space within which the cursor moves, H_T=A⁺AH [where A⁺ = A^T·(A·A^T)^–1 is the Moore–Penrose (MP) pseudoinverse of A]. The second is its 17D null-space, H_N = (I₁₉ – A^þA)H (where I₁₉ is the 19D identity matrix), which is everywhere orthogonal to the task-space (Fig. 2). Note that both task- and null-spaces are embedded in 19 dimensions. Given a point on the screen, the null-space of that point contains all glove-signal configurations that project onto that point under the mapping A (i.e., the null-space of a cursor position is the inverse image of that position under the hand-to-cursor linear map). Consider a hand gesture that generates a glove-signal vector B and suppose that this vector maps onto cursor position P. Because of the mismatch in dimensionality between the data-glove signal and cursor vectors (often referred to as “redundancy of control”), one can reach a new position Q in an infinite number of ways.

Fig. 2.

Geometrical representation. (a) The “hand space,” H, is represented in reduced dimension as a 3D space. The matrix, A, establishes a linear map from three glove signals to a 2D computer monitor. T(A) and N(A) are the task-space and the null-space of A. The line, L_P, contains all the points in H that map onto the same point P on the screen. This line is the “null-space” of A at P. A continuous family of parallel planes, all perpendicular to the null-space and each representing the screen space, fills the entire signal space. (b) The starting hand configuration, B, lies on a particular plane in H and maps to the cursor position, P. All the dotted lines in H leading from B to L_Q produce the line shown on the monitor. The “null-space component” of a movement guiding the cursor from P to Q is its projection along L_Q. The “task-space component” is the projection on the plane containing BC. Bottom: The mathematical derivation of the null-space and task-space components generated by the transformation matrix A (from Mussa-Ivaldi and Danziger, 2009).

In Fig. 2, the glove-signal space is depicted as a simplified 3D space. In this case, the null-space at q is a line (because 3 signal dimensions –2 monitor dimensions = 1 null-space dimension). Thus, one can reach Q with any configuration (C, D, E, F, etc.) on this line. However, the configuration C is special because it lies within the task-space including B and thus, the movement BC is the movement with the smallest Euclidean norm (in the glove-signal space). In this simplified representation, the hand-to-cursor linear map partitions the signal space into a family of parallel planes orthogonal at each point to the corresponding null-space. While visualizing this in more than three dimensions is impossible, the geometrical representation remains generally correct and insightful.

Consider now the problem facing the subjects in the experiments of Mosier et al. (2005). Subjects were presented with a target on the screen and were required to shape their hand so that the cursor could reach the target as quickly and accurately as possible. A number of investigators have proposed that in natural movements, the brain exploits kinematic redundancy for achieving its goal with the highest possible precision in task-relevant dimensions. Redundancy would allow disregarding performance variability in degrees of freedom that do not affect performance in task-space. This is a venerable theory, first published by Bernstein (1967) and more recently formalized as the “uncontrolled manifold” theory (Latash et al., 2001, 2002; Scholz and Schoner, 1999) and as “optimal feedback control” (Todorov and Jordan, 2002). These different formulations share the prediction that the motor system will transfers motor variability (or motor noise) to glove-signal degrees of freedom that do not affect the goal, so that performance variability at the goal—that is, at the target—is kept at a minimum. This is not a mere speculation; in a number of empirical cases the prediction matches observed behavior, as in Bernstein's example of hitting a nail with a hammer. However, in the experiments of Mosier et al. (2005) things turned out differently. As subjects became expert in the task of moving the cursor by shaping their hand, they displayed three significant trends with practice that were spontaneous and not explicitly instructed:

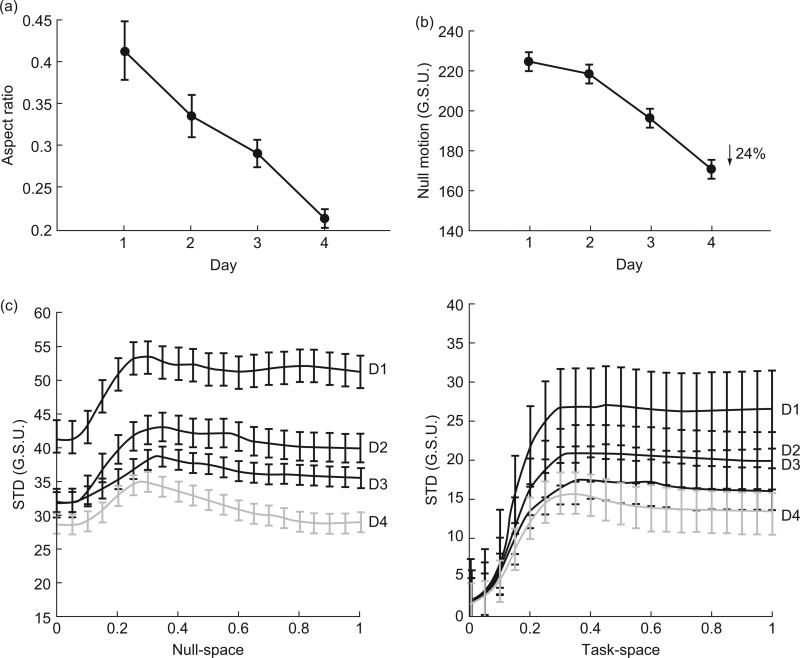
1. They executed increasingly straighter trajectories in task-space (Fig. 3a).

2. They reduced the amount of motion in the null-space of the hand-to-cursor map (Fig. 3b).

3. They reduced variability of motion in both the null-space and the task-space (Fig. 3c).

Fig. 3.

Behavioral results of the hand-to-cursor mapping experiment. (a) Subjects execute progressively straighter trajectories of the cursor on the screen. This is measured by the aspect ratio, the maximum perpendicular excursion from the straight-line segment joining the start and end of the movement divided by the length of that line segment. The aspect ratio of perfectly straight lines is zero. (b) Length of subject movements in the null-space of the task, hand motion that does not contribute to cursor movement, decreases through training. (c) Average variability of hand movements over four consecutive days (D1, D2, D3, D4). Left: average standard deviation across subjects of the null-space component over the course of a single movement. Right: average standard deviation across subjects of the task-space component over a single movement. Standard deviations are in glove-signal units (G.S.U.), that is, the numerical values generated by the CyberGlove sensors, each ranging between 0 and 255. The x axes units are normalized time (0: movement start; 1: movement end). The overall variance decreases with practice both in the task- and in the null-space (from Mosier et al., 2005).

Taken together, these three observations suggest that during training, subjects were learning an inverse geometric model of task-space. Consider that among all the possible right inverses of A, the MP pseudoinverse

$${\mathbf{A}}^{+}={\mathbf{A}}^{\mathbf{T}}\cdot {(\mathbf{A}\cdot {\mathbf{A}}^{\mathbf{T}})}^{-1}$$ (5)

selects the glove-signal solution with minimum Euclidean norm. This is the norm calculated as a sum of squares:

$$\Vert \mathbf{h}\Vert =\sqrt{h_1^2+h_2^2+\cdots +h_{19}^2}$$ (6)

Passing through each point B in the signal space (Fig. 2), there is one and only one 2D plane that contains all inverse images of the points in the screen that are at a minimum Euclidean distance from B. The subjects in the experiment of Mosier et al. (2005) demonstrated a learning trend to move over these planes and to reduce the variance orthogonal to them—both at the targets and along the movement trajectory. We consider this to be evidence that the learning process is not only driven by the explicit goal of reaching the targets but also by the goal of forming an inverse model of the target space and its metric properties. This internal representation of space is essential to generalize learning beyond the training set.

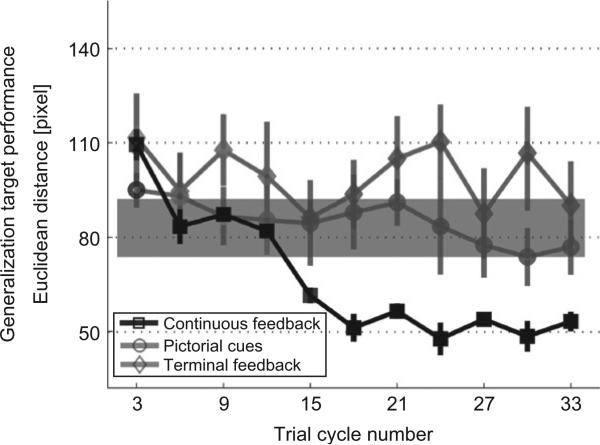
In a second set of experiments, Liu and Scheidt (2008) controlled the type and amount of task-related visual feedback available to different groups of subjects as they learned to move the cursor using finger motions. Subjects rapidly learned to associate certain screen locations with desired hand shapes when cued by small pictures of hand postures at screen locations defined by the mapping A. Although these subjects were also competent to form the gestures with minimal error when cued by simple spatial targets (small discs at the same locations as the pictures), they failed to generalize this learning to untrained target locations (pictorial cue group; Fig. 4). Subjects in a second group also learned to reduce task-space errors when provided with knowledge of results in the form of a static display of final cursor position at the end of each movement; however, this learning also failed to generalize beyond the training target set (terminal feedback group; Fig. 4). Only subjects provided with continuous visual feedback of cursor motion learned to generalize beyond their training set (continuous feedback group; Fig. 4) and so, visual feedback of endpoint motion appears necessary for learning an inverse geometrical model of the space of cursor motion. Of all the feedback conditions tested, only continuous visual feedback provides explicit gradient information that can facilitate estimation of an inverse model B̂ of the hand-to-screen mapping A.

Fig. 4.

The ability to generalize beyond the trained target set depends on the type and amount of task-related visual feedback available during practice in moving the cursor using finger motions. Subjects performed 33 cycles of six movements, wherein a cycle consisted of one movement to each of five training targets (performed with visual feedback) plus a movement to one of three generalization targets (performed entirely without visual feedback). Each generalization target was visited once every three cycles. Each trace represents the across-subject average generalization error for subjects provided with continuous visual feedback of target capture errors (black squares), subjects provided with feedback of terminal target capture errors only (gray diamonds), and subjects provided with pictorial cues of desired hand shapes (gray circles). Error bars represent ± 1 SEM. We evaluated whether performance gains in generalization trials were consistent with the learning of an inverse hand-to-screen mapping or whether the different training conditions might have promoted another form of learning, such as the formation of associations between endpoint targets and hand gestures projecting onto them (i.e., a look-up table). Look-up table performance was computed as the across-subject average of the mean distance between the three generalization targets and their nearest training target on the screen. Because each subject's A matrix was unique, the locations of generalization and training targets varied slightly from one subject to the next. The gray band indicates the predicted mean ± 1 SD look-up table performance. Only those subjects provided with continuous visual feedback of cursor motion demonstrated generalization performance consistent with learning an inverse map of task-space (adapted from Liu and Scheidt, 2008).

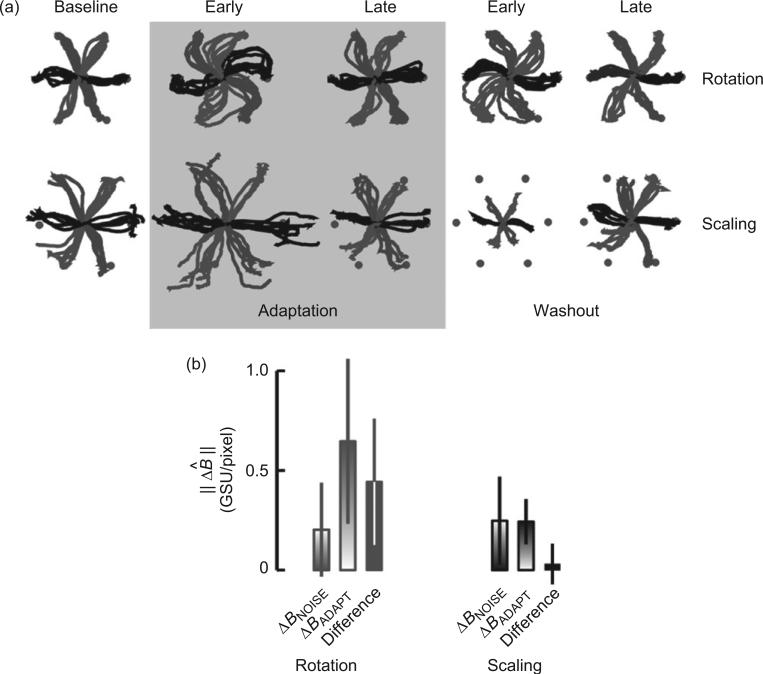
Liu and colleagues further examined the learning of an inverse geometric representation of task-space by studying how subjects reorganize finger coordination patterns while adapting to rotation and scaling distortions of a newly learned hand-to-screen mapping (Liu et al., 2011). After learning a common hand-to-screen mapping A by practicing a target capture task on one day and refreshing that learning early on the next day, subjects were then exposed to either a rotation θ of cursor motion about the origin (T_R):

$${\mathbf{P}}_{\mathbf{T}}=\left[\begin{array}{c}\hfill x_{\text{rotated}}\hfill \\ \hfill y_{\text{rotated}}\hfill \end{array}\right]={\mathbf{T}}_{\mathbf{R}}\mathbf{P}=\left[\begin{array}{cc}\text{cos}\left(\theta \right)\hfill & -\text{sin}\left(\theta \right)\hfill \\ \text{sin}\left(\theta \right)\hfill & \text{cos}\left(\theta \right)\hfill \end{array}\right]\left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right]$$ (7)

or a scaling k of cursor motion in task-space (T_S):

$${\mathbf{P}}_{\mathbf{T}}=\left[\begin{array}{c}\hfill x_{\text{scaled}}\hfill \\ \hfill y_{\text{scaled}}\hfill \end{array}\right]={\mathbf{T}}_{\mathbf{S}}\mathbf{P}\left[\begin{array}{cc}\hfill k\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill k\hfill \end{array}\right]\left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right]$$ (8)

The distortion parameters θ and k were selected such that uncorrected error magnitudes were identical on initial application of T in both cases. The question Liu and colleagues asked was whether step-wise application of the two task-space distortions would induce similar or different reorganization of finger movements. Both distortions required a simple reweighting of the finger coordination patterns acquired during initial learning of A (Fig. 5a), while neither required reorganization of null-space behavior.

Fig. 5.

Adaptation to rotation and scaling distortions of task-space 1 day after initially learning the manual target capture task. (a) Patterns of cursor trajectory errors are similar to those typically observed in studies of horizontal planar reaching with the arm. Here, we show data from representative subjects exposed to a ROTATION (top) or SCALING (bottom) of task-space during baseline (left) adaptation (early and late) as well as washout (early and late) blocks of trials. Shading indicates the adaptation block of trials. During preadaptation practice with the baseline map, cursor trajectories were well directed to the target. Imposing the step-wise counterclockwise (CCW) rotation caused cursor trajectories to deviate CCW initially but later “hook back” to the desired final position (Fig. 4a, top). With practice under the altered map, trajectories regained their original rectilinearity. When the baseline map was suddenly restored, initial trajectories deviated clockwise (CW) relative to trajectories made at the start of Session 2, indicating that subjects used an adaptive feedforward strategy to compensate for the rotation. These aftereffects were eliminated by the end of the washout period. Similarly, initial exposure to a step-wise increase in the gain of the hand-to-screen map resulted in cursor trajectories that far overshot their goal. Further practice under the altered map reduced these extent errors. Restoration of the baseline map resulted in initial cursor movements that undershot their goal. These targeting errors were virtually eliminated by the end of the washout period. (b) Adaptation to the rotation induced a significant change in the subject's inverse geometric model of Euclidean task-space whereas adaptation to a scaling did not. Here, ΔB̂ is our measure of reorganization within the redundant articulation space, for subjects exposed to a rotation (red) and scaling (black) of task-space, both before (solid bars) and after (unfilled bars) visuomotor adaptation. For the subjects exposed to the rotation distortion, B̂ after adaptation could not reasonably be characterized as a rotated version of the baseline map because ΔB_ADAPT far exceeded ΔB_NOISE for these subjects. The within-subject difference between ΔB_ADAPT and ΔB_NOISE was 0.44 ± 0.32 G.S.U./pixel (red solid bar), from which we conclude that the rotational distortion induced these subjects to form a new inverse hand-to-screen map during adaptation. In contrast, ΔB_ADAPT did not exceed ΔB_NOISE, for scaling subjects (black gradient bars; p = 0.942), yielding an average within-subject difference between ΔB_ADAPT and ΔB_NOISE of 0.03 ± 0.10 G.S.U./pixel (black solid bar). We, therefore, found no compelling reason to reject the hypothesis that after adaptation, scaling subjects simply contracted their baseline inverse map to compensate for the imposed scaling distortion. Taken together, the results demonstrate that applying a rotational distortion to cursor motion initiated a search within redundant degrees of freedom for a new solution to the target capture task whereas application of the scaling distortion did not (adapted from Liu et al., 2010).

Because A is a rectangular matrix with 2 rows and 19 columns, it does not have a unique inverse; rather, there are infinite 19 × 2 matrices B such that

$$\mathbf{A}\cdot \mathbf{B}={\mathbf{I}}_2$$ (9)

where I₂ is the 2 × 2 unit matrix. These are “right inverses” of A, each one generating a particular glove-signal vector H mapping onto a common screen coordinate P. Liu et al. (2011) estimated the inverse hand-to-screen transformation B̂ used to solve the target acquisition task before and after adaptation to T_R and T_S by a least squares fit to the data:

$$\widehat{\mathbf{B}}={\mathbf{HP}}^{\mathbf{T}}{\left({\mathbf{PP}}^{\mathbf{T}}\right)}^{-1}$$ (10)

They then evaluated how well B̂ obtained after adaptation (B_ADAPT) was predicted by rotation (T_R) or scaling (T_S) of the B̂ obtained just prior to imposing the distortion (B_BEFORE) by computing a difference magnitude ΔB_ADAPT:

$$\Delta {\mathbf{B}}_{\text{ADAPT}}=\Vert {\mathbf{B}}_{\text{ADAPT}}-{\mathbf{B}}_{\text{BEFORE}}{\mathbf{T}}^{-1}\Vert$$ (11)

They compared this to the difference magnitude obtained from data collected in two separate time intervals during baseline training on the second day (i.e., before imposing the distortion; BL₁ and BL₂). Here, T^–1 of Eq. (9) is assumed to be the identity matrix:

$$\Delta {\mathbf{B}}_{\text{NOISE}}=\Vert {\mathbf{B}}_{\mathrm{BL}1}-{\mathbf{B}}_{\mathrm{BL}2}\Vert$$ (12)

Importantly, Liu and colleagues found that adaptation to the rotation induced a significant change in the subject's inverse geometric model of Euclidean task-space whereas adaptation to a scaling did not (Fig. 5b). Because the magnitude of initial exposure error was virtually identical in the two cases, the different behaviors cannot be accounted for by error magnitude. Instead, the results provide compelling evidence that in the course of practicing the target capture task, subjects learned to invoke categorically different compensatory responses to errors of direction and extent. To do so, they must have internalized the inner product structure imposed by the linear hand-to-screen mapping, which establishes the independence of vector concepts of movement direction and extent in task-space. Under the assumption that the brain minimizes energetic costs in addition to kinematic errors (see Shadmehr and Krakauer, 2008 for a review), subjects in the current study should at all times have used their baseline inverse map to constrain command updates to only those degrees of freedom contributing to task performance. This was not the case. The findings were also inconsistent with the general proposition that once the “structure” of a redundant task is learned, such dimensionality reduction is used to improve the efficiency of learning in tasks sharing a similar structure (Braun et al., 2010).

Instead, the findings of Mosier et al. (2005) and colleagues (Liu and Scheidt, 2008) demonstrate that as the subjects learned to remap the function of their finger movements for controlling the motion of the cursor, they also did something that was not prescribed by their task instructions. They formed a motor representation of the space in which cursor was moving and, in the process of learning, they imported the Euclidean structure of the computer monitor into the space of their control signals. This differs sharply from the trend predicted by the uncontrolled manifold theory, where a reduction in the variance at the target should have been accompanied by no such decrease in performance variance in redundant degrees of freedom. The experimental observations of Bernstein, Scholz, Latash, and others (Bernstein, 1967; Latash et al., 2001; Scholz and Schoner, 1999) can be reconciled with the observations of Mosier and colleagues if one considers that the glove task is completely novel, whereas tasks such as hitting a nail with a hammer are performed within the domain of a well learned control system. Because the purpose of learning is to form a map for executing a given task over a broad target space in many different situational contexts, it is possible that once a baseline competency and confidence in the mapping is established, the abundance of degrees of freedom becomes an available resource to achieve a more flexible performance, with higher variability in the null-space.

The dual-learning problem

A HMI sets a relation from body-generated signals to control signals or commands for an external device. This relation does not need to be fixed. Intuition suggests that it should be possible to modify the map implemented by the interface so as to facilitate the learning process. In this spirit, Taylor et al. (2002) have employed a coadaptive movement prediction algorithm in rhesus macaques to improve cortically controlled 3D cursor movements. Using an extensive set of empirically chosen parameters, they updated the system weights through a normalized balance between the subject's most successful trials and their most recent errors, resulting in quick initial error reductions of about 7% daily. After significant training with exposure to the coadaptive algorithm, subjects performed a series of novel point-to-point reaching movements. They found that subjects’ performance in the new task was not appreciably different from the training task. This is evidence of successful generalization.

Danziger et al. (2009) modified the glove-cursor paradigm by introducing a nonlinear transformation between the hand signals and the cursor (Fig. 6). In their experiment, the 19D vector of sensor values was mapped to the position of a cursor presented on a computer monitor. First, the glove signals were multiplied by a 2 × 19 transformation matrix to obtain a pair of angles. These angles then served as inputs to a forward kinematics equation of a simulated 2-link planar arm to determine the end-effector location:

$$\begin{array}{cc}\hfill & \left[\begin{array}{c}\hfill {\theta }_1\hfill \\ \hfill {\theta }_2\hfill \end{array}\right]=\mathbf{A}\cdot \left[\begin{array}{c}\hfill h_1\hfill \\ \hfill h_2\hfill \\ \hfill ⋮\hfill \\ \hfill h_{19}\hfill \end{array}\right]\hfill \\ \hfill & \left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right]=\left[\begin{array}{cccc}\text{cos}\left({\theta }_1\right)\hfill & \text{cos}({\theta }_1+{\theta }_2)\hfill & 1\hfill & 0\hfill \\ \text{sin}\left({\theta }_2\right)\hfill & \text{sin}({\theta }_1+{\theta }_2)\hfill & 0\hfill & 1\hfill \end{array}\right]\cdot \widehat{\mathbf{s}}\hfill \end{array}$$ (13)

where ŝ = [l₁, l₂, x₀, y₀]^T is a constant parameter vector that includes the link lengths and the origin of the shoulder joint. The virtual arm was not displayed except for the arm's endpoint, which was represented by a 0.5-cm-radius circle. Subjects were given no information about the underlying mapping of hand movement to cursor position.

Fig. 6.

Hand posture represented as a point in “hand space,” h, is mapped by a linear transformation matrix, A, into two-joint angles of a simulated planar revolute-joint kinematic arm on a monitor. The endpoint of the simulated arm was determined by the nonlinear forward kinematics, ζ. Subjects placed the arm's endpoint into displayed targets through controlled finger motions. During training, the elements of the A matrix were updated to eliminate movement errors and assist subjects in learning the task (from Danziger et al., 2009).

The mapping matrix, A, was initially determined by having the subject generate four preset hand postures. Each one of these postures was placed in correspondence with a corner of a rectangle inside the joint angle workspace. The A matrix was then calculated as, A = Θ · H⁺, where Θ is a 2 × 4 matrix of angle pairs that represent the corners of the rectangle, and H⁺ is the MP pseudoinverse of H (Ben-Israel and Greville, 1980), the 19 × 4 matrix whose columns are signal vectors corresponding to the calibration postures. Using the MP pseudoinverse corresponded to minimizing the norm of the A matrix in the Euclidean metric. As a result of this redundant geometry, each point of the workspace was reachable by many anatomically attainable hand postures.

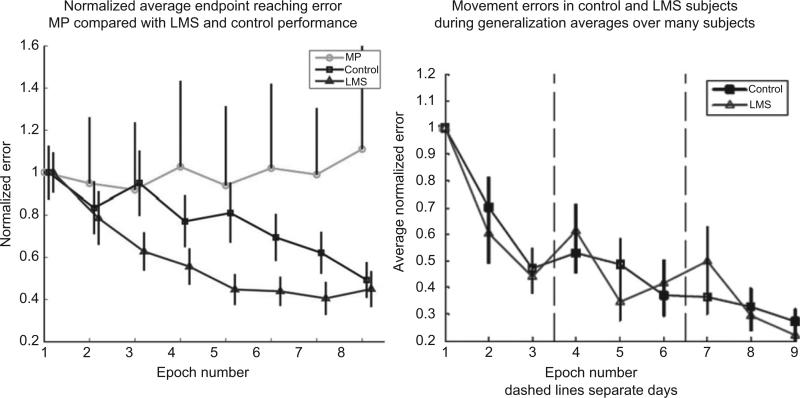
Danziger et al. asked subjects to shape their hands so as to move the tip of the simulated arm into a number of targets. The experiment proceeded in sets of training epochs. In each epoch, the mapping between the hand joint angles and the arm's free-moving tip (the “end-effector”) was updated so as to cancel the mean endpoint error in the previous set of movements. This was done in two ways by two separate subject groups: (a) by a least mean squares (LMS) gradient descent algorithm which takes steps in the direction of the negative gradient of the endpoint error function, or (b) by applying the MP pseudoinverse which offers an analytical solution for error elimination while minimizing the norm of the mapping. LMS (Widrow and Hoff, 1960) is an iterative procedure, which seeks to minimize the square of the performance error norm by iteratively modifying the elements of the A matrix in Eq. (13). The minimization procedure terminated when the difference between the old and the new matrix exceeded a preset threshold. In contrast, the MP procedure was merely a recalibration of the A matrix, which canceled the average error after each epoch. Therefore, both LMS and MP algorithms had identical goals, to abolish the mean error in each training epoch, and each method found a different solution.

The result was that subjects exposed to the LMS adaptive update outperformed their control counterparts who had a constant mapping. But, surprisingly, the MP update procedure was a complete failure, and subjects exposed to this method failed to improve their skill levels at all (Fig. 7, left). We hypothesize that this was because the LMS procedure finds local solutions to the error elimination problem (because it is a gradient decent algorithm), while the MP update may lead to radically different A-matrices across epochs. This finding highlights a trade-off between maintaining a constant structure of the map and altering the structure of the map so as to assist subjects in their learning. But perhaps the most important finding in that study was a negative result. In spite of the more efficient learning over the training set, subjects in the LMS group did not show any significant improvement over the control group on a different set of targets, which were not practiced during the training session (Fig. 7, right). The implication is that the LMS algorithms facilitated subjects’ creation of an associative map from the training targets to a set of corresponding hand configurations. However, this did not improve learning the geometry of the control space itself. Had this been the case, we would expect to see greater improvement in generalization. Finding machine learning methods that facilitate “space learning” as distinct from improving performance over a training set remains an open and important research goal in human–machine interfacing.

Fig. 7.

(Left) Average normalized movement errors for three subject groups in the experiment outlined in Fig. 6. The mapping for MP subjects was updated to minimize prior movement errors by an analytical method, which resulted in large mapping changes. The mapping for LMS subjects was also updated to minimize prior error but with a gradient descent algorithm that resulted in small mapping changes. Control subjects had a constant mapping. LMS subjects outperformed controls, while MP subjects failed to learn the task at all. (Right) Movement errors on untrained targets for control and LMS groups show that adaptive mapping updates does not facilitate spatial generalization (from Danziger et al., 2008, 2009).

A clinical perspective: the body–machine interface

The experiments of Mosier et al. (2005) and Danziger et al. (2009) demonstrated the ability of the motor system to reorganize motor coordination so as to match the low-dimensional geometrical structure of a novel control space. Subjects learned to redistribute the variance of the many degrees of freedom in their fingers over a 2D space that was effectively an inverse image of the computer monitor under the hand-to-cursor map. We now consider in the same framework the problem of controlling a powered wheelchair by coordinated upper body motions. People suffering from paralysis, such as spinal cord injury (SCI) survivors are offered a variety of devices for operating electrically powered wheelchairs. These include joysticks, head and neck switches, sip-and-puff devices, and other interfaces. All these devices are designed to match the motor control functions that are available to their users. However, they have a fixed structure and ultimately they present the users with challenging learning problems (Fehr et al., 2000). In general, the lack of customizability of these devices creates various difficulties across types and levels of disability (Hunt et al., 2004) and subjects with poor control of the upper body are at a greater risk of incurring accidents. Decades of research and advances in robotics and machine learning offer now the possibility to shift the burden of learning from the human user to the device itself. In a simple metaphor, instead of having the user of the wheelchair learning how to operate a joystick, we may have the wheelchair interface looking at the user's body as if it were a joystick.

The controller of a powered wheelchair is a 2D device, setting the forward speed and the rotation about a vertical axis. Most paralyzed SCI survivors have residual mobility much in excess of 2 degrees of freedom. Therefore, from a computational point of view one can see the control problem as a problem of embedding a 2D control surface within a higher-dimensional “residual motor space.” This is analogous to the problem of embedding the control space of a robotic arm within the signal space associated with a multiunit neural signal from a cortical area. From a geometrical standpoint, the embedding operation is facilitated by the ability of the motor control system to learn Euclidean metrics in a remapping operation, as shown in Mosier et al. (2005). While control variables may have a non-Euclidean Riemannian structure, a powerful theorem by Nash (1956) states that any Riemannian surface can be embedded within a Euclidean space of higher dimension. A simple way to construct a Euclidean space from body motions is by principal component analysis (PCA; Jolliffe, 2002). This is a standard technique to represent a multidimensional signal in a Cartesian reference frame, whose axes are ordered by decreasing variance. Using PCA, Casadio et al. (2010) developed a camera-based system to capture upper body motions and control the position of a cursor on a computer monitor (Fig. 8). Both SCI injured subjects—at or above C5—and unimpaired control subjects participated in this study. Four small cameras monitored the motions of four small infrared active markers that were placed on the subjects’ upper arms and shoulders. Since each marker had a 2D image on a camera, the net signal was an 8D vector of marker coordinates. This vector defined the “body space.” The control space was defined by the two coordinates (x,y) of the cursor on the monitor. Unlike the hand-to-cursor map of the previous study, the body-to-cursor map was not based on a set of predefined calibration points. Instead, in the first part of the experiment subjects performed free upper body motions for 1 min. This was called the “dance” calibration. A rhythmic music background facilitated the subjects’ performance in this initial phase. The purpose of the dance was to evaluate how subjects naturally distributed motor variance over the signal space. The two principal component vectors, generating the highest variance of the calibration signals, defined two Cartesian axes over the signal space. In the calibration phase, subjects could scale the axis to compensate for the difference in variance associated with them. They were also allowed to rotate and/or reflect the axis to match the natural right-left, front-back directions of body space.

Fig. 8.

Controlling a cursor by upper-body motion: experimental apparatus. Four infrared cameras capture the movements of four active markers attached to the subject's arm and shoulder. Each camera outputs the instantaneous x, y coordinates of a marker. The eight coordinates from the four cameras are mapped by linear transformation into the coordinates of a cursor, presented as a small dot on the monitor. The subject is asked to move the upper body so as to guide the dot inside a target (from Casadio et al., 2010).

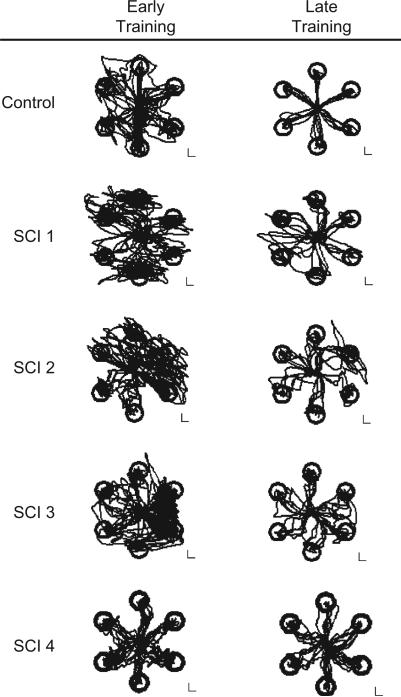
After the calibration, subjects were engaged in a set of reaching movements. Both control and SCI subjects learned to execute efficiently the required motions of the cursor on the computer monitor by controlling their upper body movements (Fig. 9). Learning in terms of error reduction, increase in movement speed, and trajectory smoothness was evident both in controls and SCI subjects. In particular, all SCI subjects were able to use their shoulder movements for piloting the cursor for about 1 h. Importantly, subjects did not merely learn to track the cursor on the monitor. Instead, they acquired the broader skill of organizing their upper-body motions in “feedforward” motor programs, analogous to the natural reaching by hand. No statistically significant effect of vision could be detected, as well as no interaction between vision and practice when comparing movement executed under continuous visual feedback of the cursor, with movements where the cursor feedback was suppressed.

Fig. 9.

Movement trajectories in early (left) and late (right) phases of learning, for a control subject and four SCI subjects. Calibration lines on bottom right corner of each panel: 1 cm on the computer screen (from Casadio et al., 2010).

Moreover, PCA succeeded in capturing the main characteristics of the upper-body movements for both control and SCI subjects. During the calibration phase, for all high-level SCI subjects it was possible to extract at least two principal components with significant variance from the 8D signals. Their impairment constrained and shaped the movements. Compared to control, they had on average a bigger variance associated with the first component and smaller variances associated with the second through fourth components. Otherwise stated, the SCI subjects had a lower-dimensional upper body motor space.

At the end of training, for all subjects the first three principal components accounted for more than 95% of the overall variance. Furthermore, the variance accounted for (VAF) by the two first principal components slightly increased with practice. However, there was a significant difference between controls and SCI subjects. Controls mainly changed the movements associated with their degrees of freedom in order to use two balanced principal movements. They learned to increase the variance associated with the second principal component (Fig. 10), thus achieving a better balance between the variance explained by the first two components. This behavior was consistent with the consideration that subjects practiced a 2D task, with a balanced on-screen excursion in both dimensions. In contrast, at the end of the training, SCI subjects maintained the predominance of the variance explained by the first component: they increased the variance explained by the first component and decreased the fourth. Their impairment effectively constrained their movements during the execution of the reaching task as well as during the free exploration of the space.

Fig. 10.

Distribution of motor variance across learning. Left panel: Results of principal component analysis on the first (gray) and last movement set (black) for control subjects (mean+SE). In the first movement set (gray) more than 95% of variance was explained by four principal components. At the end of the training session (black), unimpaired controls mainly tended to increase the variance associated with the second principal component. Right panel: Control subjects (mean + SE). Results of the projection of the data of the first (gray) and last movement set (black) over the 8D space defined by the body-cursor map. This transformation defines an orthonormal basis, where the “task-space” components a₁, a₂ determine the cursor position on the screen, and the orthogonal vectors a₃,. . .,a₈ represent the “null-space” components that do not change the control vector. For most of the control subjects, the fraction of movement variance in the null-space decreased with training in favor of the variance associated in the task-space (from Casadio et al., 2010).

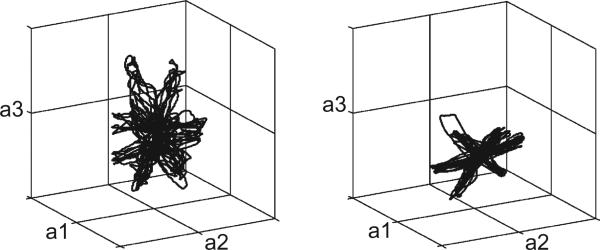
The most relevant findings of Casadio et al. (2010) concerned the distribution of variance across task-relevant and task-irrelevant dimensions. For control subjects, the VAF by the task-space with respect to the overall variance significantly increased with practice. In spite of the reduced number of training movements, the same trend was present in most SCI subjects. Therefore, as in the hand-cursor glove experiments of Mosier et al. (2005), subjects learned to reduce the variance that did not contribute to the motion of the cursor and demonstrated the ability to form an inverse model of the body-to-cursor transformation. As subjects reduced the dimensionality of their body motions, they also showed a marked tendency to align their movement subspace with the 2D space established by the body-cursor map (Fig. 11). It is important to observe that this was by no means an expected result. In principle, one could be successful at the task while confining one's movements to a 2D subspace that differs from the 2D subspace defined by the calibration. To see this, consider the task of drawing on a wall with the shadow of your hand. You can move the hand on any invisible surface with any orientation (except perpendicular to the wall!). The result of Casadio and collaborators is analogous to finding that one would prefer to move the hand on an invisible plane parallel to the wall. Taken together, these results indicate that subjects were able to capture the structure of the task-space and to align their movements with it.

Fig. 11.

Matching the plane of the task. The limited number of dimensions involved in the task allowed us to project the body movement signals in a 3D subspace where the vectors a₁, a₂ define the “task-space” and a₃ is the most significant null-space component in terms of variance accounted for. In the first movement set (early phase of learning, left panel) there was a relevant movement variance associated with the null-space dimension a₃. That component was strongly reduced in the last target set (late phase of learning, right panel) where the movement's space became more planar, with the majority of the movement variance accounted by the task-space components a₁, a₂ (from Casadio et al., 2010).

Conclusions

The concept of motor redundancy has attracted consistent attention since the early studies of motor control. Bernstein (1967) pioneered the concept of “motor equivalence” at dawn of the past century by observing the remarkable ability of the motor system to generate a variety of movements achieving a single well-defined goal. As aptly suggested by Latash (2000), the very term “redundancy” is a misnomer as it implies an excess of elements to be controlled instead of a fundamental resource of biological systems. We agree with Latash, and stick opportunistically with the term redundancy simply because it is commonly accepted and well understood. There is a long history of studies that have addressed the computational tasks associated with kinematic redundancy while others have considered the advantage of large kinematic spaces in providing ways to improve accuracy in the reduced space defined by a task. Here, we have reviewed a new point of view on this issue. We considered how the abundance of degrees of freedom may be a fundamental resource in the learning and remapping problems that are encountered in human–machine interfacing. We focused on two distinctive features:

1. The HMI often poses new learning problems and these problems may be burdensome to users that are already facing the challenges of disability.

2. By creating an abundance of signals—either neural recordings or body motions—one can cast a wide net over which a lower-dimensional control space can be optimally adapted.

Work on remapping of finger and body movements over 2D task-spaces have highlighted the existence of learning mechanisms that capture the structure of a novel map relating motor commands to their effect on task-relevant variables. Both unim-paired and severely paralyzed subjects were able with practice not only to perform what they were asked to do but they also adapted their movements to match the structure of the novel geometrical space over which they operated. This may be seen as “suboptimal” with respect to a goal of maximal accuracy. Subjects did not shift their variance from the low-dimensional task to the null-space (or uncontrolled manifold). Instead, as learning progressed, variance in the null-space decreased as well as variance in the task-relevant variables. This is consistent with the hypothesis that through learning, the motor system strives to form an inverse map of the task. This must be a function from the low-dimensional target space to the high-dimensional space of control variables. It is only after such a map is formed that a user may begin to exploit the possibility of achieving the same goals through a multitude of equivalent paths.