Parallel Transport in Diffeomorphisms Distinguishes the Time-Dependent Pattern of Hippocampal Surface Deformation due to Healthy Aging and the Dementia of the Alzheimer’s Type

Abstract

Hippocampal surface structure was assessed at twice two years apart in 26 nondemented subjects (CDR 0), in 18 subjects with early dementia of Alzheimer type (DAT, CDR 0.5), and in 9 subjects who converted from the nondemented (CDR 0) to the demented (CDR 0.5) state using magnetic resonance (MR) imaging. We used parallel transport in diffeomorphisms under the large deformation diffeomorphic metric mapping framework to translate within-subject deformation of the hippocampal surface as represented in the MR images between the two time points in a global template coordinate system. We then performed hypothesis testing on the longitudinal variation of hippocampal shape in the global template. Both subjects with early DAT and converters showed greater rates of hippocampal deformation across time than nondemented controls within every subfield of the hippocampus. In a random field analysis, inward surface deformation across time occurred in a non-uniform manner across the hippocampal surface in subjects with early DAT relative to the nondemented controls. Also, compared to the controls, the lateral aspect of the left hippocampal tail showed inward surface deformation in the converters. Using surface deformation patterns as features in a linear discriminant analysis, we were able to respectively distinguish converters and patients with early DAT from healthy nondemented controls at classification rates of 0.77 and 0.87, which were obtained in the same training set using the leave-one-out cross validation approach.

1. Introduction

MR-based volumetric assessment of the hippocampus has been widely employed in normal aging and various neuropsychiatric disorders, including DAT, mild cognitive impairment, schizophrenia, temporal lobe epilepsy, and major depression (Convit et al., 1997, Shenton et al., 2001, Cardenas et al., 2003, Wang et al., 2003, Csernansky et al., 2005, Frisoni et al., 2005, Apostolova et al., 2006a, Apostolova et al., 2006b, Frisoni et al., 2006, Wang et al., 2006, Frisoni et al., 2007, Whitwell et al., 2007). In particular, progressive hippocampal volume loss has been identified to be one of the hallmarks of DAT. Using brain warping techniques, neuroimaging studies previously found that increased rates of hippocampal volume loss as well as different patterns of hippocampal shape change distinguished early DAT from healthy aging (Fox et al., 1996, Cardenas et al., 2003, Wang et al., 2003, Apostolova et al., 2006b, Ridha et al., 2006). However, among the group of nondemented subjects, there was considerable variation in the rate of hippocampal volume loss and shape change, possibly because of the presence of subjects within this group with preclinical forms of Alzheimer’s Disease (AD) (i.e. subjects are cognitively normal but have histopathological AD). More sensitive methods for assess the degree and pattern of structural change in the hippocampus are still needed to optimally distinguish subjects with early forms of AD (including preclinical AD) from subjects who are aging in the absence of the AD process.

To precisely assess the location of volume loss within the complex structure of the hippocampus requires studying within-subject time-dependent deformation of the hippocampal surface, as illustrated in the first level analysis of Fig. 1. However, the absence of a common coordinate system across subjects can undermine hypothesis testing related to time-dependent within-subject deformation. Previously, subjects’ hippocampi at different time points were mapped to a single hippocampal atlas via brain warping techniques (Wang et al., 2003, Apostolova et al., 2006b). The difficulty with this approach is that the transformations used to assess longitudinal changes in the hippocampal surface included both the variation of the transformation between different time points within and across subjects. The weakness of this approach for detecting within-subject changes is that the variation across subjects is generally larger than the variation within subjects.

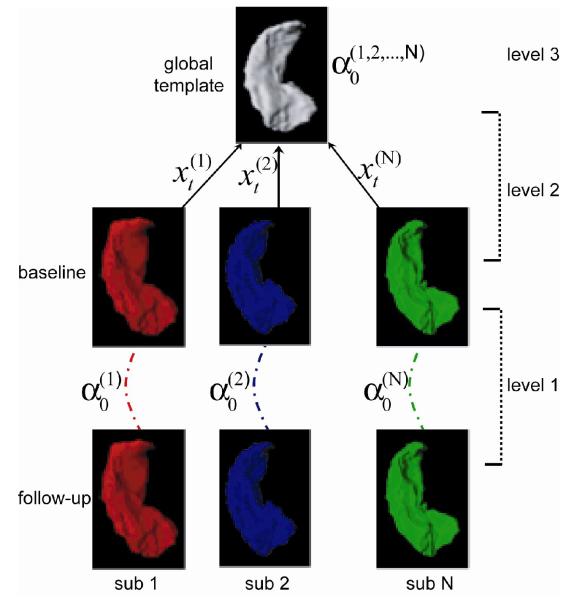
Fig. 1.

Schematics of transport in diffeomorphisms for studying longitudinal shape variation. There are three levels of analysis. In the first level, the initial momentum ${\alpha }_0^{\left(j\right)}$ encoding the deformation of the hippocampus between the baseline and follow-up within subject j is computed via LDDMM surface mapping. The geodesic $x_t^{\left(j\right)}$ connecting subject j at the baseline to the global template is also computed via LDDMM surface mapping in the second level of the analysis. Finally, ${\alpha }_0^{\left(j\right)}$ is parallel transported to the global template along $x_t^{\left(j\right)}$ via the technique described in Methods.

In this paper, we demonstrate three-level analyses under the large deformation diffeomorphic metric mapping framework (LDDMM) for comparing longitudinal shape variation of the hippocampus across clinical populations. As illustrated in Fig. 1, the first two levels assess deformations within-subjects and between a global template and subjects, respectively, via LDDMM. In the third level analysis, we use a novel technique, parallel transport in diffeomorphisms, which allows us to translate within-subject deformation between time points in a global template without incorporating across-subject deformation. We applied this approach to a study of hippocampal shape change in 26 healthy nondemented subjects (CDR 0), 18 patients with DAT (CDR 0.5), and 9 subjects who converted from being nondemented to being demented. Our aim was to distinguish subjects with very mild AD and subjects with preclinical forms of AD from healthy comparison subjects using time-dependent patterns of hippocampal surface deformation.

2. Methods

2.1 General Approach

Template-based morphometric methods have been successful for describing anatomical variations between a collection of shapes and a reference. Among these, the Large Deformation Diffeomorphic Metric Matching (LDDMM) algorithms provide a range of diffeomorphic matching methods (landmarks, images, curves, surfaces), each of which can produce a metric evaluation of the size of the variation. Moreover, LDDMM provides a mechanism that allows for the reconstitution of the variations by encoding precise variations of anatomies relative to the template. The resultant template-based representation can be interpreted as a change of coordinates, and can be used to represent anatomies in a local chart centered at the template.

In the present study, we were primarily interested in quantifying anatomical variation within each subject between two time points. This variation is naturally represented by the deformation needed to pass from the anatomy at the first time point to one at the second time point within a subject. When comparing two or more subjects, one then needs to decide how change in the anatomy of one subject can be translated into the similar deformation that occurs in another subject.

The metric structure on anatomies provided by LDDMM offers a consistent approach for the translation of this information. This operation, parallel translation taken from Riemannian geometry, displaces vectors along a curve without changing properties such as the norms of the vectors or their dot products. In Euclidean space, this operation is the standard translation of vectors; i.e., the infinitesimal displacement of subject 1 is applied to subject 2 without change. In curved spaces, however, parallel translation is nonlinear, and can be computed by solving a differential equation. The special form of this equation on our setting will be described in section 2.3, after having introduced the notation and formalism related to LDDMM in section 2.2.

We thus present three levels of analysis for studying time-dependent deformation of anatomies as schematized in Fig. 1. The first level of analysis was to characterize within-subject variations between the baseline and follow-up. The second level of analysis was to construct a curve connecting the baseline anatomies and the global template and characterize cross-subjects variations between them. In the third level, the parallel transport operation moved within-subject time-dependent variations along this curve: from the baseline to the global template. The first two levels involve spatial normalization of anatomies implemented by the LDDMM algorithm in Section 2.2. The technique of parallel transport was applied in the third level of the analysis as described in Section 2.3.

2.2 Large Deformation Diffeomorphic Metric Matching

LDDMM Background

The first and second level analyses in Fig. 1 involve the registration between two anatomical structures. In our case, the surface of the hippocampus was represented by a triangulated mesh with a finite number of points. In the LDDMM setting, we developed mapping algorithms for registering two point sets that represent three types of different anatomical manifolds: landmarks, curves, and surfaces (Joshi et al., 1999, Glaunes et al., 2004, Vaillant and Glaunes, 2005). All of these mapping algorithms provide diffeomorphic maps --- one-to-one, reversible smooth transformations that preserve topology. The use of LDDMM for studying the shapes of objects implies the placement of shapes in a metric space, provides a diffeomorphic transformation, and defines a metric distance that can be used to quantify the similarity between two shapes. We particularly chose the LDDMM-surface mapping algorithm for transforming one hippocampal surface to the other because it incorporates intrinsic geometry of the surface (normal vector) to quantify the similarity of surface shapes. The surface matching algorithm minimizes the energy

$$J({\alpha }_t,x_t)=\sum _{k,l=1}^N{\int }_0^{1}K\left(x_t\right(k),x_t(l\left)\right){\alpha }_t\left(k\right)•{\alpha }_t\left(l\right)\mathit{dt}+D(x_1,x_{\mathrm{targ}}),$$ (1)

where N represents the number of vertices on the template surface. x_t =(x_t(1),…x_t(N)) denote transformed vertex locations at time t and α_t = (α_t(1),…α_t(N)) is a collection of 3D vectors associated with x_t. The first term provides a metric that quantifies the length of the trajectory connecting x₀ and x_{t arg} in a shape space. The kernel, K is a smoothing kernel that is positive definite and penalizes the smoothness of the deformation so that the trajectory, x_t, is diffeomorphic (see more details in (Dupuis, 1998)). D(x₁,x_targ) quantifies the closeness between the surfaces at the end of the evolution, x₁, and the target x_targ, which is measured by the correlation of normal vectors at one surface with smoothed normal vectors at the other surface (Vaillant and Glaunes, 2005, Vaillant et al., 2007). Note that the time in this equation is a dummy time only used for algorithmic purposes, and should not be confused with the time at which the data is collected. The variables x_t and α_t are related by the dynamical equations

$$\frac{{\mathit{dx}}_t\left(k\right)}{\mathit{dt}}=\sum _{l=1}^{N}K\left(x_t\right(k),x_t(l\left)\right){\alpha }_t\left(l\right),k=1,\dots N$$ (2)

with initial condition x₀ = x_temp. This “optimal control” problem (because the α parameters control the evolution of the state variable x), with a specific choice of the distance D adapted to the case when x contains the vertices of a triangulated surface was formulated and solved in (Vaillant and Glaunes, 2005). The Euler-Lagrange optimality conditions for the variational problem in Eq. (1) imply

$$\frac{d{\alpha }_t\left(k\right)}{\mathit{dt}}=-\sum _{l=1}^N{\alpha }_t\left(k\right)•{\alpha }_t\left(l\right){\nabla }_{1}K\left(x_t\right(k),x_t(l\left)\right),$$ (3)

where ▽₁ denotes taking derivative of K(x, y) with respect to its first variable. Eq. (2) and (3) indicate that the evolution from one object to the other is uniquely determined given α₀. From Eq. (2), we see that α₀ carries the same information as t dx_t/dt at t = 0, and therefore corresponds to an infinitesimal variation of x₀. We shall term it as “deformation signature” that will be used to encode the shape variation between the baseline and follow-up in the subject baseline coordinates. Doing so yields ${\alpha }_0^{\left(j\right)}=\left({\alpha }_0^{\left(j\right)}\right(k),k=1,\dots ,N_j)$, in subject j. This signature is, as already pointed out, aligned with the reference surface for subject j , S(j,0), with vertices $x_0^{\left(j\right)}=\left(x_0^{\left(j\right)}\right(k),k=1,\dots ,N_j)$. It needs to be translated to a global reference frame in order to make between-subject comparisons possible. In the subsequent section, we describe how the deformation signature obtained in this first level analysis is transported to the global template along the geodesic obtained in the second level analysis in Fig. 1.

2.3 Parallel Transport in Diffeomorphisms

We describe how the signatures ${\alpha }_0^{\left(j\right)}$ are translated from subject $x_0^{\left(j\right)}$ to the global template x_temp with parallel transport. This operation is taken from Riemannian geometry, which displaces vectors along a curve without changing properties such as the norms of the vectors (as the first term in Eq (1)) or their angles (or dot products). In Euclidean space, this operation is the standard translation of vectors; i.e., the infinitesimal displacement of subject 1 is applied to subject 2 without change. In curved spaces, this operation is implemented along a curve so this starts with the computation of the best time evolution from subject j, $x_0^{\left(j\right)}$, to the global template, x_temp. This requires using again the LDDMM-surface algorithm, minimizing

$$J({\beta }_t,y_t)=\sum _{k,l=1}^N{\int }_0^{1}K\left(y_t\right(k),y_t(l\left)\right){\beta }_t\left(k\right)•{\beta }_t\left(l\right)\mathit{dt}+D(y_1,x_{\mathrm{temp}}).$$ (4)

with $y_0=x_0^{\left(j\right)}$. The last operation is to translate α₀ along the trajectory y_t. The theoretical derivation was described in (Younes, 2007). We implemented it with the following algorithm. Assume ν_t is the translation of from time 0 to time t with initial condition ${\eta }_0={\alpha }_0^{\left(j\right)}$. Then ν₁ is the representation of ${\alpha }_0^{\left(j\right)}$ at the global template.

1. Start with the optimal trajectory (y_t,β_t) minimizing (4), and set ${\eta }_0={\alpha }_0^{\left(j\right)}$ as the deformation signature that needs to be transported.

2. At time t, we study the variation of y_t, denoted by J_s, in Eq. (2) and (3) when perturbing β₀ by εν₀ and solve the following differential system over a small interval δt, with J₀ = 0, ${\tilde{\eta }}_0={\eta }_t$:

   $$\begin{array}{cc}\hfill \frac{{\mathit{dJ}}_s\left(k\right)}{\mathit{ds}}& =\sum _{l}K\left(y_{t+s}\right(k),y_{t+s}(l\left)\right){\tilde{\eta }}_s\left(l\right)+{\nabla }_{1}K\left(y_{t+s}\right(k),y_{t+s}(l\left)\right)\left)•J_s\right(k\left){\beta }_{t+s}\right(l)\hfill \\ \hfill & +{\nabla }_{2}K\left(y_{t+s}\right(k),y_{t+s}(l\left)\right)•J_s\left(l\right){\beta }_{t+s}\left(l\right)\hfill \\ \hfill \frac{d{\tilde{\eta }}_s\left(k\right)}{\mathit{ds}}& =-\sum _l{\nabla }_1\left[{\nabla }_{1}K\right(y_{t+s}\left(k\right),y_{t+s}\left(l\right)\left)\right]J_s\left(k\right){\beta }_{t+s}\left(k\right)•{\beta }_{t+s}\left(l\right)\hfill \\ \hfill & -{\nabla }_2\left[{\nabla }_{1}K\right(y_{t+s}\left(k\right),y_{t+s}\left(\underset{~}{l}\right)\left)\right]J_s\left(l\right){\beta }_{t+s}\left(k\right)•{\beta }_{t+s}\left(l\right)\hfill \\ \hfill & -{\nabla }_{1}K\left(y_{t+s}\right(k),y_{t+s}(l\left)\right)•{\eta }_s\left(k\right){\beta }_{t+s}\left(l\right)-{\nabla }_{1}K\left(y_{t+s}\right(k),y_{t+s}(l\left)\right)•{\beta }_{t+s}\left(k\right){\tilde{\eta }}_s\left(l\right)\hfill \end{array}$$ (6)

3. Solve ν_t+δt from ${\sum }_{l}K\left(y_{t+\delta t}\right(k),y_{t+\delta t}(l\left)\right){\eta }_{t+\delta t}\left(l\right)=J_s\left(k\right)∕\delta t$ and ν_t+δt is an approximation of α₀ at point y_t+δt.

4. Loop until t = 1.

In these formulae, ▽_lK(x, y) represents the derivative of K(x, y) with respect to its l th variable. K(x, y) was chosen as the form of $e^{-\frac{{\Vert x-y\Vert }^2}{2{\sigma }^2}}$ with ∥•∥ denoting the Euclidean distance between x and y.

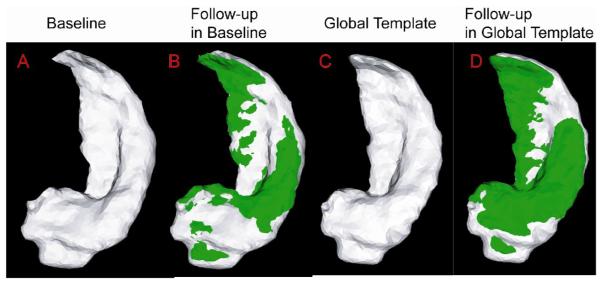
Fig. 2 intuitively illustrates one example using parallel transport to represent within subject deformation in the global template coordinates. Panel (A) shows the hippocampal surface of a subject at the baseline while Panel (B) shows the hippocampal surface of the same subject at the follow-up (green) superimposed with one at the baseline (gray). Panel (C) depicts the global hippocampal template. Panel (D) shows the hippocampal surface of this subject at the follow-up (green) represented in the global template coordinates (gray). The deformation of the hippocampal surface between baseline and follow-up represented by interlacing green and gray in panel (B) has a similar pattern as in panel (D). This indicates that the technique of parallel transport in diffeomorphism is a reasonable approach allowing us to study longitudinal shape variation within subjects in a global template coordinate system.

Fig.2.

Panel (A) shows the hippocampus of a subject at the baseline. The hippocampus surface of this subject at the follow-up (green) is superimposed with one at the baseline in Panel (B). Panel (C) shows the global hippocampus template. Panel (D) shows the hippocampus of this subject at the follow-up (green) represented in the global template coordinates (gray).

2.4 Subjects, Data Acquisition

The MR scans used in this study were collected for an ongoing longitudinal study of subjects with very mild DAT (Wang et al., 2003), and included 18 subject with very mild DAT (CDR 0.5), 26 age-matched nondemented subjects (CDR 0), and 9 subjects who converted from being nondemented (CDR 0) at baseline to having very mild DAT (CDR 0.5) at follow-up. The CDR 0 group included 12 males and 14 females with mean age of 73 (SD: 7.0) years; the CDR 0.5 included 11 males and 7 females with mean age of 74 (SD: 4.4) years; and the converter group included 2 males and 7 females with mean age 79 (SD: 8.7) years. The Clinical Dementia Rating (CDR) (Morris, 1993) was used to rate the presence or absence of dementia and, when present, its severity; i.e., with the CDR 0 indicated no dementia and CDR 0.5, 1, 2, and 3 indicated very mild, mild, moderate, and severe dementia, respectively.

All subjects had MR scans approximately two years apart – the mean scan interval for the CDR 0 group was 2.2 years (range 1.4-4.1 years), for the CDR 0.5 group, 2.0 years (range 1.0-2.6 years), and 2.8 years (range 1.8-4.3 years) for the converter group. All scans were obtained using the same Siemens Magnetom SP-4000 1.5 Tesla imaging system, a standard head coil, and a magnetization prepared rapid gradient echo (MPRAGE) sequence. A MPRAGE sequence (TR/TE - 10/4, ACQ - 1, Matrix - 256 × 256, 180 slices, Scanning time - 11.0 min) was used to produce 3D data with a 1 mm × 1 mm in-plane resolution and 1 mm slice thickness across the entire cranium.

2.5 Data Processing

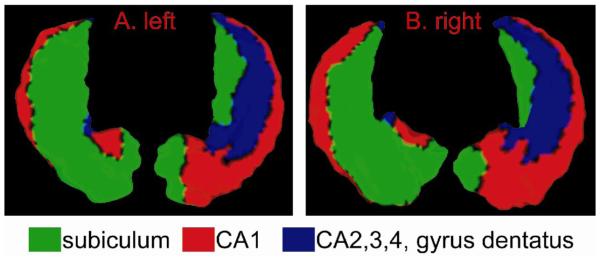
The global template was produced using an MR image from an elder control subject, which was not otherwise included in the statistical analysis. The subject selected to produce this template was from the same source as the other subjects in the study. The left and right hippocampal surfaces in this template scan were manually delineated using methods previously described (Haller et al., 1997). The anatomical description of the guidelines used for this delineation are detailed elsewhere (Wang et al., 2001). As illustrated in Fig. 3, the gray matter of the left and right template hippocampal surfaces were also manually divided into three main subfields (subiculum, cornu ammonis 1 (CA1), and the rest including CA2, 3, 4, and gyrus dentatus), as previously described (Wang et al., 2003).

Fig. 3.

The global left and right hippocampal templates were manually divided into three subfields, subiculum in green, cornu ammonis 1 (CA1) in red, and the rest (CA2,3,4, and gyrus dentatus) in blue.

Hippocampal surfaces were generated for each subject at baseline and follow-up using a template-driven approach (Wang et al., 2003), and the accuracy of this delineation was evaluated against manual hippocampal segmentation in ten scans. For the study of hippocampal shape variation across time, we applied three levels of analysis as shown in Fig. 1. In the first level of analysis, the baseline hippocampal surfaces were deformed to the follow-up surfaces within each subject via LDDMM-surface mapping. In the second level of analysis, the baseline hippocampal surfaces were deformed to the global template via LDDMM-surface mapping. Finally, in the third level of analyisis, the deformations between the baseline and follow-up surfaces were transported to the global template coordinates using the approach described in the previous section.

3. Results

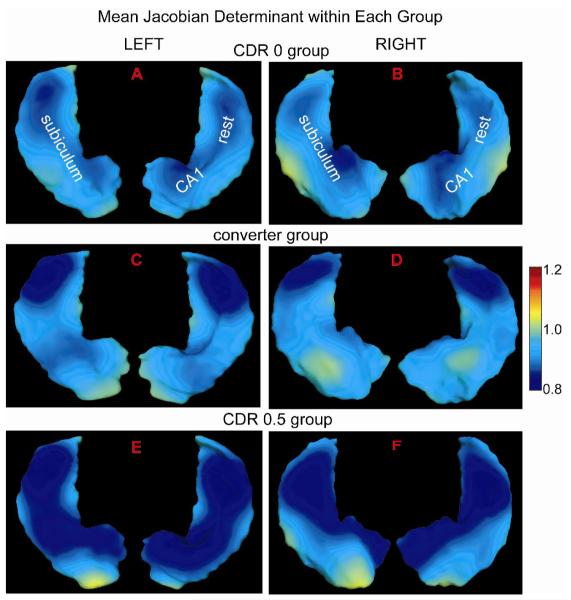
We computed Jacobian determinant of within-subject deformation between two time points on the global template to indicate hippocampal atrophy (<1) or expansion (>1) in the follow-up relative to one in the baseline. The Jacobian determinant indexed over the template coordinates measures the ratio of the hippocampal volume at the follow-up to the one at the baseline in the local region. Fig. 4 illustrates Jacobian determinant maps averaged over each clinical population in the global template coordinates. The hippocampus is displaced in the same orientation as shown in Fig. 3. The visualization of the Jacobian determinant maps in Fig. 4(A,B) indicates atrophy non-uniformly distributed over both left and right hippocampi due to healthy aging. As shown in Fig. 4(C,D), the left and right hippocampal atrophy in the converter group seems stronger in the lateral aspect of the hippocampal tail than elsewhere. In Fig. 4(E,F), the atrophy is observed throughout the entire left and right hippocampi in the CDR 0.5 group and stronger than that in the groups of CDR 0 and converter. To confirm these, we made statistical inferences on the Jacobian determinant using both a region of interest (ROI)-based approach and a localized approach in the global template below.

Fig. 4.

Figure shows Jacobian determinant of the deformation between the baseline and its follow-up surfaces averaged over each clinical population in the global template coordinates. Panels (A, C, E) illustrate those for the left hippocampus, while panels (B, D, F) show those for the right hippocampus. The bottom and top views of the hippocampus are respectively shown in the left and right sides of each panel (see the reference of subfield divisions in Figure 3).

3.1 Statistical Analysis in Subfields of the Global Hippocampal Template

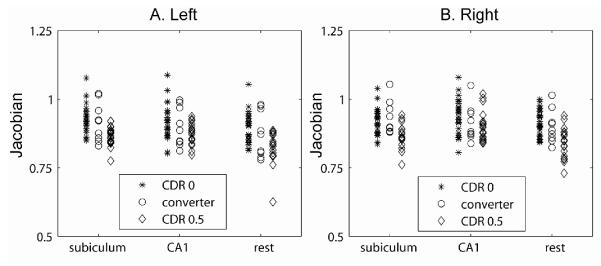
In the ROI-based analysis, we integrated the Jacobian determinant within each subfield of the global hippocampal template surface and divided it by the surface area of the subfield. Fig. 5(A, B) shows this measurement from each subject in every subfield of the left and right hippocampal surfaces, respectively. The visualization in this figure suggests systematic decreases in the Jacobian determinant from the CDR 0 group and the converter group as compared to the CDR 0.5 group within every subfield. This suggests that hippocampal deformations of every hippocampal surface subfield were progressively larger as one moves from the healthy aging group to the converter group and on to the group with very mild DAT. For instance, in the subiculum of the left hippocampus, an average Jacobian determinant was 0.924 for the CDR 0 subjects, 0.917 for the converter subjects, and 0.867 for the CDR 0.5 subjects (see Table 1). Similar trends were observed in the CA1 subfield. As listed in Table 1, the average Jacobian determinants were less than one in every subfield, which suggests that atrophy is occurring throughout the hippocampus in both healthy aging and DAT. However, the rates of atrophy within subfields were increased in both converter and CDR 0.5 groups relative to those in the CDR 0 group.

Fig. 5.

Panels (A, B) show average Jacobian determinant within each subfield of the hippocampus. Each data point represents one measurement from one subfield of the left or right hippocampus of 53 subjects.

Table1.

Average Jacobian determinant over each clinical group within subfields of the hippocampus (mean ± standard deviation).

		subiculum	CA1	Rest
left	CDR 0	0.924±0.051	0.917±0.063	0.894±0.055
	converter	0.917±0.070	0.899±0.071	0.874±0.083
	CDR 0.5	0.867±0.036	0.874±0.039	0.817±0.061
right	CDR 0	0.919±0.047	0.936±0.062	0.912±0.048
	converter	0.931±0.061	0.912±0.065	0.900±0.061
	CDR 0.5	0.869±0.046	0.904±0.055	0.843±0.057

We performed the statistical testing to examine the above observations. A generalized linear regression model was applied where Jacobian determinant averaged over each subfield was included as dependent variable. Diagnostic group (condition), subfield, and hemisphere were included as categorical predictor variables. For each subject, the Jacobian determinant from each subfield in both left and right hippocampi were considered as repeated measures, and the error term in the linear regression model was split into errors between- and within-subjects. Interactions between condition and subfield were also examined. The statistical results from this linear regression model showed a significant effect of condition (F = 8.35, P=0.007), a significant subfield effect (F=26.06, P<0.0001), a significant hemisphere difference (F=12.69, P=0.0004), and a significant condition by subfield interaction (F=3.66, P=0.0064). The post-hoc analysis indicates that the atrophy in every subfield is significantly smaller in the CDR 0 group than in the CDR 0.5 group (p<0.0001 in the subiculum, the rest subfield (CA2, 3, 4, gyrus dentatus) of left and right hippocampi, p=0.0071 and p=0.046 respectively for the left and right subfield of CA1). The atrophy in the subiculum and the rest subfield is significantly larger in the group CDR 0.5 than in the group of the converters, but not in the CA1. No significant group difference in the Jacobian determinant within every subfield is found between the groups of CDR 0 and converters. These results from the post-hoc analysis may suggest that the hippocampus shrunk in the subiculum, CA2, 3, 4, and gyrus dentatus at the similar atrophy rate in the groups of CDR 0 and converters. The CA1 may be the key region that would show significant group difference in the atrophy between the controls and converters if more samples were studied or a localized statistical analysis was applied. Thus, we discuss the localized analysis in the subsequent section.

3.2 Random Field Analysis in Global Template Coordinates

To characterize the pattern of surface deformation over time between two diagnostic groups at each location of the global template, we assumed that the anatomical deformation between the baseline and follow-up within subject arose from random processes. This was represented by the Jacobian determinant map (deformation map) F indexed over the global template M^atlas. In the global template coordinates, F was modeled as a random field and characterized by an infinite number of random variables F_i in the form of

$$F\left(x\right)=\sum _{i=1}^m{F}_i{\psi }_i\left(x\right),\text{where}{F}_i={\int }_{M^{\text{atlas}}}F\left(x\right){\psi }_i\left(x\right)d\nu \left(x\right).$$ (5)

v(x) is area measure at location x ∈M^atlas and ψ_i(x) is a basis function indexed over M^atlas. We chose ψ_i(x) to be the i th eigenfunction of the Laplace-Beltrami (LB) operator on M^atlas, the extension of the Laplacian from the regular grid to an arbitrary surface (Qiu et al., 2006). The LB eigenfunctions in Eq. (5) only depend on the geometry of the extrinsic atlas and not on F(x). The number of eigenfunctions (m) used in Eq. (5) was determined by goodness of fit, the sum square residual between observed values and the values expected under the model divided the sum square of observed values ($\frac{{\Sigma }_{j=1}^N{\mid F^{\left(j\right)}\left(x\right)-{\Sigma }_{i=1}^m{F}_i^{\left(j\right)}{\psi }_i\left(x\right)\mid }^2}{{\Sigma }_{j=1}^N{\mid F^{\left(j\right)}\left(x\right)\mid }^2}$, where j indexes subjects). At the discrepancy level of 0.05, the first twenty eigenfunctions (m = 20 ) were selected for both left and right sides of the hippocampus.

To identify the LB eigenfunctions that significantly contributed to longitudinal deformation difference between two diagnostic groups, we first examined the Wilcoxon rank-sum test on each random variable, F_i, i = 1, 2,…m in Eq. (5). Then two sets containing F_i with corresponding p-value less than 0.05 were associated with the left or right hippocampi, $S_m^L,S_m^R$, respectively, where the subscript denotes the number of eigenfunctions examined using the rank-sum test and the superscript represents left or right hippocampus. Finally, the subset of $S_m^L$ and $S_m^R$ was then chosen by optimizing the linear discriminant analysis (LDA) performance.

Assuming samples (X₁,L₁),…,(X_N,L_N) with X_i being feature vectors and L_i being the class label of subject i are independently and identically Gaussian distributed, LDA seeks best hyperplanes to separate the feature space into discriminant regions. The feature vectors, X_i, of the shape are selected from the joint set of $S_m^L$ and $S_m^R$ for fixed m and L_i take values of {1,…,L} . The linear discriminant analysis involves the estimation of prior probability π_l, the class-conditional mean vectors μ_l and covariance matrices ∑_l. Observation X is classified as belonging to class l is then obtained by maximizing the posterior probability: i. e.,

$$\underset{L}{⌢}(X\mid (X_i,L_i),i=1,\dots ,N)=\underset{l=\{1,\dots ,L\}}{\overset{\arg \max }{}}{\pi }_{l}P(X\mid L=l),$$

where P(X|L = l) is Gaussian with mean μ_l and covariance matrix ∑.

To select features from the joint set of $S_m^L$ and $S_m^R$ that best discriminated the two groups, the performance of the classifier was maximized with respect to m via leave-one-out cross validation. In every trial, one subject out of N subjects was selected as test data while the rest were used as training data. The probability of misclassification was estimated by

$$\widehat{e}(S_m^L,S_m^R)=\frac{1}{N}\sum _{i=1}^{N}I({\widehat{L}}_i\ne L_i\mid (X_j,L_j),X_j\in S_m^L\cup S_m^R,j=1,\dots ,N,j\ne i).$$

m was determined by minimizing

$$\widehat{m}=\underset{m=1,\dots ,20}{\overset{\arg \min }{}}\widehat{e}(S_m^L,S_m^R).$$

While the 26 subjects with CDR 0 and 18 subjects with CDR 0.5 were used in this analysis, it yielded the best classification performance at m = 19 with the minimal probability of $\widehat{e}(S_{19}^L,S_{19}^R)=6∕44\approx 0.13$. The p-value associated to this obtained classification rate under the hypothesis of no group difference is p = 0.0003, as estimated by permutation sampling. The same scheme was applied to distinguish converters from subjects with CDR 0, which yielded the best classification performance at m = 19 with the minimal probability of misclassification $\widehat{e}(S_{19}^L,S_{19}^R)=8∕35\approx 0.23$ (p = 0.0517).

To illustrate these results, we constructed statistically significant group difference in longitudinal shape deformation using the LB eigenfunctions in the form of

$${\widehat{F}}^{1\nu s2}\left(x\right)=\sum _{i\in S_{19}^k}({\stackrel{‒}{F}}_i^1-{\stackrel{‒}{F}}_i^2){\psi }_i\left(x\right),$$

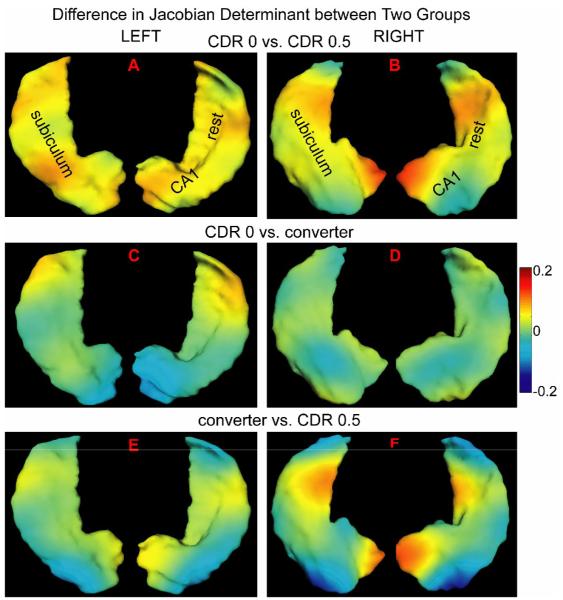
where ${\widehat{F}}^{1\nu s2}\left(x\right)$ denotes the group difference between groups 1 and 2. ${\stackrel{‒}{F}}_i^1$ and ${\stackrel{‒}{F}}_i^2$ respectively denote average F_i over group 1 and group 2: i was chosen from the set of $S_{19}^k$ containing eigenfunctions associated with p-value less than 0.05 in the rank-sum test. k corresponds to left or right side of the hippocampus. Fig. 6 illustrates the time-dependent deformation difference between any two groups. In this figure, panels (A, B) show the Jacobian difference in terms of longitudinal deformation between the CDR 0 and 0.5 groups in the left and right hippocampi, respectively. The map in panel (A) was constructed using {1,15,19}th LB eigenfunctions of the left global template while the map for the right hippocampus was using {1,4,10,16}th LB eigenfunctions of the right global template. Red denotes the outward surface deformation between the baseline and follow-up hippocampal shapes in the CDR 0 group relative to that in the CDR 0.5 group, while blue denotes the inward movement of the surface in the CDR 0. We constructed the group difference in the same way for comparisons between the CDR 0 and converter groups and between the converter and CDR 0.5 groups, respectively showing in the second and third rows of Fig. 6. Warmer colors denote an outward surface deformation between the baseline and follow-up in the former group relative to the later group, while cooler colors correspond to inward surface deformation.

Fig. 6.

Statistically significant shape difference between diagnostic groups is constructed using the eigenfunctions of the Laplace-Beltrami operator in the global template coordinates. The left and right columns respectively correspond to left and right hippocampi. Color encodes the Jacobian difference between two groups. The warm color denotes that the outward surface deformation in the former group relative to the later group, while the cool color corresponds to inward surface deformation.

The visualization shown in Fig. 6(A,B) suggest that the CDR 0.5 group showed more inward time-dependent surface deformation everywhere except the lateral aspect of the hippocampal head in the right side as compared to the CDR 0 group. The degree of inward surface deformation between the baseline and follow-up in the CDR 0.5 group slightly varied across the hippocampus. Fig. 6(C,D) also indicates that the lateral aspect of the hippocampal tail on both the left and right sides had a larger inward deformation in the converter group relative to the CDR 0 group. The head of the hippocampus had a lower rate of change in the converter group than in the CDR 0 group. The right hippocampus showed relatively similar effects of condition. In Fig. 6(E,F), the medial aspect of the hippocampus showed stronger inward surface deformation across time in the CDR 0.5 group than in the converter group. However, the lateral aspect of the hippocampal tail and head showed stronger outward surface deformation due to time in the CDR 0.5 group than in the converter group.

4. Discussion

We applied three levels of analysis for studying longitudinal shape variation of the hippocampus in subjects with early forms of AD. Moreover, we briefly introduced a novel technique, parallel transport in diffeomorphisms, under the LDDMM framework. For comparison of patterns of hippocampal deformation across time within- and between- groups, both ROI-based analysis and random field analysis via the LB eigenfunctions were applied. Our findings can be summarized as follows:

1. Time-dependent deformations of the hippocampal surface in each diagnostic group (CDR 0, converters, and CDR 0.5) were distinct (see Fig. 4). In a ROI-based analysis, there were statistically significant effects of condition, subfield, and interaction between them. The CDR 0.5 groups showed statistically significantly greater rates of inward deformation in the subfields of subiculum and the rest, as compared to the nondemented subjects and converters (see Fig. 5 and Table 1). The CDR 0.5 group also showed statistically significantly greater rates of inward deformation in the subfield of CA1, as compared to the nondemented subjects.

2. Using the random field model, we discovered possible local changes in the time-dependent deformations of the hippocampal surface between diagnostic groups as shown in Fig. 6. Inward surface deformation across time in the subjects with CDR 0.5 occurred non-uniformly across the hippocampus relative to the CDR 0 group. Compared to the CDR 0 group, the lateral aspect of the left hippocampal tail in the converters also showed inward surface deformation.

3. The surface deformation patterns were used as features in a linear discriminant analysis (LDA) and were able to distinguish subjects with early DAT from healthy aging subjects; the misclassification rate was impressively low (0.13). The misclassification rate for distinguishing converters from healthy aging subjects was larger (0.23). The misclassification rates were quantified using the training sets.

In our previous study (Wang et al., 2003), we applied large-deformation high-dimensional brain mapping to transform the hippocampus of each subject at each time point to a common template. The findings of the present study are consistent with the findings of this previous study, in that there was a greater rate of shape change (i.e., inward deformation), in the CDR 0.5 group than in the CDR 0 group. Moreover, we observed similar patterns in the head of hippocampus, the lateral aspect of the body of the hippocampus, and the most ventral surface of the hippocampus, which we interpreted as localized volume loss in the CA1 subfield and subiculum, in subjects with early DAT. However, the findings of the present study showed greater sensitivity than those in the previous study in the sense that inward progressive deformation of the hippocampal surface was observed in both healthy aging and early DAT, albeit with a different pattern. Moreover, for the first time, we report progressive deformations of the hippocampal surface in a group of subjects who converted from being non-demented to demented during the course of the study. In this particular group, we observed a greater inward deformation in the lateral aspect of the hippocampus (i.e., the region most closely associated with the CA1 subfield) relative to the CDR 0 group, but the magnitude of the deformation in the inferior-medial aspect of the hippocampus (i.e., the region most closely associated with the subiculum) was smaller as compared to that observed in the CDR 0.5 group.

Except for the frameworks for the longitudinal shape analysis proposed in this paper and in our previous study (Wang et al., 2003), tensor based morphometry has also been widely used to assess changes in brain structure in subjects with early DAT (Kipps et al., 2005, Brambati et al., 2007a, Brambati et al., 2007b). The general objective of tensor based morphometry (Ashburner et al., 1999, Ashburner and Friston, 2000, Chung et al., 2001, Chung et al., 2003) is to localize regions of shape difference among clinical population of brain images based on the deformation fields that map a template to each individual subject. Moreover, in the longitudinal studies (e.g (Kipps et al., 2005), the deformation fields can be obtained by mapping the one at baseline to the one at following. In order to perform statistical testing across subjects, such deformation fields have to be represented in a global template, which were accomplished by modulating them by the Jacobian determinants from the registration between the global template and the subject at the baseline. It thus becomes to the problem demonstrated in our previous study (Wang et al., 2003); that is, across-subject deformations, which are in general larger than within-subject deformation, can substantially the results. In contrast, the parallel transport operation presented in this paper translates within-subject deformation across time points to a global template without incorporating across-subject deformation, and thus offers increased power for detecting longitudinal shape changes. This operation also preserves the metric distance defined in LDDMM (Younes, 2007).

In summary we used a new method, parallel transport in diffeomorphisms under the LDDMM framework, to study longitudinal variation of the surface shape of the hippocampus in subjects with and without early forms of AD. This new method shows great promise for improving our ability to identify and characterize neuroanatomical changes in individuals with very early forms of AD. In the future, these methods may also help us to improve our ability to characterize neuroanatomical asymmetries, and integrate structural neuroimaging data from different sites.