Metabolic Labeling Reveals Proteome Dynamics of Mouse Mitochondria

Abstract

Mitochondrial dysfunction is associated with many human diseases. Mitochondrial damage is exacerbated by inadequate protein quality control and often further contributes to pathogenesis. The maintenance of mitochondrial functions requires a delicate balance of continuous protein synthesis and degradation, i.e. protein turnover. To understand mitochondrial protein dynamics in vivo, we designed a metabolic heavy water (²H₂O) labeling strategy customized to examine individual protein turnover in the mitochondria in a systematic fashion. Mice were fed with ²H₂O at a minimal level (<5% body water) without physiological impacts. Mitochondrial proteins were analyzed from 9 mice at each of the 13 time points between 0 and 90 days (d) of labeling. A novel multiparameter fitting approach computationally determined the normalized peak areas of peptide mass isotopomers at initial and steady-state time points and permitted the protein half-life to be determined without plateau-level ²H incorporation. We characterized the turnover rates of 458 proteins in mouse cardiac and hepatic mitochondria and found median turnover rates of 0.0402 d⁻¹ and 0.163 d⁻¹, respectively, corresponding to median half-lives of 17.2 d and 4.26 d. Mitochondria in the heart and those in the liver exhibited distinct turnover kinetics, with limited synchronization within functional clusters. We observed considerable interprotein differences in turnover rates in both organs, with half-lives spanning from hours to months (∼60 d). Our proteomics platform demonstrates the first large-scale analysis of mitochondrial protein turnover rates in vivo, with potential applications in translational research.

Mitochondrial dysfunctions are observed in disorders such as neurodegeneration, cardiovascular diseases, and aging (1–3). It is postulated that the failure to contain or replenish mitochondrial proteins damaged by reactive oxygen species directly underlies many pathological phenotypes (4). The development of effective treatments for these diseases therefore relies on understanding the molecular basis of protein dynamics. Outstanding questions are how the processes of mitochondrial proteome dynamics are regulated in different systems, and how their perturbations could progress to pathological remodeling of the organelle. Thus far, quantitative proteomics efforts have been predominated by steady-state measurements, which often provide fragmentary snapshots of the proteome that are difficult to comprehend in the context of other cellular events.

To further understand mitochondrial dynamics in vivo, we examined the turnover rates of individual heart and liver mitochondrial proteins on a proteome scale. Both the liver and the heart contain large numbers of mitochondria, but cardiac and hepatic mitochondria differ in their protein composition, oxygen consumption, substrate utilization, and disease manifestation. However, these differences are often interpreted only by protein compositions and steady-state abundance, without the consideration of protein kinetics in the temporal dimension. Abnormal protein kinetics may indicate dysfunctions in protein quality control, the accumulation of damaged proteins, misfolding, or other proteinopathies. Protein dynamics itself is an important intrinsic property of the proteome, the disruption of which could be causal of cellular etiologies.

At minimum, a kinetic definition of the proteome requires knowledge of the rate at which individual proteins are being replaced. Isotope tracers are particularly useful for tracking such continual renewal of the proteome in living systems, because they allow differentiation between preexisting and newly synthesized proteins (5). Among the available stable isotope precursors, heavy water (²H₂O) labeling offers several advantages with respect to safety, labeling kinetics, and cost (6, 7). First, ²H₂O administration to animals and humans at low enrichment levels is safe for months or even years (8). Second, maintaining constant ²H enrichment levels in body water following the initial intake of ²H₂O is easily achieved, because administrated ²H₂O rapidly equilibrates over all tissues but decays slowly (9, 10). Third, ²H₂O labeling is more cost effective than other stable isotope labeling methods. Importantly, ²H₂O intake induces universal ²H incorporation into biomolecules. Systematic insights into protein turnover in vivo could therefore be correlated to that of nucleic acids, carbohydrates, or lipids, enabling broad applications for this technology in studying mammalian systems, including humans.

A variety of methodologies have been developed to analyze the extent of ²H incorporation in proteins following ²H₂O labeling, including GC-MS measurements of hydrolyzed target proteins (11–14) and peptide analysis in MALDI-TOF MS (15) and LC-MS (16, 17). More recently, Price et al. described an approach for measuring protein turnover by calculating the theoretical number of ²H-labeling sites on a peptide sequence (18) and reported the turnover rates of ∼100 human plasma proteins. Here we describe another novel strategy to determine protein turnover rates on a proteomic scale using ²H₂O labeling. By computing the parameters needed to deduce fractional protein synthesis using software we developed, we were able to obtain protein half-life data without relying on the asymptotic isotopic abundance of peptide ions. Our approach also has the unique benefit of automating all steps of isotopomer quantification and postcollection data analysis, and it does not require knowledge of the exact precursor enrichment or labeling sites of peptides. We observed diverse kinetics from 458 liver and heart mitochondrial proteins that inform essential characteristics of mitochondrial dynamics and intragenomic differences between the two organs.

EXPERIMENTAL PROCEDURES

²H₂O Labeling of Mice and Tissue Collection

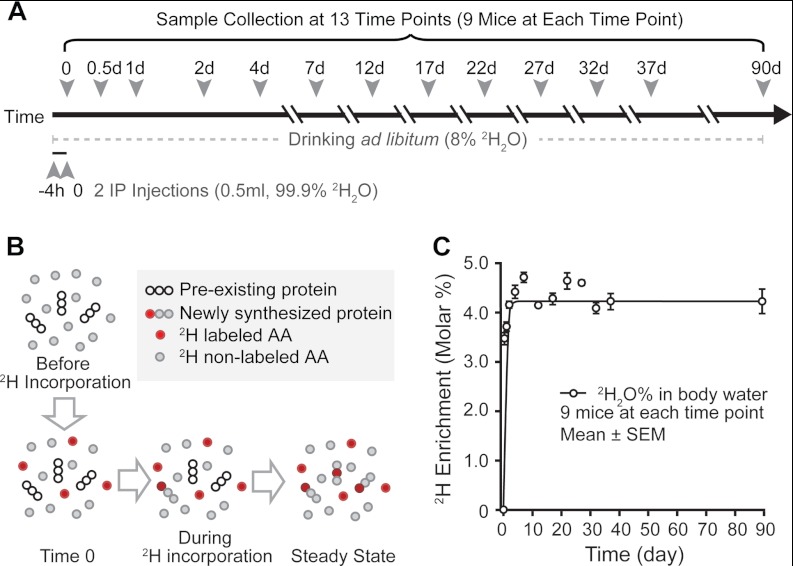
All animal experiments were conducted in accordance with the National Research Council's Guide for the Care and Use of Laboratory Animals and approved by the University of California, Los Angeles. Male Hsd:ICR (CD-1) outbred mice (8 to 10 weeks of age) (Harlan Laboratories, Indianapolis, IN) were housed upon arrival in a 12:12 h light-dark cycle with controlled temperature and humidity and free access to standard lab chow and natural water. No significant change was observed in the body weights of mice (∼40 g) during the labeling period. ²H₂O labeling was initiated by two intraperitoneal (IP) injections of 99.9% saline ²H₂O (Cambridge Isotope Laboratories, Andover, MA) spaced 4 h apart; then mice were allowed free access to 8% ²H₂O to maintain a steady-state labeling level at ∼4.5% in body water (Fig. 1A). Heart, liver, and blood were harvested at 13 time points (0, 0.5, 1, 2, 4, 7, 12, 17, 22, 27, 32, 37, and 90 d) from the second IP injection (t = 0). At each time point, three groups of three mice each were euthanized. All three groups from each time point were used to determine the extent of ²H labeling in body water; one group was used to calculate protein turnover rates.

Fig. 1.

Metabolic labeling of mice using heavy water. A, schematic of ²H₂O labeling of mouse and sample collection. Twelve groups of 9 mice were given two IP injections of 99.9% ²H₂O/saline, followed by ad libitum drinking of 8% ²H₂O to maintain enrichment levels. Samples were collected at each time point of 0, 0.5, 1, 2, 4, 7, 12, 17, 22, 27, 32, 37, and 90 d of labeling. B, ²H₂O labeling introduces ²H-labeled amino acids into the precursor pool for protein synthesis. Continuous protein turnover increases the ²H enrichment level in the protein pool until it reaches steady state. Measurement of ²H incorporation during the labeling period provides the information about protein turnover. C, molar percent enrichment of ²H in mouse serum during ²H₂O feeding was measured via GC-MS at 13 time points. Enrichment reached 3.5% within 12 h after two IP injections of 99.9% ²H₂O/saline and stayed at ∼4.3% throughout the labeling period with 8% ²H₂O feeding. Each data point represents an average of three biological replicates; error bar indicates S.E.

GC-MS Analysis of Serum Water

²H labeling in body water was measured via GC-MS after exchange with acetone as described elsewhere (13). Serum was centrifuged for 20 min at 4,000 rpm at 4 °C, and 20 μl of serum or ²H₂O standard for calibration curve was reacted with 2 μl of 10 N NaOH and 4 μl of 5% (v/v) acetone in acetonitrile (ACN). After overnight incubation at ambient temperature, acetone was extracted by adding 500 μl of chloroform and 0.5 g of anhydrous sodium sulfate, and 300 μl of the extracted solution was aliquoted and analyzed on a GC¹ mass spectrometer (Agilent 6890/5975) with an Agilent J&W DB17-MS capillary column (30 m × 0.25 mm × 0.25 μm). The column temperature gradient was as follows: 60 °C initial, 20 °C/min increase to 100 °C, 50 °C/min increase to 220 °C, and 1 min hold. The mass spectrometer operated in the electron impact mode (70 eV) and selective ion monitoring at m/z 58 and 59, with a 10 ms dwell time.

Isolation of Cardiac and Hepatic Mitochondria

Mitochondria were isolated by means of ultracentrifugation as described elsewhere (19). Hearts and livers were excised from euthanized mice, homogenized in the homogenization buffer (250 mmol/l sucrose, 10 mmol/l HEPES, 10 mmol/l Tris-HCl, 1 mmol/l EGTA, protease inhibitors (Roche Complete, 1×), phosphatase inhibitors (Sigma Phosphatase Inhibitor Mixture II and III, 1×), and 10 mmol/l of dithiothreitol (Sigma), pH 7.4), and then centrifuged at 800 relative centrifugal force (rcf) at 4 °C for 7 min. The supernatant was centrifuged at 4,000 rcf at 4 °C for 20 min. The pellets were washed, centrifuged again, resuspended in 19% (v/v) Percoll (Sigma) in the homogenization buffer, overlaid on 30% and 60% Percoll, and ultracentrifuged at 12,000 rcf at 4 °C for 20 min to remove microsomes. Purified mitochondria were collected from the 30%/60% Percoll interface, washed twice, centrifuged at 4,000 rcf at 4 °C for 20 min, and then lysed by sonication in 10 mmol/l Tris-HCl, pH 7.4.

Electrophoresis and In-gel Digestion of Proteins

Mitochondrial proteins were separated via SDS-PAGE; 200 μg of proteins were denatured at 70 °C in Laemmli sample buffer for 5 min and then separated on a 12% Tris-glycine acrylamide gel with 6% stacking gel, at 80 V, at ambient temperature for ∼19 h. The gel was Coomassie-stained and cut into 21 fractions. Each fraction was digested with 30:1 (w/w) sequencing-grade trypsin (Promega, Madison, WI) following reduction and alkylation by dithiothreitol and iodoacetamide (Sigma), respectively.

LC-MS and MS/MS

Peptide identification and mass isotopomer quantification were performed on an LTQ Orbitrap XL mass spectrometer (ThermoFisher Scientific, San Jose, CA), coupled to a nanoACQUITY UPLC system (Waters, Manchester, UK). The trapping (30 mm) and analytical (200 mm) columns for peptide separation were packed in IntegraFrit columns (New Objective, Woburn, MA) (360-μm outer diameter, 75-μm inner diameter) using Jupiter Proteo C₁₂ resin (Phenomenex, Torrance, CA) (90-Å pore, 4-μm particle). The binary buffer system consisted of 0.1% formic acid in 2% and 80% ACN for buffers A and B, respectively. The separation gradient was made by changing buffer B as follows: 0 min, 2%; 0.1 min, 5%; 70 min, 40%; 90 min, 98%; 100 min, 98%; and 105 min, 2%, with subsequent equilibrium at 2% for 5 min. Mass spectra were obtained in profile mode for MS survey scan in the Orbitrap at a resolution of 7,500 and in centroid mode for MS/MS scan in the LTQ. The top five intense peaks in the MS scan were subjected to collision-induced dissociation with an isolation window of 3 Th and a dynamic exclusion of 25 s.

Database Search for Protein Identification

The raw data were processed uisng BioWorks, version 3.3.1 SP1 (ThermoFisher Scientific), and searched using SEQUEST, version 3.3.1 (ThermoFisher Scientific), against the UniProt mouse database (July 27, 2011; 55,744 entries). Search parameters included fixed cysteine carbamidomethylation and variable methionine oxidation, trypsin enzymatic specificity, and two missed cleavages. The mass tolerances for the precursor and the product ions were 100 ppm and 1 Th, respectively. The minimum redundancy set of proteins was acquired with Scaffold, version 3.3.3 (Proteome Software, Portland, OR). At least two peptides and 99.0% protein confidence were required for protein identification, and the global false discovery rate was 0.1%. Peptides shared by multiple proteins or protein isoforms were excluded from downstream turnover rate calculations.

Quantification of Mass Isotopomers

²H in body water is metabolically incorporated into the C–H bonds of free nonessential amino acids by multiple enzymes (11). Unlike labile N–H or O–H bonds, the C–H bonds are stable, and the incorporated ²H in nonessential amino acids do not back-exchange during sample processing. Additionally, H in the α-carbon of essential amino acids is reversibly accessible to ²H via transamination. The ²H-labeled amino acids are integrated into newly synthesized protein via t-RNAs and, with each cycle of turnover, into proteins until their ²H content reaches steady-state equilibrium with surrounding ²H₂O. The rate of protein turnover is determined by tracking the time evolution of mass isotopomer distributions (Fig. 1B). To accommodate the determination of the protein turnover rate on a proteomic scale, in-house software was developed in Java that contained two modules, one for quantifying the peptide ion mass isotopomer distribution (IsotoQuan) and the other for curve fitting to determine the rate constants of protein turnover (RateQuan). RAW files were converted into mzML format using ProteoWizard (version 2.2.2913) for input. IsotoQuan extracts the extracted ion chromatogram (XIC) for each identified peptide ion using retention time and a mass isolation window of ±100 ppm. Then, the peak area under the XIC is integrated to determine the normalized abundances of all mass isotopomers corresponding to a peptide ion. At any given time point t, the normalized peak area for a designated mass isotopomer, A_i(t), is determined by dividing the peak area I of the mass isotopomer i (i.e. I_i(t), over the summation of peak areas from all mass isotopomers $\left({\displaystyle {\sum }_{j=0}^N{I}_j\left(t\right)}\right)$.

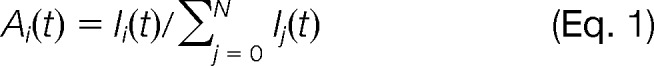where I_j is the peak area of the mass isotopomer m_j (j = 0, 1, 2, …, N).

Calculation of Protein Turnover Rates

To determine the protein turnover rate, the normalized peak intensities at t = 0, A(0), and at full enrichment, A(∞), were defined from the time-series data of each mass isotopomer via nonlinear fitting into a first-order kinetics equation.

where k is the rate constant, which describes the rate at which proteins are newly synthesized to replace the existing pool; assuming equilibrium, it equals the rate at which proteins are degraded. Subsequently, the time-series data of all mass isotopomers from a protein were transformed into fraction synthesis, f(t), which is the fraction of total protein newly synthesized through turnover, by rearranging Equation 2.

RateQuan excluded data from the curve fitting with an R² value less than 0.7 or containing fewer than five time points from the calculation of fractional synthesis. The chosen R² value of 0.7 was adjudged empirically to balance high accuracy and precision in the measurement of the kinetic data. As A(0) and A(∞) are theoretically bound between 0 and 1, only experimental values between −0.1 and 1.1, in consideration of experimental errors, were included in fractional synthesis calculation. Finally, fractional syntheses from all of the mass isotopomers corresponding to a particular protein were fitted to the first-order kinetics equation (Equation 3) to determine k for protein turnover.

Statistical Analyses

Uncertainties in rate constants were estimated using the Monte Carlo method. The distribution of the relative abundance was approximated using the absolute value of the residues. At each measured time point, a single point was synthetically generated using random numbers from a Gaussian distribution with the same width as the distribution of the absolute values of the residuals and a mean of the model value. New rate constants were determined for the 10,000 synthetic datasets, and the distribution of rates was observed to converge approximately to a Gaussian distribution. The width of this distribution (1σ) was reported as the standard error of the rate constant. (In principle, there is little difference between the standard error estimations of the Monte Carlo and nonlinear curve fitting methods. For comparison, the histograms of the errors in the rate constants for cardiac proteins are given in supplemental Fig. S4.) Quantile-quantile plots clearly suggest that degradation rates of proteins within an organ are not normally distributed. The significance of differences between groups was thus assessed via the rank-based, nonparametric Mann-Whitney U test using R. Correlations between variables were denoted by Spearman's rank-correlation coefficient (ρ).

RESULTS

Precursor Enrichment in Serum during ²H₂O Labeling

Fractional protein synthesis is calculated based on the precursor-product relationship, which states that product labeling enrichment would reach that of the precursor at steady state. To quantify the level of precursor ²H incorporation during labeling, the serum of mice was sampled at all experimental time points. As water quickly equilibrates throughout the body and permeates cellular compartments, water in the serum serves as a proxy for ²H incorporation in all organs. GC-MS experiments measured the molar percentage of ²H in serum water, which rapidly reached 3.5% within 12 h following two IP injections of 99.9% ²H₂O (Fig. 1C). Throughout the labeling period, ad libitum feeding of 8% ²H₂O maintained ²H enrichment at ∼4.3% (Fig. 1C). The speed and stability of ²H incorporation in our experiment support the calculation of fractional synthesis from constant precursor enrichment.

Time Evolution of Mass Isotopomer Abundance Distribution of ²H-labeled Peptides

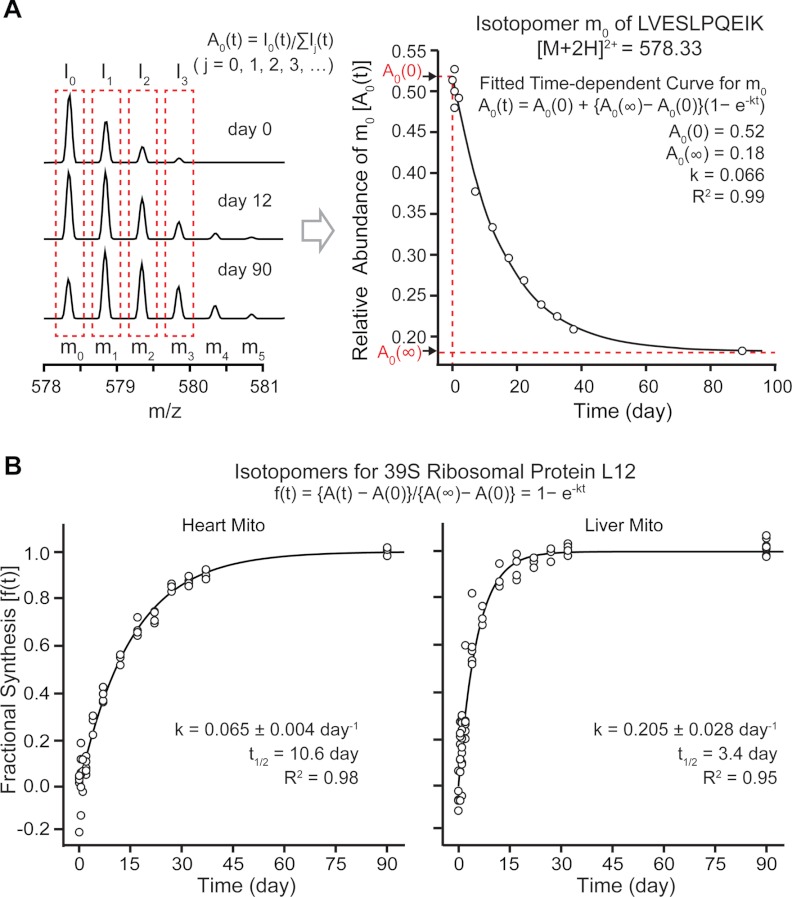
Mass isotopomer distributions of peptide ions change over time as ²H is introduced from the precursor pool into the protein pool through protein turnover. Fig. 2A displays the temporal profile (0 to 90 d) of mass isotopomer distributions for a given tryptic peptide LVESLPQEIK, [M+2H]²⁺ = 578.33 m/z, from the mitochondrial 39S ribosomal protein L12 (MRPL12). Prior to ²H₂O labeling (0 d), the first mass isotopomer (m₀) gave the most intense peak. When the labeling time reached 12 d, the peak intensity of m₀ became comparable to that of m₁, and one new feature corresponding to m₄ was observed. After 90 d of labeling, m₀ became the third most intense mass isotopomer, and the high-mass isotopomer peak m₅ appeared. In summary, ²H₂O labeling resulted in anticipated changes in isotopomer peak intensity that allowed protein fractional synthesis to be calculated. Accordingly, we proceeded with the proteome scale characterization of protein turnover from the heart and liver mitochondria isolated from the same animals.

Fig. 2.

Extracting protein turnover rates from the temporal profile of mass isotopomer distribution. A, the profile of the relative abundances for mass isotopomers of LVESLPQEIK ([M+2H]²⁺ = 578.33 m/z) from mitochondrial 39S ribosomal protein L12 as a function of labeling time. ²H₂O labeling for 90 d resulted in a decrease in the normalized peak intensity of m₀ (I₀) and appearances of extra higher mass isotopomer peaks of m₄ and m₅. The values for A₀(0) = 0.52, A₀(∞) = 0.18, and k = 0.066 d⁻¹ for m₀ of the peptide were obtained by fitting to an exponential curve (R² = 0.99) and then transformed into fractional synthesis f(t) with the following equation: f(t) = {A(t) − A(0)}/{A(∞) − A(0)}. Although the fitting also provides information on the rate constant for protein turnover (k), this parameter is neglected at this stage because our method determines the k value at the peptide level, not at the mass isotopomer level. B, the protein turnover rate was determined by fitting the fractional syntheses of mass isotopomers of a protein throughout the labeling period into an exponential curve. Individual data points represent the mass isotopomers of peptide ions belonging to mitochondrial 39S ribosomal protein L12 at the 13 labeling time points. The turnover rates for this protein in the heart and the liver are 0.065 ± 0.004 d⁻¹ (R² = 0.98) and 0.205 ± 0.028 d⁻¹ (R² = 0.95), respectively.

The intensities of mass isotopomers were quantified using computational software developed to integrate the areas under the peak in the XIC and then normalized by the intensity of all isotopomers in a particular peptide ion to determine its relative abundance (Equation 1). For every mass isotopomer with quantification data at five or more time points, the relative abundances from all time points were fitted to an exponential decay equation (Fig. 2A). For a particular mass isotopomer, multiple normalized peak intensities might exist as a result of the detection of the identical peptides in multiple gel bands, different charge states, or the oxidized forms. Identical isotopomers from multiple gel bands were combined but were otherwise fitted independently. The fitting is extrapolated to yield the normalized abundance of the mass isotopomer at its initial (A(0)) and steady (A(∞)) states.

In summary, we have applied two distinct criteria for peptide selections. The first is concerned with the protein identification, for which Scaffold was used to validate and filter peptides based on their confidence levels. The second addresses the precision of curve fitting by using an R² threshold filter. Mass isotopomers that met these two criteria (see detailed descriptions in the “Experimental Procedures” section) were accepted for protein turnover rate calculations.

Rates of Protein Turnover in Cardiac and Hepatic Mitochondria

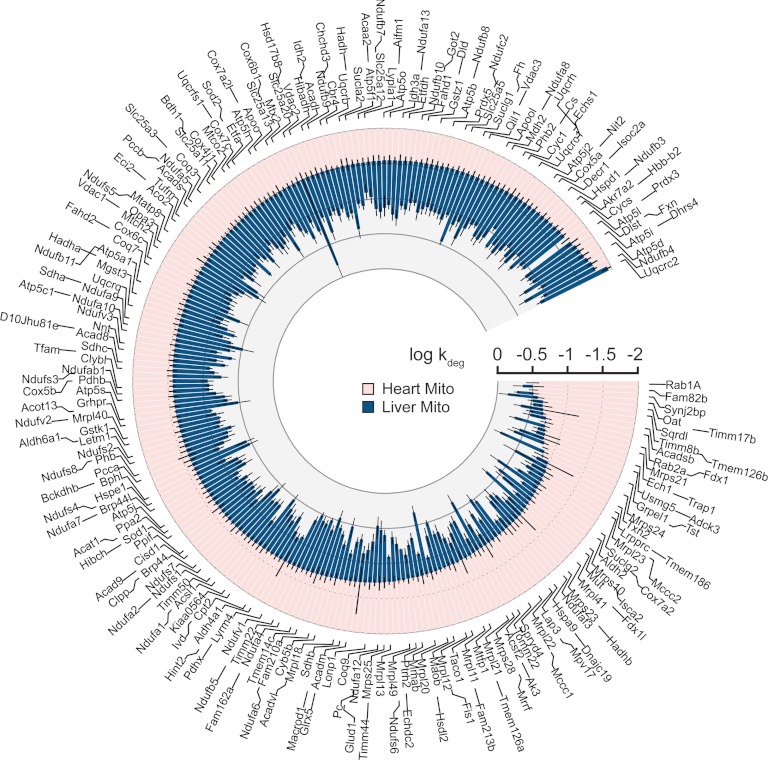
From the fitted A(0) and A(∞) values, all isotopomer data of a protein were transformed into protein fractional synthesis using Equation 3. For m₀ at some early time points, experimentally measured A(t) could be larger than the computationally determined A(0) because of the fitting error, which leads to a negative fractional synthesis value. We found that filtering by R² value at this point excluded unquantifiable isotopomers and improved the accuracy of turnover rate calculation without significantly impacting the number of analyzed proteins. Fig. 2B shows an example of fractional synthesis time evolution from the mitochondrial 39S ribosomal protein L12. The fractional synthesis data were fitted to an exponential curve to yield the protein turnover rate k. The 39S ribosomal protein L12 turns over at a rate of 0.065 ± 0.004 d⁻¹ (R² = 0.98) in the heart, but turnover is almost three times faster in the liver, at 0.205 ± 0.028 d⁻¹ (R² = 0.95) (Fig. 2B). Such differences in turnover rates were generally observed between mitochondrial proteins in the heart and in the liver; the median turnover rate was about four times higher in the liver than in the heart (0.040 d⁻¹ versus 0.16 d⁻¹). With the exception of three proteins (MRPS24, RAB1A, and SYNJ2BP), all 242 commonly analyzed proteins demonstrated slower turnover (i.e. longer half-life) in cardiac mitochondria (Fig. 3). In total, we deduced the turnover of 314 proteins in cardiac mitochondria and 386 in hepatic mitochondria, of which 458 are distinct. This study captured mitochondrial proteins in all major functional categories, spanning 5 orders of magnitude in protein abundance (see supplemental Fig. S3). The fractional synthesis curves of all proteins are in supplemental Figs. S1 and S2. All kinetic data are listed in supplemental Table S1.

Fig. 3.

Analyses of turnover rates of mitochondrial proteins identified in both heart and liver. The cardiac k_deg values (red) are plotted in ascending order on a logarithmic scale and paired with the corresponding hepatic k_deg values from the same protein (blue). Among the 242 proteins analyzed in both organs, only 3 had smaller turnover rates in the liver than in the heart. Error bars represent S.E.

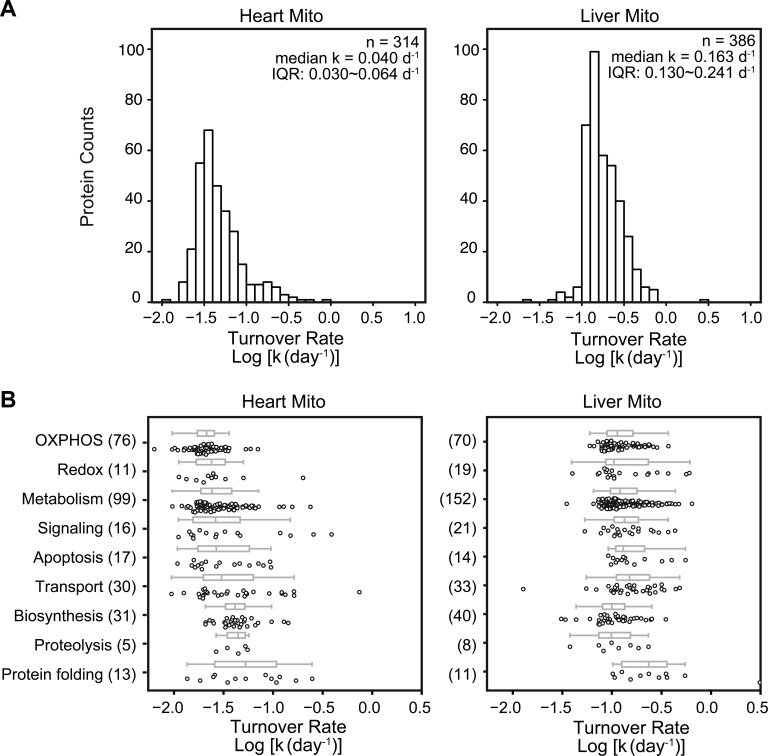
Fig. 4A shows the distribution of turnover rates in the analyzed proteins in the liver and the heart. The analyzed protein kinetics ranged over 2.4 orders of magnitude in total and spanned 1.8 and 2.2 orders of magnitude in the heart and the liver, respectively. Between the 5th and 95th percentiles, protein turnover rates differed by 7.9-fold in the heart and 4.3-fold in the liver. To determine whether the observed turnover rates correlated with biological functions, we categorized the observed cardiac and hepatic mitochondrial proteins using Gene Ontology (Fig. 4B). In both tissues, proteins associated with protein folding showed relatively faster turnover, whereas those related to redox turned over rather slowly. In contrast, proteins involved with biosynthesis and proteolysis displayed disparate turnover between the two tissues. Biosynthesis proteins had fast turnover in the heart but not in the liver. However, significant overlaps in turnover rates were observed among the functional categories in both the liver and the heart.

Fig. 4.

Distributions of protein turnover rates and their correlations with functions. A, histograms of protein turnover rates in heart and liver mitochondria. Proteins in the heart have slower turnover rates than those in the liver (median k = 0.042 d⁻¹ versus 0.163 d⁻¹). B, the measured turnover rates of murine mitochondrial proteins against their Gene Ontology categories. Boxes: interquartile range and median; whiskers: data range up to 1.5 interquartile ranges. The numbers of analyzed proteins in the category are presented in parentheses.

DISCUSSION

We demonstrated a novel strategy utilizing ²H₂O labeling to examine the kinetics of mitochondrial proteins in mouse heart and liver on a large scale. Our computational approach, created in-house, automated the characterization of fractional protein synthesis and deduced protein half-life without steady-state isotopomer abundance information. With this integrated platform of MS and informatics, we successfully obtained the turnover rates of 458 proteins in mouse cardiac and hepatic mitochondria.

Data Analysis

A recent investigation by Price and coworkers (18) further elevated the utilities of the ²H₂O labeling method in evaluating protein turnovers. In their elegantly designed study, A(∞) was determined from the precursor enrichment and the theoretical number of ²H incorporation into a peptide, derived from its sequence and established labeling sites for each amino acid. In our approach, the plateau ²H enrichment in the peptide was computationally deduced from the experimental data points. In addition, all data processing was fully automated, which enabled us to overcome the limitations in throughput.

In analyzing our large-scale set of data points, we considered the following when addressing the experimental errors, which can be contributed by multiple sources. Firstly, the experimental error is directly linked to experimental conditions, including the reliability of the peak area measurement, the separation of overlapped chromatographic peaks, spectral accuracy, and absolute peak intensities. Secondly, our study makes the assumption of first-order kinetics in our curve fitting to extract the kinetic information; under the scenario in which this kinetics is forced, a larger error will result. Ostensibly, the first-order kinetics model that we used in our study does not hold homogeneously for all experimental data. In other words, proteins whose turnover deviated from first-order kinetics would be fitted with a larger error. Thirdly, we filtered out redundant peptides from known protein isoforms to ensure that only unique peptides were selected for individual proteins, and to avoid ambiguity in the protein kinetics calculation. However, peptides shared by either undocumented or undiscovered isoforms might remain, subsequently causing an increased error formation in data processing.

Extensive fractionation and enrichment procedures were conducted to yield functionally viable mitochondria (19). The majority of the detected proteins are classically established mitochondria proteins. However, some identified proteins may be classified as mitochondria-associated proteins, whereas some nonmitochondrial contaminants inevitably remain in a mitochondrial isolation. Because of our stringent criteria in filtering both protein identification and turnover data, common contaminant proteins (e.g. keratin) were automatically expunged from the final kinetic data. We surmised that among the 458 analyzed proteins, 1 protein represented a highly likely nonmitochondrial contaminant (hemoglobin subunit beta-2 (HBB-B2)). Incidentally, our approach detected almost identical turnover rates (k = 0.021 d⁻¹) for only HBB-B2 in liver and heart mitochondria, which suggests the shared blood origin of the HBB-B2 protein from the two independent experiments. These data independently validate the reproducibility of our technology platform.

Rules Governing Turnover Rate of Proteins

Other metabolic labeling studies suggest that protein turnover rates differ across mammalian organs (20, 21). Our results demonstrate that such tissue-specific differences are preserved in the mitochondrial proteome (Fig. 3), supporting the hypothesis that intragenomic differences in organ phenotypes directly constrain mitochondrial protein dynamics. The turnover rates cannot be explained by liver cell turnover, as mouse liver DNA has a half-life exceeding 300 d (22).

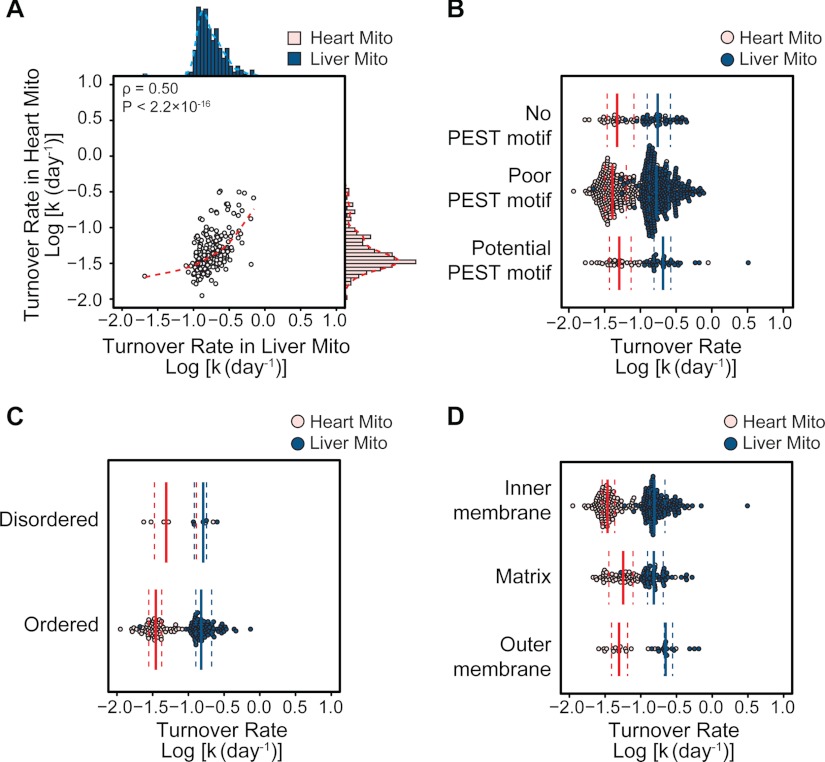
We observed good correlation between protein turnover rates in the heart and in the liver (Spearman's ρ = 0.50, p < 2.2 × 10⁻¹⁶) (Fig. 5A), suggesting that the determined distribution of protein turnover is robust. However, the correlations are not without exceptions, which indicates additional layers of regulatory mechanisms. Several models were proposed in the literature to explain the diversity in turnover rates, either within mitochondria or across the whole cell. We further investigated whether some of these intrinsic protein properties might account for the turnover rates in our large-scale dataset. The presence of the PEST motif (23) and intrinsic protein sequence disorder (24) have been proposed as determinants of protein kinetics. We found no proteome-wide evidence of distinct turnover for both features in either organ (Mann-Whitney U test, p > 0.05) (Figs. 5B and 5C), corroborating a recent report (25). Our data support previous observations that proteins on the outer mitochondrial membrane turn over faster than those on the inner membrane (Mann-Whitney U test, heart: p = 5.55 × 10⁻³; liver: p = 5.21 × 10⁻⁴) (Fig. 5D), suggesting possibilities of greater accessibility to extramitochondrial degradation mechanisms (26). A minimal inverse correlation was observed between half-life and protein abundance in both the heart (ρ = −0.46 and p < 2.2 × 10⁻¹⁶) and the liver (ρ = −0.19, p = 7.95 × 10⁻³) (supplemental Fig. S3), whereas no significant correlation was observed between turnover rate and protein molecular weight, isoelectric point, or hydrophobicity (supplemental Fig. S3). Taken together, these data argue that protein kinetics, similar to abundance, is a selectable trait of the proteome subject to cellular regulations.

Fig. 5.

Factors affecting mitochondrial protein turnover. A, protein turnover rates in the heart and the liver were significantly correlated (Spearman's ρ = 0.50). B, PEST motifs and C, intrinsic protein sequence disorders were not indicative of protein turnover rates. D, comparison between submitochondrial locations revealed that median turnover is higher in the outer membrane than in the inner membrane. The solid and dotted lines in B, C, and D denote the median and the interquartile range, respectively.

Turnover of Multiprotein Complexes

As mentioned above, protein turnover rates within mitochondrial types are quite variable. The subunits of multiprotein complexes have been suggested to have coordinated turnover (20), but notable exceptions also have been reported (25, 27). In our experiments, subunits of well-defined protein complexes displayed variable kinetics, but particular members of intermediate subcomplexes may turn over together in a tighter fashion. For instance, in the respiratory chain complex I, assembly factors turned over considerably faster than the protein complex median. In the heart, NDUFAF2 and NDUFAF3 had k = 0.053 and 0.078 d⁻¹, compared with the median complex I value of 0.036 ± 0.007 d⁻¹. The assembly factor proteins are integral to complex I topogenesis but dissociate from the mature complex. In contrast, the core subunits of the Q subcomplex (NDUFS2, NDUFS3, NDUFS7, and NDUFS8) turned over similarly (heart: k = 0.039 d⁻¹, 0.036 d⁻¹, 0.042 d⁻¹, 0.039 d⁻¹). We suggest that subunits with faster turnover might be more frequently exposed to or have existed as free monomers because of assembly sequence or topology (supplemental Table S1). Under this scenario, turnover rates are influenced by the stability of the association with the final assembly, whereas in the synchronized complex model, all constitutive subunits have similar turnover kinetics. We further examined the data on the subunit NDUFA9, which has a relatively fast turnover among all subunits only in the liver (k = 0.27 d⁻¹), but not in the heart (k = 0.035 d⁻¹). In complex I biogenesis, the Q subcomplex first assembles before NDUFA9 associates with the mitochondrial-encoded ND1 to initiate the assembly of the next intermediate (28). ND1 has a considerably lower abundance in the liver than in the heart relative to other subunits, a scenario consistent with increased surplus NDUFA9 free subunits. Likewise, the NDUFA4 and NDUFS7 subunits have above-median turnover in both organs (NDUFA4: heart, k = 0.047 d⁻¹, liver, k = 0.30 d⁻¹; NDUFS7: heart, k = 0.042 d⁻¹, liver, k = 0.028 d⁻¹) and are incorporated only after stable intermediates are formed (28). Future investigations on protein kinetics are required in order to determine in-depth mechanistic insights on complex assembly.

Protein Turnover in Mitochondria

It is known that autophagy can degrade whole mitochondria when induced (29) and act as a synchronizing mechanism for protein kinetics inside the organelle. Indeed, the overall range of mitochondrial protein turnover rates we observed is much narrower than that reported for the cellular proteome. Nevertheless, the observation that individual mitochondrial protein turnover rates span at least an order of magnitude within an organ suggests that individual mitochondria cannot be simplistically assumed to turn over only as single units. In theory, the assumption of steady-state protein abundance in inferring turnover from synthesis may be transiently offset by bouts of occasional mitophagy and remains valid over the labeling period. However, because we measured protein turnover from isolated mitochondria, we reason that given the observed variability in synthesis rates, at any moment each mitochondrion contains some proteins that have been more recently synthesized than others. If mitophagy were predominant in the process of mitochondrial protein removal, then many mitochondria in the cell would be missing critical components. As this circumstance is unlikely, a mechanism is necessary to allow mitochondria with new and old proteins to preserve homeostasis under mitophagy. Mitochondrial proteins may be synthesized in excess in the cytosol at variable rates before entering the mitochondria simultaneously. Alternatively, a sorting mechanism prior to autophagy could exist such that some protein species would be preferentially recycled during fusion-fission cycles. Given that evidence of either possibility remains scarce, we posit that it is likely that individual substrate proteolysis plays significant roles in mitochondrial dynamics. The asynchronous degradation of mitochondrial proteins is attested to by the multiple protease complexes inside mitochondria. Under this model, measuring total organellar protein synthesis as a proxy for homeostasis would be an inadequate means of capturing the details of mitochondrial protein turnover. Our findings underscore the significance of obtaining a proteome dynamics map at individual protein resolution in uncovering signatures of protein quality control dysfunctions, such as in aging and metabolic perturbation studies.

In conclusion, we demonstrated the first mitochondrial proteome-wide study of in vivo protein dynamics. The experimental platforms tailored to the analysis of changes in mass isotopomer distribution enabled us to determine the turnover rates of 458 murine mitochondrial proteins, spanning over 2 orders of magnitude in half-life. Mitochondrial protein turnover displayed both organ-specific differences and interprotein heterogeneity, and subcellular fractionation ensured that the protein kinetics were free from interference by cytosolic precursors. We envision our kinetic data will help elucidate the mechanisms of mitochondrial homeostasis. Our methodology has wide applications in the characterization of protein kinetics and temporal proteome changes in mammalian systems. The safety and economy of ²H₂O labeling also make it practical for use in measuring human protein dynamics in clinical studies.