Proteome Dynamics: Revisiting Turnover with a Global Perspective

Abstract

Although bulk protein turnover has been measured with the use of stable isotope labeled tracers for over half a century, it is only recently that the same approach has become applicable to the level of the proteome, permitting analysis of the turnover of many proteins instead of single proteins or an aggregated protein pool. The optimal experimental design for turnover studies is dependent on the nature of the biological system under study, which dictates the choice of precursor label, protein pool sampling strategy, and treatment of data. In this review we discuss different approaches and, in particular, explore how complexity in experimental design and data processing increases as we shift from unicellular to multicellular systems, in particular animals.

The use of stable isotopes to trace metabolic processes, pioneered by Schoenheimer starting in 1935, elicited a paradigm shift in the perception of proteins, such that they were no longer considered as unchanging structural components of a cell that are replaced only when damaged by general “wear and tear” (1). These seminal studies introduced the concept of continual breakdown and re-synthesis as an ongoing metabolic process that truly reflects “The Dynamic State of Body Constituents” (2). This original work, which predates the discovery of the ribosome or the elucidation of the genetic code, placed protein turnover firmly in the category of highly active metabolic processes. In the ensuing period, huge progress has been made in clarification of the mechanisms of protein turnover, although our understanding of the subtleties of protein synthesis still exceeds our understanding of the corresponding destructive processes by which a protein is converted to constituent amino acids. Even now, it is difficult to describe the complete mechanistic details of the breakdown of any specific intracellular protein; we know the beginning (the mature protein), we know the end point (amino acids), and we may know some details of the intermediate processes (whether the protein is ubiquitylated prior to proteasomal degradation, whether the proteasome is involved, and so forth), but for most proteins, it is still not possible to define the exact route from specific intact protein to its pool of constituent amino acids. Part of the problem is that protein degradation is associated with a loss of tangibility; thus, loss of a band on a western blot is easy to observe, but monitoring of transiently existing intermediates in the process of degradation is rather difficult. Higher level questions, such as those posed in a recent review (3), define some of the challenges in the development of our understanding of proteome dynamics and may well require the development of new experimental approaches.

It is (at least conceptually) convenient to distinguish between two distinct processes in the degradation of any protein: a commitment step and a completion step. The commitment step is the rate-limiting step and need not be proteolytic. For example, polyubiquitin conjugation and lysosomal internalization are both non-proteolytic commitment steps. Subsequently, the completion phase, in which the committed protein is degraded to amino acids, is proteolytic and generally held to be much faster than the commitment step, avoiding the intracellular accumulation of partially degraded proteins (4). This review is restricted primarily to the measurement of commitment; the determination of the rate-limiting step of protein degradation. In particular, we restrict the scope to studies that use the flux of stable isotope precursor into and out of the protein pool and discuss stable-isotope-mediated approaches to the recovery of degradation rates. We do not address methods based on fluorogenic or immunogenic tagging, or those that are based on decay of the protein pool after inhibition of protein synthesis; each of these approaches brings its own considerations (5). Finally, we restrict our scope to cells grown in culture and to animal systems. Some recent reviews also inform (3, 6–10).

The Central Role of Protein Turnover

Protein turnover requires energy for both biosynthesis and degradation of proteins and has a substantial metabolic demand. For example, in the young rat, the rate of synthesis of liver proteins is about 50% per day, and in the young mouse, it may be as high as 100% per day (11). A primary function of this energetically expensive constant turnover is to alter the levels of specific proteins in response to physiological changes, hormonal status, or diet. How rapidly this change in abundance is brought about depends on the rate of turnover of the protein in question; if the protein has a high rate of turnover, then the change can be rapid. It is important to remember that the abundance of a protein can be adjusted by altering the rate of synthesis or the rate of degradation; for example, if the rate of synthesis remains constant but the protein is degraded at a lower rate, then the protein pool will expand. In animals, the rates of protein turnover are maximal when the growth rate is highest (11).

It is now generally accepted that the correlation between protein and mRNA abundance is imperfect. In a recent comprehensive analysis of protein and transcript abundance and stability, the correlation between protein and transcript abundance was not matched by any correlation between protein and transcript stability (12). One reason for the weak relationship between these pairs of parameters could be the intervention of the protein turnover cycle. It can be assumed that mRNA abundance in a cell is the determinant of the rate of input into the protein pool, refined and adjusted by the overall ribosomal activity and the rate of translation initiation and elongation, as well as by diversionary losses during the protein folding and maturation process. It would be interesting to test the relationship between the transcript abundance and the rate of turnover of the cognate protein, and indeed, analysis of the data previously published (12) indicates that this is the case. A further complication may arise from the fact that most large-scale data sets are acquired using exponentially growing cells in culture. Resolving protein losses by growth-mediated dilution and true intracellular degradation is not only technically challenging, but also might impose a different relationship on the parameters. In non-dividing tissues, the modulation of protein abundance can be achieved only by intracellular turnover, as a reduction in pool size by cell division is no longer possible. Under these circumstances, different relationships between protein and transcript abundance, or in their dynamics might emerge.

By contrast, the rate of removal of proteins from the same pool reflects the commitment step in degradation. The modulation of this step can be influenced by the interaction of that protein with binding partners and by metabolites, with the latter providing an implicit connectivity between protein degradation and the metabolome. Evidence of the relationship between metabolites and protein degradation has long been available. As an early statement of the paradigm, we refer to studies on the effect of glucocorticoids or l-tryptophan administration on the levels of rat liver tryptophan 2,3-dioxygenase (13, 14). With either treatment in isolation, the level of the enzyme increased, although with notably different trajectories. Combination of the treatments potentiated the effect. When glucocorticoid treatment was discontinued, the elevated level of tryptophan 2,3-dioxygenase in rats declined to pre-treatment values. However, if tryptophan administration was continued while glucocorticoids were withdrawn, the enzyme remained at elevated levels (15). The interpretation of these data was that glucocorticoids enhanced protein synthesis, but the administration of excess substrate for the enzyme stabilized the protein and prevented intracellular degradation. Thus, the glucocorticoid exerted its effect through the transcriptome, but the influence of the metabolome was mediated through substrate-induced stabilization of the protein to the intracellular degradative mechanism. Effectors of mature proteins, such as ligands and metabolites, together with post-translational modifications, such as phosphorylation, are known to affect the rate of degradation of a protein. These changes control the commitment step and provide the coupling between the proteome and the metabolome. For example, an elevated concentration of the substrate of an enzyme, which can stabilize a protein in vitro, might also reduce the degradation rate in vivo. In such a model, an elevated substrate pool elicits an increase in the availability of the enzyme that could reduce the pool size to the homeostatic norm. By the same argument, we might expect enzyme inhibitors to destabilize their targets in vivo, although such ideas have yet to be tested on a proteome-wide scale.

Turnover rate dictates responsiveness to metabolic shifts, and thus the proteins with the highest rates of turnover might be expected to be regulatory. Indeed, often it is the high-abundance proteins that have the lowest rates of turnover and carry out more “housekeeping” roles in the cell, although these proteins nonetheless consume a large proportion of the energy budget of protein turnover because of the scale of the flux through these protein pools (12). Protein turnover is also critical to tissue remodeling during growth and is an essential part of the process whereby damaged proteins are cleared from the cell. Finally, there are some fascinating discussions of the role that protein turnover plays in thermoregulation and the role of the inappropriately named “futile cycle” as a source of heat to maintain homeothermy (16–20). In this regard, the highest rates of bulk protein turnover are observed in newborn and young animals, consistent with an increased demand for heat production in a smaller animal. The magnitude of this process should not be underestimated: a young mouse may replace all of its liver protein every 24 h, dropping in the adult to 50% per day (21). Turnover rates in skeletal muscle are lower, perhaps reflecting the relative mass of the two tissues, in addition to their different metabolic profiles and roles (11, 22). Moreover, the age-dependent decline in protein turnover in skeletal muscle is more pronounced than in liver, which might reflect the decline in muscle function in older animals. The individually evolved susceptibility of each protein to the degradative process is thus modulated and tempered by the overall activity of the proteolytic machinery in each tissue; it could therefore be assumed that the baseline activity of the degradative machinery (probably the commitment step) is quantitatively different between two tissues, and the rate of entry of an individual protein into this process will thus place it in the same position in the overall degradation profile in each tissue. If this is true, then a prediction might be that for a set of proteins that are expressed in two tissues, the relationship between the first-order rate constants should be linear with a slope that is not unity; initial indications are that with some exceptions, this prediction will hold (22).

Terminology, Parameterization, and Modeling in Turnover Measurements

The simplest model of protein turnover assumes that synthesis is a zero-order process and degradation is a first-order process. In this model, the rate of synthesis (k_syn) of a protein is not directly regulated by the size of the pool of like protein molecules (P). By contrast, abstraction from the pool by degradation is a process of proportional removal, defined by a first-order rate constant (k_deg). Synthesis has the units of molecules, or moles, per unit time, whereas degradation, being fractional removal from the pool, has the dimensions of time⁻¹. The change in protein abundance as a function of time is given by the following simple relationship:

When the protein pool size is constant, the rate of change of the protein pool dP/dt = 0, and the equation reduces to

To illustrate, if a protein has a synthesis rate of 1000 molecules/s and a degradation rate of 1%/s (k_deg = 0.01 s⁻¹), the pool size is given as 1000/0.01 = 100,000 molecules. If the degradation rate is doubled (k_deg = 0.02 s⁻¹) and synthesis is unchanged, the pool size adjusts to 50,000 molecules. Turnover is the combined process of synthesis and degradation. However, when referring to the “rate of turnover,” it is accepted practice to refer to the movement of material through the pool in terms of the rate of exit of molecules from the pool, usually expressed as the first-order rate constant.

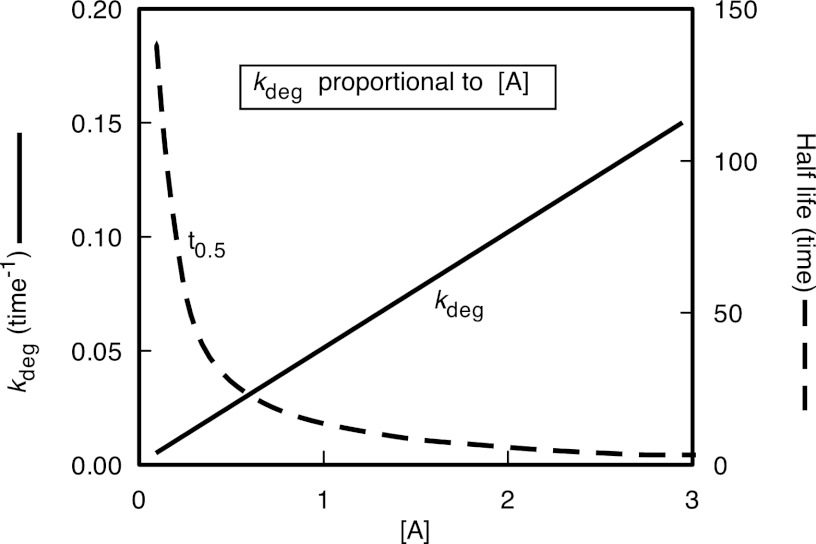
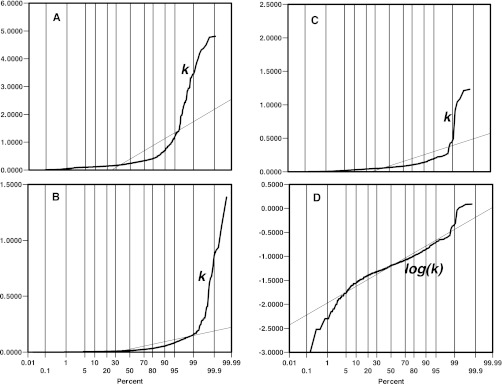
As the desired parameter of turnover experiments indicates the percentage of the existing pool that has been replaced (using terms such as, for example, 0.1 h⁻¹ or its equivalent, 10% h⁻¹), all turnover experiments must address the flux of newly synthesized molecules into the pool and their subsequent exit. As a first-order process, degradation is stochastic, and a newly synthesized protein molecule has the same probability of being committed to degradation as one that has been present in the same pool for a considerable time. The alternative, whereby a protein is retained in the protein pool for a specific period of time (lifetime kinetics), is not thought to be broadly applicable, although there may be circumstances whereby a shift in the intracellular location of a protein during the maturation process or as part of a regulatory process (e.g. nuclear/cytoplasmic shuttling of transcription factors) can create pools that have different turnover rates (23). Thus, one objective of turnover studies is normally the accurate and precise measurement of the “turnover rate,” or, more formally, the first-order rate constant for the degradation of each protein of interest. The degradation rate constant (k_deg), defined with units of reciprocal time, should ideally be the parameter reported. The conversion of k_deg to a half-life (ln(2)/k_deg or 0.693/k_deg) is often used to express turnover rates, but this is not ideal when used analytically or in comparative studies, because it is a reciprocal derivative. A plot of half-life against k_deg for theoretical or experimental data indicates the non-linear relationship between k_deg and half-life (Fig. 1). Half-life profiles are sometimes logarithmically transformed to compress the data into a convenient scale, a transformation that can make visual interpretation even more difficult. In all studies, the most appropriate parameter is the first-order rate constant for degradation, and a case can be made for the re-examination of such data in the true parameter space. In our experience (24), and from analyses of other data sets (25), the distribution of k_deg (or, indeed, half-life) does not meet tests of normality (Fig. 2), with relatively few proteins being “high turnover” and with a long tail of “low turnover” proteins (24–26). Log transformation of degradation rate constants does move the distribution toward normality (Fig. 2) and might be appropriate under some circumstances. Comparative analyses of the overall profiles should ideally be performed using non-parametric methods. Although log transformation of the data can introduce a distribution curve that is closer to normality, the potential exists for misinterpretation (27, 28). Of course, non-parametric statistical methods based on rank order of the degradation rate (however calculated) will return the same analysis.

Fig. 1.

The relationship between degradation rate constant and half-life. The plots are for theoretical data assuming that the rate of degradation of a protein (k_deg) is linearly proportional to the activity of some degradative component A. As [A] increases, so k_deg increases linearly. However, when the behavior of the protein is plotted after conversion to the reciprocal term half-life, the potential exists for misinterpretation of the relationship—a modest change in k_deg at low [A] appears as a very large decline in half-life.

Fig. 2.

Normality tests on degradation profiles. Three high-quality data sets from carefully conducted experiments were used to provide profiles of k_deg values. These data sets (panels A (43), B (12), and C (40)) are clearly not normally distributed, as evidenced by the probability plots shown and a formal test for normality (Shapiro-Wilk, p < 0.0001). The distribution of the profile more closely approximates a normal distribution after logarithmic transformation (panel D), illustrated by reanalysis of the data from C.

Stable Isotope Strategies for Determination of Protein Turnover

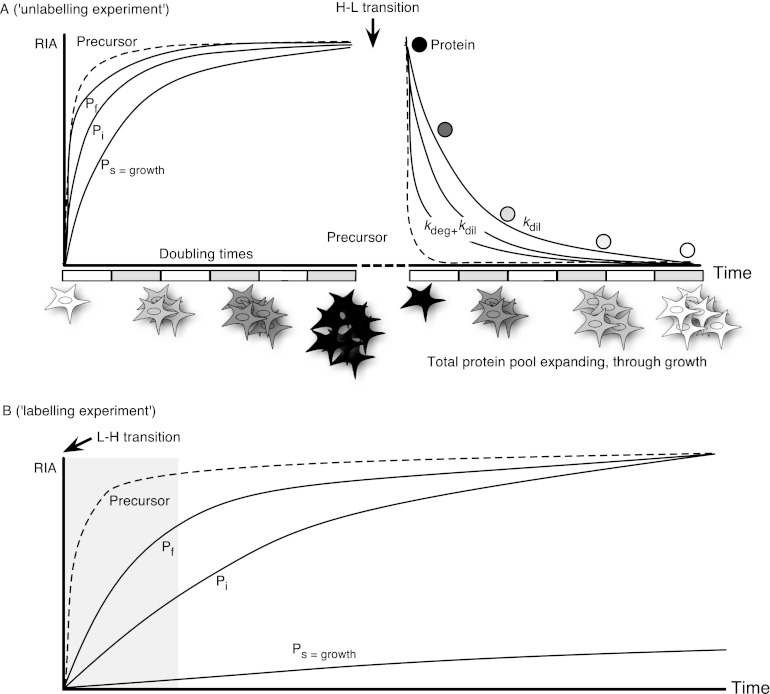
All stable-isotope-mediated turnover experiments have essentially the same design (Fig. 3), and within this broad experimental design there have been at least 30 different studies of proteome or subproteome turnover that have used stable isotope labels (Table I). A living system (ranging from cells in culture to intact mammals) is exposed to a stable isotope precursor. In the simplest experimental design, the precursor is then incorporated into proteins, and the rate of incorporation is determined (“labeling” experiment). In a slightly more complex design, cells are pre-labeled with stable-isotope-labeled precursor before the system is transferred to an unlabeled condition, and the rate of loss of label is determined (“unlabeling” experiment). Of the 30 studies reported in Table I, half focused on cells grown in culture, split equally between labeling and unlabeling experiments. The other half of the studies in Table I are all in animal systems, and here the bias is firmly toward labeling experiments—about 90% of such studies are of this design. The two approaches are formally equivalent, but one advantage of an unlabeling experiment is that it permits the use of an excess unlabeled “chase” to reduce the stable isotope enrichment of the precursor pool as quickly as possible. In animals, the cost and complexity of creating fully labeled animals prior to a degradation study is prohibitive, and the opportunity for an excess unlabeled chase phase is low; hence the predominance of labeling-type experiments. More sophisticated experimental designs using dual labeling approaches have recently been introduced (29), resonating with the early double labeling studies that used sequential labeling with [³H] and [¹⁴C] amino acids to create an isotope ratio that reported on turnover rate (30).

Fig. 3.

Overall strategies for turnover analysis. All turnover studies using stable isotopes measure the rate of entry of material into the protein pool (labeling experiments, panel B) or the rate of exit of label from previously labeled proteins (unlabeling experiments, panel A). Unlabeling experiments are most commonly used with cells grown in culture. Proteins (P_f, P_i, P_s: fast, intermediate, and slow turnover proteins, respectively) are pre-labeled through a combination of turnover and pool expansion through growth, as the cells are usually undergoing exponential growth. Irrespective of the turnover rate, all proteins will be fully labeled after six or seven doubling times. Subsequently, the medium is changed to one containing no label, and the rate of loss of label (k_loss = k_deg + k_dil) from proteins is assessed by means of mass spectrometry. Because the cells continue to divide, label is lost from proteins through a combination of growth and intracellular degradation, and the lowest rate of degradation that can be measured is equal to the dilution, or growth rate (k_dil). This can impair the measurement of turnover of slow turnover proteins. Labeling experiments (B) are more common in animal studies, in which tissue growth might be much lower. Here the stable isotope label is administered at the start of the experiment, and mass spectrometry is used to monitor the rate of label incorporation into proteins. These experiments are often conducted in the absence of significant tissue growth, and the exponential rise to plateau yields a reliable measure of the turnover rate. In both experimental modalities, the extent and rate of labeling of the precursor amino acid pool (dotted lines) is critical. In unlabeling experiments, manipulation of the media can be used to effect rapid changes in precursor RIA, such that it has minimal influence on the labeling trajectory of all but the most rapidly turning over proteins; the sampling frequency in most experiments means that these proteins will appear to transition from unlabeled to labeled, often by the time of the first sample. In labeling experiments in animals, in which label has to be introduced orally, the precursor pool might take rather longer to reach a plateau. This can be incorporated into the labeling model, or sampling can be distributed over an extended time such that the pre-plateau contribution to the error in turnover rate measurement (shaded area) is minimal.

Table I. Exemplar turnover studies using stable isotope labels.

Experimental model	Stable isotope label	Labeling protocol	RIA transition	Calculation of turnover rate	Reference
Escherichia coli	[13C6]glucose	Labeled glucose added to cell culture. Cells harvested after 30 min.	Incorporation of label monitored. Single time point.	Synthesis/degradation ratio.	(68)
Mycoplasma pneumoniae	[13C6][15N4] arginine	Cells pre-labeled and transferred to unlabeled media for time-point sampling.	Loss of label monitored at 1, 2, 4, and 8 h.	TPP Xpress algorithm used to define H:L ratios over the time points. Protein half-lives determined.	(69)
Saccharomyces cerevisiae	dl-[2H10]leucine	Cells grown in glucose-limited culture media containing heavy leucine for seven doubling times. Media changed to unlabeled leucine for sampling.	Loss of label monitored at 0, 0.17, 0.67, 1, 2, 4, 6, 8, 10, 12, 25, and 51 h.	Non-linear curve fitting of (t, RIAt) data to obtain kloss. True rate of degradation (kdeg) by subtraction of the constant dilution rate D from kloss	(39)
Saccharomyces cerevisiae	([15N]H4)2SO4	Nitrogen-limited chemostat used to culture yeast. Inflowing media then changed to contain [15N] for 16 h.	Loss of unlabeled peaks monitored at 0, 2, 4.5, 7, 10, and 16 h.	Rate of protein degradation, assuming first-order kinetics, calculated by loss of unlabeled peptide peaks, and then half-life for each protein using t1/2 = ln2/kdeg	(40)
Corynebacterium glutamicum	[15N]H4Cl	Cells cultured in media with [15N]H4Cl as the sole nitrogen source until fully labeled and then transferred to unlabeled media and heat shocked.	Loss of label monitored at 0.5, 1, 2, and 4 h.	Calculation of protein synthesis rates were based on abundance ratios of new (partly [14N]-labeled) to old (fully [15N]-labeled) proteins.	(29)
Mycobacterium smegmatis	([15N]H4)2SO4	Cells grown in [15N] media until mid-log phase, washed, and then resuspended in [14N] high-iron medium or [14N] low-iron medium until OD doubled.	Loss of label monitored at 0, 2, 3, 4, 5, 6, and 7 h.	AL, AH, and AM represent the isotopologue intensities with light, heavy, and medium label. S/D = AM/AL or S/D = AL/AH.	(70)
Streptomyces coelicolor	[13C6][15N4] arginine	Cells prelabeled in heavy media and transferred to unlabeled medium.	Loss of label monitored at 0, 2, 4, and 8 h.	iTRAQ used to tag each of four time points for multiplexed turnover analysis.	(71)
Ostreococcus tauri	Na[15N]O3 and [15N]H4Cl	Cells grown in either labeled or unlabeled media, then resuspended in the opposite form of media.	Incorporation or loss of label monitored in the different cultures. Samples at 12 h, then 24 h intervals for 6 d.	Averaged peptide H/(H + L) values were plotted against time, enabling estimation of initial linear time-dependence by linear regression, where the slope (divided by 100) returns the initial turnover rate in %/h.	(72)
HeLa cells	l-[13C615N4]arginine, l-[13C615N2]lysine and l-[13C6]arginine, l-[2H4]lysine	Amino acids were added to cell cultures in light (Arg0, Lys0), medium (Arg6, Lys4), or heavy (Arg10, Lys8) form. Label incorporation assessed after six passages.	Labeling and unlabeling compared at 0.5, 4, 7, 11, 27, and 48 h.	Data analyzed using PepTracker turnover and spatial viewer. At each time point, labeled cells were mixed with those grown in light media.	(23)
Arrested HeLa or differentiated C2C12 cells	l-[13C615N4]arginine and l-[13C615N2]lysine	Cells initially grown in media with 1:1 Arg0/Lys0:Arg10/Lys8. Cells were arrested and then transferred to 100% heavy for 24 h.	At time t = 0, H = 50%. ΔH/(H + L) calculated so RIA values can be compared to standard RIA values where H = ΔH. Sampling at 1, 2, 4, 8, or 24 h.	Half-life t1/2 calculated using the loss of “light label” as a first-order process.	(26)
Human adenocarcinoma A549 cells	l-[13C6]arginine	Cells grown in label-containing media for 13 d, then resuspended and incubated in unlabeled media for chase.	Loss of label monitored at 0, 0.25, 0.5, 1, 2, 4, or 8 h.	First-order rate constants determined via nonlinear curve fitting.	(24)
HeLa cells	l-[13C615N4]arginine, l-[13C615N2]lysine and l-[13C6]arginine, l-[2H4]lysine	Light cells transferred to media containing heavy (H) or medium-heavy (M) arg/lys. Samples are combined for analysis.	Incorporation of labels monitored. Comparison of rates of protein translation between two samples by pulse labeling. Sampling at 1, 2, 4, 6, 8, and 10 h.	H vs. M peak intensity indicates translation differences between iron-treated cells.	(73)
Mouse fibroblasts	Heavy SILAC amino acids (not specified)	Cells grown initially in light amino acids and then pulse labeled with heavy amino acids.	Incorporation of label monitored at 1.5, 4.5, and 13.5 h.	Protein half-lives calculated from log H/L ratios at all three time points using linear regression.	(12)
Mouse (Mus musculus)	U-[13C6]glucose	Continuous venous infusion of glucose tracer over effective labeling phase of 8 h.	Single labeling time point. Liver proteins compared to control, unlabelled, liver.	Half-life (days) assessed as T1/2 = ln(2)/k/24	(66)
Mouse (Mus musculus)	[15N]-enriched Spirulina-based rodent diet	Animals acclimated to the unlabeled algae-based diet, then switched to labeled diet.	Incorporation of label monitored at nine times over 32 d in proteins from the brain, liver, and blood.	Turnover rate recovered from exponential fit post-labeling delay phase.	(43)
Mouse (Mus musculus)	[15N]-enriched Ralstonia eutropha protein-based rodent diet	Animals acclimated to the unlabeled diet, then diet changed to that containing labeled protein.	Incorporation of label monitored at 1, 2, 4, 7, and 14 d in brain and plasma proteins.	Direct analysis of free amino acids for enrichment of the precursor pool. Calculation of the labeled peptide fraction (LPF) using ProTurnyzer software. Delayed exponential curve: LPFt = 1 − e−λ(t − t0)	(44)
Mouse (Mus musculus)	[2H]2O	Two intraperitoneal injections of 99.9% saline [2H]2O, 4 h apart, then free access to 8% [2H]2O.	Incorporation of label monitored; heart, liver, and blood sampled at 0, 0.5, 1, 2, 4, 7, 12, 17, 22, 27, 32, 37, and 90 d for mitochondrial enrichment.	Non-linear curve fitting: A(t) = A(0) + A(∞) − A(0) (1 − e−kt), then transformed into fraction synthesis, f(t):(t) = ((t) − (0))/(A(∞) − A(0))=1 − e−kt to determine rate of turnover (k).	(25)
Mouse (Mus musculus)	[2H8]valine	Animals fed diet containing [2H8]valine at RIA of 0.5 after first acclimating to diet containing crystalline [H8]valine.	Incorporation of label monitored at 1, 2, 5, and 12 d. Liver, kidneys, heart, and skeletal muscle sampled from two animals per time point.	Precursor RIA calculated from divaline peptides via isotopomer analysis. (RIA, t) data analyzed by means of non-linear curve fitting.	(22)
Mouse (Mus musculus)	[2H8]valine	Animals fed diet containing [2H8]valine at RIA of 0.5 after first acclimating to diet containing crystalline [H8]valine.	Incorporation of label monitored at 2, 7, 14, 21, and 35 d. Samples of seminal vesicle secretions and sperm from two animals per time point.	Precursor RIA calculated from divaline peptides. First-order rate constant of labeling and the delay (days) in appearance of label caused by sperm maturation.	(74)
Mouse (Mus musculus)	[2H3] leucine	Animals fed unlabeled synthetic diet for 1 week, then transferred to deuterated leucine-containing diet.	Incorporation of label monitored at 3, 10, and 17 d for three mice per time point. Mitochondria from liver and heart analyzed.	Topograph software used to measure isotopologue abundances and calculate peptide turnover rates using precursor RIA and pt = p0 e−λ(t − t0)	(67)
Rat (Rattus norvegicus)	[15N]-enriched Spirulina algal cells	[15N]-algal cells fed to rats for two generations, starting either from before pregnancy or during pregnancy.	Level of incorporation in liver and brain proteins compared in pups from dams labeled either pre- vs. during pregnancy.	Incorporation levels compared for different proteins.	(63)
Rat (Rattus norvegicus)	[2H]2O	Intraperitoneal injection of [2H]2O to enrich body water to 2.6% and drinking water replaced with 5% [2H]2O. Two groups of animals, fed and fasted.	Incorporation of label monitored; blood and plasma samples collected after 30 and 60 min, then at 1 h intervals for 8 h.	Fractional synthesis rate determined using a one-compartment model. Time course of total labeling of a peptide (Epeptide(t)) fit to exponential rise curve equation: Epeptide(t) = Ess * (1 − e−kt)	(75)
Rat (Rattus norvegicus)	[15N]-enriched algal cells	Female rats and offspring fed [15N] diet for 6 weeks. Offspring changed to [14N] diet after this time.	Dam rats culled when fully labeled. Proteins from liver and brain of progeny rats analyzed after 6 and 12 months.	[15N]/[14N] calculated at sampling times.	(31)
Zebrafish (Danio rerio)	[13C6]lysine	Fish were fed 2:1 ratio of [13C6]lysine:normal fish feed for 4 months. Fish split into two groups and then fed unlabeled or [13C6]lysine containing diet.	Labeling and unlabeling of brain and re-grown amputated fins compared.	SILAC-type analysis.	(45)
Common carp (Cyprinus carpio)	l-[2H7]leucine	Synthetic diet containing unlabeled leucine fed to fish twice per day for 4 weeks. Diet then switched to contain deuterated leucine for up to 7 weeks.	Incorporation of label into muscle proteins monitored at 0, 1, 2, 3, 4, 5, and 7 weeks.	Precursor pool RIA calculated from parvalbumin peptides to allow synthesis and degradation rates to be determined through non-linear curve fitting.	(76)
Chicken (Gallus gallus)	[2H8]valine	Animals fed diet containing [2H8]valine at RIA of 0.5 for 120 h.	Incorporation of label into skeletal muscle proteins monitored at 0, 1, 2, 4, 8, 14, 24, 30, 32, 48, 55, 72, 96, and 120 h for three chickens at each time point.	Precursor RIA from multiply labeled peptides applied to non-linear curve fitting. Data adjusted to correct for muscle growth.	(42)
Mouse (Mus musculus), rat (Rattus norvegicus), and human (Homo sapiens) studies	[2H]2O	Bolus injection (intraperitoneal) of [2H]2O followed by [2H]2O drinking water for all studies. Samples for body water enrichment taken at various times. In rat “decay of 2H” study, animals labeled for 8 to 10 weeks; then water changed to unlabeled.	Loss and incorporation of label monitored in variety of different samples (bone, muscle, liver, sera) and species.	MIDA calculations and GC/MS to determine RIA of M0, M1, and M2 isotopomers. Fractional protein synthesis rates, or label decay rates estimated by non-linear least squares fitting. Half-lives calculated as t = 0.693/k.	(35)
Human (Homo sapiens)	[2H]2O	Short-term (7 day) study: oral dosing of eight 50 ml 70% [2H]2O over 36 h, then two doses every 24 h.	Incorporation of label monitored via daily blood sampling.	Fractional synthesis (proportion of new protein as a fraction of total pool) and rate constant for protein turnover using SAAM program to calculate time-dependant changes in isotopic enrichment of newly synthesized peptides.	(36)
		Long-term (6 weeks) study: oral administration of three doses per day for 7 days, then two per day.

Because turnover can occur in the absence of any change in protein abundance, turnover is assessed by monitoring the incorporation or loss of a label into or from the protein pool. In the latter case, this means the loss of a stable-isotope-labeled tracer that has been metabolically incorporated into newly synthesized proteins at some time in the experiment. To recover a degradation rate from a change in labeling of a protein, the critical parameter is the variation of the extent of labeling with time. Thus, samples must be taken that map a significant part of the transition from labeled to unlabeled protein, or vice versa. A high turnover protein that has changed its label pattern almost completely by the time the first sample is taken is most unlikely to yield a reliable degradation rate. This is particularly challenging in whole animal systems in which a high turnover protein might undergo extensive replacement even before the precursor pool has attained labeling equilibrium. At the other extreme, very low turnover proteins do not incorporate label to a sufficient extent that a precise turnover rate can be assessed (31). As such, they will manifest only very small changes in labeling profile, a behavior that is more problematic in rapidly growing cells in which the process of pool expansion attributable to growth will cause label incorporation, even in the absence of intracellular turnover. Discrimination between the change in labeling due to growth and that caused by true degradation is difficult to achieve without high confidence in the two rate constants (see below). The sampling regimen must ensure that sufficient time points are taken to cover both high and low turnover proteins; a geometric progression in sampling points is desirable. Also, the rate constant used to define the proportion of labeled or unlabeled protein must be fitted in the appropriate expression (e.g. simple exponential decay or rise to plateau, exponential labeling with a delay term) in parameter space, avoiding, if possible, logarithmic transformation that can introduce a transformative distortion. A further complication relates to the distribution of effort and analytical capacity: is it preferable to distribute sampling over as many times as possible, or to take replicates at fewer time points? We would argue that the key requirement is to define the labeling trajectory as carefully as possible and that it is preferable to take as many time points as possible to define both high and low turnover proteins; the replication should be over time rather than at fewer time points, such as that exemplified by a recent study on mouse protein turnover in which 13 time points were recovered (25).

Deviations from simple exponential labeling curves are to be anticipated, and will be revealed by higher granularity in time sampling (22). Factors such as metabolic reutilization of stable isotope atoms, precursor pool equilibration, and recycling of amino acids released from protein degradation back into the protein pool will all complicate analysis, once there are sufficient data to parameterize such complications (6). However, considerable understanding can already be obtained from the most simple “zero-order, first-order” model. There is virtue in revisiting much of the historical literature on the modeling and kinetic analysis of protein turnover (see, for example, Refs. 11, 15, and 32). Issues of pool dynamics, precursor metabolism and reutilization have been addressed previously, predominantly in terms of radiolabeling, but the overall principles are equally applicable. More recently, proteome turnover studies have developed sophisticated compartmental modeling approaches (e.g. Ref. 33) that should yield higher quality analyses, although such approaches might require the acquisition of additional parameters and more measurements. Specific labeling methods may sometimes be available, such as in one of our early studies that used the excretion profile of a metabolic dead-end product of a cofactor in a compartmental analysis to measure the turnover of a specific protein in skeletal muscle (34); this study included an analysis of the sensitivity of the model to different parameters to discover which were most critical to the results obtained.

The Choice of Precursor

Whether the size of the protein pool is changing or not, all turnover studies that are based on measurement of isotopic labeling monitor the flux of a tracer precursor that is incorporated into or lost from the protein molecule. In proteomic studies, the tracer is a stable isotope, and the flux of tracer (either entry or exit) through the protein pool is monitored by means of mass spectrometry of the protein(s) of interest, usually after proteolysis to peptides. The choice of label for turnover studies is not particularly different from the choice for comparative proteomics, such as SILAC (stable isotope labelling with amino acids in cell culture) or SILAM (stable isotope labelling in mammals) (6). The precursor can be an amino acid, a mixture of amino acids, a simple metabolic precursor of amino acids ([²H₂]O, [¹⁵N]H₄Cl), or a complex metabolic precursor that is metabolized before resynthesis into amino acids ([¹³C₆]glucose) (Table I). The simplicity of the labeling precursor and the “metabolic distance” between the precursor and the amino acid pool create different degrees of complexity in the labeling profiles, but these are not insurmountable. Indeed, some of the most comprehensive turnover data sets have been obtained from protocols using simple metabolic precursors, because the multiple centers of incorporation increase the sensitivity of the measurement. An attractive approach in animal studies is to use uniform elemental labeling, in which diets are fully labeled, usually with [¹⁵N] or [¹³C] that is distributed over all biomolecules in the diet. These diets can be generated only by incorporating protein from cultured organisms, and the usual route is to compound a diet that contains algae such as Spirulina spp that is fully labeled through photosynthetic growth, as these organisms will grow using [¹⁵N]H₄Cl or [¹³C]O₂ as the sole source of label. It is also possible to replace all [¹²C] with [¹³C] if heavy glucose is used; the same is true with [¹⁵N]H₄Cl. If these two labels are combined, it is possible to assess the rates of both synthesis and degradation (29), although this approach needs rather more sophisticated analysis. There has been a notable increase in the use of [²H₂]O as a label for protein turnover measurement, particularly in intact animals and in man, coincident with the appearance of high resolution mass spectrometers and the emergence of improved algorithms for analysis of label incorporation (25, 35–38).

In animal studies, the route of administration becomes a key factor, because exposure to the label has to continue for many days. Earlier studies using radiolabeled amino acids employed bolus injections or continuous infusion, the latter usually for several hours. Because of the high specific radioactivity of the precursor and the sensitivity of scintillation counting, the short period of exposure to label was compatible with the incorporation of sufficient radiolabel to permit detection, though in most instances only for the total protein pool. In proteome studies, the need to resolve turnover behavior for individual proteins, usually via the analysis of proteolytically generated peptides, coupled with the inherent difficulties in measurement of very low levels of incorporation of a stable isotope, means that proteins must be exposed to higher levels of labeled precursor for sufficiently long a time that a significant proportion of the protein becomes labeled. There are exceptions, of course—high turnover proteins will accumulate label very quickly, and extremely long-lived proteins might never become labeled adequately (31)—but for the majority of cellular proteins (for example, in small mammals such as rat or mouse), administration periods of days or weeks are appropriate. Under these circumstances, the only feasible route for the administration of label is through the drinking water (studies based on [²H₂]O) or, for other metabolic precursors, the diet.

The Importance of Precursor Relative Isotopic Abundance

The calculation of turnover rates does require knowledge of the level of enrichment of the label in the amino acid precursor pool, the precursor relative isotopic abundance (RIA),¹ in the cell or tissue under study. The simplest turnover experiments to set up are labeling experiments in which the precursor pool is rapidly flooded with the labeled precursor through a medium change; the critical nature of this step has been emphasized by a recent study that demonstrated incomplete transition between unlabeled and labeled precursor unless media changes were repeated (23). A label shift is most readily achieved with cells in culture, in which a change in the large volume excess of medium surrounding the cells can bring about a near-instantaneous change in the extracellular precursor pool, resulting in a consequent change in intracellular precursor RIA as quickly as the precursor pool can be exchanged with the extracellular pool. Similarly, in unlabeling experiments, a rapid medium change can deplete the labeled pool virtually instantaneously. Indeed, unlabeling experiments can be designed to enhance the decline in precursor RIA if an excess of the unlabeled precursor is used. Of course, this is a change in the composition of the medium, and care must be taken to ensure that the shift in precursor concentration does not elicit other effects in the cells that perturb turnover. In one of the first studies of protein turnover at a proteome level (39) in Saccharomyces cerevisiae, cells were maintained in turbidostat culture, and thus the population was sustained at a specific growth rate (a doubling time of ∼7 h). The strain used was auxotrophic for leucine, and the only source of leucine available for protein synthesis was that provided in the medium, as no synthesis de novo was possible. A challenge with turbidostat or chemostat cultures is the difficulty of changing the growth medium rapidly, as the system is in a steady state and only a small proportion, such as 10%, of the medium will pass through the culture vessel every hour. For this reason, the S. cerevisiae experiment was conceived as an unlabeling experiment, with cells exposed to [²H₁₀]leucine for at least seven doubling times in order to fully label all proteins before the medium was changed to contain unlabeled leucine, plus a simultaneous addition of a 10-fold excess of the same unlabeled amino acid; clearly this is less expensive than the reciprocal labeling experiment. It might be argued that the addition of the excess leucine could perturb the cells, but because the cultures were set up to be glucose limited, growth was maintained at the same rate in the labeling and unlabeling phases. Subsequently, the transition from “heavy” leucine containing peptides to “light” leucine containing peptides was monitored over time. Because the cells were growing throughout this unlabeling phase, the stable isotope label was lost from protein via a combination of two exponential processes: dilution and degradation. The rate constants are additive, and loss via dilution was constant for all proteins, so the additional loss via degradation was recovered by means of simple subtraction of the first-order rate constant for dilution of label (k_dil) from the protein-specific loss of label (k_loss) to recover k_deg. In a more recent study (40) with the same organism, the culture nitrogen source was shifted from [¹⁴N]H₄Cl to [¹⁵N]H₄Cl; the logic behind this experiment was that the growth of the cells was limited by nitrogen availability, and thus there could be no residual [¹⁴N]H₄Cl remaining in the medium to dilute the labeled precursor. Because this approach measures loss of the [¹⁴N] protein pool, there was no requirement to assess the complex patterns of [¹⁵N] incorporation, provided that the nitrogen in the medium was fully depleted.

When the RIA of the precursor pool can be manipulated to unity, most readily achieved with cells grown in a culture medium, or even “mini-organs” such as atrial traberculae immersed in an organ-bath containing stable-isotope-labeled media (41), the calculation of turnover rates is relatively straightforward. In more complex systems, such as animals, it is more challenging to design dynamic labeling experiments in which the precursor RIA is unity, particularly when the precursor is a specific amino acid. Diets with a high level of labeling are generated by compounding new dietary formulations derived from algal, bacterial, or yeast cultures that have been grown in the presence of a labeled precursor and subsequently incorporated into a feed (22, 26, 42–44). The challenge in single amino acid labeling for animal studies has been met in two ways. First, there are commercially available diets in which 100% of the labeled precursor is [¹³C₆]lysine, for example. This means that the goal of a target RIA of 1 is possible. These diets are totally synthetic and protein free, and such diets might be unpalatable or create metabolic stress. In our own studies we have taken a different approach of supplementing a standard laboratory feed with crystalline stable amino acids to the same level as that in the diet before supplementation, setting the target RIA of the precursor to 0.5. We chose this approach as a compromise between the need for an adequate degree of labeling and the aim of retention of palatability (6, 22, 42). The metabolic consequences of specialized diets are assumed to be slight, but some caution might be required (45). There is a need for a more critical evaluation of the long-term effects of such diets in comparison with the carefully developed formulations that are usually used.

If the RIA range is set, for example, between 0 and 0.5, the turnover experiment is still entirely feasible, but it requires slightly different treatment. The compression of the dynamic range is readily dealt with by appropriate sampling across the time domain, so that turnover values are not derived from almost fully labeled or fully unlabeled peptides. The true precursors of protein synthesis are the charged aminoacyl-tRNAs, but isolating aminoacyl-tRNAs is not straightforward (46, 47). Analysis of free amino acid pools as a surrogate for charged tRNA molecules could produce inaccuracies in measurements of protein turnover, as amino acids from both intra- and extracellular free amino acid pools contribute to the final synthesized protein (48–50). One option to avoid this is to use a labeled source in which all of one element is labeled (e.g. where all amino acids are fully labeled with ¹⁵N). This has the benefit of giving newly synthesized proteins a greater chance of containing labeled amino acids (even with unlabeled protein still present in existing pools and tissues), and the labeled peptide fraction can be calculated from the intensity of the monoisotopic peak, which is assumed to contain only unlabeled amino acids (43, 44).

If neither the diet nor the tissues are fully labeled, any pre-existing proteins that are degraded will return unlabeled amino acids to the precursor pool, diluting the label that is present. This is much less of a problem with cultured cells, because in exponential growth the initial biomass is small relative to the final biomass, and the ratio of labeled to unlabeled amino acids can be set to be high by experimental design (26). With animal studies, which predominantly follow a labeling (rather than unlabeling) route, a substantial pool of unlabeled amino acids will pre-exist in the animal tissues. This unlabeled pool will slowly return unlabeled amino acids to the precursor pool, and these will be distributed through the tissues via the circulation. Further complication is provided by the sub-cellular compartmentalization of precursor pools both within and between different tissues (51). Thus, it cannot be assumed that the RIA of the labeled amino acid when it is introduced to an organism is equivalent to the RIA at protein synthesis (11). Yet, it is this “point of synthesis” RIA value that determines the probability that a labeled amino acid will be incorporated into a newly synthesized protein when there is a mix of labeled and unlabeled amino acids in the precursor pool. Fortunately, at least with amino acid precursors, it is possible to calculate the true precursor RIA.

The precursor RIA can be calculated at the point of protein synthesis (effectively sampling the extent of labeling of the charged tRNA pool via analysis of the incorporation of an amino acid from newly synthesized peptides) by means of direct examination of the isotopomer distribution in peptides that contain multiple instances of the precursor. This approach, based on a single amino acid label, uses the mass spectral data obtained from peptides containing more than one instance of the amino acid being labeled—a di- or tri-valine-containing peptide, for example—to calculate the precursor pool RIA specific to that protein. MIDA (mass isotopomer distribution analysis, 52, 53) uses combinational probability analysis to compare the observed isotopomer distribution of labeled and unlabeled forms of the same peptide to the expected isotopomer distribution for a known RIA; from this, the actual RIA can be determined (36, 50, 52–54).

The method is best illustrated by consideration of a peptide with two instances of the amino acid. If the RIA of the precursor pool is 1, then there can be only LL (all unlabeled, light) or HH (all labeled, heavy) variants. But if the RIA is less than unity, three distinct labeled peptide ions will be observed in a mass spectrum: peptides that are unlabeled (LL), partially labeled (HL or LH, both with the same probability of occurrence and with the same m/z value), or doubly labeled (HH). The intensity distribution of the three variants of the peptides is also contributed to by pre-existing proteins (“old”) and proteins synthesized de novo (“new”). Pre-existing protein can contribute only unlabeled peptides (LL), but this pool also contains newly synthesized protein in which two unlabeled amino acids were incorporated into the peptide. The other two peaks, which contain one or two instances of the labeled amino acid, can have arisen only by synthesis de novo. If the precursor RIA was 1, then it would be possible to detect only the HH peptide, but any lower RIA increases the probability of HL. If the RIA of the precursor pool was 0.5, the ratio of HL to HH would be 2:1 (because of binomial expansion of the labeling patterns and the equal probability of the positional variants HL and LH). It is simple to calculate the precursor RIA from the relative intensities of HH and HL (9). The trajectory of the RIA profile can be assessed in the same samples that are used for the subsequent turnover analysis, provided that appropriate, multiple-labeled peptides are recoverable; these can be miscleaved peptides or LysPro containing peptides if lysine is the label, or, for most other amino acids used in labeling protocols (including the essential branched chain amino acids), it is likely that multi-labeled peptides will be present in a sufficient number of analyzable peptides. Alternatively, a digestion with a different protease could be used to generate multi-labeled peptides. Because the intensity analysis of the peptides is internally referenced only, it is independent of the recovery of the peptides. It is not even necessary to use the same peptides in each analysis, provided they come from the same tissue and subcellular compartment.

Once the precursor RIA is known, it can be used as a parameter in the calculation of the turnover rate of individual proteins, as the all proteins would eventually reach the precursor RIA if the labeling phase continued for long enough. This can, most simply, be modeled by a single exponential curve of RIA as a function of time, with RIA being calculated as I_H/(I_L + I_H), where I_L and I_H are the intensities of the labeled and unlabeled components, rather than the I_H/I_L ratio often calculated in SILAC studies. It is now possible to use peptides containing only a single instance of the labeled amino acid, and this greatly increases the number of informative peptides.

This approach was first explored in a growing chicken (42). The label was deuterated valine ([²H₈]valine), chosen because it is an essential amino acid, is in high abundance in the proteome and substantially less costly than the equivalent amount of the [¹³C] labeled amino acid. The label was administered to 6 d old chicks through a semi-synthetic diet with a target RIA of 0.5 to ensure palatability and to maintain a high rate of growth. The chicks, housed under 23 h lighting, ate almost constantly throughout the light periods of the 5 d experiment. At each of 14 sampling times, peptides that contained multiple instances of valine were assessed to determine the precursor RIA, which rapidly reached a plateau value of 0.35, lower than the dietary input value, indicating the dilution of the label from the diet into the unlabeled amino acids in the precursor pools, as well as the result of degradation of pre-existing unlabeled proteins. Multiple peptides per protein were then analyzed over the different time points to enable calculation of the individual rates of protein turnover. It has been suggested that a similar labeling protocol would not be possible with mammalian models, as the daily fluctuations in precursor RIA would be too large (44). We have conducted similar, and successful, labeling protocols with adult mice using a diet comprising standard laboratory feed supplemented with the same quantity of labeled valine to a target RIA of 0.5, and we have indeed acquired evidence of such diurnal fluctuation (see below).

Using Secreted Proteins to Track Precursor RIA

Proteins that are constitutively secreted (as opposed to being stored in secretory vesicles) are likely, by definition, to have a very low residence time in the tissue of origin. If those proteins are secreted into the circulation, it should be possible to devise analyses of the trajectory of the precursor RIA within the tissue. Even more preferable, and avoiding frequent blood sampling, which is both undesirable and a more highly regulated procedure, if the protein is secreted/excreted in the urine, then monitoring of the precursor RIA can be non-invasive and permit sampling at a high frequency. In many rodents (55), and particularly in rats and mice, there is obligate proteinuria in the form of eight-stranded beta barrel proteins of about 19 kDa known as “major urinary proteins,” or MUPs. These proteins are present in all standard laboratory strains at high micromolar to millimolar concentrations (typically 5 to 10 mg/ml; in humans this would be a highly pathological proteinuria) and demonstrating some sexual dimorphism (56). They are synthesized in the liver and are rapidly released to the urine.

Analysis of MUPs from urine samples collected at high frequency from mice fed a semi-synthetic valine labeled diet allowed us to monitor the hepatic precursor RIA. Urinary MUPs were digested with endoprotease Lys-C (the lower frequency of cleavage increases the chance of identifiable di- or tri-valine peptides) over the time course, and a very rapid rise to a plateau was recorded. The precursor RIA value obtained from the urinary MUPs can be used only for liver proteins, as this is where their synthesis occurs, but it yields a non-invasive report on the progress of the overall labeling experiment. When the RIA value for the MUPs was analyzed, they produce a very distinctive “wave-like” labeling trajectory, explained by the 12 h dark:12 h light cycle under which these animals were housed, reflecting the nocturnal feeding behavior of this species. During the dark period, the RIA appeared to rise rapidly, reflecting feeding and possibly preferential absorption of the free synthetic labeled valine relative to the protein-bound valine in the diet. In the quiescent, light period, the RIA declined. With time, the oscillations dampened and settled to a stable RIA. In other tissues, the precursor RIA was assessed from intracellular proteins, from which it was apparent that tissues remote from the enterohepatic system all reached the same precursor RIA, but at slightly different rates (22).

In related experiments, mice were fed the semi-synthetic [²H₈]valine-containing diet for 35 d to cover the period of spermatogenesis. The labeling trajectory was again monitored through the label incorporation into MUPs. The proteins analyzed in this experiment, from seminal vesicle secretions and sperm, enabled the potential for adaptive plasticity of reproductive proteins under conditions of sperm competition to be assessed; phenotypic changes to sperm production and seminal vesicle mass are known to occur (57, 58). The high rates of turnover of the seminal vesicle proteins, even under no risk of sperm competition, suggest that these proteins are likely to be the first to adapt to changes. The sperm proteins had a range of turnover rates, from life-time labeling to rapid incorporation of the precursor. Some high turnover sperm proteins were incorporated from epididymal secretions, but some were sperm-cell derived, opposing the suggestion that sperm are metabolically quiescent during maturation.

Although sampling of major urinary proteins was used as a non-invasive route to monitor liver precursor pool labeling, we are intrigued by the notion that exosomes might contain adequate material to permit a minimally invasive analysis of tissue protein turnover (59).

General Conclusions and Future Perspective

Large-scale analysis of protein turnover rates can address key biological questions regarding the process and mechanisms of protein degradation. The availability of large turnover profiles permits the exploration of structural factors that might predispose proteins to a specific rate of commitment. It is increasingly clear that there are no obvious determinants of protein stability and that there are unlikely to be simple motifs or rules that can explain the degradation of the bulk of cellular proteins (23, 40, 42). This promises to be a fruitful area for further research.

Although most studies adopt the bottom-up strategy to obtain data for large numbers of proteins, the proteolysis step can also conceal variation between different isoforms of the protein. The use of two-dimensional PAGE brings benefits, as it enables “trains” of protein spots to be visualized. It has been suggested that the sequence of gel spots might represent proteins at different stages of degradation, or with different rates of turnover. However, we have shown that the labeling profile using [²H₈]valine was consistent across the different spots for some muscle or cardiac proteins (22). The consistency of the RIA_t values indicates that these different subunits have similar rates of turnover or that the interconversion between the different charge-modified isoforms must happen very rapidly; if not, there would be differences in the ratio of [²H₈]valine to [H₈]valine between the isoforms, as the unmodified isoform would have been synthesized earlier. Top-down turnover studies may well contribute to the debate of the role of successive protein modifications in an “aging” process.

At present, virtually all studies on proteome turnover with cells in culture have focused on nutrient-rich growth conditions in which cells are undergoing exponential growth. Under such conditions, the rate of protein degradation might be biased toward the few proteins that require high turnover rates commensurate with the cell cycle and thus might not reflect the true balance of synthesis and breakdown that a system in steady state would demonstrate. As suggested, the rate of turnover of many proteins in such cells is extremely low, consistent with a model wherein protein abundance can be manipulated by dilution into progeny cells rather than requiring intracellular degradation. Moreover, exponentially growing cells elicit rapid labeling (or unlabeling) of the total protein pool because the protein pool is expanding exponentially, and thus the kinetics of labeling must be corrected for the expansion of the protein pool through growth. From our data on a limited subset of proteins in S. cerevisiae (39) and from a more recent comprehensive study, also in chemostat culture (40), we can make some interesting inferences. We quantify the abundance of the total yeast proteome as ∼60,000,000 protein molecules (60, 61). Moreover, the median half-life of the most abundant category of protein is ∼10 h (40), yielding a first-order rate constant of 0.07 h⁻¹. Thus, the entire yeast proteome turned over at that median value would require a flux of ∼4,000,000 protein molecules degraded per hour. If we make the dangerous assumption that all of the degradation was channeled through the 20S proteasome, then calculations of average throughput can be made. We have estimated via intensity-based label-free quantification that the total number of 20S proteasome subunits in exponentially growing S. cerevisiae cells is ∼8000 copies per cell,² and thus each 20S subunit is, on average, processing about 500 substrate molecules per hour, or fewer than 10 molecules per minute. There are many caveats that should be attached to such calculations, but they serve to illustrate that in rapidly growing cells the degradative processes might be largely idling and handling the degradation of only a few key proteins plus any misfolded/damaged proteins. Studies performed with non-dividing cells (26) or adult animals (22, 25, 26, 31, 43, 44, 62–67) might give a more realistic picture of steady-state protein turnover, reflecting the process in cells that are non-dividing and which must adjust the intracellular protein abundance via manipulation of intracellular turnover. Although experimentally more challenging, the recent large-scale studies obtained with complex systems (22, 25, 26, 31, 43, 65–67) are beginning to give insights into the maintenance of individual protein abundance in tissues, in organelles, and in species—a proteome-scale test of those observations initially made with total protein.

It will not be possible to capture in protein databases a single parameter for the rate of turnover of a protein. Any conditions under which the absolute abundance of the protein changes must, by definition, display a difference in either k_syn or k_deg or, indeed, in both parameters (26). Within any animal, the same gene product is likely to vary in turnover rate, depending on the tissue in which it is expressed (22); for example, liver and kidney both have a high average rate of turnover, whereas skeletal and cardiac muscle have rather lower rates of turnover. Our study in mice showed that kidney and liver proteins had similar rates of turnover in the two tissues, with the exception of isocitrate dehydrogenase (NADP), which had a higher rate of turnover in the kidney, and catalase, which had a much higher rate of turnover in the liver; the asymmetry in the turnover of such proteins can be anticipated to have as yet unknown functional consequences. All proteins expressed in both cardiac and skeletal muscle were turned over faster in the heart, although the rates of turnover of aldolase and pyruvate kinase were considerably different (22). At present, we cannot ascribe functional significance to such changes in turnover, but such variances in specific protein degradation are promising avenues for further research.

Finally, overall rates of protein turnover scale with metabolic rate, and so a degradation rate constant obtained from a mouse is unlikely to be maintained in a larger mammal such as man. It is less apparent whether overall rates of protein turnover vary significantly between, for example, different human cell lines, although there are signs of this being the case (26)—certainly there is considerable variation in the reported k_deg figures that are being accumulated. Given the considerable variation in cellular systems under study, in experimental approach and labeling strategies, and in data processing and reporting, it is evident that there is considerable scope for further studies that combine the exquisite sensitivity and selectivity of proteomics with imaginative labeling strategies and a full appreciation of the importance of the compartmental modeling of precursor and reutilization pools. The future of proteome turnover is far from a “degrading business” and offers considerable hope for a clearer understanding of the mechanisms by which cells perform their essential housekeeping.