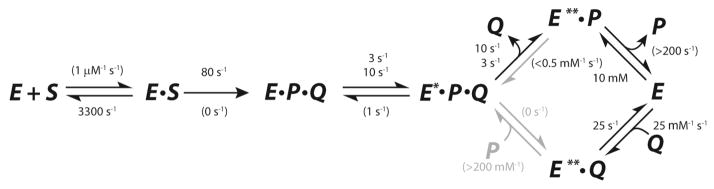A Pre-Steady State Kinetic Analysis of the αY60W mutant of trans-3-Chloroacrylic Acid Dehalogenase: Implications for the Mechanism of the Wild-type Enzyme

Abstract

The bacterial degradation of the nematicide 1,3-dichloropropene, an isomeric mixture, requires the action of trans- and cis-3-chloracrylic acid dehalogenase (CaaD and cis-CaaD, respectively). Both enzymes are tautomerase superfamily members and share a core catalytic mechanism for the hydrolytic dehalogenation of the respective isomer of 3-haloacrylate. The observation that cis-CaaD requires two additional residues raises the question of how CaaD carries out a comparable reaction with fewer catalytic residues. As part of an effort to determine the basis for the apparently simpler CaaD-catalyzed reaction, the kinetic mechanism was determined by stopped-flow and chemical quench techniques using a fluorescent mutant form of the enzyme, αY60W-CaaD, and trans-3-bromoacrylate as the substrate. The data from these experiments as well as bromide inhibition studies are best accommodated by a six-step model that provides individual rate constants for substrate binding, chemistry, and a proposed conformational change occurring after chemistry followed by release of malonate semialdehyde and bromide. The conformational change and product release rates are comparable and together they limit the rate of turnover. The kinetic analysis and modeling studies validate the αY60W-CaaD mutant as an accurate reporter of active site events during the course of the enzyme-catalyzed reaction. The kinetic mechanism for the αY60W-CaaD-catalyzed reaction is comparable to that obtained for the cis-CaaD-catalyzed reaction. The kinetic model and the validated αY60W-CaaD mutant set the stage for an analysis of active site mutants to explore the contributions of individual catalytic residues and the basis for the simplicity of the reaction.

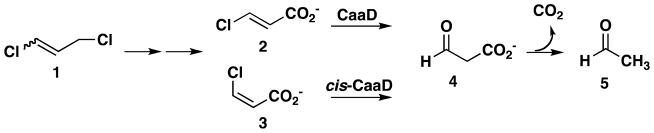
A mixture of cis- and trans-1,3-dichloropropene (1, Scheme 1) constitutes the active ingredient in nematicides marketed as Telone II and Shell D-D.¹ The effectiveness of 1 in soil is limited by its rapid degradation due, in part, to the bacterial 1,3-dichloropropene catabolic pathway.^1–3 In three enzyme-catalyzed steps, the isomeric mixture is processed to the trans- and cis-isomers of 3-chloroacrylic acid (2 and 3, respectively).^3,4 Subsequently, these compounds are processed by the isomer-specific dehalogenases trans- and cis-3-chloroacrylic acid dehalogenase (CaaD and cis-CaaD, respectively) to malonate semialdehyde (4).^4–6 Malonate semialdehyde decarboxylase (MSAD) converts 4 to acetaldehyde (5), which is channeled into the Krebs cycle.⁷ The three enzymes are members of the tautomerase superfamily, a group of structurally homologous enzymes characterized by a β–α–β building block and a catalytic amino-terminal proline (Pro-1).^{8, 9} These three enzymes evoke interesting mechanistic, structural, and evolutionary questions including how they became part of the same pathway. Hence, their properties have been extensively characterized.⁹

Scheme 1.

The 1,3-dichloropropene catabolic pathway.

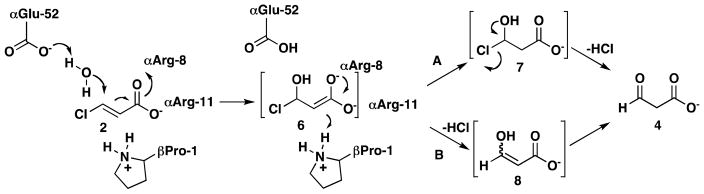
Sequence analysis coupled with mechanistic and structural studies identified Pro-1, from the β-subunit, and Arg-8, Arg-11, and Glu-52, from the α–subunit, as key catalytic residues in the heterohexameric CaaD.^{4, 5, 10, 11} In the current working hypothesis for the mechanism (Scheme 2), αGlu-52 functions as a general base catalyst to activate a water molecule for attack at C-3 of 2.^{10, 11} The two arginines (αArg-8 and αArg-11) interact with the C-1 carboxylate group to align the substrate in the active site and draw electron density away from C-3, which facilitates the addition of water to C-3 to produce the enediolate species, 6. In one scenario (Scheme 2, route A), βPro-1 (pK_a ~9.2) protonates C-2 to complete the conjugate addition of water and form a chlorohydrin intermediate (7), and the chemical or enzyme-catalyzed decay of 7 then yields 4. In a second scenario (Scheme 2, route B), 6 rearranges to enol 8, which is coupled with the elimination of the chloride (i.e., an α,β-elimination of HCl), and subsequent ketonization (chemical or enzyme-catalyzed) yields 4, where the C-2 proton is again provided by βPro-1.

Scheme 2.

The proposed mechanisms for the CaaD-catalyzed reaction.

Given the similarities in the overall active site organization, it was initially thought that the mechanisms of CaaD and cis-CaaD were largely the same, with differences in the primary (70 and 75 amino acids for the α- and β-subunits of CaaD vs 149 amino acids in cis-CaaD) and quaternary structures (heterohexamer vs trimer), and the corresponding isomer specificities.⁶ However, in light of additional results, it became apparent that there are at least three major differences in the catalytic mechanisms. First, two extra residues, His-28 and Tyr-103, are involved in the dehalogenation of the cis-isomer. ¹² The positions of these residues in a crystal structure suggest that His-28 aligns with the arginine pair and Tyr-103 assists a glutamate residue (Glu-114) in the activation of water. There are no obvious counterparts for these residues in CaaD. Second, a loop may be involved in cis-CaaD catalysis, where substrate binding induces loop closure, facilitating catalysis.¹³ A similar event has not been discovered in the catalytic cycle of CaaD. Third, there is very recent evidence that cis-CaaD utilizes a covalent intermediate (via Pro-1) to process an alternate substrate, 2,3-butadienoate, and that some fraction of the reaction using cis-3-haloacrylates might also function by covalent catalysis.¹⁴

Potential roles for the loop and the covalent intermediate in the cis-CaaD mechanism were suggested in part from pre-steady state kinetic experiments.^{13, 14} The experiments reported here were part of a larger effort to delineate similarities and difference between CaaD, cis-CaaD, and their mutants, and to establish a basis for their catalytic differences. In this report, we use trans-3-bromoacrylate (9) as the substrate because the release of bromide can be accurately quantified, as in our previous studies on cis-CaaD. ¹³ The stopped-flow fluorescence experiments on cis-CaaD relied on a change in the enzyme fluorescence after the addition of 3.¹³ CaaD does not have a significant native fluorophore: it only contains 2 tyrosine residues (αTyr-9 and αTyr-60), one of which (αTyr-60) is located near the active site.¹⁰ Hence, a tryptophan residue was introduced to provide a stronger signal for stopped-flow fluorescence experiments. In silico docking studies guided our selection of a point mutation to introduce a tryptophan residue to provide a strong fluorescence signal to monitor enzyme states during catalysis. Mutation at αTyr-60 had a minimal effect on the observable CaaD reaction, as assessed by the steady state kinetic parameters, rapid quench experiments, and bromide inhibition studies. Transient state kinetic data obtained using stopped-flow fluorescence and rapid chemical quench flow methods, and full progress curve kinetic traces were fit by global simulation to yield a minimal six-step model with individual rate constants for chemistry, a proposed conformational change occurring after the chemistry, and a biased-random product release.

MATERIALS AND METHODS

Materials

Chemicals, biochemicals, buffers, and solvents were purchased from Sigma-Aldrich Chemical Co. (St. Louis, MO), Fisher Scientific Inc. (Pittsburgh, PA), Fluka Chemical Corp. (Milwaukee, WI) or EMD Chemicals, Inc (Gibbstown, NJ). The reagents used in the ion chromatography (IC) and rapid quench experiments were acquired from sources reported elsewhere.^{13, 14} The centrifugal filter devices (3,000 MW cutoff) were obtained from PALL Life Sciences (Ann Arbor, MI). Column resins were obtained from Sigma-Aldrich.

Bacterial Strains, Plasmids, and Growth Conditions

Escherichia coli strain BL21-Gold(DE3) was obtained from Stratagene (La Jolla, CA). The E. coli DH5α cells were obtained from Invitrogen (Carlsbad, CA). The construction of the pET-24a(+) vector (EMD Chemicals, Inc.) containing caad1 and caad2 (the α- and β-subunits of CaaD, respectively) is described elsewhere.^{4, 5, 15} Cells were grown at 37 °C in Luria-Bertani (LB) media that contained kanamycin (Kn, 30 μg/mL).

General Methods

The PCR amplification of DNA sequences was conducted in a GeneAmp 2700 thermocycler (Applied Biosystems, Carlsbad, CA). Techniques for restriction enzyme digestion, ligation, transformation, and other standard molecular biology manipulations were based on methods described elsewhere.¹⁶ DNA sequencing was performed by the DNA Core Facility in the Institute for Cellular and Molecular Biology (ICMB) at the University of Texas at Austin. Mass spectrometer (MS) data were collected on an LCQ electrospray ion-trap mass spectrometer (Thermo, San Jose, CA) housed in the ICMB Protein and Metabolite Analysis Facility at the University of Texas. Steady state kinetic assays were performed on an Agilent 8453 diode-array spectrophotometer at 22 °C.⁵ Non-linear regression data analysis was performed using the program Grafit (Erithacus Software Ltd., Staines, U.K.). Protein concentrations were determined according to the method of Waddell.¹⁷ Sodium dodecyl sulfate-polyacrylamide gel electrophoresis (SDS-PAGE) was carried out on denaturing gels containing 15% or 20% polyacrylamide.¹⁸ The pre-steady state kinetic data were fit by simulation using KinTek Global Kinetic Explorer (KinTek Corp. Austin, TX).

Docking Studies

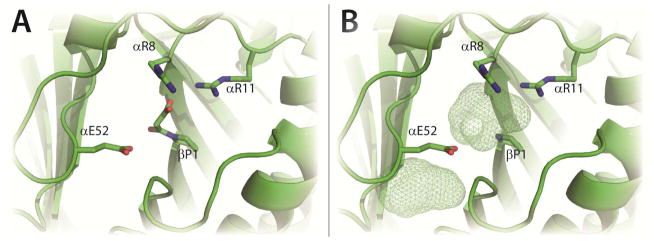
In order to identify and optimize positions for a tryptophan residue in the CaaD active site, docking studies were carried out using PyMOL with Autodock Vina.^{19, 20} To minimize differences in the active sites of the different CaaD crystal structures, 21 active sites in four reported crystal structures were compared (PDB codes: 1S0Y1, 3EJ3, 3EJ7, 3EJ9). [Each heterohexamer contains 3 active sites. One crystal structure (PDB code 3EJ9) contains a single heterohexamer, whereas those for PDB codes 1S0Y, 3EJ3, and 3EJ7 contain two heterohexamers. This gives a total of 21 active sites.] The crystal structures include those with covalent (malonic acid, 1S0Y) and non-covalent ligands (acetate and phosphate, 3EJ3), and those without any ligands (3EJ7 and 3EJ9). The side chains of αGlu-52 and αLeu-57 adopt different rotomers depending on the bound ligand limiting the available active site space. One active site from the crystal structure with the covalently bound malonyl adduct was chosen as the receptor for docking studies (Figure 1A). The covalent adduct on the prolyl nitrogen of βPro-1 results from the reaction of CaaD with 3-bromo or 3-chloropropiolate, as described elsewhere.^{5, 10} The adduct was removed before docking experiments were performed (Figure 1B). This crystal structure (1S0Y) was chosen because it shows the heterotrimer and the α–chain has well-defined electron density out to residue 63. A 10Å × 15Å × 10Å box centered on the βPro-1 residue was selected as the origin of docking. The side chains of αGlu-52 and αLeu-57 were designated as flexible during docking routines.

Figure 1. CaaD Active Site.

Two views of the active site of CaaD (PDB code 1S0Y). A) The key catalytic residues of CaaD shown as sticks with βPro-1 covalently attached to malonate after reaction with 3-bromopropiolate.¹⁰ B) The approximate active site volume as predicted in Pymol is shown in mesh after the malonate moiety has been removed from the active site. The mesh area below αE52 shows unoccupied space near the active site. The figure was prepared using PyMOL.²⁰

Construction of the CaaD Mutants

Four CaaD mutants were constructed using a pET-24a(+) vector containing both caad1 and caad2 genes as the template. Mutations were introduced at the appropriate position using the QuikChange Site-Directed Mutagenesis Kit (Stratagene) following the manufacturer’s instructions. Oligonucleotide primers (coding and complementary) with the desired change to make the αY60W, αM7W, αL57W, and βI37W CaaD mutants were obtained from Sigma-Aldrich. The forward and reverse primers used to introduce the mutations were respectively: 5′-CTGCCGGACTGGGTGCCAG-3′ and 5′-CTGGCACCCAGTCCGGCAG-3′ (αY60W); 5′-CTTGCGACTGGCGCTATGGGAG-3′ and 5′-CTCCCATAGCGCCAGTCGCAAG-3′ (αM7W); 5′-CGAGCATTGGCCGGACTAC-3′ and 5′-GTAGTCCGGCCAATGCTCG-3′ (αL57W); and 5′-CGACCCCAAGTGGATCAATG-3′ and 5′-CATTGATCCACTTGGGGTCG-3′ (βI37W). The DNA products were purified using the MiniElute PCR Purification Kit (Qiagen, Valencia, Ca.) and transformed into E. coli DH5α cells for plasmid preparation. Single colonies were used to inoculate 20 mL of LB/Kn media. The cultures were grown overnight at 37 °C and plasmids were isolated using the GenElute Plasmid Miniprep Kit (Sigma-Aldrich).

Expression and Purification of CaaD and CaaD Mutants

CaaD was grown and expressed in E. coli BL21-Gold(DE3) cells and purified by a variation of published protocols.^{5, 15} An overnight starter culture (40 mL) was grown at 37 °C from a single colony and used to inoculate five 2 L Erlenmeyer flasks (each containing 500 mL of LB/Kn media). The cultures were incubated for ~2 h at 37 °C. Protein expression was induced with isopropyl β-D-thiogalactopyranoside (1 mM, final concentration), followed by a 4–5 h induction period at 37 °C. Cells were harvested by centrifugation (4,000 × g), to yield ~7 g of cells and stored at −80 °C. Cells were suspended in 10 mM Na₂HPO₄ buffer, pH 8 (Buffer A) and lysed by sonication. The resulting solution was centrifuged for 30 min (23,500 × g) and the supernatant was subjected to an additional 30 min of centrifugation (330,000 × g). Solid (NH₄)₂SO₄ (for a final concentration of 1.6 M) was slowly added (over 10 min) to the supernatant and the resulting solution was stirred on ice for 1 h, and then centrifuged for 15 min (23,500 × g). The clarified supernatant was filtered (0.2 μM pore) and loaded onto a Phenyl-Sepharose 6 Fast Flow column (0.5 × 10 cm, ~4 mL resin) pre-equilibrated with Buffer A containing 1.6 M (NH₄)₂SO₄ (Buffer B). The column was washed (~1 mL/min) with 5 mL of Buffer B followed by a linear salt gradient [1.6-0 M (NH₄)₂SO₄]. Protein typically elutes 45–60 min after initiation of the salt gradient. Protein purity in the individual fractions was evaluated by SDS-PAGE and activity assays. Fractions with the highest activity and purity were pooled and exchanged into Buffer C (50 mM Na₂CO₃ buffer, pH 10.5) using an Amicon stirred-cell concentrator (10,000 MW cutoff). Exchanged protein was then loaded onto a Q-Sepharose 6 Fast Flow column (~7 mL of resin) pre-equilibrated with Buffer C and washed (~1 mL/min) with Buffer C (5 mL), followed by elution using a linear salt gradient (0–0.1 M Na₂SO₄). Protein typically elutes 15–45 min after the start of the salt gradient. The appropriate fractions, assessed as described above, were pooled. The combined fractions were exchanged into 100 mM Na₂HPO₄ buffer, pH 8, using an Amicon stirred-cell concentrator (10,000 MW cutoff) and concentrated to ~16 mg/mL (~1 mM). Yields were typically ~75 mg of homogenous protein from 2.5 L of culture.

Mass Spectral Analysis of CaaD and CaaD Mutants

The monomer molecular masses of CaaD and the CaaD mutants were determined by electrospray ionization mass spectrometry (ESI-MS) using LCQ electrospray ion-trap mass spectrometer. Samples for ESI-MS analysis were made 1 mg/mL and prepared as reported.⁵ The observed molecular mass (MH⁺) for the α- and β-subunits of CaaD are 8343 Da and 7505 Da, respectively. The α-subunits of Y60W, M7W, and L57W-CaaD give molecular masses of 8367, 8398, 8416 Da, respectively. The β-subunit of I37W-CaaD shows a molecular mass of 7578 Da. These masses agree with the calculated masses (within experimental error).

Steady State Kinetics

The steady state kinetic parameters for CaaD and the four CaaD mutants were measured using trans-3-bromoacrylate (9).⁵ The assays were carried out at 22 °C in 100 mM Na₂HPO₄ buffer, pH 8.1, using a 2 μM enzyme solution (based on the α-β dimer molecular mass). [Other buffers (with better buffering properties) were examined, but they inhibited the reaction or reacted with malonate semialdehyde.] Enzyme solutions were equilibrated for 1 h prior to use. The assay was initiated by the addition of 9 from a 20 mM stock solution (made up in 100 mM phosphate buffer, final pH 8.1). The decrease in absorbance at 224 nm, corresponding to the hydration of 9 (ε₂₂₄= 9100 M⁻¹ cm⁻¹), was monitored over a 60 s time period, with readings recorded every 3 s. Initial rates were plotted vs. substrate concentration and fit to the Michaelis-Menten equation using Grafit to determine k_cat and K_m. Data for full time course experiments (300 s) were collected using five concentrations of 9 (20, 50, 80, 100, and 150 μM).

Stopped-Flow Experiments

The stopped-flow experiments were carried out on a SF 2004 series stopped-flow apparatus (KinTek Corp). Wild-type, αY60W- and αM7W-CaaD, were separately made up in 100 mM Na₂HPO₄ buffer, pH 8.1, to final concentrations of 20 μM (based on the α-β dimer molecular mass), and allowed to equilibrate at 22 °C for 1 h. Various concentrations of 9 (0–20,000 μM) were made up in 100 mM Na₂HPO₄ buffer, pH 8.1. The enzyme (10 μM after mixing) and substrate (0–10,000 μM after mixing) solutions were then mixed in the stopped-flow apparatus at 22 °C. The fluorescence was excited at 280 nm and emission was observed using a 340 nm band pass filter (Semrock, Rochester, NY). The slit width on the monochromator and the light filter were set at 0.6 mm. Traces represent an average of at least five runs at each substrate concentration. The time courses range between 1–300 s with 1000 data points collected for each trace. Stopped-flow fluorescence traces were fit initially to defined exponential functions by non-linear regression using the KinTek stopped-flow software. Data were fit either to a single exponential (Eq. 1) or double exponential function (Eq 2).

$$Y=A·exp(-\lambda t)+C$$ (Eq. 1)

$$Y=A_1·exp(-{\lambda }_{1}t)+A_2·exp(-{\lambda }_{2}t)+C$$ (Eq. 2)

The concentration dependence of the rate was fit to a hyperbola (Eq. 3) using non-linear regression (Grafit).

$$\lambda =\frac{k_{\mathit{for}}[S]}{K_d+[S]}+k_{\mathit{rev}}$$ (Eq. 3)

Light transmittance (280 nm) was also monitored in the stopped-flow apparatus with various concentrations of 9 in buffer.

Rapid-Quench Experiments

The rapid-quench experiments were carried out at 22 °C on a RFQ-3 quench-flow apparatus (KinTek Corp). The experimental procedure followed previously published ones with the modifications noted below.¹³ To correct for dilution errors introduced by sample preparation and the rapid quench apparatus, tartrate was included as an internal standard. Tartrate is well-resolved from other peaks (e.g. bromide, phosphate, and sulfate), readily quantified by ion chromatography (IC), and does not inhibit CaaD at concentrations of 4 mM. Typically, ~8 mM tartrate (4 mM final concentration) was added to a concentrated enzyme solution (400–1000 μM) in 100 mM Na₂HPO₄ buffer, pH 8.1, and allowed to equilibrate for 1 h. For each experiment, one syringe was loaded with enzyme solution (400–1000 μM) containing 8 mM tartrate and a second syringe was loaded with freshly prepared 9 (from a 20 mM stock solution, pH 8.1). The reaction mixture (~15 μL enzyme and ~15 μL substrate) was quenched at intervals ranging from 3 ms to 1.5 s (depending on the k_cat of the enzyme) with 0.6 M H₂SO₄ (~90 μL). The individually quenched reaction mixtures (~110 μL) were then transferred to a PALL centrifugal filter device (3,000 MW cutoff), and centrifuged at 11,000 rpm for 30 min to remove enzyme. The effluent was saved (~80 μL) and used for bromide and tartrate quantification. An aliquot of the effluent (~25 μL) was diluted into 475 μL of 20 mM NaHCO₃ buffer, pH 9.0, to give a final volume of 500 μL, pH ~3.0. To quantify the amount of tartrate added to the concentrated enzyme solutions, an unreacted enzyme control sample (~100 μL) was filtered (as above) to remove enzyme and 10 μL aliquots of effluent were added to 490 μL of 20 mM NaHCO₃ buffer, pH 9.0, to give a final volume of 500 μL. These control samples were made up in triplicate and the tartrate concentration was quantified by IC analysis. A dilution factor for each sample was determined by dividing the final tartrate concentration by the average initial tartrate concentration added to the enzyme solution. The bromide ion concentration was determined using IC on an ICS-1500 instrument as previously described with the following modifications.¹³ The contents of the mixture elute over a 18 min period. Bromide ion was detected by suppressed conductivity with an applied current of 25 mA and quantified as described.¹³ A linear plot of the peak area vs. the concentration of bromide gives a slope of 0.018 ± 0.002 μS × min⁻¹ × ppm⁻¹ (correlation coefficient ~ 0.995), where μS is microsiemens and ppm is parts per million. The calibration curve for tartrate was constructed using a stock solution of 100 mM sodium tartrate in 20 mM NaHCO₃ buffer, pH 9.0. Seven serial dilutions (0.08–50 mM) were made from the 100 mM sodium tartrate solution stock. A linear plot of the peak area vs. the concentration gave a slope of 0.0020 ± 0.0001 μS × min × mM⁻¹ (correlation coefficient ~ 0.995).

Data were fit to the burst equation to estimate the rate (λ) and amplitude (A) of the reaction followed by steady state turnover (k_ss):

$$Y=A·exp(-\lambda t)+k_{ss}·t$$ (Eq. 4)

In this equation, the fitted line was constrained to begin at the origin (Y=0 at t=0).

Inhibition of CaaD by Bromide Ion

Product inhibition of CaaD by bromide ion was determined under the steady state conditions described above. The assays were carried out at 22 °C in 100 mM Na₂HPO₄ buffer, pH 8.1 using a 2 μM enzyme solution. Aliquots of a sodium bromide solution (0.5 M in 100 mM Na₂HPO₄ buffer, pH 8.1) were added to 1 mL portions of enzyme solution to yield a total of six final inhibitor concentrations (0, 5000, 10000, 15000, 30000, 50000 μM). The assay was initiated by the addition of six different concentrations of 9 (35, 50, 75, 120, 160, and 200 μM), obtained from a 50 mM stock solution. The initial rate of the hydration of 9 was monitored over a 60 s time period, recording readings every 3 s. [To avoid significant signal interference due to bromide absorbance at 224 nm, the kinetic traces were followed at 234 nm.] The inhibition patterns were determined by plotting the initial rate of the reaction vs. the concentration of bromide at different concentrations of 9 in a Dixon plot.^{13, 21, 22} Full time courses (220 s) at each inhibitor concentration were recorded under the same conditions using 300 μM of 9.

Binding of Bromide Ion to αY60W-CaaD

The binding of bromide ion to αY60W-CaaD was observed in the stopped-flow apparatus, where the change in fluorescence at 340 nm was monitored. The assay was conducted under the conditions described in the previous section using 10 μM enzyme solution. Various concentrations of bromide (0–100,000 μM) were made up in 100 mM Na₂HPO₄ buffer, pH 8.1. The enzyme (10 μM after mixing) and substrate (0–50,000 μM after mixing) solutions were mixed in the stopped-flow apparatus at 22 °C. At least five 1 s traces were collected and averaged for each concentration of bromide ion. Stopped-flow fluorescence traces were unchanged over 1 s. Therefore, the collected data for each trace were averaged (yielding a single fluorescence value) and plotted against the bromide ion concentration. The data in the resultant plot was fit to a hyperbola using Grafit. Stopped-flow traces were also fit by simulation using KinTek Global Kinetic Explorer and resulting values were used as constraints during global fitting.

Binding of Malonate Semialdehyde (4) to αY60W-CaaD

The binding of 4 to αY60W-CaaD was monitored in the stopped-flow apparatus (monitoring the change in fluorescence at 340 nm). The assay was conducted as described in the preceding section using a 10 μM enzyme solution. To generate 4, cis-CaaD (20 μM) and propiolic acid (10,000 μM) were mixed in 100 mM Na₂HPO₄ buffer, pH 8.1 (W.H. Johnson, Jr., J.P. Huddleston, G.K. Schroeder, and C.P. Whitman, unpublished observations, 2012). After 4 min, the mixture was transferred to a PALL centrifugal filter device (3,000 MW cutoff), and centrifuged at 11,000 rpm for 10 min to remove enzyme. This procedure generates ~10,000 μM of 4 (assuming the reaction is quantitative.) [Malonate semialdehyde (4) is a mixture of the aldehyde (~25%) and hydrate (~75%)⁷.] Various concentrations of 4 (0–10,000 μM) were made up in 100 mM Na₂HPO₄ buffer, pH 8.1, immediately before use. The αY60W-CaaD (10 μM after mixing) and different concentrations of 4 (0–5,000 μM after mixing) were mixed (1 s) in the stopped-flow apparatus at 22 °C. Stopped-flow traces were fit to a single exponential using the KinTek stopped-flow software. The k_obs and constant values (C) were plotted vs. the concentrations of 4. The plots of C vs. [4] and k_obs vs. [4] were fit to hyperbolic and linear equations, respectively. In addition to this conventional analysis, the data were fit by simulation and resulting values were used as constraints for global fitting.

Data and Global Fitting Analysis

Conventional data fitting of pre-steady state kinetic data (including concentration dependence) by non-linear regression using the program Grafit provided initial estimates for rate constants and a minimal number of steps in the overall reaction pathway. The steady state k_cat/K_m value was used as a lower limit for the rate of substrate binding and the k_cat value provided a lower limit for individual first order rate constants following substrate binding and proceeding through product release.^{14, 23} All of the collected data were then globally fit to a single kinetic model using KinTek Global Kinetic Explorer, as described elsewhere. ^{13, 14, 24} During the process of global optimization, the data collected over a series of concentrations within a given experiment were scaled using a correction factor (less than 5%) for each trace to correct for slight lamp drift between traces. The simulated traces also contain a correction factor to account for the change in the fluorescence intensity resulting from the reduced transmitted light (280 nm) due to absorbance by substrate (9, ε₂₈₀ = 110 M⁻¹ cm⁻¹) and product (4, ε₂₈₀ ~ 27 M⁻¹ cm⁻¹). The reduced light intensity (I) is provided by the logarithmic function, I = I_ref 10^{−ε•c•(l/2)}, where ε is the extinction coefficient at 280 nm, c is the concentration of the species, and l is the path length of the cell (0.5 cm). The average light intensity across the full fluorescence window was approximated by l/2 (0.25 cm).¹⁴

RESULTS

In silico Docking Experiments

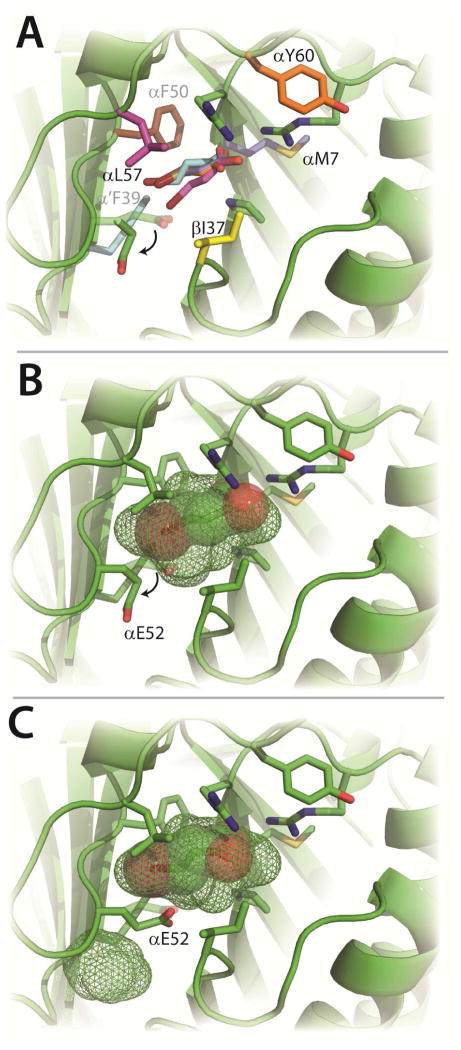
In order to provide a stronger signal for stopped-flow fluorescence experiments on CaaD, a tryptophan residue was introduced at a position near the active site. Several sites were evaluated where the mutation would have a minimal impact on the reaction kinetics and enzyme structure. Inspection of the crystal structures of CaaD (1S0Y, 3EJ3, 3EJ7, 3EJ9) and cis-CaaD (2FLZ) combined with a series of docking studies, identified six potential sites for the insertion of the tryptophan (αPhe-39, αPhe-50, αLeu-57, βIle-37, αMet-7, αTyr-60). Docking studies were carried out in silico with wild-type CaaD and six tryptophan mutants (αF39W, αF50W, αM7W, αY60W, αL57W, and βI37W generated by in silico using the PyMOL mutagenesis wizard) and 9 (Figure 2A).²⁰ With the exception of the αF39W and αL57W in silico mutants, (the tryptophan side chain of the αL57W mutant was held fixed during the docking studies) the consensus binding orientation for 9, as assessed by the lowest predicted free energies of binding (Table S1), places the carboxylate group near the two arginine residues and the bromide moiety buried near the back of the active site, facing a potential halide binding pocket consisting primarily of αPhe-39 and αPhe-50. Interestingly, in this consensus binding mode, the side chains of αGlu-52 and αLeu-57 adopt rotomers that increase the size of the active site pocket (Figure 2B). This increase in the active site volume (shown in mesh, Figure 1B vs. Figure 2B) allows 9 to fit in the active site.

Figure 2. Substrate Docking Studies.

A) Six docking poses of 9 in the CaaD active site having the lowest energies of binding (ΔG values can be found in Table S1) after each residue (shown in color) was independently replaced with a tryptophan (in silico). Four poses of 9 are superimposable, whereas the poses of 9 in the α’F39W (cyan) and αL57W (pink) enzymes are slightly different. All poses rotate E52 as illustrated by the arrow. B) Docking of 9 (spheres) into wild-type CaaD.¹⁹ Shown in mesh is the in silico active site pocket volume. The movement of αE52 to expand the active site volume is shown by the arrow. C) An alternative docking mode for 9 with αE52 in a position to perform the proposed chemistry with the newly predicted active site volume shown in mesh. The figure was prepared using PyMOL.²⁰

At first glance, αPhe-39 and αPhe-50, seemed to be the most promising sites for a tryptophan substitution: αPhe-39 superimposes on Trp-101 in cis-CaaD and αPhe- aligns with a tryptophan in two other tautomerase superfamily members [i.e., a heterohexamer 4-oxalocrotonate tautomerase and a 4-OT homologue in the tomaymycin biosynthetic pathway designated TomN].^{25, 26} However, in silico mutagenesis of these residues indicates that the CaaD active site cannot accommodate the larger indole side chain of the tryptophan residue. In the αF39W in silico mutant, there are steric clashes with nearby residues and a significant volume reduction of the putative halide binding pocket. In the αF50W in silico mutant, all rotomers exhibit significant steric clashes including one with the β1 strand containing αArg-8. Moreover, docking studies using 2 and 9 show steric clashes with the halide moiety of each substrate. These results may partially explain the intractable kinetic data previously obtained with the αF39W mutant of CaaD using 9. ²⁷ Hence, the αF39W and αF50W positions were no longer considered as possible sites for a tryptophan.

The αY60W in silico mutant has a predicted energy of binding (with 9) that is comparable to wild-type (−5.1 kcal/mol vs. −4.8 kcal/mol).¹⁹ Moreover, docking conformations in which the side chain of αGlu-52 points into the active site (Figure 2C) such that it can carry out the proposed chemistry, (i.e., activation of a water molecule for attack at C-3), were observed for both the in silico αY60W mutant and wild-type CaaD (−3.5 kcal/mol). A similar conformation for αGlu-52 is observed in the crystal structure of CaaD (1S0Y) containing the covalent malonyl adduct on βPro-1, perhaps reflecting the position of αGlu-52 after the attack of water on 9. Based upon our in silico analysis, four mutants, αM7W, αY60W, αL57W, and βI37W were constructed and their properties analyzed.

Steady state Kinetic Parameters of Wild-type and CaaD Mutants

Four CaaD mutants, αM7W, αY60W, αL57W, and βI37W, were constructed and purified. Mass spectral analysis shows nearly homogenous proteins (>95%) with the predicted subunit molecular masses (monomeric). The αL57W and βI37W mutants of CaaD have no activity with 2 or 9. Stopped-flow experiments using the βI37W mutant and 9 suggest that βI37W-CaaD binds 9 weakly with a K_d > 40 mM. Due to the similar locations of βI37 and αL57 in the active site, it appears that the substrate can no longer enter the active site because the indole side chain of tryptophan forms a “gate” that blocks the active site. No further experiments were carried out on these two mutants and their positions were no longer considered as possible sites for a tryptophan.

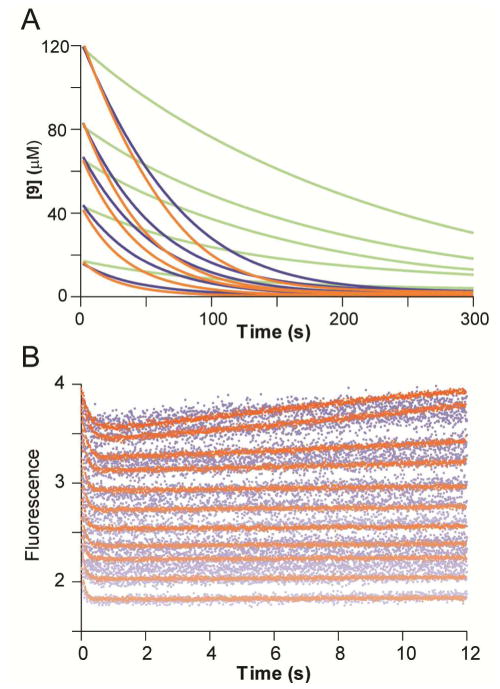
In contrast, the αM7W and αY60W mutants have steady state kinetic parameters (with 9) comparable to those of wild-type enzyme (Table 1). The K_m value for αM7W-CaaD is similar to that of wild-type, whereas the k_cat decreases ~4-fold. As a result, there is a 4-fold decrease in k_cat/K_m compared with wild-type. The K_m value for αY60W-CaaD decreases ~1.5-fold compared with wild-type, but the values of k_cat and k_cat/K_m are identical within experimental error. Full progress curves (300 s) were also carried out with these two mutants following the disappearance of various concentrations of 9 at 224 nm. At all concentrations of 9, the UV traces for αY60W-CaaD (shown in orange in Figure 3A) mirror those of wild-type CaaD (shown in blue in Figure 3A), reflecting the similar k_cat values. However, those corresponding to the αM7W mutant (shown in green in Figure 3A) exhibit slightly slower rates compared with wild-type, reflecting the reduced k_cat value.

Table 1.

Steady state Kinetic Parameters for CaaD and the CaaD Mutants Using trans-3-Bromoacrylate (9).^a

Enzyme	Km (OM)	kcat (s−1)	kcat/Km (M−1s−1)
Wild-type	120 ± 10	2.5 ± 0.1	1.3 ± 0.1 × 104
αM7W	120 ± 10	0.6 ± 0.1	0.3 ± 0.1 × 104
αY60W	70 ± 3.5	2.5 ± 0.1	1.2 ± 0.1 × 104
βI37W	> 40,000b	-	-

^aThe kinetic parameters were measured in 100 mM Na₂HPO₄ buffer (pH 8.1) at 22 °C following a decrease in absorbance at 224 nm.⁵ Errors are standard deviations.

^bDetermined in a stopped-flow experiment using 9, as described in the text.

Figure 3. Comparison of Wild-type and αY60W Mutant CaaD.

A) The UV traces following the disappearance of 9 (18, 42, 63, 83, and 125 μM) at 224 nm catalyzed by CaaD (blue), the αY60W mutant (orange), and the αM7W mutant (green). The full time courses for wild-type and the αY60W mutant are comparable. The full time course for the αM7W mutant is slower. B) Stopped-flow enzyme fluorescence (12 s) monitoring the reaction of wild-type CaaD (blue) and the αY60W-CaaD mutant (orange) with 9. Both show single exponential decay in fluorescence in the first 1 s, but the αY60W CaaD mutant shows a significant improvement in the signal-to-noise ratio. (Note that the wild-type data set has been normalized to superimpose it on the αY60W-CaaD mutant data set.)

Pre-Steady State Stopped-Flow Kinetic Experiments

The newly-created fluorescent CaaD mutants, αM7W and αY60W, were examined for their ability to report active site changes during the course of the enzymatic reaction. Changes in the enzyme fluorescence of both mutant proteins were monitored during the initial phases (12 s) and full time course (120 s) of the reaction with 9 (Figure S1). In the first second of the initial time course, the αY60W and αM7W mutants exhibited 2- and 3.5-fold decreases in fluorescence, respectively (Figures S1A and B). The full time course (120 s) shows that this decrease was followed by an increase in fluorescence, which eventually plateaus, as the reaction reaches completion (Figures S1C and D). Neither mutant shows significant photobleaching under the reaction conditions. Both mutants have similar initial reaction kinetics, which can be approximated by a single exponential, ignoring a possible lag at the beginning of the trace (vida infra). However, notable differences between the two mutants were observed in the full time course data (Figures S1C and D). The αY60W-CaaD mutant rapidly returns to a final fluorescence plateau, whereas the αM7W-CaaD showed a slower return to the final fluorescence value due to slower catalytic turnover by this mutant (Table 1 and Figure 3A).

Stopped-flow fluorescence measurements were also performed using wild-type CaaD, monitoring native enzyme fluorescence at 340 nm (with excitation at 280 nm). The fluorescence in the wild-type enzyme is likely due to αY60 because of the location near the active site and the similarities observed for the wild-type (shown in blue in Figure 3B) and αY60W CaaD mutant (shown in orange in Figure 3B). Due to the lower quantum yield of tyrosine, the wild-type fluorescence data have a reduced signal-to-noise ratio. However, the data sets from both wild-type and the αY60W-CaaD mutant showed the same initial single exponential drop in fluorescence, and conventional analysis of both data sets (Table S2) yielded the same maximum rates (vida infra), observed at the higher concentrations where the signal with wild-type enzyme was sufficient to afford reliable data fitting. Note that in both data sets, traces obtained at increasing substrate concentrations were offset due to the absorption of incident light by the substrate.

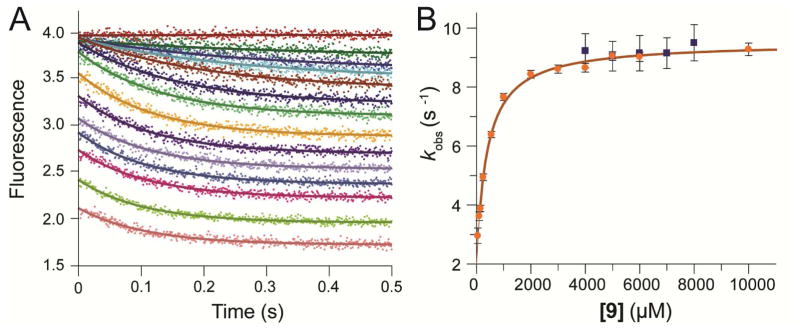
Data obtained with the αY60W-CaaD mutant gave a significantly larger signal at all concentrations, allowing more extensive analysis as shown in Figure 4. Initially, the first second of each trace was fit to a single exponential function (Figure 4A, Eq. 1). The concentration dependence of the rate (obtained from the single exponential) was fit to a hyperbola (Figure 4B, Eq. 3) suggesting a minimal two-step model with a rapid equilibrium step (K_d) followed by rate-limiting isomerization governed by forward and reverse rate constants (k_for and k_rev). Analysis of the concentration dependence of the rate defined an apparent K_d = 400 μM for initial substrate binding followed by a maximum rate of the fluorescence change of ~10 s⁻¹. A well-defined intercept on the y-axis afforded resolution of a net forward rate (k_for ~ 8 s⁻¹) and an apparent reverse rate (k_rev ~ 3 s⁻¹). The numerical values above are summarized in Table S3. As described below, because the enzyme turns over product and the actual reverse rate appears to be negligible (k_-2 = 0), the observed “reverse rate” is equal to k_cat. A more rigorous interpretation and explanation of these results are detailed below.

Figure 4. Stopped-Flow Fluorescence.

A) The stopped-flow fluorescence traces (0.5 s) showing reaction of αY60W-CaaD with 9 were fit to a single exponential (eq 1) shown in solid lines. The concentrations of 9 are: 0, 50, 100, 150, 250, 550, 1000, 2000, 3000, 4000, 5000, 6000, 8000, 10000 μM. B) The observed rate constant (k_obs) from the 1 s stopped-flow data for the wild-type (■) and the αY60W (●) CaaD plotted versus the concentration of 9. Error bars for the k_obs values are representative of the scatter in the data. Within error, the rate at high concentrations are identical. At lower concentrations, the signal to noise is too low to accurately resolve the rate. The solid line is a fit of the data to the hyperbolic equation (eq 3).

Rapid-Quench Experiments with CaaD and αY60W-CaaD

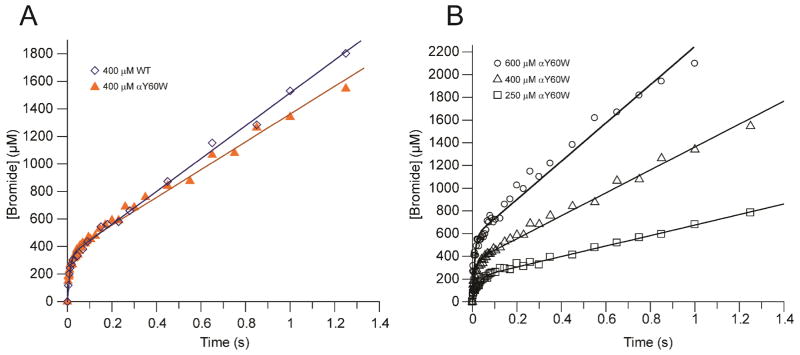
In light of the similarities in the kinetic parameters for wild-type and αY60W CaaD, rapid quench experiments were carried out with both enzymes, to provide a more rigorous comparison. Experiments were conducted by mixing equal volumes of various concentrations of enzyme (CaaD: 400 μM; αY60W-CaaD: 250, 400, and 600 μM, after mixing) and an excess of 9 (10 mM, after mixing). At fixed intervals (3–1500 ms), the reactions were quenched with acid, and the amount of bromide ion quantified by IC and plotted versus time (Figures 5A and B). A pre-steady state burst of product (bromide) formation was observed for both enzymes in all experiments, with a fast initial burst rate followed by a slower steady state turnover rate. The observation of a pre-steady state burst implies that a step after chemistry is at least partially rate limiting in both the CaaD- and αY60W-CaaD- catalyzed reactions.²³ Data were fit to the burst equation (Eq. 4) to yield the kinetic parameters summarized in Tables 2 and 3, defining the rate of the burst as approximately 85 s⁻¹, followed by steady state turnover of 3 s⁻¹. The sum of these observations, along with the steady state kinetic parameters and stopped-flow data presented above, indicated that the αY60W mutant of CaaD was a suitable candidate for subsequent in-depth analysis and use as a model for the wild-type CaaD reaction.

Figure 5. Rate of a Pre-steady State Burst.

Rapid quench experiments using CaaD and αY60W-CaaD fit to the burst equation. A) A comparison of the wild-type CaaD (⋄) and the αY60W-CaaD (▲) showing the burst of bromide followed by steady state turnover. The concentration of enzyme was 400 μM. B) Rapid quench experiment for three concentrations of αY60W CaaD: 250 μM (□), 400 μM (△), and 600 μM (○).

Table 2.

Burst Experiment Parameters Obtained using CaaD and the αY60W mutant^a

Enzyme (400 μM)	kburst (s−1)	kcatb (s−1)	Burst Amplitude (A)
Wild-type	90 ± 20c	3 ± 0.5	0.8
αY60W	86 ± 10	2.5 ± 0.5	0.9

^aThe kinetic parameters were measured in 100 mM Na₂HPO₄ buffer (pH 8.1) at 22 °C with a saturating concentration of 9.

^bCalculated from the burst equation.²³

^cErrors are standard deviations.

Table 3.

Burst Experiment Parameters Obtained at Different Concentrations of αY60W-CaaD^a

Enzyme concentration (μM)	kburst (s−1)	kcatb (s−1)	Burst Amplitude (A)
200	43 ± 3c	1.8 ± 0.5	0.85
400	86 ± 20	2.5 ± 0.5	0.9
600	107 ± 15	2.8 ± 0.5	0.94

^aThe kinetic parameters were measured in 100 mM Na₂HPO₄ buffer (pH 8.1) at 22 °C with saturating concentration of 9 (10,000 μM).

^bCalculated from the burst equation.²³

^cErrors are standard deviations.

Inhibition and Binding of Bromide to αY60W-CaaD

The mode of inhibition of bromide was investigated by monitoring the changes in the initial rate of the αY60W-CaaD- catalyzed reaction using 9 (35–200 μM) in the presence of various concentrations of bromide (0–50,000 μM). The inhibition pattern observed in the Dixon plot is consistent with competitive inhibition where the K_i value is ~10 mM (Figure S2).^{21, 22} Full time courses (300 s) were monitored using the αY60W-CaaD mutant at a fixed concentration of 9 (300 μM) in the presence of various concentrations of bromide ion (Figure S3B). A reduction in the rate of the reaction can only be observed at very high bromide concentration, consistent with the observed weak inhibition constant. Stopped-flow binding experiments were conducted using bromide ion and the αY60W-CaaD mutant (Figure S3A). At all bromide concentrations examined, the fluorescence change reached equilibrium within the dead time of the instrument (1.3 ms). Based on the saturation of the fluorescence signal, the αY60W-CaaD mutant binds bromide with a predicted K_d of 7.4 mM (similar to the K_i observed in the Dixon plot, Figure S2) with a ~14% increase in fluorescence (Figure S4, Table S3).

In addition to conventional fitting, binding data were fit by simulation using KinTek Global Kinetic Explorer (Figure S3A).²⁴ Due to rapid equilibration between the αY60W-CaaD mutant and bromide ion (faster than the dead time, <1.3 ms), the k_{off, Br} (release of Br⁻ from species E^**P) was held fixed at an arbitrarily fast rate (200 s⁻¹) where it didn’t affect the simulated traces and fitting was based upon finding the optimal value for k_on, _Br- (binding of Br⁻ to free E). Accordingly, the data only define the equilibrium constant (K_{d, Br}-) for bromide binding to free enzyme, but not the individual on and off rate constants. Fitting by simulation defines the fluorescence factor of 1.17 for enzyme-bound bromide, and a k_{on, Br}- affording the calculation of a K_{d, Br}- of 12 mM. The values of k_{off, Br}- and the fluorescence factor for enzyme-bound bromide were used as constraints for subsequent global fitting of the reactions of 9 with αY60W-CaaD. Steady state bromide inhibition experiments using wild-type CaaD (not shown) also suggest weak binding of bromide (~10 mM).

Binding of 4 to the αY60W-CaaD Mutant

Stopped-flow binding experiments were conducted with 4 (0–5000 μM after mixing) and the αY60W-CaaD mutant (Figure S5). Upon mixing αY60W-CaaD with 4, a 16% increase in the fluorescence signal was observed (Figure S6), like that observed for bromide. However, in contrast to the bromide binding (fast equilibration within the dead time), the binding of 4 occurs more slowly and requires ~100 ms to reach equilibrium. After approximately 0.5 s, the fluorescence signal decays, which we attributed to the instability of 4 and subsequent degradation to a chromophoric species, which absorbs strongly at 280 nm, thereby reducing the fluorescence signal (W.H. Johnson, Jr., G.K. Schroeder, J.P. Huddleston, and C.P. Whitman, unpublished observations, 2012). Data were fit using both conventional analysis (fitting to equations) and simulation-based methods (fitting based on numerical integration of the rate equations) (Figure S5 A-B). The initial phase of the time course (250 ms) for each trace was fit to a single exponential (Figure S5A). A plot of the resulting first order rate constants versus the concentration of 4 is nearly linear and fitting to equation S3 gave values of k_{on, 4} = 0.025 μM⁻¹s⁻¹ and k_{off, 4} = 28 s⁻¹ (Figure S6A). These values provide an estimate of the K_d (k_off / k_on) for 4 of 1100 μM. Based on the end-point fluorescence titration fit to Equation S2, the K_d for 4 was predicted to be 380 μM (Figure S6B). Fitting the data (250 ms) by simulation gave a k_{on, 4} of 0.028 μM⁻¹s⁻¹ and a k_{off, 4} of 17 s⁻¹ which affords the calculation of K_{d, 4} ~ 600 μM with a fluorescence factor of 1.14 for enzyme-bound to 4. These values are summarized in Table S2. The values for k_{on, 4} and the fluorescence factor for enzyme bound to 4 were used as constraints for subsequent global fitting of the reactions of 9 with αY60W-CaaD, yielding refined estimates for k_{off, 4} and K_{d, 4} by accounting for the rate and amplitude of the reactions simultaneously.

Kinetic Model Development

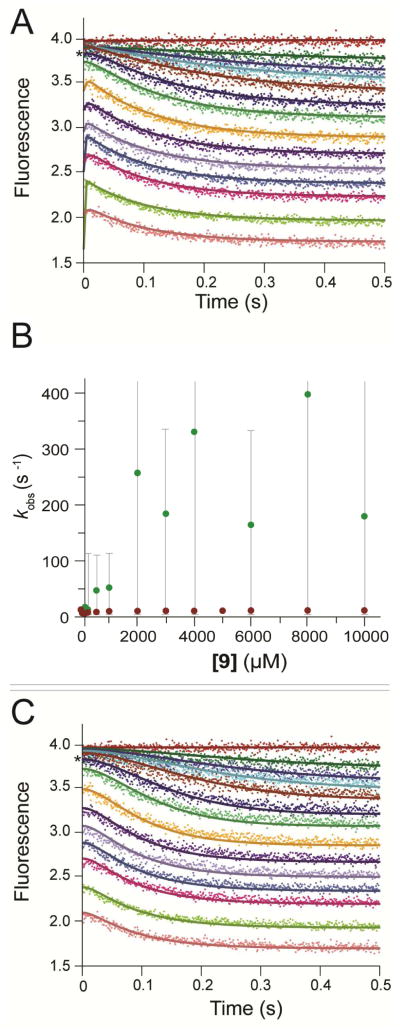
A kinetic model was developed to allow global fitting of the full data set in order to provide a more comprehensive test of the model. Conventional analysis (i.e. fitting to equations and plotting the observed rates versus concentration) was used to provide the initial kinetic model and estimates for some of the rate constants.²³ We initially fit the stopped-flow fluorescence data to a two-step model because the data appeared to be adequately fit to a single exponential function, reaching a maximum rate of ~10 s⁻¹. However, the rate of the pre-steady state burst of bromide product was approximately 100 s⁻¹ (Table 3), which defines the sum of the rates of chemistry and subsequent steps leading to release of product. These data imply that the chemistry step precedes the fluorescence change, and predicts that the fluorescence data should show a brief lag phase. Closer inspection of the stopped-flow fluorescence data revealed the data could be fit to a double exponential function (Figures 6A,B) but resolution of the lag phase was unreliable due to the large errors stemming from the low amplitude of the lag phase, and the inherent difficulties in fitting kinetic data to double exponential functions with arbitrary amplitude terms. In Figure 6C, we show a fit to the same data set based on computer simulation using the full kinetic model described below. The predicted lag phase is most prominent at the intermediate substrate concentrations. The simulated traces show the rate and the amplitude of the lag phase are consistent with the measured rates of the chemistry step, resulting in a more accurate representation of the lag phase kinetics.

Figure 6. Fitting a Lag in the Stopped-flow Fluorescence Data.

A) The stopped-flow fluorescence traces (0.5 s) of αY60W-CaaD with 9 were fit to a double exponential (eq 2) yielding the solid lines shown. The concentrations are the same as those listed in Figure 4A. B) The observed rate constants (λ₁ and λ₂) from the fit to eq 2 to the first 0.5 s of the stopped-flow data for the αY60W CaaD are plotted versus the concentration of 9. The faster rate constants are shown in green while the slower rate constants are shown in red. Shown in gray lines are the error bars on the first observable rate values. Note that some of these rates are off the y-axis and some of the error values exceed the rate constants values. Values for the slower rate constants and errors are similar to the rates observed from the single exponential fits shown in Figure 4B. C) The stopped-flow fluorescence traces (0.5 s) of αY60W-CaaD with 9 fit by global simulation are shown in solid lines. The simulation lines are able to account for the lag phase significantly better than conventional methods. The concentrations are the same as those listed in Figure 4A.

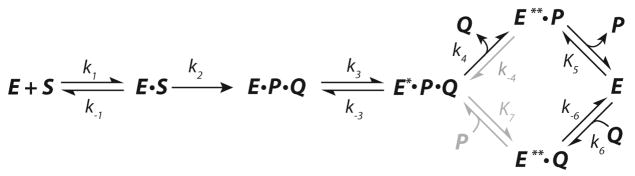
The sum of all of our results suggests a minimal model shown in Scheme 3 (with individual rate constant values shown in Scheme 4), with a fluorescence change occurring after the chemistry step. Product release is proposed to follow a biased random pathway with kinetic preference for the upper branch of the pathway (see Discussion). Three distinct fluorescence states (E, E^* and E^**) were proposed based upon quantitative analysis of the kinetic and equilibrium titration data. Fitting of the data set using this model, and the features of the data requiring each element of the model are discussed below.

Scheme 3.

Minimum kinetic pathway for the αY60W CaaD-catalyzed reaction. E is free enzyme, S is substrate (9), P is bromide, Q is malonate semialdehyde (4), and E^* and E^** are distinct forms of the enzyme with differing fluorescence quantum yield as described in the text.

Scheme 4.

Minimum kinetic pathway for the αY60W CaaD-catalyzed reaction with individual rate constants.

Global Fitting of Kinetic Data

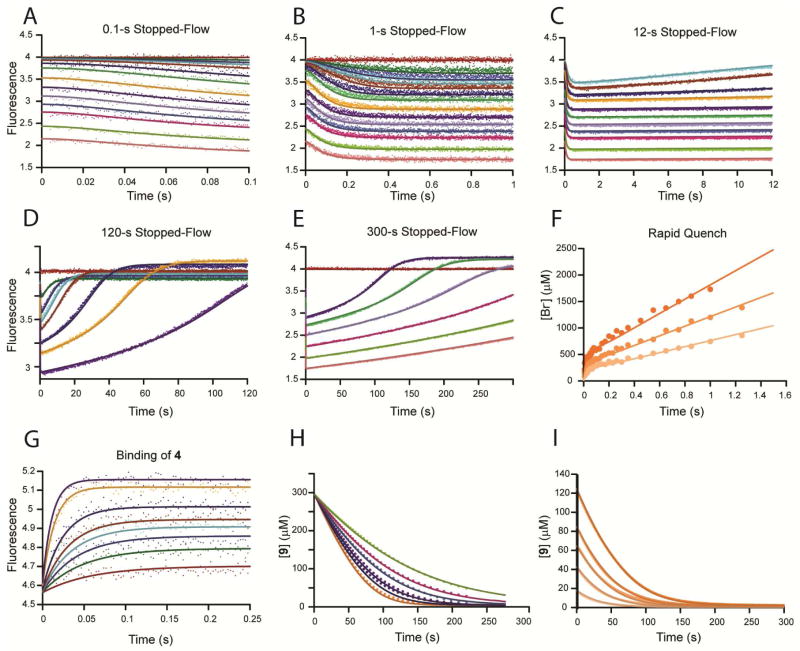
The complete data set for the αY60W-CaaD mutant reacting with 9 was subjected to global data fitting using KinTek Global Kinetic Explorer²⁴ in order to rigorously test our model and provide a more comprehensive analysis of the lag phase in the stopped-flow fluorescence data relative to the observed rate of the pre-steady state burst. The global fit of the data according to Scheme 3 is shown in Figures 7A–I, where the smooth lines represent the global fit to the entire data set based upon Scheme 3 with the rate constants summarized in Table 4 and shown in Scheme 4. The stopped-flow data at various concentrations of 9 (0–10,000 μM) are shown in Figures 7A–E. Figures 7A–B (see also Figure 6C) show the initial portion (100 ms) and first 1 s of the stopped-flow data, respectively, while Figure 7C shows the first 12 s of the reaction. Figures 7D–E (see also Figure S1C) show the change in fluorescence over the full-time course of the reaction (120 s and 300 s, respectively). Figure 7F (see also Figure 5) shows the pre-steady state burst of bromide formation (using 9) at various concentrations of αY60W-CaaD (250–600 μM). Figure 7G shows the time dependence for the binding of 4 to αY60W-CaaD (data from Figure S5A–B). This data set was not included explicitly in the global fit. However, the fit to this data by conventional analysis and simulation-based fitting of the single data set yielded a binding rate constant of ~0.025 s⁻¹ (Table S2 and Figure S6A); and this value was used for k₆ (Scheme 3) and held fixed during global fitting. Figure 7H (data from Figure S3B) shows the dehalogenation of 9 by αY60W-CaaD in the presence of various concentrations of bromide (0–50,000 μM). Figure 7I (data from Figure 3A) shows the full progress curves of the dehalogenation of 9. A single fluorescence factor for enzyme bound product species (E^**P and E^**Q in Scheme 3) was defined based upon the conventional analysis and fits by simulation of the individual data sets; because these data were not included in the global analysis (Table S2), the fluorescence factor was held constant at a value of 1.13 during global fitting, a value within the error ranges of each estimate (Table S2).

Figure 7. Global Data Fitting.

The αY60W-CaaD kinetic data with 9 and bromide (A–I) globally fit by simulation (solid lines) to the mechanism shown in Scheme 3 and (G) αY60W-CaaD kinetic data with 4 fit by simulation (solid lines) to give constraints on rates defined in Scheme 3 and Table 4.²⁴ (A–E) Stopped-flow fluorescence traces (0.1–300 s) for 9 (0–10000 μM) and αY60W-CaaD. Concentrations of 9 are: 0, 50, 100, 150, 250, 550, 1000, 2000, 3000, 4000, 5000, 6000, 8000, 10000 μM. Colors corresponding to the concentrations of 9 are maintained for graphs A–E. (F) Rapid-quench of αY60W-CaaD (200, 400, and 600 μM) with 9. (G) Stopped-flow fluorescence traces for 4 (100, 200, 300, 400, 500, 750, 1500, and 2000 μM) and αY60W-CaaD. (H) Full time progress curves following 300 μM of 9 at 224 nm with increasing concentrations of bromide (0, 5000, 10000, 20000, 30000, and 50000 μM). (I) Full time progress curves following the decrease of 9 (18, 42, 63, 83, and 125 μM) at 224 nm.

Table 4.

Rates Constants Derived from the Global Analysis of the αY60W-CaaD Reaction with 9^a

Rate	Lower Limitb	Upper Limitb	% Rangec	Best fit	Rate	Lower Limitb	Upper Limitb	% Rangec	Best fit
f/f0d	0.708	0.715	0.5%	0.710	k3e	5.0	13.0	41%	9.6 s−1
					k4	2.6	4.0	21%	3.3 s−1
k-1f	2600	4700	32%	3300 s−1	Kd,Br g	9100	20000	43%	12500 μM
k2	65	100	22%	78 s−1	k-6h	20	33	26%	25 s−1

^aThe data are fit globally to the mechanism shown in Scheme 4. Chemistry and the initial release of malonate semialdehyde (4) were assumed to be irreversible with reverse rates fixed at zero during global fitting.

^bThe upper and lower limits reflect a threshold of 3% deviation from the minimal SSE in the confidence contours. FitSpace error confidence contours are shown in Figure S7.²⁸

^cThe percentage range was calculated by dividing the mean of the range by the best fit value as (upper-lower) / (2*best fit). This reflects the allowable variation of each best fit value as a percentage.

^dThe fluorescence scaling factor is shown as the fractional change in enzyme fluorescence (see text).

^eFormation of E^*PQ was modeled as a reversible step associated with a conformational change in the enzyme. The value of k-₃ was held fixed at 1 s⁻¹ during global fitting (see text).

^fThe value for k₁ (substrate binding) was assumed to be fast and held fixed at 1 μM^{− 1} s⁻¹, so fitting to derive k_-1 defined only K_d,S (see text).

^gThe value for k₅ (release of bromide ion) was assumed to be fast (Figure S3A) and held fixed at 200 s⁻¹ (see text). As bromide binding is in rapid equilibrium with free enzyme, the data only defines the K_d for bromide

^hThe value for k₆ was defined by fitting the binding of 4 to free enzyme (Figure S5 and Table S2) and held fixed at 0.025 μM⁻¹ s⁻¹ during global fitting (see text). Errors for this value estimated by FitSpace results to the binding of 4 to free enzyme can be found in Figure S7 inset. The value f/f₀ for the product bound enzyme species (E^**) was determined by fitting the products, 4 and bromide, binding to free enzyme, individually, (Table S2) and held fixed at 1.13 during global fitting (see text). Rates for the alternate fit (see text) are provided in Table S4.

Data were not sufficient to define all of the rate constants in Scheme 3, so the ill-defined rate constants were assigned nominal values in order to fit the data to the full model. Because of the nature of the chemistry, we propose that the chemical reaction at the active site is essentially irreversible (k_-2 = 0). The proposed conformational change occurring after chemistry (vida infra), was allowed to be reversible with the value of k_-3 set at 1 s⁻¹, which represents a upper limit for k_-3 based upon analysis by computer simulation; that is, in fitting the data we noted that any rate greater than 1 s⁻¹ begins to affect the simulated traces, but rate constants below 1 s⁻¹ have no effect, so any value less than or equal to 1 s⁻¹ accounts for the data. The rate of bromide release from E^**P appears to be rapid and therefore was held fixed at an arbitrarily fast rate (k₅ = 200 s⁻¹) during global fitting. Accordingly, the data only define the K_d for bromide, not the individual rate constants for binding and release.

Fitting with the constraints described above provide individual rate constants for each step in the model shown in Scheme 3 with error ranges shown in Table 4. Error ranges were provided by FitSpace²⁸ confidence contour analysis (Figure S7) and represent the upper and lower limits of a 3% threshold on the summation of squared error (SSE).²⁸ Global simulation of the data to the model shown in Scheme 3 with the constraints described above accounts for all aspects of the data and yields well-bounded rate constants. The final model with our best estimates for each rate constant is shown in Scheme 4. Numbers in parentheses represent values of rate constants that were assigned nominal values and held fixed during fitting. Stacked values, 3 over 10 and 10 over 3, represent ambiguity in assigning these two rates to individual steps in the pathway as described below.

Discussion

Enzymes have evolved ingenious catalytic strategies to remove halogens bonded to alkane, aromatic, and alkene substrates without the use of metal ions or other cofactors.^{29, 30} The haloalkane dehalogenase designated DhlA^30–33, 4-chlorobenzoyl-CoA dehalogenase^34–38, CaaD^{2–5, 10, 11, 15}, and cis-CaaD^{6, 12–14} illustrate the reactions and their similarities and differences. The first two of these enzymes catalyze reactions that proceed by a well-characterized covalent ester intermediate^{29, 30}, whereas cis-CaaD and CaaD do not.^{5, 6, 9} Extensive mechanistic, structural, and kinetic studies have defined key features of all four enzyme-catalyzed reactions including the catalytic and binding residues, rate limiting steps, conformational changes, and the presence or absence of a halide-binding pocket.

Although cis-CaaD and CaaD have the same core catalytic residues (the amino-terminal proline, two arginines, and a glutamate), the cis-CaaD reaction appears to be more complex than that of CaaD because two additional active site groups (i.e., His-28 and Tyr-103) are required for activity.¹² There is no obvious explanation for the additional complexity, and the hydration of the cis-isomer is not expected to be energetically more difficult. As part of an effort to understand the basis for this difference and to define the fundamental reaction scheme, a kinetic analysis of both enzymes and their mutants is being pursued. The kinetic mechanism for cis-CaaD has been determined (Scheme 5).¹³ A comprehensive analysis of the CaaD reaction was precluded by the absence of a strong fluorophore in the active site to provide a signal to define kinetically significant enzyme states.¹⁰ This prompted the construction of the αY60W mutant of CaaD and the validation of this mutant as an accurate reporter of active site events. Indeed, the αY60W- and wild-type-CaaD behave comparably and show statistically equivalent results in all experiments including the steady state kinetic experiments (Table 1 and Figure 3A), the stopped-flow enzyme fluorescence (Figure 3B) and rapid quench (Table 2 and Figure 5A) experiments, and steady state bromide inhibition studies (not shown).

Scheme 5.

Minimum kinetic pathway for the cis-CaaD-catalyzed reaction with individual rate constants.

Based on the highly similar αY60W- and wild-type-CaaD-catalyzed reactions, a more in-depth analysis of the αY60W CaaD data was pursued. Global fitting of the αY60W CaaD data provided values for individual rate constants without many of the additional assumptions and deconvolution of complex rate functions required for conventional analysis.²⁴ Prior to global fitting, a minimal kinetic model was proposed based upon conventional analysis of the data.²⁴ To minimize the total number of variables during global fitting, experimental results not included in the fit and supplementary knowledge about the system were utilized to hold some parameters fixed during the fitting process. The kinetic model (Scheme 3) used to account for the data was developed as follows. Observation of a pre-steady state burst in the rapid quench experiments imply that a step after chemistry is at least partly rate limiting. Fitting the burst data to the burst equation (i.e., Eq. 4)²³ defines the rate of the burst (~85 s⁻¹) and the rate of steady state turnover, governed by k_cat (~3 s⁻¹). Analysis of the pre-steady state stopped-flow data provided estimates for the rate constants governing a possible conformational change occurring at a rate slower than chemistry.^13,23 The stopped-flow fluorescence data could be fit to a double exponential decay with a fast (lag) phase occurring with a rate comparable to the rate of the pre-steady state burst of product formation. Although conventional analysis failed to provide reliable estimates for the rate constant governing the lag (fast) phase, simulation-based fitting confirmed the existence of a lag phase consistent with the rate of chemistry preceding the fluorescence change. It is useful to note that the lag will be most noticeable when the rates governing the fast and slow phases are comparable, which should occur at a concentration of approximately 500 μM substrate according to the fitted parameters. This is evident in the data, as marked by an asterisk (*) in Figures 6A and C. At higher concentrations of substrate, the lag phase becomes less distinct. This makes resolution of the lag by conventional fitting difficult. However, in the concentration range where the lag is most prominent (~100–1000 μM), the rates approach the burst rate (~85 s⁻¹) with much reduced error ranges (Figure 6B). The overall trend agrees with the global fitting results, which reinforces confidence in the results.

The slower phase of the fluorescence transients occurred at a maximum rate of ~10 s⁻¹, which defines the sum of all rate constants contributing to the final approach to the steady state,²³ including the rate constant that limits steady state turnover. Because chemistry appears to be irreversible, the actual reverse of the fluorescence change occurs via the release of products to return the enzyme to the free E state. Accordingly, fitting the concentration dependence of the rate of the fluorescence change to Eq. 3, gives k_for = k₃ = 8 s⁻¹ and k_rev = k_cat = k₄ = 3 s⁻¹ (Table S2).

Estimation of the equilibrium constant (K_d,S) for substrate binding was based on a rapid equilibrium assumption (k_-1 ≫ k₂) in globally fitting the entire data set. In particular, the K_d,S (1/K₁) was defined by the concentration dependence of the fluorescence transients and the need to account for the k_cat and K_m values derived from the full time course kinetic traces. Although there was no observable lag in the burst data, suggesting a rapid equilibrium binding of the substrate prior to chemistry, this conclusion is not exact, but reasonable given the relatively weak apparent K_d (~ 400 μM). By assigning a second order rate constant of k₁ = 1 μM⁻¹ s⁻¹, where k_-1 ≫ k₂, fitting the data to derive k_-1 affords a simplistic calculation of the K_d,S = k_-1/1 μM⁻¹ s⁻¹. This value k₁ was significantly larger than the lower limit defined by k_cat/K_m (0.01 μM⁻¹ s⁻¹).

Because the rate of the fluorescence change was significantly slower than chemistry, the formation of species E^*PQ is proposed to occur after chemistry and the binding and chemistry steps occur without a change in fluorescence. That is, the lag phase in the fluorescence transients can be accurately accounted for in the simulated traces by assigning the same fluorescence to all enzyme species through chemistry (i.e., E, ES, and EPQ). The maximum burst of product rate (~ 85 s⁻¹) provides an initial estimate of the chemistry rate (k₂), but is actually the sum of the rate constants governing formation and decay of the EPQ complex.

Two product release steps are required to regenerate free enzyme, which we suggest occurs by a biased, random release pathway with kinetic preference for the upper branch of the pathway. This assignment was based on the following data and analysis. As described above, bromide (P) was observed to be purely a competitive inhibitor (K_i ~ 12 mM). This might suggest an ordered product release pathway with loss of Q (4) preceding the release of P (Br⁻).³⁹ However, malonate semialdehyde (Q, 4) was shown to bind to free enzyme 20-fold more tightly than bromide (Table S2, K_{d, 4} ~ 600 μM), perhaps suggesting a random pathway as shown in Scheme 3. Unfortunately, the product, Q (4) was too unstable to carry out accurate product inhibition studies to further probe product release. Although a random pathway predicts a mixed inhibition pattern for both products, the apparent competitive inhibition pattern for P (Br⁻) could be explained if the binding of P to E^**•Q is too weak to have an observable effect. Thermodynamic box arguments based on the available product binding measurements (see Text S1) imply that P binds to E^**•Q 20-fold more weakly than Q (4) binds to E^**•P, consistent with a competitive inhibition pattern for P, according to the upper (preferred) pathway. This also agrees with the docking results of 9 to CaaD, which indicate that substrate appears to bind with the halide oriented toward the back of active site pocket (Figure 2A), implying that the physical release of bromide would occur second. In addition, an ordered product release model, with halide release as the final step, was proposed earlier for the related enzyme cis-CaaD.¹³ Therefore, we prefer a biased-random product release pathway favoring the release of Q (4) first (slow) followed by bromide (fast), but accounting for the rebinding of Q to free enzyme as one leg of a random pathway. As there is no direct evidence for the release of P (Br⁻) from E^*PQ or the binding of P to E^**•Q, this reaction step is shown in gray in Scheme 3 and 4.

In Scheme 3, the formation of a new fluorescent state of the enzyme (E^*PQ) occurs after chemistry (k₂). Comparable rates of formation for E^*PQ were observed for wild-type (Figure 3B), αY60W, and αM7W-CaaD enzymes (Table S3), suggesting that the slow formation for E^*PQ is not an artifact caused by the αY60W mutation. The rebinding of Q (4) to form E^**•Q was included to account for direct binding measurements (vida supra). The E^**•P and E^**•Q states accounted for an increase in the fluorescence endpoint (~13%) relative to that of the free enzyme when either product (i.e., 4 or bromide) was bound to the enzyme (Figure S3A and S5, Table S2).

Global fitting to the model shown in Scheme 3, constrained by the above information, yielded estimates for the individual rates constants for each step of the kinetic mechanism (Table 4). A more accurate error analysis for the individual rate constants was obtained using FitSpace²⁸, which indicates that all of the rates are constrained as shown in Figure S7. Moreover, the kinetic parameters derived by global simulation provide reasonable estimates in agreement with the Michaelis-Menten parameters obtained from steady state initial velocity measurements. Using the numbers in Table 4 and Scheme 3, we calculate k_cat = 2.2 s⁻¹ and K_m = 95 μM. The experimentally determined values for k_cat and K_m are 3.0 s⁻¹ and 70 μM, respectively. Additionally, the calculated K_d values for bromide and 4 binding to free enzyme are in good agreement with those predicted from the individual fits by simulation and conventional analysis.

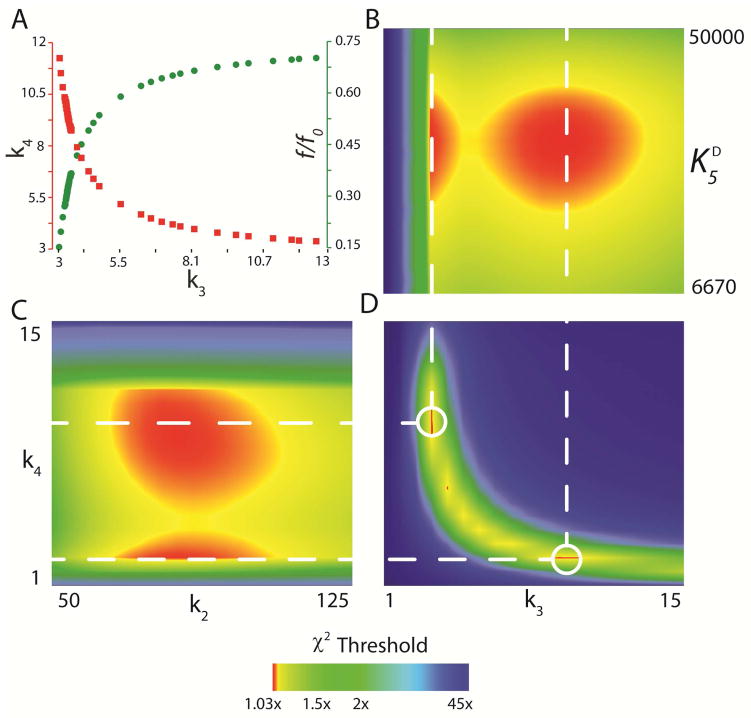
Inspection of the FitSpace confidence contours (Figure 8) highlights various limitations of the data set and provides a more realistic estimation of errors on the rate constants (~20% Table 4) compared to conventional data analysis.^{23, 28} For example, conventional analysis of the stopped flow fluorescence data based upon fitting to exponential functions yields two rate constants for k₃ and k₄ (Scheme 3) ~8 s⁻¹ and ~3 s⁻¹, respectively. Global fitting using these values as initial estimates for the rate constants k₃ and k₄, respectively, results in a fit shown in Figure 7 (with normal error estimates on all rate constants of <1%). However, FitSpace analysis revealed that an equivalent fit to the data can be obtained when the values of k₃ and k₄ are reversed (i.e. k₃ = 3 s⁻¹ and k₄ = 10 s⁻¹), with a corresponding adjustment of the fluorescence scaling factor (f/f₀) to compensate for changes in the predicted transient concentration of E^*PQ. This is illustrated in Figure 8A which depicts the parameter variation among k₃, k₄, and f/f₀ (the fluorescence scaling factor) required to maintain the χ² value (within 3% of the minimum). Figure 8A shows that as the value for k₃ increases from 3 s⁻¹ to 12 s⁻¹, the value of k₄ decreases from 12 s⁻¹ to 3 s⁻¹, following a hyperbolic relationship. Conversely, as the value for k₃ increases from 3 s⁻¹ to 12 s⁻¹, the value for f/f₀ increases from 0.15 to 0.70 following the an inverse hyperbolic relationship in which k₄ decreases. This suggests that the data can be fit equally well (maintaining an acceptably small χ²) when k₃ and k₄ are defined as any appropriate combination of rates (i.e. following the hyperbolic relationship) from 3 s⁻¹ to ~12 s⁻¹ by proper adjustment of the fluorescence factor value (f/f₀). However, when comparing k₃ or k₄ to other rate constants, (e.g., k₃ vs. K_d,Br-, Figure 8B, or k₂ vs. k₄, Figure 8C) two sets of rates centered around ~3 s⁻¹ and ~10 s⁻¹ emerge as acceptable values. Therefore, all FitSpace confidence contours describing k₃ or k₄ in relation to other rate constants have two regions of minimum χ² (red spots) centered around 3 s⁻¹ and 10 s⁻¹. In the direct comparison of k₃ vs. k₄, (Figure 8D) the hyperbolic relationship in the parameter variation is apparent, with two primary regions of a minimum χ² occurring when k₃ and k₄ are defined as 10 s⁻¹ and 3 s⁻¹, or 3 s⁻¹ and 10 s⁻¹, respectively (dashed lines in Figure 8D). Also, Figure 8D shows that when k₃ and k₄ divert from these rate constants (i.e. the hyperbolic relationship), the χ² increases rapidly, resulting in large areas of blue (45× the minimum χ²).

Figure 8. Confidence Contour Analysis.

Selected FitSpace confidence contours for the global fit to the kinetic data shown in Figure 7 (αY60W-CaaD and 9). (A) Parameter variation for k₄ (■, left axis) and f/f₀ (●, right axis) plotted as a function of the value of k₃ required to maintain an SSE value within 3% of the minimum χ². FitSpace confidence contours for (B) k₃ vs. K_d,Br (C) k₂ vs. k₄, and (D) k₃ vs. k₄. The dashed lines illustrate two sets of values for k₃ and k₄ that yield equivalent fits to the data (within 3% of the minimum χ² value). Graphs were generated using gnuplot 4.6 (www.gnuplot.info).

The uncertainty in the order of these two rate constants is primarily due to the fact that the data lack explicit information to quantify the fluorescence factor for the species, E^*PQ. For example, a fast/slow sequence predicts a higher concentration of E^*PQ requiring a lower scaling factor to achieve the same fluorescence amplitude, compared to the slow/fast sequence of rate constants. This observation emphasizes the inability of kinetic analysis to provide the order of the two sequential rates in the absence of data to define the absolute amplitude of the intermediate species (E^*PQ in this case). Conventional methods of determining standard error drastically underestimate the error ranges for these rate constants because error analysis is based upon only exploring the area around a local minimum and the covariance analysis fails to reveal nonlinear relationships between fitted parameters.²⁸ The global fit to all the data with the confidence contour analysis reveals two acceptable fits to the data.

Although the data cannot define the order for k₃ and k₄, they do provide strict lower and upper limits for both rate constants. The lower limit for both k₃ and k₄ is 2.5 s⁻¹ defined by k_cat and depicted in the FitSpace confidence contours by a rapid increase in χ² at rate constants below 2.5 s⁻¹. The upper limits for these rate constants are controlled by the range of allowable adjustments in the fluorescence factor values (f/f₀) (Figure 8A). The upper limit for k₃ is ~13 s⁻¹ and is well constrained (Figures 8A and B). As k₃ increases, f/f₀ increases and begins to approach unity yielding a smooth, well defined upper limit (Figure 8B). Conversely, like the lower limits, the upper limit on k₄ is strictly defined. As seen in Figure 8A, as k₄ increases, f/f₀ decreases exponentially, reaching zero when k₄ is ~12 s⁻¹. At all values above 12 s⁻¹, the χ² drastically increases, resulting in a strict upper limit for k₄ in the FitSpace confidence contours (Figure 8C). However, even at these limits, the values of k₃ and k₄ are within 5-fold of one another. This suggests that both the formation of E^*PQ and release of 4 are partially rate limiting.

A previous report indicated that product release is not rate limiting.⁴⁰ Horvat et al. based this conclusion on the observation that increasing solvent viscosity with trehalose did not decrease the values of k_cat or k_cat/K_m, based upon the simplistic analysis suggesting that viscosity effects probe the extent to which diffusion limits the observed rate.⁴⁰ At first glance, the observation of a burst of product formation appears at odds with this conclusion. However, the observation of a burst only implies that a step after chemistry, not necessarily product release per se (e.g. a conformational change), is rate limiting.²³ In the case of CaaD, product release appears to be only partially rate limiting, which may have led to the observed results of the viscosity experiments. Moreover, the release of Q (4) from the E^*PQ state is accompanied by a change in enzyme state (to E^**P) as indicated by the different fluorescence level. Although the structural basis for the fluorescence change is not known with certainty, it is reasonable to propose that a change in enzyme structure precedes and limits the net rate of release of Q, defining k^cat. Therefore, the viscosity effect would have failed to reveal the rate-limiting product release, governed by a change in enzyme structure. It is most reasonable to suppose that many slow product release steps are governed by rate-limiting conformational change steps that lead to rapid product release and weaken product rebinding. Such conformational change steps occurring before and after chemistry may provide a critical component contributing to enzyme specificity.⁴¹ Our experimental results also provide a more accurate estimate of the rate enhancement for the CaaD reaction (k₂/k_non = 3.6 × 10¹³), a value that is an order of magnitude greater than previously reported.⁴⁰ Our analysis suggest caution in interpreting viscosity effects.

Our results raise the question about the nature of the partially rate-limiting conformational change steps following chemistry. One possible explanation is found in the docking results, which provide molecular details for the observed conformational change. Inspection of the docking poses suggests that αGlu-52 would have to rotate out of the active site after participating in the chemistry in order to facilitate product release. In the crystal structure of covalently modified CaaD (1S0Y), αGlu-52 is observed in the active site.¹⁰ A possible conformational change, with measurable changes in fluorescence (E^*PQ), might rotate αGlu-52 out of the active site so the products, 4 followed by bromide, can be released from the enzyme. This proposed conformational change could partially limit the rate of turnover. It is also reasonable to speculate that with further evolution to improve the efficiency of this enzyme that the rate of this conformational change may be accelerated.

The results largely parallel those found for cis-CaaD (Scheme 5). The kinetic data for the cis-CaaD reaction using cis-3-bromoacrylate (9) are best accommodated by a fivestep kinetic model¹³ in which substrate binding is followed by a rapid isomerization to a new fluorescent state (Scheme 5). Chemistry occurs next yielding an enzyme complex containing both products with no further change in fluorescence. (If 7 or 8 in Scheme 2 exist as discrete intermediates, their production and decomposition are not rate limiting.) Subsequent product release from the complex is ordered and rate-limiting: malonate semialdehyde is released first by the enzyme (and rate-limiting), followed by the rapid release of bromide. The model suggested only two states for the enzyme, which could be associated with an open state and a closed state observed in the absence or presence of ligands, respectively. A comparison of the unliganded and liganded cis-CaaD structures provides a structural basis for this hypothesis.^{12, 13}

The similarities between CaaD and cis-CaaD include the ordered product release of malonate semialdehyde followed by bromide. Bromide is a competitive inhibitor for both enzymes and the dissociation of malonate semialdehyde is at least partially rate determining for each enzyme. The only differences are the nature of the conformational change (movement of an active site group in CaaD after chemistry vs open and closed states in cis-CaaD) and in the product inhibition. Malonate semialdehyde binds more tightly to CaaD than bromide (~10-fold), whereas bromide binds more tightly to cis-CaaD than malonate semialdehyde (not quantifiable because of the instability of malonate semialdehyde). These differences do not explain the greater simplicity of the CaaD-catalyzed reaction (compared with that of the cis-CaaD reaction). This remains an active area of investigation, which can now be pursued based upon the foundation provided here.

Abbreviations

CaaD and cis-CaaD

trans- and cis-3-chloroacrylic acid dehalogenase, respectively

ESI-MS

electrospray ionization mass spectrometry

IC

ion chromatography

Kn

kanamycin, LB, Luria-Bertani

MSAD

malonate semialdehyde decarboxylase

4-OT

4-oxalocrotonate tautomerase

PCR

polymerase chain reaction

SDS-PAGE

sodium dodecyl sulfate-polyacrylamide gel electrophoresis

SSE

sum square error