Mathematical Modeling of Drug Delivery from Autocatalytically Degradable PLGA Microspheres—A Review

Abstract

PLGA microspheres are widely studied for controlled release drug delivery applications, and many models have been proposed to describe PLGA degradation and erosion and drug release from the bulk polymer. Autocatalysis is known to have a complex role in the dynamics of PLGA erosion and drug transport and can lead to size-dependent heterogeneities in otherwise uniformly bulk-eroding polymer microspheres. The aim of this review is to highlight mechanistic, mathematical models for drug release from PLGA microspheres that specifically address interactions between phenomena generally attributed to autocatalytic hydrolysis and mass transfer limitation effects. Predictions of drug release profiles with mechanistic models are useful for understanding mechanisms and designing drug release particles.

1. Introduction

Poly(lactic-co-glycolic acid) (PLGA) microspheres are controlled-release drug delivery alternatives to conventional drug therapy regimens. By releasing drug molecules in a controlled manner over extended periods of time from a single administration, controlled-release systems have the potential to maintain drug concentrations within target ranges, diminish side effects caused by concentration extremes and repeated administrations, and improve patient compliance as compared to conventional regimens. Despite these advantages, the implementation of controlled-release drug delivery devices composed of PLGA microspheres for human patients has been gradual as the characterization and design of the microspheres depends heavily on trial- and-error experiments, and the interplay between complex phenomena that contribute to the drug release is still being deciphered.

PLGA microspheres have been extensively studied for controlled-release drug delivery [1-4] mainly because of the biodegradable and bioabsorbable qualities that allow for the passive degradation of the polymer in aqueous environments such as living tissues and for the harmless incorporation of degradation products into the surrounding media [5-7].

Several processes contribute to the overall kinetics of drug release from PLGA microspheres including chemical degradation of the polymer by autocatalytic ester hydrolysis, polymer erosion, evolution of pore structure as a result of mass erosion, and diffusive transport of the drug through the polymer matrix and the aqueous pore structure [8]. In the present work, the term degradation refers to the process through which the polymer chain bonds are hydrolyzed to form oligomers and monomers. The term erosion refers to the loss of mass due to diffusion of water-soluble, small oligomers and monomers out of the polymer matrix. The definitions of degradation and erosion are the same as those given by Göpferich [5] and have been widely adopted in the literature.

Three main phenomena—PLGA degradation, PLGA erosion, and drug transport—are discussed in Section 2, and mathematical models that mechanistically address these phenomena and the interactions between them are described in Section 3. The coupling between the three phenomena is important for understanding how a phenomenon may dominate or work in conjunction with the others under different conditions. The autocatalytic degradation mechanism may lead to acceleration of degradation and erosion in the center of microspheres and size-dependent drug transport enhancements. The complex effects of autocatalysis are difficult to predict without understanding of the relative strengths of the phenomena and their dynamics.

Mathematical models can reduce the number of experiments needed to deepen the understanding of the physical and chemical mechanisms of drug release, particularly when the effects of different phenomena are coupled, and to probe different conditions and designs. Empirical or correlative models, which are commonly applied in the drug delivery field, have very limited predictive capability outside of the specific experimental conditions used to fit parameters in the models [9]. In contrast, mechanistic models aim to account for the physical and chemical phenomena that contribute to the overall drug release kinetics [10] and are applicable over a wide range of conditions to be used in the model-based design of microspheres to produce desired release profiles (e.g., constant rate of release for uniform therapeutic dosage). Here, only semi-empirical and mechanistic models are addressed.

2. Background concepts

Polymeric drug delivery can be categorized based on the mechanisms of drug release [11-13]: diffusion-controlled systems (diffusion from non-degrading polymers), swelling-controlled systems (enhanced diffusion from polymers that swell in aqueous media), and erosion-controlled systems (release as a result of degradation and erosion of polymers). For biodegradable polyesters such as PLGA, drug release occurs through a combination of degradation and erosion of polymer and transport of drug and is classified as being erosion-controlled. Drug transport through and release from the microspheres can occur by diffusion through the polymer matrix and/or water-filled pores depending on the water-solubility and molecular weight of the drug molecule. The mechanisms of each of these processes for erosion-controlled drug release from PLGA microspheres and how their effects are combined are overviewed in this section.

2.1. PLGA degradation

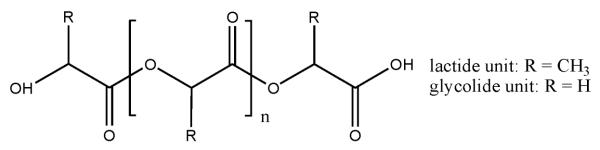
PLGA is a poly(α-hydroxy-ester) (see Fig. 1) that is depolymerized in the presence of water. The hydrolysis reaction cleaves the ester bonds of polymer chains. The reaction can be catalyzed by acids or bases, but experimental data on the acidic local pH within PLGA particles [14-18] suggest that only the reaction mechanism catalyzed by acid is relevant. The acid-catalyzed ester hydrolysis proceeds by the bimolecular, acyl-oxygen cleavage A_AC2 mechanism [19,20] summarized by

$${\text{P}}_n+{\text{H}}_2\text{O}+{\text{H}}^{+}\to {\text{P}}_m+{\text{P}}_{n-m}+{\text{H}}^{+},n=2,3,\dots \text{and}m=1,2,\dots ,n-1,$$ (1.1)

where P_n, P_m, and P_n–m denote polymer chains with degrees of polymerization n,m, and n – m, respectively, and H⁺ is the acid catalyst.

Figure 1.

Structure of poly(α-hydroxy-esters). PLGA has a fraction of functional groups with lactide units and the remaining fraction with glycolide units. n is the number of interior lactide and/or glycolide monomeric units.

The source of the acid catalyst can be external from strong acid in the medium (non-autocatalytic reaction) or internal from the carboxylic acid end groups of the polymer chains (autocatalytic reaction)[21]. In autocatalysis, the reaction product catalyzes further hydrolysis in the manner

$$A+B\to 2B,$$ (1.2)

where A is water and B is acidic polymer chains in the context of PLGA degradation.

2.2. PLGA erosion

Polymer erosion is classified as surface-eroding or bulk-eroding [4,5,22,23]. For surface-eroding polymers such as polyanhydrides, the rate of polymer degradation at the surface is faster than the rate of penetration of water from bodily fluids in vivo or from the buffer medium in vitro into the polymer bulk. Surface-eroding polymers react from the surface inward. Bulk-eroding polymers exhibit a faster rate of water penetration than rate of polymer degradation. The degradation and erosion in bulk-eroding polymers occurs throughout the polymer bulk. PLGA is a bulk-eroding polymer at the length scales used in drug delivery microspheres (10s to 100s of microns) as the hydration time scale is on the order of a few minutes compared to weeks or months for degradation [24-26].

Erosion depends on the degradation, dissolution, and diffusion processes [27]. For PLGA, the dissolution of water-soluble oligomers up to nonamers [28-30] and of drug molecules is often assumed to occur with faster time scales than diffusion and polymer degradation in many mathematical models and is neglected. A few models propose that dissolution is rate-limiting for PLGA oligomers [31].

2.3. Drug transport

An “initial burst” of drug release often occurs wherein a significant percentage of the drug is released during the early stage of the release process. This effect has been reported for many formulations of PLGA microspheres. The initial burst can be diminished or eliminated by adjusting the fabrication technique [32-34].

The subsequent controlled release of drug molecules from PLGA microspheres depends on the transport properties of the drug and the dynamic conditions of the degrading polymer. The drug compound in PLGA microspheres may be released by some combination of diffusion through the polymer matrix, diffusion through aqueous pores, and dissolution coincident with polymer dissolution [8]. Diffusion through the dense polymer matrix is possible [35] but is limited to small, hydrophobic molecules [8] as the PLGA matrix is hydrophobic. For highly water-soluble and macromolecular drugs such as protein and peptides, diffusion through the aqueous pores is an important mode of transport [36].

Dissolution of the polymer matrix to release the drug without mass transport is typical of surface-eroding polymers rather than bulk-eroding polymers. Drug dissolution dynamics may need to be considered for drug compounds with low water solubility [37,38].

Drug diffusion through the PLGA matrix and through the aqueous pores can be considered as the parallel modes of release from the polymer microsphere to treat small and large drug molecules and to account for transport prior to and after significant development of the pore network. Water-soluble drugs diffuse more easily through aqueous pores than in the polymer matrix, so the effective diffusivity of the drug increases as the pore network develops. After the pore network is sufficiently developed such that the pores are larger than the size of the drug molecules, the drug transport increases rapidly.

2.4. Coupling between phenomena for drug release

PLGA can sometimes exhibit heterogeneous erosion behavior where the interior degrades faster than the surface of the polymer. This phenomenon is size-dependent: larger microspheres and thicker slabs have been observed to experience faster erosion in their centers than smaller microspheres and thinner films [17,39-43]. The effective diffusivity has been observed to increase with increasing microsphere diameter [35,43]. The cause of the heterogeneous mass loss in bulk-eroding polymers is generally attributed to the combined effects of autocatalytic degradation and mass transport limitations [17,43-46].

The coupled mechanism for PLGA degradation and erosion consists of three stages [26]. In the first stage, the polymer solid is hydrated, and degradation proceeds predominantly by non-catalytic hydrolysis homogeneously throughout the polymer bulk while the concentration of carboxylic acid end groups on the polymer chains is low. In the second stage, the autocatalytic hydrolysis reaction becomes important as the catalyst concentration is significant. The third stage involves dissolution of small oligomers and monomers into the aqueous medium. Significant mass loss of the polymer occurs as more oligomers are solubilized into the pores and are transported through the growing pore network.

Drug release profiles can exhibit different shapes, such as zero-order, monophasic, biphasic, and triphasic, depending on the dynamics of the initial burst, diffusion through the polymer matrix and pores, and the stages of degradation and erosion [8]. Diffusion of acidic degradation products may occur quickly in small or porous microspheres suppressing the heterogeneities in internal pH and erosion due to autocatalysis [6,47]. Drug release rates under these conditions are diffusion-controlled with relatively smaller microspheres releasing drugs faster than larger microspheres as the diffusion pathways are shorter and the concentration gradients are larger in smaller microspheres. Contrary to this intuitive diffusion-controlled behavior, the autocatalytic polymer degradation and erosion can influence the drug release rates in such a way to allow larger microspheres to release drugs at a faster rate than smaller microspheres [32].

In domains close to the external surfaces of microspheres (indicated with arrows in Fig. 2), the diffusion lengths are sufficiently small for the acidic oligomer hydrolysis byproducts to diffuse out of the microspheres without reacting with the polymer; in smaller microspheres, the entire volume can have such short diffusion lengths. Acidic polymer fragments that remain in the microspheres have hindered mobility in regions farther from the external surfaces where transport is limited by greater diffusion lengths. This leads to an accumulation of acidic degradation byproducts in the interior of larger microspheres, which results in a decrease in the microenvironment pH. The acidic end groups further catalyze the hydrolysis reaction leading to accelerated degradation particularly in the interior of large microspheres due to the limited acid transport out of the center (illustrated by lighter interior in larger microsphere in Fig. 2). Over time, the autocatalytic effect becomes more pronounced, and microspheres can form heterogeneous, hollow interiors [32,46]. Small microspheres without long diffusion lengths are less susceptible to acidic buildup and heterogeneous degradation.

Figure 2.

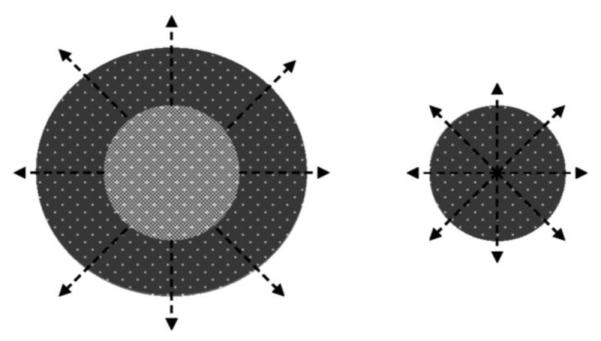
Size-dependent autocatalysis in PLGA microspheres. Arrows indicate regions where diffusion lengths are not prohibitive for reaction products to diffuse out of the particle before leading to enhanced autocatalysis. Lighter shading indicates more accelerated autocatalysis. Autocatalysis becomes more significant with time in the interior of the large particle than in the small particle.

Polymer microsphere size plays a strong role in the coupling between degradation, erosion, and drug transport and the effects of autocatalysis. Descriptions of factors in addition to microsphere size that affect degradation and release kinetics can be found in the literature [8,23,48,49].

3. Mathematical models

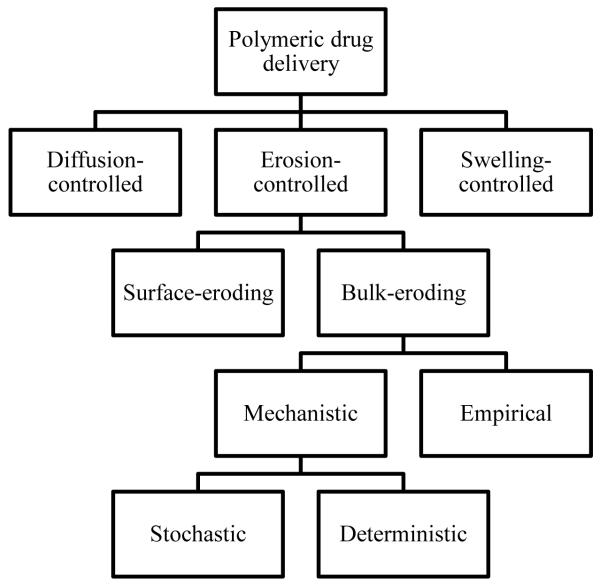
Several mathematical models have been developed for the in vitro drug release kinetics from polymeric drug delivery devices (see Tables 1 and 2). This review aims to highlight mechanistic, mathematical models that address the role of autocatalysis in the mass transport and chemical reaction phenomena of drug delivery from PLGA microspheres. The place of these types of models in the broader context of mathematical models for polymeric drug delivery systems is illustrated in Fig. 3. In vivo drug delivery is outside the scope of the present article, and the reader is referred to Grassi et al. [50] for a review of mathematical models for simultaneous drug release and in vivo drug absorption. For comprehensive coverage of both empirical and mechanistic mathematical models including stochastic methods for PLGA microspheres as well as thorough discussions of mathematical models for diffusion-controlled and swelling-controlled drug delivery systems, the reader is referred to the reviews listed in Table 1 and citations therein.

Table 1.

Reviews of mathematical models for polymeric drug delivery.

Scope	Review articles
Polymeric drug delivery systems	Kanjickal and Lopina [13] Arifin et al. [10] Siepmann and Siepmann [9] Aguzzi et al. [51]
Diffusion-controlled systems	Siepmann and Siepmann [52]
Erosion-controlled systems	Siepmann and Göpferich [25] Sackett and Narasimhan [27]
Bulk-eroding systems	Lao et al. [23]

Table 2.

Mathematical models for polymeric drug delivery systems with autocatalytic effects.

Article	Phenomena modeled	Delivery system	Role of autocatalysis
PLGA degradation
Siparsky et al. [54]	Pseudo-first order, second- order, and 1.5th-order degradation	PLA in solution	Autocatalytic hydrolysis kinetics
Nishida et al. [55]	Second-order degradation	PLA films in atmosphere of saturated water vapor	Autocatalytic hydrolysis kinetics
Lyu et al. [56]	Water-dependent third-order and 2.5th-order degradation	PLA discs	Autocatalytic hydrolysis kinetics
Antheunis et al. [53,57]	Second-order degradation	PLA and PLGA rods	Autocatalytic hydrolysis kinetics
PLGA erosion
Göpferich [58]	Stochastic degradation and erosion	PLGA discs	Not explicitly autocatalytic, pore percolation may cause lag and burst of mass loss rather than autocatalysis
Chen et al. [59]	Stochastic degradation and erosion	PLA films and scaffolds, PLGA microspheres	Empirical multiplicative factor representing the strength of autocatalytic effects
Batycky et al. [28]	Pseudo-first-order degradation, erosion with pore formation, diffusive drug release with constant diffusivity after induction time	PLGA microspheres	Not explicitly autocatalytic, pore formation theory based on experimental polymer erosion
Ding et al. [60]	Erosion by dissolution to determine microclimate pH	PLGA films	Not explicitly autocatalytic; average microclimate pH as a function of time
Arosio et al. [61]	Eroding core grows as interface moves due to pseudo-first-order degradation and transport	PLA cylinders	Geometry consist with autocatalytic erosion, degradation not explicitly autocatalytic
Wang et al. [62]	Non-catalytic and autocatalytic degradation, monomer diffusivity linearly dependent on porosity	PLA films, cylinders, and three- dimensional blocks	Regimes where autocatalytic degradation dominates and where autocatalytic degradation is coupled to other effects is mapped to material parameters
Drug release
Charlier et al. [63], Faisant et al. [64], Raman et al. [35], Berchane et al. [65]	Empirical fits between drug diffusivity and degradation	PLGA films and microspheres	Not explicitly autocatalytic, variable drug diffusivity fit to data
He et al. [66]	Empirical fits between drug diffusivity and degradation	PLA and poly(lactide-co- ε-caprolactone) microspheres and discs	Empirical factor for contribution of matrix erosion on drug release
Siepmann et al. [43]	Empirical fit of drug diffusivity to analytical drug diffusion as a function of microsphere radii	PLGA microspheres	Size-dependent drug diffusivity captured autocatalytic behavior while constant diffusivity did not
Mollica et al. [67]	Drug diffusion and dissolution in microsphere with empirical degradation front	PLGA microspheres	Geometry consistent with autocatalytic erosion, degradation not explicitly autocatalytic
Coupled phenomena
Thombre and Himmelstein [68], Joshi and Himmelstein [69]	Second-order degradation, erosion by diffusion, diffusive drug release	Poly(orthoester) slabs and discs	Autocatalytic hydrolysis kinetics, drug diffusivity is a function of extent of catalytic polymer degradation
Siepmann et al. [70]	Stochastic degradation and erosion, drug diffusion coupled to stochastic porosity	PLGA microspheres	Probabilistic effects for random hydrolysis and erosion with parameters sensitive to autocatalysis
Lemaire et al. [71]	Erosion with linear correlation, diffusive drug release with constant drug diffusivities in two compartments with interface moving as erosion progresses	PLA microspheres	Not explicitly autocatalytic, erosion rate modulates drug release between diffusion-controlled and erosion-controlled
Zhang et al. [72]	Drug dissolution and diffusion from eroding polymer, erosion defined by mathematical functions rather than polymer degradation	Bulk- and surface-eroding microspheres	Not explicitly autocatalytic, erosion patterns empirically capture autocatalytic effects
Prabhu and Hossainy [73]	Non-catalytic and autocatalytic degradation in parallel, erosion by diffusion, diffusive drug release	PLA films for drug eluting stents	Autocatalytic hydrolysis kinetics, drug diffusivity is a function of extent of catalytic polymer degradation
Rothstein et al. [74,75]	Drug dissolution and diffusion dependent on pore growth, empirical fits of porosity to pseudo-first-order degradation and diffusivity to microsphere size	Bulk- and surface-eroding microspheres	Not explicitly autocatalytic, pore formation and drug diffusivity empirically dependent on autocatalytic effects
Zhao et al. [76]	Erosion with non-catalytic degradation kinetics and pore formation, transient drug diffusivities using hindered diffusion theory	PLGA microspheres	Not explicitly autocatalytic, pore formation and drug diffusivity based on degradation kinetics
Ford et al. [77]	Second-order autocatalytic degradation, erosion by diffusion, linear coupling of drug diffusivity to porosity, diffusive drug release	PLGA microspheres	Autocatalytic degradation, mass transport of polymer and drug coupled to void fraction in polymer due to erosion

Figure 3.

Hierarchy of mathematical model categories for bulk-eroding, polymeric drug delivery systems. Mechanistic models for PLGA microspheres with autocatalytic effects are the subject of this article.

In this review, mathematical models are categorized by the phenomena on which they focus: degradation, erosion, and drug transport (see Table 2). Models that treat the phenomena in a coupled manner are discussed separately. Some models for polymeric drug delivery systems other than PLGA microspheres are discussed if they explicitly address autocatalysis in a manner consistent with the mechanisms of PLGA. Particularly, hydrolysis kinetics for poly(lactic acid) (PLA) are often used as the basis of hydrolytic degradation theory for poly(α-hydroxy acids) including PLGA [53].

3.1. Mathematical models for PLGA degradation

Often polymer degradation is assumed to follow well-mixed, pseudo-first-order kinetics where degradation rate is a function of the concentration of only one of the three species involved—water, polymer (or ester bonds), and acid catalyst—with the other two concentrations either ignored or assumed constant and polymer molecular weight decreases exponentially with time [35,43,47,78,79]. The assumption of constant water concentration is reasonable in polyester solids as the concentration is determined by water solubility[26]. Pseudo-first-order kinetics are appropriate for general non-catalytic depolymerization reactions [80-82] and do not include the mathematics of autocatalytic behavior [57]. Pseudo-first-order kinetics should only be used in the early stages of degradation when the ester bond concentration and molecular weight have not decreased significantly [47]. Siparsky et al. [54] showed that pseudo-first-order kinetics approximated hydrolysis catalyzed by an external strong acid well but was insufficient for modeling autocatalysis where the catalyst was the internal weak carboxylic acid from the polymer end groups.

Autocatalytic hydrolysis kinetics have been studied for polyester hydrolysis reactions in solution [54,55] and for the hydrolytic degradation of solid PLGA microspheres without drug diffusion [26,62,83]. According to Lyu and Unterker [26], hydrolysis in solid polyesters is controlled by chemical reactions rather than constraints on molecular mobility as the diffusion of water is faster than the reaction time scale. This allows for analyses of solution hydrolysis kinetics to be applied to solid polyester hydrolysis for the kinetics of degradation. The dissolution and diffusion effects should also be considered for solids.

Second-order, autocatalytic hydrolysis kinetics for PLA and PLGA have been modeled in several reports [53-55,57] where the catalyst and ester bond concentration are allowed to vary while the water concentration is assumed constant for the duration of degradation. Nishida et al. [55] solved the differential equation for the total polymer concentratration subject to catalysis by carboxylic acid end groups using moment analysis. The moments were coupled with assumptions on the molecular weight distribution in order to determine approximations for the average degree of polymerization, the polymer polydispersity, and the weight-average molecular weight as functions of time. Antheunis et al. [53] proposed a kinetic model explicitly calculating the full distribution of ester bonds and polymer chains subject to autocatalysis through coupled ordinary differential equations. The model was simplified [57] to treat the total ester bonds concentration and the acid catalyst concentration rather than the full distribution of polymer chains. The model accurately predicted sigmoidal curves for the decrease of number-average molecular weight for PLA and PLGA before polymer mass loss occurred. The limitation of second-order kinetics for autocatalysis is the inability to capture the effects of partial dissociation of the carboxylic acid end groups [54].

Siparsky et al. [54] derived an 1.5^th-order kinetic expression for PLA hydrolysis that included partial dissociation effects with square-root dependence on carboxylic acid by the theory of equilibrium dissociation of weak acids. This model fit the kinetic data very well except near the extrema of the data set. Lyu et al. [56] observed that the hydrolysis kinetics of amorphous PLA transitioned after long times at some critical molecular weight from third-order with variable water concentration to 2.5^th-order kinetics consistent with Siparsky et al. [54] with variable water concentration.

3.2. Mathematical models for PLGA erosion

Mechanistic models for erosion-controlled drug delivery systems often are sorted into two categories [10]: discrete stochastic models and continuum-scale deterministic models. The first category considers erosion as a random process using Monte Carlo simulations and cellular automata, while the second treats the overall polymer erosion process as a combination of transport and chemical reactions through use of deterministic equations. Models that consider stochastic or deterministic PLGA erosion in tandem with drug transport are described in Section 3.4.

3.2.1. Stochastic models for PLGA erosion

Stochastic models have been used to model the evolution of pore structure through hydrolytic degradation and dissolution of a polymer and subsequent drug transport from surface-eroding and bulk-eroding systems [9,25]. Göpferich [58] proposed a model for PLGA based on stochastic mass erosion as an alternative to autocatalytically accelerated degradation to explain sigmoidal profiles of polymer mass loss. Erosion with first-order hydrolysis kinetics resulted in early polymer molecular weight loss followed by subsequent onset and burst of polymer mass loss. The delay in mass loss was explained by the lag time needed for pores to form a continous network to the surface to enable mass loss. The model underestimated mass loss during late mass erosion. Göpferich attributed the discrepancy to neglecting polymer swelling and loss of contiguous small polymer pieces, but alternatively, it could have been due to autocatalytic effects that were not considered.

Chen et al. [59] combined stochastic hydrolysis [58] with diffusion-governed autocatalysis through the use of an empirical factor to relate the carboxylic acid concentration and the autocatalytic effect to simplify the exponential coupling of the diffusivity of polymer degradation products to the mass of degraded polymer chains. Realistic size-dependent degradation and erosion behavior was predicted with the model when the parameter for autocatalysis was fitted to experimental data with a value representing a significant autocatalytic effect.

3.2.2. Deterministic models for PLGA erosion

Batycky et al. [28] proposed a model that calculated the amount of initial drug burst via a desorption mechanism, accounted for pseudo-first-order degradation kinetics using a combined random and chain-end scission mechanism, and simulated pore creation mechanistically. The erosion portion of the model related pore growth to the rate of coalescence of small pores caused by breaking of polymer chains. The rate of coalescence was experimentally estimated based on polymer erosion to determine the induction time when the average pore size became larger than the Stokes-Einstein radius of the drug. Drug transport was not allowed to begin until after the induction period and was represented as simple diffusion with a constant effective diffusivity after the pores were formed. Diffusion was not coupled to erosion after it began.

Ding et al. [60] derived an equation for calculating the average microclimate pH in thin PLGA films using the charge balance on species and the mole balance on water-soluble acidic PLGA degradation products in the polymer matrix involving equilibrium partitioning of the acidic products from the polymer bulk into aqueous pores and dissociation of the acidic products giving the acidic microclimate in the pores. Parameters that were straightforward to measure were used in the calculation of microclimate pH. The knowledge of the microclimate pH is useful for characterizing autocatalytic degradation and erosion of PLGA even though the microclimate pH calculation did not explicitly involve autocatalysis as the water-soluble acid content was measured experimentally rather than predicted from autocatalytic degradation kinetics.

Arosio et al. [61] developed a model for cylindrical PLA that imposed the autocatalytic effects of interior erosion geometrically. The cylindrical geometry consisted of an inner core of degraded polymer surrounding by an outer layer of non-degraded polymer with the interface between the layers moving such that the inner core grew over time. Two kinetic models were used with the first considering only the production of monomers and the second treating the production of oligomers and monomers. The equilibrium between the forward depolymerization reaction and the reverse polymerization reaction was included in the degradation model, but the hydrolysis kinetics were not catalytic. The reactions and mass transport were assumed to occur only along the moving interface between the degraded and non-degraded polymer. The model failed to predict published data well, and the authors pointed to the need to model the diffusional processes throughout the device structure to improve the model accuracy.

Wang et al. [62] modeled monomer diffusivity as a linear function of the porosity, which was approximated by concentrations of the ester and monomer. The ester concentration depended on degradation, while the monomer concentration depended on degradation and diffusion. The hydrolytic degradation proceeded both with and without a catalyst. A biodegradation map for planar and cylindrical geometries was constructed to quantitatively show the zones where diffusion and reaction have strong or weak influences depending on the nondimensional parameters characterizing monomer diffusivity and the relative reaction rate between non-catalytic and autocatalytic degradation. The map presented zones where erosion was controlled by non-catalytic degradation when degradation products diffused rapidly or the degradation was fast, autocatalytic degradation when the degradation products diffused rapidly and the non-catalytic degradation was not fast, and by combinations of autocatalytic and non-catalytic degradation and monomer diffusion in intermediate conditions.

3.3. Mathematical models for drug transport

The discrepancy between widely used theoretical predictions made from classic diffusion models with constant drug diffusivity and actual drug release experimental data has been attributed to the models’ failure to adequately treat size-dependent effects of autocatalysis [43]. Models that propose non-constant drug diffusivity in some manner are reviewed here. Models that focus mechanistically on the effects of polymer erosion on the drug diffusivity are described in Section 3.4.

A common approach has been to correlate the effective diffusivity of drug to the exponentially decreasing molecular weight based on an empirical fit to data [35,63-65]. The exponential dependence on molecular weight was based on pseudo-first-order degradation kinetics. The variable effective diffusivity in each model was used in an analytical solution to the equation for Fick’s second law of diffusion.

He et al. [66] used the correlation for effective diffusivity of drug proposed by Charlier et al. [63] in an approximate solution to the Fickian diffusion equation for time-dependent, exponentially-growing diffusivity with an empirical factor accounting for the contribution of the autocatalytic matrix erosion process on drug release. The model predicted triphasic drug release with contributions from initial burst, diffusion-controlled release, and accelerated release due to erosion.

Siepmann et al. [43] proposed a slightly different empirical method for drug transport where each microsphere size was fitted with its own effective diffusivity using the analytical solution for diffusion. The effective diffusivity was observed to vary significantly with the size of the microspheres. They correlated diffusion coefficient to microsphere radius and concluded that the strong dependence of drug mobility on microsphere size illustrated the importance of autocatalysis. The solution to the Fickian diffusion equation with a single value for the effective diffusivity for the entire range of microsphere sizes did not match the experimental data. This failure to predict the drug release profiles was attributed to the need to incorporate autocatalytic effects into models to explain drug release behavior from bulk-eroding, polyester microspheres.

Mollica et al. [67] presented a model that described the time-dependent radial concentration profiles for two populations of a protein dispersed in a PLGA microsphere. The immobile fraction of protein was stationary in unopened pores not connected to the microsphere surface through hydrated pores. The mobile fraction of protein was able to diffuse through the open, hydrated pores resulting from a degradation front that extended with time from the microsphere center to the surface. The model assumed that the conversion from immobile to mobile populations followed first-order kinetics within the front boundary. The immobile species concentration only changed due to the conversion between populations. The mobile species concentration changed as a result of diffusion and conversion from immobile to mobile protein. The diffusion coefficient for the protein was treated as a piecewise constant function with the larger diffusion coefficient outside the reaction front to capture the accelerated diffusion of mobile protein through the hydrated pores between the eroded interior and the surface of the microsphere. The erosion front moved with the square root of time multiplied by an adjustable parameter. The erosion front geometrically represented autocatalytic erosion from the center of the microsphere towards the surface.

3.4. Mathematical models with coupling between phenomena for drug release

As illustrated by the models reviewed in the previous sections, many models focus on only one of the processes involved in the drug release from PLGA microspheres or treat the processes independently rather than in a coupled manner. The nonlinearity, tight coupling, and dynamics of the processes contributing to drug release make it critical to model the effects in a coupled manner rather than independently to obtain models that are predictive rather than merely correlative. Models that have treated polymer erosion and drug transport simultaneously to better approximate the interplay between the physical and chemical processes are highlighted in this section in chronological order.

Thombre and Himmelstein [68] developed a model for simultaneous reaction within and diffusive transport from a 1-dimensional slab of surface-eroding poly(orthoester) with an encapsulated anhydrous acid source, and Joshi and Himmelstein [69] extended the model for disc geometries. While the reaction mechanisms for degradation of PLGA and poly(orthoester) differ, both polymers experience autocatalytic degradation via an acidic reaction product in the polymer. The model included autocatalytic effects by having the acidic reaction product as the only acid source and having second-order reaction terms for each species produced or consumed by catalytic reactions with the acidic reaction product. The partial differential equations for the mass balance of each species coupled the generation of the species by reaction to the Fickian diffusion for transport of drug, acid, and acid-producing species out of the slab and water into the slab. The polymer was assumed to degrade but not to diffuse. Rather than using constant diffusion coefficients in the diffusion equation, the effective diffusivity of each species increased exponentially as a function of the extent of polymer degradation. The diffusivities for each mobile species ranged between the diffusivity through the polymer and the diffusivity in water. The model used the Thiele modulus, the ratio of time scales for diffusion and reaction, to characterize the transition between surface and bulk erosion by competition between the degradation and transport phenomena.

Siepmann et al. [70] used a model for stochastic degradation and erosion to quantify the heterogeneities in the porosity throughout a three-dimensional microsphere. The effective diffusivity of the drug was assumed to be a product of a critical diffusion coefficient and the porosity at each position and time from the stochastic erosion simulation. The eroding polymer pixel lifetime and the critical diffusion coefficient enabled the model to be sensitive to autocatalysis. Drug diffusion was modeled with Fick’s second law for cylindrical geometry with axial and radial mass transfer and the variable effective diffusivity functions. Drug solubility was accounted for by limiting the amount of drug available for diffusion at each grid point at each time step dependent on the local concentrations of water and drug. The model predicted triphasic drug release with initial burst, approximately zero-order release, and final accelerated release due to diffusion through the eroded microsphere, consistent with release mechanisms where autocatalysis plays a role.

Lemaire et al. [71] described a microstructural model involving the effects of porous networks on diffusion rates of drug. An aqueous pore was approximated as a cylinder surrounded by a concentric cylinder of degrading polymer. The drug was assigned constant effective diffusivities in each of these domains, with smaller effective diffusivity in the polymer phase. The moving interface between the domains was calculated through the average pore size as the pores grew by erosion. Lemaire et al. approximated the expression for average pore size from Batycky et al. [28] as a linear function of time with some constant erosion velocity and initial pore radius. Varying the parameters for the erosion velocity and the effective diffusivity of drug in the pores allows for modeling of the transition from diffusion-controlled to erosion-controlled drug release regimes.

Zhang et al. [72] presented a model for drug diffusion, dissolution, and erosion based on mathematical expressions for dissolution and erosion rather than the polymer degradation and erosion mechanisms. They explored the effects of the functional forms for linear, S-shaped, and hyperbolic erosion profiles on drug transport. Solid and dissolved phases were tracked to calculate the porosity of the microsphere. The effective diffusivity was defined as proportional to the porosity. The effects of parameters for relative strength of the coupled phenomena on the drug cumulative release profiles under the different erosion models were explored.

Prabhu and Hossainy [73] modified the reaction-diffusion model proposed by Thombre and Himmelstein [68] to treat the kinetics for PLA degradation rather than poly(orthoester). The kinetic mechanism included non-catalytic hydrolysis dependent on the concentrations of polymer (non-diffusing bulk and soluble oligomers) and water in parallel with autocatalytic hydrolysis additionally dependent on the acidic monomer concentration. The non-catalytic and autocatalytic mechanisms had different rate constants. The concentrations of water, non-diffusing polymer bulk, soluble oligomers, soluble monomers, and drug were tracked with the reaction-diffusion model. The effective diffusivity of each water-soluble species increased exponentially as a function of the extent of polymer degradation in the same manner as in Thombre and Himmelstein [68].

Rothstein et al. [74] developed a model to simulate drug diffusion through a bulk-eroding polymer with effective diffusivity defined as the product of the polymer matrix porosity and the maximum diffusivity through the porous matrix. The time-dependent porosity was assumed to follow a cumulative normal distribution with two fitted parameters—the mean time for pore formation and the variance in time required to form pores. The mean time for pore formation depended on pseudo-first-order degradation kinetics and a critical molecular weight of polymer that permitted diffusion of the drug through the pore structure of the polymer. The maximum diffusivity through the porous matrix was correlated to polymer microsphere radius, and the critical molecular weight of polymer was correlated to drug molecular weight. The model includes initial burst of drug from a domain close to the surface subject to constant effective diffusivity. The authors acknowledged that their correlation of effective drug diffusivity to particle size lacked a physically relevant expression to incorporate size-dependent autocatalytic effects. The model was later extended [75] to apply to surface-eroding polymers as well as bulk-eroding polymers. In addition to drug transport, the extended model included drug dissolution kinetics and water transport and contribution of water concentration on the degradation kinetics. The model results showed good agreement between theory and experiments for bulk- and surface-eroding polymers for short release periods (up to 30 days).

Zhao et al. [76] presented a mechanistic method for coupling degradation and variable effective diffusivity through hindered diffusion and pore evolution. The model proposed a proportional relationship between the rate of growth of average pore size and the rate of generation of soluble monomers and oligomers. The mechanistic relationship improved upon the empirical correlations between pore growth and erosion rate given by Batycky et al. [28] and Lemaire et al. [71]. Though the model used non-catalytic pseudo-first-order degradation kinetics, the pore growth expression could be generalized for autocatalysis with the appropriate degradation kinetics. Zhao et al. linked the transient average radius of eroding pores to drug diffusivities using hindered diffusion theory, where aqueous transport of solutes in fine pores is reduced from the diffusion of the solute in water at infinite dilution due to hydrodynamic and steric restrictions [84]. Zhao et al. proposed using the variable effective diffusivity for the drug in Fick’s second law of diffusion but showed no results for the drug concentration or amount of drug released.

Ford et al. [77] proposed a reaction-diffusion model similar to Thombre and Himmelstein [68] to treat second-order, autocatalytic degradation for PLGA microspheres. The concentrations of water-soluble small oligomers up to length of nine, the carboxylic acid end groups, non-diffusing polymer bulk, and drug were tracked with the reaction-diffusion model. The effective diffusivity of each water-soluble species increased linearly as a function of the void fraction in the polymer bulk due to transport of soluble oligomers. The effective diffusivity was bounded by the diffusivity of the soluble species in the bulk polymer at the initial porosity and the diffusivity of the soluble species at infinite dilution in water. The numerical solutions to the model equations were compared to the drug release profiles with constant diffusivity at different values of the initial time constant for diffusion. Cumulative release profiles for constant diffusivity scaled by fraction of total release time collapsed onto a single curve as expected while release profiles with variable effective diffusivity scaled in the same manner showed size-dependence. Larger microspheres were predicted to release drugs faster than smaller microspheres with sigmoidal release profiles consistent with autocatalytic, erosion-controlled drug release.

4. Conclusions

Numerous mathematical models have been published for predicting degradation, erosion, and drug transport and overall drug release from PLGA microspheres. In this review, models that incorporated autocatalysis have been categorized according to the phenomena they treated. Collectively, the models have provided insights into the mechanisms of drug release occurring under different conditions. The more sophisticated models that treated the coupled interactions between phenomena brought predictive capability to the regimes where autocatalysis plays a significant role in drug release dynamics. Models could be improved further by considering the effects of autocatalysis on degradation kinetics and oligomer transport and by continuing to explore the mechanistic coupling between polymer erosion and increasing effective diffusivity of the drug.

With accurate predictions of the effects of many possible PLGA microsphere fabrication designs under a range of conditions, the optimum design for producing microspheres exhibiting a desired drug release profile could be determined for use in patients. Mixing monodisperse microspheres of different sizes yields release profiles that are mass-weighted averages of the release profiles for the individual sizes [85,86]. Predictive, high accuracy models that rigorously include autocatalytic effects could decrease the number of experimental trials needed to explore release from different microsphere distributions by optimizing controlled drug release in silico.