Abstract
Current thoracic artificial lungs (TALs) possess blood flow impedances greater than the natural lungs, resulting in abnormal pulmonary hemodynamics when implanted. This study sought to reduce TAL impedance using computational fluid dynamics (CFD). CFD was performed on TAL models with inlet and outlet expansion and contraction angles, θ, of 15°, 45°, and 90°. Pulsatile blood flow was simulated for flow rates of 2–6 L/min, heart rates of 80 and 100 beats/min, and inlet pulsatilities of 3.75 and 2. Pressure and flow data were used to calculate the zeroth and first harmonic impedance moduli, Z0 and Z1, respectively. The 45° and 90° models were also tested in vitro under similar conditions. CFD results indicate Z0 increases as stroke volume and θ increase. At 4 L/min, 100 beats/min, and a pulsatility of 3.75, Z0 was 0.47, 0.61, and 0.79 mmHg/(L/min) for the 15°, 45°, and 90° devices, respectively. Velocity band and vector plots also indicate better flow patterns in the 45° device. At the same conditions, in vitro Z0 were 0.69 ± 0.13 and 0.79 ± 0.10 mmHg/(L/min), respectively, for the 45° and 90° models. These Z0 are 65% smaller than previous TAL designs. In vitro, Z1 increased with flow rate but was small and unlikely to significantly affect hemodynamics. The optimal design for flow patterns and low impedance was the 45° model.
Keywords: Thoracic artificial lung (TAL), Impedance, Computational fluid dynamics (CFD)
INTRODUCTION
Currently there is no sufficient long-term bridge to lung transplant for patients with end-stage lung disease, nor is there an adequate long-term alternative to mechanical ventilation for patients with acute respiratory failure. Available devices and support methods are unable to provide complete respiratory support for these patients without causing significant long-term blood damage or further deterioration of the disease state, often resulting in multiple organ failure.10 Thoracic artificial lungs (TALs) are being developed without blood pumps for these patients to minimize blood damage, coagulation, and inflammation. TALs are attached to the pulmonary circulation, and thus their blood flow is provided by the right ventricle (RV). These devices must therefore have low impedance to prevent overloading the RV and causing RV dysfunction.
Current TALs possess blood flow impedances greater than the natural lungs, resulting in abnormal pulmonary hemodynamics when implanted in series with the natural lung or in parallel with high flows to the TAL.1,11 The most physiologically relevant impedances in this setting are those at the zeroth and first harmonic frequencies.5,6 These represent, respectively, the opposition to blood flow that is steady and periodic at a frequency equal to the heart rate. Moreover, cardiac output (CO) during TAL attachment is affected mostly by the magnitude of the zeroth and first harmonic impedance moduli (Z0 and Z1). Sato et al.11 suggest that most RV dysfunction during TAL attachment is due to an increase in Z0 due to its effects on average system pressures, and a smaller decrease in CO is caused by Z1 because of its effect on systolic pressures. Kuo et al.6 confirmed that Z0 is the key determinant of RV output in their study examining the effect of pulmonary system impedance on CO. For every 1 mmHg/(L/min) increase in Z0, there is an approximate 3.65% decrease in CO. Likewise, for every 1 mmHg/(L/min) increase in Z1, there is a 0.08Z0% decrease in CO. Therefore, the foremost goal of TAL design should be to reduce Z0, with a secondary requirement to limit increases in Z1.
Studies using a compliant housing TAL (cTAL) showed the majority of device impedance was because of excessive inlet/outlet impedances.2 It was thus theorized that the abrupt expansions and contractions at the inlet and outlet regions cause flow recirculation that, in turn, leads to higher device impedance. If this is the case, then more gradual expansions and contractions could improve flow patterns and reduce device impedance. Therefore, this study explored the effect of different inlet and outlet geometries on impedance and flow patterns within the device. The inlet and outlet expansion angle, θ, was adjusted, and flow patterns and impedances were determined at a variety of blood flow rates and heart rates (HR). Physical models were then created and tested in vitro to verify computer results.
METHODS
Computational Fluid Dynamics Studies
The effects of θ on TAL blood flow patterns and impedance were evaluated using designs with θ = 15°, 45°, and 90° (Fig. 1). SolidWorks (Dassault Systèmes SolidWorks Corp., Concord, MA) computer-aided design (CAD) software was used to create each housing model, which was then imported into the ADINA (ADINA R&D Inc., Watertown, MA) computational fluid dynamics (CFD) software program (Fig. 2). In these models, blood flows through the inlet, expands into the inlet manifold, flows through the fiber bundle at the center of the device, then travels through the outlet manifold and exits through the device outlet. The inlet/outlet diameter, height, and width of each TAL model are 0.016, 0.103, and 0.102 m, respectively. The fiber bundle length, path length (the distance blood must flow through the bundle), and frontal area (the cross-sectional area perpendicular to blood flow through the bundle) are 0.140 m, 0.038 m, and 0.016 m2, respectively, for each model. The 15°, 45°, and 90° models have total lengths of 0.350, 0.229, and 0.191 m, respectively. Since the inlet/outlet tube diameter and the housing body geometry is fixed, as θ changes, the lengths of the expansion/contraction sections must change (see Fig. 1).
FIGURE 1.
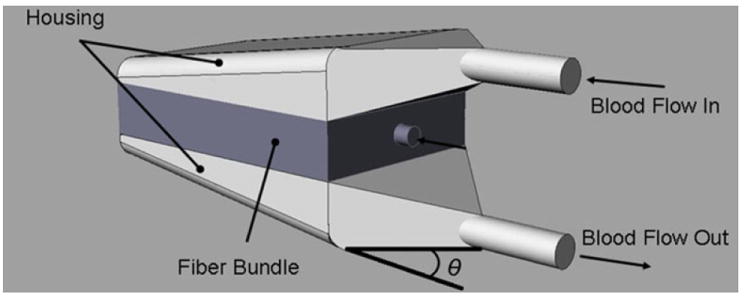
TAL model showing blood flow path and inlet and outlet expansion angle, θ.
FIGURE 2.
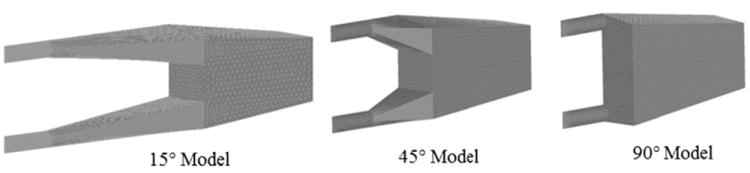
TAL housing models used for CFD study with θ = 15°, 45°, and 90°.
CFD: Problem Formulation
Program assumptions included a transient solution with incompressible flow. Turbulent flow was assumed to occur in the inlet and outlet sections. The average Reynolds numbers in the inlet and outlet sections at flow rates of 2, 4, and 6 L/min are 920, 1800, and 2760, respectively. The material properties of the rigid housing and fiber bundle, along with the fluid characteristics of blood were defined in the program. Blood viscosity and density were set to 0.003 Pa s (3.0 cP) and 1040 kg/m3, respectively. The fiber bundle region was modeled as porous media with fluid density, porosity, permeability, and fluid viscosity defined as 1040 kg/m3, 0.75, 2.81 × 10−9 m2, and 0.003 Pa s (3.0 cP), respectively. Permeability, k, was calculated from preliminary cTAL data2 using Darcy’s Law:
| (1) |
where Q is blood flow rate, μ is viscosity, L is the fiber bundle path length, A is the fiber bundle frontal area, and ΔP is the pressure drop across the fiber bundle. The hollow fiber bundle was modeled using a porous media theory to determine flow characteristics within the bundle.3,4,8,12
The fluid motion outside the fiber bundle is governed by the Navier–Stokes equations with constant density and fluid properties, together with the continuity equation as follows:
| (2) |
| (3) |
where ρf is the blood density, μf is the blood viscosity, P is the pressure, and V is the velocity vector.
CFD: Boundary Conditions
A symmetry condition was utilized in ADINA, allowing the model to be cut in half, thus reducing computational time. This was done by applying a zero velocity fixity perpendicular to the symmetry face. A no-slip wall boundary condition was also applied to the inlet and outlet housings, while a slip wall boundary condition was applied to the bundle walls. The initial pressure condition was set to 10 mmHg. A time-dependent velocity was applied to the inlet face, and a constant pressure of 10 mmHg was applied to the outlet face.
Pulsatile blood flow through the device was simulated in ADINA at average flow rates (Q) of 2, 4, and 6 L/min, and HR of 80 and 100 beats/min (Fig. 3). This inlet flow waveform, Qi, is a simulated RV output with a pulsatility of 3.75. Pulsatility is defined as (maximum flow rate − minimum flow rate)/average flow rate. The inlet waveform was created with the equation13:
| (4) |
where Vs is the stroke volume defined as
| (5) |
tes is the end-systolic time defined as
| (6) |
ted is the end-diastolic time defined as
| (7) |
and A is the flow pulse scaling factor used for scaling flows to match the CO. The duration of regurgitation is assumed to be 0.04 s. In reality, device inflow is less pulsatile since the TAL is attached to the pulmonary artery (PA) which dampens the pulse. Thus, this waveform represents the most extreme case the device would encounter. A more typical inlet waveform with a lower pulsatility of 2 was also investigated (Fig. 3).2 This waveform is created by sending the previously discussed RV output waveform through a windkessel model with R = 1.25 mmHg/(L/min) and C = 1.78 mL/mmHg.
FIGURE 3.
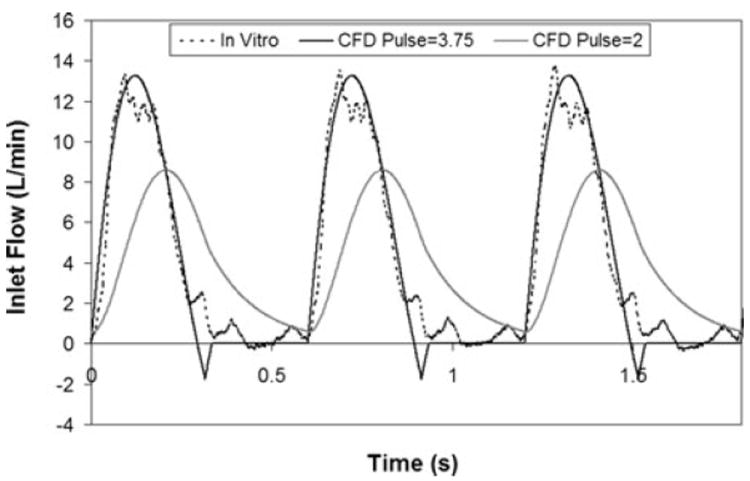
TAL inlet flow waveform for CFD and in vitro studies at 4 L/min, 100 beats/min, and pulsatilities of 2 and 3.75.
CFD: Numerical Scheme
A finite element formulation based on the Galerkin method was utilized to solve the governing equations. A tighter convergence tolerance was used in this investigation to obtain accurate results. A value of 10−5 was set for the relative error. The mesh size and time step of the model were varied until a converged solution was reached. The convergence criterion was set at ≤1.5% difference in impedance between models of different time step or mesh size. A variable grid size system was employed in the present study to capture the rapid changes in the velocity and pressure variables. A finer mesh was implemented at the inlet and outlet faces to accurately determine pressure and flow data. Also, a finer mesh along the inlet and outlet cylindrical regions was required for convergence. In the end, the mesh size was 3 mm for the bodies, 0.25 mm for the inlet and outlet sections, and 1.0 mm for the inlet and outlet faces. A time step of 0.005 s was used.
CFD: Data Analysis
The simulation was run for three consecutive heart beats to achieve a converged periodic solution. Inlet and outlet pressures and overall flow rate data from the final beat were obtained from the program for presentation and analysis. To determine the impedance moduli, Fourier transforms were used to convert the inlet pressure and flow in the time domain to a series of sinusoids at their respective harmonic frequencies:
| (8) |
| (9) |
where P0 and Q0 are the average pressure and flow magnitudes, respectively, Pn and Qn are the pressure and flow magnitudes at the nth harmonic, respectively, ωn is the frequency at the nth harmonic, t is time, and ϕn is the phase shift at the nth harmonic. Impedance moduli at the nth harmonic, Zn, are the ratio of the amplitudes of pressure and flow at the same harmonic:
| (10) |
where Pi and Po are the inlet and outlet device pressures, respectively. Values of Z0 and Z1 were calculated and used to asses TAL impedance. Pressure and flow data were also obtained from the top and bottom fiber bundle faces to determine bundle resistance.
In order to separately investigate the viscous pressure drop, the average pressure drop due to an expansion or contraction, ΔPec, was calculated:
| (11) |
where ρ is the density of blood, Q(t) is the time-dependent blood flow through the device at Q = 4 L/min and HR = 100 beats/min, A1 is the cross-sectional area of the inlet/outlet, and A2 is the cross-sectional area of the fiber bundle. Equation (11) was numerically integrated using the trapezoidal rule. The viscous resistance was then calculated for the inlet (Rv,in) and outlet (Rv,out) sections:
| (12) |
| (13) |
where ΔP is the pressure drop for the inlet, bundle, or outlet section, and Q = 4 L/min. No adjustment is necessary for the fiber bundle resistance, as it does not include an expansion or contraction. The percentage of total device resistance was then calculated for the inlet, bundle, and outlet sections.
Velocity band plots were created in ADINA to investigate flow uniformity in the housing and fiber bundle of each model. Plots were created on a cross section along the y-axis (top down view) for several sections in the housing and fiber bundle of the device. In these plots, color is used to indicate velocity magnitude where red represents the highest velocity in the plot range (0.14 m/s) and blue represents a velocity of 0 m/s. These plots were created at peak systole in the cardiac cycle. Velocity vector plots were also created to investigate areas of recirculation in each housing model. In these plots, color and the size of the vectors are used to indicate velocity magnitude where red represents a velocity of 0.67 m/s and blue represents a velocity of 0 m/s.
In Vitro Testing
Experimental tests were run on two TAL rigid housing models to validate the computer results. The models tested had θ = 45° and 90°. To create the fiber bundle, woven mats of polypropylene fibers with a fiber diameter of 200 μm were wound into compact bundles with porosity, path length, and frontal area of 0.75, 0.038 m, and 0.016 m2, respectively. The bundle was potted with WC7-53, a two-part polyurethane, into an acrylic box. Three sets of housings for each θ were machined from PVC blocks and then clamped above and below a fiber bundle. The blocks were carved out in the center, so that they are the negative of the housing shown in Fig. 1. In vitro testing was conducted with a circuit consisting of a pulsatile pump (Harvard Apparatus, Holliston, MA), TAL model, and reservoir. The entire circuit was primed with a 3.0 cP glycerol solution (Fig. 4).
FIGURE 4.
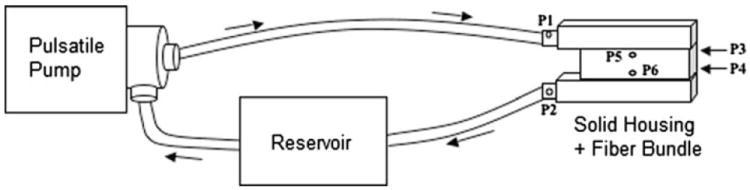
In vitro test circuit consisting of a pulsatile pump, TAL model, and reservoir filled with 3.0 cP glycerol solution. Six pressure lines were connected to the model at the inlet (P1), outlet (P2), top of the bundle (P3 and P5), and bottom of the bundle (P4 and P6).
Pressure transducers (see Fig. 4) were connected to six lures on the model to monitor device pressure at the inlet (P1), outlet (P2), top of the bundle (P3 and P5), and bottom of the bundle (P4 and P6). A blood flow probe was placed before the device inlet to monitor flow rate. Using the pulsatile pump, testing was conducted for HR = 80 and 100 beats/min and Q = 2, 4, and 6 L/min. Average pulsatilities for these flows were 3.33. A representative inlet flow rate waveform at a HR = 100 beats/min, Q = 4 L/min, and pulsatility = 3.33 is shown in Fig. 3. In addition, the 45° model was tested at a pulsatility of 1.7 with HR = 100 beats/min and Q = 4 L/min to examine the effects of pulsatility on device impedance. To reduce the pulsatility, a compliance chamber11 with C = 0.5 was placed in the circuit before the device inlet. The BIOPAC MP150 data acquisition system (Biopac Systems, Inc.) was used to acquire pressure and flow data. Fourier transforms were then performed on this data to calculate Z0 and Z1. Fiber bundle resistance was calculated by averaging bundle pressures:
| (14) |
Viscous resistances were calculated at Q = 4 L/min and HR = 100 beats/min for the inlet, bundle, and outlet sections of each model in a similar fashion as the CFD simulation.
Comparisons between in vitro Z0 and Z1 were performed with SPSS (SPSS, Chicago, IL) using a mixed model with device as the subject variable, stroke volume as a fixed, repeated-measure variable, and θ as a fixed variable. Stroke volume, SV, was calculated as Q/HR. Correlations between Z0 and SV and between Z1 and Q were created.
RESULTS
Computational Fluid Dynamics
Figure 5 displays TAL Z0 CFD results for varying stroke volumes at a pulsatility of 3.75. Device Z0 increases linearly as SV increases, as well as increasing with larger θ. At Q = 4 L/min and HR = 100 beats/min (SV = 0.04 L), Z0 was 0.47, 0.61, and 0.79 mmHg/(L/min) for the 15°, 45°, and 90° devices, respectively. The correlations relating Z0 to SV were:
| (15) |
| (16) |
| (17) |
FIGURE 5.
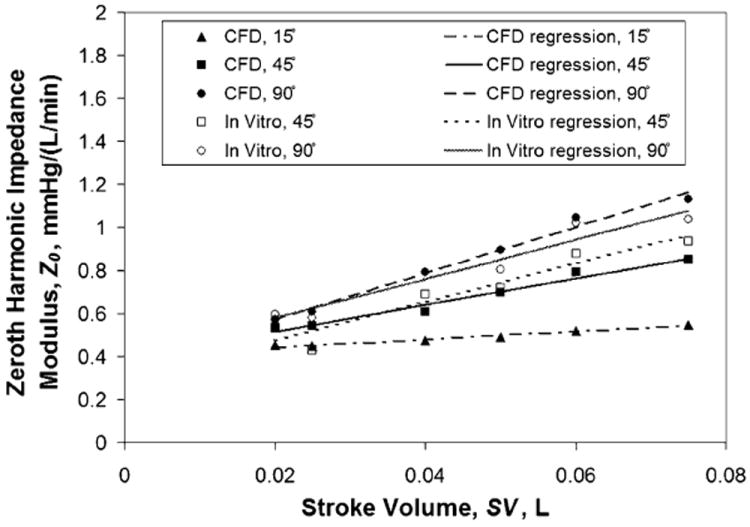
Effect of θ on TAL Z0 for varying stroke volumes: comparison between in vitro and CFD results.
Figure 6 displays Z1 CFD results at varying HR and flow rates at a pulsatility of 3.75. The values of Z1 increase linearly with flow rate for the 15° model; however, they remain more uniform at each flow rate for the 45° and 90° models. Z1 is larger at HR = 100 beats/min for all three models. Finally, Z1 was similar between the 45° and 90° models but noticeably greater for the 15° model. At Q = 4 L/min and HR = 100 beats/min, Z1s were 0.67, 0.40, and 0.35 mmHg/(L/min) for the 15°, 45°, and 90° models, respectively.
FIGURE 6.
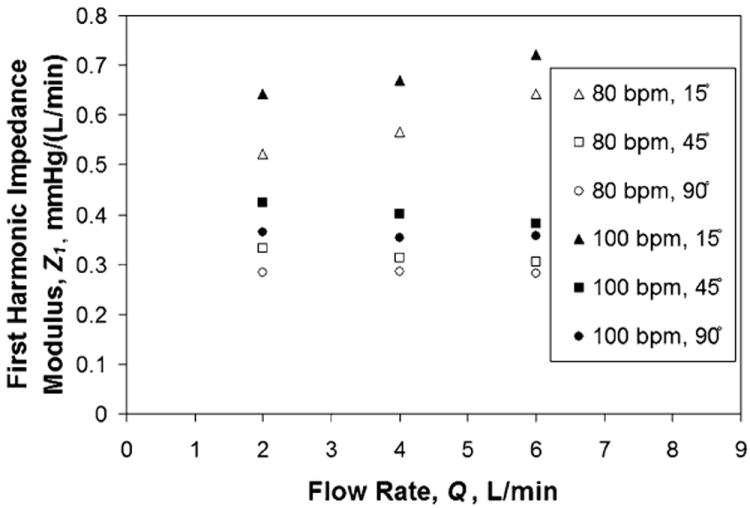
Effect of θ on TAL Z1 for varying heart and flow rates: CFD results.
Device Z0 was reduced slightly under more typical in vivo conditions with a lower inlet flow pulsatility; however, Z1 was not affected. At Q = 4 L/min and HR = 100 beats/min, the 45° model Z0 was 0.53 mmHg/(L/min) at a pulsatility of 2 vs. 0.61 mmHg/(L/min) at a pulsatility of 3.75. The 45° model Z1 was 0.41 mmHg/(L/min) at a pulsatility of 2 vs. 0.40 mmHg/(L/min) at a pulsatility of 3.75. Finally, fiber bundle resistance for all models was 0.31 mmHg/(L/min). The majority of device resistances came from the fiber bundle and inlet housing sections in each design. Table 1 lists the viscous resistances in the inlet, bundle, and outlet sections for the 45° and 90° models at an example condition of Q = 4 L/min and HR = 100 beats/min.
TABLE 1.
Viscous resistance in the inlet, bundle, and outlet sections for the 45° and 90° in vitro and CFD models at Q = 4 L/min and HR = 100 beats/min.
| Resistance | In vitro, 45° | CFD, 45° | In vitro, 90° | CFD, 90° |
|---|---|---|---|---|
| Inlet, mmHg/(L/min) | 0.25 ± 0.06 | 0.21 | 0.26 ± 0.09 | 0.31 |
| Inlet, % of total | 36.2 ± 10.5 | 34.2 | 32.2 ± 10.9 | 39.4 |
| Bundle, mmHg/(L/min) | 0.31 ± 0.11 | 0.31 | 0.28 ± 0.09 | 0.31 |
| Bundle, % of total | 43.5 ± 14.1 | 49.4 | 35.1 ± 12.9 | 38.7 |
| Outlet, mmHg/(L/min) | 0.14 ± 0.16 | 0.10 | 0.26 ± 0.12 | 0.17 |
| Outlet, % of total | 20.3 ± 19.2 | 16.4 | 32.7 ± 12.4 | 22.0 |
| Total, mmHg/(L/min) | 0.70 ± 0.14 | 0.62 | 0.81 ± 0.10 | 0.79 |
Band plots taken at peak systole for Q = 4 L/min, HR = 100 beats/min, and pulsatility = 3.75 are shown in Fig. 7a along a section in the device inlet region. These plots indicate areas of little to no flow at the distal ends of the 15° and 45° device, as indicated by the blue color. During diastole (not pictured), no more flow is entering the device, and thus the velocity plots show even less flow getting to the back of each model. Band plots taken during systole across the bundle indicate a uniform flow in the 15° and 45° model with slightly lower flow near the front of the device in the 90° model (Fig. 7b).
FIGURE 7.
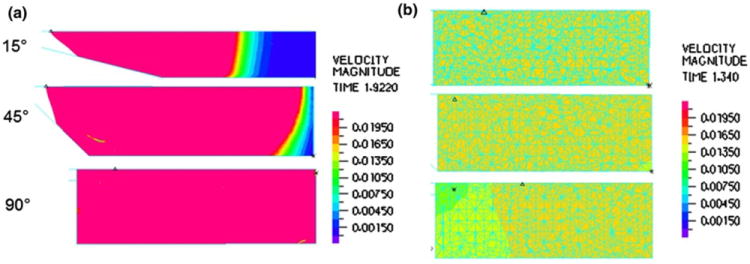
Velocity band plots for the 15°, 45°, and 90° CFD TAL models at peak systole in the (a) inlet housing region and (b) fiber bundle.
Velocity vector plots of the inlet housing region, taken at the beginning of diastole (t = 1.58 s) for Q = 4 L/min, HR = 100 beats/min, and pulsatility = 3.75, are shown in Fig. 8. A magnified view of the major recirculation regions (indicated in Fig. 8a) are shown in Fig. 8b. Large vortices occur near the distal end of the 90° device while smaller recirculation regions occur in the proximal end of the 15° and 45° devices. In the 90° model at peak systole (not shown), large vortices occur in the proximal end, as well as smaller one at the distal end of the device. The large vortices in this device travel from the proximal end to the distal end of the model (with flow) as time in the cardiac cycle progresses. The 15° and 45° models also have vortices occurring throughout the cardiac cycle; however, these are smaller and mainly occur in the proximal end of the device. Velocity vector plots taken in the housing outlet (not pictured) showed small regions of recirculation in the outlet tube and proximal end of the housing during diastole only. However, the velocities in these vortices were very small compared to those in the housing inlet.
FIGURE 8.
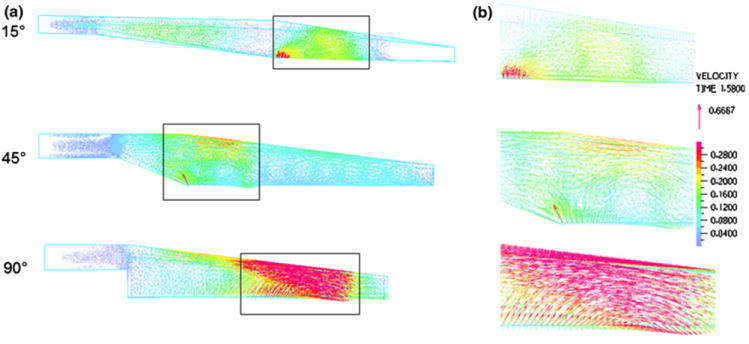
(a) Velocity vector plots for the 15°, 45°, and 90° CFD TAL models at the beginning of diastole (t = 1.58 s) in the inlet housing region. (b) Magnified view of the major recirculation areas in each model. A magnified view of the major recirculation regions (indicated in Fig. 8a) are shown in Fig. 8b.
In Vitro Testing
The effects of θ on TAL in vitro Z0 and Z1 are shown in Figs. 5 and 9, respectively, for an average pulsatility of 3.3. Z0 varied significantly with SV (p < 10−19) and θ (p < 0.01). The 45° model had a significantly lower Z0 than the 90° model overall. At Q = 4 L/min and HR = 100 beats/min (SV = 0.04 L), Z0 = 0.69 ± 0.13 and 0.79 ± 0.10 mmHg/(L/min) for the 45° and 90° models, respectively. The correlations relating in vitro Z0 to SV were
| (18) |
| (19) |
Values for Z1 varied significantly with HR (p < 0.01), Q (p < 10−30), and θ (p < 10−6). The effect of HR was very small compared to Q and θ, but indicated that Z1 increased with HR. The 90° model had significantly lower Z1 than the 45° model. Under the same conditions, Z1 = 1.23 ± 0.27 and 0.91 ± 0.0.13 mmHg/(L/min) for the 45° and 90° models, respectively. The correlations relating in vitro Z1 for each θ and HR are
| (20) |
| (21) |
| (22) |
| (23) |
FIGURE 9.
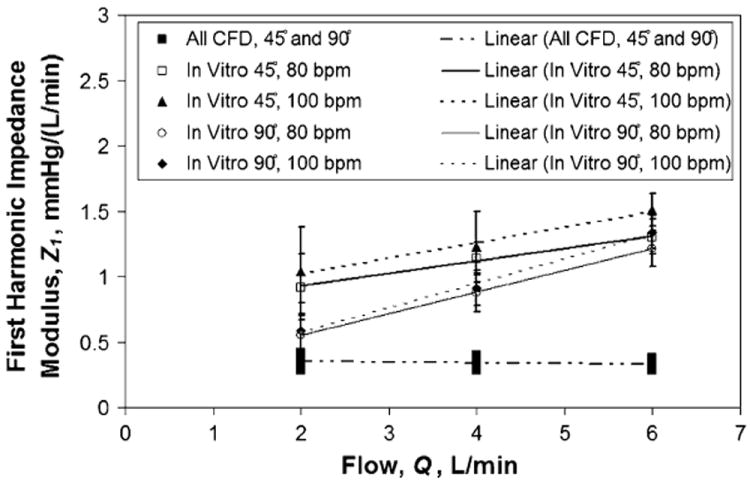
Effect of θ on TAL Z1: comparison between in vitro and CFD results for varying heart and flow rates.
Overall, in vitro Z1s were larger and showed stronger dependence on θ and Q than CFD results. These larger Z1s were due to larger peak pressures in vitro, even though average pressure drops were similar between the CFD and in vitro studies. Average fiber bundle resistance for all models was 0.29 mmHg/(L/min), nearly identical to CFD results. In the 45° model, the majority of device resistance came from the fiber bundle and inlet housing sections. However, in the 90° model, the relative contribution to total device resistance was almost identical for each section (Table 1).
Finally, at a lower pulsatility of 1.7 with Q = 4 L/min and HR = 100 beats/min (SV = 0.04 L), the 45° model had Z0 = 0.65 mmHg/(L/min) and Z1 = 1.29 mmHg/(L/min). The Z0 and Z1 are 0.69 and 1.23 mmHg/(L/min) at the same conditions with pulsatility equal to 3.2. Therefore, as predicted in the CFD study, pulsatility does not greatly influence impedance in vitro.
DISCUSSION
The impedances of all the TAL designs tested in this study are significantly lower than previous designs. Experiments with the MC3 Biolung (MC3, Ann Arbor, MI)9 and a cTAL2 report Z0 = 1.8 and 1.9 mmHg/(L/min), respectively, at Q = 4 L/min and HR = 100 beats/min. At the same flow and heart rate, the 45° and 90° models in the current study had Z0 = 0.69 ± 0.13 and 0.79 ± 0.10 mmHg/(L/min), respectively. These values are also significantly lower than the impedance of the natural lung: Z0 = 1.25 mmHg/(L/min). Z1 in the healthy, natural lung is 0.49 mmHg/(L/min)7 compared to 1.23 mmHg/(L/min) in the 45° model in this study.
The effect of SV and θ on Z0 was very similar in the CFD and in vitro results. However, CFD modeling predicted lower Z1 values overall with a minimal effect of θ and Q. The Z1 is more heavily influenced by differences in flow rate patterns and thus has a higher variability than Z0 during in vitro testing. Overall, the Z1 values measured for both models are small and unlikely to influence device function in vivo.6
The 45° device tested in this study had a 65% lower in vitro Z0 than previous designs. This decrease should improve RV function during attachment in vivo. The ultimate effect of lower impedance on cardiac function depends on attachment mode. The most likely clinical application for these devices is attachment in parallel with the natural lung in a PA to left atrium (LA) configuration. If attached in parallel with the natural lung, then lower TAL impedance may allow patients to more easily exercise during device attachment. Akay et al.1 attached the MC3 Biolung in parallel with the pulmonary circulation in sheep with chronic pulmonary hypertension and varied the percentage of CO through the device under simulated rest, ambulatory, and exercise conditions. At ambulatory and resting conditions, CO was maintained as the percentage of CO to the device increased. At exercise conditions, CO decreased with increasing flow to the TAL up to 23 ± 5% at 90% flow diverted through the TAL. TAL impedance increases, and the natural lung impedance decreases with increasing blood flow. Thus, during exercise with elevated CO, a higher percentage of CO may travel through the native lungs reducing respiratory support when attached in parallel. Further decreases in device impedance may allow for complete exercise tolerance and optimal device performance.
If attached in series with the natural lung, from the proximal to distal PA, then lower impedance should reduce the drop in CO that has been observed experimentally. Previous studies by Kim et al.5 and Kuo et al.6 developed relationships between acute increases in Z0 and Z1 and the resultant percent decrease in CO. These studies can be used to predict the improvement in CO using these devices vs. previous designs. In the devices tested here, Z1 values are small in all devices, regardless of design, and should not have a measureable effect on CO.6 Values of Z0 should, on the other hand, contribute to lowering CO. The increase in pulmonary system impedance (ΔZ) due to the TAL impedance (ZTAL) can be calculated using the equation.
| (24) |
where f is the fraction of flow to the TAL. If we assume CO to be 6 L/min and allow 4 L/min to travel through the TAL then f = 2/3. Using the 45° model, in vitro data at Q = 4 L/min, HR = 100 beats/min, and a pulsatility of 1.7 for ΔZ0 and ΔZ1 are 0.43 and 0.86 mmHg/(L/min), respectively. If one assumes that the impedance of the device is purely additive, the flow rate is 4 L/min, and the 45° model is used, then the Kim and Kuo relationships predict 0.1 and 11% decreases in CO, respectively, because of the impedance change of the device alone. For the previous TAL designs, we would predict decreases of 5 and 14%. Based on these predictions, the 45° model should cause a small decrease in CO. This decrease may be tolerable in patients with normal pulmonary vascular resistance or mild pulmonary hypertension and normal right ventricular function. It would not be tolerable in patients with marked pulmonary hypertension and right ventricular dysfunction. In addition, the anastomoses used to attach the device to the pulmonary circulation would further increase impedance and thus further decrease CO. Unfortunately, appropriate anastomoses’ impedances are not available in the literature. If necessary, f could be reduced to further decrease the drop in CO.
The CFD model also provided important information on how device design affects flow patterns in both the housing and fiber bundle. Changes in Z0 can be explained in large part by examining blood flow recirculations in the TAL. Recirculation occurred in the inlet of all three models; however, recirculations decreased as θ decreased. The 90° housing inlet had several regions of large vortices throughout the cardiac cycle, while the 15° and 45° models had smaller areas of recirculation. Device design also affected flow uniformity in the housing inlet and fiber bundle. Flow uniformity is essential to the short- and long-term functions of the device. Regions of little or no flow offer little gas exchange when they occur in the fiber bundle and, worse yet, can lead to a buildup of activated clotting factors and clot formation, when they occur at any of the device artificial surfaces. The 15° and 45° models had areas of little to no flow near the distal end of the inlet. These areas were larger in the 15° model where flow was barely reaching past the middle of the housing body. The stasis regions in the back of the device can never completely be eliminated for the angled housings, but further geometry changes may help, such as a shorter distance between the inlet and the back and tapered corners in the back. Tapered corners are easily incorporated during the production process when the fiber bundle is “potted” in urethane to separate the blood and gas phases of the device.
Ultimately, the optimal device must have a combination of low impedance, even flow, and reasonable size for use by an ambulatory patient. While the 15° model had smaller recirculation regions and low impedance, it had a large stasis region near the distal end of the device. Also, the long inlet and outlet lengths of the 15° model may make it unwieldy to use with patients. Therefore, the 45° model has the optimal combination of low impedance, better flow patterns, and relatively compact size. This device will be prototyped and tested further in vivo. The low impedance of the 45° model should allow for a minimal, acute decrease in CO at rest if implanted in series with the natural lung and increased exercise tolerance when compared to previous TAL designs if attached in parallel with high flows to the TAL.
Acknowledgments
Financial support for this project was provided by the NIH Heart, Lung, and Blood grant #R01HL089043.
References
- 1.Akay B, Reoma JL, Camboni D, et al. In-parallel artificial lung attachment at high flows in normal and pulmonary hypertension models. Ann Thorac Surg. 2010;90:259–265. doi: 10.1016/j.athoracsur.2010.03.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cook KE, Perlman CE, Seipelt R, et al. Hemodynamic and gas transfer properties of a compliant thoracic artificial lung. ASAIO J. 2005;51:404–411. doi: 10.1097/01.mat.0000169707.72242.8f. [DOI] [PubMed] [Google Scholar]
- 3.Funakubo A, Taga I, McGillicuddy JW, et al. Flow vectorial analysis in an artificial implantable lung. ASAIO J. 2003;49(4):383–387. [PubMed] [Google Scholar]
- 4.Gage KL, Gartner MJ, Burgreen GW, Wagner WR. Predicting membrane oxygenator pressure drop using computational fluid dynamics. Artif Organs. 2002;26(7):600–607. doi: 10.1046/j.1525-1594.2002.07082.x. [DOI] [PubMed] [Google Scholar]
- 5.Kim J, Sato H, Griffith GW, Cook KE. Cardiac output during high afterload artificial lung attachment. ASAIO J. 2009;55:73–77. doi: 10.1097/MAT.0b013e318191500a. [DOI] [PubMed] [Google Scholar]
- 6.Kuo AS, Sato H, Reoma JL, Cook KE. The relationship between pulmonary system impedance and right ventricular function in normal sheep. Cardiovasc Eng. 2009;9:153–160. doi: 10.1007/s10558-009-9083-2. [DOI] [PubMed] [Google Scholar]
- 7.Laskey WK, Ferrari VA, Palevsky HI, Kussmaul WG. Pulmonary artery hemodynamics in primary pulmonary hypertension. J Am Coll Cardiol. 1993;21:406–412. doi: 10.1016/0735-1097(93)90682-q. [DOI] [PubMed] [Google Scholar]
- 8.Matsuda N, Nakamura M, Sakai K, Kuwana K. Theoretical and experimental evaluation for blood pressure drop and oxygen transfer rate in outside blood flow membrane oxygenator. J Chem Eng Jpn. 1999;32(6):752–759. [Google Scholar]
- 9.McGillicuddy JW, Chambers SD, Galligan DT, et al. In vitro fluid mechanical effects of thoracic artificial lung compliance. ASAIO J. 2005;51:789–794. doi: 10.1097/01.mat.0000182473.47668.f1. [DOI] [PubMed] [Google Scholar]
- 10.Plötz FB, Slutsky AS, van Vught AJ, Heijnen CJ. Ventilator-induced lung injury and multiple system organ failure a critical review of facts and hypotheses. Intensive Care Med. 2004;30:1865–1872. doi: 10.1007/s00134-004-2363-9. [DOI] [PubMed] [Google Scholar]
- 11.Sato H, McGillicuddy JH, Griffith GW, et al. Effect of artificial lung compliance on in vivo pulmonary system hemodynamics. ASAIO J. 2006;52:248–256. doi: 10.1097/01.mat.0000208961.67272.fa. [DOI] [PubMed] [Google Scholar]
- 12.Taga I, Funakubo A, Fukui Y. Design and development of an artificial implantable lung using multiobjective genetic algorithm: evaluation of gas exchange performance. ASAIO J. 2005;51(1):92–102. doi: 10.1097/01.mat.0000150645.23825.f0. [DOI] [PubMed] [Google Scholar]
- 13.Van Grondelle A. Thesis. Evanston, IL: Northwestern University; 1982. Analysis of Pulmonary Arterial Blood Flow Dynamics with Special Reference to Congenital Heart Disease. [Google Scholar]


