Supralinear increase of recurrent inhibition during sparse activity in the somatosensory cortex

Abstract

The balance between excitation and inhibition in the cortex is crucial in determining sensory processing. Because the amount of excitation varies, maintaining this balance is a dynamic process; yet the underlying mechanisms are poorly understood. We show here that the activity of even a single layer 2/3 pyramidal cell in the somatosensory cortex of the rat generates widespread inhibition that increases disproportionately with the number of active pyramidal neurons. This supralinear increase of inhibition results from the incremental recruitment of somatostatin-expressing inhibitory interneurons located in layers 2/3 and 5. The recruitment of these interneurons increases tenfold when they are excited by two pyramidal cells. A simple model demonstrates that the distribution of excitatory input amplitudes onto inhibitory neurons influences the sensitivity and dynamic range of the recurrent circuit. These data show that through a highly sensitive recurrent inhibitory circuit, cortical excitability can be modulated by one pyramidal cell.

Sensory stimuli both excite and inhibit cortical neurons^1–6. The fraction of cortical neurons that respond to a sensory stimulus, and the timing of these neuronal responses, depend on the relative amount of synaptic excitation and inhibition they receive^2,6–8. Disrupting this balance, for example through pharmacological manipulations, interferes with the response of cortical neurons to several properties of the stimulus, including orientation, contrast and the receptive field size^9–11.

Maintaining a balance between excitation and inhibition is a dynamic process. Variations in stimulus intensity are accompanied by large changes in the amount of excitation received by cortical neurons. These changes in excitation are rapidly countered by changes in synaptic inhibition within several primary sensory areas^2,4,6. However, the mechanisms by which cortical circuits vary the strength of inhibition during ongoing changes in excitation are not well understood. Although recurrent inhibitory circuits seem to be well suited to provide this dynamic regulation^12–15, their specific contribution to the inhibition of primary sensory areas is not known. Furthermore, the relative proportion of excitation and inhibition experienced by cortical neurons in response to sensory stimuli is still debated. Although some data indicate that inhibition increases linearly with the amount of excitation received by cortical neurons^2,4,6, other results and theoretical considerations suggest that a nonlinear increase of inhibition may better account for the observed cortical responses to sensory stimuli¹⁶.

The somatosensory ‘barrel’ cortex of the rat receives sensory information from the whiskers. The number of cortical neurons excited by whisker deflection increases with the velocity of the deflection¹⁷. However, even strong stimuli trigger spikes in only a very small fraction of synaptically excited cortical neurons¹⁸. Whether this small fraction is sufficient to recruit inhibition and how inhibition increases with increasing number of activated neurons are unknown.

Here we show that even very sparse excitation triggers widespread synaptic inhibition in layer 2/3 cortical neurons by recruiting intra- and translaminar recurrent inhibitory circuits. Furthermore, this inhibition increases disproportionately with increases in excitation. A simple model based on experimentally determined parameters captures the essential properties of this behavior and illustrates the cellular mechanism affecting the scaling between excitation and inhibition in response to the spiking of a few pyramidal cells. During the revision of this manuscript, another group reported the presence of a recurrent inhibitory circuit with similar properties to the one described here in layer 5 of the somatosensory cortex⁴². Together, these findings suggest common principles of operation of elementary circuits across cortical layers.

RESULTS

Recurrent inhibition triggered by a single pyramidal cell

To determine the minimal conditions¹⁹ required to generate inhibition in the somatosensory cortex, we performed double or triple recordings from pyramidal cells in layer 2/3 of slices of rat somatosensory cortex (distance between cell bodies ≤50 μm; 194 pairs tested in 305 directions; each double recording corresponds to one pair that can be tested in maximally two directions, and each triple recording corresponds to three pairs that can be tested in maximally six directions). In 12.5% of all directions tested (38 of 305), a train of ten action potentials at 100–125 Hz triggered in an individual pyramidal cell elicited an outward current in the simultaneously recorded ‘target’ pyramidal cell (voltage clamped at −40 mV; Fig. 1a). The onset of the outward current occurred, on average, between the fourth and the fifth action potential in the train (4.9 ± 0.31, n = 38), and its peak amplitude was 15.5 ± 2.1 pA (n = 38; Fig. 1b). When the target cell was recorded in current clamp (V_m = −50.2 ± 1.0 mV, n = 9), the resulting synaptic hyperpolarization averaged 1.1 ± 0.2 mV (n = 9; Fig. 1c). The outward current was blocked by the GABA_A receptor antagonist gabazine (5 μM; n = 6) and was evoked in the presence of the GABA_B receptor antagonist CGP54626 (2 μM; n = 31). Furthermore, the outward current was abolished by the glutamate receptor antagonist NBQX (10 μM; n = 12; Fig. 1d), indicating that it resulted from synaptic recruitment of GABAergic interneurons rather than from monosynaptic GABA release between two recorded neurons. These results demonstrate that, under the present conditions, recurrent inhibitory circuits in layer 2/3 of the somatosensory cortex can be recruited by as few as four action potentials in a single pyramidal cell.

Figure 1.

Unitary recurrent inhibitory circuits. (a) The spiking (ten action potentials at 100 Hz) of a layer 2/3 pyramidal cell (black trace) evokes outward currents in a simultaneously recorded target layer 2/3 pyramidal cell (blue traces; V_H, −40 mV). The top trace is the average of 15 sweeps, 3 of which are shown superimposed in the middle. Upper left, schematic of the recording configuration. Vclamp, voltage clamp; Iclamp, current clamp. (b) Summary current, averaged over all experiments (n = 38), recorded in layer 2/3 pyramidal cells in response to a train of action potential in a neighboring pyramidal cell (the dots indicate the time of the spikes). Individual currents were normalized by their peak amplitudes. Inset, peak current for each recurrent IPSC (n = 38; open symbols) and the averaged peak of all experiments (solid symbol). (c) Same configuration illustrated in a (different pair), except that target pyramidal cell is recorded in current clamp (blue traces; V_m = −52 mV). Inset, peak hyperpolarization for nine similar experiments (open symbols) and the average of all experiments (solid symbol). (d) Same recording configuration illustrated in a (different pair). Application of the AMPA/kainate receptor antagonist NBQX (10 μM) completely abolishes the outward current. (e) Simultaneous recording from three layer 2/3 pyramidal cells. The spiking of one of the cells (black trace) evokes outward current in the two other pyramidal cells (blue and green traces; V_H, −40 mV). The top traces are the average of 23 sweeps. Lower traces show four individual sweeps recorded simultaneously in the green and blue pyramidal cells. Black–blue pair same as in d.

To determine the fraction of neighboring pyramidal cells inhibited by these unitary recurrent inhibitory circuits, we first assessed the activation of recurrent inhibitory circuits on a target pyramidal cell in response to the spiking of a neighboring pyramidal cell and then established the probability of observing inhibition on a second target pyramidal cell. For this we recorded from three pyramidal cells (either as sequential pairs or as simultaneous triples): two in the voltage-clamp configuration to monitor synaptic currents and one in current clamp to elicit action potentials. In 20.4% (21 of 103) of all recordings, inhibition could be confirmed in at least one of the two voltage-clamped target cells. If inhibition was confirmed in one of the pyramidal cells, the chance of observing inhibition in the other was 38.1% (8 of 21; Fig. 1e).

These results demonstrate that, through the activation of recurrent inhibitory circuits, a single layer 2/3 pyramidal cell of the somatosensory cortex can inhibit about 40% of its neighbors.

Direct excitatory monosynaptic connections between pairs of pyramidal cells (Supplementary Fig. 1a; input resistance 64.6 ± 4.3 MΩ, n = 82; membrane time constant 20.9 ± 0.9 ms, n = 81) occurred with a frequency of 10.5% (32 of 305 directions: 22 unidirectionally and 5 reciprocally connected pairs)^20,21. The amplitude of the unitary excitatory postsynaptic current (EPSC) (recorded in pyramidal cells voltage clamped at −40 mV) averaged 9.4 ± 2.2 pA (n = 28), and the ratio between the fourth and the first unitary EPSC evoked with presynaptic trains of action potentials at 100–125 Hz was 0.77 ± 0.1 (n = 23), indicating synaptic depression. In 7 of the 32 monosynaptic connections, a train of spikes in the presynaptic pyramidal cell also evoked an inhibitory current in the target pyramidal cell resulting in an EPSC–inhibitory postsynaptic current (IPSC) sequence (Supplementary Fig. 1b).

Supralinear increase of recurrent inhibition

To determine whether inhibition increases when more pyramidal cells are synchronously active, we next performed simultaneous triple recordings and triggered trains of action potentials in two pyramidal cells while monitoring inhibition in a third voltage-clamped target pyramidal cell.

When two pyramidal cells were activated together, the probability of triggering inhibition in a target pyramidal cell was much higher than what would be expected if the two pyramidal cells were activating independent inhibitory circuits. Whereas the probability (p) of eliciting inhibition in a target pyramidal cell with spikes triggered in a single pyramidal cell was 0.125 (that is, 12.5%, 38 of 305, see above), the probability increased to 0.477 (56 of 120) when two pyramidal cells were spiking simultaneously (Fig. 2a). This is about twice the expected probability ((1 − (1 − p)²) = 0.234) if each individual pyramidal cell recruited independent inhibitory circuits, suggesting that pyramidal cells cooperate in the recruitment of recurrent inhibition.

Figure 2.

Supralinear increase of inhibition. (a) Simultaneous recording from three layer 2/3 pyramidal cells (PC1, blue; PC2, black; PC3, green). Left, a train of action potentials in PC2 elicits no current in PC1 nor PC3 (V_H, −40 mV). Middle, a train of action potentials in PC3 elicits no current in PC1 or PC2 (V_H, −40 mV). Right, simultaneous trains of action potentials in PC2 and PC3 elicit an outward current in PC1. All current traces are averages of multiple sweeps. (b) Same recording configuration as in a (different cells). Left, the spiking of either PC2 or PC3 alone elicits outward currents in PC1. Note the earlier onset of inhibition in PC1 (blue trace) when PC2 and PC3 are spiking simultaneously (the PC2-PC1 pair is the same one as in Fig. 1a). Right top, gray trace: algebraic sum of the currents elicited in PC1 in response to the spiking of PC2 and PC3 alone. Blue trace, outward current elicited in response to the simultaneous spiking of PC2 and PC3. Right bottom, running integral of the two currents illustrated on top. Note that the inhibitory charge in response to the simultaneous spiking of PC2 and PC3 is larger than the inhibitory charge of the algebraic sum of the responses of PC1 to the spiking of PC2 and PC3 alone. All current traces are averages of multiple sweeps. (c) Cumulative distribution of the nonlinearity index (see Results for details) for 38 similar experiments. Note that most values are larger than 0, indicating supralinear increase in recurrent inhibition when PC2 and PC3 are spiking simultaneously.

We next determined whether the inhibition evoked in a target pyramidal cell (PC1) in response to the simultaneous activity of two pyramidal cells (PC2 and PC3) was merely the sum of inhibition triggered when either PC2 or PC3 were active independently or whether inhibition increased in a nonlinear manner (Fig. 2b,c). Trains of action potentials evoked simultaneously in PC2 and PC3 elicited an inhibitory current in PC1 whose integral (the inhibitory charge) was three times larger (see below) than the sum of the inhibitory charges elicited in PC1 by independently spiking PC2 and PC3. To quantify the increase of inhibition, we computed the nonlinearity index NL as (I_PC2PC3 − (I_PC2 + I_PC3))/I_PC2PC3, where I_PC2 and I_PC3 are the inhibitory charges recorded in PC1 in response to the spiking of either PC2 or PC3, respectively, and I_PC2PC3 is the inhibitory charge recorded in PC1 when PC2 and PC3 are active simultaneously. NL is 1 when supralinearity is maximal (that is, I_PC2 = 0, I_PC3 = 0 and I_PC2PC3 > 0; for example, Fig. 2a), 0 when inhibition sums linearly (that is, I_PC2 + I_PC3 = I_PC2PC3), and negative for sublinearity (that is, I_PC2+I_PC3 > I_PC2PC3). The NL averaged 0.68 ± 0.06 (n = 38; Fig. 2c; and thus I_PC2PC3 ≈ 3 × (I_PC2 + I_PC3)), indicating that there was a strong supralinear increase of inhibition when PC2 and PC3 were spiking together.

To determine whether the timing of recurrent inhibition is modulated by the number of active pyramidal cells, we compared the onset of inhibitory currents elicited by the spiking of one versus two pyramidal cells. When recurrent inhibition was generated by the spiking of two pyramidal cells, its onset occurred significantly earlier. Specifically, in response to the spiking of either PC2 or PC3, inhibition in PC1 occurred between the fourth and the fifth action potential in the train (4.6 ± 0.5, n = 27; consistent with the results described above). In contrast, the onset was moved to between the second and the third action potential in the train (2.6 ± 0.4; n = 24; P = 0.0014; Fig. 2b) when PC2 and PC3 spiked together (see Methods). These results indicate that, as the number of spiking pyramidal cells increases, both the probability and the amount of recurrent inhibition generated in layer 2/3 of the somatosensory cortex increase supralinearly; furthermore, the onset of inhibition occurs earlier.

Recurrent inhibition via somatostatin-expressing interneurons

Which type of inhibitory interneuron generates this recurrent inhibition in layer 2/3 in response to the activity of one or a few pyramidal cells? Any interneuron receiving excitatory inputs from and projecting back to layer 2/3 pyramidal cells could, in principle, participate in the observed recurrent inhibition^21–24. Through recordings from pairs of connected pyramidal cells and interneurons (Fig. 3), we subdivided the interneuron population into two broad categories: those that received unitary EPSCs that depressed in response to a train of spikes in pyramidal cells (ratio between the fifth and first EPSC = 0.17 ± 0.02, n = 32; Fig. 3a,b,e) and those that received facilitating EPSCs (ratio between fifth and first EPSC = 3.8 ± 1.3, n = 36; Fig. 3c,e)^20,21. The membrane potential of interneurons receiving depressing inputs reached maximal depolarization at the beginning of the train of spikes triggered in the pyramidal cell (by the 1.7 ± 0.29 spike in the train; n = 18; Fig. 3f) and then rapidly decayed toward rest, consistent with the dynamics of their EPSCs. This category could be further subdivided into two neuronal types based on the spiking response to depolarizing current steps: those that showed high-frequency non-adaptive spiking behavior (fast-spiking (FS) cells^25,26; Fig. 3a; input resistance 83.4 ± 6.1 MΩ, n = 29; membrane time constant 10.1 ± 1.0 ms, n = 28) and those that showed an adaptive spiking pattern (regular spiking neurons receiving depressing excitatory inputs (dRS cells); Fig. 3b; input resistance 235.7 ± 20.7 MΩ, n = 13; membrane time constant 23.2 ± 3.6 ms, n = 12). On the other hand, the membrane potential of interneurons receiving facilitating input depolarized progressively and reached its peak toward the end of the train of spikes in the pyramidal cell (by the 9.52 ± 0.17 spike in the train; n = 31; Fig. 3f). In response to depolarizing current steps, these neurons showed an adaptive spiking behavior (regular spiking neurons receiving facilitating excitatory inputs (fRS cells)²¹; Fig. 3c; input resistance 215.8 ± 14.9 MΩ, n = 27; membrane time constant 26.6 ± 2.2 ms, n = 26). Both categories of inhibitory neurons, those receiving facilitating inputs (fRS cells) and those receiving depressing excitatory inputs (FS and dRS cells), formed inhibitory synapses with layer 2/3 pyramidal cells (average unitary IPSC amplitude mediated by fRS cells onto pyramidal cells, 19.14 ± 16.4 pA, n = 31; average unitary IPSC amplitude mediated by FS and dRS cells (pooled) onto pyramidal cells, 44.4 ± 10.1 pA, n = 21), confirming their potential involvement in the observed recurrent inhibition (Fig. 3a–d) and consistent with previous observations in layer 2/3 and other cortical layers^{20,21,24,27–29}.

Figure 3.

Intra- and translaminar recurrent inhibitory circuits. (a) Reciprocal connection between a layer 2/3 pyramidal cell (black traces) and a layer 2/3 fast-spiking (FS) cell (blue traces) receiving depressing inputs. Upper, a train of action potentials in the pyramidal cell elicits depressing unitary EPSCs or EPSPs in the FS interneuron recorded in the voltage- or current-clamp mode, respectively. Inset, spiking response of the interneuron to a 2-s-long square current pulse. Lower, same pair: a train of action potentials in the interneuron elicits unitary IPSCs in the pyramidal cell (V_H, −40 mV). (b) Reciprocal connection between a layer 2/3 pyramidal cell (black traces) and a layer 2/3 regular spiking interneuron receiving depressing inputs (dRS cell; blue traces). Protocols same as in a. (c) Reciprocal connection between a layer 2/3 pyramidal cell (black traces) and a layer 2/3 interneuron (blue traces) receiving facilitating inputs (fRS cell). Protocols same as in a. Note the summation of consecutive EPSPs. (d) Reciprocal connection between a layer 2/3 pyramidal cell (black traces) and a layer 5 fRS cell (blue traces). Protocols same as in a. (e) Summary graph of unitary EPSC amplitudes normalized by the amplitude of the largest EPSC in the train and plotted against presynaptic action potential number. Closed circles, fRS cells (n = 36); open circles, FS and dRS cells (n = 21 and 13, respectively, pooled). (f) Summary graph of the time course of membrane depolarization plotted against presynaptic action potential number. The peak depolarization achieved after each action potential is normalized by the maximum depolarization achieved during the train. Closed circles, fRS cells (n = 31); open circles, FS and dRS cells (n = 12 and 6, respectively, pooled). (g) z projection of a confocal stack showing a biocytin-filled fRS interneuron (streptavidin–Alexa 488, green; left), anti-SOM immunostaining of the same field (Alexa 594, red; middle) and their superimposition (right). Scale bar, 20 μm. Pial surface is to the top.

fRS cells receiving inputs from and projecting back to layer 2/3 pyramidal cells (not necessarily the same pyramidal cell they received input from) were found in both layers 2/3 and 5 (layer 2/3 pyramidal cells to layer 2/3 fRS cells, n = 33 connections; layer 2/3 fRS cells to layer 2/3 pyramidal cells, n = 28 connections; Fig. 3c; layer 2/3 pyramidal cells to layer 5 fRS cells, n = 5 connections; layer 5 fRS cells to layer 2/3 pyramidal cells, n = 3 connections; Fig. 3d), indicating that recurrent inhibitory circuits involving this category of interneurons can cross cortical layers (Fig. 3d). In contrast, FS and dRS cells receiving input from and projecting back to layer 2/3 pyramidal cells were found exclusively in layer 2/3.

fRS cells invariably expressed somatostatin (SOM; 10 of 10 processed neurons)²¹, as shown by the colocalization of the post hoc fluorescently labeled biocytin dialyzed into the cell during the recording with the antibody labeling against SOM (Fig. 3g). Hence, we will hereafter refer to fRS cells as SOM interneurons. SOM-positive labeling was never observed in FS and dRS cells.

To determine which of the two categories of interneurons mediates the observed recurrent inhibition, we reasoned as follows: the timing of spikes elicited in the interneuron in response to a train of action potentials in a pyramidal cell must account for the time course of the inhibitory current recorded in the target pyramidal cell. The suitability of the candidate interneuron category can thus be evaluated by convolving the distribution of spike times with the average unitary IPSC generated onto pyramidal cells. This convolution should match the time course of the observed recurrent inhibition.

Through paired recordings, we determined the distribution of spike times in the two interneuron categories in response to a train of action potentials in pyramidal cells (see Methods). The convolution of the distribution of spike times triggered in SOM interneurons (Fig. 4a,b) with the unitary IPSC (10–90% rise time of 2.3 ± 0.2 ms, n = 19; decay time constant 12.12 ± 1.9 ms, n = 20) that they generate onto pyramidal cells resulted in an outward current with a time course that was markedly similar to that of the inhibition observed in pyramidal cells in response to a train of action potentials triggered in a neighboring pyramidal cell (Fig. 4c). In contrast, the distribution of spike times of interneurons receiving depressing excitatory inputs peaked much earlier (Fig. 4d), indicating that they are recruited at the onset of a train of action potentials¹². Accordingly, the convolution of this spike time distribution with the unitary IPSC that these interneurons generate on layer 2/3 pyramidal cells (10–90% rise time 1.0 ± 0.1 ms, n = 18; decay time 9.4 ± 1.3 ms, n = 14) resulted in an outward current with a much earlier onset and peak than the observed one (Fig. 4e).

Figure 4.

Spike timing of somatostatin-positive interneurons determines the time course of recurrent inhibition. (a) A train of spikes at 100 Hz in a layer 2/3 pyramidal cell (black trace) elicits action potentials in an SOM interneuron (threshold for action potential generation was achieved in some (blue races; 12 superimposed sweeps) but not all (gray traces, 14 superimposed sweeps) trials (V_m interneuron, −63 mV)). Inset, the interneuron was reciprocally connected with the pyramidal cell: spiking of the interneuron (blue trace) triggered outward currents in the pyramidal cell (black trace). (b) Summary graph of the distribution of spike times in SOM interneurons in response to trains of action potentials at 100Hz in the presynaptic pyramidal cells (n = 12). (c) The blue trace illustrates the result of the convolution of the spike time distribution (in b) with a fit to an average unitary IPSC (sum of two exponential functions; τ_rise, 1.7 ms; τ_decay, 11 ms). The convolution is superimposed onto the time course, averaged over all experiments, of the outward current elicited by the spiking of a single pyramidal cell onto a neighboring pyramidal cell (gray trace, from Fig. 1b). Note the similarity of the rising and decaying phase of the two currents. Inset: gray trace, standard IPSC; black trace, unitary IPSC from a. (d) Summary graph of the distribution of spike times in interneurons receiving depressing inputs in response to trains of action potentials at 100 Hz in the presynaptic pyramidal cells (n = 2). Inset, a train of spikes at 100 Hz in a layer 2/3 pyramidal cell (black trace) elicits action potentials in an interneuron receiving depressing inputs (blue traces; five superimposed sweeps where threshold for action potential generation was achieved (V_m interneuron, −63 mV)). (e) Convolution (blue trace) of the spike distribution (in d) with the fit of an average IPSC (sum of two exponential functions; τ_rise, 0.8 ms; τ_decay, 9.4 ms). The convolution is superimposed onto the time course, averaged over all experiments, of the outward current elicited by the spiking of a single pyramidal cell onto a neighboring pyramidal cell (gray trace, from Fig. 1b). Note the very different rising and decaying phases of the two currents. (f) Simultaneous recording from three layer 2/3 pyramidal cells (blue, PC1; black, PC2; green, PC3). A train of spikes in PC2 alone leads to inhibition with late onset in PC1 (V_H, −40 mV; black traces), similar to that illustrated in Figures 1 and 2. A train of spikes in PC3 alone leads to no inhibition in PC1 (green traces). A simultaneous train of spikes in PC2 and PC3 leads to the appearance of an early component of inhibition (open arrow) followed by the late component (black arrow) in PC1 (blue trace).

Despite the high connectivity between pyramidal cells and FS cells (that is, one of the two interneuron types receiving depressing excitatory inputs; pyramidal cell to FS cell 47.5%, 19 of 40 pairs; FS to pyramidal cell 66.7%, 26 of 39 pairs), recurrent inhibition with such an early onset and peak was never observed in response to the spiking of a single pyramidal cell (0 of 305). This suggests that the activity of a single pyramidal cell is not sufficient to recruit interneurons receiving depressing inputs. However, in response to the simultaneous spiking of two pyramidal cells, early inhibition was evoked in 1.7% of all triple recordings (2 of 120; Fig. 4f).

These data show that sparse activity in layer 2/3 results in the preferential recruitment of SOM interneurons located both in layer 2/3 and layer 5.

A tenfold increase in the recruitment of SOM interneurons

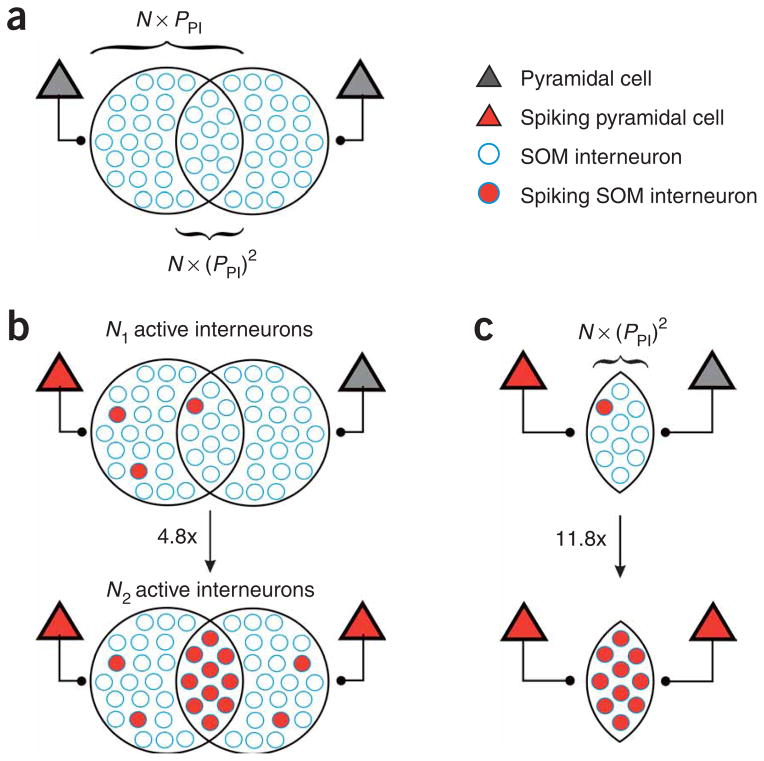
Having identified the type of interneuron that generates recurrent inhibition in response to sparse activity in layer 2/3, we can now determine the mechanism underlying the observed supralinear increase in inhibition. Toward this end, we first estimated the increase in the average number of recruited SOM interneurons when two pyramidal cells are active, as compared to one. Then we determined the increase in the probability of recruiting SOM interneurons that receive input from both active pyramidal cells (Fig. 5).

Figure 5.

Increase in the recruitment of somatostatin-expressing interneurons. (a) Schematic of the projection of two pyramidal cells onto SOM interneurons. N is the total population of SOM interneurons; P_PI is the probability of a pyramidal cell contacting a SOM interneuron; N × P_PI is the population of SOM interneurons contacted by one layer 2/3 pyramidal cell; and N × (P_PI)² is the population of interneurons targeted by both pyramidal cells. The number of interneurons assigned to each population is for illustration purpose only. (b) Top, when only one of the two pyramidal cells is spiking, the N₁ SOM interneurons are recruited (filled red circles). Bottom, when two pyramidal cells are spiking, almost five times more interneurons (N₂) are recruited. (c) Within the population of interneurons receiving convergent input from two pyramidal cells (N × (P_PI)²), the fraction that is recruited in response to the activity of two pyramidal cells (bottom) is 11.8 times larger than the one that is recruited by one pyramidal cell only (top; see Methods).

As shown above, when the number of active pyramidal cells increases from 1 to 2, the chance of a neighboring pyramidal cell being inhibited increases from 0.125 (P_inh1) to 0.477 (P_inh2). Can we use this information to deduce the increase in the average number of recruited SOM interneurons? Unfortunately, we do not know how many SOM inter-neurons participate in the inhibition of a pyramidal cell. However, in the cases where no inhibition is observed (1 − P_inh1), none of the recruited interneurons contacts the recorded pyramidal cell. Thus, given the connectivity of an SOM interneuron to a pyramidal cell (P_IP), we can determine the number of SOM interneurons recruited, N₁ and N₂, when one or two pyramidal cells are active, respectively: (1 − P_inh1) = (1 − P_IP)^N1; (1 − P_inh2) = (1 − P_IP)^N2.

By applying the experimentally determined P_IP (0.49; 19 connections out of 39 pairs; see Methods), we can solve for N₁ and N₂ (N₁ = 0.2; N₂ = 0.96; Fig. 5b). Thus, increasing the number of pyramidal cells spiking from 1 to 2 increases the average number of recruited SOM interneurons by a factor of 5 (N₂/N₁ = 4.85; Fig. 5b).

We can now estimate the increase in the probability of recruiting SOM interneurons in the subpopulation that receives convergent input from both active pyramidal cells. Because only the fraction (P_PI)2 of SOM interneurons receives convergent input from both pyramidal cells (where P_PI is the connectivity of a pyramidal cell to an SOM interneuron), only part of the fivefold increase is due to cooperative recruitment. We determined the probability P_PI that a layer 2/3 pyramidal cell excites an SOM interneuron (0.29; n = 29 pairs; see Methods). The probability of recruiting those SOM interneurons receiving convergent input from two active pyramidal cells increased 11.8 times (Fig. 5c; see Methods).

Thus, these results show that the supralinear increase in inhibition when two pyramidal cells are spiking is due to a fivefold increase in the number of recruited SOM interneurons. This increase in the number of active SOM interneurons mainly results from the fact that the recruitment of SOM interneurons contacted by two active pyramidal cells increases by an order of magnitude.

Range and sensitivity

How does the increase in inhibition progress when more than two pyramidal cells are active simultaneously? Based on the experimentally determined properties of the circuit, we first constructed a simple model that captures the observed increase in inhibition. We then used this model to predict the dynamic behavior of the circuit for a wider range of pyramidal cell activity (Fig. 6).

Figure 6.

Model describing range and sensitivity of recurrent inhibition. (a) Left, mean EPSP amplitude recorded in SOM interneurons after the tenth action potential evoked in the presynaptic pyramidal cell, plotted against the standard deviation (s.d.) of the EPSP, for each of the 31 unitary connections. Middle, distribution of EPSP amplitudes (blue bars) and alpha function (black curve) that fits the distribution. Right, cumulative distribution of EPSP amplitudes (blue line) and alpha function (black line). (b) Left, distribution of EPSP amplitudes evoked by one pyramidal cell (D₁: black line) or two pyramidal cells (D₂: gray line) in the interneuron populations contacted by one pyramidal cell or by either of two pyramidal cells, respectively. Values at zero represent the fraction of unconnected interneurons (black: 1 − P_PI, gray: 1 − (1 − P_PI)²). The threshold for action potential generation (11.3 mV above resting potential) is shown by a dashed line. Right, prediction of the fraction of recruited SOM interneurons (INs) plotted against the number of active pyramidal cells (interneuron activation curve). The blue dotted lines illustrate half activation. (c) Left: black line, D₁ (same as in b; values at zero have been cut; mean 4.6 mV, s.d. ± 2.8 mV); continuous gray line, EPSP distribution with same mean but small s.d. (mean 4.6 mV; s.d. ± 0.5 mV); dotted gray line, EPSP distribution with large mean (mean 10.3 mV, s.d. ± 0.5 mV), yet same fraction of EPSPs above threshold as D₁. Right: interneuron activation curves for the three EPSP distributions shown on the left (black trace same as in b). Note the faster saturation of the activation curve for the EPSP distribution with a large mean (dotted gray trace) and the right-shifted onset for the EPSP distribution with a small s.d. (continuous gray trace). The blue dotted lines illustrate half activation. Inset, the minimum number of pyramidal cells required to activate inhibitory circuit for experimental EPSP distribution is 1, as compared to 3 for the normal distribution of the same mean with a smaller s.d.

The model incorporates three parameters: the probability of a layer 2/3 pyramidal cell exciting an SOM interneuron (P_PI = 0.29; n = 29 pairs, see above), the distribution of the peak amplitudes of the EPSPs recorded in SOM interneurons in response to ten action potentials in a pyramidal cell (mean, 3.3 mV; median, 2.8 mV; s.d., 2.7 mV; range, from <1 mV to >10 mV; n = 31; Fig. 6), and the threshold for action potential generation in SOM interneurons³⁰. The EPSP amplitude distribution used for the model, D₁, was obtained by fitting the experimentally determined EPSP distribution with an alpha function (Fig. 6a; see Methods). Using P_PI, we then calculated the distribution of EPSP amplitudes, D₂, received by the interneuron population when two pyramidal cells are spiking. With a threshold of 11.3 mV above resting membrane potential (see Methods), D₂ leads to a fivefold increase in the fraction of interneurons that are active as compared to D₁, indicating that our model captures the specific behavior of the recurrent inhibitory circuit onto layer 2/3 pyramidal cells (Fig. 6b).

With the same parameters, we can now use the model to predict the evolution of inhibition when more than two pyramidal cells are simultaneously spiking. The activation curve (Fig. 6b) shows that the recruitment of inhibitory interneurons begins with only one active pyramidal cell and increases supralinearly when up to about four pyramidal cells are simultaneously active. Inhibition then progresses linearly over a relatively wide range, and half-maximal activation of the interneuron population occurs when nine pyramidal cells are firing (Fig. 6b).

What properties of the EPSP distribution between layer 2/3 pyramidal cells and SOM interneurons dictate this dynamic behavior? The distribution of EPSPs has a relatively small mean, yet is skewed toward larger amplitudes (see above; Fig. 6a). These few large-amplitude EPSPs provide ‘sensitivity’ to the circuit because they allow the spiking of a single pyramidal cell to excite a fraction of its target SOM interneurons above threshold for spike generation. In fact, a hypothetical EPSP distribution with the same mean but no skew yields an activation curve with an onset shifted to the right; that is, more active pyramidal cells are needed before the first interneuron is recruited (Fig. 6c, thin gray line). The relatively small mean of the EPSP distribution, on the other hand, allows the activation of SOM inter-neurons to progress over a relatively wide ‘range’ of activities in the pyramidal cell population. In fact, a hypothetical EPSP distribution in which the same fraction of EPSPs are above threshold, yet with a larger mean as compared to the experimentally observed distribution, yields an activation curve where the spiking of only five pyramidal cells is necessary to recruit half of the SOM interneuron population. Furthermore, by increasing with a steeper slope, the function reaches saturation rather quickly (Fig. 6c, thick gray line). Thus, the distribution of EPSPs onto SOM interneurons (with a small mean but skewed toward large amplitudes) provides both sensitivity and a broad dynamic range to recurrent inhibition of layer 2/3 pyramidal cells.

This model illustrates the progression in the recruitment of SOM interneurons with increasing numbers of simultaneously active pyramidal cells each firing ten action potentials. How does this progression change if pyramidal cells are firing only three action potentials (a situation that may be closer to the brief burst of spikes recorded in vivo in response to sensory stimulation^31,32)? The distribution of EPSP amplitudes recorded in SOM interneurons in response to the third action potential in the presynaptic pyramidal cell can be directly extracted from our dataset (Fig. 3f). Unsurprisingly, the recruitment of SOM interneurons in response to three action potentials requires the activity of more active pyramidal cells (half-maximal activation 14; Supplementary Fig. 2). Further, the recruitment of SOM interneurons increases with a shallower slope, thereby covering a broader range.

Hence, even during very sparse activity in layer 2/3 of the somatosensory cortex, intra- and translaminar recurrent inhibitory circuits involving SOM interneurons are recruited, resulting in widespread inhibition of pyramidal cells. Because of the large increase in the probability of spiking of SOM interneurons, recurrent inhibition increases supralinearly with increases in the number of active pyramidal cells. Our model shows that both the sensitivity of recurrent inhibition and its dynamic range result from the skewed distribution of EPSPs onto SOM interneurons.

DISCUSSION

In the cortex, changes in excitation are continuously countered by corresponding changes in inhibition^{2,4,6,8,13,33}. The cellular mechanisms underlying this balancing are poorly understood. Neither the minimal conditions required to generate inhibition nor the dynamics of the increase of inhibition are known. Here we show that sparse excitatory activity in layer 2/3 of the somatosensory cortex specifically recruits a recurrent inhibitory circuit involving SOM interneurons that are located in layers 2/3 and 5. Through this circuit a single pyramidal cell can cause inhibition of almost 40% of its neighbors. Furthermore, when two pyramidal cells are spiking simultaneously, recurrent inhibition increases disproportionately owing to the tenfold increase in the recruitment of SOM interneurons receiving convergent inputs. A simple model, based on experimentally determined parameters, illustrates how the specific distribution and connectivity of excitation onto interneurons dictates the sensitivity and the dynamic range of the circuit.

Recurrent inhibition via SOM interneurons

Different types of cortical inhibitory interneurons have been shown to receive excitation from and project back to excitatory neurons^{20–24,27,28,34–37}, indicating their potential involvement in recurrent inhibition. Our study shows, however, that among these possible circuits, one in particular involving SOM interneurons^21,26,30,38 is activated when one or a few layer 2/3 pyramidal cells are spiking. This circuit recruits SOM interneurons located in both layer 2/3 and layer 5, indicating that recurrent inhibition of layer 2/3 pyramidal cells is mediated by both intra- and translaminar circuits. Several electrophysiological and synaptic properties reported here, including the relative high input resistance, the long membrane time constant and the facilitating excitatory inputs, are consistent with previous descriptions of SOM interneurons^21,30,38, also referred to as low-threshold spiking neurons^27,28. Although SOM interneurons are not a homogeneous class, those present in layers 2/3 and 5 seem to match the morphological criteria of Martinotti cells^30,38,39. Notably, a recurrent inhibitory circuit with very similar dynamics and involving interneurons known to express SOM, the so-called oriens-lacunosum-molecolare interneurons, has been identified in the hippocampus¹².

Despite the relatively high connectivity rate between layer 2/3 pyramidal cells and other types of inhibitory neurons (for example, FS interneurons), inhibition with an early onset (such as would be expected if these types of interneurons were recruited) was evoked only by the simultaneous activity of two pyramidal cells. The reasons for the specific recruitment of recurrent inhibitory circuits involving SOM interneurons with respect to others remains to be elucidated. Several parameters, including resting membrane potential, unitary EPSP amplitude distribution, spike threshold, synaptic dynamics and probability of receiving excitatory inputs from layer 2/3 pyramidal cells, are likely to be important in determining the conditions necessary to activate each specific type of inhibitory interneuron. Irrespective of the mechanism, however, recurrent inhibitory circuits involving SOM interneurons require very little cortical activity to be recruited. Thus, the process where excitation is balanced with inhibition occurs even at the lowest activity levels, supporting the idea that in primary sensory cortices excitation and inhibition are inseparable events¹⁵.

Dynamics of recurrent inhibition in cortical layer 2/3

Not only do recurrent inhibitory circuits through SOM interneurons necessitate that little cortical activity be recruited, but their recruitment progresses supralinearly with slight increases in excitation. We show that the number of spiking interneurons increases fivefold (N₁/N₂ = 4.85) when a second pyramidal cell is engaged. Two key parameters determine the increase in the recruitment of inhibitory neurons with increasing number of active pyramidal cells: the distribution of the amplitudes of excitatory inputs onto SOM interneurons with respect to spike threshold and the convergence of pyramidal cells onto SOM interneurons. If, for example, layer 2/3 pyramidal cells evoked sufficiently large EPSPs to trigger a spike in all their target SOM interneurons, yet the probability of contacting an SOM inter-neuron were very low, the fraction of activated SOM interneurons would grow almost linearly with the number of active pyramidal cells. In contrast, if the probability of contacting SOM interneuron were high, the fraction of activated SOM interneurons would reach its maximum very quickly.

Our study shows that, in contrast to the above example, the distribution of unitary EPSPs onto SOM interneurons is skewed toward small values, such that only a fraction of interneurons receiving inputs from any given pyramidal cell will reach threshold for spike generation. However, because of the relatively large convergence of pyramidal cells onto SOM interneurons (~0.3), about 10% (0.3²) of the interneuron population will receive convergent inputs from any two active pyramidal cells. The recruitment of SOM interneurons increases by ten times for that population receiving convergent inputs from two active pyramidal cells. Thus, the supralinear increase in inhibition can be accounted for by the tenfold increase in the recruitment of 10% of the SOM interneuron population.

The absolute synchrony in the activation of pyramidal cells used here may facilitate the recruitment of SOM interneurons, yet is unlikely to be strictly necessary. On one hand, the simultaneous arrival of EPSPs will lead to a rapid change in the membrane potential, thereby increasing the chances of triggering a spike⁴⁰ in the SOM interneuron. On the other hand, the slow membrane time constant of SOM interneurons (26 ms) gives them a broad integration time window, as illustrated by the sustained postsynaptic depolarization experienced by these neurons during the 10-ms interval in between presynaptic action potentials (see Fig. 3b,c). Thus, an increase in the recruitment of SOM interneurons will probably occur as long as pyramidal cells are concurrently active within a time window comparable to the membrane time constant of SOM interneurons.

The dynamics of the increase in inhibition, however, are likely to be very sensitive to the specific conditions of the tissue. Factors such as temperature, extracellular ionic composition (which only approximated physiological conditions in our experiments) and the possible presence of neuromodulators (which may depend on the behavioral state of the animal) will certainly influence the excitability of SOM interneurons, as well as the properties of their excitatory inputs. Thus, it is likely that the conditions necessary to recruit SOM interneurons in vivo may change depending on the state of the cortex.

In the present study, recurrent inhibition is evoked through trains of ten action potentials at 100–125 Hz in pyramidal cells, a protocol that allows one to follow the time course of the inhibitory current over a prolonged period and, through convolution, to identify the underlying interneuron type. Recurrent inhibition, however, can be observed already by the second to fourth action potential depending on the number of pyramidal cells spiking simultaneously, a situation that more closely resembles the brief bursts of spikes recorded in vivo in response to sensory stimulation^31,32. In the somatosensory cortex, the fraction of neurons responding to whisker stimulation can vary over a wide range depending on the velocity of the stimulus¹⁷. Our data suggest that recurrent inhibitory circuits involving SOM inter-neurons not only are likely to be recruited by stimuli with the lowest deflection velocity, but also may be highly sensitive to changes in stimulus velocity.

By using a simple model that incorporates experimentally determined connectivity parameters, we can, at least qualitatively, predict the behavior of recurrent inhibition when many pyramidal cells are active. Our model shows that, after an early supralinear recruitment of interneurons, increases in inhibition become proportional to those of excitation over a relatively wide range. For a given connectivity between layer 2/3 pyramidal cells and SOM interneurons, both the early recruitment and the wide linear range of increase depend on the shape of the EPSP distribution. The few large-amplitude EPSPs ensure that even the activity of a single pyramidal cell will activate a fraction of the interneuron population, thus providing sensitivity to the circuit. Because of the skew of the distribution, large-amplitude EPSPs are likely to be under-sampled in our database, and hence the distribution used in our model is only an approximation of the real distribution. Furthermore, because of the cutting of axonal and dendritic processes during the slicing procedure, both the connectivity between neurons and the size of unitary EPSPs are probably underestimated. However, this underestimation is unlikely to qualitatively affect our conclusions, as larger amplitudes would further enhance the capacity of individual pyramidal cells to recruit SOM interneurons.

The small mean of the EPSP distribution ensures that during stronger cortical activity, recruitment of interneurons proceeds almost linearly over a wide range before reaching saturation. Notably, during relatively high levels of excitation, linear changes in cortical inhibition have been observed both in vitro¹³ and in vivo^2,6,33, suggesting that the distributions of EPSP amplitudes and the specific connectivity of the circuit may have a crucial role in correctly balancing excitation with inhibition in the cortex.

Besides activating only a small fraction of neurons in the somatosensory cortex¹⁸, whisker deflections often evoke bursts of action potentials in layer 2/3 pyramidal cells^31,32. Our data show that high-frequency trains of action potentials in one or a few layer 2/3 pyramidal cells are ideally suited to recruit SOM interneurons. This suggests that in response to tactile stimuli, recurrent inhibitory circuits involving SOM interneurons may be specifically engaged in the balancing of cortical excitation, thereby contributing to the processing of sensory information.

METHODS

All experiments were carried out in accordance with the animal care and handling guidelines set forth by the University of California.

Slice preparation and recordings

Parasagittal slices of primary somatosensory cortex (300–400 μm) were prepared from Wistar rats 23 ± 5 (mean ± s.d.; n = 67) days of age. Animals were anesthetized in isoflurane or a mixture of ketamine and xylazine (4/1). Slices were cut with a Vibratome (DSK) in a chilled solution containing (in mM): 85 NaCl, 2.5 KCl, 1.25 NaH₂PO₄, 0.5 CaCl₂, 4 MgCl₂, 25 NaHCO₃, 75 sucrose, 25 glucose and 0.5 ascorbic acid (95% O₂, 5% CO₂) and incubated for 30 min at 34 °C in artificial cerebrospinal solution containing (in mM): 122 NaCl, 2.5 KCl, 1.25 NaH₂PO₄, 2 CaCl₂, 1 MgCl₂, 26 NaHCO₃, 25 glucose and 3 sodium pyruvate. Slices were stored in an interface chamber at room temperature until being placed in a submerged chamber for recordings at 32–34 °C.

Pyramidal cells in cortical layer 2/3 and interneurons in layers 2/3 and 5 were visually identified by infrared differential interference contrast videomicroscopy. Whole-cell patch-clamp recordings were performed using Multiclamp 700B and Axopatch 200A amplifiers (Axon Instruments) and digitized at 20 kHz. For recordings in pyramidal cells, pipettes (2–4 MΩ) were filled with either (in mM) 122 potassium gluconate, 1 MgCl₂, 10 L-glutamic acid, 10 HEPES, 4 magnesium ATP, 0.3 sodium GTP, 10 sodium phosphocreatine and 5.5 biocytin (pH 7.25, 290 mOsm)⁴¹ or 150 potassium gluconate, 1.5 MgCl₂, 5 HEPES, 1.1 EGTA, and 10 phosphocreatine (pH 7.25; 280–290 mOsm). For recordings in interneurons, internal solutions contained (in mM) 134 potassium gluconate, 1.5 MgCl₂, 10 HEPES, 0.1 EGTA, 3 magnesium ATP, 10 sodium phosphocreatine and 5.5 biocytin (pH 7.25, 290 mOsm). Trains of action potentials were elicited by somatic current injection (2 ms, 0.8–4 nA). Voltage measurements were not corrected for the experimentally determined liquid junction potential of 13 ± 0.4 mV (n = 3). The drugs used were NBQX, gabazine (SR95531) and CGP54626 (all from Tocris Bioscience).

Data analysis

Amplitudes of recurrent IPSCs and inhibitory postsynaptic potentials were measured relative to baseline, over a window of 4–6-ms duration, 4 ms after the action potential, on averages of 6–100 sweeps. To determine the onset of recurrent IPSCs, a threshold criterion of 2 × s.d. of the noise was applied to the averaged traces. To determine the shift in the onset of the recurrent IPSC when two pyramidal cells are spiking simultaneously, we compared the onset of the current recorded in PC1 when either PC2 or PC3 were spiking alone with the onset of the current recorded in PC1 when PC2 and PC3 were spiking simultaneously. Thus, this analysis does not include the set of triple recordings, in which neither the individual activity of PC2 nor of PC3 evoked a detectable inhibition of PC1.

Input resistance was measured in response to a 2-s step current injection of −10 to −50 pA. Membrane time constants were measured by fitting a single exponential to the late portion of the membrane potential relaxation from a step current injection of −10 to −50 pA. Amplitudes of monosynaptic EPSCs and IPSCs in pyramidal cell–interneuron pairs were measured over a window of 0.5–2 ms around the peak of the averages of 5–50 sweeps. If the decay of the averaged response to the previous action potential in a train did not return to baseline, the decay of the previous signal was fitted with a single exponential and the baseline extrapolated.

Average values in the text and figures are expressed as mean ± s.e.m. unless stated otherwise. The Student’s t-test was used for statistical comparisons. All traces are the average of more than ten sweeps, unless stated otherwise.

Immunohistochemistry and imaging

After recordings, slices were fixed overnight in sodium phosphate buffer (PB; 0.1 M, pH 7.4) containing 4% paraformaldehyde. After rinsing (all rinses were performed in PB), slices were incubated overnight in a solution containing 30% sucrose for cryoprotection. Slices were then frozen in 2-methylbutane on dry ice and stored at −20 °C. For biocytin-SOM immunohistochemistry, slices were rinsed and transferred in a PB solution (all solutions were made in PB) containing 3% H₂O₂ and 10% methanol for 15 min. After rinsing, slices were incubated for 3 h in 3% Triton X-100 and 10% normal donkey serum (NDS). Subsequently, slices were incubated for 30–35 h at 4 °C in the primary polyclonal antibody to SOM (rabbit anti–somatostatin-14 IgG, Peninsula no. T-4102, 1:1,000; with reactivity to somatostain-14 and -25) 3% Triton X-100 and 10% NDS. After rinsing, the secondary antibody solution was applied for 20–24 h at 4 °C. The solution contained a secondary donkey anti-rabbit-IgG–Alexa 594 antibody (1:500; Molecular Probes no. A21203) as well as streptavidin–Alexa-488 (to label biocytin; 1:1,000; Molecular Probes no. S11223) in 0.3% Triton X-100 and 2% NDS. After rinsing, slices were mounted on slides and embedded in GelMount (Biomeda). Control experiments in which either the primary or the secondary antibodies were omitted resulted in no labeling. In addition, incubating the slices in a mixture of SOM primary antibody together with an excess of the corresponding exogenous antigen (somatostatin-14 peptide; Peninsula no. H1490) resulted in no labeling. Staining was analyzed with confocal microscopy (Leica TCS NT) in sequential mode to exclude channel crosstalk. Single optical sections along the z plane were imaged in 0.8–1.0-μm increments. Images were contrast adjusted and maximum-intensity z projections were created using Adobe Photoshop (Adobe Systems) or ImageJ (NIH) software.

Spike distribution and convolution

Current injection was used to set the membrane potential such that the postsynaptic interneuron would reach threshold for spike generation in ~50% of all trials. Thus, depending on the size of the unitary EPSP and on the membrane potential of the interneuron, positive or negative current injections were used.

Interneuron action potential times were binned at 0.1 ms and normalized to create the probability distribution. Unitary IPSCs were described by the difference of two exponentials: f(t) = (exp(t/−τ_rise) − exp(t/−τ_decay).

For the unitary IPSC evoked by interneurons receiving depressing excitatory inputs, τ_rise = 0.8 ms and τ_decay = 9.4 ms. For the unitary IPSC evoked by interneurons receiving facilitating excitatory inputs, τ_rise = 1.7 ms and τ_decay = 11 ms. Using MATLAB, the probability distribution was convolved with f(t). Because fewer than 95% of the trials evoked more than one action potential in the postsynaptic interneuron, we only convolved the distribution of the first spike and, accordingly, did not consider any short-term plastic change of the unitary IPSC.

Connectivity

To determine P_PI, we first identified the recorded interneuron through the characteristic facilitating excitation it receives from a simultaneously recorded presynaptic pyramidal cell. Then, while keeping the identified interneuron, we recorded sequentially from additional pyramidal cells. Notably, P_PI was computed exclusively using the additional pairs—that is, it did not include the initial pair used to identify the interneuron.

To determine P_IP, we first identified the recorded interneuron through the characteristic facilitating excitation it receives from a simultaneously recorded presynaptic pyramidal cell and then, while keeping the identified interneuron, recorded sequentially from additional pyramidal cells. P_IP also included pairs used to identify the interneuron when they were reciprocally connected.

Quantifying the recruitment of SOM interneurons

We determined experimentally that when the number of active pyramidal cells increases from 1 to 2, the probability that a neighboring pyramidal cell is inhibited increases from 0.125 to 0.477. By assuming that SOM interneurons contact pyramidal cells statistically independently, we calculated that this increase in probability occurs because of a fivefold increase (N₂/N₁ = 4.85) in the number of SOM interneurons recruited. How much of this increase is contributed by cooperativity? To answer this question we determined the increase in probability of recruiting SOM interneurons receiving convergent excitation from two active pyramidal cells as compared to the probability of recruiting SOM interneurons receiving excitation from only one pyramidal cell as follows: assuming that pyramidal cells contact SOM interneurons statistically independently, we compute N₁ and N₂, the number of recruited SOM interneurons when one or two pyramidal cells are active, respectively, as

$$\begin{array}{c}{N}_1=F_1{P}_{\text{PI}}N\\ N_2[2F_1(P_{\text{PI}}-{(P_{\text{PI}})}^2)+F_{1\&2}{(P_{\text{PI}})}^2]N\end{array}$$

where F₁ is the probability of SOM interneurons being recruited in the subpopulation contacted by only one of the two pyramidal cells, and F_1&2 is the probability of SOM interneurons being recruited in the subpopulation contacted by both pyramidal cells. P_PI is the probability that a pyramidal cell contacts a SOM interneuron (that is, connectivity) and is experimentally determined. N is the total number of SOM interneurons in the local circuit. Solving for F_1&2/F₁ using N₂/N₁ (see above), we find that F_1&2/F₁ = 11.83.

The probability F_1&2 consists of SOM interneurons that are contacted by both pyramidal cells but may be recruited by the independent activity of either pyramidal cell or the cooperative activity of both pyramidal cells; thus we subtract the fraction that is due to independent pyramidal cell activity ((F_1&2 − (2F₁ − (F₁)²)/F₁). The probability of recruiting SOM interneurons through the cooperative activity of two pyramidal cells is approximately 9.8 times larger than if they were recruited by one pyramidal cell. This result is an underestimate because we approximated that the term (F₁)², which represents the probability of SOM interneurons recruited by both pyramidal cells independently, to be zero. Because 0 < F₁ ≤1, this underestimate is small.

Note that F₁ and F_1&2 are the probabilities that an SOM interneuron is recruited at least once, given n trials. These probabilities are distinct from the fraction of trials in which the spiking of a pyramidal cell recruits an SOM interneuron.

Model

We experimentally quantified the probability that pyramidal cells recruit inhibition onto neighboring ‘target’ pyramidal cells (see Results). This probability is a measure of the capacity of a pyramidal cell, given n trials, to at least once recruit at least one inhibitory circuit that impinges onto the target pyramidal cell. Note that this probability is distinct from the fraction of trials in which the spiking of a pyramidal cell evokes inhibition on a given target pyramidal cell.

Accordingly, the probability of recruiting an interneuron determined in the study is a measure of the capacity of a pyramidal cell, given n trials, to recruit an interneuron at least once, and not the fraction of trials in which the spiking of the pyramidal cell recruits a given interneuron.

Consequently, the activation curves (Fig. 6) describe the maximal (not the average) fraction of interneurons that could be activated at any individual trial by the simultaneous spiking of n pyramidal cells.

We sought to design a simple model constrained by experimentally determined parameters (EPSP distribution and anatomical connectivity) for the purpose of (i) determining whether the experimentally observed increase in the probability of recruiting the SOM interneuron circuit can be explained based only on these parameters, and (ii) providing qualitative insight into how connectivity, EPSP distribution and the number of active pyramidal cells affect the fraction of interneurons recruited.

Our model predicts the fraction of interneurons activated as a function of the number of spiking pyramidal cells. We created a distribution of EPSP amplitudes from paired recordings between connected pyramidal cells and SOM interneurons. The EPSP amplitude and standard deviation (s.d.) was measured after the third or tenth action potential. We then fit an alpha function (B = xe^−ax, a = 0.58) to this distribution of mean EPSP amplitudes (similar results were obtained using a Gaussian smoothed EPSP distribution). A fraction of these EPSP amplitudes are above threshold (as the activity of a single pyramidal cell is sufficient to recruit recurrent inhibition). This fraction is equal to the fraction of active interneurons. However, the distribution of average EPSP amplitudes does not take into account the trial-to-trial variability inherent in synaptic transmission. Namely, some EPSPs may fluctuate such that in only a minority of trials they are suprathreshold while their average remains subthreshold. To ensure that the model design accounted for a pyramidal cell’s capacity for recruiting inhibition (rather then just the average behavior), the average EPSP s.d. (s.d. = 1.2 mV) was added to the distribution of EPSP amplitudes. Based on this shifted distribution, we obtained the maximum fraction of interneurons above threshold for any individual trial. To create D₁ (see Fig. 6b), the connectivity between pyramidal cells and interneurons was introduced into the distribution by adding zeros to B (that is, if P_PI = 0.29, then 0.71 of D₁ must be zeros). Finally, the distribution of EPSP amplitudes when two pyramidal cells are spiking (D₂) was generated from the linear sum of two EPSPs picked randomly out of D₁ (see gray trace in Fig. 6b, left). We used the same method to generate D₃–D_N.

On the basis of our experiments, we deduced that two pyramidal cells have the capacity to recruit five times as many interneurons as one pyramidal cell can. These data can be used to determine the threshold (T) for interneuron activity in our model. The ratio of the integral of D₂ > T to D₁ > T (that is, ${\sum }_T^{\infty }{D}_2/{\sum }_T^{\infty }{D}_1$) should equal 4.85. A threshold, T, of 11.3 mV above resting membrane potential is consistent with this fivefold increase (Fig. 6b, left). This T is consistent with the range of experimentally measured thresholds for SOM interneurons³⁰. We then used this threshold, together with D₁–D_N, to predict the fraction of interneurons recruited when more than two pyramidal cells are active (Fig. 6b,c). Clearly, as more pyramidal cells simultaneously excite interneurons, reductions in driving force and membrane resistance will result in sublinear summation of EPSPs. So our model will underestimate the number of active pyramidal cells required to fully activate the interneuron population.