Spatial Modeling of Cell Signaling Networks

Abstract

The shape of a cell, the sizes of subcellular compartments and the spatial distribution of molecules within the cytoplasm can all control how molecules interact to produce a cellular behavior. This chapter describes how these spatial features can be included in mechanistic mathematical models of cell signaling. The Virtual Cell computational modeling and simulation software is used to illustrate the considerations required to build a spatial model. An explanation of how to appropriately choose between physical formulations that implicitly or explicitly account for cell geometry and between deterministic vs, stochastic formulations for molecular dynamics is provided, along with a discussion of their respective strengths and weaknesses. As a first step toward constructing a spatial model, the geometry needs to be specified and associated with the molecules, reactions and membrane flux processes of the network. Initial conditions, diffusion coefficients, velocities and boundary conditions complete the specifications required to define the mathematics of the model. The numerical methods used to solve reaction-diffusion problems both deterministically and stochastically are then described and some guidance is provided in how to set up and run simulations. A study of cAMP signaling in neurons ends the chapter, providing an example of the insights that can be gained in interpreting experimental results through the application of spatial modeling.

I. Introduction

The cell is distinctly non-homogeneous and the spatial distribution of molecules can be of critical importance to cellular pathways. Signaling events initiated within the two dimensional plane of the membrane move through the three dimensional volume of the cytosol and propagate through multiple intracellular compartments. Spatial segregation of interacting molecules, whether by localization to different cellular compartments or by associations with supramolecular complexes, is a common mechanism of regulating pathway activity. Mathematical modeling and simulation in these situations requires spatial simulation methods that incorporate actual cell geometry, compute local concentrations and account for changes that arise from transport processes (diffusion and active processes).

Spatial modeling of signaling pathways has already begun to provide unique insights into how cellular geometry intersects with the kinetic behavior of signaling components to create spatially encoded information in the cell. We are now beginning to understand at a quantitative level not only how surface to volume effects impact signaling pathways that arise on a membrane (e.g. (Fink et al., 2000), but also how geometry effects are transmitted to downstream components. Spatial modeling studies have demonstrated that the creation of signaling molecules at the membrane and their destruction or inhibition throughout the cytosol can create gradients that vary as the local geometry of the cell changes (Kholodenko et al., 2010). Local gradients likewise can have significant downstream effects. For example, regulation of calcium levels during repetitive firing of synapses is highly dependent on the specialized geometry of the neuronal spine, leading to new hypotheses for coincidence detection localized to individual synapses, a key aspect of learning and memory (Brown et al., 2008; Hernjak et al., 2005). Also in neuronal cells, experiments coupled to spatial simulations demonstrated that while microdomains of elevated cAMP arise from the localization of receptors and adenyl cyclase to the membrane, the kinetics of negative regulators localized to the cytosol creates spatially distinct regions of activity of downstream targets such as PKA and MAPK (Neves et al., 2008).

Events at the plasma membrane that dictate polarized cellular responses, such as chemotaxis and cell migration as well as yeast budding and cell division, are among the more obvious cases where spatial modeling can lead to new insights into how signaling pathways evoke spatially discrete responses in the cell. Already modeling efforts have led to a number of new hypotheses in these fields. Some examples include the local excitation, global inhibition (LEGI) model to explain how cells respond to shallow gradients of chemoattractants (Ma et al., 2004), a hypothesis that Turing-type activator-inhibitor dynamics involving the small Rho GTPase Cdc42 can explain the selection of only a single budding site in yeast (Goryachev and Pokhilko, 2008), and a proposed mechanism by which spatial gradients of two regulatory molecules evaluates cell size in yeast mitotic checkpoints (Vilela et al., 2010).

In addition to testing and developing new hypotheses, spatial modeling also provides an exceptional tool for analyzing and interpreting the ever expanding arsenal of fluorescence-based microscope imaging methods. Spatial simulations help one to extract quantitative information about the dynamic behavior of molecules and the detailed kinetics of molecular interactions and enzymatic events within the exact geometry of experimental cells. This allows direct comparison of simulation results of different models and parameters with experimental image time series. Most current methods for quantitative analysis of dynamic fluorescence imaging experiments rely on analytic solutions that assume simple analytic geometries for the cell. The ability of numerical simulation approaches to account for exact morphologies of real cells dramatically broadens the range of these experimental techniques. Simulation based approaches have been used to analyze many different types of experiments including uncaging experiments (Roy et al., 2001) and fluorescence photobleaching or photoactivation experiments (Holt et al., 2004; Kapustina et al., 2010; Moissoglu et al., 2006; Shen et al., 2008). Indeed, any experimental data based on changes in fluorescence distributions over time and space can be amenable to analysis by spatial simulation methods. Particularly exciting is the promise of spatial simulation based analysis to extract high temporal and spatial resolution information on pathway dynamics from the array of new fluorescence biosensors for kinase and phosphatase activities (Saucerman et al., 2006; Zhong et al., 2009).

This chapter provides a discussion of the problems that spatial modeling can effectively address in cell signaling, and different overall strategies for developing models of cellular pathways. Using our web-based Virtual Cell (VCell) modeling environment to illustrate the process (http://vcell.org), we discuss some of the important issues that need to be addressed in order to build a useful spatial model and how to negotiate the important choices and parameters involved in running numerical simulations of the models. This is followed by working through a specific example of a VCell spatial model and exploring how the model can be used to simulate specific experimental or conceptual conditions to generate predictions of the model (i.e. simulation data) that can be tested experimentally.

II. Overview of spatial modeling

A spatial model is a mathematical system that accounts for processes such as reactions kinetics, diffusion, advection and membrane transport. A pair of equations serves to summarize the physical chemistry of cell signaling systems with explicit consideration of the voyage of a molecule from one region of the cell to another:

$$\frac{\partial C_i}{\partial t}=-\text{div}{\mathit{F}}_i+R_i\left(C_j,C_k,\dots ,\mathrm{\Phi }\right)$$ (1)

$${\overrightarrow{\text{F}}}_i=-D_i\nabla C_i-C_i{\overrightarrow{\text{V}}}_i-z_i{\mu }_i{C}_i\nabla \mathrm{\Phi }$$ (2)

The first equation describes the change in concentration, C_i, of a molecular species, i as a function of time at some point within the cell. It is a partial derivative of C_i with respect to time; C_i can also vary over spatial coordinates, x,y,z. On the right hand side of eq. (1), R_i is the rate expression for the formation or destruction of species i; it can be a function of the concentration of any of the other molecular species in the system, as well as the electrical potential across the membrane, Φ, for a voltage-sensitive membrane bound species. The first term on the right side is the divergence of the flux of i, F_i, which is further described in the second equation. Eq. (2) is the Nernst-Planck flux equation with an added advection term, showing the factors that govern the net flow of molecules: the gradient of concentration times the diffusion coefficient, D_i; the velocity field, V→_i (possibly driven by molecular motors); and an electrical term, where z_i is the charge, μ_i is the electrical mobility and ∇Φ is the voltage gradient (i.e. the electric field; the electrical term is unimportant within the cytosol, but can, of course, control ionic transport across membranes). The geometry specification for the model should include all the morphological features of the cell that might influence the molecular processes; it should also account for the heterogeneous distribution of the molecules within this geometry. The resulting set of partial differential equations (PDEs) for all the molecular species represent a continuous deterministic mathematical description of the system and also serve to summarize all the biophysical mechanisms hypothesized to govern the biological process under study (Slepchenko et al., 2003). However, when the number of molecules involved in the process is small (<100), a deterministic mathematical description may prove to be inaccurate because it fails to account for the probabilistic nature of the reactions of single molecular species and of the Brownian dynamics of single molecules that underlie diffusion. In such a case, a stochastic mathematical formulation needs to be employed.

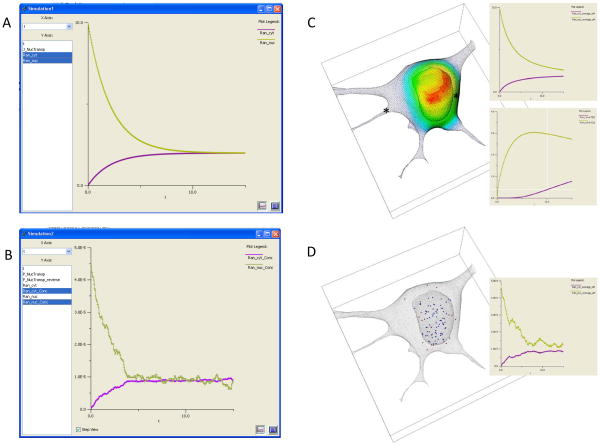
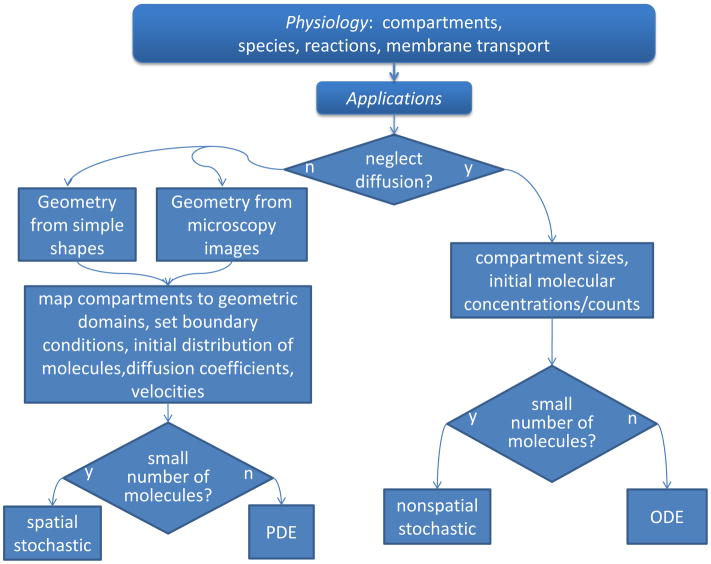
But it is important to ask how much detail is actually required to address a specific cell biological problem. Clearly, the more detail, the more likely that the investigator will not overlook a key contribution to the biology. However, the more detail, the greater the computer power and the longer the computation time required for the numerical methods to compute a simulation. Furthermore, the simpler the model, the easier it is to analyze and understand the simulation results; that is, when simulations from simple models fail to reproduce an experimental result, it is easier to uncover what may be missing or incorrect in the model. Arguably, this process of interacting with experiment is the most important reason for building a model and running simulations. We will therefore discuss varying choices for posing a model mathematically, in order of increasing computational intensity, describing the limitations of each. These can all be modeled and simulated with the Virtual Cell software system, as illustrated in Figure 1, which shows simulation results for the passive flux of a molecule through the nuclear membrane from 4 different mathematical models.

Figure 1.

At the simplest level, if all diffusive and advective processes are fast compared to any of the reaction rates in the system, the flux term in equation (1) can be ignored; that is, the cell is behaving like a well-mixed reaction vessel. Instead of PDEs, this would result in a set of ordinary differential equations (ODEs) describing all the changes in species concentrations as a result of reactions or membrane transport processes. By definition, an ODE model is classified as a non-spatial model because it cannot simulate spatial gradients within volumes or surfaces. However, the geometry can still be represented in ODE models by accounting for the sizes of compartments and membranes; indeed, the surface areas of membranes and the volumes of compartments can influence the dynamics of the molecular components of the system. For example, consider a molecular flux of a molecule from a small compartment into a larger compartment, e.g. from the nucleus to the cytosol. Because of the difference in volume, a flux through the nuclear membrane will produce a larger change in concentration within the nucleus than in the cytosol; these changes can be represented in the math as simple rate expressions for the species in each compartment, scaled by their relative volumes. A screenshot of the VCell simulation results for this compartmental ODE model are shown in Figure 1A, where the nuclear concentration of our molecule (green curve), set initially to 10μM, decays much more than the cytosolic concentration (violet curve) increases. This is because the volume of the cytosolic compartment is about 5 times larger than the volume of the nucleus. The two curves reach equilibrium at the same concentrations after about 10s. These simulations were carried out with the “Combined Stiff Solver”, one of 8 numerical solvers for ODEs available in VCell.

The same compartmental model can also be solved stochastically, as illustrated in Figure 1B. The results for this single trajectory for 100 molecules initially in the nucleus, are qualitatively similar to the deterministic results in Figure 1A. To be able to make this comparison, the stochastic results are plotted in terms of concentrations rather than number of molecules, where an initial concentration in the nucleus of 45 pM corresponds to 100 molecules. Notice that at the steady state there are still fluctuations of concentration and these fluctuations are greater for the nuclear species than for the cytosolic species; this is because the nucleus contains a smaller number of molecules, so fluctuations are more significant. This simulation used the Gibson-Bruck variation (Gibson and Bruck, 2000b) of the Gillespie next reaction step algorithm (Gillespie, 1977; Gillespie, 2001) to calculate the trajectory; this is one of 4 stochastic solvers available in VCell. VCell also provides a utility for running multiple stochastic trajectories and generating a histogram for the final time point to evaluate the distribution of the species numbers. Stochastic simulations can capture behaviors due to the intrinsic fluctuations of molecular processes, but they are more computationally intensive than ODE simulations. For large numbers of molecules, such simulations become both impractical, because of the long computing times, and unnecessary, because fluctuations are relatively insignificant.

Diffusion is important in a cell biological process when it is slower than the reaction rates producing or consuming the diffusing species. This produces spatial gradients in concentration. A number of examples were given in the introduction and a specific example will be analyzed in detail in the final section of this chapter. Here, in Figure 1C, we explore how our simple model of nucleocytoplasmic transport behaves in a real 3D cell geometry. We used a cell geometry based on a 3D confocal microscope image that had the same nucleus and cytoplasm volumes as the compartmental model used for the simulations of Figure 1A and 1B (actually, VCell derived the size parameters in the compartmental model from the real geometry). Figure 1C shows a volume rendering of the distribution of the concentration at the 1s time point with the standard rainbow color scheme corresponding to the full range of concentration (red~9μM; blue~1μM). As can be seen in this simulation, which used a diffusion coefficient of 10μm²/s (typical for a protein in cytoplasm), the distribution of the species is far from the uniform distribution that is assumed in a compartmental model. Furthermore, the overall kinetics are strongly affected, as demonstrated by the time plots shown in the inset for the same 15s duration used in Figure 1A. The upper inset shows the concentration of the nuclear and cytosolic species not reaching steady state even after 15s (compare Figure 1A); this is because the slow diffusion prevents the molecule from instantly equilibrating within each compartment. The lower inset shows time plots at the 2 spatial points indicated by the asterisks in the cell image; the cytoplasmic concentration for the point (green curve) where the nucleus is close to the outer membrane actually overshoots the steady state value because of the restricted diffusion in this crowded region of the cell. The other point, at the mouth of a process at the left side of the cell, shows (violet curve) a several second lag period in the appearance of our molecule – again a behavior that cannot be captured in a compartmental model. Clearly spatial models provide details that may be missed in a compartmental model. But not always: if the diffusion coefficient in our model was an order of magnitude greater (as for a metabolite or a nucleotide), the results of the spatial model would be virtually identical to those of the compartmental ODE model. Of course the disadvantage of a spatial simulation is that it is computationally intensive; the model in Figure 1C, with 367,000 grid points, took about 100s to simulate on a single processor compared to essentially instantaneous for the ODE model of 1A. We used the fully implicit adaptive time step finite volume solver in VCell to run this simulation; it is fully described in Section IV. on spatial simulation methods, below.

The most detailed (and computationally intensive) mathematical model to simulate for cell biology is a spatial stochastic model. The results of a spatial stochastic simulation for 100 molecules are shown in Figure 1D. These simulations are performed with the Smoldyn algorithm developed by Steven Andrews (Andrews et al., 2010b). This model accounts for both probabilistic reactions of individual molecular species and Brownian dynamics of the motion of individual molecules in solution. The image in Figure 1D is taken at the 1s time point and therefore can be directly compared to 1C. The blue molecules are in the nucleus and the red molecules are in the cytosol (some of the red molecules appear to be in the nuclear region but they are actually above or below the nucleus in this 3D rendering). The inset shows the time course of change in concentration for the entire nucleus and cytosol – a noisy version of the upper inset in Figure 1C. The computing time for the Smoldyn algorithm was about 600s (compared to 100s for the PDE simulation of Figure 1C). However, there is siginificant overhead for special geometry handling required by Smoldyn for non-analytic geometries such as the one we used (as opposed to analytical geometries such as a sphere or cylinder); such image-based geometries could add hours to the computation time. But even without the geometry issue, spatial stochastic simulations are the most computationally expensive; furthermore, multiple simulations will often be required to develop statistics for the overall behavior of the system. Alternative algorithms and software packages for spatial stochastic simulations are described in Section IV.

III. Building a Spatial Model

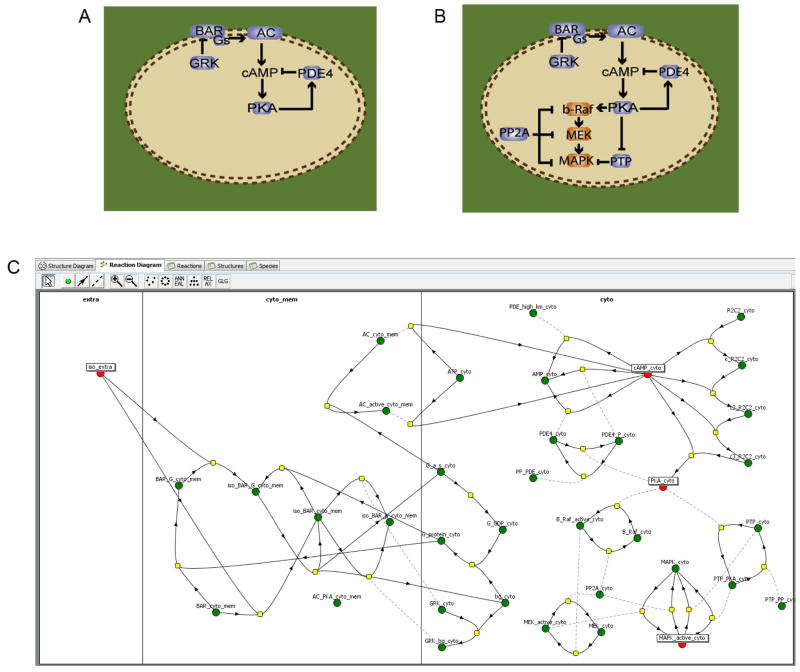
In the Virtual Cell, a biological model is described in a layered branched fashion within the graphical user interface know as the “BioModel Workspace”. The trunk is the “Physiology”, describing the underlying network of quantitative reaction and transport mechanisms that are associated with volumetric and membrane cellular compartments (Figure 2). These mechanisms makes no explicit reference to spatial coordinates, but rather describes the local time rate of change of concentration for reaction rates and the local molecular flux density for membrane transport mechanisms (flux reactions) in terms of the local environment. The Physiology in Figure 2C consists of 2 compartments, “extra” and “cyto” separated by a membrane, “cyto_mem”. The small circles represent species, 4 of which are highlighted; note how many species are required to fully represent all the states and interactions represented by the cartoon diagram of (B). The yellow squares each contain a rate expression for the quantitative mechanism of the reaction specified by the connecting lines. This Physiology is taken from a public model found in the VCell database as ‘susana:neves_cell_2008’; it contains the model and simulations published by Neves et al. (2008), which is discussed in Section E of this chapter. This type of description is very flexible, allowing a single Physiology to simultaneously form the basis of multiple spatial, non-spatial, deterministic and stochastic computational experiments (Applications), such as the four mathematical models already discussed in Section II. (Figure 1). An Application together with its parent Physiology is sufficient to completely define the mathematical system. The remainder of this section will discuss the geometry definition and other specifications required to define an Application in VCell.

Figure 2.

The cellular distributions of organelles, fixed structures and free and bound molecules are far from homogeneous. To begin, consider those cellular compartments which are encapsulated by membranes, and are thus capable of maintaining distinct cellular environments with specialized composition (e.g. the organelles). Some organelles are small, punctate and numerous and could be considered as either discrete objects, spatially resolved compartments, or as a continuous average density (e.g. volume fraction of cytoplasm). The endoplasmic reticulum (ER) presents the problem of fine structure which is contiguous and distributed throughout the cytoplasm. The fine structure of the ER is difficult to spatially resolve, and therefore it is more readily modeled as a continuous average density. For most models of eukaryotic cells, spatially resolving the plasma membrane and the nuclear envelope provide the basic encapsulation, while the finer structures are represented in a mean field manner by considering their effects to be continuously distributed within these compartments. Thus a spatial model can be a hybrid where some features are represented with an explicit geometry, while fine structures are represented as compartments within the geometry that occupy a continuous volume fraction with a continuous surface to volume ratio. Importantly, these continuously distributed compartments may be non-uniform.

To build a spatial model in VCell, a cellular geometry must be defined using either raw experimental images, segmented images, or shapes described using mathematical expressions (Analytic Geometry). The analytic geometry capability of VCell allows arbitrary inequalities in x, y and z combined with Boolean operators to identify volume domains (e.g. “(x²+y²+z² < 3² ) OR ((x-2)²+y²+z²<3²)” is the union of two spheres of radius 3, centered at (0,0,0) and (2,0,0)). Through the use of a universal image format library (Linkert et al., 2010), various native microscopy formats (e.g. Zeiss LSM) can be imported into VCell as raw image data and additional microscope data information describing the size of the field of view and space between image planes. Thus the imported image data can be treated as samples from a scalar field, which can be used to describe protein distributions. The experimental images can also be used to define the geometry of the cell or subcellular structures.

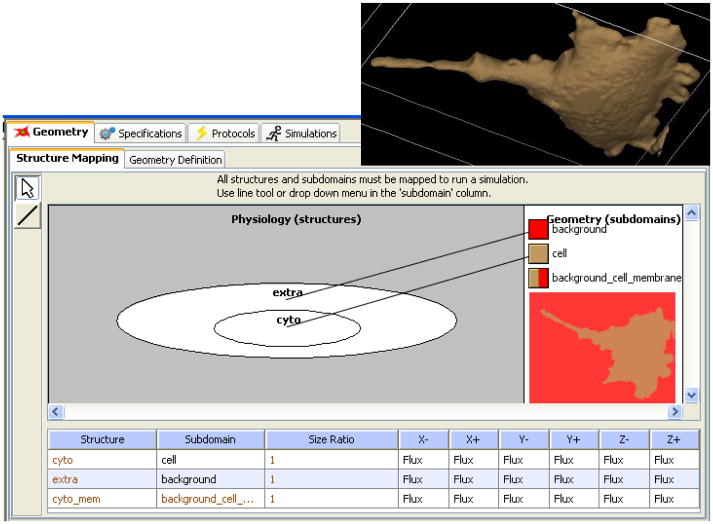
To assist in this process, VCell provides tools for image processing and segmentation (Figure 3). For example, if the cell interior is fluorescently labeled, then the cell membrane can often be determined by using an isosurface of pixel intensities and the set of all pixels that are brighter than a specified threshold in the cell interior. VCell provides a tool for 2D or 3D intensity histogram segmentation which can apply a low pass filter to accommodate noise and punctate staining. Thin or narrow processes (e.g. dendrites, lamellipodia and filopodia) have a relatively weaker observed fluorescence and are often underrepresented by threshold segmentations. Therefore, manual editing tools are provided as well as tools for merging numerous small objects due to uneven staining. This process is repeated for each resolved cellular feature (e.g. nucleus and cytosol) and the resulting geometric domains are given appropriate labels. In Figure 3, one cell is chosen with the cropping tool and segmented by this combined process of histogram thresholding and manual editing. The resultant 3D surface rendered geometry is shown in the inset on the upper right of Figure 4.

Figure 3.

Figure 4.

Once the geometry is complete, one must map the compartments from the Physiology to the geometric domains defined in the geometry so that the reaction and transport mechanisms can be distributed spatially. Figure 4 shows how the “extra” and “cyto” compartments in the Physiology (Figure 2) are mapped, respectively, to the geometry domains labeled “background” and “cell” in the segmented geometry produced from Figure 3; the software simply requires the user to draw a line connecting the compartment to the color assigned to the corresponding domain in the geometry. The same geometry can be reused in multiple models as it is accessible through the VCell database. In this example, the compartment to domain mapping is one-to-one. Often, however, multiple physiological compartments may be mapped to the same geometric domain, with specification of the volume fraction of each compartment within the domain. For example, the “cytosol” and “ER lumen” compartments can be mapped to the same “cellular” geometric domain with volume fractions of 0.85 and 0.15 respectively. This approximation assumes that the ER structure is fine enough to be not resolvable on the spatial scale of the model and avoids having to represent the difficult geometry and expensive computation of a spatially resolved ER.

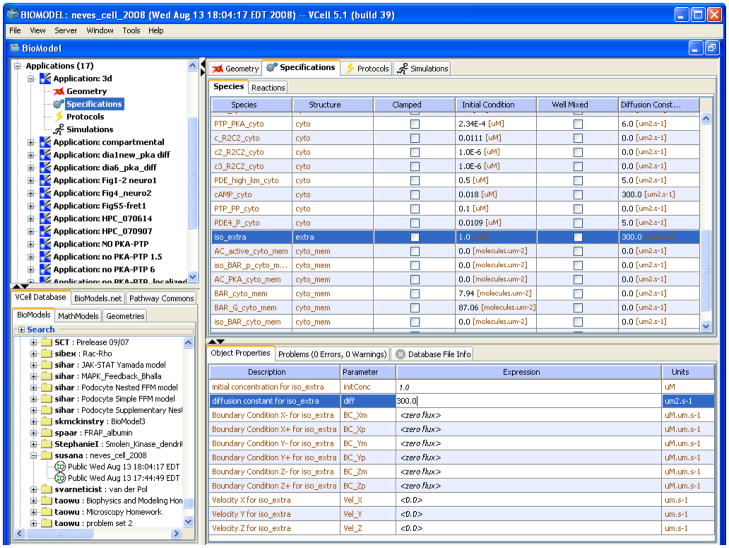
To complete a spatial model, initial concentrations, diffusion coefficients and velocities need to be specified (Figure 5). In this example, we highlight the species iso_extra, the only species in the “extra” compartment in the reaction network of Figure 2. Its initial concentration is set to 1μM. Diffusive transport is specified by the diffusion coefficient which defaults to 10 μm²s⁻¹ for volumetric species and 0.1 μm²s⁻¹ for membrane species; iso_extra represents a small drug molecule with a much higher diffusion coefficient than a protein, so it is set at 300 μm²/s. The flux due to advection of a molecular species can be specified by the x, y and z components of the velocity for each molecular species; these are all set to 0 for our example, but if the Application is meant to simulate a microfluidics experiment, it could be set to a value representing the perfusion rate. Spatially invariant initial concentration, diffusion coefficient or the velocity components are specified with numerical constants. The initial concentration, diffusion and advection specifications need not be constants, however, but can be expressions of spatial coordinates, time or variables in the model. An initial concentration may be specified as an explicit function of spatial coordinates. It can also be based on an image of a protein distribution as a fieldData object, which is imported as an image file. This object is a named dataset that may be a function of time as well as being multivariate for multichannel recordings. Thus, the concentration of a species may be clamped in both space and time to drive the evolution of other system variables. Diffusion and advection coefficients may also be explicit functions of coordinates or of fieldData. If other model parameters must be specified as a nonuniform distribution, then one may define a dummy species which can then be referenced anywhere in the model, and can be given a spatial or spatiotemporal profile using explicit functions or fieldData. Finally, in models which aim to directly fit experimental spatiotemporal fluorescence image data, the simulated fluorescence and the experimental measurements may be directly compared to evaluate the fitting error.

Figure 5.

The flux density of a molecular species at a membrane results from the sum of the trans-membrane transport and adsorption and desorption due to surface binding reactions. This flux density is constrained to equal the flux due to diffusion and advection at the surface of the membrane and results in the generation of gradients near the membrane for nonzero flux. Thus, VCell handles boundary conditions of domains bounded by membranes automatically, based on the specified membrane-associated reactions and transport mechanisms. Boundary conditions at the edges of the simulations geometry, however, must be specified for any species that exists in a domain that intersects with one or more of these edges, as is the case for iso_extra in Figure 5.. The portion of the domain boundary that coincides with the walls of the geometry’s bounding box represents an artificial truncation of a larger geometric domain and so either the concentration or flux density must be given as a boundary condition at these walls to recover a unique solution. If the concentration is specified at a wall (i.e. “value” boundary condition), then this wall acts as a perfect buffer at the given concentration and will supply the required molecular flux to maintain the given concentration at the boundary. If instead the molecular flux density is given at the wall (i.e. “flux” boundary condition), then the concentration at the wall will be such that the diffusive (and advective) flux at the wall is equal to the given flux density. This “flux” boundary condition is often specified with zero flux, as is the case for the example in Figure 5; 0 flux is equivalent to either a plane of symmetry or an impermeable wall. In all cases, the influence of the boundary condition will be made smaller as the geometry’s bounding box is made larger (at the expense of simulation time).

To summarize, the VCell BioModel workspace provides the flexibility to map a single physiological model to multiple mathematical frameworks, ordinary differential equations, partial differential equations, nonspatial stochastic, and spatial stochastic (Fig. 1). This rich set of simulation capabilities enables the modeler to independently consider and evaluate spatial effects and stochastic effects as illustrated in Figure 6, which summarizes the process for specifying multiple Applications based a single Physiology. Of note, even within a single physical formulation, say a deterministic spatial model, there can be many Applications, each with different initial concentrations of species, clamped species concentrations, different geometries for different cell types, etc. In other words, any combination of the specifications described in Fig. 6 can be chosen to exercise the parent Physiology. A VCell Application is thus akin to a “virtual experiment”. After an Application is completely specified, VCell automatically generates a full mathematical description, which contains all the constants, variables, functions, ODEs, PDEs or stochastic processes of the system. This can be viewed and even copied into an editable “MathModel” workspace. This mathematical description (whether generated automatically in the BioModel workspace or edited manually in the MathModel workspace), is directly translated into the input to our various simulation solvers. This separation of biological model construction from the mathematics of numerical simulation enables independent development and verification of modeling and simulation capabilities. The considerations required to set up and run spatial simulations are the subject of Section IV.

Figure 6.

IV. Running spatial simulations with VCell: numerical method and simulation parameters

Mathematically, spatial aspects of cell signaling are deterministically modeled by systems of PDEs that involve rates of change of concentrations of signaling molecules both in space and time (time and spatial derivatives), as described in Section II., equations (1) and (2). Most spatial mathematical models, particularly models with realistic geometries and complex nonlinear behaviors, do not have analytical solutions, and the problems need to be solved numerically.

Numerical solution of a PDE entails discrete sampling of both spatial domains and a time interval of interest. The spatial sampling should be fine enough to capture the essential geometric features of both the volumetric and surface domains of the geometry. The temporal sampling should be fine enough to capture any fast events in the mathematical system. This spatiotemporal sampling produces a solution in the form of tables of floating point numbers. It is important to realize that the numerical solution of a PDE is approximate: what the computer actually solves is not the original PDE but rather a system of algebraic equations that approximates the original PDE. This algebraic system of equations is obtained through discretization of time and spatial derivatives included in a PDE. While this can be done using different discretization approaches (i.e. a PDE can be approximated by different algebraic systems), the numerical solution of the algebraic system converges to the exact solution of the original PDE with increasing sampling density, i.e. the numerical solution can in principle be made as close to the exact solution of a PDE as desired, by refining the spatial grid and decreasing the integration time step.

Still, various discretization schemes have different characteristics with respect to order of convergence, numerical stability, conservation of mass and other parameters. In Virtual Cell, for example, spatial discretization of PDEs is performed using a finite volume scheme (Ferziger and Peric, 2002), a conservative method with a built-in mass balancing, a feature that is particularly important in biological applications (Novak et al., 2007; Schaff et al., 1997; Schaff et al., 2000; Slepchenko and Loew, 2010; Slepchenko et al., 2000; Slepchenko et al., 2003). More details about handling geometry in Virtual Cell can be found in (Novak et al., 2007; Resasco et al., 2011; Schaff et al., 2001; Slepchenko and Loew, 2010).

Time discretization methods can differ by how they advance the solution from one time point to the next. The methods that advance the system based on the rates evaluated at the “old” time point (explicit solvers) require a sufficiently small integration step to ensure numerical stability (numerical instability can manifest itself as qualitatively wrong behaviors, such as unphysical oscillations or negative concentrations, or an exponential growth of numerical error resulting in machine infinity). In contrast, the implicit methods that propagate the system on the basis of rates corresponding to the “new” time point are unconditionally stable but they result in a system of nonlinear algebraic equations that must be solved iteratively.

Efficient numerically stable solvers have long been provided for simulating temporal behaviors of cell signals (Alves et al., 2006). In particular, systems biologists have come to rely on so-called stiff solvers that retain their numerical stability and good performance in the presence of vastly disparate time scales – a common situation in biological applications. However, for the case of spatially resolved systems described by PDEs, solvers that meet such requirements and apply to a general class of problems are less common. A relatively new addition to the list of Virtual Cell spatial algorithms is a fully implicit spatial simulator (Resasco et al., 2011; Slepchenko and Loew, 2010), which meets requirements of numerical stability and efficiency that modelers are used to in non-spatial simulators. With a built-in automatic time-step control and in combination with automatic meshing, the new spatial integrator in Virtual Cell is easy to use. It is freely accessible through the VCell user interface (www.vcell.org).

The fully implicit spatial solver in VCell is based on the well-known method of lines (MOL) (Schiesser, 1991): after applying spatial discretization, a system of PDEs is first replaced with a large system of ODEs, which is then solved using a stiff ODE solver. The stiff solver advances the solution in time using implicit differentiation formulas and adaptive time step control. The latter allowed us to relieve the user of the burden of specifying the integration time step, which is generally a nontrivial task. Based on model parameters and tolerances, the solver automatically determines the initial integration time step and adjusts it along the way: the required accuracy is maintained by applying small time steps during periods of rapid change in the solution, whereas the time step is allowed to safely grow outside of these periods. The adaptive time step control essentially eliminates the time discretization error and significantly enhances efficiency of the solver.

The method, however, results in a large coupled nonlinear system of algebraic equations that must be solved at each step in time. A commonly used alternative called operator-splitting (Sportisse, 2000) avoids solving large, coupled nonlinear systems of algebraic equations, but it can carry more error and is not always applicable, especially in situations when stiffness originates from binding of molecules to membranes, interactions that are represented in terms of fast, nonlinear boundary conditions. The fully implicit approach, although sometimes dismissed as inefficient because of the large size and complexity of the non-linear solves, can in fact be efficient when implemented with the use of effective technologies designed to optimize storage requirements and computation time. In particular, the adaptive control of the time step and order of the integration method, efficient iterative approaches to solving large-scale sparse nonlinear systems (see e.g. (Knoll and Keyes, 2004) and references within), and the application of effective physics-based preconditioners (Saad, 2003) are the main ingredients that contribute to the robustness and good performance of this solver. More details of the implementation of the fully implicit solver in VCell are provided in (Resasco et al., 2011).

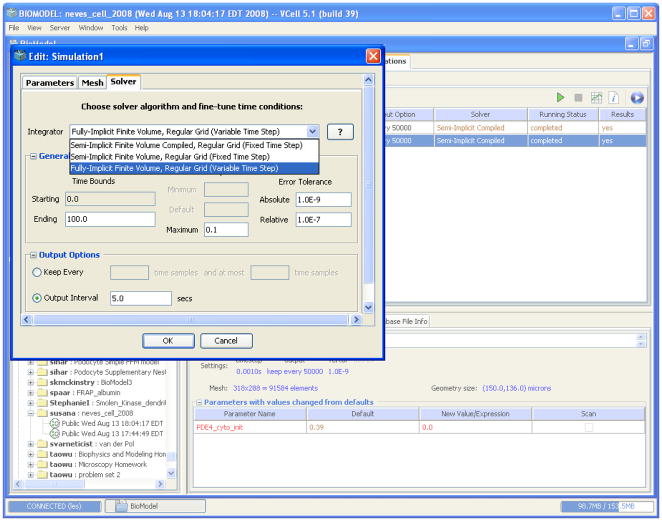
The Virtual Cell fully implicit simulator is essentially turn-key. The solver is accessed through a Solver dialog box from the Simulation Editor (Figure 7). Using this panel, one can switch between the solvers using a drop-down menu. This, plus simulation start and end times and the desired output time interval, is all the information needed to run the fully implicit solver. The user may also choose to adjust the relative and absolute tolerances for local (time-discretization) errors and the maximum integration time-step allowed. These simulation parameters are initially set at default values: 1e-7 and 1e-9, for the relative and absolute tolerances respectively, and 0.1 for the maximum integration time step.

Figure 7.

The other two tabs of the Simulation Editor reveal panels for Parameter and Mesh specification. The Mesh panel allows a user to refine or coarsen the mesh by changing the mesh size for each Cartesian direction. In this way, the user can increase or decrease the number of grid points for which the solution is computed. In the Parameter panel, the user can vary model parameters, such as rate constants or initial concentrations, for a given run. This can be done individually or through the option of parameter scanning. The latter allows a user to run a batch of simulations for a selected set of combinations of parameter values. For this, the user specifies parameter ranges and the number of values within a range, which will be selected, either uniformly or logarithmically, for scanning. This is done by checking boxes in the ‘Scan’ column, under the ‘Edit>Parameters’ tab. VCell then automatically initiates simulations for all combinations of selected parameters. The results for individual parameter combinations can be viewed by selecting a set of parameter values from the table at the bottom of the ‘Results’ window, in which simulation results are displayed.

The continuous description in terms of PDEs becomes inadequate when concentrations of signaling molecules are relatively low and stochastic fluctuations need to be taken into account. Instead, spatial stochastic approaches should be applied. Stochastic modeling of signaling events seeks to predict dynamics of a probability distribution over states of signaling molecules and their spatial location. Realistic models formulated in terms of stochastic processes rarely have exact solutions (Gardiner, 2004; Kim and Shin, 1999; van Kampen, 1992), and computer simulations have inevitably become a method of choice for stochastic applications to cell biology.

Numerical methods for modeling stochastic processes often rely on random number generators, which are nowadays built in every computer; such algorithms are called Monte Carlo methods. In recent years, there has been significant progress in developing Monte Carlo algorithms designed for applications in cell biology (Andrews et al., 2010a; Andrews et al., 2010b; Elf et al., 2003; Isaacson and Peskin, 2006; Kerr et al., 2008; Morelli and ten Wolde, 2008; Morton-Firth and Bray, 1998; Plimpton and Slepoy, 2005; Saxton, 2007; van Zon and ten Wolde, 2005). Some of these methods have been implemented in software packages such as MCell (http://www.mcell.cnl.salk.edu), StochSim (http://www.pdn.cam.ac.uk/groups/comp-cell/StochSim.html) , Smoldyn (http://www.smoldyn.org/), ChemCell (http://ipal.sandia.gov/ip_details.php?ip=8030), and MesoRD (http://mesord.sourceforge.net/).

Stochastic simulators utilize different approaches and yield results with a varying degree of detail. A method based on a reaction-diffusion master equation (Elf et al., 2003; Isaacson and Peskin, 2006; Stundzia and Lumsden, 1996) approximates volume elements as well-stirred compartments and describes a system in terms of a number of copies of each signaling molecule in each volume element. Diffusion fluxes between neighboring locations are treated as a subset of unimolecular reaction steps, and Gillespie-type (event-driven) algorithms (Gibson and Bruck, 2000a; Gillespie, 1976; Gillespie, 1977) optimized for spatial simulations (Fange and Elf, 2006) are used to generate stochastic trajectories of the system. While conceptually appealing, the method does not have a well defined scope of applicability and diverges as the mesh is refined.

In a more detailed description, the state of the system is defined in terms of locations and states of every signaling molecule (velocities of the molecules are considered to be in equilibrium at any time because of low Reynolds numbers). Particle-based Brownian Dynamics algorithms that advance a system in time with a fixed time step are widely used to simulate dynamics of interacting molecules in cells (Andrews and Bray, 2004; Kerr et al., 2008; Plimpton and Slepoy, 2003). In one of most recent developments, Virtual Cell has implemented Smoldyn (Andrews et al., 2010b) (Figure 1D), which is among the most efficient particle-based spatial stochastic simulators. Interpolation techniques implemented in Smoldyn become exact in the diffusion-controlled limit. The algorithm is designed to reproduce observable on- and off- reaction rates, and therefore results are expected to be sufficiently accurate even when obtained with relatively large steps. Still, numerical error cannot be regularly estimated, other than for the case of diffusion-limited reactions. In this regard, more accurate, but likely less efficient, methods were recently proposed in (Morelli and ten Wolde, 2008; van Zon and ten Wolde, 2005).

V. Application to a specific example: cAMP signaling in neuronal cells

Intracellular signal transduction often leads to localized regulation of specific cellular processes. Such spatial heterogeneity can be experimentally observed by in vivo high resolution subcellular imaging and can involve localized production of small molecule messengers and/or localized activation of protein kinases, protein phosphatases and other signaling components. Concentration gradients of key signaling components can form dynamic subcellular regions, called signaling microdomains, where selected molecules have elevated (or decreased) levels compared to other contiguous areas. It has long been thought that some of the specificity observed in the effects of signals that use similar or identical signaling pathways arise from such spatial domains of signaling components within the cells. Signaling microdomains involving cAMP and protein kinase cascades have been recently studied in a number of different cell types. These studies revealed a surprising complexity that is not easily explained by simple reaction mechanisms and the geometrical shape of the particular cells. Performing quantitative simulations of the biochemistry in spatially resolved geometries using software such as VCell can be of critical help to guide experiments and unravel this complexity. This is illustrated in this Section by example, using a recent study of beta-adrenergic receptor signaling in hippocampal neurons (Neves et al., 2008).

Initial hypothesis and overall approach

The overall goal was to study the role of morphology and spatial anisotropy in regulating intracellular signaling in neurons. The original hypothesis was the following: due to the shape of hippocampal neurons, microdomains of cAMP may form in response to global beta-adrenergic receptor stimulation, and this would then lead to localized activation of the downstream effector, mitogen activated protein kinase (MAPK; active in its phosphorylated state, P-MAPK). The approach used was to resolve the information flow within the cell using spatial specifications from realistic cell shapes and locations of relevant components. Models were developed using VCell and simulations were used to analyze how the various factors (signaling network connectivity map, individual reaction kinetics, diffusion constraints, shape, etc.) could affect the dynamics of the signaling microdomains. The predictions generated from these simulations were tested experimentally in an iterative cycle of model building/refinement – simulation predictions – new experiments. This work has resulted in exciting new insights into the interplay between signaling network topology, biochemical kinetics, and spatial anisotropy in the regulation of the cellular response to receptor stimulation.

Creating and testing the model and the initial hypothesis

The first step was to build a simple, but quantitatively accurate model of signal transduction at the membrane that controls the concentration of the cytosolic second messenger, cAMP. This initial model included the extracellular ligand (iso-proterenol), the beta-adrenergic membrane receptor, the G-protein cascade leading to adenlyl cyclase activation, cAMP generation, the activation of protein kinase A (PKA), and the cAMP degradation by PKA activation of phosphodiesterase (PDE4) (see Fig. 2A). This simple stimulatory pathway with one negative feed-back loop had many parameters known from experimental measurements. The unknown parameters were constrained by running simulations as a compartmental (i.e. ODE) model to fit time curves and dose-response curves of a few selected components whose average concentration was measured in brain slice experiments.

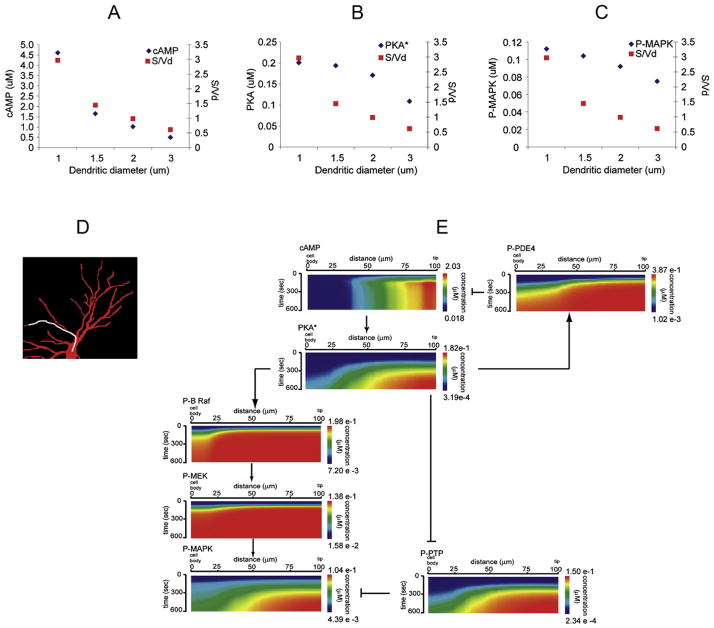
The second step was to use microscope images of cultured hippocampal neurons as geometries for simulating the spatially-resolved activity of this signaling network (an example is shown in Fig. 8D). All molecules involved were assumed to be evenly distributed at the initial steady state. The time-course simulations after ligand stimulus predicted that cAMP microdomains would form, with relatively steep concentration gradients (strong activation in the dendrites and essentially no activation in the cell body). This was then confirmed by live cell measurements of cAMP in slice experiments (using a cAMP FRET sensor) which were compared to further simulations that used the actual geometries of the neurons from the slice experiments microscope images. Theoretical analysis of this (still relatively simple) model had shown that a critical parameter that influences the cAMP gradients is dendrite diameter. This mathematical analysis was confirmed by simulation results on idealized geometries where the dendrite diameter was varied and a strong correlation was seen with cAMP concentrations (Fig. 8A).

Figure 8.

First unexpected model prediction

The model was then extended to include the signaling elements connecting the second messenger production to effector activation: a stimulatory (PKA → b-Raf → MAPK) and an inhibitory (PKA ¬ PTP ¬ MAPK) feed forward link, both with negative regulation by phosphatases (PPP2A and PP1, respectively). The schematic overview of the extended signaling network is shown in Fig. 2B and the detailed reaction diagram of the corresponding VCell model is shown in Fig. 2C. Spatially resolved simulations of the extended model were started by activating the receptors with saturating concentrations of isoproterenol, and they showed that, similar to the case of cAMP, distinct microdomains for P-MAPK were also formed in the distal dendrites, as originally hypothesized. However, when analyzing the dependency of the P-MAPK microdomains on dendrite diameter, the results were very different than for the cAMP microdomain, in that the P-MAPK microdomain was far more robust (compare Fig. 8A and 8C). Thus the model predicted that localized cAMP signaling is directly dependent on cellular geometry, but other factors must contribute to the control of the spatial distribution of MAPK activation. One possible hypothesis was that this was due to differences in diffusion constants of the different molecules involved, e.g cytosolic proteins diffuse much slower than the small molecule cAMP. This hypothesis was tested in silico, by performing parameter scan simulations where the diffusion constants of several of the molecules were changed to higher values. (It is worth noting that this was a quite important model analysis step independent of the hypothesis, since many of these diffusion constants were estimated based on molecular radius and not experimentally measured values). These simulations showed, however, that the characteristics of the P-MAPK microdomains were not significantly affected when any of the diffusion constants were increased (within physically reasonable bounds). So what could be the cause? When looking at the simulation data for other cytosolic proteins, the very first protein in the signaling path, PKA* (the cAMP-activated PKA), also exhibited a microdomain formation that was more robust to changes in dendrite size and shape, similar to the case of P-MAPK (Fig. 8B). A natural hypothesis was that the cause must reside in the upstream part of the signaling – e.g. the phosphodiesterase-mediated upper negative feed-back loop. An in silico “virtual knock-out” experiment was performed where simulations where run with the PDE4 activity set to zero. These simulations showed a complete loss of microdomain formation for both PKA* and P-MAPK. This important prediction was then confirmed experimentally: hippocampal tissue slices were treated with the PDE4 inhibitor rolipram before beta-adrenergic stimulation, and as a result, global activation (body + dendrite) of P-MAPK was seen, perfectly matching simulation predictions.

More unexpected model predictions

While doing the above model analysis to compare microdomain characteristics for the second messenger cAMP vs. the downstream effectors PKA* and P-MAPK, a second surprising feature was observed. Looking at the spatial dynamics of all of the diffusible components involved, the proteins that form the intermediary link between them in the stimulatory pathway, P-b-Raf and P-MEK, not only do not have robust spatial microdomains, they essentially do not form any microdomain, and show little difference in activation between different areas of the cell (Fig. 8E). Given the previous insight gained into the importance of the upper negative feed-back loop in propagating spatial information, a new round of in silico and in vivo experiments was done, focused on the negative feed-back component of the downstream activation path: phosphatases PP2A and P1. Simulations of inhibited PP2A/PP1 activity showed a disappearance of the downstream P-MAPK microdomain, while the upstream PKA* microdomain was unaffected. This was then confirmed experimentally by treatment with the phosphatase inhibitor, okadaic acid.

Given the apparent critical role of negative regulators, further efforts were made to understand the role of the parallel inhibitory feed-forward loop (PTP inhibition by PKA followed by MAPK inhibition by PTP). Indeed, P-PTP (currently not measurable experimentally) also showed a similar robust microdomain like PKA* and P-MAPK (Fig. 7E). A PTP “virtual knockout” experiment in silico (where phosphatase activities were kept normal) resulted in simulations where only shallow P-MAPK microdomains were formed, which were also not at all robust to changes in cellular shape characteristics such as dendrite vs. cell body surface/volume ratios. Experimental testing of this prediction was far more complicated, since no good specific direct inhibitor of PTP was available. Gene knock-down experiments were performed, where animals were treated with antisense oligonucleotides that were designed to reduce the expression of the PTPRR gene products prior to sacrificing them for tissue slice experiments. Comparison of P-MAPK imaging after isoproterenol stimulation in tissue slices from the antinsense oligonucleotide-treated animals vs. those from scrambled oligonucleotide-treated controls matched the simulation predictions. This also prompted further more detailed analyses to study the relative role of kinetic parameters of the reactions in the stimulatory and inhibitory feed-forward paths, as well as of their respective reverse loops via phosphatases.

Conclusions

This study achieved a new understanding of how cell morphology characteristics, biochemical parameters, and network topology combine in subtle ways to control the propagation of spatial information through the signaling networks (in the particular case of beta-adrenergic stimulation of neurons). To put in perspective the complexity of the study, it should be noted that the presentation here only briefly summarizes the stepwise progression from an initial hypothesis through many cycles of in silico and in vivo experiments. Considerable more data is provided and discussed in the original paper by Neves et al. (2008): the 6 multi-paneled results figures are accompanied by a 50-page supplement with more simulation and experimental data (34 more figures and tables) as well as additional theoretical mathematical analyses. Overall, this study is an excellent example of how geometry can control cell signaling and how modeling and experiment can interact to solve a complex cell biological problem.