Use of Virtual Cell in studies of cellular dynamics

Abstract

The Virtual Cell (VCell) is a unique computational environment for modeling and simulation of cell biology. It has been specifically designed to be a tool for a wide range of scientists, from experimental cell biologists to theoretical biophysicists. The models created with VCell can range from the simple, to evaluate hypotheses or to interpret experimental data, to complex multi-layered models used to probe the predicted behavior of spatially resolved, highly non-linear systems. In this Chapter, we discuss modeling capabilities of VCell and demonstrate representative examples of the models published by the Virtual Cell users.

1. Introduction

Why computational modeling in cell biology? A short answer is because it can help gain new insights and knowledge and make testable predictions (1). More specifically, given the complexity of cell processes, qualitative reasoning alone may not be sufficient for adequate interpretation of experimental data or for predicting the system behavior. Formulating assumptions mathematically allows an experimentalist to perform a rigorous logical test of a `theory' that he or she might have in mind. An adequate model almost always yields interesting predictions that, in turn, can be tested experimentally, but even a failure of the model to explain experimental observations often leads to a better understanding of the process under study.

While cell biology, unlike physics, remains largely qualitative and mathematical modeling may not always be appropriate (2) or even possible, certain areas of cell science have benefited from combining experimental studies with physics-based modeling (3). A model of action potential by A. Hodgkin and A. Huxley (4), developed as part of the Nobel Prize-winning study of electric pulses in a giant squid axon, is perhaps one of the most successful examples of an application of modeling in cell-biological research. It is striking how a careful quantitative analysis of ion currents led to the prediction of gating mechanisms even before ion channels were discovered and characterized (5). Not only had the Hodgkin-Huxley model explained the dynamics of membrane potential in neurons, it also became a prototype for modeling the dynamics of other excitable cells, such as cardiac myocytes, pancreatic beta-cells, gonadotrophs etc., and more broadly, laid a foundation for a new field: the theory of excitable systems (6).

Theoretical methods have been successfully applied to other areas of cell biology as well, such as gene networks (7), cell metabolism (8, 9), molecular motors (10, 11), cell signaling (12), chemotaxis (13), cell cycle (14), calcium dynamics (15), cell motility (16), and others.

It is hardly possible to specify with certainty the circumstances under which a mathematical model would be a useful tool in a cell-biological study: usually, you know it when you see it. Still, it is probably safe to say that a modeling effort is likely to succeed in situations where experimental studies have resulted in a substantial amount of quantitative information. The Hodgkin-Huxley model is an excellent example of the “data-driven” modeling. A typical goal of this type of analysis is to predict or explain the behavior of a complex system by building a model from multiple components that are carefully constrained by experimental data.

A different modeling approach is utilized in investigating particular behaviors (oscillations, waves) or features (e. g. amplification of sensitivity). For these cases, building a model might not require precise knowledge of parameter values; rather, the analysis itself should yield conditions that need to be imposed on the model structure and/or parameters so that certain qualitative patterns could emerge. One such example is a seminal theoretical study of sensitivity amplification in activation-inactivation cycles and signaling cascades by A. Goldbeter and D. Koshland (17).Their predictions were later used to explain enhanced sensitivity of the mitogen-activated protein kinase (MAPK) cascade in Xenopus oocyte extracts (18), and recent in-depth analyses of the Goldbeter- Koshland model have shown that the sensitivity amplification in signaling cascades is likely to be a fine-tuned property, as it requires a rare combination of unsaturated activation and saturated inhibition of enzymes (19, 20).

Finally, modeling proved to be helpful in analyzing raw experimental data. One can simulate an experiment in order to find a correct way of extracting valuable parameters, e.g. diffusion or reaction rate constants (21, 22), and in some cases, the model can even provide guidance for designing experiments (23–25).

Two developments have recently sparked renewed interest in quantitative approaches to cell-biological studies. First, new fluorescent biosensors have been discovered, especially the naturally fluorescent proteins (26, 27), that are used to quantify spatiotemporal dynamics of proteins in vivo (28). Second, development of new computational tools, accessible to cell biologists (29, 30), has made it possible to run simulations based on realistic models within reasonable computation time, owing to the exponential growth of computer power in the past two decades and development of new numerical techniques. As cell biology becomes more quantitative and a new generation of cell scientists with adequate mathematical training enters the field, their arsenal of research tools will most likely include computational modeling.

This review is focused on the usage of the Virtual Cell (VCell) (29, 31–37), www.vcell.org, arguably the most versatile software tool for computational modeling in cell biology (38) designed for both experimental biologists and theoretical biophysicists. VCell is developed at the Richard D. Berlin Center for Cell Analysis and Modeling (CCAM) in the University of Connecticut Health Center.

After discussing modeling capabilities of VCell in Section 2, we review recent publications in which various cell-biological processes have been simulated using VCell (Section 3). The chapter concludes with a discussion of directions in developing new tools for modeling in cell biology in Section 4.

2. Modeling capabilities of VCell

A computational project usually includes: formulating a biological model, casting it in a mathematical form, solving the mathematical model, and comparing predictions from the model with experimental data. Implementation of these steps requires, in addition to expertise in cell biology, some knowledge in the areas of mathematical physics, applied mathematics, and computer programming, and therefore presents obvious technical challenges.

The Virtual Cell was designed to help biologists overcome these barriers. Accordingly, VCell includes two workspaces, biological (BioModel) and mathematical (MathModel), of which the first, described in detail in section 2.2, was developed to be used by experimentalists (theorists might find it attractive as well, given the ease of setting up a nontrivial model). It includes an intuitive graphical user interface that facilitates formulating biological models by allowing a user, in effect, to draw corresponding diagrams. While it is generally true that modeling is in essence the art of simplifying assumptions (1–3), the very structure of user input in VCell (what are the compartments to be modeled? what are the molecules that populate the compartments? how are the molecules wired through their interactions?) may help the user formulate a model.

Once the biological model is fully specified, VCell automatically translates it into a corresponding mathematical description. This is done by applying physics principles, such as local mass conservation and, in the context of membrane potential, conservation of electric charges (36). The math description in the BioModel workspace is read-only in order to maintain one-to-one correspondence with the BioModel from which the math has been generated (since in general, it is not possible to unambiguously propagate the changes made in the math description back to the BioModel). This math description, however, can be moved to the MathModel workspace for further editing. In this case, it becomes a standalone mathematical model with no ties to any VCell BioModel, and the user takes on the responsibility to ensure its physical soundness (consistency with conservations laws, etc.). It is also possible, of course, to enter the mathematical description manually in the MathModel workspace from scratch.

The Virtual Cell solves mathematical models numerically. This means that the solutions are obtained in the form of arrays of floating point numbers and therefore are not exact, although numerical error can be made very small. VCell solvers are described in section 2.5 where we also discuss some pitfalls of the numerical procedures. The results, visualized as images and graphs, can also be exported in various formats, such as spreadsheets, images, and movies, so that the user can further analyze them with the aid of familiar software tools (see also section 2.2).

2.1 Scope of applicability

VCell accommodates modeling of a wide range of cellular phenomena, which include molecular interactions and transport in various subcellular compartments, as well as dynamics of membrane potential. These mechanisms might be interconnected and can be modeled as such. For example, VCell provides tools for coupling the membrane electrophysiology with reaction-diffusion processes in the volume (36). These tools can be applied to modeling an interdependence of dynamics of membrane potential and concentrations of ion species, such as calcium (39): the membrane potential regulates calcium fluxes through the plasma membrane voltage-sensitive channels and thus affects both spatial distribution of calcium and its overall content in the cytosol. The latter in turn affects the behavior of the membrane potential. Similar situations arise in the context of processes in mitochondria (40).

What distinguishes VCell from most of the other software packages designed for biological applications is that it allows one to simulate cellular dynamics not only in time but also in space, using realistic experimental geometries taken from microscope images (41). In section 2.4.1, we explain how VCell handles geometry. Spatial applications in VCell can include both diffusive and directed molecular transport. The latter is exemplified by molecular motors moving along cytoskeletal tracks. In a continuous approximation that does not resolve individual molecules and filaments, directed transport is modeled as advective flow (42).

A newly developed capability to model diffusion on curved surfaces (43) permits coupling of a volumetric reaction-transport system to diffusion and reactions of molecules in the embedding membrane. This capability is necessary for modeling a mobile cytosolic protein that can bind to a mobile molecule in the plasma membrane, so that the complex can diffuse in the membrane, and then return to the cytosol upon unbinding (21).

Overall, the scope of applicability of VCell can be summarized as the dynamics of reaction-diffusion-advection (flow) systems on arbitrary geometries with arbitrary cross-membrane fluxes; these systems can be coupled to reaction-diffusion systems in the embedding membrane and, for non-neuronal cells, to the dynamics of membrane potential. Note that the geometry in the spatial model does not have to be necessarily geometry of a whole cell or of only one cell: one can model a part of the cell or a multicellular system.

VCell resolves the dynamics of a system based on its initial state, or initial conditions. In mathematical terms, VCell solves an initial value problem. For most cases, this problem has a unique solution, or is well posed (44). In the situations where the model is designed to determine how the cell responds to stimuli, it is important to make sure that the system is at a stable steady state in the absence of the stimulus, or, in other words, that the initial conditions of the problem correspond to a steady state of the system. Otherwise, the simulated behavior will include internal dynamics of the system that can be confused with a response to the stimulus. For a stationary steady state, which is often the case, the check is easy: one should simply run the simulation for some time with the stimulus turned off and make sure that molecular concentrations remain nearly constant.

VCell solvers can in principle be used to find a steady state, again by running a sufficiently long simulation, so that the state variables (concentrations, membrane potential) have a chance to stabilize within an acceptable error. It is important to bear in mind, however, that the models in biological applications are often nonlinear (that is they include rates that are nonlinear functions of the state variables), which may have multiple stable steady states (multistability) (45). In this case, the initial value solvers may result in different steady states, depending on the initial conditions. It is also important to realize that steady states are not always stationary: they may be oscillatory, wave-like, or even chaotic (46).

2.2 BioModel Workspace

Among the most useful and innovative design features of the VCell software is the hierarchical multilayered structure of a BioModel. The idea is similar to hypothesis-driven research, where a hypothesis can generate multiple experimental protocols (e.g. in vitro biochemistry; in vivo biosensor; gene knockouts, etc.) to probe the hypothesis and the experiments may be performed with multiple minor changes in conditions (e.g. titrations of ligand concentrations; varying current clamp steps; differing durations for following dynamic changes, etc.). Experimental results can then be interpreted in relation to the hypothesis. In a BioModel, the parent layer is called the Physiology, which can generate several Applications, which, in turn, can spawn multiple Simulations. This structure is illustrated in Figure 1.

Figure 1.

Computational modeling with the VCell BioModel workspace.

A set of mechanisms in Physiology generates multiple Applications, each of which in turn can spawn multiple simulations utilizing different solvers, spatial resolutions and parameter values.

The Physiology is a container for the identity of all the molecular species and variables within the model, where they are located within cellular structures and how they interact with each other through rate expressions and membrane transport processes. Cellular structures are created by specifying the topological arrangement of membranes and membrane bounded compartments. Biochemical reactions are defined within volumetric compartments of the cell as well as in membranes; molecular fluxes, and electrical currents are defined across membranes. The reaction rate or flux rate is determined as an explicit function of the local environment (e.g. concentrations, surface densities, membrane potential) and one or more kinetic parameters (e.g. k_on and k_off). Mass action and Michaelis-Menten rate laws are available automatically, but user-defined general kinetic expressions are also readily entered. Membrane transport kinetics can be specified with expressions for molecular flux or, for ions, the electric current. The transport kinetics can be described in terms of standard electrophysiological formulas (e.g. Goldman-Hodgkin-Katz permeability or Nernst conductance) or as user defined molecular flux or current.

Several Applications can probe the Physiology. These contain specification of the geometrical features of the model, boundary and initial conditions of the system and the kind of mathematical physics to apply to the model. For the latter, VCell offers choices of continuum reaction kinetics, discrete (stochastic) reaction kinetics, or continuum spatial reaction-diffusion models with geometries that can be derived from experimental images. These three categories of Applications will be described in more detail in sections 2.3, and 2.4. For spatially explicit Applications, the structures defined in the Physiology are mapped to the corresponding regions within a geometry. As further detailed in 2.4, the geometry can be derived from either an analytical expression in Cartesian coordinates or from an experimentally derived image, two-dimensional (2D) or three-dimensional (3D). An Application (together with the parent Physiology) is sufficient to completely specify a mathematical model. As noted above, VCell automatically generates a math description language from this input.

The Application further branches to permit multiple Simulations. These might invoke different numerical solvers or discretization schemes (detailed in Section 2.5), or different durations. Among the most convenient and common reason to generate multiple simulations is to do parameter scans, where the effect of differing initial concentrations of molecular species or different rate constants can be tested. Simulation results are visualized as graphical outputs in a number of convenient formats. For spatial simulations, the variables and rates are displayed as spatial fields mapped onto the model geometry; membrane variables in 3D geometries can be visualized as textured surface renderings. Results can also be exported to spreadsheets and, for spatial models, as images or movies.

This hierarchical branching BioModel structure is extremely convenient for exploring the implications of a hypothesis describing a complex mechanism of a cellular process. The Physiology encompasses the major features of the hypothesis, while the Applications represent different scenarios for testing the hypothesis – akin to “virtual experiments”. Simulations drill down further in exploring the quantitative predictions of the model. Once the Physiology is defined, most of the work in formulating the model is done. Depending on the complexity of the model, it can take minutes to hours to months to develop a Physiology. But once a Physiology is formulated, Applications can be set up in minutes to hours and Simulations can be set up in seconds to minutes. Of course, the database structure of VCell also permits reuse of the components of a Physiology as components of new BioModels.

2.3 Compartmental applications

Diffusion within a compartment can be fast compared to reactions and cross-membrane fluxes (this is generally true for relatively small compartments). For this case, spatial gradients of concentrations are small and concentration dynamics are similar at all locations of the compartment. There is no need for spatially resolving the compartment in these conditions; therefore the concentrations become functions of time only. The model reduction based on fast equilibration of variables in space is sometimes called a `well-mixed' or a whole-cell approximation. While the latter term refers to a single compartment, generally there might be multiple well-mixed compartments in the model. In VCell, the applications that are concerned only with time dependences of state variables are termed compartmental. In a deterministic mathematical model, functions of a single independent variable (time) are governed by ordinary differential equations (ODEs) as opposed to partial differential equations (PDEs) which describe functions of multiple independent variables (spatial coordinates and time). The deterministic compartmental model is therefore described by a set of ODEs.

The VCell tool for modeling the membrane potential is designed for non-neuronal cells (as well as for space-clamped neurons) where equilibration of charges is fast. The membrane potential in VCell is therefore a variable that depends only on time and thus is described in compartmental applications by an ODE. When coupled to spatially resolved concentration dynamics, the membrane potential is governed by an integro-differential equation, since its rate of change in this case is obtained by integrating electric current densities over the membrane.

Compartmental models might be a good starting point even when the ultimate goal is spatial modeling. The practical reason is that solving ODEs is obviously much faster than solving PDEs which involve multiple grid points in space. Thus the compartmental approximation provides a quick preview of `averaged' system dynamics governed by reactions and cross-membrane fluxes and in particular, gives the user an idea about time scales that should be expected for the full spatial solution. This information helps manage computationally expensive spatial simulations. By default, new applications in the BioModel workspace are generated as compartmental.

2.3.1 Stochastic applications

When the number of molecules in a system is small, the deterministic approach to simulating a compartmental model may not be appropriate. In such cases changes in the state of the system should be described according to discrete stochastic events. In the stochastic approach, the system is described by a probability distribution P over a range of possible values of state variables. Stochastic processes are described by time-dependent probabilities and governed by local conservation. For cases, where the rate of change of the process is fully determined by the current state of the system, i.e. the system has no memory (Markov processes), the conservation law is known as `master equation' (47). VCell solves the master equation numerically, using methods based on sampling individual trajectories (Monte Carlo simulations). VCell stochastic solvers, described in more detail in section 2.5.4, utilize the Gibson-Bruck Next Reaction algorithm (48), an optimized version of one of the Gillespie algorithms (49), which interpret reactions as Poisson stochastic processes.

The VCell stochastic tool allows a user to simulate individual trajectories as well as multiple trials with either default or user-specified seeds. In the case of multiple trials, VCell automatically calculates histograms of the number of copies for the species of interest. While the algorithm simulates events as they randomly occur, the user can specify regular time intervals at which the results should be displayed.

One problem with deriving stochastic applications from a general VCell BioModel is that the reaction kinetics are introduced in the model as deterministic, and the default option for reaction kinetics in the BioModel workspace, `general kinetics', allows for arbitrary rate expressions. However, an unambiguous interpretation of deterministic rates in terms of Poisson stochastic processes is possible only for mass-action kinetics, and even for this case, the reversible reactions should be decoupled into separate processes. (Indeed, one can be show that generally, different stochastic models can have the same deterministic limit).

A special analyzer tool in VCell automatically maps mass-action reaction rates to probabilistic propensities, and facilitates the mapping of other reactions. The tool identifies the kinetic type of a reaction or membrane flux, and in the case of general kinetics, automatically determines, by parsing the rate expression, whether the mechanism might be a combination of individual Poisson processes (for example, if they are passive fluxes). It then informs the user: (i) which of the mechanisms with kinetics other than mass action can be directly translated into probabilistic propensities (and asks permission to do it automatically), and (ii) which of the mechanisms have to be recast manually by the user into a combination of one or more mass-action types.

2.4 Spatial applications

For situations, where spatial concentration gradients are of importance, VCell provides tools for running spatial simulations. In spatial applications, the set of mechanisms defined in `Physiology' are mapped onto a geometry that must be created in a `Geometry' workspace (details of how to operate VCell can be found in VCell User Guide at http://vcell.org/userdocs/Rel/user_guide.pdf). Geometry is either defined analytically or taken from experimental images. In analytical geometry, the shape of compartments is specified by inequalities in Cartesian coordinates; for instance, a unit sphere centered at the origin is defined as x²+ y²+ z² <1. A most recent version of VCell, VCell 4.7 Beta (http://www.vcell.org/vcell_software/login.html), includes `an assistant' that automatically generates inequalities for a number of predefined primitives.

Geometry can also be created using an experimental image. For this, VCell requires segmented images, in which all pixels belonging to a given compartment have the same pixel value and different compartments have different colors (a 3D image is entered as an ordered stack of 2D segmented slices in a .zip format). Standard image processing tools, such as thresholding, can be utilized to segment the raw image. While currently this is done outside VCell, a set of relatively simple tools are being developed in VCell to help a user prepare a segmented image. As of this writing, these are set to be deployed in the next beta release.

A spatial application is mathematically described by a set of PDEs; it may also include a subset of ODEs for the model that includes immobile molecules whose concentrations vary only due to reactions. Concentrations of immobile molecules may still vary in space because of their binding interactions with mobile components. Since numerical solution to a set of PDEs can be obtained only for a finite set of points in space, the spatial domain for which the solution is sought has to be discretized. The next section describes how this is achieved in VCell.

2.4.1 Handling geometry

Discretization of space in VCell is performed using a relatively simple procedure which is automatic and fast. The geometry of interest, either analytical or experimental, is placed in a rectangular box (computational domain), to which uniform orthogonal meshing is applied (Figure 2). The meshing of the computational domain generates a uniform grid of points with a default resolution and decomposes the computational domain into volume elements centered at grid points (except for `partial' subvolumes adjacent to the domain boundaries). The automatically generated default resolution can be modified by the user by specifying new numbers of mesh points for each Cartesian direction (in doing so, it is important to bear in mind that equilateral volume elements, cubes in 3D and squares in 2D, provide better accuracy, particularly in resolving surfaces, see below). The grid points define locations for which the solution is computed. For a given spatial resolution, approximate geometry is built by assigning a whole volume element to the compartment in which its center (the grid point) is located in the `exact' geometry defined analytically or by a fully resolved segmented image, as described in the preceding section. This automatically yields membranes as watertight pixilated surfaces separating different compartments. The membrane elements are rectangular facets between the volume elements belonging to different compartments; their centers form a surface grid for which densities of the cross-membrane fluxes and surface densities of the membrane-bound molecules are computed.

Figure 2.

A simple 2D example of handling geometry in VCell. A. Computation domain and a cell of an arbitrary shape. B. Mesh lines and grid points.

Structured orthogonal gridding, adopted in VCell, facilitates automatic sampling of cell geometry, particularly when it is based on experimental microscope images where one can only tell whether a square pixel in the image lies inside or outside a compartment. It also allows one to move easily from one-dimensional to two- to three-dimensional simulations. The downside of this approach is that it results in a 'staircase' approximation of cell membranes. While volumes and overall shapes of the compartments converge with an increasing spatial resolution to those prescribed by the user, neither a surface area of the 'staircase', nor distances between the points on the pixilated surface converge to those for a smooth surface when the mesh is refined. This creates difficulties in approximating cross-membrane fluxes and lateral diffusion in the membranes. In VCell, this issue is addressed by applying an optimized approximation of normal vectors to the exact surface in the presence of quantization noise (41, 43). A “flux correction” method and methods for modeling lateral diffusion, which are based on this approximation, produce converging solutions, as demonstrated in (43).

2.4.2 Boundary conditions

Solution to a spatial initial value problem depends on conditions at the boundaries of the computational domain. Imagine that a large number of molecules are injected at the center of the box and allowed to diffuse. It is clear that eventually their distribution will become uniform but the concentration level will depend on properties of the box walls. Indeed, for the impermeable walls (no flux boundary conditions), the final concentration of the molecules in the box will be given by the ratio of the total number of injected molecules and the box volume. However, if the walls are leaky and the outside concentration is clamped at zero or if the walls are ideally absorbing (zero-value boundary conditions), the final concentration of the molecules will be zero. Thus, in order to run spatial simulations, boundary conditions must be specified.

In VCell, the term `boundary conditions' is reserved for the boundary planes, i.e. the walls of the rectangular box enclosing the geometry. The VCell boundary conditions can be of two types, `flux' or `value'. For either type, the boundary condition can be specified as a constant or as an appropriate function of time and place on the boundary plane. They can also be functions of state variables.

Conditions at surfaces representing membranes inside the computational domain, are technically termed `jump conditions', as they determine a jump of concentration across the membrane. However, this term is not explicitly used in the VCell BioModel interface. Rather, the jump conditions are generated automatically in accordance with the membrane mechanisms, such as fluxes through channels and/or reactions of binding to the membrane-associated molecules and unbinding from the membrane. Thus, the jump conditions are generally functions of state variables. They can also depend on spatial coordinates, as is the case for polarized cells, and/or on time like in modeling of photobleaching (section 3.4). The dependence on time and spatial coordinates, however, cannot be introduced directly in the reaction editor of the `Physiology' panel because by design, the mechanisms defined in `Physiology' can be combined with various geometries and experimental protocols specified in different Applications of the BioModel. Instead, one can introduce an auxiliary `regulator' reflecting the spatiotemporal attribute of the process. For example, if a certain membrane flux occurs only at the brush border of an epithelial cell, a `species' Brush_Border can be included in the BioModel as a `regulator' for the corresponding flux. In the Application with a particular geometry, an appropriate spatial dependence can then be specified by using an expression of the Cartesian coordinates, corresponding to the region of the brush border membrane, as an initial condition for the `species' Brush_Border. At the same time, Brush_Border should be flagged as `clamped', which will tell VCell that Brush_Border is not in fact a variable but rather a prescribed function of spatial coordinates.

The MathModel workspace is less restrictive, and the dependence on spatial coordinates and time can be included in the jump conditions directly. Still, to ensure correct implementation of the jump conditions in the MathModel, one should carefully follow certain conventions used in VCell. In particular, the adopted notations for a volumetric concentration of molecule X near the membrane are X_INSIDE and X_OUTSIDE, and the `inside-outside' relation is encoded in the order in which the names of the adjacent compartments appear in the subtitle for a membrane subdomain. Consider a simple example of reversible binding of a cytosolic protein A to a nuclear pore complex NPC. The format of the equation for the bound state A_NPC and the corresponding jump condition for the diffusing protein A is shown below:

In the description above, `InFlux' denotes the flux (per unit area) coming from the membrane into an inside compartment. According to the convention, the name of the inside compartment, which in this case is the nucleus, comes first in the membrane subtitle. Because the binding of the cytosolic protein to the nuclear pore does not produce flux from the membrane into the nucleus, InFlux is zero. `OutFlux' stands for the flux coming from the membrane into the outside compartment, which in our example is the cytosol. Then OutFlux is minus the rate of binding, and the concentration of the protein A near the membrane on the cytosolic side is appended by `_OUTSIDE'. The conversion factor KMOLE is unity if the surface density of A_NPC is in molecules per μm² and the concentration [A] is measured in molecules per μm³; if [A] is measured in μM and the flux density units are μMμm/s, as is the standard for VCell BioModels, then KMOLE=1/602.

The `inside-outside' relationship will not be required in a new VCell release, VCell 5. This will result in a more intuitive notation for the membrane fluxes and the volumetric concentrations near the membrane: the `_INSIDE' and `_OUTSIDE' labels of will be replaced with the names of the corresponding compartments.

2.5 VCell solvers

Realistic biological models do not generally lend themselves to an analytical treatment and therefore must be solved numerically. VCell provides a number of deterministic and stochastic solvers that can be found in the `Simulation-> Edit->Advanced' panel.

The numerical approach to deterministic models, which are formulated continuously in terms of differential equations, requires that the time interval and the spatial domain for which the solution is sought be sampled. The differential equations are then approximated by finite differences with respect to selected grid and time points. Essentially, they are replaced by a system of algebraic equations from which the concentrations can be found for a selected set of points in time and space. While the algebraic system is usually solved with high precision, it is important to realize that the solution is an approximation to that of the original system of differential equations. The magnitude of error depends on the time step and the mesh size (discretization parameters); as they decrease, the solution of the algebraic system should converge to the correct solution. However, small integration time steps and mesh sizes will result in a long computation time, hence a tradeoff between algorithm's accuracy and efficiency.

There are various discretization schemes – ways, in which differential equations can be approximated by a set of algebraic equations, and some of them can become numerically unstable if, for example, the integration time step is insufficiently small to resolve fast processes in the system. Numerical instability can manifest itself as qualitatively wrong behaviors, such as unphysical oscillations or negative concentrations, or an exponential growth of numerical error resulting in machine infinity. Thus, even when the goal of modeling is to get an idea about qualitative behavior of the system and numerical accuracy is not of major concern, the discretization parameters might still be constrained by conditions of numerical stability of the solver. On the other hand, when accuracy is the issue, it is important to remember that even unconditionally stable methods can produce inaccurate results if the time step is not small enough or tolerances are insufficiently strict. It is therefore a good practice to double-check results by running simulations with varying discretization parameters (tolerances) or with different solvers.

2.5.1 ODE solvers

A VCell suite of ODE solvers includes algorithms with fixed and variable time steps. The fixed time step solvers included in VCell sample the time interval uniformly with a step specified by the user and advance the solution from one time point to the next using rates evaluated at the “old” time point (explicit solvers). The explicit time discretization is not unconditionally stable but the methods with higher order of convergence are less susceptible to numerical instability (the order of convergence n determines the rate with which numerical error ε decreases with decreasing time step Δt, n ~ log(ε)/log(Δt)). Solvers with adaptive (variable) time steps do not require a user to specify the integration time step. They automatically adjust the time step within given bounds so that the solution remains sufficiently accurate; for these algorithms, the solution error is controlled by setting up tolerances in the `Advanced' panel of the `Simulation->Edit' window.

Two of the solvers with variable time step, IDA and CVODE, are unconditionally stable (50). They propagate the solution in time on the basis of rates corresponding to the “new” time point. This is a so-called implicit discretization scheme resulting in a system of nonlinear algebraic equations that must be solved iteratively. These solvers are the best choice when dealing with `stiff' systems that involve disparate time scales (for more details about stiff systems, see section 2.5.3).

2.5.2 PDE solvers

VCell currently provides two solvers for running spatial simulations: semi-implicit and fully implicit. There are two versions of the semi-implicit solver, compiled and interpreted. The interpreted version has better error annotation, while the compiled version might be more efficient. The semi-implicit solver is a fixed time-step integrator that requires a user to specify the integration time step (note that simulation results do not have to be saved for each integration step; a time interval at which the data should be saved is specified separately). Numerical errors can be estimated by comparing results obtained with different time steps.

The algorithm is based on a discretization scheme that converts a system of m PDEs (m is the number of variables in the model) into m independent systems of linear algebraic equations. The systems of equations are solved using a robust iterative linear solver based on preconditioned conjugate gradients (a general minimal residual algorithm (GMRES), PCGPAK (Scientific Computing Associates, New Haven, CT) (51). Linearization of equations is achieved by treating reactions and fluxes explicitly, which makes the method prone to numerical instability if the time step is insufficiently small to resolve fast processes in the system.

A recently developed fully implicit spatial solver, accessible through VCell version 4.7 (and later), is unconditionally stable. The algorithm uses the method of lines (52) to convert the system of PDEs into mN coupled nonlinear ODEs (N is the number of grid points), which are then solved using robust solvers from SUNDIALS (Lawrence Livermore National Laboratory, CA) (53). These are adaptive time step solvers; therefore the user does not have to worry about the integration time step when using the fully implicit spatial solver. Accuracy of the solution is controlled by tolerances. The default relative and absolute tolerances are set in VCell at 1e-9.

2.5.3 Handling disparate time scales

Biological models often include processes with drastically different time scales, e.g. some reactions can be several orders of magnitude faster than others. Mathematically, the systems with disparate time scales (`stiff' systems) are particularly prone to numerical instabilities, as they require small time steps to resolve fast processes. As a consequence, stiffness impedes efficiency of computations, since in order to avoid numerical instabilities, very short time steps must be used even if only the long timescale behavior of the system is of interest. Because adaptive `stiff' solvers (IDA and CVODE, for ODEs, and the fully implicit spatial solver) are unconditionally stable, they are generally suitable for treating stiff systems, but they can also be inefficient.

In situations where some reactions continue to be much faster than others during the entire simulated time, as is the case, for example, with calcium buffering (54), a quasi-steady-state approximation (QSSA) provides an accurate and efficient alternative. In this approximation, fast reactions are considered to be near equilibrium, and the corresponding ODEs are replaced with algebraic equations corresponding to steady-state conditions (55) (the mathematically accurate formulation of this approach is sometimes called singular perturbation theory). VCell supports automatic implementation of QSSA with respect to any reactions labeled as `fast' (56). In fact, this is all that a user has to do to invoke QSSA in VCell. The underlying algorithm automatically transforms the original model into a differential- algebraic system, where the subsystem of differential equations includes only slow reaction rates whereas the algebraic subsystem reflects instantaneous equilibration of fast reactions. For compartmental applications, where this transformation is exact, QSSA is performed in combination with Forward Euler or IDA ODE solvers (in VCell 4.7, also with the Combined Stiff Solver). For spatial simulations, QSSA is implemented in combination with the semi-implicit solver. In this case, the separation of the fast and slow subsystems is not exact and results in an additional `splitting' error (57) which is usually comparable to the error of solving diffusion. Overall, applying QSSA can improve simulation times by several orders of magnitude and make it practical to explicitly include the effects of rapid binding of buffers and fluorescent indicators on the behavior of molecules to which they bind.

2.5.4 Stochastic solvers

Methods for simulating stochastic processes are based on generating (pseudo)random numbers. They are called Monte Carlo methods; the term was originally introduced by S. Ulam and J. von Neumann in the days of the Manhattan Project, as throwing a dice is actually a way of generating random numbers. The Monte Carlo algorithms rely on the quality of a random number generator which produces pseudorandom sequences that mimic a random variable ξ uniformly distributed on the segment [0,1], and on a variety of methods that then transform ξ into a new variable η with the probability distribution of interest (58).

Similarly to deterministic models, stochastic systems can be advanced in time using a fixed time step; this approach is utilized, for instance, in Brownian Dynamics simulations (59). Generation of random numbers is used to determine whether a reaction will occur during the time step. The fixed time step methods are approximate, with the error determined by the size of the time step. In contrast, the exact, or event-driven, algorithms, introduced in chemical dynamics by D. Gillespie (49, 60), are free of this error, as they simulate stochastically both the reaction that occurs next and the time between consecutive reaction events. The latter is achieved by taking into account that discrete reaction events are Poisson processes. In the so-called `first reaction' method, for example, one uses current probability rates (propensities) to sample putative reaction times for all reactions, then the reaction with the least time is deemed to be occurring next and the system is updated accordingly.

In VCell, stochastic simulations of compartmental models are based on the `next reaction' algorithm (48), which uses certain properties of Poisson processes and other important observations to drastically improve efficiency of the first-reaction method. It takes advantage of the fact that connectivity of reactants through reactions is usually sparse, which allows one to reuse reaction times that have not been affected by the current event, and uses a fast heap-like sorting algorithm, an `indexed priority queue', in searching for the reaction with a minimal projected time.

The exact stochastic simulator may be inefficient when applied to stiff systems with vastly different reaction rates. For this case, a number of approximate `hybrid' solvers have been proposed (61–63). They advance the system in time with a reasonably large fixed time increment and thus allow for an appropriate compromise between accuracy and efficiency. The idea behind the hybrid methods is to treat fast reactions by superimposing Gaussian noise over deterministic dynamics, while simulating slow reactions exactly. A challenge is to account for a possible feedback from the fast subsystem onto the slow one. VCell incorporates an open source library Hy3S (hysss.sourceforge.net/index.shtml) written by H. Salis, which implements hybrid methods optimized for accuracy (64–66). Still, it is important to remember that hybrid methods are approximate, as they use certain `reasonable' criteria for separating fast and slow reactions. The user may want to modify default parameters of these criteria, that are accessible in the 'Simulation->Edit->Advanced' panel, to achieve a best-suited tradeoff between accuracy and efficiency of the simulation.

2.6 Managing complexity

VCell provides a number of tools that facilitate the analysis and building of complicated models.

2.6.2 Parameter scanning and parameter estimation

The option of parameter scanning allows a user to run a batch of simulations for a selected set of combinations of parameter values. For this, the user specifies ranges and the number of values within a range that will be selected, either uniformly or logarithmically, for scanning. This is done by checking boxes in the `Scan' column, under the `Edit>Parameters' tab. VCell then automatically initiates simulations for all combinations of selected parameters. The results can be viewed for each parameter combination separately, by selecting parameters from the table at the bottom of the `Results' window.

The parameter estimation option includes two optimization solvers that automatically find a combination of parameters that minimizes differences between experimental time series and predictions form a compartmental model. Details of how to perform parameter estimation in VCell can be found in VCell User Guide at http://vcell.org/userdocs/Rel/user_guide.pdf. Caution should be exercised in using optimization techniques. First, optimization of a complex nonlinear model may yield different results for different initial guesses, i.e. the optimization problem might have multiple solutions. Second, a minimum found by the solver might be shallow so that even large deviations from “optimal” parameters would result only in slight changes of the fit. This might indicate that the model parameters cannot be faithfully identified based on a given set of experimental data. Overall, it is important to bear in mind that fitting the data by parameter optimization may yield misleading results unless it is accompanied by a careful analysis of sufficiency of the available data for unique parameterization of the model.

2.6.1 Analysis of sensitivities

One way to estimate the 'goodness-of-fit' is to analyze how the model responds to deviations of parameters from the optimal values. The model is usually expected to be not very sensitive to parameter changes unless there are reasons to believe that certain parameters have been fine-tuned by natural selection. The sensitivity analysis might also yield predictions that could be tested experimentally. These tests either validate the model or require its revision. Knowing local sensitivities of the model might also be helpful in finding the path of “steepest descent” when the fitting is done manually by trial and error.

The local sensitivities (also known as control coefficients in the metabolic control analysis) are defined as the change in the model output, Δ[X], caused by perturbation of a particular parameter α, divided by the magnitude of the perturbation, Δ α More precisely, the local sensitivity is the derivative ∂[X ] / ∂α evaluated at a particular point in the parameter space. Sometimes it is more informative to compute the ratios of relative changes of the output and the parameter; these ratios are called logarithmic sensitivities, ∂ log[X ] / ∂ logα. VCell provides a tool for the local sensitivity analysis of the compartmental models. When invoked, it prompts VCell to solve the initial value problem for the local sensitivities (or logarithmic sensitivities) along with the solution of the model for a particular parameter set.

2.6.3 BioNetGen@VCell

Building a large BioModel, involving binding interactions among multiple molecular species that generate numerous intermediate complexes, might be tedious. An intuitive and convenient way of handling combinatorial complexity that arise from molecules with multiple binding sites, known as rule-based modeling, has been implemented in the software called BioNetGen (67). In this approach, each molecule in the system is characterized by a set of binding sites which may carry attributes (e. g. a tyrosine residue can be phosphorylated or unphosphorylated). Interactions between molecular species are governed by a set of reaction rules that specify reaction probability rates and conditions in which the reaction can occur. The rule also specifies modifications of attributes of interacting molecules as a result of their interaction. This method, which is particularly efficient for the case of noncooperative interactions, automatically keeps track of changes of attributes and connectivity.

A VCell user can access this method through a BioNetGen@VCell service by clicking the `BioNetGen' button on the tool bar of the BioModel workspace. This will allow the user to write or upload a BioNetGen input file and perform reaction network generation and time courses simulation. A VCell BioModel can then be automatically generated and processed by the Virtual Cell.

3. What one can accomplish with the Virtual Cell (review of published studies)

The goal of this section is to demonstrate how VCell can be applied to various cell biological problems. For this, we review studies published by different research groups in which they used VCell to create and solve models. We discuss biological contexts of these applications and methods used to build models and run simulations. In some cases, we also discuss published models that were reproduced in VCell.

3.1 Quantitative studies of calcium dynamics

Calcium plays a central role in relaying intracellular signals in both excitable and non-excitable cells. Because it can readily be measured in cells with fluorescent indicators and quantitative microscopy and because calcium channels can be quantitatively studied with electrophysiological methods, a wealth of data is available for model input, constraint and validation. In addition, calcium signals can display intriguing behaviors in cells such as oscillations and waves. For these reasons, intracellular calcium dynamics has become the subject of hundreds of mathematical models (68–72). It was natural, therefore, that calcium was the target of the first VCell models (31, 73–75) and continues to be a subject that is especially appropriate for the VCell software (76–88).

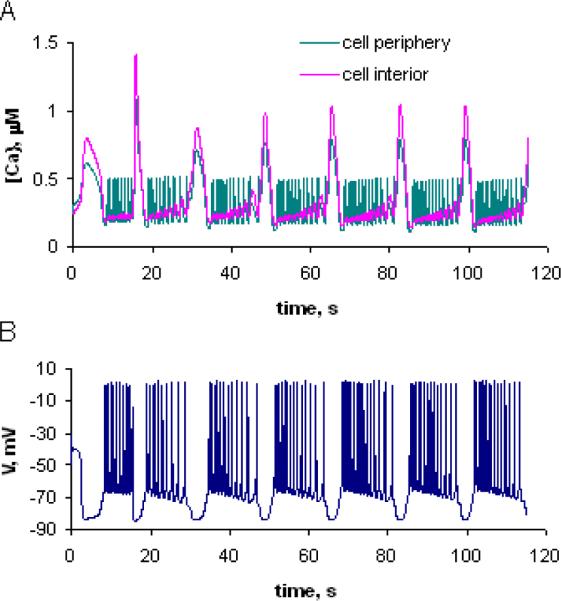
The two papers by Fink et al. on calcium dynamics in a cultured neuronal cell line (73, 74) serve as good examples of how modeling can aid in the interpretation of experimental results, i.e. “data-driven modeling”. The basic experimental result is shown on the left in Figure 3. In these experiments, bradykinin, an agonist for a G-protein coupled receptor, is added to a coverslip with adherent differentiated N1E-115 neuroblastoma cells. The experiment in Figure 3 shows that calcium increases after a delay of about 2.5s after addition of bradykinin. It first peaks in the thin neurite of the cell and shortly thereafter spreads to the soma. The calcium level reaches about 1.2μM in all regions of the cell before decaying over the next 30s. Time courses for the calcium changes in the neurite (green) and soma (yellow) are shown in the adjacent plots. These features of the spatiotemporal calcium response to bradykinin were stereotypical for cells with this general morphology. Simulations can then predict the bradykinin-induced changes in free Ca²⁺ within the experimental geometry derived from microscope images. Fluorescence microscopy of the calcium indicator Fura-2 provided the data (left of Figure 3) for validation of a model.

Figure 3.

Calcium dynamics in a neuroblastoma cell: experiment and modeling

While the two papers (73, 74) used the MathModel workspace to create a series of VCell models, subsequent improvements in the BioModel workspace permitted us to implement them as multiple Applications within one BioModel (see the public model “Ca_Release_Fink_etal_1999&2000” under username CMC). The Physiology contained structures corresponding to the extracellular space, the cytosol, the ER and the nucleus. Activation of the bradykinin receptor leads to activation of phospholipase C, which produces inositol-1,4,5-trisphosphate (IP₃) at the cytosolic side of the plasma membrane. IP₃ then binds to the IP₃ receptor in the endoplasmic reticulum (ER) membrane, activating it to release calcium. The IP₃ receptor is also regulated by calcium in a complex and still somewhat controversial mechanism with evidence for both positive and negative feedback at different levels of calcium (68). Other components of the mechanism that also must be included in the model are calcium leak and calcium pump fluxes across the ER membrane, binding of calcium by cytoplasmic buffers, extrusion of calcium form the cell via plasma membrane ATPase and degradation of IP₃ via metabolic enzymes in the cytosol. All of the rate laws for these individual mechanisms as well as the concentration of the relevant molecular species could be derived from experiments.

The Applications include a compartmental model, to establish the steady state distributions of all the species before activation of the bradykinin receptor, and several 2D spatial models. For the latter, the extracellular space, cytosol and nucleus were mapped to the corresponding regions within the experimental geometry; but the ER, because it is too fine and convoluted a structure to be resolved, was modeled as a continuously distributed compartment within the cytosol, using a volume fraction of 0.15. The simulation in the Figure 3 labeled “Best Fit” recapitulates the experimental results very well, but the Application that was implemented first in this study (labeled “Uniform ER”) gave a very poor match to the experiment. This initial model produced a much higher calcium signal in the neurite than in the soma. This result was a consequence of the higher levels of IP₃ that were produced in the neurite compared to the soma and this was a consequence, in turn, of the higher surface to volume ratio in the neurite: diffusion of IP₃ was too slow to equalize concentrations throughout the cell before substantial degradation of the IP₃ due to metabolic enzymes. However, this led to the realization that the higher transient levels of IP₃ in the neurite could be compensated by a higher sensitivity to IP₃ in the soma. One way to achieve this would be to have a higher density of ER in the soma compared to the neurite. This hypothesis was then tested by extensive immunofluorescence imaging of ER markers, including the IP₃ receptor itself. The result was a finding that the ER density was, indeed, ~ 2 fold higher in the soma than in the neurite. When this non-uniform distribution of ER was mapped onto the geometry in a new spatial Application, the simulation labeled “Best Fit” in Figure 3 was the result. Thus, this study showed how iterations between experiment and modeling can yield new insights into how morphology can be fine tuned to control cell signaling.

To perform a calcium imaging experiment, an indicator is required. But the indicator binds to free calcium and must be present at concentration of 20–100μM for sufficient fluorescence signal. The “Best Fit” model included the calcium indicator, Fura-2, at a level of 75μM, as this was the intracellular concentration used in the experiment. But once this full model is constructed and validated, it is a simple operation to run a simulation in which the [Fura-2] is set to zero. The results, shown in the rightmost column of Figure 3, reveal that the Fura-2 has a profound effect on the measurement; the Ca²⁺ appears much earlier (0.8s vs. 2.5s) and has twice the amplitude compared to the model containing Fura-2. Thus the simulations can be used to back out the perturbing effect of the fluorescent indicator.

In the original papers (73, 74), additional validations of the model against experiments were carried out, including experiments where bradykinin was applied focally to different regions of the cells and where IP₃ was released simultaneously throughout the volume of the cell via photolysis of a caged IP₃ that had been microinjected. In all cases, the simulations recapitulated the results of the experiments. This lends credibility to the basic accuracy of the “Best Fit” model.

3.2 Nucleocytoplasmic transport: experiment and models

Nucleocytoplasmic transport of proteins and nucleic acids is crucial for normal functioning of eukaryotic cells. It occurs by way of nuclear pore complexes (NPC); small molecules passively diffuse through the nuclear pores, whereas passage of large molecules is facilitated by binding to transport receptors (carriers). In the nucleus, unloading of the imported cargo from the carrier requires binding to RanGTP, a GTP-bound form of a small GTPase Ran. After the transport receptor, free of cargo but bound to RanGTP, returns to the cytosol, it unbinds from Ran when RanGTP is hydrolyzed by the GTPase-activating protein RanGAP, which completes the cycle. The process is thus controlled by activation and inactivation of Ran, which in turn cycles between the cytosol and the nucleus. Because at least one molecule of Ran is translocated in each direction for each complete cycle of carrier-cargo transport, the cargo flux can be estimated if the steady-state flux of Ran is known.

Experimental and computational approaches were combined in a study of Ran transport (89), aimed at determining factors that contribute most toward the overall regulation of the nucleocytoplasmic flux at steady state. The computational component of the paper is another example of data-driven modeling. Given that measuring parameters of the overall transport in intact cells is hardly feasible, the behavior of the system is analyzed by building a model from well characterized components of Ran transport.

An overall kinetic scheme of the Ran cycle that underlies the model is shown in Figure 4. Directionality of fluxes of Ran in a strongly non-equilibrium steady state is maintained by a spatial separation of RanGAP localized exclusively to the cytosol from the Ran exchange factor RCC1 bound to chromatin. Hydrolysis of RanGTP in the cytosol, catalyzed by RanGAP, is irreversible and consumes metabolic energy. Nucleotide exchange in the nucleus facilitated by RCC1, while comprised of reversible reactions, is effectively irreversible as well, due to strong asymmetry in concentrations of GTP and GDP maintained at the expense of metabolic energy. All other mechanisms are reversible, including the passage of RanGTP and RanGDP through NPC. The latter is facilitated by binding to the nuclear transport factor NTF2.

Figure 4.

Diagram of a minimal model of nucleocytoplasmic transport.

The model was implemented and simulated with VCell. Results of spatial simulations performed on experimental 3D geometry were close to the compartmental approximation, indicating that the latter was sufficiently accurate. The reversible reactions of the type X+A↔AX were described by the mass action kinetics, v=−k_on[X][A]+k_off[AX]; the irreversible enzyme-mediated reactions were approximated with the Michaelis-Menten rates, v_X=k_cat[E][X](K_m+[X])⁻¹, where [E] is the enzyme concentration. The nuclear membrane flux densities were modeled as j_X = P_X([X]_cytosol − [X]_nucleus).

Parameters of reversible binding interactions and enzyme-mediated reactions were constrained by reported data. To determine other parameters, in particular the permeability of NPC to NTF2:RanGDP and carrier:RanGTP, the fluorescently labeled recombinant Ran was injected into the cytosol of BHK-21 cells, and the nuclear accumulation of Ran was imaged at 0.5-s intervals until steady state was reached, usually within 12 to 30 s (at 23 °C) (89). Additionally, microinjection of a fluorescently labeled mutant Ran(T24N) defective in binding NTF2 showed that passive diffusion of Ran through a pore constitute less than 4% of the facilitated transport. Both initial accumulation rates and the steady-state nucleus-to-cytosol ratio of total concentrations of fluorescent Ran were used to constrain the permeabilities and the activity of RCC1. Comparing experimental results with simulations was facilitated by explicit incorporation of fluorescent Ran in the model (note that in this case, the tagged molecules, X_tag, compete with the endogenous molecules X for the same enzyme and therefore the Michaelis-Menten rates for a tagged species should be v_{X_tag}=k_cat[E][X_tag]/(K_m+[X]+[X_tag])).

Once the model was established, it was used to estimate the rate of the steady state nucleocytoplasmic transport and its sensitivity to various contributing factors. The total in vivo flux was estimated to be 260 molecules per NPC per second per direction, assuming 3000 pores per nucleus. The nucleocytoplasmic transport was found to be sensitive to the permeability of NPC to NTF2:RanGDP, the concentration of NTF2 and, most of all, to the activity of RCC1. Additional experiments with microinjection of NTF2 and RanBP1 were performed to validate results of the sensitivity analysis. Simulations also indicated a very steep gradient of Ran GTP across the nuclear envelope which was later confirmed by direct measurements (90). Three public math models can be accessed under user `boris' : `AliciaProblem1_5' (the basic compartmental model in (89)); `AliciaProblem1_5Fast' (compartmental model where mass action kinetics are treated as fast; this model was used to obtain initial conditions for spatial simulations). `AliciaSpatial_NewFast' (the spatial model used in (89). A public Biomodel can be found under user `les' and is entitled `Smith et al System Analysis of Ran Transport'. This is a later version of the model and is corrected for the competition between RanGDP and NTF2:RanGDP for the same site on RCC1.

A conceptually similar model of nucleocytoplasmic transport was published in (91). Constrained by experiments with HeLa cells, it predicted surprisingly different transport sensitivities: the authors arrived at the conclusion that the transport is much more sensitive to the NPC permeability for RanGDP than to the activity of RCC1. Comparative analysis of the two models is obscured by their apparent structural differences. Gorlich et al. (91) provided a detailed description of the chain of reactions involving RCC1, whereas in the VCell model this was modeled by approximate Michaelis-Menten kinetics. On the other hand, Smith et al. (89) explicitly introduced binding of Ran to `generic' karyopherins, whereas in (91) this was modeled by an equivalent `load'. A careful comparison of the models showed that the effective Michaelis-Menten constants of the nucleotide exchange computed on the basis of detailed modeling of reactions involving RCC1, V_max= 9.6 μM/s and K_m =1.7 μM, were indeed somewhat different from the values V_max= k_cat[RCC1]_total=3.4 μM/s and K_m =1.1 μM used in the VCell model. But the major factor that led to the reversal in the prediction of a limiting factor was an almost 20-fold difference in the pore permeability to RanGDP (1). Indeed, Smith et al. estimated the permeability of the nuclear envelope to RanGDP (in effect, to NTF2:RanGDP) as 3.73 μm/s, which, when converted to the `bulk' permeability with respect to the nucleus using the surface-to-volume ratio of 0.6 μm⁻¹, yields 2.24 s⁻¹, compared to 0.12 s⁻¹ used in (91).

How has this discrepancy come about, given that the initial accumulation rates upon injection of ~1μM of fluorescent Ran are similar: ~0.4 μM/s in BHK-21 cells vs. 0.48 μM/s in HeLa cells? The raw data indicate that both cell types have apparent `bulk' permeabilities in the 0.3 to 0.5 s⁻¹ range. However, based on these data, the actual permeability for NTF2:RanGDP must be significantly higher because only a small fraction of the injected Ran gets to bind NTF2. Thus, the apparent value of the permeability, utilized in (91) in order to avoid explicit incorporation of NTF2 in the model, is an underestimation of the actual permeability (the additional four-fold reduction was apparently an adjustment to the NTF2 level of 0.3 μM; in (89), an estimate for the NTF2 average concentration was the equivalent of 1.5 μM of NTF binding sites). While this approximation yields reasonable predictions for the overall Ran transport, it significantly overestimates the sensitivity of transport with respect to facilitated diffusivity of RanGDP through NPC.

More detailed models of Ran transport (92, 93), created on the basis of the minimal models discussed above, were simulated with the aid of VCell in (92).

3.3 Compartmental and spatially resolved models of cell signaling

Many experimental groups have been using VCell to create models for, and numerically simulate, various aspects of cell signaling. These include mechanisms of G-protein-coupled receptor signaling (94, 95), processes involving PIP2 (phosphatidylinositol 4,5-bisphosphate) (76, 83, 96–98), the JAK-STAT signaling pathway (99), spatiotemporal dynamics of cAMP (82, 100–103), pathways of small GTPases (104–106), signaling events in cell cycle (107, 108), spatial gradient sensing in chemotaxis and signaling in cell migration (13, 109–111). Both compartmental and spatial applications have been implemented. To access them, simply click the `access' link at www.vcell.org/vcell_models/published_models.html and follow the instructions. Below we discuss two representative applications of VCell to cell-signaling problems.

3.3.1 A compartmental model of G-protein receptor signaling

In a recent paper (95), a comprehensive kinetic model of G_q-coupled M₁ muscarinic (acetylcholine) receptor signaling has been formulated. The study is another characteristic example of data-driven modeling, where the authors seek to reproduce the time courses and concentration-response relationships that they measured using Föster resonance energy transfer (FRET). The model was implemented in VCell and the results of compartmental simulations were compared with whole-cell measurements. The public model `FalkenburgerJGP2010' can be found in the BioModel Shared folder under the username `hillelab'.

We will consider the part of the model that is common for many different G-protein coupled receptors (Figure 5): binding of the agonist (ligand, L) to the receptor (R) increases the receptor's affinity for G proteins whose Gα_q subunit is in the inactive GDP-bound form; binding of G proteins to the bound receptor amplifies nucleotide exchange on Gα_q subunit, which leads to dissociation of the GTP-bound form of the Gα_q subunit from the G-protein αβγ trimer. The GTP-bound form of the Gα_q subunit is active and acts as an effector for the downstream events (in particular, it activates PLC, which eventually turns off KCNQ2/3 channels). All the mechanisms in the model occur in the plasma membrane and all the species, except for the agonist, are membrane-bound and are assumed to diffuse freely. The binding of the ligand to the receptor is modeled without accounting for `resting' forms of the receptor because the available FRET data are insufficient for distinguishing between the different ligand forms. On the same grounds, the model does not discriminate between the events of nucleotide exchange and G-protein dissociation. For demonstration purposes, we simplify the model further by ignoring the slow `parallel' processes, such as the binding of G protein to the receptor that is not bound to the ligand and the nucleotide exchange on G proteins that are not bound to the receptor or bound to the receptor that is not bound to the ligand.

Figure 5.

Diagram of G-protein receptor activation.

All reaction rates in the pathway, v_reaction, are described by the mass-action kinetics:

L-R binding:	vR-L=kfR-L[R][L]-krR-L [RL],
G-RL binding:	vG-RL=kfG-RL[G][RL]- krG-RL [RLG],
Nucleotide exchange and trimer dissociation:	vRLG= kNX_RLG[RLG].

One of the key steps in building a kinetic model is constraining rate constants and initial concentrations. In cases where direct measurements are not feasible, the parameters are estimated by fitting the model to dynamics of the system as a whole. In that case, it is important to analyze sufficiency of available experimental information for unique parameterization of the model. In (95), the concentrations were measured directly, whereas the model kinetic constants were constrained by time courses recorded for the intermediate components of the system using FRET. The authors carefully annotated parameter values and provided their detailed discussion. For the reactions outlined above, the parameter values were as follows: k_f^R-L =2.8 μM⁻¹s⁻¹, k_r^R-L = 5.5 s⁻¹, k_f^G-RL = 2.7×10⁻³ μm² s⁻¹, k_r^G-RL =0.68 s⁻¹, k_{NX_RLG} = 0.65 s⁻¹. The endogenous total concentrations were: [R] = 1 μm² and [G] = 40 μm². The results of Figure 5 in (95) were obtained for the total concentration of the ligand [L]= 10 μM. This information is sufficient for implementing the model in VCell and running simulations. We encourage readers to do this exercise and compare results with those obtained in (95).

3.3.2 A spatial model of gradient sensing in chemotaxis

We now consider an example of `conceptual' modeling which, unlike data-driven modeling, does not seek an accurate fit for a particular set of experimental data, but rather aims at elucidating a qualitative phenomenon, in this case, robustness of adaptation along with persistent gradient sensing in chemotaxis.

Cells are able to detect chemical gradients in which the concentration of a chemoattractant varies by only a few percent across the cell size. Furthermore, gradient detection is robust over a wide range of average background concentrations. This excludes a simple threshold mechanism and requires a more sophisticated design of directional sensing.

In a `local excitation global inhibition (LEGI)' model proposed in (112), an effector (signal S, Figure 6A), activated by a G-protein receptor, regulates a downstream enzyme (a response element) R through activating intermediate activator and inhibitor enzymes (A and I, respectively). The model is based on three main ideas: (i) robust adaptation can be achieved if S activates both A and I with functionally similar kinetics but the activation of the inhibitor is slower than that of the activator; (ii) robust adaptation can coexist with signal amplification if A and/or I also regulate the supply of R; and (iii) polarization of the cell by spatial gradients of active R is achieved if A localizes to the membrane and does not diffuse, whereas cytosolic I diffuses rapidly throughout the cell.

Figure 6.

LEGI model. A. Mechanism of perfect adaptation (for notations, see text). B. Simulated chemoattractant gradient (Application `Needle' of the public BioModel `LEGI', username `LiuYang'). C. Simulated distribution of activated PI3K induced by the chemoattractant gradient in B.

A generic version of the model was implemented and simulated in VCell (13). The BioModel `LEGI', found in the shared BioModel folder under the username `LiuYang', describes emergence of a polar distribution of the membrane-bound molecules of activated PI3K in response to spatial gradients of the chemoattractant L (Figure 6B,C). The spatial application `Needle' employs a simple 2D geometry with a point-like source of chemoattractant located at one of the corners of the computational domain. The cell shape is circular and all initial distributions are uniform.

In the model, the source of chemoattractant is implemented by introducing an auxiliary `species' `L_source' mimicking a pipette in the extracellular (`EC') compartment. At the level of Application, this species is flagged as `clamped' in the subpanel `Initial Conditions'. This tells VCell that `L_source' is not actually a variable and therefore does not have to be solved for. Instead, it is assigned a value specified in the column `Initial Conditions'. For a `clamped' species, this value can be a number or any expression in terms of Cartesian coordinates and time, and can therefore be used to define geometry, location, and duration of the source. In the application `Needle', the source is permanent and defined as a small circle of radius 1 centered at a corner with coordinates [15, 15]. Correspondingly, the value is specified as inequality, (x-15)<sup>2</sup>+(y-15)<sup>2</sup><1. This is a logical (Boolean) expression evaluated as either zero, for points whose coordinates do not satisfy the inequality, or one, otherwise. Note that `LEGI' is a minimal model which does not include signal amplification mechanisms (see assumption (ii) above).

3.4 Analysis of fluorescence microscopy data

In a number of studies, VCell was used as a tool for analyzing microscopy data obtained in experiments that use the techniques of fluorescence redistribution after photobleaching (FRAP), photoactivation or photorelease (21, 113–116).

Roy et al. (114) explored light-directed perturbation techniques by activating a caged form of thymosin ß4 (Tbeta4) in a defined local region of locomoting fish scale keratocytes. Computer simulations of a 2D VCell model of uncaging Tbeta4 (model `7_12_00_model1' under username `partharoy') predicted that rapid sequestration of actin monomers by uncaged Tbeta4 and the consequent reduction in the diffusional spread of the Tbeta4-actin complex could potentially affect locomotion of the keratocyte. Indeed, local uncaging of Tbeta4 at the wings of locomoting keratocytes resulted in a specific turning about the photorelease site thus providing insight into possible mechanisms of the turning behavior of keratocytes.

A detailed model of a FRAP experiment was implemented in VCell (username 'Lagnado Lab', public model 'TIR_FRAP') to analyze FRAP data in the study of vesicle dynamics at the ribbon synapse of retinal bipolar cells (115). The model includes excitation and emission processes, by which fluorescing and non- fluorescing states of a labeled particle alternate, and a photobleaching step. The distribution of light is specified through the initial conditions of an auxiliary `species' Light_spec, defined as `clamped' in the Application `FrapIt'. The laser was turned on between 1 and 2 s, which was implemented by a multiplier `Light' in the rate expressions for excitation and bleaching: Light= 1.0 + 315.2 * ((t >= 1.0) && (t < 2.0)). Simulations, run in an analytically defined 3D geometry, produced a reasonable fit to the experimental data with an effective diffusion coefficient of approximately 0.01μm² s⁻¹.

Two-photon photoactivation of a postsynaptic scaffolding protein PSD-95 tagged with photoactivatable GFP (paGFP) was used in (113) to study dynamics of PSD-95 in the postsynaptic density (PSD), a protein-enriched postsynaptic region of a dendritic spine. Dendritic spines, on which most excitatory synapses terminate, vary in size and synaptic strength. PSD-95 is an abundant scaffolding protein that clusters glutamate receptors and is thought to determine the size and strength of synapses. Clusters of synaptic PSD-95 were photoactivated in layer 2/3 dendrites in the developing barrel cortex. While a subset of PSD-95 clusters was stable for days, a rapidly turning over dynamic pool of PSD-95 was observed, with retention times ~ 1 hr, which exchanged by diffusion with PSD-95 in neighboring spines. To simulate dynamics of PSD-95:paGFP, the authors created a 2D VCell model, using reasonable estimates of binding constants and diffusion rates. The analysis suggested that individual PSDs compete for PSD-95 and that the kinetic interactions between PSD molecules and PSDs are tuned to regulate the PSD size.

Similar observations were made in a study of a different biological system, also thought to be very stable, the tight junctions of epithelial cells (116). Photoactivation and photobleaching experiments indicated that some of the tight-junction proteins, such as ZO-1 and occludin, were turning over on ~ 1-hr scale. A set of VCell BioModels (username `leshen') were created to simulate the experiments. As in (115), photomanupilation was implemented in the models by introducing a `clamped' species `Laser' that was used in Applications to define the location of the area affected by the laser and the duration of irradiation. By changing the duration of the beam, the same model can be used to simulate FRAP, where the laser is turned on for a short time, and FLIP (fluorescence loss in photobleaching), where bleaching is continuous. Similarly, by varying the size and location of the bleached area, one can simulate photobleaching of small and large parts of the tight junction or the bleaching of the cytosol or the plasma membrane in FLIP experiments. Simulations in (116) were run on an analytically defined 3D geometry. Analysis of the experimental data showed that the fluorescence recovery of ZO-1 was largely due to binding of the cytosolic ZO-1 to the tight junction. In contrast, the main mechanism behind the turnover of occludin was diffusion within the tight junction, with a possible contribution from binding of occludin from the surrounding membrane.

FLIP was used in (21) to quantify the in vivo interaction between the plasma membrane and a small GTPase Rac, a regulator of actin cytoskeleton. Rac cycles between the membrane and the cytosol as it is activated by nucleotide exchange factors (GEFs) and inactivated by GTPase-activating proteins (GAPs). Solubility in the cytosol is conferred by binding of Rac to guanine-nucleotide dissociation inhibitors (GDIs). To determine the dissociation rate constant (k_off) of the membrane-bound Rac, NIH3T3 fibroblasts expressing GFP-Rac were bleached continuously by a laser beam everywhere except for a small masked region at cell periphery (Figure 7A). Using a confocal microscope, fluorescence loss was simultaneously recorded in the unbleached region and in the proximal area in the bleached region (Figure 7B). Decay of the signal in the unbleached region was caused by dissociation of Rac from the membrane followed by diffusion in the cytosol and, as it turned out, also by diffusion of the membrane-bound Rac out of the unbleached region.

Figure 7.

Modeling FLIP experiments.

A. Diagram of the experimental setup.

B. Fluorescence time courses measured in the bleached and unbleached areas.

C. 3D geometry used in (43) to simulate FLIP experiments. The geometry was reconstructed in VCell from a z-stack of confocal slices. The cut shows the cell interior including the nucleus. The mask over the unbleached region, shown in black, mimics the experimental setup.

A simple compartmental model built on the assumption of fast diffusion of Rac in the cytosol pointed to a two-step procedure of retrieving k_off from the raw data: first, fit the fluorescence decay in the bleached region by a two-exponential function (the second component was likely due to inhomogeneity of light in z-direction); second, fit the fluorescence decay in the unbleached region by a some of three exponentials, two of which are the same as in step 1; then the rate constant of the third exponential is k_off + k_diff, where k_diff, the rate constant due to the lateral diffusion of Rac, was estimated in a separate experiment. Using this procedure, the following values of k_off were found: 0.048 s⁻¹, for the wtRac, and approximately 10-fold less (0.004 s s⁻¹) for G12VRac, the mutant that remained constitutively in its GTP-bound conformation. Overexpression of the GEF Tiam1 unexpectedly decreased k_off for wtRac, most likely by converting membrane-bound GDP-Rac back to GTP-Rac. Both overexpression and small hairpin RNA-mediated suppression of RhoGDI strongly affected the amount of membrane-bound Rac but surprisingly had only slight effects on k_off. These results showed that RhoGDI controls Rac function mainly through influencing activation and/or membrane association.

The method of measuring k_off was derived on the assumption that diffusion of Rac in the cytosol is much faster than the processes contributing to the loss of fluorescence in the unbleached area. To assess the accuracy of this assumption, a 3D VCell MathModel was constructed to simulate the FLIP experiment on a realistic cell geometry (Figure 7C) (43). The idea was to mimic the experimental protocol, collect the data in the way they were collected in real experiments, subject the simulated data to the fitting procedure and compare the obtained estimates of k_off with the “exact” values used in the model. These numerical tests generally validated the fitting procedure but also pointed to a possible underestimation of k_off (up to 30%) in cases where Rac is tightly bound to the membrane, because tight binding effectively slows down diffusion of Rac in the cytosol. The corresponding MathModel, `Schwartz_3D_FLIP', can be accessed in the MathModel Database under username `boris'.

3.5 Modeling of cell electrophysiology

VCell can be used to model dynamics of membrane potential and ion currents (81–83, 86, 94, 95, 98, 117, 118). In the BioModel workspace, this is done at the Application level by using the `Electrical Mapping' tool. This tool allows one to model voltage and current clamp protocols or stay in the default `no clamp' configuration. In modeling voltage/current clamps, the applied voltage/current can be specified either as a constant or as an arbitrary function of time. The latter can include inequalities, such as (t>t₁)&&(t< t₂), to model turning the clamp on and off at particular times t₁ and t₂ (>t₁). In the `no clamp' configuration, one should check the box `Calculate V?' and specify the initial conditions for the membrane potential V. The user can also override the default value of specific membrane capacitance set at 0.01 pF/μm². The ion currents are defined in the `Physiology' window as membrane mechanisms, with an option to automatically account for the corresponding molecular fluxes. A default `General Current' kinetic type in the Reaction Editor window allows a user to enter an arbitrary equation for the ion current. Alternatively, one of the predefined approximations of the membrane ion currents can be selected.

These tools were used in (83, 94, 95, 98, 117) to create compartmental (nonspatial) electrophysiological models. The models can be accessed in the Shared folder of the BioModel Database under username `hillelab'.

In the MathModel workspace, compartmental models include the membrane potential as an ODE variable with the rate of change (I − Σ^I_X) /C_m where I is the applied current in the current clamp protocol (otherwise I=0), the sum of ion currents is taken over all ion molecules X crossing the membrane, and C_m is the membrane capacitance. The membrane potential (voltage) is conventionally defined as V =ϕ_in−ϕ_out where ϕ_in and ϕ_out are the potentials inside and outside the cell, respectively. This convention assigns a positive direction to outward currents. The MathModel workspace was used in (81, 82, 86, 118) to create compartmental models for simulating dynamics of membrane potential coupled to calcium dynamics in pancreatic beta-cells; these models can be accessed in the MathModels Database under username `Fridlyand'.

VCell can also be used to reproduce previously published models. In 1997, Li et al. (39) developed a model of an excitable endocrine cell gonadotroph. The model involves technically nontrivial coupling between spatially resolved dynamics of calcium and dynamics of membrane potential. VCell provides tools for the implementation of this type of model (see the BioModel `Gndph_wBuffer' under username `boris'). The model is essentially a combination of two models, one for Ca²⁺ oscillations mediated by the endoplasmic reticulum (ER) through the inositol 1,4,5-trisphosphate (IP₃)-receptor channels and another for Ca²⁺ oscillations driven by the plasma membrane potential. It is instructive to implement complex models by parts, each of which could be tested separately. The first two compartmental applications of the BioModel `Gndph_wBuffer' were designed for testing separately the voltage and calcium modules of the model. The modules were then combined to run spatial simulations on a simple analytical geometry (Application `spatial_analyt'). The results from one such simulation are illustrated in Figure 8.

Figure 8.

Results of a simulation of the BioModel `Gdnph-wBuffer'. A. Calcium dynamics at cell periphery (green) and cell interior (red). B. Dynamics of membrane potential.

The spatial model of calcium dynamics coupled to dynamics of membrane potential can also be implemented in the MathModel workspace as a standalone mathematical model. The format of the VCell math description required for the implementation this coupling can be gleaned from the description that is automatically generated in the BioModel workspace. For this, one should use the `View Math' tab in the Application window and then select `View Model Description Language'. Of note, the membrane potential in this description, as well as the corresponding equation type, is declared as `MembraneRegionVariable'.

Li et al. demonstrated that their model agreed with existed experimental records of cytosolic and ER Ca²⁺ concentrations and electrical activity in gonadotrophs. On this basis, they argued that the sensing of ER Ca²⁺ content could occur without the Ca²⁺ release-activated Ca²⁺ current (Icrac), but rather through the coupling of IP₃-induced Ca²⁺ oscillations to plasma membrane voltage spikes that gate Ca²⁺ entry. They concluded that in excitable cells that do not express Icrac, profiles of cytosolic Ca²⁺ provide a sensitive mechanism for regulating net calcium flux through the plasma membrane during both ER depletion and refilling.

Mathematically, both of the excitable components of the gonadotroph model are essentially based on the Hodgkin-Huxley mechanism. The classic Hodgkin-Huxley model has also been implemented in VCell and can be accessed under username `Tutorial' in the Shared Model folder of the BioModel Database.

3.6 Intracellular transport: interplay of binding, flow and “active” diffusion

VCell supports implementation of models that include diffusion and/or directed transport. The VCell capability of modeling directed flow has been recently used to describe possible effects of fluid flow inside moving keratocytes (119, 120) and for modeling intracellular transport of organelles driven by molecular motors (42). Similarly to diffusion, directed transport in VCell is described using a continuous approximation, i.e. without resolving individual particles; this approximation is applicable when the number of particles participating in directed transport is sufficiently large.

To invoke this capability, the user needs to define the direction and magnitude of the velocity of species experiencing directed flow, or in mathematical terms, to specify their `velocity vector field' everywhere in the computational domain. This is done by providing Cartesian components of the velocity, either as constant values or as functions of spatial coordinates (the velocities can also be functions of time and the state variables of the system). Below we discuss in more detail how this capability can be used for modeling intracellular organelle transport (42).

In cells, organelles and vesicles are transported along cytoskeletal tracks by molecular motors: the motors of kinesin and dynein families pull cargos along microtubules (MTs), whereas myosins move along actin filaments (AFs). MTs generally serve as tracks for long-range transport, whereas AFs support local movements. Because the organelle may bind simultaneously all types of motors, it can switch tracks along the way. The switching events in vivo cannot be detected reliably by light microscopy because of the high density of MTs and AFs in the cytoplasm.

In (42), the rate constants for the switching of organelles between MT and AF transport systems were estimated for fish melanophores, pigment cells whose major function is redistribution of membrane-bounded pigment granules to ensure color changes of the fish in response to environmental cues: intracellular signals can induce aggregation of pigment granules at the cell center or their uniform dispersion throughout the cytoplasm, and during these movements the granules use both MT and AF tracks. Pigment aggregation occurs predominantly along MTs, while dispersion involves a combination of MT-based and AF-based transport; so the switching between the two types of cytoskeletal tracks must be tightly regulated by intracellular signals.

Given that individual movements along MT and AF had been well characterized by particle tracking during aggregation or dispersion in cells where one of the two transport systems was disabled, the idea was to use a computational model with the two well constrained modules coupled by the switching events. The switching rate constants could then be determined from fitting the model to an additional set of data - spatiotemporal dynamics of pigment measured at low magnification.

The model was formulated in terms of pigment densities associated, for a given location and time, with MT and AF (the MT-associated density, in turn, was composed of densities of granules that were driven by plus- or minus-end motors, or pausing). Given random directionality of AFs, the AF-bound transport was approximated by effective diffusion (the approximation is sometimes termed `active diffusion' because the movements of granules are not just thermal fluctuations but rather motor-driven). The movements of MT-associated pigment densities were described as directed flows.

How are velocities defined for these flows? First, it is reasonable to approximate the geometry as two-dimensional, because the lamellum where the pigment redistribution takes place is essentially flat. Second, given that MTs originate from a centrosome, one can assume, for modeling purposes, that they form an ideal radial array. Individual microtubules are not resolved in the continuous approximation, but their spatial organization defines directions of velocities of the MT-associated flow of pigment. By placing the origin of the coordinate system at the position of the centrosome, the velocity projections of the MT-associated plus-end flow can be approximated as $v_x=v_k\frac{x}{\sqrt{x^2+y^2+{\epsilon }^2}},v_y=v_k\frac{y}{\sqrt{x^2+y^2+{\epsilon }^2}}$, where v_K is the kinesin velocity and ε is a technical parameter, which should be much smaller than the spatial resolution of geometry, included to avoid division by zero. The velocities of the minus-end flow have the opposite direction and should be scaled by the dynein velocity v_D. Note that the circular symmetry reduces the spatial dimensionality of the problem, as all unknowns become dependent only on the distance to the center (42).

Special care is required in formulating jump and boundary conditions for variables described by directed flow. For example, modeling pigment dispersion can easily produce spikes of pigment density at the cell periphery that were not seen in the experimental data. In (42), this problem was overcome by including in the model a realistic distribution of the MT plus ends; this distribution was a decreasing function approaching zero near the cell edge.

Fitting of the spatiotemporal dynamics of the pigment density by the model (Figure 9) yielded the following switching rate constants: for dispersion, k_MT->AF = 6.5 min⁻¹ and k_AF>MT<=0.0025 min⁻¹, whereas for aggregation, k_MT->AF = 4.5 min⁻¹ and k_AF->MT=10.7 min⁻¹. Note that k_AF->MT is spatially dependent because it is proportional to the local MT density which decreases towards the cell periphery; the values shown above correspond to the cell interior. Also, the aggregation value of k_MT->AF might be overestimated because the binding of the pigment granule to MT, occurring in the model with equal probability everywhere on the microtubule, can in fact be biased towards the MT plus end, as has been shown for frog melanophores(121); in these cells, the bias is caused by CLIP-170 bound to MT tips. Still, the results indicate that signals that induce transitions from dispersion to aggregation largely affect the rate constant for the transferring of granules from AFs to MTs, k_{AF -> MT}, and to a lesser extent, k_MT->AF. This correlates with sharp changes in the activity of the cytoplasmic dynein, indicating that the primary role in these transitions is played by regulation of dynein.

Figure 9.

Intracellular transport of pigment granules in fish melanophores (42). A. Experiment: a snapshot of pigment aggregation (top); time courses averaged over multiple scans in several cells, shown for equidistant locations along cell “radius” during dispersion (middle) and aggregation (bottom). B. Model: idealized geometry, with the black circle mimicking the location of the pigment aggregate (top); simulated time courses of pigment density during dispersion (middle) and aggregation (bottom).

3.7 Deterministic and stochastic modeling of gene regulatory networks

VCell supports stochastic simulations of compartmental (nonspatial) models. As with deterministic simulations, there are two ways to set up a stochastic simulation in VCell: (i) by automatically generating a stochastic application in the BioModel workspace or (ii) by manually creating an editable stochastic math description in the Math Model workspace following a VCell template. As an example, below is shown a stochastic math description corresponding to the enzymatic reaction depicted in Figure 10.

Figure 10.

Stochastic simulations of a simple reaction network. A. Diagram of an enzymatic reaction: substrate S reversibly binds enzyme E, after which intermediate compound ES irreversibly decays into E and product P (for parameter values, see the math description in the text). B. Stochastic time course of the number of ES molecules. C. Probability distribution of the ES copy number at time t=4.0 obtained from 10000 trials.

In the description above, the constant `Size_Cell' describes the cell volume in cubic microns. Copying this description into the MathModel workspace creates a valid VCell stochastic model. Figure 10 illustrates simulation results obtained with this model. Note that stochastic trajectories from different runs of the same model may differ unless the corresponding pseudorandom sequences are obtained with the same seed (by default, the seed is generated randomly but can be specified by the user in the `Advanced' panel). In contrast, histograms built on the basis of a large number of trials should be close for different runs of the same model.

The stochastic modeling tool in VCell is designed to make it easy to treat the same model both deterministically and stochastically. In fact, the `Copy As' option in the Application dialog allows one to create a stochastic version of the model by a push of a button. This is how a stochastic version of a model was created within the VCell BioModel `CSH_09_circadian_clock` (username `boris'), that reproduces a generic model of circadian clocks proposed in (122, 123). The papers represent another example of `conceptual' modeling where the emphasis is placed on demonstrating the system design and mechanisms that are required to achieve particular properties, in this case for sustaining regular oscillations in the face of external and internal noise. Particular parameter values in this type of model are not an issue so long as they are in appropriate ranges.

Circadian clocks are periodic biological processes by which organisms keep sense of daily time and regulate their behavior accordingly. Most of these clocks utilize intracellular genetic networks based on positive and negative regulatory elements. The minimal model described in (123) includes essential components commonly found in experiments. It involves two genes, an activator and a repressor, which are transcribed into mRNA and subsequently translated into protein. The activator protein A binds to promoters of both genes which increases their transcription rate. It therefore acts as the positive element in transcription. The repressor protein sequesters the activator upon forming an inactive complex with it: the complex decays into a repressor molecule. Thus, the repressor acts as a negative regulator. Oscillatory behavior occurs when the dynamics of activators is significantly faster than those of the repressors and inactive complexes (for detailed analysis, see (123)).

When creating a VCell model with the intention to analyze it both deterministically and stochastically (the way the model was studied in (123)), it is advisable to avoid using the `catalyst' tool but instead to implement the binding explicitly, as it is done in the BioModel `CSH_09_circadian_clock`(Figure 11). The reason is that in VCell the mass-action kinetics, required for stochastic simulations in the BioModel workspace, cannot be applied to reactions implemented with the `catalyst' tool.

Figure 11.

Implementation of translation events in the BioModel workspace. The mRNA_A can be included as a catalyst (A, dashed line) or through explicit binding (B, solid lines). Both variants are equivalent but in VCell only variant B allows for the mass-action kinetic type required for stochastic simulations in the BioModel workspace.

The model in (123) demonstrates that with the positive and negative feedbacks at the gene level, circadian clocks need not rely on mRNA dynamics to oscillate, which makes them resistant to fluctuations. Oscillations persist even when the time average of the number of mRNA molecules becomes less than one. Moreover, simulations of the model indicate that stochasticity may even enhance robustness of oscillations: in the stochastic version of the model in (123), oscillations exist in a wider parameter range than in the deterministic model.

3.8 Problems in cell migration: Actin dynamics

The Virtual Cell was applied to the analysis of various aspects of cell migration including cell signaling (see BioModels under username `CMC') and gliding motility of keratocytes in which the cell shape does not change (e.g., MathModels under username `ignovak'). This section reviews these applications with the emphasis on actin dynamics.

Actin, one of the most abundant molecules in the cell, is present as coexisting pools of monomer, called G-actin, and polymer, called F-actin. The F-actin polymer cytoskeleton provides structural support for the cell cortex. What's more, the fascinating dynamics of these actin containing structures are critical for such diverse morphological changes as muscle contraction, neurite pathfinding, endocytosis, cytokinesis, and cell motility. These varied and precisely controlled functions of the actin cytoskeleton require the interaction with many regulatory proteins and signaling molecules to control the dynamic organization of the actin polymer network. Indeed, scores of actin binding partners have been identified and the functions of many are known (124–128). In particular, the molecules controlling actin-driven protrusions at the leading edge of migrating cells have been intensely studied over the last 15 years. A key step in this process is activation of the Arp2/3 complex at the cytoplasmic face of the plasma membrane in the lamellipodium, which then binds to actin filaments and nucleates new F-actin (129, 130) to produce a dense, highly branched actin polymer network (130–133). Electron microscopy of the lamellipodium reveals a thin, dense meshwork of filaments composed of relatively short segments compared to less branched, longer F-actin distributions to the rear of the cell (134). The force produced by the rapidly polymerizing F-actin against the plasma membrane results in rearward movement of this network and also produces the protrusive force that drives the lamellipodium forward (132, 135–137).

As was the case for modeling of calcium (Section 3.1), mathematical analysis of actin dynamics benefits from a wealth of quantitative data on the kinetics of polymerization in the presence of actin binding proteins, which provides excellent input data for models, as well as live cell imaging experiments against which models can be validated (131–133, 138–141). However, modeling of polymerization, especially the complex mechanisms of regulated actin polymerization, presents some special challenges. This is because the rate of assembly and disassembly is different at the two ends of the polymer (the “barbed” and “pointed” ends); it also depends on the state of the subunits within the polymer and where those subunit states reside relative to either end. In particular, actin subunits can exist in three nucleotide bound states within the polymer and can be associated with various binding proteins. Furthermore, the rate of fragmentation or annealing of filaments as well as their diffusion rates depend on the length of the filaments. Detailed discrete stochastic models that follow individual monomers and filaments (142–145) can solve this problem by keeping track of all the individual states, but this becomes computationally prohibitive for realistic numbers of actin molecules and their binding partners in a cell. There have also appeared continuum models that can recapitulate in vitro experiments on steady state distributions of filament size and turnover, where the number of different species is relatively low (146–151) and several of these have employed Virtual Cell to help analyze the experiments (114, 149–151).

Another modeling approach is to avoid the details and develop phenomenological mathematical models that use physical principles to reproduce a specific cellular mechanism – `conceptual models'. This approach has indeed proven powerful in suggesting or explaining experiments. For example, recent papers have shown how models with a relatively small number of variables that abstract essential features of actin dynamics can explain the variable shape of motile keratocytes (152), show that G-actin diffusion is sufficient to deliver monomers to the actively polymerizing leading edge (119), the relationship of protrusion velocity and the concentration of barbed ends (147) or the relationship between severing and capping in controlling acting polymerization (153). Again, models of this type have used VCell (119, 120).

But detailed models that explicitly include as many of the known mechanisms as possible would also be extremely useful. First, they can permit simulations that mirror experimental manipulations and thus help to guide the design and interpretation of experimental results. For example, how would knockdown of a protein that caps filament ends change F-actin accumulation in the lamellipodium? At first glance, one might expect that if capping proteins inhibit addition of monomers to ends, such an experiment should increase F-actin. But that fails to account, for example, for the effect of capping on the available pool of G-actin, which is required for stimulated polymerization at the leading edge. Furthermore, this pool might depend not only on capping protein, but also on several other molecules that interact with both F-actin and G-actin. A model that explicitly includes all of these molecules and their interactions can be very useful in sorting out the key factors and making experimentally testable predictions. Second, computational models that integrate many mechanisms and molecules involved in a complex cellular process provide a powerful means for organizing our knowledge about the components of the system. Building the model requires evaluating differing, sometimes conflicting, data sources and deciding how to best formulate a biochemical or biophysical rate expression. These choices amount to an intense level of integration and curation of the available information. Of course, the modeling software has to be designed with layers to permit the expression of abstractions related to biochemical and biophysical mechanisms. As discussed in section 2, this separate layer in VCell is the Physiology. The database structure of VCell allows each of the species and reactions comprising the Physiology to be treated as components that can be searched and cut, copied or pasted from one model to another. Thus, in addition to producing simulations, the VCell model serves as a flexible container for biochemical and biophysical data that is readily interpretable and extensible and is much richer than a pathway database.

A detailed model of this type was built in VCell for the process of actin dendritic nucleation, which governs cell protrusion (154). The model was formulated in a continuous approximation, i.e. in terms of concentrations of molecules. The molecules included in the model were actin, a generic nucleation promoting factor associated with the membrane (called NWASP in the model), Arp2/3, capping protein, profilin (which catalyzes exchange of ATP for ADP on G-actin), ADF/cofilin (a filament severing protein) and thymosin-ß4 (a molecule that act as a buffer for G-actin); also included were the association of the various actin species with ATP, ADP and ADPPi (an intermediate in which ATP has been hydrolyzed, but phosphate has not yet fully dissociated to produce ADP). To describe all the mechanisms associated with this seemingly limited list of building blocks required 60 species and 155 reactions. It is important to appreciate that even this large number of reactions included many approximations where multiple individual transformations were lumped into single rate expressions. This was necessitated by the infinite number of states accessible to a polymerizing system. But, adding to the challenge of this “lumping” process, the rates of these individual transformations are often dependent on the length and nature of the polymer. An example will serve to illustrate how these approximations were made by Ditlev et al. (154). For polymeric actin, a single fixed diffusion coefficient would not be appropriate, given the large spatial and temporal variation in the size and degree of branching of the filaments following localized stimulation of polymerization. Therefore, the F-actin diffusion was modeled according to the following equation:

$$\frac{D_{GActin}}{FilamentLength}\ast (1-BranchFraction)$$

The inverse relationship of diffusion to length for a linear polymer is well established in polymer physical chemistry (155); the FilamentLength at each point in space is calculated from the state variables of the system as the sum of all F-actin species (i.e. the total F-actin) divided by the sum of all pointed end species. To account for the diminution of diffusion for a highly interconnected branched network, the equation reduces the diffusion coefficient by the fraction of filaments associated with branches; BranchFraction is determined from the state variables as the sum of all the species corresponding to an Arp2/3 capped pointed end bound to a mother F-actin filament (giving the concentration of branched filament segments), divided by the sum of all the pointed end species (whether Arp2/3 capped or not; giving the total concentration of filament segements). Full details on how other key modeling challenges were met (e.g. addition and dissociation of nucleotide-bound subunits to the pointed and barbed ends of filaments with varying nucleotide compositions) can be found in the paper (154) and in several public VCell models under username `les': BioModels “Actin Dendritic Nucleation” and “Actin Dendritic Nucleation_Detailed Mechanism”; MathModels “Actin Advection and Diffusion” and “Actin Advection and Diffusion 2D Cylindrical Transform”. Parenthetically, at the time the work for this paper was carried out, it was not possible to express velocity fields and spatially variable diffusion within a BioModel, which is why MathModels were used to produce spatial simulations; since the paper was published, all of these features have been added to the BioModel interface.

Simulations performed with this model were able to quantitatively reproduce many of the features of both in vivo and in vitro actin dynamics including: the accumulation of F-actin in the lamellipodium (Figure 12b), the high concentration of barbed ends at the cell edge, the average lengths of filaments as a function of capping protein, the dependence of actin turnover on capping protein and profilin and the branching and filament length distributions within the lamellipodium. The model was also able to resolve conflicting reports on the affect of ADF/cofilin activity on the accumulation of F-actin in the lamellipodium: ADF/cofilin was shown in the model to be able to both inhibit and potentiate polymerization depending on the capping protein activity. Here, we will highlight one outcome of the simulations that illustrates how VCell simulations can provide valuable insights on not just the distribution of molecular species but also on the rates of reactions. Using a 3D analytical geometry that captures the generic structure of a cell migrating on a flat substrate, Figure 12d shows how the model recapitulates the sharp boundary between polymerization and depolymerization discovered by speckle microscopy experiments (Figure 12c) (156–159). The model shows that this behavior does not require any special hypothetical depolymerization factor behind the leading edge, but rather emerges from the interplay of rearward flow of the actin network, barbed end capping, and dissociation of Arp2/3 branches to expose free pointed ends. In particular, the model predicts that stabilizing Arp2/3 branches should move the boundary toward the rear and decrease its sharpness.

Figure 12.

Selected features of the actin dendritic nucleation model. (a) Surface rendering of the outer membrane of the 3D geometry used for the VCell simulations. A graded band of active NWASP on the front of the lamelipodium membrane recruits and activates Arp2/3 to initiate nucleation. (b) Simulations run to steady state produce F-actin accumulation in the lamellipodium, as shown in this plane at the bottom of the 3D geometry. The scale shows how the colors are mapped to concentrations of actin subunits within filaments. (c) Map of net polymerization and depolymerization activity in the lamellipodium of an epithelial cell derived from speckle microscopy experiments (156). Note the sharp transition between polymerization at the edge and depolymerization within 2μm of the edge (white scale bar is 5μm). (d) Simulation result for net actin polymerization rates at steady state. The white band shows a region of strong polymerization and is 2μm wide before a sharp transition to depolymerization (negative rates). Behind these two bands of activity, the bulk of the cell displays near zero actin filament assembly rates. Figure 12 c is reproduced from ….by permission of the copyright owner.

4. Future directions in developing tools for modeling in cell biology

VCell and other software packages designed for cell biologists provide a variety of tools for modeling a wide range of cell phenomena. Still, a number of limitations preclude realistic modeling of important processes that are of interest to biologists. For example, modeling diffusion in VCell with a constant diffusion rate amounts to describing the cytoplasm as uniform, a hardly realistic assumption. One can introduce the diffusion coefficient as a function of spatial coordinates but that might not be an accurate way of including effects of heterogeneity caused by internal membranes and cytoskeletal structures (160). Implementation of rigorous coarse-grain approaches that would account for processes occurring on multiple spatial scales might be necessary for fully understanding the properties of the intracellular environment (161).

Multi-scale modeling is also required for adequate description of reactions in crowded spaces. Methods that are currently employed in VCell do not resolve individual molecules, effectively assuming that they do not take any space. This `ideal gas' approximation hampers modeling of important cellular processes, such as molecular aggregation and polymerization.

VCell provides tools for spatial simulations on experimental geometries, but the geometry must be fixed. This does not permit modeling of dynamic changes of cell shape which play an important role in cytokinesis, chemotaxis, and generally, in cell migration. Implementation of tools for simulating these processes within a general-purpose infrastructure is challenging, as it requires coupling of mechanics and chemical dynamics, fast automated front tracking, and solving diffusion-flow-reaction systems on domains with moving boundaries, which are all areas of active research in computational physics.

But should all modeling tools be implemented within a single general-purpose computational framework? One could argue that that would mirror the way in which cells work. However, efficiency and manageability requirements place limits beyond which the software becomes slow and difficult to use and maintain. For some cases, a lightweight specialized package designed for a particular purpose might be more practical (162).

Resolving these and other issues will determine how VCell can be made even more useful and give direction for development of a new generation of tools for modeling in cell biology.