Representation Theoretic Patterns in Three-Dimensional Cryo-Electron Microscopy II—The Class Averaging Problem

Abstract

In this paper we study the formal algebraic structure underlying the intrinsic classification algorithm, recently introduced in Singer et al. (SIAM J. Imaging Sci. 2011, accepted), for classifying noisy projection images of similar viewing directions in three-dimensional cryo-electron microscopy (cryo-EM). This preliminary classification is of fundamental importance in determining the three-dimensional structure of macromolecules from cryo-EM images. Inspecting this algebraic structure we obtain a conceptual explanation for the admissibility (correctness) of the algorithm and a proof of its numerical stability. The proof relies on studying the spectral properties of an integral operator of geometric origin on the two-dimensional sphere, called the localized parallel transport operator. Along the way, we continue to develop the representation theoretic set-up for three-dimensional cryo-EM that was initiated in Hadani and Singer (Ann. Math. 2010, accepted).

1 Introduction

The goal in cryo-EM is to determine the three-dimensional structure of a molecule from noisy projection images taken at unknown random orientations by an electron microscope, i.e., a random Computational Tomography (CT). Determining three-dimensional structures of large biological molecules remains vitally important, as witnessed, for example, by the 2003 Chemistry Nobel Prize, co-awarded to R. MacKinnon for resolving the three-dimensional structure of the Shaker K+ channel protein [1, 4], and by the 2009 Chemistry Nobel Prize, awarded to V. Ramakrishnan, T. Steitz and A. Yonath for studies of the structure and function of the ribosome. The standard procedure for structure determination of large molecules is X-ray crystallography. The challenge in this method is often more in the crystallization itself than in the interpretation of the X-ray results, since many large molecules, including various types of proteins, have so far withstood all attempts to crystallize them.

Cryo-EM is an alternative approach to X-ray crystallography. In this approach, samples of identical molecules are rapidly immobilized in a thin layer of vitreous ice (this is an ice without crystals). The cryo-EM imaging process produces a large collection of tomographic projections, corresponding to many copies of the same molecule, each immobilized in a different and unknown orientation. The intensity of the pixels in a given projection image is correlated, [5], with the line integrals of the electric potential induced by the molecule along the path of the imaging electrons (see Fig. 1). The goal is to reconstruct the three-dimensional structure of the molecule from such a collection of projection images. The main problem is that the highly intense electron beam damages the molecule and, therefore, it is problematic to take projection images of the same molecule at known different directions as in the case of classical CT¹. In other words, a single molecule is imaged only once, rendering an extremely low signal-to-noise ratio (SNR), mostly due to shot noise induced by the maximal allowed electron dose.

Fig. 1.

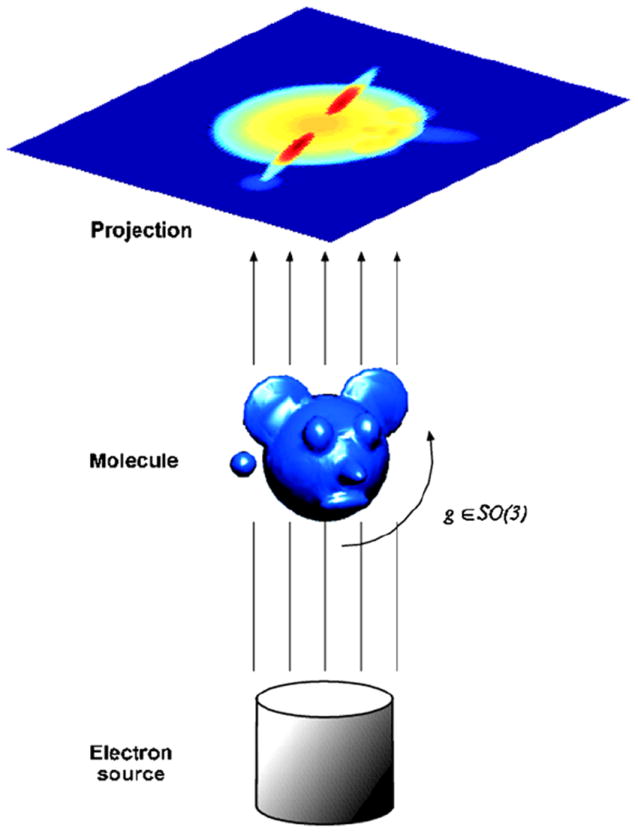
Schematic drawing of the imaging process: every projection image corresponds to some unknown spatial orientation of the molecule

1.1 Mathematical Model

Instead of thinking of a multitude of molecules immobilized in various orientations and observed by an electron microscope held in a fixed position, it is more convenient to think of a single molecule, observed by an electron microscope from various orientations. Thus, an orientation describes a configuration of the microscope instead of that of the molecule.

Let (V, (·, ·)) be an oriented three-dimensional Euclidean vector space. The reader can take V to be ℝ³ and (·, ·) to be the standard inner product. Let X = Fr(V) be the oriented frame manifold associated to V; a point x ∈ X is an orthonormal basis x = (e₁, e₂, e₃) of V compatible with the orientation. The third vector e₃ is distinguished, denoted by π(x) and called the viewing direction. More concretely, if we identify V with ℝ³, then a point in X can be thought of as a matrix belonging to the special orthogonal group SO(3), whose first, second and third columns are the vectors e₁, e₂ and e₃ respectively.

Using this terminology, the physics of cryo-EM is modeled as follows:

• The molecule is modeled by a real valued function ϕ : V → ℝ, describing the electromagnetic potential induced from the charges in the molecule.

• A spatial orientation of the microscope is modeled by an orthonormal frame x ∈ X. The third vector π(x) is the viewing direction of the microscope and the plane spanned by the first two vectors e₁ and e₂ is the plane of the camera equipped with the coordinate system of the camera (see Fig. 2).

• The projection image obtained by the microscope, when observing the molecule from a spatial orientation x is a real valued function I : ℝ² → ℝ, given by the X-ray projection along the viewing direction:

  $$I(p,q)={\mathrm{Xray}}_x\varphi (p,q)={\mathit{\int }}_{t\in ℝ}\varphi (p{e}_1+q{e}_2+t{e}_3)\mathrm{d}r.$$

  for every (p, q) ∈ ℝ².

Fig. 2.

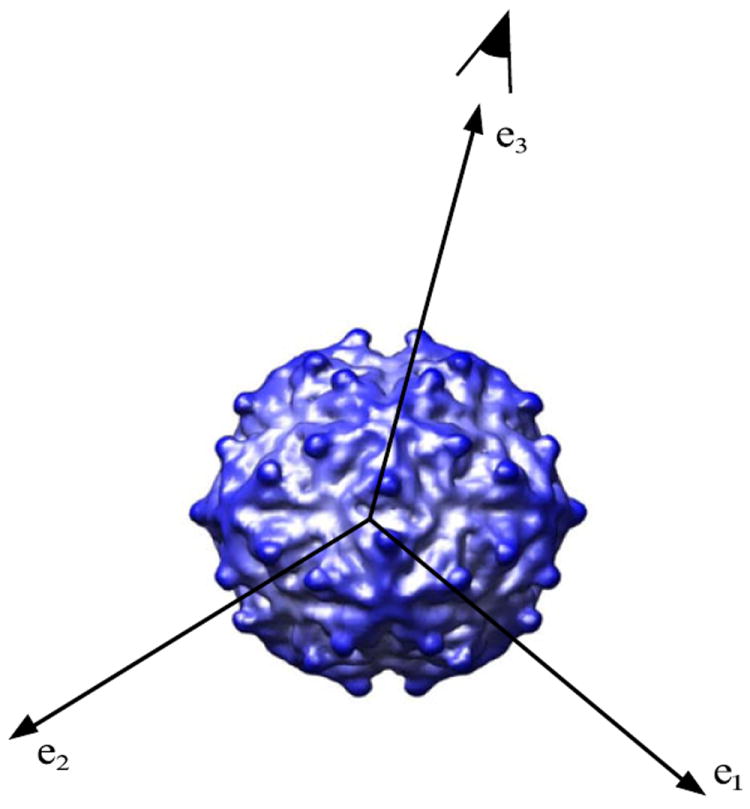
A frame x = (e₁, e₂, e₃) modeling the orientation of the electron microscope, where π(x) = e₃ is the viewing direction and the pair (e₁, e₂) establishes the coordinates of the camera

The data collected from the experiment are a set consisting of N projection images P = {I₁, …, I_N}. Assuming that the potential function ϕ is generic², in the sense that each image I_i ∈ P can originate from a unique frame x_i ∈ X, the main problem of cryo-EM is, [7, 13], to reconstruct the (unique) unknown frame x_i ∈ X associated with each projection image I_i ∈ P.

1.2 Class Averaging

As projection images in cryo-EM have extremely low SNR³ (see Fig. 3), a crucial initial step in all reconstruction methods is “class averaging” [2]. Class averaging is the grouping of a large data set of noisy raw projection images into clusters, such that images within a single cluster have similar viewing directions. Averaging rotationally aligned noisy images within each cluster results in “class averages”; these are images that enjoy a higher SNR and are used in later cryo-EM procedures such as the angular reconstitution procedure, [11, 12], which requires better quality images. Finding consistent class averages is challenging due to the high level of noise in the raw images.

Fig. 3.

The left most image is a clean simulated projection image of the E.coli 50S ribosomal subunit. The other three images are real electron microscope images of the same subunit

The starting point for the classification is the idea that visual similarity between projection images suggests vicinity between viewing directions of the corresponding (unknown) frames. The similarity between images I_i and I_j is measured by their invariant distance (introduced in [6]) which is the Euclidean distance between the images when they are optimally aligned with respect to in-plane rotations, namely

$$d(I_i,I_j)=\underset{g\in \mathrm{SO}(2)}{\min }\Vert R(g)I_i-I_j\Vert ,$$ (1.1)

where

$$R(g)I(p,q)=I(g^{-1}(p,q)),$$

for any function I : ℝ² → ℝ.

One can choose some threshold value ε, such that d(I_i, I_j) ≤ ε is indicative that perhaps the corresponding frames x_i and x_j have nearby viewing directions. The threshold ε defines an undirected graph G = (Vertices, Edges) with vertices labeled by numbers 1, …, N and an edge connecting vertex i with vertex j if and only if the invariant distance between the projection images I_i and I_j is smaller than ε, namely

$$\{i,j\}\in \mathrm{Edges}\iff d(I_i,I_j)\le \epsilon .$$

In an ideal noiseless world, the graph G acquires the geometry of the unit sphere S(V), namely, two images are connected by an edge if and only if their corresponding viewing directions are close on the sphere, in the sense that they belong to some small spherical cap of opening angle a = a(ε).

However, the real world is far from ideal as it is governed by noise; hence, it often happens that two images of completely different viewing directions have small invariant distance. This can happen when the realizations of the noise in the two images match well for some random in-plane rotation, leading to spurious neighbor identification. Therefore, the naïve approach of averaging the rotationally aligned nearest neighbor images can sometimes yield a poor estimate of the true signal in the reference image.

To summarize

From this point of view, the main problem is to distinguish the good edges from the bad ones in the graph G, or, in other words, to distinguish the true neighbors from the false ones (called outliers). The existence of outliers is the reason why the classification problem is non-trivial. We emphasize that without excluding the outliers, averaging rotationally aligned images of small invariant distance (1.1) yields a poor estimate of the true signal, rendering the problem of three-dimensional reconstruction from cryo-EM images non-feasible. In this respect, the class averaging problem is of fundamental importance.

1.3 Main Results

In [8], we introduced a novel algorithm, referred to in this paper as the intrinsic classification algorithm, for classifying noisy projection images of similar viewing directions. The main appealing property of this new algorithm is its extreme robustness to noise and to the presence of outliers; in addition, it also enjoys efficient time and space complexity. These properties are explained thoroughly in [8], which includes also a large number of numerical experiments.

In this paper we study the formal algebraic structure that underlies the intrinsic classification algorithm. Inspecting this algebraic structure we obtain a conceptual explanation for the admissibility (correctness) of the algorithm and a proof of its numerical stability, thus putting it on firm mathematical grounds. The proof relies on the study of a certain integral operator T_h on X, of geometric origin, called the localized parallel transport operator. Specifically:

• Admissibility amounts to the fact that the maximal eigenspace of T_h is a three-dimensional complex Hermitian vector space and that there is a canonical identification of Hermitian vector spaces between this eigenspace and the complexified vector space W = CV.

• Numerical stability amounts to the existence of a spectral gap which separates the maximal eigenvalue of T_h from the rest of the spectrum, which enables one to obtain a stable numerical approximation of the corresponding eigenspace and of other related geometric structures.

The main technical result of this paper is a complete description of the spectral properties of the localized parallel transport operator. Along the way, we continue to develop the mathematical set-up for cryo-EM that was initiated in [3], thus further elucidating the central role played by representation theoretic principles in this scientific discipline.

The remainder of the introduction is devoted to a detailed description of the intrinsic classification algorithm and to an explanation of the main ideas and results of this paper.

1.4 Transport Data

A preliminary step is to extract certain geometric data from the set of projection images, called (local) empirical transport data.

When computing the invariant distance between images I_i and I_j we also record the rotation matrix in SO(2) that realizes the minimum in (1.1) and denote this special rotation by T̃ (i, j), that is,

$$\stackrel{\sim }{T}(i,j)=\underset{g\in \mathrm{SO}(2)}{\mathrm{argmin}}\Vert R(g)I_i-I_j\Vert ,$$ (1.2)

noting that

$$\stackrel{\sim }{T}(j,i)=\stackrel{\sim }{T}{(i,j)}^{-1}.$$ (1.3)

The main observation is that in an ideal noiseless world the rotation T̃ (i, j) can be interpreted as a geometric relation between the corresponding frames x_i and x_j, provided the invariant distance between the corresponding images is small. This relation is expressed in terms of parallel transport on the sphere, as follows: define the rotation

$$T(x_i,x_j)=\left(\begin{array}{cc}\cos ({\theta }_{\mathit{ij}})& -\sin ({\theta }_{\mathit{ij}})\\ \sin ({\theta }_{\mathit{ij}})& \cos ({\theta }_{\mathit{ij}})\end{array}\right),$$

as the unique solution of the equation

$$x_i⊲T(x_i,x_j)=t_{\pi (x_i),\pi (x_j)}{x}_j,$$ (1.4)

where t_{π(xi), π(xj)} is the parallel transport along the unique geodesic on the sphere connecting the points π(x_j) with π(x_i) or, in other words, it is the rotation in SO(V) that takes the vector π(x_j) to π(x_i) along the shortest path on the sphere and the action ◁ is defined by

$$x⊲\left(\begin{array}{cc}\cos (\theta )& -\sin (\theta )\\ \sin (\theta )& \cos (\theta )\end{array}\right)=(\cos (\theta )e_1+\sin (\theta )e_2,-\sin (\theta )e_1+\cos (\theta )e_2,e_3),$$

for every x = (e₁, e₂, e₃). The precise statement is that the rotation T̃ (i, j) approximates the rotation T (x_i, x_j) when {i, j} ∈ Edges. This geometric interpretation of the rotation T̃ (i, j) is suggested from a combination of mathematical and empirical considerations that we proceed to explain.

• On the mathematical side: the rotation T (x_i, x_j) is the unique rotation of the frame x_i around its viewing direction π(x_i), minimizing the distance to the frame x_j. This is a standard fact from differential geometry (a direct proof of this statement appears in [8]).

• On the empirical side: if the function ϕ is “nice”, then the optimal alignment T̃ (i, j) of the projection images is correlated with the optimal alignment T (x_i, x_j) of the corresponding frames. This correlation of course improves as the distance between π(x_i) and π(x_j) becomes smaller. A quantitative study of the relation between T̃ (i, j) and T (x_i, x_j) involves considerations from image processing; thus it is beyond the scope of this paper.

To conclude, the “empirical” rotation T̃ (i, j) approximates the “geometric” rotation T (x_i, x_j) only when the viewing directions π(x_i) and π(x_j) are close, in the sense that they belong to some small spherical cap of opening angle a. The latter “geometric” condition is correlated with the “empirical” condition that the corresponding images I_i and I_j have small invariant distance. When the viewing directions π(x_i) and π(x_j) are far from each other, the rotation T̃ (i, j) is not related any longer to parallel transportation on the sphere. For this reason, we consider only rotations T̃ (i, j) for which {i, j} ∈ Edges and call this collection the (local) empirical transport data.

1.5 The Intrinsic Classification Algorithm

The intrinsic classification algorithm accepts as an input the empirical transport data {T̃ (i, j) : {i, j} ∈ Edges} and produces as an output the Euclidean inner products {(π(x_i), π(x_j)) : i, j = 1, …, N}. Using these inner products, one can identify the true neighbors in the graph G as the pairs {i, j} ∈ Edges for which the inner product (π(x_i), π(x_j)) is close to 1. The formal justification of the algorithm requires the empirical assumption that the frames x_i, i = 1, …, N are uniformly distributed in the frame manifold X, according to the unique normalized Haar measure on X. This assumption corresponds to the situation where the orientations of the molecules in the ice are distributed independently and uniformly at random.

The main idea of the algorithm is to construct an intrinsic model, denoted by W_N, of the Hermitian vector space W = CV which is expressed solely in terms of the empirical transport data.

The algorithm proceeds as follows:

• Step 1 (Ambient Hilbert space): consider the standard N-dimensional Hilbert space

  $$H_N={\mathrm{C}}^N.$$
• Step 2 (Self-adjoint operator): identify ℝ² with C and consider each rotation T̃ (i, j) as a complex number of unit norm. Define the N × N complex matrix

  $${\stackrel{\sim }{T}}_N:H_N\to H_N,$$

  by putting the rotation T̃ (i, j) in the (i, j) entry. Notice that the matrix T̃_N is self-adjoint by (1.3).
• Step 3 (Intrinsic model): the matrix T̃_N induces a spectral decomposition

  $$H_N=\underset{\mathrm{\lambda }}{\oplus }{H}_N(\mathrm{\lambda }).$$

Theorem 1

There exists a threshold λ₀such that

$$\dim \underset{\mathrm{\lambda }>{\mathrm{\lambda }}_0}{\oplus }{H}_N(\mathrm{\lambda })=3.$$

Define the Hermitian vector space

$${\mathrm{W}}_N=\underset{\mathrm{\lambda }>{\mathrm{\lambda }}_0}{\oplus }{H}_N(\mathrm{\lambda }).$$

• Step 4 (Computation of the Euclidean inner products): the Euclidean inner products {(π(x_i), π(x_j)) : i, j = 1, …, N} are computed from the vector space W_N, as follows: for every i = 1, …, N, denote by φ_i ∈ W_N the vector

  $${\phi }_i=\sqrt{2/3}·{\mathrm{pr}}_i^{\ast }(1),$$

  where pr_i : W_N → C is the projection on the ith component and ${\mathrm{pr}}_i^{\ast }:\mathrm{C}\to {\mathrm{W}}_N$ is the adjoint map. In addition, for every frame x ∈ X, x = (e₁, e₂, e₃), denote by δ_x ∈ W the (complex) vector e₁ − ie₂.

The upshot is that the intrinsic vector space W_N consisting of the collection of vectors φ_i ∈ W_N, i = 1, …, N is (approximately⁴) isomorphic to the extrinsic vector space W consisting of the collection of vectors δ_xi ∈ W, i = 1, …, N, where x_i is the frame corresponding to the image I_i, for every i = 1, …, N. This statement is the content of the following theorem:

Theorem 2

There exists a unique (approximated) isomorphism ${\tau }_N:W\stackrel{\simeq }{\to }{\mathrm{W}}_N$ of Hermitian vector spaces such that

$${\tau }_N({\delta }_{x_i})={\phi }_i,$$

for every i = 1, …, N.

The above theorem enables us to express, in intrinsic terms, the Euclidean inner products between the viewing directions, as follows: starting with the following identity from linear algebra (which will be proved in the sequel):

$$(\pi (x),\pi (y))=|\langle {\delta }_x,{\delta }_y\rangle |-1,$$ (1.5)

for every pair of frames x, y ∈ X, where 〈·, ·〉 is the Hermitian product on W = CV, given by

$$\langle u+\mathrm{i}\upsilon ,u^{\prime }+\mathrm{i}{\upsilon }^{\prime }\rangle =(u,\upsilon )+(\upsilon ,{\upsilon }^{\prime })-\mathrm{i}(u,{\upsilon }^{\prime })+\mathrm{i}(\upsilon ,u^{\prime }),$$

we obtain the following relation:

$$(\pi (x_i),\pi (x_j))=|\langle {\phi }_i,{\phi }_j\rangle |-1,$$ (1.6)

for every i, j = 1, …, N. We note that, in the derivation of Relation (1.6) from Relation (1.5) we use Theorem 2. Finally, we notice that Relation (1.6) implies that although we do not know the frame associated with every projection image, we still are able to compute the inner product between every pair of such frames from the intrinsic vector space W_N which, in turns, can be computed from the images.

1.6 Structure of the Paper

The paper consists of three sections besides the introduction.

• In Sect. 2, we begin by introducing the basic analytic set-up which is relevant for the class averaging problem in cryo-EM. Then, we proceed to formulate the main results of this paper, which are: a complete description of the spectral properties of the localized parallel transport operator (Theorem 3), the spectral gap property (Theorem 4) and the admissibility of the intrinsic classification algorithm (Theorems 5 and 6).

• In Sect. 3, we prove Theorem 3: in particular, we develop all the representation theoretic machinery that is needed for the proof.

• Finally, in the Appendix, we give the proofs of all technical statements which appear in the previous sections.

2 Preliminaries and Main Results

2.1 Set-up

Let (V, (·, ·)) be a three-dimensional, oriented, Euclidean vector space over ℝ. The reader can take V = ℝ³ equipped with the standard orientation and (·, ·) to be the standard inner product. Let W = CV denote the complexification of V. We equip W with the Hermitian product 〈·, ·〉 : W × W → C, induced from (·, ·), given by

$$\langle u+i\upsilon ,u\prime +i\upsilon \prime \rangle =(u,\upsilon )+(\upsilon ,\upsilon \prime )-i(u,\upsilon \prime )+i(\upsilon ,u\prime ).$$

Let SO(V) denote the group of orthogonal transformations with respect to the inner product (·, ·), preserving the orientation. Let S(V) denote the unit sphere in V, that is, S(V) = {υ ∈ V : (υ, υ) = 1}. Let X = Fr(V) denote the manifold of oriented orthonormal frames in V, that is, a point x ∈ X is an orthonormal basis x = (e₁, e₂, e₃) of V compatible with the orientation.

We consider two commuting group actions on the frame manifold: a left action of the group SO(V), given by

$$g⊳(e_1,e_2,e_3)=(g{e}_1,g{e}_2,g{e}_3),$$

and a right action of the special orthogonal group SO(3), given by

$$(e_1,e_2,e_3)⊲g=(a_{11}{e}_1+a_{21}{e}_2+a_{31}{e}_3,a_{12}{e}_1+a_{22}{e}_2+a_{32}{e}_3,a_{13}{e}_1+a_{23}{e}_2+a_{33}{e}_3),$$

for

$$g=\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right).$$

We distinguish the copy of SO(2) inside SO(3) consisting of matrices of the form

$$g=\left(\begin{array}{ccc}{a}_{11}& a_{12}& 0\\ a_{21}& a_{22}& 0\\ 0& 0& 1\end{array}\right),$$

and consider X as a principal SO(2) bundle over S(V) where the fibration map π : X → S(V) is given by π(e₁, e₂, e₃) = e₃. We call the vector e₃ the viewing direction.

2.2 The Transport Data

Given a point υ ∈ S(V), we denote by X_υ the fiber of the frame manifold lying over υ, that is, X_υ = {x ∈ X : π(x) = υ}. For every pair of frames x, y ∈ X such that π(x) ≠ ± π(y), we define a matrix T (x, y) ∈ SO(2), characterized by the property

$$x⊲T(x,y)=t_{\pi (x),\pi (y)}(y),$$

where t_π(x),π(y) : X_π(y) → X_π(x) is the morphism between the corresponding fibers, given by the parallel transport mapping along the unique geodesic in the sphere S(V) connecting the points π(y) with π(x). We identify ℝ² with C and consider T (x, y) as a complex number of unit norm. The collection of matrices {T (x, y)} satisfy the following properties:

• Symmetry: for every x, y ∈ X, we have T (y, x) = T (x, y)⁻¹, where the left hand side of the equality coincides with the complex conjugate $\overline{T(x,y)}$. This property follows from the fact that the parallel transport mapping satisfies:

  $$t_{\pi (y),\pi (x)}=t_{\pi (x),\pi (y)}^{-1}.$$
• Invariance: for every x, y ∈ X and element g ∈ SO(V), we have T (g ▷ x, g ▷ y) = T (x, y). This property follows from the fact that the parallel transport mapping satisfies:

  $$t_{\pi (g⊳x),\pi (g⊳y)}=g\circ t_{\pi (x),\pi (y)}\circ g^{-1},$$

  for every g ∈ SO(V).
• Equivariance: for every x, y ∈ X and elements g₁, g₂ ∈ SO(2), we have $T(x⊲g_1,y⊲g_2)=g_1^{-1}T(x,y)g_2$. This property follows from the fact that the parallel transport mapping satisfies:

  $$t_{\pi (x⊲g_1),\pi (y⊲g_2)}=t_{\pi (x),\pi (y)},$$

  for every g₁, g₂ ∈ SO(2).

  The collection {T (x, y)} is referred to as the transport data.

2.3 The Parallel Transport Operator

Let H =C(X) denote the Hilbertian space of smooth complex valued functions on X (here, the word Hilbertian means that H is not complete)⁵, where the Hermitian product is the standard one, given by

$$\langle f_1,f_2\rangle H={\mathit{\int }}_{x\in X}{f}_1(x)\overline{f_2(x)}\mathrm{d}x,$$

for every f₁, f₂ ∈ H, where dx denotes the normalized Haar measure on X. In addition, H supports a unitary representation of the group SO(V) × SO(2), where the action of an element g = (g₁, g₂) sends a function s ∈ H to a function g · s, given by

$$(g·s)(x)=s(g_1^{-1}⊳x⊲g_2),$$

for every x ∈ X.

Using the transport data, we define an integral operator T : H → H as

$$T(s)(x)={\mathit{\int }}_{y\in X}T(x,y)s(y)\mathrm{d}y,$$

for every s ∈ H. The properties of the transport data imply the following properties of the operator T :

• The symmetry property implies that T is self-adjoint.

• The invariance property implies that T commutes with the SO(V) action, namely T (g · s) = g · T (s) for every s ∈ H and g ∈ SO(V).

• The implication of the equivariance property will be discussed later when we study the kernel of T.

  The operator T is referred to as the parallel transport operator.

2.3.1 Localized Parallel Transport Operator

The operator which arises naturally in our context is a localized version of the transport operator. Let us fix a real number a ∈ [0, π], designating an opening angle of a spherical cap on the sphere and consider the parameter h = 1 − cos(a), taking values in the interval [0, 2].

Given a choice of this parameter, we define an integral operator T_h : H → H as

$$T_h(s)(x)={\mathit{\int }}_{y\in B(x,a)}T(x,y)s(y)\mathrm{d}y,$$ (2.1)

where B(x, a) = {y ∈ X : (π(x), π(y)) > cos(a)}. Similar considerations as before show that T_h is self-adjoint and, in addition, commutes with the SO(V) action. Finally, note that the operator T_h should be considered as a localization of the operator of parallel transport discussed in the previous paragraph, in the sense that now only frames with close viewing directions interact through the integral (2.1). For this reason, the operator T_h is referred to as the localized parallel transport operator.

2.4 Spectral Properties of the Localized Parallel Transport Operator

We focus our attention on the spectral properties of the operator T_h, in the regime h ≪ 1, since this is the relevant regime for the class averaging application.

Theorem 3

The operator T_h has a discrete spectrum λ_n(h), n ∈ ℕ, such that dim H (λ_n(h)) = 2n + 1, for every h ∈ (0, 2], Moreover, in the regime h ≪ 1, the eigenvalue λ_n(h) has the asymptotic expansion

$${\mathrm{\lambda }}_n(h)=\frac{1}{2}h-\frac{1+(n+2)(n-1)}{8}{h}^2+O(h^3).$$

For a proof, see Sect. 3.

In fact, each eigenvalue λ_n(h), as a function of h, is a polynomial of degree n + 1. In Sect. 3, we give a complete description of these polynomials by means of a generating function. To get some feeling for the formulas that arise, we list the first four eigenvalues:

$$\begin{array}{lll}{\mathrm{\lambda }}_1(h)& =& \frac{1}{2}h-\frac{1}{8}{h}^2,\\ {\mathrm{\lambda }}_2(h)& =& \frac{1}{2}h-\frac{5}{8}{h}^2+\frac{1}{6}{h}^3,\\ {\mathrm{\lambda }}_3(h)& =& \frac{1}{2}h-\frac{11}{8}{h}^2+\frac{25}{24}{h}^3-\frac{15}{64}{h}^4,\\ {\mathrm{\lambda }}_4(h)& =& \frac{1}{2}h-\frac{19}{8}{h}^2+\frac{27}{8}{h}^3-\frac{119}{64}{h}^4+\frac{7}{20}{h}^5.\end{array}$$

The graphs of λ_i(h), i = 1, 2, 3, 4 are given in Fig. 4.

Fig. 4.

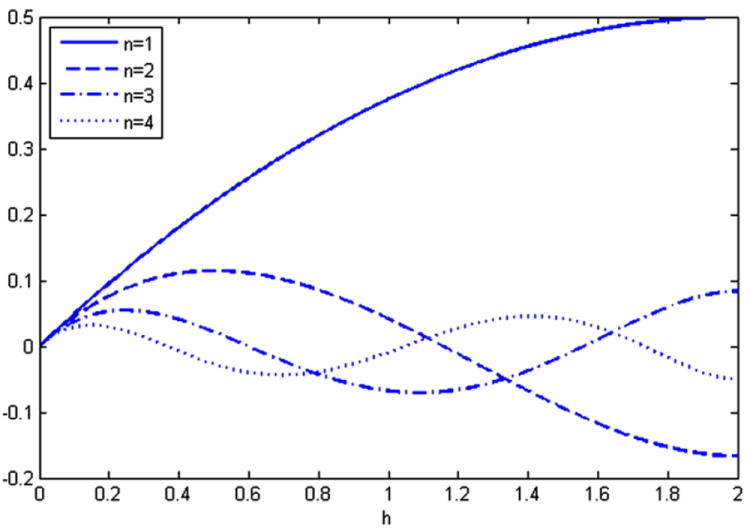
The first four eigenvalues of the operator T_h, presented as functions of the variable h ∈ [0, 2]

2.4.1 Spectral Gap

Noting that λ₂(h) attains its maximum at h = 1/2, we have

Theorem 4

For every value of h ∈ [0, 2], the maximal eigenvalue of T_h is λ₁(h). Moreover, for every value of h ∈ [0, 1/2], there is a spectral gap G (h) of the form

$$G(h)={\mathrm{\lambda }}_1(h)-{\mathrm{\lambda }}_2(h)=\frac{1}{2}{h}^2-\frac{1}{6}{h}^3.$$

For a proof, see the Appendix. Note that the main difficulty in proving the second statement is to show that λ_n(h) ≤ λ₂(h) for every h ∈ [0, 1/2], which looks evident from looking at Fig. 4.

Consequently, in the regime h ≪ 1, the spectral gap behaves like

$$G(h)~\frac{1}{2}{h}^2.$$

2.5 Main Algebraic Structure

We proceed to describe an intrinsic model W of the Hermitian vector space W, which can be computed as the eigenspace associated with the maximal eigenvalue of the localized parallel transport operator T_h, provided h ≪ 1. Using this model, the Euclidean inner products between the viewing directions of every pair of orthonormal frames can be computed.

• Extrinsic model: for every point x ∈ X, let us denote by δ_x : C → W the unique complex morphism sending 1 ∈ C to the complex vector e₁ − ie₂ ∈ W.

• Intrinsic model: we define W to be the eigenspace of T_h associated with the maximal eigenvalue, which by Theorems 3 and 4, is three-dimensional. For every point x ∈ X, there is a map

  $${\phi }_x=\sqrt{2/3}·{({\mathrm{ev}}_x\mid \mathrm{W})}^{\ast }:\mathrm{C}\to \mathrm{W},$$

  where ev_x : H → C is the evaluation morphism at the point x, namely,

  $${\mathrm{ev}}_x(f)=f(x),$$

  for every f ∈ H. The pair (W, {φ_x : x ∈ X}) is referred to as the intrinsic model of the vector space W.

The algebraic structure that underlies the intrinsic classification algorithm is the canonical morphism

$$\tau :W\to H,$$

defined by

$$\tau (\upsilon )(x)=\sqrt{3/2}·{\delta }_x^{\ast }(\upsilon ),$$

for every x ∈ X. The morphism τ induces an isomorphism of Hermitian vector spaces between W equipped with the collection of natural maps {δ_x : C → W } and W equipped with the collection of maps {φ_x : C → W}. This is summarized in the following theorem:

Theorem 5

The morphism τ maps W isomorphically, as an Hermitian vector space, onto the subspace W ⊂ H. Moreover,

$$\tau \circ {\delta }_x={\phi }_x,$$

for every x ∈ X.

For a proof, see the Appendix (the proof uses the results and terminology of Sect. 3).

Using Theorem 5, we can express in intrinsic terms the inner product between the viewing directions associated with every ordered pair of frames. The precise statement is

Theorem 6

For every pair of frames x, y ∈ X, we have

$$(\pi (x),\pi (y))=\left|\langle {\phi }_x(\upsilon ),{\phi }_y(u)\rangle \right|-1,$$ (2.2)

for any choice of complex numbers υ, u ∈ C of unit norm.

For a proof, see the Appendix. Note that substituting υ = u = 1 in (2.2) we obtain (1.6).

2.6 Explanation of Theorems 1 and 2

We end this section with an explanation of the two main statements that appeared in the introduction. The explanation is based on inspecting the limit when the number of images N goes to infinity. Provided that the corresponding frames are independently drawn from the normalized Haar measure on X (empirical assumption), in the limit the transport matrix T̃_N approaches the localized parallel transport operator T_h : H → H, for some small value of the parameter h. This implies that the spectral properties of T̃_N for large values of N are governed by the spectral properties of the operator T_h when h lies in the regime h ≪ 1. In particular,

• The statement of Theorem 1 is explained by the fact that the maximal eigenvalue of T_h has multiplicity three (see Theorem 3) and that there exists a spectral gap G(h) ~ h/2, separating it from the rest of the spectrum (see Theorem 4). The later property ensures that the numerical computation of this eigenspace makes sense.

• The statement of Theorem 2 is explained by the fact that the vector space W_N is a numerical approximation of the theoretical vector space W and Theorem 5.

3 Spectral Analysis of the Localized Parallel Transport Operator

In this section we study the spectral properties of the localized parallel transport operator T_h, mainly focusing on the regime h ≪ 1. But first we need to introduce some preliminaries from representation theory.

3.1 Isotypic Decompositions

The Hilbert space H, as a unitary representation of the group SO(2), admits an isotypic decomposition

$$H=\underset{k\in \mathbb{Z}}{\oplus }{H}_k,$$ (3.1)

where a function s ∈ H_k if and only if s(x ◁ g) = g^k s(x), for every x ∈ X and g ∈ SO(2). In turn, each Hilbert space H_k, as a representation of the group SO(V), admits an isotypic decomposition

$$H_k=\underset{n\in {\mathbb{N}}^{\ge 0}}{\oplus }{H}_{n,k},$$ (3.2)

where H_n,k denotes the component which is a direct sum of copies of the unique irreducible representation of SO(V) which is of dimension 2n + 1. A particularly important property is that each irreducible representation which appears in (3.2) comes up with multiplicity one. This is summarized in the following theorem:

Theorem 7

(Multiplicity one) If n < |k| then H_n,k = 0. Otherwise, H_n,k is isomorphic to the unique irreducible representation of SO(V) of dimension 2n + 1.

For a proof, see the Appendix.

The following proposition is a direct implication of the equivariance property of the operator T_h and follows from Schur’s orthogonality relations on the group SO(2):

Proposition 1

We have

$$\underset{k\ne -1}{\oplus }{H}_k\subset \ker T_h.$$

Consequently, from now on, we will consider T_h as an operator from H₋₁ to H₋₁. Moreover, since for every n ≥ 1, H_{n, −1} is an irreducible representation of SO(V) and since T_h commutes with the group action, by Schur’s Lemma T_h acts on H_{n, −1} as a scalar operator, namely

$$T_h\mid H_{n,-1}={\mathrm{\lambda }}_n(h)Id.$$

The reminder of this section is devoted to the computation of the eigenvalues λ_n(h). The strategy of the computation is to choose a point x₀ ∈ X and a “good” vector u_n ∈ H_{n, −1} such that u_n(x₀) ≠ 0 and then to use the relation

$$T_h(u_n)(x_0)={\mathrm{\lambda }}_n(h)u_n(x_0),$$

which implies that

$${\mathrm{\lambda }}_n(h)=\frac{T_h(u_n)(x_0)}{u_n(x_0)}.$$ (3.3)

3.2 Set-up

Fix a frame x₀ ∈ X, x₀ = (e₁, e₂, e₃). Under this choice, we can safely identify the group SO(V) with the group SO(3) by sending an element g ∈ SO(V) to the unique element h ∈ SO(3) such that g ▷ x₀ = x₀ ◁ h. Hence, from now on, we will consider the frame manifold equipped with commuting left and right actions of SO(3).

Consider the following elements in the Lie algebra so(3):

$$\begin{array}{ccc}{A}_1& =& \left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right),\\ A_2& =& \left(\begin{array}{ccc}0& 0& 1\\ 0& 0& 0\\ -1& 0& 0\end{array}\right),\\ A_3& =& \left(\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right).\end{array}$$

The elements A_i, i = 1, 2, 3 satisfy the relations

$$\begin{array}{ccc}[A_3,A_1]& =& A_2,\\ [A_3,A_2]& =& -A_1,\\ [A_1,A_2]& =& A_3.\end{array}$$

Let (H, E, F) be the following sl₂ triple in the complexified Lie algebra Cso(3):

$$\begin{array}{lll}H& =& -2\mathrm{i}{A}_3,\\ E& =& \mathrm{i}{A}_2-A_1,\\ F& =& A_1+\mathrm{i}{A}_2.\end{array}$$

Finally, let (H^L, E^L, F^L) and (H^R, E^R, F^R) be the associated (complexified) vector fields on X induced from the left and right action of SO(3) respectively.

3.2.1 Spherical Coordinates

We consider the spherical coordinates of the frame manifold ω : (0, 2π) × (0, π) × (0, 2π) → X, given by

$$\omega (\phi ,\theta ,\alpha )=x_0⊲{\mathrm{e}}^{\phi A_3}{\mathrm{e}}^{\theta A_2}{\mathrm{e}}^{\alpha A_3}.$$

We have the following formulas.

• The normalized Haar measure on X is given by the density

  $$\frac{\sin (\theta )}{2{(2\pi )}^2}\mathrm{d}\phi \mathrm{d}\theta \mathrm{d}\alpha .$$
• The vector fields (H^L, E^L, F^L) are given by

  $$\begin{array}{lll}{H}^{\mathrm{L}}& =& 2\mathrm{i}{\partial }_{\phi },\\ E^{\mathrm{L}}& =& -{\mathrm{e}}^{-\mathrm{i}\phi }(\mathrm{i}{\partial }_{\theta }+\cot (\theta ){\partial }_{\phi }-1/\sin (\theta ){\partial }_{\alpha }),\\ F^{\mathrm{L}}& =& -{\mathrm{e}}^{\mathrm{i}\phi }(\mathrm{i}{\partial }_{\theta }-\cot (\theta ){\partial }_{\phi }+1/\sin (\theta ){\partial }_{\alpha }).\end{array}$$
• The vector fields (H^R, E^R, F^R) are given by

  $$\begin{array}{lll}{H}^{\mathrm{R}}& =& -2\mathrm{i}{\partial }_{\alpha },\\ E^{\mathrm{R}}& =& {\mathrm{e}}^{\mathrm{i}\alpha }(\mathrm{i}{\partial }_{\theta }+\cot (\theta ){\partial }_{\alpha }-1/\sin (\theta ){\partial }_{\phi }),\\ F^{\mathrm{R}}& =& {\mathrm{e}}^{-\mathrm{i}\alpha }(\mathrm{i}{\partial }_{\theta }+\cot (\theta ){\partial }_{\alpha }-1/\sin (\theta ){\partial }_{\phi }).\end{array}$$

3.3 Choosing a Good Vector

3.3.1 Spherical Functions

Consider the subgroup T ⊂ SO(3) generated by the infinitesimal element A₃. For every k ∈ ℤ and n ≥ k, the Hilbert space H_n,k admits an isotypic decomposition with respect to the left action of T:

$$H_{n,k}=\underset{m=-n}{\overset{n}{\oplus }}{H}_{n,k}^m,$$

where a function $s\in H_{n,k}^m$ if and only if s(e^{−t A₃} ▷ x) = e^imt s(x), for every x ∈ X. Functions in $H_{n,k}^m$ are usually referred to in the literature as (generalized) spherical functions. Our plan is to choose for every n ≥ 1, a spherical function $u_n\in H_{n,-1}^1$ and exhibit a closed formula for the generating function

$$\sum _{n\ge 1}{u}_n{t}^n.$$

Then, we will use this explicit generating function to compute u_n (x₀) and T_h (u_n) (x₀) and use (3.3) to compute λ_n(h).

3.3.2 Generating Function

For every n ≥ 0, let ${\psi }_n\in H_{n,0}^0$ be the unique spherical function such that ψ_n(x₀) = 1. These functions are the well known spherical harmonics on the sphere. Define the generating function

$$G_{0,0}(\phi ,\theta ,\alpha ,t)=\sum _{n\ge 0}{\psi }_n(\phi ,\theta ,\alpha )t^n.$$

The following theorem is taken from [10].

Theorem 8

The function G_0,0 admits the following formula:

$$G_{0,0}(\phi ,\theta ,\alpha ,t)={(1-2t\cos (\theta )+t^2)}^{-1/2}.$$

Take u_n = E^L F^R ψ_n. Note that indeed $u_n\in H_{n,-1}^1$ and define the generating function

$$G_{1,-1}(\phi ,\theta ,\alpha ,t)=\sum _{n\ge 1}{u}_n(\phi ,\theta ,\alpha )t^n.$$

It follows that G_{1, −1} = E^L F^R G_0,0. Direct calculation, using the formula in Theorem 8, reveals that

$$\begin{array}{lll}{G}_{1,-1}(\phi ,\theta ,\alpha ,t)& =& e^{-i(\alpha +\phi )}[3\sin {(\theta )}^2{t}^2{(1-2t\cos (\theta )+t^2)}^{-5/2}\\ & & -t\cos (\theta ){(1-2t\cos (\theta )+t^2)}^{-3/2}\\ & & -t{(1-2t\cos (\theta )+t^2)}^{-3/2}].\end{array}$$ (3.4)

It is enough to consider G_{1, −1} when φ = α = 0. We use the notation G_{1, −1} (θ, t) = G_{1, −1} (0, θ, 0, t). By (3.4)

$$\begin{array}{lll}{G}_{1,-1}(\theta ,t)& =& 3\sin {(\theta )}^2{t}^2{(1-2t\cos (\theta )+t^2)}^{-5/2}\\ & & -t\cos (\theta ){(1-2t\cos (\theta )+t^2)}^{-3/2}\\ & & -t{(1-2t\cos (\theta )+t^2)}^{-3/2}.\end{array}$$ (3.5)

3.4 Computation of u_n (x₀)

Observe that

$$G_{1,-1}(0,t)=\sum _{n\ge 1}{u}_n(x_0)t^n.$$

Direct calculation reveals that

$$\begin{array}{lll}{G}_{1,-1}(0,t)& =& -2t{(1-t)}^{-3}\\ & =& -2t\sum _{n\ge 0}\left(\begin{array}{c}-3\\ n\end{array}\right){(-1)}^n{t}^n\\ & =& -2\sum _{n\ge 1}\left(\begin{array}{c}-3\\ n-1\end{array}\right){(-1)}^{n-1}{t}^n.\end{array}$$

Since $\left(\begin{array}{c}-3\\ n-1\end{array}\right)=\frac{{(-1)}^{n-1}}{2}n(n+1)$, we obtain

$$u_n(x_0)=-n(n+1).$$ (3.6)

3.5 Computation of T_h (u_n) (x₀)

Recall that h = 1 − cos(a).

Using the definition of T_h, we obtain

$$T_h(u_n)(x_0)={\mathit{\int }}_{y\in B(x_0,a)}T(x_0,y)u_n(y)\mathrm{d}y.$$

Using the spherical coordinates, the integral on the right hand side can be written as

$$\frac{1}{{(2\pi )}^2}{\mathit{\int }}_0^{2\pi }\mathrm{d}\phi {\mathit{\int }}_0^a\frac{\sin (\theta )}{2}\mathrm{d}\theta {\mathit{\int }}_0^{2\pi }T(x_0,\omega (\phi ,\theta ,\alpha ))u_n(\omega (\phi ,\theta ,\alpha )).$$

First

$$\begin{array}{lll}T(x_0,\omega (\phi ,\theta ,\alpha ))& =& T(x_0,x_0⊲{\mathrm{e}}^{\phi A_3}{\mathrm{e}}^{\theta A_2}{\mathrm{e}}^{\alpha A_3})\\ & =& T(x_0,{\mathrm{e}}^{\phi A_3}⊳x_0⊲{\mathrm{e}}^{\theta A_2}{\mathrm{e}}^{\alpha A_3})\\ & =& T({\mathrm{e}}^{-\phi A_3}⊳x_0,x_0⊲{\mathrm{e}}^{\theta A_2}{\mathrm{e}}^{\alpha A_3})\\ & =& {\mathrm{e}}^{\mathrm{i}\phi }T(x_0,x_0⊲{\mathrm{e}}^{\theta A_2}){\mathrm{e}}^{\mathrm{i}\alpha },\end{array}$$ (3.7)

where the third equality uses the invariance property of the transport data and the second equality uses the equivariance property of the transport data.

Second, since $u_n\in H_{n,-1}^1$ we have

$$u_n(\omega (\phi ,\theta ,\alpha ))={\mathrm{e}}^{-\mathrm{i}\phi }{u}_n(x_0⊲{\mathrm{e}}^{\theta A_2}){\mathrm{e}}^{-\mathrm{i}\alpha }.$$ (3.8)

Combining (3.7) and (3.8), we conclude

$$\begin{array}{lll}{T}_h(u_n)(x_0)& =& {\mathit{\int }}_0^a\frac{\sin (\theta )}{2}T(x_0,x_0⊲{\mathrm{e}}^{\theta A_2})u_n(x_0⊲{\mathrm{e}}^{\theta A_2})\mathrm{d}\theta \\ & =& {\mathit{\int }}_0^a\frac{\sin (\theta )}{2}{u}_n(x_0⊲{\mathrm{e}}^{\theta A_2})\mathrm{d}\theta ,\end{array}$$ (3.9)

where the second equality uses the fact that x₀ ◁ e^{θ A₂} is the parallel transport of x₀ along the unique geodesic connecting π(x₀) with π(x₀ ◁ e^{θ A₂}).

Denote

$$I_n(h)={\mathit{\int }}_0^a\frac{\sin (\theta )}{2}{u}_n(x_0⊲{\mathrm{e}}^{\theta A_2})\mathrm{d}\theta .$$

Define the generating function $I(h,t)={\sum }_{n\ge 0}{I}_n(h)t^n$ and observe that

$$I(h,t)={\mathit{\int }}_0^a\frac{\sin (\theta )}{2}{G}_{1,-1}(\theta ,t)\mathrm{d}\theta .$$

Direct calculation reveals that

$$\begin{array}{lll}I(h,t)& =& 1/2[h{(1+2t(h-1)+t^2)}^{-1/2}\\ & & -\mathit{th}(2-h){(1+2t(h-1)+t^2)}^{-3/2}\\ & & -t^{-1}({(1+2t(h-1)+t^2)}^{1/2}-(1-t))].\end{array}$$ (3.10)

3.6 Proof of Theorem 3

Expanding I (h, t) with respect to the parameter t reveals that the function I_n(h) is a polynomial in h of degree n + 1. Then, using (3.3), we get

$${\mathrm{\lambda }}_n(h)=-\frac{I_n(h)}{n(n+1)}.$$

In principle, it is possible to obtain a closed formula for λ_n(h) for every n ≥ 1.

3.6.1 Quadratic Approximation

We want to compute the first three terms in the Taylor expansion of λ_n(h):

$${\mathrm{\lambda }}_n(h)={\mathrm{\lambda }}_n(0)+{\partial }_h{\mathrm{\lambda }}_n(0)+\frac{{\partial }_h^2{\mathrm{\lambda }}_n(0)}{2}+O(h^3).$$

We have

$$\begin{array}{rrr}{\mathrm{\lambda }}_n(0)& =& -\frac{I_n(0)}{n(n+1)},\\ {\partial }_h{\mathrm{\lambda }}_n(0)& =& -\frac{{\partial }_h{I}_n(0)}{n(n+1)},\\ {\partial }_h^2{\mathrm{\lambda }}_n(0)& =& -\frac{{\partial }_h^2{I}_n(0)}{n(n+1)},\end{array}$$

Observe that

$${\partial }_h^{k}I(0,t)=\sum _{n\ge 1}{\partial }_h^k{I}_n(0).$$

Direct computation, using Formula (3.10), reveals that

$$\begin{array}{ccc}\hfill I(0,t)& =& 0,\hfill \\ \hfill {\partial }_{h}I(0,t)& =& -\sum _{n\ge 1}n(n+1)t^n,\hfill \\ \hfill {\partial }_h^{2}I(0,t)& =& \frac{1}{4}\sum _{n\ge 1}n(n+1)(1+(n+2)(n-1))t^n.\hfill \end{array}$$

Combing all the above yields the desired formula

$${\mathrm{\lambda }}_n(h)=\frac{1}{2}h-\frac{1+(n+2)(n-1)}{8}{h}^2+O(h^3).$$

This concludes the proof of the theorem.

Appendix: Proofs

A.1 Proof of Theorem 4

The proof is based on two technical lemmas.

Lemma 1

The following estimates hold:

1. There exists h₁ ∈ (0, 2] such that λ_n(h) ≤ λ₁(h), for every n ≥ 1 and h ∈ [0, h₁].

2. There exists h₂ ∈ (0, 2] such that λ_n(h) ≤ λ₂(h), for every n ≥ 2 and h ∈ [0, h₂].

The proof appears below.

Lemma 2

The following estimates hold:

1. There exists N₁ such that λ_n(h) ≤ λ₁(h), for every n ≥ N₁ and h ∈ [h₁, 2].

2. There exists N₂ such that λ_n(h) ≤ λ₁(h), for every n ≥ N₂ and h ∈ [h₂, 1/2].

The proof appears below.

Granting the validity of these two lemmas we can finish the proof of the theorem.

First we prove that λ_n(h) ≤ λ₁(h), for every n ≥ 1 and h ∈ [0, 2]: By Lemmas 1 and 2, we get λ_n(h) ≤ λ₁(h) for every h ∈ [0, 2] when n ≥ N₁. Then we verify directly that λ_n(h) ≤ λ₁(h) for every h ∈ [0, 2] in the finitely many cases when n < N₁.

Similarly, we prove that λ_n(h) ≤ λ₂(h) for every n ≥ 2 and h ∈ [0, 1/2]: By Lemmas 1 and 2, we get λ_n(h) ≤ λ₂(h) for every h ∈ [0, 1/2] when n ≥ N₂. Then we verify directly that λ_n(h) ≤ λ₁(h) for every h ∈ [0, 1/2] in the finitely many cases when n < N₂.

This concludes the proof of the theorem.

A.2 Proof of Lemma 1

The strategy of the proof is to reduce the statement to known facts about Legendre polynomials.

Recall h = 1 − cos(a). Here, it will be convenient to consider the parameter z = cos(a), taking values in the interval [−1, 1].

We recall that Legendre polynomials P_n(z), n ∈ ℕ appear as the coefficients of the generating function

$$P\left(z,t\right)={\left(t^2-2\mathit{tz}+1\right)}^{-\left(1/2\right)}.$$

Let

$$J_n\left(z\right)=\{\begin{array}{ll}\frac{1}{2\left(1-z\right)}& n=0,\\ \frac{1}{2\left(1-z\right)}& n=1,\\ {\partial }_z{\mathrm{\lambda }}_{n-1}\left(z\right)& n\ge 2.\end{array}$$

Consider the generating function

$$J\left(z,t\right)=\sum _{n=0}^{\infty }{J}_n\left(z\right)t^n.$$

The function J(z, t) admits the following closed formula:

$$J\left(z,t\right)=\frac{t+\mathit{tz}+t^2+1}{2\left(1-z\right)}{\left(t^2+2\mathit{tz}+1\right)}^{-1/2}.$$ (A.1)

Using (A.1), we get for n ≥ 2

$$J_n\left(z\right)=\frac{1}{2\left(1-z\right)}\left(Q_n\left(z\right)+\left(1+z\right)Q_{n-1}\left(z\right)+Q_{n-2}\left(z\right)\right),$$

where Q_n(z) = (−1)ⁿ P_n(z). In order to prove the lemma, it is enough to show that there exists z₀ ∈ (−1, 1] such that for every z ∈ [−1, z₀] the following inequalities hold:

• Q_n (z) ≤ Q₃ (z) for every n ≥ 3.

• Q_n (z) ≤ Q₂ (z) for every n ≥ 2.

• Q_n (z) ≤ Q₁ (z) for every n ≥ 1.

• Q_n (z) ≤ Q₀ (z) for every n ≥ 0.

These inequalities follow from the following technical proposition.

Proposition 2

Let n₀ ∈ ℕ. There exists z₀ ∈ (−1, 1] such that Q_n (z) < Q_n0 (z), for every z ∈ [−1, z₀] and n ≥ n₀.

The proof appears below.

Take h₀ = h₁ = 1 + z₀. Granting Proposition 2, verify that J_n (z) ≤ J₂ (z), for n ≥ 2, z ∈ [−1, z₀] which implies that λ_n(h) ≤ λ₁(h), for n ≥ 2, h ∈ [0, h₀] and J_n (z) ≤ J₃ (z), for n ≥ 3, z ∈ [−1, z₀] which implies that λ_n(h) ≤ λ₂(h), for n ≥ 3, h ∈ [0, h₀].

This concludes the proof of the lemma.

A.2.1 Proof of Proposition 2

Denote by a₁ < a₂ < … < a_n the zeroes of Q_n(cos(a)) and by μ₁ < μ₂ < … < μ_n−1 the local extrema of Q_n (cos(a)).

The following properties of the polynomials Q_n are implied from known facts about Legendre polynomials (Properties 1 and 2 can be verified directly), which can be found for example in the book [9]:

• Property 1: a_i < μ_i < a_i+1, for i = 1, …, n − 1.

• Property 2: Q_n (−1) = 1 and ∂_z Q_n+1 (−1) < ∂_z Q_n (−1) < 0, for n ∈ ℕ.

• Property 3: |Q_n (cos(μ_i))| ≥ |Q_n (cos(μ_i+1))|, for i = 1, …, [n/2].

• Property 4: (i − 1/2)π/n ≤ a_i ≤ iπ/(n + 1), for i = 1, …, [n/2].

• Property 5: $\sin {\left(a\right)}^{1/2}·|Q_n\left(\cos \left(a\right)\right)|<\sqrt{2/\pi n}$, for a ∈ [0, π].

Granting these facts, we can finish the proof.

By Properties 1, 4

$$\frac{\pi }{2n}<{\mu }_1<\frac{2\pi }{n+1}.$$

We assume that n is large enough so that, for some small ε > 0,

$$\sin \left(a_1\right)\ge \left(1-\epsilon \right)a_1,$$

In particular, this is the situation when n₀ ≥ N, for some fixed N = N_ε. By Property 5

$$\begin{array}{lll}\left|Q_n\left(\cos ({\mu }_1)\right)\right|& <& \sqrt{2/\pi n}·\sin {({\mu }_1)}^{-1/2}\\ & <& \sqrt{2/\pi n}·\sin {(a_1)}^{-1/2}\\ & <& \sqrt{2/\pi n}·{\left(\left(1-\epsilon \right)a_1\right)}^{-1/2}=\frac{2}{\pi \sqrt{1-\epsilon }}.\end{array}$$

Let a₀ ∈ (0, π) be such that $Q_{n_0}\left(\cos \left(a\right)\right)>2/\pi \sqrt{1-\epsilon }$, for every a < a₀. Take z₀ = cos(a₀).

Finally, in the finitely many cases where n₀ ≤ n ≤ N, the inequality Q_n (z) < Q_n0 (z) can be verified directly.

This concludes the proof of the proposition.

A.3 Proof of Lemma 2

We have the following identity:

$$\mathrm{tr}\left(T_h^2\right)=\frac{h}{2},$$ (A.2)

for every h ∈ [0, 2]. The proof of (A.2) is by direct calculation:

$$\begin{array}{lll}\mathrm{tr}(T_h^2)& =& {\mathit{\int }}_{x\in X}{T}_h^2(x,x)\mathrm{d}x=\\ & =& {\mathit{\int }}_{x\in X}{\mu }_{\mathrm{Haar}}{\mathit{\int }}_{y\in B\left(x,a\right)}{T}_h(x,y)\circ T_h(y,x)\mathrm{d}x.\end{array}$$

Since T_h (x, y) = T_h (y, x)⁻¹ (symmetry property), we get

$$\mathrm{tr}(T_h^2)={\mathit{\int }}_{x\in X}{\mathit{\int }}_{y\in B(x,a)}\mathrm{d}x\mathrm{d}y={\mathit{\int }}_0^a\frac{\sin (\theta )}{2}\mathrm{d}\theta =\frac{1-\cos (a)}{2}.$$

Substituting, a = cos⁻¹ (1 − h), we get the desired formula $\mathrm{tr}(T_h^2)=h/2$.

On the other hand,

$$\mathrm{tr}(T_h^2)=\sum _{n=1}^{\infty }\mathrm{tr}\left(T_{h\mid H_{n,-1}}^2\right)=\sum _{n=1}^{\infty }(2n+1){\mathrm{\lambda }}_n{(h)}^2.$$ (A.3)

From (A.2) and (A.3) we obtain the following upper bound:

$${\mathrm{\lambda }}_n(h)\le \frac{\sqrt{h}}{\sqrt{4n+2}}.$$ (A.4)

Now we can finish the proof.

First estimate: We know that λ₁(h) = h/2 − h²/8; hence, one can verify directly that there exists N₁ such that $\sqrt{h}/\sqrt{4n+2}\le {\mathrm{\lambda }}_1(h)$ for every n ≥ N₁ and h ∈ [h₁, 2], which implies by (A.4) that λ_n(h) ≤ λ₁(h) for every n ≥ N₁ and h ∈ [h₁, 2].

Second estimate: We know that λ₂(h) = h/2 − 5h²/8 + h³/6; therefore, one can verify directly that there exists N₂ such that $\sqrt{h}/\sqrt{4n+2}\le {\mathrm{\lambda }}_2(h)$ for every n ≥ N₂ and h ∈ [h₂, 1/2], which implies by (A.4) that λ_n(h) ≤ λ₂(h) for every n ≥ N₂ and h ∈ [h₂, 1/2].

This concludes the proof of the lemma.

A.4 Proof of Theorem 5

We begin by proving that τ maps W = CV isomorphically, as an Hermitian space, onto W = H (λ_max(h)).

The crucial observation is that H (λ_max(h)) coincides with the isotypic subspace H_{1, −1} (see Sect. 3). Consider the morphism $\alpha =\sqrt{2/3}·\tau :W\to H$, given by

$$\alpha (\upsilon )(x)={\delta }_x^{\ast }(\upsilon ).$$

The first claim is that Im α ⊂ H₋₁, namely, that ${\delta }_{x⊲g}^{\ast }(\upsilon )=g^{-1}{\delta }_x^{\ast }(\upsilon )$, for every υ ∈ W, x ∈ X and g ∈ SO(2). Denote by 〈·, ·〉_std the standard Hermitian product on C. Now write

$$\begin{array}{lll}{\langle {\delta }_{x⊲g}^{\ast }(\upsilon ),z\rangle }_{\mathrm{std}}& =& \langle \upsilon ,{\delta }_{x⊲g}(z)\rangle =\langle \upsilon ,{\delta }_x(\mathit{gz})\rangle \\ & =& {\langle {\delta }_x^{\ast }(\upsilon ),\mathit{gz}\rangle }_{\mathrm{std}}={\langle g^{-1}{\delta }_x^{\ast }\left(\upsilon \right),z\rangle }_{\mathrm{std}}.\end{array}$$

The second claim is that α is a morphism of SO(V) representations, namely, that ${\delta }_x^{\ast }(g\upsilon )={\delta }_{g^{-1}⊳x}(\upsilon )$, for every υ ∈ W, x ∈ X and g ∈ SO(V). This statement follows from

$$\begin{array}{lll}{\langle {\delta }_x^{\ast }\left(g\upsilon \right),z\rangle }_{\mathrm{std}}& =& \langle g\upsilon ,{\delta }_x\left(z\right)\rangle =\langle \upsilon ,g^{-1}{\delta }_x\left(z\right)\rangle \\ & =& \langle \upsilon ,{\delta }_{g^{-1}⊳x}\left(z\right)\rangle ={\langle {\delta }_{g^{-1}⊳x}^{\ast }\left(\upsilon \right),z\rangle }_{\mathrm{std}}.\end{array}$$

Consequently, the morphism α maps W isomorphically, as a unitary representation of SO(V), onto H_{1, −1}, which is the unique copy of the three-dimensional representation of SO(V) in H₋₁. In turns, this implies that, up to a scalar, α and hence τ, are isomorphisms of Hermitian spaces. In order to complete the proof it is enough to show that

$$\mathrm{tr}\left({\tau }^{\ast }\circ \tau \right)=3.$$

This follows from

$$\begin{array}{lll}\mathrm{tr}\left(\tau \circ {\tau }^{\ast }\right)& =& \frac{3}{2}\mathrm{tr}\left({\alpha }^{\ast }\circ \alpha \right)\\ & =& \frac{3}{2}{\mathit{\int }}_{\upsilon \in S\left(W\right)}{\langle {\alpha }^{\ast }\circ \alpha \left(\upsilon \right),\upsilon \rangle }_H\mathrm{d}\upsilon \\ & =& \frac{3}{2}{\mathit{\int }}_{\upsilon \in S\left(W\right)}{\langle \alpha \left(\upsilon \right),\alpha \left(\upsilon \right)\rangle }_H\mathrm{d}\upsilon \\ & =& \frac{3}{2}{\mathit{\int }}_{\upsilon \in S\left(W\right)}{\mathit{\int }}_{x\in X}{\langle {\delta }_x^{\ast }\left(\upsilon \right),{\delta }_x^{\ast }\left(\upsilon \right)\rangle }_{\mathrm{std}}\mathrm{d}\upsilon \mathrm{d}x\\ & =& \frac{3}{2}{\mathit{\int }}_{\upsilon \in S\left(W\right)}{\mathit{\int }}_{x\in X}2\mathrm{d}\upsilon \mathrm{d}x=3,\end{array}$$

where dυ denotes the normalized Haar measure on the five-dimensional sphere S(W).

Next, we prove that τ ∘ δ_x = φ_x, for every x ∈ X. The starting point is the equation $\mathrm{e}{\mathrm{v}}_x\mid W\circ \alpha ={\delta }_x^{\ast }$, which follows from the definition of the morphism α and the fact that Im α = W. This implies that ${\phi }_x^{\ast }\circ \tau ={\delta }_x^{\ast }$. The statement now follows from

$$\begin{array}{lll}{\phi }_x^{\ast }\circ \tau ={\delta }_x^{\ast }& \Rightarrow & {\phi }_x^{\ast }\circ \left(\tau \circ {\tau }^{\ast }\right)={\delta }_x^{\ast }\circ {\tau }^{\ast }\\ & \Rightarrow & {\phi }_x^{\ast }={\delta }_x^{\ast }\circ {\tau }^{\ast }\Rightarrow {\phi }_x=\tau \circ {\delta }_x.\end{array}$$

This concludes the proof of the theorem.

A.5 Proof of Theorem 6

We use the following terminology: for every x ∈ X, x = (e₁, e₂, e₃), we denote by δ̃_x : C → V the map given by δ̃_x(p + iq) = pe₁ + qe₂. We observe that δ_x(υ) = δ̃_x(υ) − iδ̃_x (iυ), for every υ ∈ C.

We proceed with the proof. Let x, y ∈ X. Choose unit vectors υ_x, υ_y ∈ C such that δ̃_x(υ_x) = δ̃_y(υ_y) = υ.

Write

$$\begin{array}{lll}\langle {\delta }_x({\upsilon }_x),{\delta }_y({\upsilon }_y)\rangle & =& \langle {\stackrel{\sim }{\delta }}_x({\upsilon }_x)-\mathrm{i}{\stackrel{\sim }{\delta }}_x(\mathrm{i}{\upsilon }_x),{\stackrel{\sim }{\delta }}_y({\upsilon }_y)-\mathrm{i}{\stackrel{\sim }{\delta }}_y(\mathrm{i}{\upsilon }_y)\rangle \\ & =& \left({\stackrel{\sim }{\delta }}_x({\upsilon }_x),{\stackrel{\sim }{\delta }}_y({\upsilon }_y)\right)+\left({\stackrel{\sim }{\delta }}_x(\mathrm{i}{\upsilon }_x),{\stackrel{\sim }{\delta }}_y(\mathrm{i}{\upsilon }_y)\right)\\ & & -\mathrm{i}\left({\stackrel{\sim }{\delta }}_x(\mathrm{i}{\upsilon }_x),{\stackrel{\sim }{\delta }}_y({\upsilon }_y)\right)+\mathrm{i}\left({\stackrel{\sim }{\delta }}_x({\upsilon }_x),{\stackrel{\sim }{\delta }}_y(\mathrm{i}{\upsilon }_y)\right).\end{array}$$ (A.5)

For every frame z ∈ X and vector υ_z ∈ C, the following identity can easily be verified:

$${\stackrel{\sim }{\delta }}_z\left(\mathrm{i}{\upsilon }_z\right)=\pi \left(z\right)\times {\stackrel{\sim }{\delta }}_z\left({\upsilon }_z\right).$$

This implies that

$$\begin{array}{lll}{\stackrel{\sim }{\delta }}_x(\mathrm{i}{\upsilon }_x)& =& \pi (x)\times {\stackrel{\sim }{\delta }}_x({\upsilon }_x)=\pi (x)\times \upsilon ,\\ {\stackrel{\sim }{\delta }}_y(\mathrm{i}{\upsilon }_y)& =& \pi (y)\times {\stackrel{\sim }{\delta }}_y({\upsilon }_y)=\pi (y)\times \upsilon .\end{array}$$

Combining these identities with (A.5), we obtain

$$\langle {\delta }_x({\upsilon }_x),{\delta }_y({\upsilon }_y)\rangle =\left(\upsilon ,\upsilon \right)+\left(\pi \left(x\right)\times \upsilon ,\pi \left(y\right)\times \upsilon \right)-\mathrm{i}\left(\pi \left(x\right)\times \upsilon ,\upsilon \right)+\mathrm{i}\left(\upsilon ,\pi \left(y\right)\times \upsilon \right).$$

Since υ ∈ Im δ̃_x ∩ Im δ̃_y, it follows that (π(x) × υ, υ) = (υ, π(y) × υ) = 0. In addition,

$$\left(\pi \left(x\right)\times \upsilon ,\pi \left(y\right)\times \upsilon \right)=\det \left(\begin{array}{cc}\left(\pi \left(x\right),\pi \left(y\right)\right)& \left(\pi \left(x\right),\upsilon \right)\\ \left(\pi \left(y\right),\upsilon \right)& \left(\upsilon ,\upsilon \right)\end{array}\right)=\left(\pi \left(x\right),\pi \left(y\right)\right).$$

Thus, we obtain that 〈δ_x(υ_x), δ_y(υ_y)〉 = 1 + (π(x), π(y)). Since the right hand side is always ≥ 0 it follows that

$$\left|\langle {\delta }_x\left({\upsilon }_x\right),{\delta }_y\left({\upsilon }_y\right)\rangle \right|=1+\left(\pi \left(x\right),\pi \left(y\right)\right).$$ (A.6)

Now, notice that the left hand side of A.6 does not depend on the choice of the unit vectors υ_x and υ_y.

To finish the proof, we use the isomorphism τ which satisfies τ ∘ δ_x = φ_x for every x ∈ X, and get

$$\left|\langle {\phi }_x\left({\upsilon }_x\right),{\phi }_y({\upsilon }_y)\rangle \right|=1+\left(\pi \left(x\right),\pi \left(y\right)\right).$$

This concludes the proof of the theorem.

A.6 Proof of Proposition 7

The basic observation is that H, as a representation of SO(V) × SO(3), admits the following isotypic decomposition:

$$H=\underset{n=0}{\overset{\infty }{\oplus }}{V}_n\otimes U_n,$$

where V_n is the unique irreducible representation of SO(V) of dimension 2n + 1, and, similarly, U_n is the unique irreducible representation of SO(3) of dimension 2n + 1. This assertion, principally, follows from the Peter–Weyl Theorem for the regular representation of SO(3).

This implies that the isotypic decomposition of H_k takes the following form:

$$H_k=\underset{n=0}{\overset{\infty }{\oplus }}{V}_n\otimes U_n^k,$$

where $U_n^k$ is the weight k space with respect to the action SO(2) ⊂ SO(3). The statement now follows from the following standard fact about the weight decomposition:

$$\dim U_n^k=\{\begin{array}{cc}0& n<k\\ 1& n\ge k\end{array}.$$

This concludes the proof of the theorem.