Anomalous diffusion of brain metabolites evidenced by diffusion-weighted magnetic resonance spectroscopy in vivo

Abstract

Translational displacement of molecules within cells is a key process in cellular biology. Molecular motion potentially depends on many factors, including active transport, cytosol viscosity and molecular crowding, tortuosity resulting from cytoskeleton and organelles, and restriction barriers. However, the relative contribution of these factors to molecular motion in the cytoplasm remains poorly understood. In this work, we designed an original diffusion-weighted magnetic resonance spectroscopy strategy to probe molecular motion at subcellular scales in vivo. This led to the first observation of anomalous diffusion, that is, dependence of the apparent diffusion coefficient (ADC) on the diffusion time, for endogenous intracellular metabolites in the brain. The observed increase of the ADC at short diffusion time yields evidence that metabolite motion is characteristic of hindered random diffusion rather than active transport, for time scales up to the dozen milliseconds. Armed with this knowledge, data modeling based on geometrically constrained diffusion was performed. Results suggest that metabolite diffusion occurs in a low-viscosity cytosol hindered by ∼2-μm structures, which is consistent with known intracellular organization.

Introduction

Cellular biology is governed by the transport of metabolites, macromolecules, and organelles from synthesis sites to utilization and degradation sites. Translational displacement of materials in the cytoplasm is a key parameter and a rate-limiting step for biochemical reactions and biological processes. Efficient transport capacities over large distances are of particular importance for cells presenting complex structures, strong elongation and marked polarization, such as neurons, and the study of intracellular motion has raised much interest. Over the years, various methods have been proposed to investigate the motion of exogenous or labeled probes in the cytoplasm, including autoradiography, electron spin resonance, and optical techniques such as fluorescence recovery after photobleaching, fluorescence correlation spectroscopy, and single particle tracking. Diffusion-weighted (DW) magnetic resonance imaging (MRI) and spectroscopy (MRS) have also been used to assess the motion of endogenous water and metabolites (for review see Nicolay et al.¹).

Measurement methods mentioned above generally allow extracting an estimate of the displacement variance 〈x²〉 along one axis (where 〈〉 denotes the ensemble average), or an apparent diffusion coefficient ADC∼〈x²〉/2t_d (t_d being the diffusion time, i.e., the time during which displacement is measured). Molecular motion in complex media such as the intracellular space potentially depends on many factors, including active transport (either specific transport, e.g., inside vesicles, or general motion of the cytosol, known as cytoplasmic streaming), cytosol viscosity and molecular crowding, tortuosity resulting from cytoskeleton and organelles, and restriction barriers. The importance of these different factors remains debated. Measurements are generally performed for a single t_d, providing a composite picture of molecular motion where it is generally impossible to untangle the different factors contributing to motion, unless these factors can be varied independently and the resulting variation in molecular motion can be observed.² In contrast, performing measurements at different diffusion times, and observing the time dependence of 〈x²〉, may allow an intrinsic identification and quantification of the different parameters governing molecular displacement. For free diffusion, 〈x²〉 linearly depends on t_d, that is, the ADC does not depend on t_d and is equal to the free diffusion coefficient. Deviations from this behavior are referred to as ‘anomalous diffusion.' The study of anomalous diffusion is relatively recent and still represents an emerging field. Anomalous diffusion has already been reported for fluorescent proteins (for review see Malchus and Weiss³). Anomalous diffusion of exogenous and inert low-molecular-weight probes has also been reported using optical techniques,⁴ including in the brain cells.⁵ Anomalous diffusion of endogenous water has been evidenced using DW-MRI.⁶ As far as we know, anomalous diffusion of endogenous metabolites has only been reported in skeletal muscle, using DW-MRS.⁷ In contrast to muscle, anomalous diffusion has never been reported for endogenous brain metabolites.

In this work, we designed an original DW-MRS method using oscillating gradients allowing diffusion times an order of magnitude shorter than in the past studies, to probe molecular motion at subcellular scales in the rat brain in vivo. This led to the first observation of anomalous diffusion of endogenous intracellular metabolites in the brain. The time dependence of the ADC strongly suggests that random diffusion is the main mechanism for metabolite transport for time scales up to the dozen milliseconds, and that a major contribution of active transport is very unlikely. Then, data modeling based on hindered random diffusion suggests that metabolite anomalous diffusion results from diffusion in a low-viscosity fluid-phase hindered by ∼2-μm distant structures, which is very consistent with known cellular architecture. Altogether, these results allow clarifying mechanisms governing metabolite displacement in the brain, and refining the interpretation of DW-MRS data.

Materials and methods

Probing Diffusion Using Oscillating Gradients

The ADC can be simply derived from measured magnetic resonance signal attenuation S/S₀ when diffusion-weighting gradients G are applied:

In the above equation, the diffusion-weighting factor b is defined as:

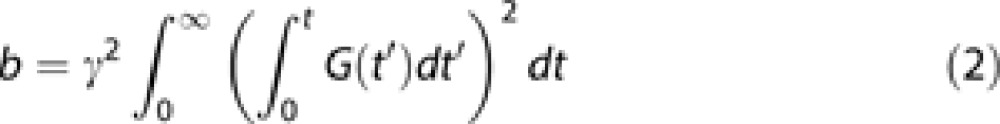Cosine-modulated diffusion gradients were used in the present work. In practice, as gradient rise cannot be infinite, cosine gradient are apodized by inserting a sine period at the beginning and at the end of the gradient:⁶

G_max is the maximal applied gradient amplitude, T is the total gradient duration, and N is the number of periods during T. For this waveform we get the following b value:

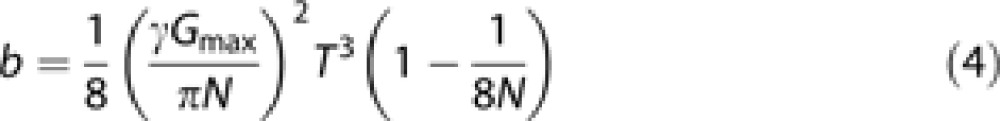It is intuitive that the higher the gradient frequency, the shorter the diffusion time, since particles magnetization is rapidly dephased and rephased by the gradient. For oscillating gradients with effective moment integrating to zero, the most accurate description of the diffusion measurement is given in the frequency domain, and directly relates to the Fourier transform of particles velocity autocorrelation function D(ω), which reflects the motion characteristics of detected molecules. The temporal properties of the measurement are then defined by a diffusion frequency ω_d∼2πN/T (equality is strict when T tends towards infinity), and one gets ADC∼D(ω_d). ω_d can be exactly determined as the position of the main peak on the gradient modulation spectrum, which is the Fourier transform of the diffusion gradient first moment.^{8, 9} For apodized cosine-modulated gradients, practical relationship between the diffusion frequency and the effective diffusion time is given by t_d=0.25/ω_d.⁶

Magnetic Resonance Spectroscopy Methods Implementation

Magnetic resonance spectroscopy methods were developed on a horizontal 7 T Varian/Agilent scanner running with VnmrJ (Palo Alto, CA, USA). Maximal gradient strength was 600 mT/m along each direction. We designed an original spectroscopy sequence derived from a LASER sequence (Localization by Adiabatic SElective Refocusing)¹⁰ implemented in-house. This localization scheme was chosen to maintain a high signal-to-noise ratio and an accurate localization due to adiabatic properties, high bandwidth, and well-defined profile of the hyperbolic secant radiofrequency pulses (pulse-bandwidth product R=20, pulse duration 2 milliseconds). The sequence was made asymmetric, and two 60-millisecond diffusion blocks were inserted around the first refocusing pulse (Figure 1). Resulting TE (echo-time) was 154 milliseconds. Different cosine-modulated gradient waveforms were generated with Matlab (The Mathworks, Natick, MA, USA) using equation (3), each waveform corresponding to a different number of periods N within each 60-millisecond diffusion block, chosen to span the frequency domain at regular intervals. Waveforms were generated for N=1 (corresponding to ω_d=19 Hz, t_d=12.9 milliseconds), N=5 (ω_d=86 Hz, t_d=2.9 milliseconds), N=8 (ω_d=134 Hz, t_d=1.9 milliseconds), N=10 (ω_d=169 Hz, t_d=1.48 milliseconds), N=12 (ω_d=201 Hz, t_d=1.24 milliseconds), and N=16 (ω_d=267 Hz, t_d=0.94 milliseconds). The exact ω_d/t_d was actually calculated by numerical integration and Fourier transform of the effective gradient chronogram. With this design, b=1 millisecond/μm² could be reached for all t_d when applying gradients in the three directions simultaneously.

Figure 1.

Modified asymmetric LASER spectroscopy sequence with diffusion-weighting oscillating gradients inserted around the first adiabatic full passage pulse. Slice selection gradients are in gray, and spoiler gradients are in black.

Animal Experiments

Experiments were performed on 20 Wistar rats (body-weight ∼300 to 350 g). Protocol was approved by the local ethical committee of the Commissariat à l'Energie Atomique (French Atomic Energy Commission). All animal experimental procedures were performed in accordance with the recommendations of the European Union (86/609/EEC) for care and use of laboratory animals, and conformed to the ethical guidelines of the French Ministry of Agriculture and Forests (Animal Health and Protection Veterinary Service). Animals were anesthetized with 1.5% isoflurane in a 1:1 mixture of air/dioxygen. Radiofrequency transmission was performed with a volume coil, while reception was performed with a quadrature surface coil. Body temperature was monitored using an endorectal probe and maintained at 37°C using heated air flow (SA Instruments Inc., Stony Brook, NY, USA). Anatomical images were acquired using a high-resolution 2D fast spin-echo sequence. A large 450 μL voxel was positioned in the brain, in which 12 to 14 Hz shimming was achieved. Water and metabolite spectra (128 repetitions, with repetition time TR=2 seconds) were acquired at b=0 and for each t_d at b=1 millisecond/μm².

Data Processing

Data processing was minimized in an effort to remain as close as possible to the original raw data. No phase variation could be observed between individual scans for each t_d (either on metabolite signal or on repeated water signal measurements), demonstrating the absence of movement artifact, which can be ascribed to the use of rapidly oscillating gradients. Spectra corresponding to a given t_d were therefore summed without individual scan phasing. The water reference signal acquired for each gradient waveform was used for standard eddy-currents correction on metabolite spectra. Spectra were analyzed with LCModel,¹¹ using a basis-set generated with home-made routines based on the density matrix formalism. At the long TE used in the present study, macromolecule and lipid signal vanishes, so that no particular modeling or subtraction of this signal was necessary, avoiding further postprocessing. The ADC was simply evaluated as −1/b × ln(S/S₀), where S₀ is the reference signal at b=0 and S is the signal at b=1 millisecond/μm² for a given t_d, as derived by LCModel. This was done for the most reliably quantified metabolites (LCModel's Cramér-Rao lower bounds <10%), that is, N-acetylaspartate (NAA), total creatine (tCr), and choline compounds (tCho).

Diffusion Models

To model measured ADC, we turned to the formalism of the velocity autocorrelation function and motion spectrum, which is well adapted to oscillating gradients as used in the present work. The theoretical motion spectrum, which is the Fourier transform of the velocity autocorrelation function, was calculated for simple restricted systems, based on Gaussian approximation of the phase distribution which holds for NMR experiments:¹²

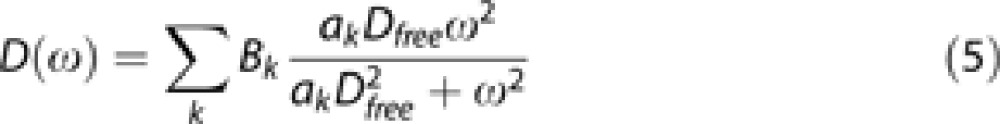D_free is the free diffusion coefficient and a_k and B_k are coefficients that depend on the geometry of the compartments where diffusion occurs. Two geometrical models were implemented in Matlab and evaluated using equation (5) to reflect diffusion in the brain. These two models were chosen since they represent two extreme situations that are expected to occur in the brain. Error on estimated parameters was evaluated using a standard Monte-Carlo approach (N=1,000 draws).

First model: neurite model

In this model, which accounts for diffusion in long fibers such as axons and dendrites, diffusion occurs in impermeable hollow cylinders oriented isotropically in three dimensions. There are two free parameters: D_free and the cylinder diameter d. When gradients are in the direction perpendicular to the axis of the cylinder, coefficients a_k and B_k are given by the following expressions:

In the above expressions, the μ_k are the roots of J′₁(μ)=0, where J' is the derivative of the Bessel function of the first kind.

As cylinders are isotropically oriented, gradients make a variable angle θ with cylinder's axes. Therefore, for any given cylinder, two diffusion regimes have to be considered: (i) restricted diffusion in the plane perpendicular to cylinder's axis, resulting in signal attenuation according to D(ω) calculated by injecting equation (6) in equation (5) and b calculated with equation (4) and effective gradient strength G_maxsin(θ) and (ii) free diffusion in the direction of the cylinder's axis, resulting in signal attenuation according to D_free and b calculated with effective gradient strength G_maxcos(θ). Signal attenuation in the fiber distribution is calculated by summing over all θs corresponding to an isotropic distribution in three dimensions, and resulting theoretical ADC for any D_free and d can then be evaluated.

Second model: cell body model

This model accounts for diffusion in the tortuous internum of large cell bodies, which is modeled by interconnected spherical pores of diameter d. In this model, cell walls are neglected due to the use of short diffusion times, so that most molecules do not have time to experience restriction by cell walls. In such structure, metabolites can move from pore to pore. As a result, as the frequency decreases (long t_d), D does not tend towards zero but towards an effective diffusion coefficient D_free/T², where the tortuosity T reflects to what extent pores are interconnected.⁹ Therefore, the term D_free/T² is added to the sum in equation (5), and the resulting model has three free parameters: D_free, T and d. Expressions of a_k and B_k for spherical pores are given by:

In equation (7) , the μ_k are the roots of μ × J′_s/2(μ)−0.5 × J_s/2(μ)=0, where J is the Bessel function of the first kind and J′ its derivative.

Results

Observing Anomalous Diffusion of Brain Metabolites In Vivo

The goal of the present work was to observe metabolite diffusion at short t_d (<1 millisecond versus >13 milliseconds in the literature), to assess the potential dependency of the ADC on t_d in this short t_d regime. To do so, we first developed a new NMR spectroscopy sequence using oscillating magnetic field gradients for diffusion-weighting. With this sequence, the gradient modulation spectrum frequency ω_d could be varied between 19 and 267 Hz, corresponding to t_d varying between 12.9 milliseconds and 0.94 milliseconds (with t_d=0.25/ω_d), by changing only gradient waveform and amplitude, while keeping constant diffusion-weighting factor (b=1 millisecond/μm²) and sequence timing unchanged, thus preserving metabolite spectral pattern and relaxation for all t_d.

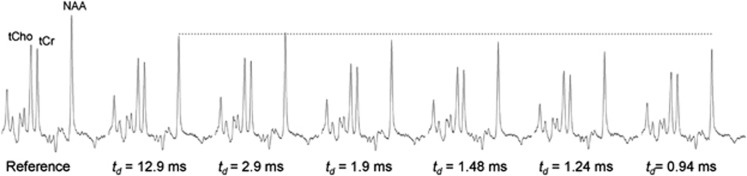
Diffusion-weighted MRS experiments were first carried out on our 7 T scanner on a liquid phantom containing NAA dissolved in water. As expected for free diffusion, the ADC of NAA and water exhibited no dependency on t_d, demonstrating the absence of diffusion artifacts due to eddy-currents or nonlinear gradient calibration. Experiments were then performed in the rat brain. The tendency of metabolite signal to decrease as t_d decreased could be visually assessed on data from individual animals, as shown in Figure 2. The dependence of signal attenuation on t_d is a direct experimental manifestation of anomalous diffusion, demonstrating the ability of our strategy to detect brain metabolite anomalous diffusion for the first time.

Figure 2.

Diffusion-weighted NMR spectra acquired in the rat brain during a single scanning session, for different diffusion times t_d and diffusion-weighting b=1 millisecond/μm². The tendency of metabolite signal to decrease as t_d decreases can be visually assessed on data, as exemplified for N-acetylaspartate (NAA) (dotted horizontal line represents the NAA peak height for the longest t_d). This is a direct experimental manifestation of anomalous diffusion.

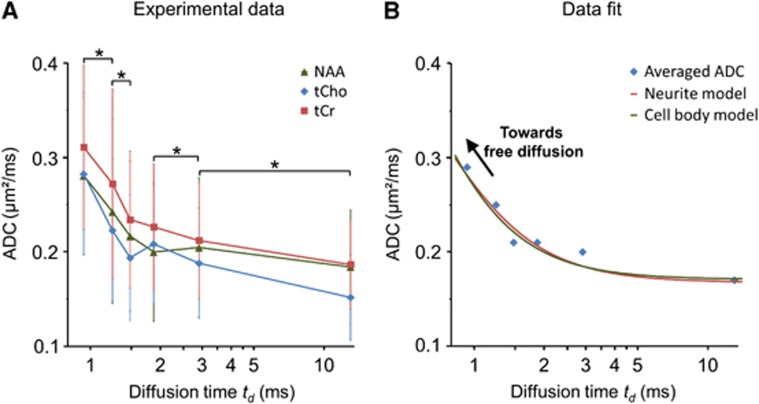
Apparent diffusion coefficient (ADC) was quantified as the logarithm of signal attenuation for three endogenous metabolites: NAA, total creatine tCr (i.e., creatine and phosphocreatine), and choline compounds tCho (essentially phosphocholine and glycerophosphocholine). Resulting ADC are displayed in Figure 3A. Values at longer t_d are in good agreement with literature values (0.18 μm²/millisecond for NAA, 0.19 μm²/millisecond for tCr, 0.15 μm²/millisecond for tCho), while ADC exhibit a clear tendency to increase as t_d decreases (+50% for NAA, +70% for tCr, and +90% for tCho between extreme t_d). This is a characteristic signature of subdiffusion, as described in studies using other measurement techniques.

Figure 3.

(A) The apparent diffusion coefficient (ADC) measured for N-acetylaspartate (NAA), total creatine tCr, and choline compounds tCho, over 20 sessions, as a function of t_d (represented in log-scale). The increase of ADC at shorter t_d is a characteristic signature of subdiffusion, and evidence that hindered random diffusion is the dominant transport mechanism for the metabolites. Statistical significance of the ADC variation between two consecutive t_d, averaged over the three metabolites, was assessed using Student's paired t-test (the star symbol stands for P<0.01). (B) The ADC averaged for the three metabolites, and the best fit using the ‘neurite' and the ‘cell body' geometrically constrained diffusion models (see text for details). Both models yield a free diffusion coefficient D_free=0.55 μm²/millisecond, slightly lower than in free water, and typical 1.8-μm distance between obstacles, which is consistent with known cellular architecture. Although best fits are represented in the time domain, modeling was actually performed in the frequency domain.

Anomalous diffusion is sometimes described by a phenomenological power-law 〈x²〉∼t_d^α, with anomalous exponent 0<α<1 corresponding to ‘subdiffusion,' and α>1 to ‘superdiffusion.' Data fit using a power-law (ADC∼t_d^α−1) yields α∼0.8, which is comparable to values reported for proteins undergoing subdiffusion in various cells (0.5<α<0.8),³ for lipid granules in human-derived fibroblast cells (α∼0.75)⁴ for fluorescent dextran in smooth dendrites of Purkinje cells (α∼0.7).⁵

Modeling Brain Metabolite Diffusion

Experimental ADC was fitted using models based exclusively on geometrically constrained diffusion. Two models were considered to embrace the variety of cellular geometry in the brain. The first model (‘neurite model') basically consists in hollow cylinders isotropically oriented in three dimensions, to account for diffusion in long fibers such as axons and dendrite. Unknown parameters are the free diffusion coefficient D_free and the fiber diameter d. The second model (‘cell body model') consists in interconnected spherical pores, to account for the internum of a large cell body filled with packed organelles and cytoskeleton. Unknown parameters were D_free, the pore diameter d and the tortuosity T. Data analysis was first performed for ADC averaged over the three metabolites. Fit was performed in the frequency domain rather than temporal domain since it is better adapted to oscillating gradients. Both models yielded a good fit of experimental ADC, as shown in Figure 3B. For the neurite model, results of the fit are D_free=0.55±0.03 μm²/millisecond and d=1.82±0.08 μm. For the cell body model, best fit yielded D_free=0.55±0.20 μm²/millisecond, d=1.80±0.12 μm, and T=1.75±0.34. Data modeling performed on individual metabolites yields similar values (see Table 1). These values are very consistent between each other and, despite the extreme simplicity of both models, agree reasonably well with known cellular organization. Estimated d is indeed consistent with axon, dendrite or astrocytic process typical size, or with the characteristic size of and distance between organelles. Estimated D_free is ∼20% lower compared with metabolite diffusion in pure water at 37°C, which is in excellent agreement with the low fluid-phase viscosity in the cytoplasm measured through rotational correlation times² and may also include some contribution of molecular crowding over very short distances.

Table 1. Parameters determined from the neurite and cell body models (see text for details), for individual metabolites and for averaged ADC.

	NAA	tCr	tCho	Averaged ADC
Neurite model
Dfree (μm2/millisecond)	0.59±0.02	0.60±0.03	0.52±0.05	0.55±0.03
d (μm)	1.70±0.04	1.88±0.06	1.76±0.13	1.82±0.08
Cell body model
Dfree (μm2/millisecond)	0.53±0.15	0.55±0.18	0.52±0.24	0.55±0.20
d (μm)	1.69±0.09	1.81±0.11	1.77±0.20	1.80±0.12
T	1.7±0.3	1.7±0.3	1.8±0.4	1.75±0.34

ADC, apparent diffusion coefficient; NAA, N-acetylaspartate; tCho, choline compounds; tCr, total creatine.

Standard deviations were estimated using Monte-Carlo simulations. D_free stands for the free diffusion coefficient, d for the cylinder diameter in the neurite model and for the pore diameter in the cell body model. T is the pore tortuosity in the cell body model.

Discussion

Relevance of Methodological Choices

Beyond the use of oscillating gradients, two striking methodological differences appear between the present work and most previous DW-MRS studies: the use of only two b-values to determine the ADC, and the relatively low maximal b-value used. Both points actually relate to an underlying assumption of the present work, namely the linearity of the logarithm of signal attenuation. This assumption allows using only two b-values to determine the ADC, and is also essential for interpretation and modeling using the velocity autocorrelation function formalism. However, for constrained diffusion, the logarithm of signal attenuation is known to deviate from linearity as b is increased. This is because the phase distribution of the spins strongly deviates from a Gaussian distribution at high b. It turns out that, when sufficiently small b are used, the Gaussian phase distribution assumption remains valid even when diffusion is not free,¹³ and the logarithm of signal attenuation can be considered linear.

Using the MRS sequence of the present work, it was possible to reach b up to 5 milliseconds/μm² for the three longest t_d (12.9, 2.9, and 1.9 milliseconds). Additional experiments were therefore performed in the rat brain to check that signal attenuation was indeed linear between b=0 and 5 milliseconds/μm² for the three longest t_d. Two rats were scanned for each t_d, and spectra at b=0, 1, 2, 3, 4, and 5 milliseconds/μm² were acquired for each rat. Linear regression of signal logarithm yielded R²>0.99 for each metabolite at all three t_d, demonstrating that we indeed are in the low b-value regime even for b up to 5 milliseconds/μm², so that signal attenuation logarithm is indeed clearly linear in the present work, and phase distribution can safely be assumed Gaussian.

Note that ADC determined by log-linear regression using the six b-values (ADC=0.15, 0.20, and 0.22 μm²/millisecond for t_d=12.9, 2.9, and 1.9 milliseconds, averaged over NAA, tCho, and tCr) are consistent with the values reported in the Results section using only b=0 and 1 millisecond/μm² (0.17, 0.20, and 0.21 μm²/millisecond for t_d=12.9, 2.9, and 1.9 milliseconds, respectively).

Major Contribution of Active Transport to Metabolite Motion is Unlikely

Molecular transport may be achieved passively by random diffusion, that is, Brownian motion, at no energetic cost. In that case, although intracellular diffusion is hindered by binding, macromolecular crowding, and obstacles such as cytoskeleton and membranes, the mechanism for transport is random diffusion. Alternatively, active transport mechanisms exist. Many are based on motor proteins conveying their cargoes on microtubules. Convection of the cytosol, also known as cytoplasmic streaming or cyclosis, which is occasioned by gel-sol transitions of actin, actin flow or myosin contraction entraining fluid, or syneresis, is well known in plants and amoeboids, and has been reported in mammal cells.^{14, 15} Some have even hypothesized that cytoplasmic streaming is a fundamental characteristic of life, and is the dominant mechanism by which metabolites and proteins are transported inside all cells.^{16, 17, 18} As a matter of fact, the failure of energy-dependent active transport, in particular cytoplasmic streaming, has been repeatedly evoked as a possible explanation for the observed massive ADC drop of intracellular molecules observed in ischemic stroke.^{19, 20, 21, 22, 23}

It turns out that anomalous diffusion is an interesting theoretical framework to address this question. Indeed, although some special cases may be imagined, active transport will in general result in superdiffusion, that is, 〈x²〉 increases more than linearly with time,⁴ or the ADC increases with time. For example, when individual particles evolve at constant speed in straight lines, a situation referred to as the ballistic regime, one simply gets 〈x²〉∼t_d². In contrast, for hindered diffusion, obstacles to motion will result in subdiffusion, that is, 〈x²〉 increases less than linearly with time, or the ADC decreases with time.²⁴ Unlike exogenous and inert low-molecular-weight probes studied by techniques other than NMR or ubiquitous water molecules studied by DW-MRI, whose anomalous subdiffusion has already been reported in the brain,^{6, 5} endogenous metabolites studied in the present work are implied in specific and active metabolic pathways. N-acetylaspartate has been reported to regulate protein synthesis, to be a storage form of acetate and aspartate, and to be implied in lipogenesis and myelination. Creatine and phosphocreatine have a major role in brain energy metabolism regulation via the creatine kinase system, by maintaining low levels of adenosine diphosphate and constant levels of adenosine triphosphate. Choline compounds are involved in membrane phospholipids synthesis and degradation. Therefore, the proportion of these metabolites engaged in efficient active transport systems may potentially be much larger than for exogenous or ubiquitous molecules. Yet metabolite unambiguous subdiffusive behavior, as observed for the first time in the present work, strongly suggests that hindered random diffusion is the dominant transport mechanism for brain intracellular metabolites over the observed time window.

This view is also consistent with the formalism of velocity autocorrelation function, which can be preferred when using oscillating gradients. Briefly, the velocity autocorrelation function is defined as VAF(t)=〈v(0)v(t)〉, where v(t) is the speed of an individual molecule along the magnetic field gradient direction at time t. For free diffusion, no correlation exists on average between a particle's speed and its speed a few moments later, that is, VAF(t)=0 for t>0. For hindered random diffusion, the impossibility for some particles to cross obstacles will impose movement's reversal, that is, VAF(t) drops below 0 as soon as t>0. For active transport or any kind of coherent motion, the movement of any single particle will tend to be preserved over a certain amount of time, that is, VAF(t) is positive. In a complex and heterogeneous medium, motion is expected to be dispersive, and progressive loss of coherence in the long-time tail makes VAF smoothly converge to 0 as t increases, but with constant sign (negative for hindered random diffusion and positive for active transport). The VAF can be equivalently described by its Fourier transform, the motion spectrum D(ω). A negative VAF typical of hindered random diffusion corresponds to D(ω) increasing at higher ω, while positive VAF corresponds to D(ω) decreasing at higher ω, D(ω) tending in both cases to D_free as ω approaches infinity.⁶ Since the use of oscillating gradients of frequency ω_d result in ADC=D(ω_d), our data demonstrate that D(ω) is increasing at higher ω, which suggests negative VAF resulting from hindered random diffusion rather than active transport.

We think that our results bring a strong argument against the minority but persisting idea of significant intracellular active transport, in particular cytoplasmic streaming, and retrospectively give solid grounds to the relatively common practice of using diffusion theory when describing or modeling the motion of small molecules in the cytoplasm. Although significant active transport may occur for a fraction of metabolite pool (e.g., in the case of vesicular transport), the fraction of metabolites whose motion is characteristic of random diffusion eventually dominates when averaged over the whole metabolite pool. Another view can be that the entire metabolite pool is potentially embarked in active transport (e.g., in the case of cytoplasmic streaming), but at negligible speed compared with the effective speed of random diffusion in the observed time window.

Two important caveats that prevent totally ruling out the possibility of dominant active transport should be mentioned. First, DW-MRS is not sensitive to phase coherent motion (pure ballistic motion for example), that is, such motion would not contribute to signal attenuation. Second, some special kinds of motion (such as oscillatory motion) will not result in superdiffusion or in a positive VAF converging to zero, so that measured ADC would not increase with t_d despite active transport. Although it cannot be excluded that such motions occur for brain metabolites, we think that this is unlikely, due to the complex geometry and heterogeneity of brain cells.

A Retrospective Look at Literature Data

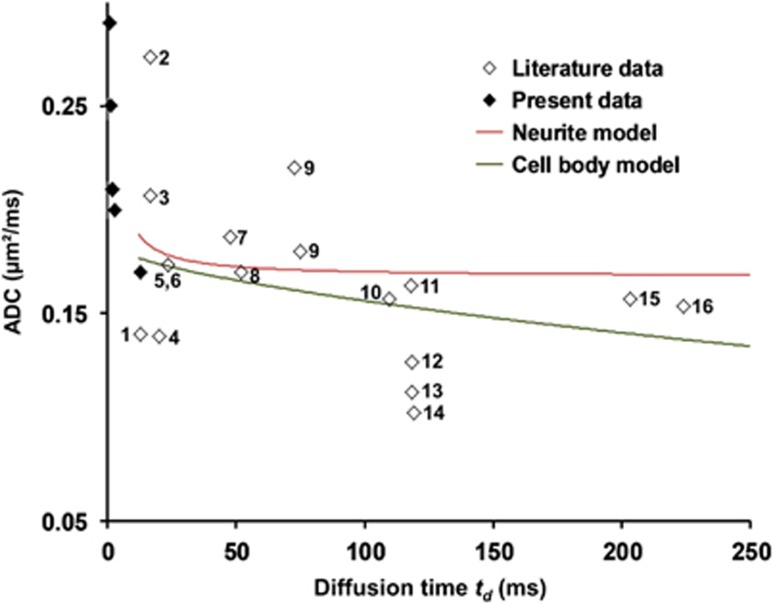
Past DW-MRS studies reporting measurements of brain metabolite diffusion in vivo used t_d ranging from 13 milliseconds²¹ to 224 milliseconds.²⁵ Average ADC for NAA, tCho, and tCr as determined in those works is plotted in Figure 4, as a function of t_d. Keeping in mind that comparisons between studies are always subject to caution, no dramatic dependence of the ADC on t_d can be observed over this large time window, although a small tendency of ADC to decrease at longer t_d may seem to emerge. Interestingly, using geometry and diffusion parameters as determined in the present study at short t_d, the neurite and cell body models can be extended over the time window of past studies (see Appendix for details), reconciling the dramatic ADC variations reported here with the relative stability reported in the literature. For the neurite model, after the initial fast decrease of ADC at short t_d, we rapidly approach a constant ADC∼D_free/3 corresponding to free diffusion along isotropically distributed fiber axes and complete restriction along the two directions perpendicular to fibers, which can account for literature data (Figure 4). For the cell body model, going to longer t_d requires a slight adaptation of the model, since restriction by cell walls will have an increasing importance, while diffusion within the cell internum will approach a tortuous regime as the distance traveled by metabolites becomes large compared with pore size. Encompassing this tortuous cytoplasmic medium (with effective diffusion coefficient D_free/T²) within 80-μm diameter spherical cell bodies accounts very well for the relatively stable literature values, with a slight decrease of ADC as t_d increases (Figure 4). Although 80 μm may seem very large for cell bodies, and is actually realistic only for the largest pyramidal neurons, it should be reminded that this value should rather be considered as an order of magnitude only, since interstudy comparison does not allow the accurate determination of this parameter. It appears that a description of metabolite diffusion based only on geometric restriction either in narrow fibers or large, tortuous cell bodies, allows accounting for the values and time dependence of metabolite ADC as measured in the present study, as well as for the absolute values and stability of ADC in the literature. It is interesting to note that this is achieved without invoking active transport that may become significant at longer t_d and compensate for the ADC drop due to restriction. In our opinion, the explanatory power of these models also reinforces a conclusion of the present work, namely the dominance of random diffusion as the main mechanism for metabolite transport at a global scale in the brain, and leaves only little room to significant active transport over time scales up to hundreds milliseconds.

Figure 4.

A compilation of apparent diffusion coefficient (ADC) averaged for N-acetylaspartate (NAA), tCr, and tCho, as reported in the past published studies when data are available, illustrating the relative stability of metabolite diffusion at long t_d. Extending the ‘neurite' and the ‘cell body' models at long t_d using parameters derived on our own data allows accounting very well for ADC stability as reported in the literature. Note that averaged ADC as measured in the present study are also presented in the time domain (black diamonds at very short t_d), for comparison only. Numbers next to diamonds stand for the referenced published articles: 1 (ref. 21); 2 (ref. 26); 3 (ref. 27); 4 (ref. 28); 5 (ref. 20); 6 (ref. 23); 7 (ref. 22); 8 (ref. 29); 9 (ref. 30); 10 (ref. 31); 11 (ref. 32); 12 (ref. 33); 13 (ref. 34); 14 (ref. 35); 15 (ref. 36); 16 (ref. 25).

Rationale for the Neurite and Cell Body Models

Two geometrical models have been used to fit experimental ADC in the present study. These models represent two extreme situations of what can be expected for brain cells. The reality certainly lays in-between, with cell bodies whose dimensions are not sufficiently large to neglect restriction by cell walls, some being prolonged by long fibers being themselves hindered by organelles. The rationale of using these two models was not to discriminate between them, but rather to assess that, even in two extreme situations, the derived parameters (intracellular D_free and typical structure size d) are consistent between the models and have reasonable values. In our opinion, this ensures that these parameters can be estimated relatively well, although we cannot tell what the 1.8-μm distant obstacles exactly consist in.

Determining which model yields the best description of metabolite diffusion could in theory be possible by going to very long diffusion times, since ADC is expected to decay towards zero as t_d increases in the case of diffusion in closed compartments such as cell bodies, while it is expected to remain fairly stable for diffusion in long fibers where diffusion is not restricted along fiber direction. This will be the object of future investigations.

Estimation of Intracellular Free Diffusion Using Diffusion-Weighted Magnetic Resonance Spectroscopy

A few works have attempted to estimate the ADC of brain metabolites along fiber directions (ADC_∣∣), reporting values from 0.25 to 0.36 μm²/millisecond for NAA,^{37, 38} or 0.37 to 0.45 μm²/millisecond for ADC averaged over NAA, tCr, and tCho.^{36, 39} Some authors went a step further and assumed that diffusion was actually free along fiber directions, so that ADC_∣∣ was considered equal to intracellular D_free. It resulted in an estimated intracellular viscosity twice as large as free water.³⁷ However, these works were performed at longer t_d (from 18 to 203 milliseconds) compared with the present work. At long t_d, it becomes more and more unlikely that diffusion along fibers is free, due to the potential presence of organelles or structures that will establish a tortuous diffusion regime. Hence, it seems unlikely that metabolite ADC_∣∣ reported in these previous works is indeed an estimate of D_free, but rather a tortuous ADC_∣∣∼D_free/T², where T is the tortuosity inside fibers. Free diffusion cannot be experimentally distinguished from tortuous diffusion when measurements are performed at long t_d. In contrast, D_free can be measured as the limit of the ADC value when t_d tends towards zero, as metabolites escape tortuous diffusion regime and approach free diffusion. In the present work, ultra-short t_d measurements combined with modeling suggests that D_free averaged for NAA, tCr, and tCho is ∼0.55 μm²/millisecond, that is, higher than reported ADC_∣∣. This value of D_free corresponds to intracellular viscosity being only ∼25% larger than for free water (average D_free for the three metabolites being ∼0.70 μm²/millisecond in free water at 37°C). This is consistent with the idea of tortuous diffusion along fibers directions for works performed at long t_d, and suggests that going to ultra-short t_d might be required to measure D_free and intracellular viscosity.

Note that the long echo time (TE=154 milliseconds) used in the present work may lead to an attenuated contribution of short T₂ metabolite pools, if any, as already suggested for tCho.³⁴ Since short T₂ are expected to be associated with long rotational correlation times, which are themselves associated with high viscosities, the above estimation of intracellular D_free might largely reflect the viscosity of the most liquid intracellular compartments. Further studies performed at shorter TE with stronger gradients should be useful to investigate this point.

Conclusion

In the present work, we reported the first evidence of anomalous diffusion for brain metabolites. This observation was made possible by the use of an original DW-MRS sequence using oscillating gradients at ultra-short diffusion times.

The subdiffusive behavior of brain metabolites is a strong experimental argument for hindered random diffusion being the correct framework to describe motion of small solutes inside brain cells, with little contribution of active transport, at least in the time scales of DW-MRS. In addition, our work reveals that brain metabolite motion can be quantitatively explained by diffusion in a low-viscosity intracellular compartment with ∼2-μm distant structures. These results should allow more specific interpretations of translational displacement in the intracellular space. For example, variations in the ADC of various intracellular molecules, as observed during ischemic stroke, should therefore be explained by viscosity or structure alterations rather than by the failure of active transport mechanisms.

Beyond the fundamental interest in elucidating the main determinants of metabolite motions, the ability to observe and quantify anomalous diffusion in the intracellular space noninvasively, as demonstrated here using endogenous molecular probes monitored by DW-MRS, may also have practical applications, in particular in the early characterization of neurodegeneration when intracellular viscosity and microstructure may be altered: it has for example been shown that dendritic spine density modulates the anomalous exponent α of fluorescent dextran in Purkinje cells,⁵ the dendritic spine density or accessibility being itself reduced in models of tauopathy and Huntington's disease.⁴⁰

Appendix: Extending the neurite and cell body models to literature data

The gradient modulation spectrum of the usual pulsed-gradient spin-echo diffusion-weighting strategy, which has been used in all previously published DW-MRS works, does not present sharp peaks as for the cosine-modulated gradients, and the expected ADC is not simply D(ω_d). Instead, the gradient modulation spectrum F(ω) is the integral of a square function of duration t_d (assuming short-gradient pulses), which is a sinc function centered around ω=0 and full width at half maximum approximately 1/t_d:

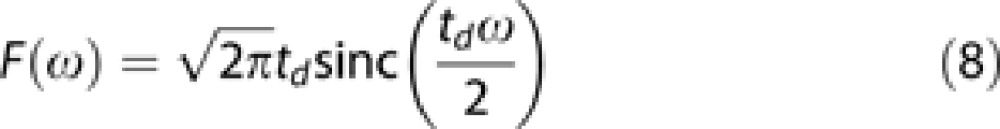Therefore, when extending modeling to literature data, the expected ADC was calculated by integrating D(ω)F(ω)², where D(ω) is calculated as described above.

Extending the cell body model to the long t_d of the literature requires further modification. As t_d increases, the distance traveled during t_d becomes significantly larger than pore diameter (i.e., when t_d>>0.5 × d/D_free∼2 milliseconds, which can be considered valid for literature data), and the effective diffusion coefficient inside the cell internum approaches D_free/T². In the meantime, molecules start experiencing restriction against cell walls. Hence, the cell body model becomes a model of molecules diffusing at rate D_free/T² inside disjoint spherical pores of diameter d, where the pores now account for the whole intracellular space enclosed within cell walls, and where d is now the cell diameter.

The authors declare no conflict of interest.