Using Wikipedia to learn semantic feature representations of concrete concepts in neuroimaging experiments

Abstract

In this paper we show that a corpus of a few thousand Wikipedia articles about concrete or visualizable concepts can be used to produce a low-dimensional semantic feature representation of those concepts. The purpose of such a representation is to serve as a model of the mental context of a subject during functional magnetic resonance imaging (fMRI) experiments. A recent study [19] showed that it was possible to predict fMRI data acquired while subjects thought about a concrete concept, given a representation of those concepts in terms of semantic features obtained with human supervision. We use topic models on our corpus to learn semantic features from text in an unsupervised manner, and show that those features can outperform those in [19] in demanding 12-way and 60-way classification tasks. We also show that these features can be used to uncover similarity relations in brain activation for different concepts which parallel those relations in behavioral data from human subjects.

1. Introduction

Over the last few years machine learning classifiers have increasingly been used to demonstrate that the pattern of brain activation measured with functional magnetic resonance imaging (fMRI) contains information about stimuli being seen, subject decisions and many other aspects of task performance (see [9], [18], [26], [10] and [29]). Recently, however, interest has expanded to discovering how the information present is encoded and also to testing hypotheses about that encoding. One approach to doing this is to postulate a model for the information being created in response to stimuli and learning a mapping between that information and brain activation patterns; this model can then be tested on new stimuli not used in building it and for which the true brain activation patterns are known (a very elegant example of this for visual cortex by [11]). Conversely, one can also test such models by trying to reproduce the stimulus that gave rise to the brain activation patterns from those patterns. Examples of these would be reconstruction of a simple visual stimulus [20], a pattern of dots mentally visualized by the subject [32] and producing a structural and semantic description of a stimulus scene [23].

All of the examples above pertain to visual cortex and pictorial stimuli, as there are many models for the information processing being carried out by visual cortex. But what model should one consider if one is interested in the meaning of a concept, as opposed to its visual representation?

When considering the representation of the meaning of a concept in someone’s mind, one possible view is that the representation is made up of several semantic features, present to varying degrees. Examples could be whether it is alive versus inanimate or, if the latter, a man-made artifact versus something natural. Features can also be shared between concepts belonging to the same semantic category, e.g. one would expect “saw” and “hammer” to share something by virtue of their both being tools.

A pioneering study [19] showed that one could predict the brain activation in response to a line drawing of a concrete concept, together with the noun naming it, if given semantic feature values for that concept and the patterns of brain activation for other concepts. The authors also introduced a procedure for obtaining semantic feature values from a text corpus which required specifying a number of verbs and computing their occurrence with nouns naming concepts in a large corpus.

Our paper is close in spirit to this, and is motivated by two related questions. The first is whether one can discover a “semantic space” to represent concrete concepts, by learning semantic features from a relatively small corpus. Our first contribution is to show that this can be done from a corpus containing Wikipedia articles defining concepts, rather than just instances of the words naming the concepts, as would be the case in standard corpora. Furthermore, the use of topic models [3] for this means that any number of features may be produced in principle, sidestepping the need to specify verbs. The second question is how to determine whether such a corpus reflects, to some degree, the semantic representations of those concepts in the mind of human subjects, using fMRI data. For this we will show that we can use the semantic feature representation learned to predict semantic feature values from brain activation, instead of brain activation from semantic feature values. This semantic feature representation can be used to decode the subject’s mental context, as well as reveal similarity structure between representations of related concepts that is not readily apparent if we solely consider fMRI data.

2. Related work

There are many theories for how semantic information is represented in the brain (see [22] for an extensive review). Almost all of these theories rely to some extent on the notion of features, the attributes of a particular concrete concept [16] (e.g. “is alive” or “is made of wood”). From that perspective, features are used for including or excluding concepts from particular categories, for judging similarity between concepts or for making semantic judgments (often in conjunction with categorical or taxonomic structure).

One way of obtaining features is by painstakingly asking subjects to produce them for many different concrete concepts, and tallying those that are named often, those that are deemed most important to distinguishing concepts or categories, etc. The result of this is known as a semantic feature production norm [16]. This does not guarantee that every relevant feature will be generated – in fact, those that are distinctive are more likely to come up – and has the further problem that no data is available for concepts not included in the norm.

It is possible to address this issue without resorting to subjects by making the assumption that semantic features which distinguish the meanings of concepts are reflected in the usage statistics of the nouns naming them within a very large text corpus. This relies on the notion that those features would be shared by most people thinking about the same concept, as talking to someone about concepts such as chair or table requires a common understanding of the characteristics of that concept. The pioneering paper that inspired our work [19] uses this approach, relying on one further assumption.

Some of the theories treat semantic knowledge as something stored amodally, independent of perception or action relevant to the acquisition and use of the knowledge [6]. Others postulate that that knowledge is stored involving sensory or functional processing areas and, furthermore, making a semantic judgment might require retrieval of interaction or perception with the situation the judgment is about and possibly even a simulation of that (e.g. What does a peach feel like when held? What happens once it is dropped?) [1].

Motivated by the latter perspective, [19] assumed that key semantic features in the meaning of a concept would correspond to basic sensory and motor activities, actions performed on objects, and actions involving changes to spatial relationships. They then hand-picked 25 verbs¹ related to these activities and actions and computed the co-occurrence of the noun naming each concept with those 25 verbs in a large text corpus (Google n-gram corpus http://ngrams.googlelabs.com). The 25 co-occurrence counts for each concept became the semantic feature values, after normalization to a unit length vector. The hypothesis underlying this procedure is that the 25 verbs are a good proxy for the main characteristics of a concept, and that their frequent co-occurrence with the corresponding noun in text means that many different sources (and people) have that association in mind when using the noun.

The authors then showed that these features corresponded, to some degree, to information present in the brain of a subject; this was accomplished by showing that one could predict the brain activation in response to a line drawing of a concrete concept, together with the noun naming it, if given semantic feature values for that concept and the patterns of activation for other concepts.

There are multiple approaches for learning features from text data, with Latent Semantic Analysis (LSA,[13]) being perhaps the best known, and a tradition of using them to perform psychological tasks or tests with word stimuli (see [31], [8] or [21] for applications to EEG, for instance). This work can be seen analytically as operating on a word-by-document matrix and using that to derive a lower-dimensional vector space (or a simplex) where words reside; an excellent review of this and related vector space approaches is [33]. [12] has shown that features similar to those in [6] – in the form concept-relation-feature – could be extracted from a subset of 500 articles of Wikipedia about the concepts in that study, showing in addition that definitional text carried more information for this purpose than a general purpose corpus (independently of our work, an early version of which [28] appeared at the same workshop). In [7] the same method was used to extract features from the British National Corpus data set [14], which were then used to replicate the analysis in [19], with the goal of validating the features extracted. [15] learns semantic features from a matrix of co-occurrences between the 5000 most common words in English, to perform the same prediction task as [19], on their data set and also using the Google n-gram corpus. This is perhaps the most closely related work, though both our approach to producing semantic features and the classification tasks we use are different. [4] uses semantic features derived from the [6] feature norm to predict fMRI activation.

The approach we will deploy is Latent Dirichlet Allocation (LDA, [3]). LDA produces a generative probabilistic model of text corpora where a document is viewed as a bag-of-words (i.e. only which words appear, and how often, matters), with each word being drawn from a finite mixture of an underlying set of topics, each of which corresponds to a probability distribution over vocabulary words; this is also known as a topic model. Note that, in either LSA or LDA, what is being modeled are documents, in terms of the learned semantic features specific to the approach used; the models can then be used to make psychological predictions about words and the concepts they refer to. A particularly relevant example of the use of topic models for our purpose is [8], which works with a text corpus containing educational text used in various school grades. The authors show that a topic model of this corpus is capable of capturing much of the structure of human semantic representation, as evidenced by its ability to predict the human subject word association patterns in [25] or its success in a number of other tasks that involve memory or linguistic processing in human subjects. While this work could have been done using LSA to extract a representation vector for each document, LDA was preferable both for practical reasons (the topic probability vectors are not forced to be orthogonal, and are restricted to add up to 1, thus making the presence of one topic detract from the presence of another) and more conceptual ones (LDA can deal with certain aspects of word association that are troublesome for LSA, as detailed in [8]).

We will analyze the same data set as [19], which was very generously made public by the authors. In this experiment, the task in each trial was to think of the meaning of a given concept for three seconds, after seeing a line drawing of that concept and the noun naming it. Before the experiment, subjects were asked to think about certain aspects of the concept to have in mind (properties, interaction, etc) and write them down next to the corresponding line drawing/noun for that concept. Subjects reported that this helped them reliably think of the same things in response to the same stimuli, and this is the precise notion of mental context that we will use.

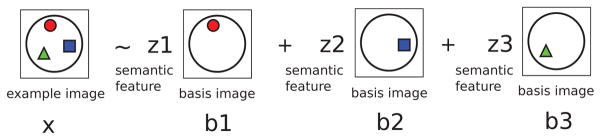
The problem we want to address is how the mental representation of that concept is present throughout the brain, as measured through fMRI. If we accept that the mental representation is composed of semantic features, then one could envisage decomposing the pattern of brain activation while thinking about the concept into a combination of basis patterns corresponding to key semantic features of the stimulus. This is illustrated in Figure 1, where a complex pattern is split into three simpler ones forming a basis. The value of each semantic feature indicates the degree to which its basis pattern is present; given those values, these patterns can be learned from fMRI data.

Figure 1.

A complex pattern of activation is expressed as a combination of three basic patterns.

As described earlier, [19] finds semantic feature values by computing 25 co-occurrence values for each concept. This approach is limited by the fact that it requires stipulating 25 verbs The verbs were selected to capture a range of characteristics described above, but this does not guarantee that those will be all the ones that are relevant, even for concrete concepts.

We will use topic models to learn semantic features from a text corpus selected for this purpose, which we describe in more detail in Section 3. This happens in an unsupervised manner and without a need to specify verbs or any other proxy indicator. The essential characteristic of the corpus is that it is composed of Wikipedia (http://en.wikipedia.org) articles about concrete or visualizable concepts, including those corresponding to the 60 used in [19]). Articles are definitional in style, refer to many other concrete concepts, and also edited by many people to contain essential shared knowledge about the subject of the article. We make the assumption that this instance of language is particularly suitable to reflect the structure of the real world as represented in multiple minds [30], but this is not something that has been conclusively demonstrated.

A very important advantage of definitional articles is that one can take the semantic feature representation of the article for a concept under the topic model (its topic probabilities), as it is a document, and use it directly as the semantic feature representation for the corresponding stimulus concept. This is in contrast to representing words in a low-dimensional space and using the representation of a word naming a concept as the representation of that concept, as one might do if using LSA. This relieves us from the burden of having to perform word sense disambiguation [24] when generating features, as a word might have different meanings in different documents. From the [33] perspective, we are deriving a document representation from a term-document matrix (whereas [12], for instance, is using a word-context matrix).

In order to show that these semantic features do indeed capture relevant semantic structure, we will 1) learn the mapping between a feature and a brain activation pattern, 2) classify brain images taken while the subject sees a novel concept not used in the training set, by predicting the values of semantic features present and 3) use the model to uncover similarity relations in brain activation paralleling similarity structures in human semantic representations.

3. Materials and methods

3.1. Data

We use the 9 subjects in the data set from [19]. The experimental task was to see a line drawing of a concept and the noun naming it, for three seconds, thinking about its properties. The stimulus set contained 60 concepts from 12 categories: animals, body parts, buildings, building parts, clothing, furniture, insects, kitchen, man-made objects, tools, vegetables and vehicles. The experiment had 360 trials, divided into 6 epochs during which the 60 concepts appeared as stimuli (there were hence a total of 6 presentations of each concept). An example image is the average of images taken 4–7 seconds after stimulus onset in a trial and has two labels, the concept and the category it belongs to.

3.2. Semantic Features

The experiments described in this paper rely on using two different kinds of semantic features: Wikipedia Semantic Features (WSF) and Google Co-occurrence Features (GCF, used in [19]. These will act as low-dimensional representations of fMRI data, to be used in decomposing each example into constituent basis images.

To obtain the Wikipedia Semantic Features we started with the classical lists of words in [27] and [2], as well as modern revisions/extensions [5] and [34], and compiled words corresponding to concepts that were deemed concrete or imageable, be it because of their score in one of the lists or through editorial decision. We then identified the corresponding Wikipedia article titles (e.g. “airplane” is “Fixed-wing aircraft”) and also compiled related articles which were linked to from these (e.g. “Aircraft cabin”). If there were words in the original lists with multiple meanings we included the articles for at least a few of those meanings, as suggested by disambiguation pages or free association (e.g. including “Bear claw (pastry)” and “Claw” together with “Bear”).

We stopped the process when we had a list of roughly 3500 concepts and their corresponding articles. We had to restrict the number of articles included for two reasons. The first is that we hadn’t yet developed a good, semi-automatic way of finding Wikipedia articles for concepts we knew were concrete and visualizable, as well as those related to them (e.g. “airplane” is “Fixed-Wing Aircraft” in Wikipedia, and we might want to include “Airplane Seat” and “Airplane Cabin”). The second is that training topic models quickly became more computationally demanding as the number of articles increased.

We used Wikipedia Extractor ² to remove HTML, wiki formatting and annotations and processed the resulting text through the morphological analysis tool Morpha [17] to lemmatize all the words to their basic stems (e.g. “taste”,”tasted”,”taster” and “tastes” all become the same word).

The resulting text corpus was processed with the topic modeling software from [3] to build several LDA models. The articles were converted to the required format, keeping only words that appeared in at least two articles, and words were also excluded resorting to a custom stop-word list. We run the software varying the number of topics allowed from 10 to 100, in increments of 5, setting the α parameter to $\frac{25}{\#\mathit{topics}}$ (following [8], though a range of multiples of the inverse of the number of topics yielded comparable experiment results in terms of peak accuracy, albeit using different numbers of topics). Intuitively, α controls how semantically diverse documents are, i.e. the number of different topics a document will tend to be represented as having. For a given number of topics K, this yielded distributions over the vocabulary for each topic and one vector of topic probabilities per article/concept; this vector is the low-dimensional representation of the concept, as depicted in Figure 2A. Note also that, since the probabilities add up to 1, the presence of one semantic feature trades off with the presence of the others, something that is desirable if expressing one brain image as a combination of basis images weighted by the features. The 60 × 75 matrix on the right of Figure 3 shows the value of these features in a 75 topic model for the 60 concepts considered, sorted by category. A visualization of the topic representations of concepts and the word distributions associated with them in a 40-topic model can be found at http://www.princeton.edu/~matthewb/wikipedia.

Figure 2.

A: The Wikipedia sub-corpus is transformed so that each article is associated with a vector of topic probabilities and each topic with a probability distribution over words. B: The 4 stages in which topic probabilities are used: 1) learning basis images, 2) predicting topic probabilities for test images, 3) using these to do classification and 4) comparing their similarity to predicted topic probabilities for test images of other concepts. This is an iteration of a cross-validation loop, with example images for “hammer” as the test set.

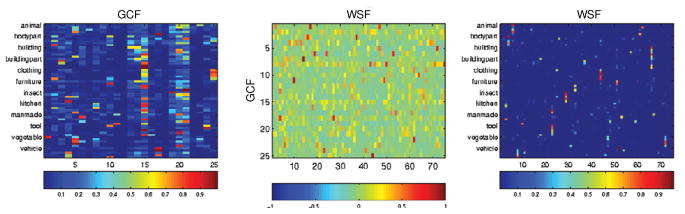
Figure 3.

The value of semantic features for the 60 concepts considered, using GCF with 25 verbs (left) and WSF with 75 topics (right). The 60 concepts belong to one of 12 categories, and those are arranged in sequence (5 animals are followed by 5 body parts, which are followed by 5 buildings, etc). Between GCF and WSF (center) is a matrix of correlations between every pair of GCF and WSF vectors of predicted features across concepts.

The Google Co-occurrence Features are the semantic features used in [19] to represent a given stimulus. They were obtained by considering co-occurrence counts of the noun naming each stimulus concept with each of 25 verbs in a text corpus, yielding a vector of 25 counts which was normalized to have unit length. The low-dimensional representation of the brain image for a given concept is thus always a 25-dimensional vector. The 60 × 25 matrix on the left of Figure 3 shows the value of these features for the 60 concepts considered.

Finally, we can consider the question of how similar GCF and WSF representations are, i.e. whether a given GCF feature has values across examples similar to a given WSF feature. We computed the correlation between each possible pair of GCF and WSF features across 60 concepts, which is shown on the center of Figure 3. Qualitatively speaking, around half of the GCF have high correlation with WSF, but the rest have no direct counterpart; GCF is thus not a subset of WSF. The fact that several of those remaining features correlate partially with WSF suggests that the latter, being more sparse, may correspond to groupings of examples that are not clearly distinguished from others by GCF.

3.3. Using semantic features with fMRI data

Overview

Figure 2B shows the 4 stages where semantic features play a role in our experiments, all of which are described in detail later. These 4 stages take place inside a cross-validation loop, where all the examples images for the “hammer” concept are left out as the test set and example images for the remaining concepts are the training set. In stage 1 the topic probability representations of the articles corresponding to the training set concepts are used together with their example images, to learn an image basis with one image per topic. In stage 2, the image basis is used with the example images of the test concept to predict a topic representation for each example image. In stage 3, we classify by considering whether the predicted topic representation is closest to the topic representation of the test concept (concept classification) or of any of the concepts in its semantic category (category classification). The predicted topic representation is also stored for a different purpose in stage 4, comparing it to the predicted topic representations for all other examples when they were in the test set.

Notation

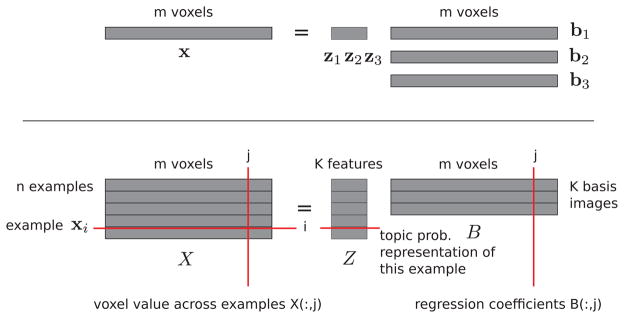
As each example is a 3D image divided into a grid of voxels, it can be unfolded into a vector x with as many entries as voxels containing cortex. A data set is a n×m matrix X where row i is the example vector x_i. Similarly to [19], each example x will be expressed as a linear combination of basis images b₁, …, b_K of the same dimensionality, with the weights given by the semantic feature vector z = [z₁, …, z_K], as depicted in the top of Figure 4. The low-dimensional representation of data set X is a n × K matrix Z where row i is a semantic feature vector z_i and the corresponding basis images are a K × m matrix B, where row k corresponds to basis image b_k, as shown in the bottom of Figure 4. If referring to columns of matrices, e.g. column j of X, we will use the notation X(:, j). The notation x′ indicates the transpose of vector x.

Figure 4.

top: An example brain image can be written as a row vector, and the combination as a linear combination of three row vectors. bottom: A data set contains many such brain images, forming a matrix X where rows are examples and whose low-dimensional representation is a matrix Z.

Learning and prediction

Learning the basis images given matrices X and Z (left of Figure 5) can be decomposed into a set of independent regression problems, one per voxel j, i.e. the values of voxel j across all examples, X(:, j), are predicted from Z using regression coefficients B(:, j), which are the values of voxel j across basis images. Predicting the semantic feature vector z for an example x is a regression problem where x′ is predicted from B′ using regression coefficients z′ = [z₁, …, z_K]′. For WSF, the prediction of the semantic feature vector is done under the additional constraint that the values need to add up to 1, as they are probabilities. Any situation where linear regression was unfeasible because the square matrix in the normal equations was not invertible was addressed by using a ridge term with the trade-off parameter set to 1.

Figure 5.

left: The semantic feature classification experiment requires learning an image basis from a set of training examples and their respective semantic feature representations. This is used to predict semantic feature values for test set examples and from those one can classify against the known semantic feature values, either which of 12 categories or which of 60 concepts. right: The voxel classification experiment replicates the main one in [19]. Semantic feature representations of the 2 test concepts are used, in conjunction with the image basis learned on the training set, to predict their respective test examples and use that prediction in a 2-way classification.

4. Results

4.1. Classification experiments

Classification using semantic features

We would like to ascertain how much information about the category and the identity of a stimulus there is in an example image coming from a single task trial. We do this by predicting semantic features – either WSF or GCF – for an example and classifying category (12-way) or concept (60-way) from them. As illustrated on the left of Figure 5, training examples get used together with their semantic feature representation to learn a set of basis images, with the goal of reconstructing those training examples as well as possible. The basis images are used, in turn, to predict semantic feature values for test examples determining, in essence, which semantic features are active during a test example. Classification is done by assigning the label for the example in the original data with the most similar semantic feature values, as judged using correlation.

We use a 60-fold leave-one-concept-out cross-validation, testing on all 6 examples of the withheld concept and performing the following steps in each fold:

1. from each training set X_train and corresponding semantic features Z_train, select the top 1000 most reproducible voxels and learn an image basis B using those (see below for more information on this selection criterion)

2. use the test set X_test and basis B to predict a semantic feature representation Z_pred for those examples

3. use nearest-neighbor classification to predict the labels of examples in X_test, by comparing Z_pred for each example with known semantic features Z

There is always one semantic feature vector for each different concept in Z. This procedure is unbiased, and we tested this empirically using a permutation test (examples permuted within epoch) to verify the accuracy results for either task in that situation were at chance level.

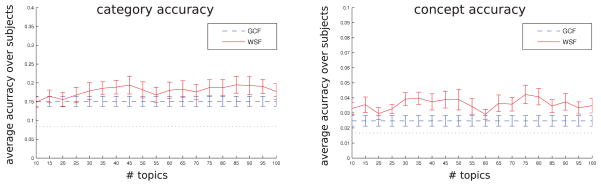
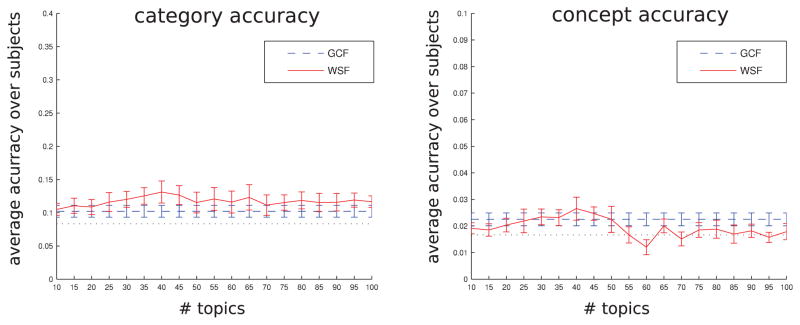
Figure 6 shows the results for both category (left) and concept (right) classification; each plot contrasts the accuracy obtained using GCF with that obtained using WSF with 10–100 topics, in increments of 5, averaged across all subjects. We also performed a per-subject comparison at each number of topics, testing whether WSF was better than GCF, as deemed by a paired t-test (0.05 significance level, uncorrected). In general, WSF is either significantly better or slightly above GCF in both category and concept classification. Chance levels for the category/concept tasks are $\frac{1}{12}=0.0833$ and $\frac{1}{60}=0.0167$, with thresholds for a p-value of 0.01 under the null hypothesis that accuracy is at chance level of 0.12/0.035, respectively. One could ask whether the improvement is solely due to the ability to generate more than 25 features or also to the fact we used LDA, and this is something we address on the next section.

Figure 6.

A comparison between the performance of GCF and WSF (10–100 topics) accuracy in the category (left) and concept (right) classification tasks. Curves are the average over 9 subjects. In each plot WSF is red (full line), GCF is blue (constant dashed line) and chance level is black (constant dotted line). These results were obtained using leave-one-concept-out cross-validation.

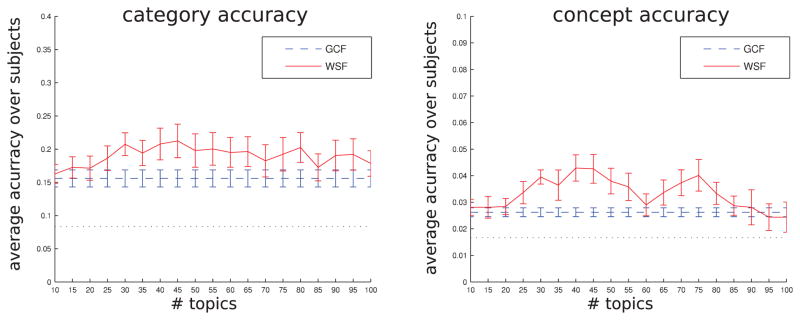
Voxel selection is necessary to obtain the best results in this experiment; that said, results without it are still above chance at least for the category task, as seen in Figure 8. The reproducibility criterion we used identifies voxels whose activation levels across the training set concepts bear the same relationship to each other over epochs (mathematically, the vector of activation levels across the sorted concepts is highly correlated between epochs). As [19] points out, we do not expect all – or even most – of the activation to be differentially task related, rather than uniformly present across conditions, or consistent between the various presentations of the same stimulus concept. We chose to use 1000 rather than 500 reproducible voxels, as the results were somewhat better (and still comparable with 2000 voxels, say), but it is legitimate to consider how sensitive the results are to this choice. Given that the reproducibility criterion for selecting voxels is essentially a correlation computation, one can find a threshold at which the null hypothesis of there being no correlation has a given p-value, using the Fisher transformation. For instance, given that 59 voxel values are compared across 6 × 5/ pairs of runs, observed correlation r = 0.1 has a p-value of 0.01 if the true correlation ρ = 0. Using this threshold gives us a different number of voxels in each subject, ranging from approximately 200 to well over 2000, but the results are still very similar to those obtained with 1000 voxels, as seen in Figure 7.

Figure 8.

Same as Figure 6, but using no voxel selection.

Figure 7.

Same as Figure 6, but using a statistical criterion for determining how many voxels to select per subject.

Classification using co-occurrence features learned from our corpus

A reasonable question one can ask is whether it is really necessary to use topic models over this corpus in order to learn new features that are useful for classification. In order to test this, we applied the same approach as [19] to our corpus, computing co-occurrence counts between the 60 nouns naming the concepts and the 25 verbs they chose and generating normalized features from these (Wikipedia Co-occurrence features, WCF). A verb and a noun were deemed to co-occur if they appeared within 5 words of each other.

Table 1 shows the results in both category and concept tasks using GCF and WCF. Across most subjects performance was often worse using WCF than GCF, especially in the category task. A possible explanation might be that n-gram co-occurrence does carry information, as shown by GCF, but requires a large corpus to yield reasonable co-occurrence estimates. WSF uses co-occurrence of multiple words in an article in determining the probability distribution for each topic, and hence appears to make a more efficient use of the information available.

Table 1.

Classification accuracy in the category (12-way) and concept (60-way) tasks, using the 25 semantic features in [19] (GCF) and the 25 semantic features derived from our corpus using their approach (WCF), across 9 participants.

	P1	P2	P3	P4	P5	P6	P7	P8	P9
category task
GCF	0.217	0.169	0.133	0.211	0.144	0.122	0.119	0.108	0.133
WCF	0.181	0.128	0.125	0.217	0.103	0.089	0.125	0.083	0.139
noun task
GCF	0.019	0.031	0.025	0.028	0.044	0.031	0.008	0.017	0.019
WCF	0.022	0.017	0.008	0.033	0.022	0.011	0.031	0.014	0.017

4.2. Comparison of low-dimensional representations

In the previous section we were concerned with accuracy as a quantitative gauge of how well a given low-dimensional representation of the fMRI data could be used to decompose it into a basis of images with generalization power. Intuitively, if the feature representation of the examples of a given concept at test time allows classification, then the basis images used to predict that representation do capture patterns of brain activation that correspond to semantic features underpinning the representation of that concept. In order to show how one might go beyond this, we will analyze a model for subject whose data yielded the highest classification accuracies (subject P1, close to 40%/10% for category/concept prediction using a WSF model with 75 topics).

A more nuanced measure of how good a model is is whether it assigns semantic feature representations to the various concepts that mirror those in the minds of subjects. In particular, we are interested in whether concepts which are related in practice are represented by a model in more similar ways than those which are not. In this experiment relatedness maps roughly to being in the same semantic category, or in semantic categories that are connected in some way (e.g. “Buildings” and “Building parts”).

While not having direct access to mental representations, if our interest is in concept relatedness we can consider behavioral data from word association norms such as [25]. In this particular experiment, subjects were given cue words and asked to produce a new word associated with the cue. The end result was a probability distribution of associates for each cue word. These data were used by [31] to produce a low-dimensional Word Association Space (WAS), in which each word was represented as a vector and words with similar association patterns were placed in similar regions of the space (i.e. vector distance reflects similarity of association pattern). One way to use this information for our purpose is to compute a matrix with word similarities as a summary of the structure of semantic association.

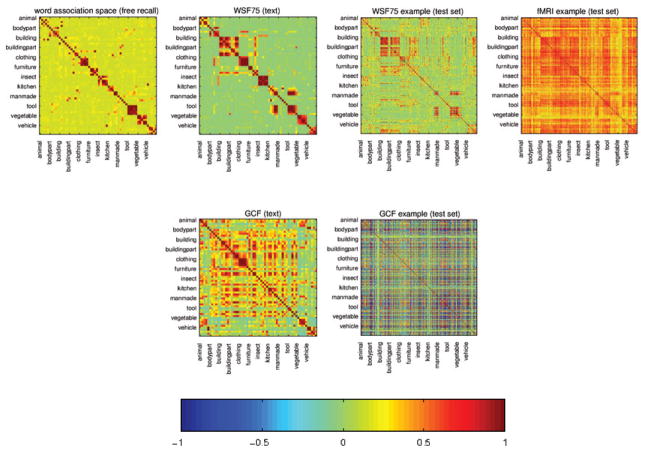
We selected the WAS vectors for the nouns naming the 60 concepts we considered and computed their correlations, a result shown in the leftmost column of Figure 9. There are salient blocks along the diagonal that correspond to concepts in the same category, but the similarity stretches across categories as well, e.g. body parts and tools, buildings with building parts and man-made objects (yellow to orange rather than the more intense brown). The WAS similarity matrix will act as a reference for whether any pair of concepts is related.

Figure 9.

This figure compares several representations of either the 360 examples (6 presentations of each concept) or 60 concepts (if fMRI, the average of those 6 presentations). The concepts/examples in each plot are always arranged so that those belonging to the same semantic category appear in sequence and the first member of each sequence is labeled with the category name (if considering examples, multiple presentations of the same concept are adjacent). left: Correlation between the low-dimensional representation of nouns naming the concepts in Word Association Space, derived from human subject behavior. middle left: Correlation between the low-dimensional representation of concepts in WSF75 (top) and GCF (bottom), both learned from text corpora. middle right: Correlation between the low-dimensional representations predicted for test examples with WSF75 (top) and GCF (bottom), from fMRI data (these plots are 360 × 360). right: Correlation between each example image at test time with all other examples, computed across the 1000 voxels selected from them (this plot is 360 × 360).

Before considering fMRI data, we can examine the similarity structure of WSF and GCF representations of the 60 concepts as obtained from text alone. This is shown in the middle left column of Figure 9, with WSF above and GCF below. For each concept, the plot shows the correlation of its semantic feature vector with the semantic feature vectors of the other concepts. There are diagonal blocks in both representations, corresponding to within-category similarity, but the pattern of confusion between categories is more similar between WSF and WAS. We had no a priori expectation regarding whether GCF or WSF would be closer to WAS, since for the latter it was possible that nouns naming related concepts would both appear close to the same verbs, giving rise to the similar feature values. These results indicate both that the WSF representation reflects relatedness of concepts and that GCF representations are similar for many unrelated concepts (as indicated by the density of high similarity across many between-categories concept pairs).

Armed with the above, we can now examine the extent to which the semantic feature values predicted from an fMRI example using a GCF or WSF image basis have any of the similarity structure in WAS or in the matrices derived solely from text. This is shown in the middle right column of Figure 9, with WSF above and GCF below. The matrices contain the similarity between the semantic features predicted for each concept when it was in the test set – all 6 presentations of a concept are in the test set at the same time – and all other examples when they were in the test set. These matrices are thus 360 × 360, sorted by category, with the 6 presentations of each concept adjacent to each other. WSF recovers much of the similarity structure between each concept and the others that was seen on text, using fMRI data from a single trial. This indicates that the basis images learned on the training set do generalize to the extent that they can help predict the topic probabilities for a new image at least at the category level. It is far less clear that the GCF features can recover the similarity structure obtained with them in text.

Finally, we can look directly at the similarity between fMRI patterns for different concepts, shown on the rightmost column of Figure 9. Each entry in the matrix is the similarity between each example when it was in the test set and all other examples in the training set, obtained by computing the correlation across the 1000 voxels selected over the latter. The first thing worth noting is that similarity is high for most pairs of concepts, possibly because voxels are selected for stability rather than how informative they are in distinguishing concepts. The second is that the matrix looks rather similar to the GCF matrix produced from the fMRI data, suggesting that in that case the GCF text model has less of an influence in the representations predicted than happens with WSF.

This analysis is an attempt at understanding the structure of similarity between concept representation and giving us a sense of how these echo the relatedness between concepts measured in behavioral data, rather than a systematic study. Although we are presenting a single subject, the overall results remain similar for other subjects, degrading as the peak accuracy in category/concept prediction degrades. One could also conceive of using other measures of semantic behavior, or using our model to generate predictions about word association (as suggested in [8]).

Replication of the 2-way classification experiment using voxel values in [19]

Classification using voxel values

The main experiment in [19] entailed predicting the fMRI activation for unseen stimuli and using that to perform a forced-choice 2-way classification from the predicted brain image, as schematized in the right of Figure 5. Note that this is a completely different prediction task from what was described in previous section, both in terms of what is predicted – fMRI activation rather than semantic features – and also in being 2-way. We replicated this experiment using both GCF and WSF representations.

In more detail, the authors considered the 60 average examples for each stimulus concept (averaging over the 6 presentations) and, in turn, left out each of 1770 possible pairs of such average examples. For each left out pair, they learned a set of basis images using the remaining 58 examples and their respective GCF representations. They then used the GCF representation of the two left-out examples and the basis to generate a predicted example for each one of them. These were used in a two-way matching task with the actual average examples that were left out, where the outcome was deemed correct if the predicted image for either concept was closer to the image of the corresponding left-out concept than that of the other concept. Note that learning the basis or making the prediction was not done over the entire brain but over a selection of 500 stable voxels, as determined by computing their reproducibility over the 58 examples in each of the 1770 training sets.

Table 2 shows the mean accuracy across 1770 leave-2-out pairs using GCF, the mean accuracy reported in [19] and the mean accuracy using WSF with 25, 50, 75 and 100 topics, for the 9 subjects. Figure 10 shows the same results averaged across subjects. We were not able to exactly reproduce the GCF numbers in [19], despite the same data preprocessing, as far as we could ascertain through supplementary materials and personal communication with one of the authors. The data preprocessing we used was to make each example mean 0 and standard deviation 1, prior to averaging all the repetitions of each concept, and then subtracting the mean of all average examples from each one. We used the same voxel selection procedure (using 500 voxels, code yields the same voxel ranking) and the same ridge regression function (although [19] does not mention the value of the ridge parameter γ, which we assumed to be 1).

Table 2.

Results of a replication of the leave-2-concepts-out 2-way classification experiment in [19].For subjects P1–P9, GCF represents the mean accuracy obtained using GCF (across 1770 leave-2-out pairs), Org the mean accuracy reported in [19] and the remaining columns the mean accuracy obtained using WSF with 25, 50, 75 and 100 topics.

	P1	P2	P3	P4	P5	P6	P7	P8	P9
GCF	0.79	0.75	0.73	0.79	0.82	0.73	0.75	0.74	0.70
Org	0.83	0.76	0.78	0.72	0.78	0.85	0.73	0.68	0.82
WSF25	0.78	0.60	0.66	0.83	0.67	0.71	0.79	0.56	0.64
WSF50	0.84	0.63	0.68	0.85	0.68	0.72	0.77	0.67	0.73
WSF75	0.88	0.73	0.78	0.87	0.74	0.74	0.79	0.71	0.74
WSF100	0.74	0.65	0.67	0.77	0.64	0.67	0.74	0.65	0.71

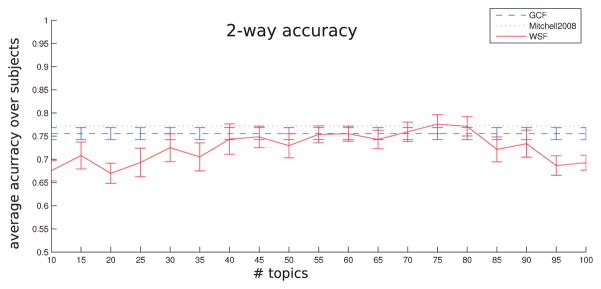
Figure 10.

Results of a replication of the leave-2-concepts-out 2-way classification experiment in [19]. Average score across the 9 subjects for all numbers of topics.

It takes around 75 topics for most subjects to display a performance equal to or better than GCF, which we think is due to two different aspects in which our models are sparse. The first is that many topics have probability close to 0 across all concepts, as those topics are used to represent other parts of the corpus. The second is that concepts tend to be represented by very few topics, mostly one or two category related ones and later, as the number of topic increases, possibly a few that are more concept specific.

We believe these two factors combine so that, with fewer than 40/50 topics, each basis image learned will correspond to a category-focused topic, and hence share common activation for various concepts in that category rather than anything concept-specific. As there won t be that many topics available – as some have probability close to 0 regardless of how many topics the model has – it makes sense that this would happen. This would lead the predicted patterns of brain activation for concepts in the same category to be very similar until models with 40/50 topics or more are used.

Given that the 2-way classification task involves matching predicted brain images for 2 left-out nouns with their actual brain images, the inability to predict concept-specific brain activation may disproportionately affect classification (whereas predicting topic probabilities from brain images at a category granularity in the classification problems in the main paper would be helped by this). In contrast, [19] use fewer features but more of them are involved in the representation of each concept, so the basis images should more effectively capture concept-specific brain activation.

5. Discussion

As discussed earlier, this work was motivated by two related questions. The first is whether one can learn a “semantic space” to represent concrete concepts from a relatively small corpus, if that corpus contains articles defining the concepts. The second is how to determine whether such a corpus reflects, to some degree, the semantic representations of those concepts in the mind of human subjects.

The fact that we could extract this from a corpus an order of magnitude smaller than the one used in [13] or [8] suggests that definitional text is informative. That said, this could only be demonstrated conclusively by learning topic models on another corpus of the same size that was not definitional but where a document and its representation could still be associated with a concept. The other contrast to make is with the semantic feature representation of concepts used in [19], obtained from considering co-occurrence of nouns naming the concepts with verbs over 1, 2, 3, 4, 5-grams in a massive corpus. In this case, the fact that we can learn indicates the power of leveraging co-occurrence of multiple words in a document – and the fact that each topic can account for a large set of words at once. Our data set is naturally sparse – 3500 articles × 50000 words – and hence a topic can easily account for the words appearing in several related articles.

In order to tackle the second question we turned to fMRI images obtained while a subject thought about different concepts. Together with the corresponding topic-probability representation of those concepts obtained from text, they can be used to derive a basis of fMRI images corresponding to the brain activation pattern elicited by each topic. To show that the basis images generalize, we do this in a cross-validated fashion and learn basis images from 59 out of 60 concepts in our fMRI data set. The basis images can then be used to predict a topic probability representation from the example images of the left-out concept. Any evaluation relying on this predicted representation is then an evaluation of how well the basis images generalize to new concepts; this is a function both of how good the test model is and the extent to which the process of using basis images to derive the topic probabilities from fMRI data predicts topic probabilities similar to those in the model.

We evaluated the model quantitatively by doing classification tasks at the concept category and individual concept levels; category classification is a 12-class problem with 30 examples per class whereas concept classification is a 60-class problem with 6 examples per class. Both because of these numbers and because some topics clearly capture category level structure, we expected the former to be substantially easier than the latter, which proved to be the case. Performing above chance in the latter task indicates that there is some concept-specific information in the topic probability representation, though the relatively low accuracy – under 5% for most subjects –indicates this is absent for most of the concepts or harder to extract from the fMRI data. From a more qualitative angle, and wanting to consider a criterion beyond accuracy, we looked at the similarity of topic probability representations of concepts and the strength of association between those concepts in a behavioral task. As [8] suggests, the topic model could be used to predict the associations between words directly, providing a more quantitative measure instead, but this is beyond the scope of the current paper. That said, an interesting avenue of research would be to attempt to predict the results of classical norms (e.g. rankings of concreteness or visualizability [27] [5], most common items in a semantic category [2] [34]) using our models and subsets of the results in those norms. This would provide a completely different source of constraints and evaluations for the quality of the representation embodied by the model.

We compared our topic model concept representation with that used in [19] because it seemed the most obvious benchmark. For predicting concept representation from brain images of new concepts, our approach is as good or better; for predicting brain images for new concepts, it takes several topics to reach the same performance as [19].

This comparison was made mostly to show that the model performed reasonably. Our main interest is not, however, in showing an improvement with respect to [19] but rather in demonstrating that this approach is feasible. Given that we do not have to specify verbs to obtain semantic features, and that we can obtain models with any number of topics (up to certain practical constraints), there is a lot of room for further improvement. One possibility would be to have topics correspond to semantic features at a finer grain than “category”. An example could be a “made of wood” topic that would place heavy probability on words such as “brown”, “grain”, “pine”, “oak”, etc. In this situation, there would be far more topics, each spreading probability over fewer words; each concept would be represented by assigning probability to more of these topics than is currently the case. It is conceptually straightforward to modify parameters of topic models to yield this and other characteristics in each model, and we are currently working on this direction.

A second possibility is the fact that this type of model opens the door to fMRI experiments where a subject can read, instead of having purely visual stimuli. Starting with a probability assignment over topics, perhaps suggested by task, a topic model provides a formal mechanism for updating that assignment as each stimulus word is read, and this could be used as a model of mental context on an image by image basis. The ability to read would allow experiments on metaphor processing – given example images for the concrete concepts underpinning the metaphors components and meaning – or even possibly on abstract concepts; while it is straightforward to produce a topic representation for the latter from the respective Wikipedia articles, we do not yet know how useful those representations will be. We are currently piloting a reading experiment to validate the idea of tracking mental context using the topic model.