Abstract
Four experiments investigated the classic issue in semantic memory of whether people organize categorical information in hierarchies and use inference to retrieve information from them, as proposed by Collins & Quillian (1969). Past evidence has focused on RT to confirm sentences such as “All birds are animals” or “Canaries breathe.” However, confounding variables such as familiarity and associations between the terms have led to contradictory results. Our experiments avoided such problems by teaching subjects novel materials. Experiment 1 tested an implicit hierarchical structure in the features of a set of studied objects (e.g., all brown objects were large). Experiment 2 taught subjects nested categories of artificial bugs. In Experiment 3, subjects learned a tree structure of novel category hierarchies. In all three, the results differed from the predictions of the hierarchical inference model. In Experiment 4, subjects learned a hierarchy by means of paired associates of novel category names. Here we finally found the RT signature of hierarchical inference. We conclude that it is possible to store information in a hierarchy and retrieve it via inference, but it is difficult and avoided whenever possible. The results are more consistent with feature comparison models than hierarchical models of semantic memory.
Hierarchical classification has long been identified as one of the most important aspects of human knowledge representation. In the sciences, management, and law, hierarchies have been used to structure the relations among domain entities, and tree diagrams representing such relations can be found in many different texts. Hierarchical structure has also been found in human knowledge representation (Markman & Callanan, 1984; Rosch, 1978). Our concepts seem to be structured in levels of classification in which specific concepts fall under increasingly higher-level concepts. For example, an object identified as a beach novel also falls under more general classes of novel, book, and publication, forming a series of inclusion relations: Beach novels are novels, novels are books, and books are publications.
The advantage of hierarchical representation has long been noted (Linnaeus, 1758; Quillian, 1968). The main benefit is that facts known about higher-level concepts apply to lower ones as well. So, after learning that all publications have an author, one knows that all novels have an author. This is an important benefit, because there are dozens or even hundreds of types of dogs, cars, musical instruments, hammers, contracts, investments, cultures, and so on, and if we had to learn the properties of each type separately, it would be extremely difficult and time-consuming. For example, if you had to learn that Scottish terriers have skin, move, breathe, have livers, have a four-chambered heart, and all their other biological properties, you might never get around to learning about Airedales, Jack Russell terriers, or Yorkshire terriers (much less poodles). However, by knowing that those properties are true of animals or mammals, you don’t have to relearn them for dogs, terriers, and every type of terrier separately. Over and above this benefit, the power and flexibility of the representational format is greatly increased with the notion of a “default hierarchy” (Quillian, 1968), in which lower branches can contain exceptions to the general properties stored higher up. For example the fact that penguins do not fly is treated as an exception to the general rule stored higher up that birds do fly. Default hierarchies are an essential tool in database design and in knowledge-based systems architecture in Artificial Intelligence, suggesting their direct relevance for representing human conceptual knowledge.
The hierarchical structure of categories seems to be descriptively correct of a significant subset of semantic memory, but what is less well understood is how that knowledge is stored and accessed in memory. A major research question in the 1970s proposed two general approaches to explaining hierarchical structure (see Smith, 1978, for an excellent contemporary review). One view proposed that something much like an actual hierarchy was represented in memory, through an associative network in which different categories were connected by “IS-A” links: a terrier IS-A dog, a dog IS-A mammal, and so on (Collins & Quillian, 1969). To represent the information associated with each category, other links such as “HAS” or “CAN” would connect properties to the categories. So, the dog concept would have a HAS link to the legs concept, and the animal concept would have a CAN link to the breathes concept. Such a structure follows the principle of cognitive economy. By linking “breathes” to the animal concept, one does not have to link it to the concepts of fish, birds, mammals, and all of their many subtypes—the information is placed at the highest level in the hierarchy only. However, a corresponding drawback to such efficiency is that processing is slowed when deriving general features for lower-level categories (Collins & Quillian, 1969). To realize that Airedales breathe, one must traverse the hierarchy through the concepts dog and mammal to arrive at animal, which is linked to the breathes feature. Similarly, classification judgments such as that an Airedale is a living creature, require traversing the links in memory between Airedale and the living creature concept, which must take longer than judging that the Airedale is a dog, since these two concepts are linked directly. In short, there is a distance effect between levels of the hierarchy, such that the farther apart information is stored in the hierarchy, the longer it takes to retrieve or confirm it. Although Collins and Quillian found such a distance effect, others have not or have questioned whether it is due to the inferential process they propose (see Chang, 1986; Smith, 1978).
The inferential-network model has had as much lasting power as any idea in cognitive psychology. A survey of our cognition textbooks finds very similar illustrations to Collins and Quillian’s (1969) Figure 1 in almost every one, ranging from 1972 (Lindsay & Norman, 1972) through 2010 (Ashcraft & Radvansky, 2010).
Figure 1.
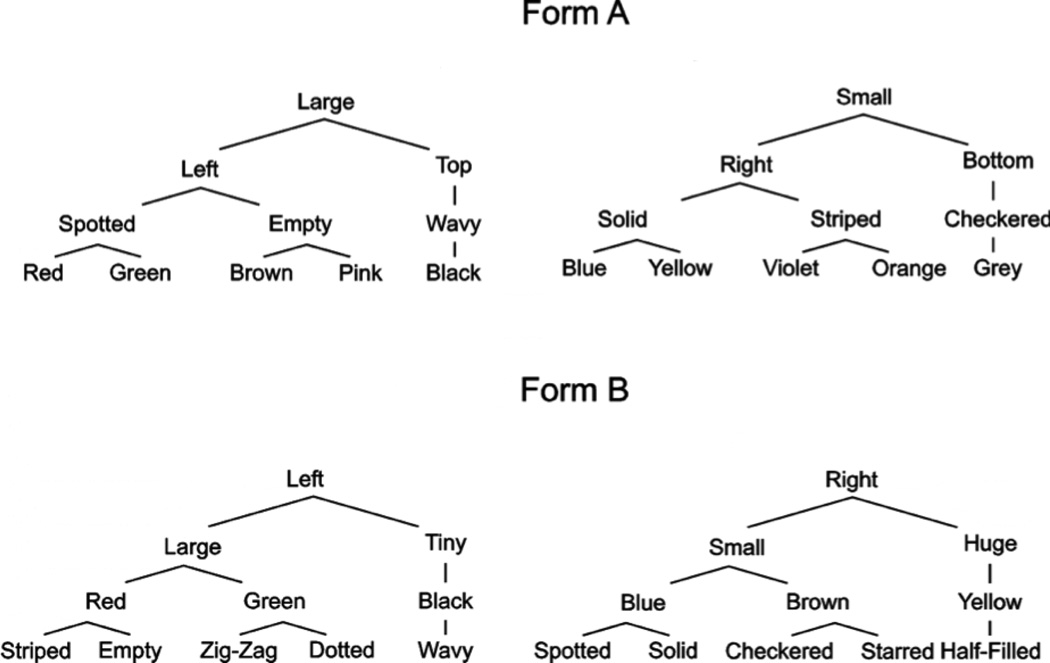
The taxonomies used in Experiment 1. Subjects learned either Form A or Form B.
A different approach to hierarchies in semantic memory proposes that the hierarchies are only implicit in our category knowledge rather than characterizing memory structures. Instead, each concept is represented by its defining and characteristic features (Smith, Rips, & Shoben, 1974). The relations between the features of different concepts would define their categorical relation, if any. For example, the concept animal is associated with the relatively few features that are common to (all) animals. To decide whether an Airedale is an animal, one could check whether those animal features are found in the features known of Airedales: Given that Airedales move independently, breathe, and reproduce, they must be animals. This feature-comparison process yields no distance effect. Furthermore, given that categories are associated to characteristic features, the similarity of two concepts could determine how long it took to judge their relation, independently of their distance in the hierarchy. Such typicality effects are extremely widespread (Hampton, 1979; 1997; McCloskey & Glucksberg, 1979; Rips, Shoben, & Smith, 1973; Rosch, 1973; Rosch & Mervis, 1975).
Ultimately, these two approaches generated considerable research but no clear resolution. Chang’s (1986) comprehensive review makes it clear that all models have unexplained phenomena. Our interpretation of this is that people take advantage of both processes proposed by these approaches, in various combinations. Imagine learning that your friend has a new kind of dog, a muffelet. Without knowing anything about it, you can infer that muffelets have four legs, breathe, probably bark, wag their tails, and so on. You would hardly be puzzled if your friend said that her muffelet chewed up her slippers. Since you have no features associated to the name muffelet, you couldn’t have been using the feature comparison process to draw these conclusions but were likely performing the kind of inference envisioned by Quillian’s theory: The muffelet chews slippers because it is a dog, and that is what juvenile dogs do. On the other hand, the evidence that this inference process takes place when making judgments about familiar categories is weak. The distance effect is often not found and unpredicted effects often are (Chang, 1986). Sometimes inference is not transitive, as it should be according to this view (Hampton, 1982).
Hampton (1997) demonstrated that categorization can use both stored associations and featural similarity, finding independent effects of category production frequency (how likely an exemplar is to be generated as a category member) and typicality (how representative a member is of its category) on categorization times. A double dissociation was obtained, with a priming task removing frequency effects, and a manipulation of task difficulty affecting typicality effects (see also Moss et al., 1995). Similarly, Kounois, Osman, and Meyer (1987), in a study using speed-accuracy decomposition, proposed fast retrieval of some facts followed by a slower feature comparison process as one explanation of their results.
Typicality effects fall more readily out of the similarity-comparison model (McCloskey & Glucksberg, 1979; Smith et al., 1974), and it now seems to be the more popular approach—except for a general rejection of the notion of defining features (Hampton, 1979; Rosch, 1973). However, even featural similarity may not explain all category judgments (e.g., Hampton, 1998).
More Recent Approaches
The importance of hierarchically organized knowledge has been recognized in recent models of semantic memory, most notably the very ambitious project of Rogers and McClelland (2004; see Close & Pothos, in press, for an alternative). They addressed issues of why very general categories may be learned first and are the most resistant to effects of brain damage. They also addressed the presence of a preferred, basic level of categorization (Rosch, Mervis, Gray, Johnson, & Boyes-Braem, 1976).
Their connectionist model does not align neatly with either of the two previous approaches. They used a Rumelhart network in which input nodes interpreted as objects activate two hidden layers, which, along with context units, activate an output layer containing features and category names. After training, the network was able to respond that a given object breathes or is a canary. The context units refer to behaviors/functions, properties, and names, serving to selectively access the information in the output layer. So, with one context unit activated, the network might respond that a given object has legs, wings, and eyes; with another context unit activated, the same object might yield the response that it is a canary and a bird.
Because of the distributed nature of the conceptual representations and the network architecture, the Rogers and McClelland model is different from the two approaches we have been discussing. Perhaps the greatest difference is that there are no “concept nodes” in the system. Input nodes correspond to objects, and output nodes include features and the objects’ names. In between are hidden nodes that form semantic representations of the kinds of objects the network has learned. There is no node corresponding to the concept of canaries, which is then related to its features or subordinate and superordinate categories. Instead, the semantic representations in the hidden layers activate various features in a graded response. This directly yields typicality effects, as typical objects (like robins) will activate category names and properties most strongly, whereas less typical objects (like penguins) will activate them less strongly.
There is no distance effect in the network corresponding to the Collins and Quillian inference effect. The semantic representations activate specific and general names, and there is no link between the names themselves. As a result, their model does not provide a simple way to evaluate statements such as “A robin is a fish.” However, following a procedure they use for introducing novel category exemplars (p. 64), one can derive a way for the model to answer such questions. If the node representing the first term of the sentence is activated, that activation can be backwards-generated to derive the hidden layer representation that is most compatible with it (the prototypical robin). Then, that activation pattern can be run forward in order to discover whether the second term of the sentence is activated (whether the prototypical robin is a fish). As this description shows, name activation in the model occurs through semantic representations and not through networks of associations between categories or category names. As a result, this model is closer to the feature-based accounts of semantic memory than to the network-based accounts. It seems very likely that the model, like Smith et al.’s (1974), could predict that some long-distance inferences like “A penguin is an animal” are faster to confirm than short-distance links like “A penguin is a bird,” if the penguin’s features overlap more with the typical animal’s than with the typical bird’s. (Indeed, Rogers & McClelland, 2004, ch. 5, document in detail the effects of the similarity of such atypical items to other categories.)
In summary, Rogers and McClelland’s (2004) semantic memory model seems much closer to the featural approaches, as do recent competitors such as Close and Pothos (in press). It clearly does not contain a hierarchical network of associations that directly lead to the Collins and Quillian effects, and its predicted effects are largely based on semantic similarity and details of the learning regimen (ch. 5). In Experiment 2, which had stimuli comparable to their simulations, we will attempt to draw specific predictions from their model.
The Present Study
It is not our intention to attempt to resolve the semantic memory debate 25 years on. If our conclusion is correct, there is no simple right answer to the question of how hierarchical information is represented. It may be either inferred or explicitly represented, depending on the categories and features. As people become experts or learn specific facts, their knowledge could pre-empt more general retrieval processes. Someone with great experience with killer whales might well store the fact “killer whales breathe air” but would not store the fact “robins breathe air.” Therefore, retrieving information about breathing killer whales might not involve hierarchical inference, whereas retrieving this fact about robins might.
One reason for confusion in the literature is that researchers do not have experimental control over the stimuli of semantic memory and people’s experience with them. People may form implicit categories such as four-legged mammals, which investigators do not take into account, making predictions of hierarchical distance incorrect. People may also have learned some of the specific categorical relations tested in an experiment, like whales being mammals, but have never even encountered others. Familiarity with properties and categories has also been argued to underlie some effects (Malt & Smith, 1982; McCloskey, 1980). Such confounding variables could obscure the basic properties of semantic memory retrieval but are very difficult to control in naturally occurring semantic domains.
In part because of such problems, it is still not clear how people structure and retrieve information from hierarchically organized domains. One important question is whether people spontaneously form memory structures of the Quillian type—efficient hierarchical networks of associations. Although such a structure seems ideal, in practice people may make redundant links or omit links in a way that results in a much more complex memory structure. Another question is whether retrieval of information about hierarchically structured material has the profile that Collins and Quillian (1969) originally identified for it, and in particular, whether it shows the distance effect. Later theorizing weakened that prediction (e.g., Collins & Loftus, 1975), but this was in large part due to uncontrolled associations of the whale-mammal sort.
Whether people form internal hierarchies when all those confounding variables are absent remains an open question. Our goal was to investigate not retrieval of information from familiar semantic domains but the underlying psychological question of whether people create and use mental hierarchies when the conditions are ideal to do so. The answer to this question will then inform the debate about how information is stored in the messier, more complex world of actual semantic memory. If people do not form mental hierarchies even under these ideal circumstances, this will cast strong doubt on whether such hierarchies play a role with real semantic information. If they do so, this will suggest a stronger potential role for such hierarchies in everyday semantic memory.
Our approach was to teach people novel, hierarchically organized information and then to perform the classic tests of information retrieval. In the first experiment, the hierarchy was implicit in the features of a set of learned exemplars. For example all the shapes of a given color were always shaded in a particular manner. In this case, people would have had to notice the hierarchical structure on their own and use it to represent the information. Since it is possible that the usual profile of hierarchical retrieval will only be found when the information is presented as explicitly hierarchical (“Robins are birds; birds are animals.”), in a further two experiments we explicitly taught people this information. An early experiment by Smith, Haviland, Buckley, and Sack (1972) also taught people hierarchies with novel features. However, their hierarchies were considerably more modest than ours, and they used already familiar categories such as hawk-bird-animal. Thus, they did not avoid the problems associated with familiar items.
Like the traditional semantic memory literature, our experiments focused on categorical relations, comparable to verifying sentences such as “A fish is an animal” or “A claw hammer is a tool.” The main effect to be expected according to the hierarchical retrieval model (Collins & Quillian, 1969) is the distance effect. When the two categories are directly linked, confirming their relationship should be faster than when there is an intervening category; and that should be faster than when there are two intervening categories. By using novel categories and names, we avoided problems such as implicit categories people might form (e.g., four-legged mammals) and specific facts that people might memorize, pre-empting inference (e.g., killer whales being mammals and breathing air).
Learning hierarchically organized categories is not a trivial task. People can only learn and remember so much information in an experimental session, and hierarchies have the unfortunate property of expanding by a factor of two or more with each level that is added. (If they do not, then they are probably not really hierarchies, as we explain below.) We constructed hierarchies with four levels, each of which had a binary branching structure. However, we pruned the category tree in order to limit the number of categories to be learned.
Past research using a similar method has found that order of learning the levels can have an effect. Murphy and Smith (1982) found that the first-learned level was faster in perceptual classification, and it is likely advantaged in sentence verification tasks as well. We addressed this issue by using two different learning orders. If there is a distance effect, it should be present when averaged across such orders. In addition, there may be an effect of the overall level of category asked about. For example, questions involving the highest level of categories could be answered faster than those involving lower levels, as in Rogers and McClelland’s (2004) model. The distance and level effects can be partly separated (see below), and the effects of these different variables should give insight into how hierarchical information is represented and then retrieved. Of course, retrieving information from recently learned material may be different from retrieving it from very familiar concepts, a possibility we address in the General Discussion.
Our expectation was that under some conditions, with the confounds of differing familiarity and pre-emptive associations gone, people would show the classic distance effect proposed by Collins and Quillian (1969). We thought it was an open question whether such evidence of hierarchical memory structure would be found in all conditions or only when the hierarchy was clearly evident. The pattern of results would be revealing about when we might expect such effects in natural categories. However, our expectations were not actually met, as we did not find distance effects until Experiment 4, and so we postpone consideration of interpretations until the General Discussion.
Experiment 1
The first experiment used a set of items that had an implicit hierarchical structure: The properties of the stimuli were structured in inclusion relations as shown in Figure 1. The stimuli were all rectangular colored shapes with different sizes, screen locations, and textures. Initially, people simply studied these shapes for a memory test. Afterwards, they judged the truth of sentences about the stimuli, such as “All pink things are empty” or “All left things are small.” Of the possible ways of establishing a hierarchy, this condition is perhaps the least amenable to the classic distance effect, since the “categories” were never explicitly learned but were implicit in the stimuli. Finding a distance effect here would therefore provide the strongest evidence for the hierarchical representation of information.
Each item is described by a vertical path through the taxonomy. For example the first stimulus in Form B (Figure 1) was striped, red, large, and on the left; another stimulus was empty, red, large, and on the left. Because there were ten such paths in the taxonomy, there were ten distinct items, although subjects saw many examples of each one. We limited the size of the hierarchies by not using the complete binary branching structure, which would have resulted in 16 distinct items and 32 nodes in the taxonomy. This seemed too many for people to learn accurately (and this was especially true for later experiments when we taught the categories explicitly). Therefore, we divided each taxonomy into two branches: a fully branching hierarchy and a pruned branch with only one stimulus. For example, in Figure 1, Form B, the left taxonomy is divided into a fully branching hierarchy (the large items) and the pruned branch (the tiny, black, wavy figure). The pruned branch was necessary to obtain four distinct levels. To understand why, consider the pruned branch itself. We have maintained its levels of attributes in the figure so that size is the second level, color the third, and texture the fourth, as in the rest of the stimuli. In reality, there is no way to establish higher or lower-order attributes when there is no branching. That is, although all wavy things are black, all black things are also wavy; although all black things are tiny, all tiny things are black. Therefore, none of these attributes is “above” any of the others, because none of them includes two different kinds of things. The feature tiny would be above black only if there were two or more colors of tiny things, so that the colors are a subset of tiny objects. For the same reason, in order to ensure that the category of things on the left is superordinate to large things, there need to be two kinds of left things, and the same for right things. (That is, without the pruned branch, left and large would be at the same level.) Thus, the pruned branches were necessary to establish the taxonomic structure shown, but they were not themselves organized hierarchically and were not involved in the predictions.
We used two different sets of materials that had the identical taxonomic structure but with different attributes at each level. In Form B, location was at the top level, followed by size, color, and texture. In Form A, size was at the top, followed by location, texture, and color. This helped to ensure that the effects would not be due to idiosyncrasies of a particular property. We could not create four different versions with each dimension (shape, texture, color, size) at each level, however, because people could not learn to distinguish ten different sizes or locations (at the bottom level), whereas they could distinguish ten colors or textures.
The goal of the experiment, then, was to discover whether people formed a hierarchical memory structure of the sort shown in Figure 1 and retrieved information in the classic manner indicated by the distance effect. For example, if those who learned Form B realized that there were two different kinds of large figures, red and green, and that the green items were either dotted or zig-zagged, then they might be very fast to verify that all dotted items are green (distance = 1) but slower to verify that all dotted items are large (distance = 2).
We also considered an alternative process, in which people used exemplar retrieval to judge the sentences. When answering whether all dotted shapes are green, one could attempt to retrieve examples of dotted shapes and see if all are green. After completing retrieval, failure to identify any non-green items would lead to a “true” answer. In contrast, if asked whether all striped things are green, retrieval of remembered striped exemplars should lead to the recall of red striped objects, yielding a “false” answer.
This exemplar retrieval strategy does not yield a distance effect. It should be just as easy to verify that dotted items are all green (in Form B) as to verify that they are all on the left, because all of the retrieved dotted items are both green and on the left. The fact that many other items are on the left (leading to its higher placement in the taxonomy) does not affect this decision. However, what should lead to difficulties in the exemplar strategy is the size of the subject category in true trials. There are relatively few dotted figures, so retrieving and judging them should be simple. There are four times as many large figures in this hierarchy, so any judgment about them should require more retrieved items, leading to longer RTs. As a result, there should be a level effect, such that questions about higher-level categories take longer: “All dotted things are green” should be confirmed faster than “All large things are left.” In contrast, if people form a taxonomic structure in memory and use it to retrieve information, there should be a clear distance effect (“All dotted things are green” much faster than “all dotted things are left”) but no strong level effect.
In summary, in Experiment 1, people memorized colored figures whose features were structured in a hierarchy. They were tested in the standard semantic memory sentence verification task. In particular, we looked for evidence of distance and level/category size effects.
Method
Subjects
Twenty-four students from New York University received course credit for their participation in the experiment. They were tested individually on a PC.
Materials
Two hierarchically structured sets of colored shapes, Forms A and B, served as the stimuli. The taxonomies had four levels, each level represented by a particular feature dimension: size, position on the screen, pattern, and color. The assignment of features to levels in the hierarchical structure was different in the two forms, as shown in Figure 1. The taxonomy’s branching was binary with the exception of one pruned branch described above (see Figure 1). Each taxonomy defined ten types of exemplar, which were the stimuli shown to the subjects in the learning phase.
Forty sentences of the form All S things are P were constructed for purposes of sentence verification, where S and P referred to features in the taxonomy (e.g., green, tiny, left), e.g., All red things are spotted. We describe sentences with a numerical code in which the first digit represents the level of the S term in the hierarchy, and the second digit represents the level of the P term. This represents both the level of the sentence (the taxonomic level of the S term) and, implicitly, its distance (the difference between the two numerals). Sentence 2–4 is thus a sentence where the first term is from level 2 and the second term from level 4, yielding a distance of 2. The true sentences were constructed so that each feature from one level was paired with all the values above it in the hierarchy. This resulted in the lowest features appearing in sentences of distances 1, 2, and 3, when they were paired with the features at levels 2, 3, and 4, respectively. Features at level 2 varied in distance from 1 to 2, and features at level 3 only had true sentences with distance of 1.
An equal number of false sentences were constructed by pairing S features with higher-level features that did not appear above them in the taxonomy. These false P features were the nearest neighbor to the true P features. For example, in Form B a true sentence was “All starred things are brown,” and the corresponding false sentence would be “All starred things are blue,” since blue is the sibling of brown in the taxonomy. This type of false item was used by Smith et al. (1973; see Table 1) and Collins and Quillian (1969; they also used same-level false items in Experiment 2). This design has the desirable property of yielding equal numbers of true and false responses for each S and P term, even though there are more possible true statements for lower-level than higher-level categories. Since the number of possible sentences decreases at the higher levels in taxonomy, the sentences of the 3–4 type were repeated, resulting in a total of 42 true and 42 false sentences in the test.
Table 1.
Mean sentence verification RTs (and accuracies) in Experiment 1
| True sentences | False sentences | ||||||
|---|---|---|---|---|---|---|---|
| Distance | Distance | ||||||
| Level | 1 | 2 | 3 | Level | 1 | 2 | 3 |
| 1 | 2196 (.72) | 2386 (.76) | 2382 (.78) | 1 | 2075 (.89) | 2249 (.90) | 2335 (.85) |
| 2 | 2525 (.73) | 2453 (.78) | 2 | 2078 (.92) | 2192 (.87) | ||
| 3 | 2746 (.57) | 3 | 2671 (.85) | ||||
Procedure
Subjects were randomly assigned to one of the two forms. There were two phases, learning and sentence verification. In the learning phase, subjects observed all exemplars from the taxonomy they were studying. We wanted to ensure that subjects would attend to all the features of an item and also that they would encode them using the words that would be tested in the test phrase. Therefore, a verbal description of the item’s features appeared for 4 s in a randomized order (e.g. pink, empty, left, large). After an ISI of 1 s, the image of the exemplar with the listed features was presented for 5 seconds. Subjects were instructed to learn the attributes of the presented objects. Subjects were also instructed to think of features of the exemplar in exactly the terms presented before the image because they were going to be tested on verbal descriptions of features later during the experiment. Nothing else was said about the nature of the upcoming test. The exemplars were presented in three randomly ordered blocks for a total of 30 presentations.
After the learning phase, subjects performed sentence verification. All sentences were presented in each of two blocks in a randomized order. On each trial, a fixation cross was presented for 500 ms in the left middle of the screen and then replaced by the sentence, which remained on screen until response. The next trial began 1 s after response. Subjects were instructed to respond as fast as they could without sacrificing accuracy.
Results
The main theoretical questions involve the effects of level (of the S term) and distance (between S and P). However, the nature of hierarchies does not permit a completely crossed design with these two variables, because as level in the hierarchy increases, the greatest possible distance decreases correspondingly. Therefore, we performed two analyses that focused on the theoretically significant variables. In an analysis of level, we kept distance constant at 1 and varied the level of the S term. In an analysis of distance, we kept the S term constant at level 1 and compared the distances 1–3 created by varying the P term. Correct reaction times (RTs) within 2 SD of the condition mean for each subject were included in the analyses. Four subjects with missing cells were omitted from the RT analysis of level in true sentences. Table 1 shows the mean RTs and accuracies of each condition (including all subjects).
The first analysis tested the effect of the level of the S term in true sentences by including only sentences with distance 1 (i.e., sentence types 1–2, 2–3, and 3–4) in a 2 × 3 ANOVA with variables form (A or B) and level (1–3). The effect of level was reliable, F(2, 36) = 11.13, p < .01, MSE = 2212062, as RT increased steadily from level 1 to level 3 (2157 to 2525 to 2746 ms). There was also a main effect of form, F(1, 18) = 7.03, p < .02, MSE = 21224518, as well as an interaction of the two variables, F(2, 36) = 7.00, p < .005, MSE = 1392111. Form B showed a particularly large increase from level 2 to 3 (3044 to 3846 ms), with a smaller increase from level 1 to 2 (2721 to 3044ms), whereas in Form A, the greatest difference was between levels 1 and 2 (1781 to 2178ms), with levels 2 and 3 about the same (2178 and 2012 ms). These effects appear to have been caused by greater difficulty in answering questions about location (top, left, bottom, right), perhaps due to the slightly unusual syntax of these sentences (“Striped things are top”), which was used to maintain uniformity of the questions across features. In any case, there was a strong effect of the taxonomic level of the S term.
Analysis of the accuracy data (see Table 1) yielded a similar pattern. There was a strong effect of level, primarily shown by a reduction in accuracy at level 3 (only 57% correct, compared to about 72% for the other levels), F(2, 44) = 10.30, p < .001, MSE = 0.197. There were again effects of form, F(1, 22) = 14.97, p < .002, MSE = 1.509, and the interaction of form and level, F(2, 44) = 14.05, p < .001, MSE = 0.269. As in the RTs, the biggest effect was between levels 2 and 3 in Form B.1
The second analysis used only sentences whose S term was at the lowest level, varying the distance of the P term. There was no distance effect in the RTs, F(2, 44) = 1.21, MSE = 283365, nor was there an interaction with form, F < 1. Form B was slower overall, as before, F(1, 22) = 9.42, p < .01, MSE = 18779535. Thus, the signature effect of retrieval from hierarchical memory structures was not obtained. The analysis of accuracy data had the same pattern, with no effect of distance p’s > .10, but marginally higher accuracy of set A, F (1, 22) = 3.65, p < .10, MSE = .34.
We also analyzed the results of the false sentences. Such sentences do not allow as firm predictions as the true ones, absent a clear model of how the false answer is derived. (For example, Collins & Quillian, 1969, considered three different proposals for how false sentences were evaluated, none of which received strong support. See Holyoak & Glass, 1975, for more discussion of false judgments.2)
In the levels analysis, there was a main effect of level, such that level 3 was slower than the lower levels, F(2, 44) = 13.96, p < .001, MSE = 2830849. The pattern was stronger for Form B, but was found in both, F(2, 44) = 3.60, p < .04, MSE = 729204, for the interaction. And Form B was again slower overall, F(1, 22) = 7.01, p < .02, MSE = 13379832. There was only a marginal effect of level on accuracy, F(2, 44) = 3.12, p < .06, MSE = 0.027.
As in the true sentences, there was no significant distance effect, F(2, 44) = 1.60, p > .20, MSE = 421550, and Form B was slower than Form A, F(1, 22) = 8.90, p < .01, MSE = 354691008. In accuracy, there were no significant differences at all. In short, the false sentences were quite similar to the true sentences.
Discussion
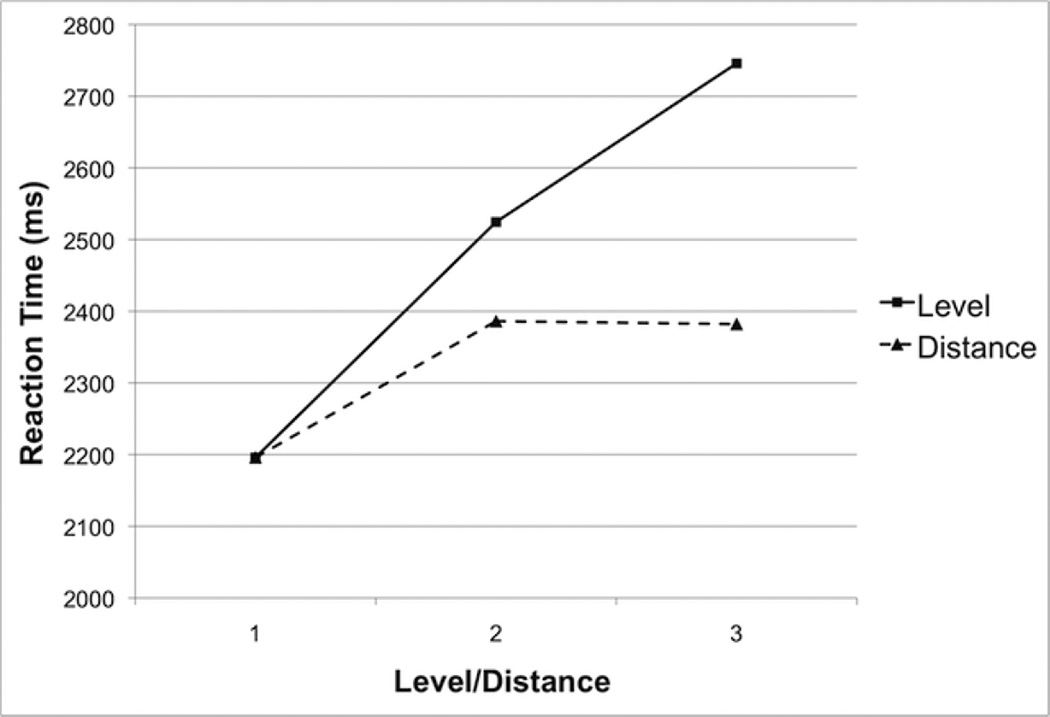
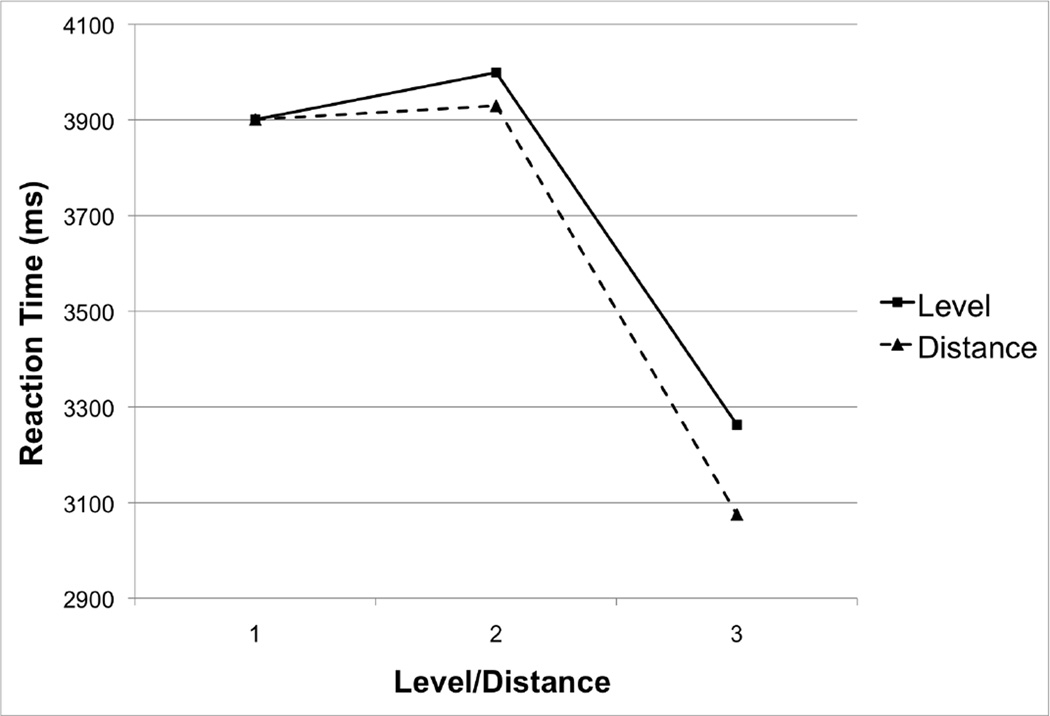
As one might expect, there were some idiosyncratic effects of the different features that characterized the levels in our hierarchy, such that people found it somewhat difficult to keep track of location and also seemed to find the two-size alternation easier than distinguishing four sizes. Such effects probably account for the interactions involving set. However, what is striking is that the results do not show a distance effect. Instead, the strongest effect is that people took longer to answer questions when the S term was higher in the taxonomy—that is, when it included a larger set. Figure 2 illustrates the two effects for the true RTs.
Figure 2.
Mean sentence verification reaction times in Experiment 1 as a function of level of the S term (solid line) and distance in the hierarchy (dotted line).
This profile of results is not consistent with the hierarchy-in-memory notion originally proposed by Collins and Quillian (1969). Instead, it seems much more in keeping with a strategy in which people retrieve exemplars using the S term as the cue, and then test them to see if they have the P feature. The number of exemplars retrieved by the S term would clearly affect RT, as the more items to be checked, the longer it will take to arrive at an answer. However, the distance in the taxonomy between S and P should have no effect on RT, since there is no “distance” between features in retrieved exemplars.
It is interesting that category size influenced RT, because people could have answered the “All” question via a simpler “Some” question and not produced this effect. If one empty square was large, then all empty squares were large, and so other empty squares didn’t need to be checked. However, answering the “Some” question actually makes the false sentences more difficult. A single counterexample can disconfirm an “All” sentence, but all items have to be checked to disconfirm “Some” statements. That may explain why subjects apparently did not adopt this strategy, taking longer to answer questions about the larger categories.
An important result is simply that people could confirm the hierarchical structure of the stimuli in spite of not having been trained on the hierarchy, or, indeed, its ever having been mentioned. As we noted in the Introduction, hierarchical structure can be implicit in semantic memory; here, by retrieving memories of individual exemplars, hierarchical relations could be accurately evaluated without being directly represented. There was one clear failure of this process, involving the highest level of set B (where four subjects had zero accuracy), which we suspect has to do with left-right confusion of some kind. Either the subjects reversed the directions or suffered response competition (when confirming a correct statement about a figure being on the left, they might have pressed the left button rather than the “true” button on the right). However, even when these subjects were omitted, the RT results showed a level effect and no distance effect.
One limitation of this study is that the nodes in the hierarchy are not traditional categories but rather features. The taxonomy in Figure 1 does not refer to classes of entities like Airedales, dogs, and mammals, but rather to properties of the entities. There is much similarity between these two situations, as a given item is simultaneously in all its higher-level categories in both cases. In Figure 1, a single item is checkered (level 1), brown (level 2), small (level 3), and on the right (level 4). Similarly, a given Airedale is also a dog, a mammal, and an animal. However, the latter categories are not defined by a single feature and generally have nouns as names rather than the adjectival forms used in our taxonomies. For these reasons, we turned next to teaching people category hierarchies of the more traditional sort. Unlike Experiment 1, the hierarchical structure was now very transparent during the learning process itself. After subjects had learned the lower-level categories, when they were then taught higher-level categories it was immediately apparent that the stimuli just learned were also in these categories. Experiment 2 asks whether subjects will encode such categorical relations into memory and confirm statements using the resulting hierarchical structure.
Experiment 2
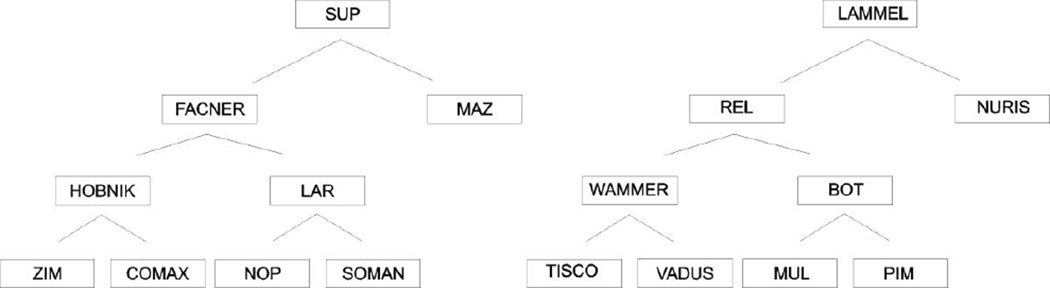
Figure 3 depicts one of the taxonomies used in Experiment 2, and Figure 4 shows exemplars of two categories, HOBNIKs and LARs. The stimuli were schematic drawings of bugs which varied in their shape, pattern, number of legs, and color. We constructed categories at four different levels, as shown in Figure 3, by successively combining lower-level categories into more general ones. To make learning easier, the categories at each level were defined by the features of the category immediately above them together with one new stimulus dimension to differentiate the categories at that level. For example, the highest-level categories separated the two shapes, oval and angular, and the next level additionally grouped the bugs by the number and arrangement of their legs, and so on. As in natural categories, more specific categories were therefore associated with more features—SUPs were rounded; ZIMs were rounded, brown, spotted, and two-legged. Each category was given a pseudo-word name.
Figure 3.
The taxonomy used in Experiments 2–4.
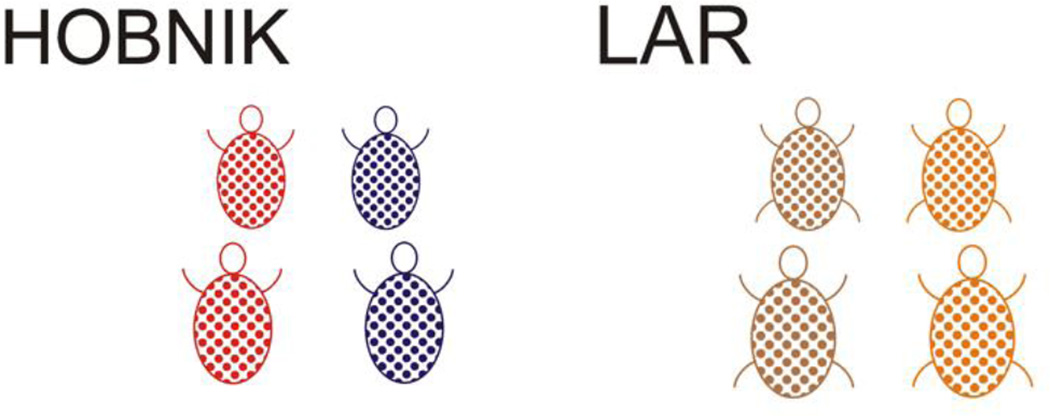
Figure 4.
Two of the categories from Experiment 2. In the original presentation, the two bugs on the left in the HOBNIK category were red, and the other two were blue. In the LARs, the first two were brown and the second two orange. Each distinct bug appeared in two sizes, as shown.
The learning procedure and structure of the stimuli made it clear that the categories were hierarchically organized, but subjects did not see a depiction of that hierarchy, nor were they trained on the IS-A relations (cf. Experiment 3). Therefore, it was possible for a subject to learn all the categories without abstracting the hierarchical structure. Our assumption was that most subjects would identify the inclusion relations, and the question was whether they would form a memory structure in which the hierarchical connections have functional consequences. In particular, would they form something like the tree structure shown in Figure 3 and use the links to draw inferences such as all BOTs being LAMMELs? Because all our subjects would have had vast experience with hierarchically organized categories, it seems very possible that they would abstract the categorical hierarchy, and we would now find the distance effect we did not observe in Experiment 1.
Rogers and McClelland (2004) taught their network hierarchies of roughly this sort. They generally found that when category names did not have their frequencies restricted, the highest level categories were learned fastest and were more strongly activated after learning. However, when they provided category names in learning proportionally to their real-life frequencies (basic-level category terms much more frequent than superordinates), they then found a basic-level advantage. In our experiment, frequencies were not specifically controlled: During learning each category received its own page depicting its exemplars, and in the tests each object had all its names tested equally often. Such uncontrolled frequencies result in larger categories being tested more often (as in Rogers & McClelland’s earlier simulations), because there are more animals (SUPs) than there are birds (LARs), and so animal would be tested more than bird in such a paradigm. Therefore, we suggest that if Rogers and McClelland’s approach is psychologically correct, we should find that the highest-level categories have an advantage in this task, as in their simulations with uncontrolled frequencies. This is because networks have a preference to learn broader distinctions before narrower distinctions and because the unequal frequencies favor the higher levels. As a result, sentences about the higher levels should be answered faster than questions about lower levels.
Method
Subjects
We tested 33 NYU undergraduates. Since the RT data are only interpretable for subjects who correctly learned the categories and their relations, we analyzed the data only from the 23 subjects who scored 85% or higher on the categorization and sentence verification tasks described below. Given the amount of material to be learned, this high drop-out rate was not unexpected.
Materials
We designed a hierarchically structured set of schematic bugs. The bugs differed in their shape (oval or angular), pattern (striped, spotted, empty, or solid), number and arrangement of legs, and color (red, blue, brown, orange, white, light blue, green, pink, gray, and violet). The hierarchy was produced by nesting the categories in four levels, as shown in Figure 3. Each level was characterized by distinctions in different stimulus dimensions. The top two categories distinguished bugs on the basis of overall shape; categories at the next level also differed in pattern; the next categories differed also in the number and arrangement of legs; and the lowest categories also differed in color. This structure avoided creation of a basic level in which information would be accumulated at one preferred level of categorization (Murphy, 2002, ch. 7). Each category received a pseudo-word name. Within the most specific categories (e.g., NOP or PIM), there were two bugs with identical values on all four dimensions but differing in size. Thus, all categories contained multiple distinct objects.
For the study phase, we prepared a sheet of paper for each category containing its name and pictures of all the bugs in that category: 16 bugs for the top level, and 8, 4, and 2 bugs for the lower levels.
Sentences for the verification test were constructed in the form “All Ss are Ps.” True sentences matched an S term with a P term at a higher level of the same taxonomical branch. There were 34 such sentences. False sentences matched the S term with the nearest corresponding category name from the higher level not on the same branch of the hierarchy. For the ZIM category, the false sentences would be “All ZIMs are LARs,” “All ZIMs are MAZes,” and “All ZIMs are LAMMELs.” There were 34 such false sentences. As in Experiment 1, we repeated the true and false 3–4 sentences to result in 72 total test sentences.
Procedure
Subjects were randomly assigned to one of two learning orders in the study phase. In the bottom-up order, they learned category names at the lowest level in the taxonomy first, and then progressed to the second, third, and fourth levels. The top-down order was the reverse. At the beginning of the study phase, subjects were told they would learn categories of artificial bugs whose drawings would be presented on separate pages and that their task was to learn the bugs’ names such that they could produce the name when presented with a drawing of a bug. They were informed of the relevant stimulus dimensions. After reading the instructions, the experimenter handed the pages containing the categories of the first level to be learned. For example, if the order of learning was bottom-up, the subject would first receive eight pages each presenting a category belonging to the lowest level of the taxonomy. The subjects were told that they could choose any way of learning the categories’ names they liked and that they should call the experimenter when they felt they had learned the categories.
Subjects then took a test on their knowledge of the categories. The computer presented a single bug together with a list of category names from the corresponding level in the taxonomy. Subjects had to choose the correct category name of that bug. For example, after learning the third level of the taxonomy, FACNER, MAZ, REL, and NURIS, the subjects would view all the bugs one by one and press a key corresponding to one of these four names. Subjects received feedback on their responses. If any response was incorrect, the subject had to review the drawings and repeat the test until performance was perfect.
After successfully passing the test of each level and completing the study phase, subjects reviewed all the categories that they had previously learned. The experimenter handed all the pages of each category of bugs to the subject in the same order in which they were learned in the study phase. The subjects were thus able to remind themselves of all categories and their names. The categorization task was then conducted on a computer. A category name appeared for 1000 ms followed by a blank screen for 500 ms, and then a picture of a bug. The subjects’ task was to respond by pressing the “Yes” key if the presented bug was a member of the category and “No” if it was not. There was no feedback, and the next trial started 500 ms after the response. Each bug was paired with all its true category names. The false items were produced by matching a bug with the closest incorrect category from a particular level. There were 48 pairs of bugs and category names in total, tested in a random order. The subjects were told that they had unlimited time to respond and that they should try to be as accurate as possible.
After the categorization task, the subjects performed the sentence verification task. There were two blocks, resulting in a total of 144 sentences per subject, randomized within each block. The sentences were presented on a screen of a PC, flush left and centered vertically. The fixation point appeared for 250 ms, followed by the sentence. The subjects were instructed to respond whether a sentence was true or false by pressing the Z and M keys labeled as “Yes” and “No” on a keyboard as quickly as possible without sacrificing accuracy. No feedback was provided; 750 ms after response, the next trial began.
Results
Categorization
Prior to sentence verification, subjects took a picture categorization task in which they had to confirm that a picture had a given name. After removing 10 subjects who failed to learn (see above), the remaining subjects performed well, scoring at least 94% correct overall, as shown in Table 2. There was a significant main effect of level on accuracy, F(3, 69) = 3.13, p < .05, MSE = 0.024, and an interaction of level and learning order, F(3, 69) = 2.99, p < .05, MSE = 0.023. Accuracy was fairly flat across levels in the bottom-up condition, and the highest and lowest levels were most accurate in the top-down condition. Most importantly, accuracy was generally high and did not differ greatly across learning orders.
Table 2.
Mean categorization accuracies (and SDs) in Experiment 2
| Order of Learning | Level | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Bottom-up | .97 (.04) | .94 (.07) | .97 (.03) | .93 (.10) |
| Top-down | .99 (.02) | .92 (.11) | .86 (.15) | .95 (.07) |
Sentence Verification
Table 3 presents the mean RTs and accuracies. As in Experiment 1, the analyses focused on two effects: the level of the first term in the sentence (comparing 1–2, 2– 3, and 3–4 sentences) and the distance between the terms in the sentence (comparing 1–2, 1–3, and 1–4 sentences). There was a marginal effect of hierarchical level on the RTs for TRUE sentences, F(2, 46) = 2.91, p < .07, MSE = 3622111, and no effect of learning order. Subjects responded fastest to the 3–4 sentences, contrary to the effect in Experiment 1. The highest level sentences were also answered most accurately, F(2, 46) = 7.30, p < .01, MSE = .073. There was no effect of learning order. In the false sentences, there was no level effect in RTs—only a marginal interaction of order of learning and level, F(2, 46) = 2.72, p < .08, MSE = 7916470. However, the higher levels were more accurate than the lowest level, F(2, 46) = 5.13, p < .01, MSE = .177, with no order effect.
Table 3.
Mean sentence verification RTs (and accuracies) in Experiment 2
| True sentences | |||||||
| Bottom-Up | Top-Down | ||||||
| Distance | Distance | ||||||
| Level | 1 | 2 | 3 | Level | 1 | 2 | 3 |
| 1 | 3465 (.83) | 3340 (.86) | 2907 (.88) | 1 | 4244 (.79) | 4393 (.83) | 3208 (.91) |
| 2 | 3762 (.83) | 3638 (.92) | 2 | 4185 (.82) | 3609 (.90) | ||
| 3 | 3217 (.88) | 3 | 3299 (.95) | ||||
| False sentences | |||||||
| Bottom-Up | Top-Down | ||||||
| Distance | Distance | ||||||
| Level | 1 | 2 | 3 | Level | 1 | 2 | 3 |
| 1 | 4059 (.77) | 2306 (.95) | 3196 (.84) | 1 | 4093 (.78) | 4072 (.79) | 3467 (.92) |
| 2 | 2529 (.97) | 3470 (.92) | 2 | 4560 (.82) | 3584 (.93) | ||
| 3 | 3072 (.93) | 3 | 3176 (.94) | ||||
The analysis of the distance in true sentences revealed a significant main effect in RT, F(2, 46) = 7.10, p < .01, MSE = 5295480, and accuracy, F(2, 46) = 3.88, p <.05, MSE = .044. In both cases, subjects performed better in the longer distances, contrary to the expected distance effect with hierarchies. There were no effects of learning order. The distance and level effects are presented in Figure 5.
Figure 5.
Mean sentence verification reaction times in Experiment 2 as a function of level of the S term (solid line) and distance in the hierarchy (dotted line).
The false sentences showed a similar “negative” distance effect, except for the data point of distance 2 in bottom-up learners, which was faster and more accurate than distance 3 in that group. One subject with missing cells was omitted from this analysis. This pattern resulted in a main effect of distance in RTs, F(2, 44) = 3.50, p < .05, MSE = 5473612, plus a marginally significant interaction with learning order, F(2, 44) = 3.15, p = .053, MSE = 4916086. Both effects were marginally reliable in the accuracy data, F(2, 46) = 2.47, p < .10, MSE = .092; F(2, 46) = 2.50, p < .10, MSE = .093.
Discussion
The results were quite different from those of Experiment 1 (compare Figures 2 and 5), which is perhaps not surprising given the differences in the stimuli. However, like Experiment 1, the data did not follow the expected pattern of hierarchical retrieval. First, there was a levels effect in which the more general categories were responded to significantly more accurately and marginally faster than the lower-level categories. This could potentially be due to the fact that there are fewer categories at these levels than at lower ones, thereby reducing memory interference. However, it should be noted that when tested on categorization, there was no general advantage for classifying into the highest category, and in fact the lowest level was slightly more accurate there (Table 2). Smith et al. (1972) paired familiar categories with novel features and also found faster responses for higher-level categories and features.
Second, and more significant, there was a distance effect, but it was opposite to the expected one. Rather than people being faster in verifying categorical relations of adjacent levels, they were faster the farther apart the categories were. Putting the two effects together, one possible explanation is that people were faster in answering questions when the sentence P term was from the highest level (3–4 and 1–4 in the two analyses). This does not seem to be caused by learning the highest level first, because the pattern is also evident in the bottom-up learners (see Table 3).
One possible explanation for this advantage for level 4 P terms is that as the categories move up in the hierarchy, they become more abstract, that is, are associated with fewer features. So, the bugs in the VADUS category (level 1) were all angular, striped, and green, with four rear legs. In contrast, the LAMMEL bugs (level 4) had only one feature in common, their angular shape. According to the feature-comparison account (Smith et al., 1974), people judge category relations by comparing the concepts’ features and looking for overlap. The fewer the features in the P term, the quicker the comparison can be, because there are fewer features to be checked (Smith et al., 1972, give a similar explanation for their results). For example, when asked if VADUSes are LAMMELs, one might judge whether VADUSes are angular, which is the only feature common to LAMMELs. However, to decide whether VADUSes are WAMMERs, one must judge their shape, pattern, and legs to ensure that the WAMMER features are also found in VADUSes.
If the highest level categories were unusual for some reason, one might wonder if there were signs of the expected distance effect when that category was not involved. This can be answered by examining distances 1 vs. 2 at level 1 in Table 3. One can see that across the four cases (truefalse × 2 learning orders), there is no sizeable slowdown or loss of accuracy at distance 2. In fact, by far the largest effect is in the false sentences, bottom-up order, where accuracy and RT are much better for the longer distance. So, it does not seem that the advantage of the highest level—whatever its cause—is masking a distance effect.
The results are broadly consistent with predictions we attributed to Rogers and McClelland (2004). There was no (normal) distance effect, and questions about the highest level seemed to have an advantage. They provide detailed analyses and explanation of why more global features should be learned prior to features used to distinguish specific categories. Like our explanation, their proposal is that superordinate categories have the advantage of a small number of features that distinguish large categories of objects. Without actually running our stimuli in their model, it is difficult to say exactly what it predicts, because we controlled the learning order by presenting the categories from specific to general or vice versa. The former order might have negated their model’s preference for global features and categories. However, the overall results seem consistent with their analysis of semantic memory.
Experiment 3
Our goal in this research has been to investigate the development and use of hierarchical memory structures for artificial materials that did not have the potential confounding variables that could influence natural category hierarchies. For example, if children are told that penguins are birds or worms are animals, these learned facts could influence their sentence verification, probably pre-empting the use of hierarchical inference or feature comparison. After all, a learned fact is likely to be retrieved faster than an inference can be drawn. Therefore, in Experiments 1 and 2, we did not make any mention of the hierarchies and inclusion relations.
However, in real life people know some taxonomic relations. Students encounter taxonomic trees in biology classes; bird-watchers read about the orders, genera, and species of different birds; people encounter statements in the media such as palm trees not being “real trees”; and so on. Possibly such explicit information is necessary for people to form hierarchies in memory that conform to the Collins and Quillian retrieval processes. We interpreted Experiment 2 as revealing a feature comparison process, but that may have arisen because people learned the items’ names and not the taxonomy per se. Perhaps when people explicitly learn a taxonomy, this useful tool will organize their memory and their answering of questions about the categories.
To explore this possibility, we investigated how people would perform the sentence verification task if they only knew the taxonomy and did not have conceptual knowledge. That is, subjects were shown a tree structure like Figure 3, and they learned the category names and their relations. They did not learn, however, that VADUSes were angular, green, etc. bugs—they only learned that VADUSes were at the bottom level of the hierarchy, subordinate to WAMMER, which was subordinate to REL, and so on. With only this schematic information, it seems more likely that memory retrieval will follow the Collins and Quillian profile. If VADUS is associated to WAMMER, which is associated to REL, which is associated to LAMMEL, then it might well take longer to confirm that a VADUS is a LAMMEL than that a VADUS is a WAMMER. We used the same taxonomy as in Experiment 2, so that a direct comparison of their results would be interpretable.
Method
Participants
Twenty students from New York University received course credit for their participation in the experiment. They were randomly assigned to one of the two presentation orders. Four other subjects were omitted because they did not follow instructions or had accuracy below .65 in the sentence verification task.
Materials
The hierarchical category structure used in Experiment 3 was identical to the one used in Experiment 2 except for a few changes in category names to make them more distinctive. We presented subjects with an illustration of the hierarchy itself, as shown in Figure 3.
Procedure
Subjects read instructions that mentioned biological taxonomies and told them that they would learn category taxonomies with novel names. No information was given about the nature of these categories. They initially saw a schema of the taxonomy containing empty boxes rather than category names. They were instructed that they would be given the category names level by level and that they should learn the whole taxonomy with the category names in correct positions. As in Experiment 2, there were two orders of learning: 11 subjects learned the taxonomy starting from the bottom level, and 9 started at the top level. There were no exemplars or features associated with the categories—the sole task was to learn the structure of the taxonomy and the category names as shown in Figure 3. A sentence in the instructions emphasized the importance of learning the inclusion relations in the taxonomy. After the presentation of the empty schema of the taxonomy, the experimenter provided a picture of the taxonomy with the category names of one level filled in (replacing the empty boxes). The subjects could spend as much time as they wanted to study each level. They then had to draw the entire hierarchy and write down in correct positions all the category names that they had previously learned. If this reproduction was correct, the experimenter would hand the taxonomy with the next level’s category names filled in. If the drawing was incorrect, the study taxonomy with the category names was presented again, followed by another test. This procedure was repeated until subjects could reproduce the drawing with all elements of the taxonomy.
The sentence verification phase was identical to the one employed in Experiment 2.
Results
Mean RTs and accuracies are presented in Table 4. We again performed two analyses in order to test the levels and distance effects. The analyses of true RTs revealed a significant main effect of the level of the first term in the sentence, F(2, 36) = 12.88, p < .01, MSE = 34587377, and a marginally significant interaction of level and order of learning, F(2, 36) = 2.80, p = .07, MSE = 7512771. This pattern seems to reflect two effects: First, the highest level was faster than the others, and second, the level learned first had an advantage. As a result, in the top-down order, the highest level (which benefited from both effects) was confirmed almost 3 s faster than the other levels, but in the bottom-up order, the lowest level (learned first) was also relatively fast. The accuracy data showed a very similar pattern and revealed the same two effects: the main effect of level, F(2, 36) = 18.03, p < .01, MSE = .277, and a marginally significant interaction of level and order, F(2, 36) = 2.80, p = .07, MSE = .043.
Table 4.
Mean sentence verification RTs (and accuracies) in Experiment 3
| True sentences | |||||||
| Bottom-Up | Top-Down | ||||||
| Distance | Distance | ||||||
| Level | 1 | 2 | 3 | Level | 1 | 2 | 3 |
| 1 | 4872 (.84) | 5761 (.65) | 3807 (.89) | 1 | 5711 (.81) | 4641 (.85) | 3694 (.94) |
| 2 | 6865 (.64) | 3445 (.91) | 2 | 5565 (.78) | 3823 (.92) | ||
| 3 | 4253 (.94) | 3 | 2964 (.94) | ||||
| False sentences | |||||||
| Bottom-Up | Top-Down | ||||||
| Distance | Distance | ||||||
| Level | 1 | 2 | 3 | Level | 1 | 2 | 3 |
| 1 | 4918 (.78) | 4960 (.78) | 3748 (.87) | 1 | 5085 (.76) | 4568 (.87) | 3461 (.84) |
| 2 | 5154 (.78) | 3997 (.88) | 2 | 5266 (.79) | 4248 (.88) | ||
| 3 | 4604 (.88) | 3 | 3156 (.86) | ||||
In the false sentences, there was only a significant main effect of level in RTs, in which the highest level was again fastest, F(2, 36) = 3.67, p < .05, MSE = 10132534. There were no reliable differences in the accuracy data of the false sentences, but the overall pattern was consistent with the levels effect in the RTs.
The second set of analyses tested for the distance effect. As in Experiment 2, the RTs for true sentences showed a negative distance effect, F(2, 36) = 8.93, p < .01, MSE = 14808954, along with another marginally significant interaction of distance and presentation order, F(2, 36) = 2.86, p = .07, MSE = 4750611. Distance 3 was over a second faster to confirm than the others, and there was also an effect that the 1–2 sentences were relatively fast when level 1 was learned first. The same pattern appeared in accuracy: a distance effect, F(2, 36) = 11.79, p < .01, MSE = .140, and interaction with order, F(2, 36) = 5.82, p < .01, MSE = .069. In the false sentences, the only reliable result was the same distance effect in RTs, F(2, 36) = 7.55, p < .01, MSE = 11067474.
Discussion
Surprisingly, the results of Experiment 3, in which people learned only the taxonomy without knowing anything about the categories themselves, were very similar to those of Experiment 2, in which people learned the categories but not the hierarchies. In particular, both experiments showed a levels effect in which the sentences with terms 3–4, highest in the hierarchy, were answered faster than others. Both experiments also showed a negative distance effect in which sentences with the greatest distance, 1–4 sentences, were faster than sentences with adjacent terms, like 1–2. As in Experiment 2, the absence of the expected distance effect was not solely due to the speed of answering questions about the top level. There was no consistent increase in RT (or decrease in accuracy) from distance 1 to distance 2 (at level 1) in Table 4. These results are inconsistent with the usual predictions involving inferences from hierarchies in memory. We discuss possible explanations of this unexpected reversal in the General Discussion.
Experiment 4
The repeated finding of no distance effect—or even a negative distance effect—within hierarchies is surprising. In fact, the result may raise a concern that there is something wrong with our tested hierarchy, the names, or some aspect of the testing procedure. There is a certain logic to the claim that drawing inferences must take longer than retrieving known information and that inferences involving more steps must take longer than those involving fewer steps. The failure to find such effects in experiment after experiment naturally raises the concern that something has gone wrong.
We addressed this concern by using the same hierarchy as in previous experiments but with a different training regimen designed to reveal the expected distance effects. In the previous experiments, people learned colored shapes, categories, or a visual depiction of a hierarchy. It is possible (and in light of the results, likely) that with such materials they could develop specific processing strategies that obviate the need for inference within the hierarchy. For example, memories of exemplars could be consulted, or the spatial characteristics of the displayed hierarchy could be used to answer questions.
Experiment 4 used a learning procedure that seemed much less open to such possibilities—a simple verbal learning procedure in which pairwise links were memorized. Subjects learned sentences such as “All FACNERs are SUPs,” “All HOBNIKs are FACNERs,” and “All ZIMs are HOBNIKs.” During the learning phase, people learned only the individual sentences; they saw neither the taxonomic tree nor category exemplars, though they were told that these names referred to categories that were nested. At test, subjects had to confirm not only the learned sentences but also the ones that are true by inference—e.g., for the above, “All HOBNIKs are SUPs” and “All ZIMs are FACNERs.” Under the assumption that most people would not spontaneously draw and learn the inferences during the learning procedure, we should now find a distance effect. The learned sentences should be fastest, and the sentences requiring a one- or two-step inference should be correspondingly slower and less accurate.
Such a finding would confirm that there is nothing in the hierarchy, names, testing procedure, and so on that is preventing the distance effect from revealing itself in our experiments. Furthermore, a finding of the distance effect will support the contention that in “normal” circumstances, when people have more knowledge about the categories and stimuli than simple pairwise associations, the hierarchical retrieval model does not apply to newly learned conceptual hierarchies.
Method
Subjects
Twenty-two NYU undergraduates served in the experiment to receive course credit.
Stimuli
The materials were the same category names as in the previous two experiments, organized into all the set-inclusion sentences from one level to the next highest level in the form “All PIMs are BOTs.” There were 16 such sentences, all of which were distance 1 category relations. The test sentences were identical to those used in Experiments 2 and 3, so that the questions and answers were the same across the two experiments. Thus, in addition to the learned sentences, longer-distance true and false sentences also appeared in the test.
Procedure
A fair test of the distance effect can only be made if people have actually learned the original sentences. Clearly, no one can draw an inference that a PIM is a REL, if they do not know both that PIMs are BOTs and that BOTs are RELs. We used a learning procedure similar to that of the Experiment 2, in which we presented the sentences from one level first, followed by a test of that level, and then presented sentences from the next level, its test, and so on. Learning proceeded either from top to bottom through the hierarchy or from bottom to top, as before. The sentences were said to describe category relations similar to all chairs being furniture or all whales being mammals.
For each level, subjects viewed a list of all the inclusion sentences at that level on the computer screen and were instructed to remember them. When they had indicated they were done, they received a cued recall test in which the first category name was provided and the second had to be filled in: “All PIMs are ____.” In the second and third levels, there were fewer sentences, and so each was tested twice. When subjects gave the wrong category name, an error message appeared along with the correctly completed sentence. If performance was not perfect in the test of a given level, the original screen of all its sentences was re-presented for more study, followed by another test.
After all levels had been learned, there was a final phase to remind subjects of the sentences that had been learned earlier. They reviewed the sentences from each level separately and could cycle through the three lists of sentences as many times as they wanted. They then received a cued recall test in the same format as the previous tests. Subjects needed to get at least 80% correct to move on to the next phase. If they scored below 80%, they reviewed the sentences as before, and took the test again.
At test, subjects were reminded that the sentences described category relations, which are transitive. So, if All Xs are Ys and all Ys are Zs, it follows that all Xs are Zs. The final task was to read each sentence and to decide whether it was true based on what was learned. Obviously, the learned sentences were true, but other sentences would be as well. It was stressed that accuracy was important and that subjects should take the time to remember the relevant sentences to respond correctly. However, they were to press the response button as soon as they had arrived at an answer.
Results and Discussion
All subjects successfully passed the final test of all learned sentences and entered the test phase. The mean number of blocks in that final learning test was 2.2, with proportion correct of .91 in the final block. Some people’s performance in the test phase was nonetheless low, and subjects were dropped from the RT analyses if they had empty cells in that particular analysis (reflected in the degrees of freedom). We included learning order as a variable but mention it only when it interacts with the theoretically relevant variables. Because of the difficulty of this task, we expected that more of the effects might be seen in accuracy than in the previous experiments. Results are shown in Table 5.
Table 5.
Mean sentence verification RTs (and accuracies) in Experiment 4
| True sentences | |||||||
| Bottom-Up | Top-Down | ||||||
| Distance | Distance | ||||||
| Level | 1 | 2 | 3 | Level | 1 | 2 | 3 |
| 1 | 3152 (.89) | 4945 (.80) | 6896 (.77) | 1 | 3364 (.85) | 5604 (.54) | 6965 (.61) |
| 2 | 5958 (.92) | 4139 (.76) | 2 | 4345 (.69) | 5560 (.65) | ||
| 3 | 5203 (.87) | 3 | 4233 (.83) | ||||
| False sentences | |||||||
| Bottom-Up | Top-Down | ||||||
| Distance | Distance | ||||||
| Level | 1 | 2 | 3 | Level | 1 | 2 | 3 |
| 1 | 5245 (.70) | 5587 (.69) | 6982 (.83) | 1 | 4500 (.87) | 4430 (.81) | 6491 (.72) |
| 2 | 5448 (.70) | 6102 (.73) | 2 | 4137 (.76) | 4726 (.74) | ||
| 3 | 4601 (.81) | 3 | 4473 (.83) | ||||
There was no effect of level in the accuracy analyses of either the true or false sentences, F(2, 40) < 1, F(2, 40) = 1.45, p > .20. This is perhaps not surprising, as all of these sentences involved distances of 1 that were directly presented and learned. However, even for distance 2, which was inferred, there was no difference between level 1 and level 2 sentences (.67 and .70 accuracy in the trues).
There was an effect of level in true RTs, with the lowest level faster than the other two, F(2, 38) = 3.84, p < .05. There were no differences due to level in the False RTs, F < 1. Across the dependent measures, there seems to have been no consistent effect of level.
In contrast, there was a clear distance effect, as accuracy declined from learned to inferred sentences (Ms of .87, .67, and .69 for distances 1–3), F(2, 40) = 8.44, p < .001. There was no distance effect in the False sentences, F < 1. That result could reflect a bias to answer “false” when unsure of the answer, inflating accuracy of the false responses at the unlearned higher distances. There was also an interaction with learning order in the false sentences, F(2, 40) = 4.95, p < .02, which may derive from an advantage to the most recently learned levels (the most accurate condition was the 1-1 sentences in the top-down order).
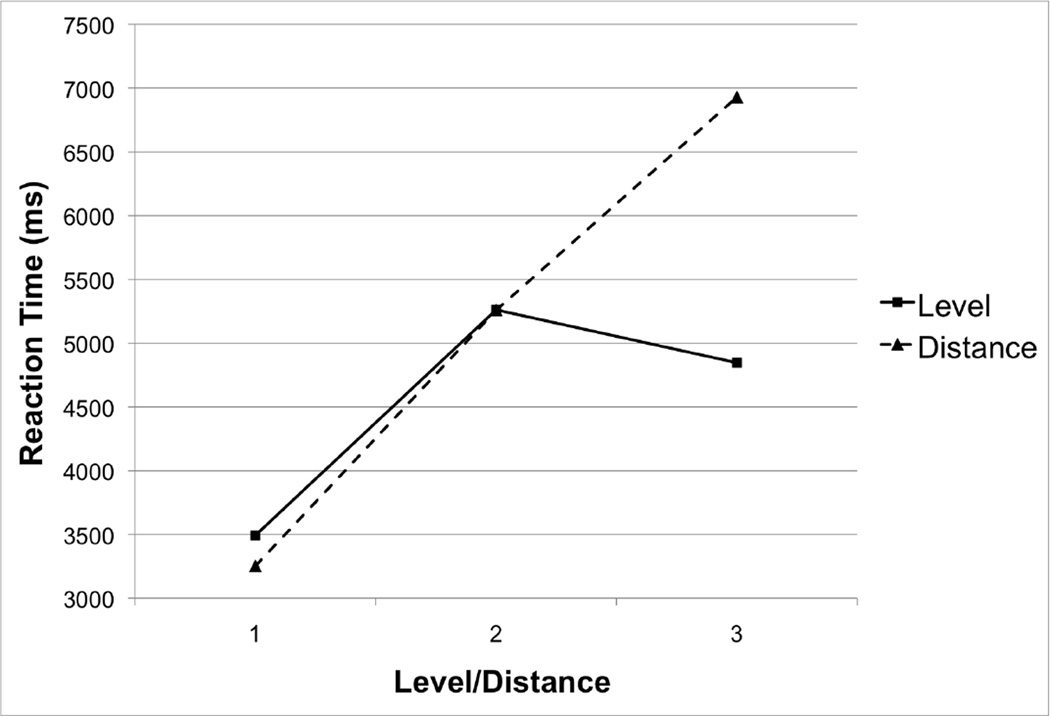
As can be seen in Figure 6, the true RTs showed a strong distance effect, increasing from 3.3 to 5.3 to 6.9 s with distances of 1–3, F(2, 38) = 25.10, p < .001. A similar though less dramatic pattern obtained with false RTs, F(2, 40) = 6.22, p < .01. The most important effect is probably the increase from distance 2 to 3, as sentences with distance 1 were learned and therefore would be faster than the others on any account. A key test, then, is to show that it takes longer to make two inferences than one, and this was in fact the case t(20) = 2.47, p < .02.
Figure 6.
Mean sentence verification reaction times in Experiment 4 as a function of level of the S term (solid line) and distance in the hierarchy (dotted line).
Overall, there was a clear distance effect, which was especially noticeable in RT. This shows that the Collins and Quillian distance effect does in fact obtain when the memory structure is likely to be what that model assumes. That is, if people store pairwise associations, they can then draw inferences across those associations, from lower levels to higher levels. The inferences were less accurate than the learned relations, and their RT increased monotonically with the number of steps required.
It is possible that subjects did not view the items as categories, given that they knew nothing about their contents. However, the instructions did present them as nested categories, analogous to real-life examples, and people were generally accurate in verifying the inferred IS-A relations. There is nothing in the hierarchical inference account that requires that the categories be richly represented—indeed, we can draw inferences about categories we know virtually nothing about other than their IS-A relations (like rheas or Lamborghinis).
The importance of this result is in its contrast to the results of all the previous experiments, which found either no distance effect or a negative effect. Even though the names and hierarchical structure were the same as those of Experiments 2 and 3, and even though the test phases of all three experiments were identical, only this experiment conformed to the expected pattern of results for hierarchical inference. This shows that the hierarchy tested, names, and test procedure of the previous experiments had no unknown problem that prevented a distance effect from revealing itself. Instead, it seems clear that when people learn categories or explicitly learn the hierarchy as a whole, they do not produce the predicted distance effects.
General Discussion
We began this investigation by asking whether retrieval of information from a newly learned set of categories would produce the pattern predicted by Collins and Quillian (1969) in their classic semantic memory model, when confounding effects of familiarity, differences in associations, and specific learned facts are removed. This question is really two interrelated questions: Do people actually form mental representations in the efficient hierarchical structure C&Q assume? and Does retrieval from such representations reveal the effect of number of intervening links, the distance effect? Questions of representation and process of this sort cannot be answered independently (Anderson, 1978). However, the results are clear enough that we can provide a joint answer.
To start at the end, the results of Experiment 4 suggest that when we are fairly certain that people’s mental representations consist of pairwise linked associations in memory (PIMs are BOTs; BOTs are RELs; etc.), the results do in fact follow the expected predictions. The more links required to answer the question, the longer subjects took to respond and the more errors they made.
One issue with that experiment might be the extremely long RTs, ranging as high as 7 s for the longest distances, which are much higher than category membership verification in most studies (e.g., means of around 1 s in McCloskey & Glucksberg, 1979). Of course, our RTs reflect judgments of newly learned materials with nonsense names, so longer times are to be expected. However, note that the RTs in Experiments 2 and 3 were shorter, with the same test materials. As we suggest below, the shorter RTs in other kinds of tasks may reflect a reorganization of memory that is inconsistent with the simple hierarchical model. That is, it may be no coincidence that the experiment with longest RTs was the only one to show the distance effect.
The problem for the hierarchical inference model is that its predicted pattern appeared only when people engaged in what was essentially a verbal-learning task, in which all inferences had to be drawn at test. Of course, it would have been logically possible for people to draw the inferences during study. However, given the need to memorize and pass a test on 16 sentences with novel names, the task no doubt discouraged the learning of inferences that were not on the test. When people were exposed to a depicted hierarchy (Experiment 3) or learned meaningful content with the categories (Experiments 1 and 2), the distance effect failed to appear. Instead, effects of category level (specificity) or even a negative distance effect obtained. Understanding these effects, which are not predicted by the hierarchy model, will tell us more about how people structured this information in memory.
The Unpredicted Effects
In Experiment 1, questions about more general properties took longer than questions about properties lower in the hierarchy. This effect seems most explicable as due to exemplar retrieval. Because the more general properties appeared in more items, they engendered more checking. If there were eight items on the left but only two that were red, it would take longer to answer questions beginning “All left objects…” than “All red objects…,” because there would be more exemplars to retrieve and check in the former. This explanation entails that people did not form a hierarchy like that shown in Figure 1 but remembered the stimuli as distinct exemplar types. This experiment did not use traditional categories or category names, so perhaps the failure to organize the material according to the hierarchical relations of the features is not very surprising.
Experiments 2 and 3 did use categories and discovered a surprising negative distance effect in which the longer the distance to be traversed in the hierarchy, the shorter the RT and more accurate the judgment. This result directly contradicts the prediction of inference in a hierarchy and also raises the question of just why it occurs. One possible explanation is that the effect is really an overall preference for answering questions about the highest level of the taxonomy. Both experiments revealed a reliable effect of hierarchy level, with the highest level being fastest; that level is involved in the longest distance (1–4) sentences as well. So, a simple explanation of much of the results may be that questions about level 4 are generally easier than questions about other levels.
It is not obvious why this should happen in both Experiments 2 and 3, however, because their stimuli and learning procedures were so different. In Experiment 2, people learned actual categories and were not trained on the taxonomy per se. The highest categories were the most inclusive, and they were associated with a single feature. Therefore, the semantic simplicity of that level could have made it easier, since only one feature had to be retrieved and compared to the representation of the subject term. SUPs were all rounded, but HOBNIKs were rounded, dotted figures with two feet, so it should take less time to judge whether something was a SUP than whether it was a HOBNIK. Under this explanation, people represented the categories as features, and the number of features involved predicts performance, as in feature comparison accounts. However, that explanation cannot account for Experiment 3, where there were no features known of the categories. Those subjects only learned the hierarchical structure.
One possible explanation of the results in Experiment 3 refers to the spatial nature of the taxonomic representation. A salient feature of each category may have been whether it was in the tree shown on the left or right (see Figure 3). If people learned these locations and associated them with the top nodes of the tree on each side, it might have been easy for them to answer questions of the sort “Ss are SUPs” or “Ss are LAMMELs,” because they would have essentially been judging whether both terms occurred on the same side. Perhaps all the left categories were encoded as the SUP categories, and the right ones as the LAMMEL categories. This strategy would help only the highest categories. Given the visual presentation of the hierarchy, we suspect that physical location accounts for the ease with which judgments were made regarding the top two categories, and this accounts for the negative distance and level effects.
Thus, it may well be coincidence that Experiments 2 and 3 had such similar results, given the large differences in what was learned about the two sets of categories. However, both illustrate that people may actively organize the material they receive into representations that are efficient for information retrieval. The Quillian hierarchy is particularly efficient in terms of the number of nodes and associations that need to be stored—that is, memory space. However, preserving memory space may not be the most important form of efficiency. If memory is cheap but processing time is valuable, then storing information redundantly could lead to better overall performance (Logan, 1988). Just as it is probably useful to memorize the fact that whales are mammals rather than deriving it every time this information is needed, it may be useful to remember categories’ features or the spatial locations in a viewed taxonomy. Given that in real life it is the content of concepts that is essential, people may well compare concepts in terms of their features and learned short-cuts rather than relying on inference to save memory space. It is important to have quick access to conceptual information about what a dog or a chair is in language comprehension and in dealing with everyday objects. Thus, even though one could save memory by storing the fact that mammals breathe and give birth to live young and by not representing the same facts about dogs, this may conflict with the more useful ability to retrieve information about dogs quickly and accurately.
In Experiments 2 and 3, which included conceptual content or spatial relations, subjects responded much faster to long-distance test questions than when such information was lacking in Experiment 4. Thus, all the “confounds” that make it difficult to provide a fair test of semantic memory models, like familiarity or specific associations, may be exactly the things in real life that people use in order to avoid the slow inference process that is necessary within a hierarchical network (though see the Limitations section). Certainly, people can make long-distance inferences when faced with novel questions such as whether wombats have heart valves or whether ambulances have rudders. But the results of the present research suggest that people try to avoid relying on those inferences when possible.
If we are right, then the inferential model proposed by Collins and Quillian is more of a fall-back measure than the preferred way that semantic information is stored and retrieved. In that sense, the model is not wrong so much as being only one possible way of retrieving information, a slow and onerous one.
Implications for Theories
The semantic memory models of the 1970s and 80s may seem somewhat simplistic in the light of newer, large connectionist models of conceptual knowledge (Rogers & McClelland, 2004) or sophisticated mathematical models of semantic organization (Close & Pothos, in press; Shafto et al., 2006; Tenenbaum, 1999). However, our own feeling is that these earlier models capture some aspects of how people can represent and retrieve information from memory.
The Collins and Quillian approach can explain how we can derive novel inferences. This occurs when we think about general properties of a specific object (e.g., that tea roses must perform photosynthesis) or about properties of a newly learned kind of thing (e.g., that a long-tailed dachshund is an animal and probably barks). Models in which concepts are represented as feature lists cannot explain such cases, given that the concept and features have never been encoded together. Assuming that such cases of retrieval by inference exist, Experiment 4 shows that they occur in the way that the original Collins and Quillian model would predict.
When people learned richer representations of our materials (Experiments 1 and 2), however, the results did not support this model. Instead, people seemed to rely on exemplar retrieval or feature comparison. Experiment 2 seems to be the experimental situation that is closest to real-world categories, which are richly represented and hierarchically organized (though our stimuli were not nearly as rich as actual categories). Subjects could have formed a hierarchical network of category names when learning these categories but failed to do so, suggesting that people prefer to compare conceptual representations. Feature comparison models (Hampton, 1979; McCloskey & Glucksberg, 1979; Smith et al., 1974) have generally seemed more consistent with the overall results in the field, though there are still phenomena they do not account for (Chang, 1986; Smith, 1978).
The use of an exemplar strategy in Experiment 1 is reminiscent of exemplar models in category learning (Medin & Schaffer, 1978). Indeed, the experiment had the properties argued to be ideal for exemplar learning—small numbers of items, presented repeatedly (Smith & Minda, 1998). Such a strategy seems less likely to work for most real-world categories. One likely cannot retain distinct memories of every chair, car, dog, or reality-TV contestant one encounters. Furthermore, no exemplar-based model of hierarchical categorization has yet been proposed (see Murphy, 2002, ch. 7).
One cannot confirm universally quantified statements by retrieving a finite number of exemplars, so exemplar retrieval is not logically able to confirm statements such as “All birds have feathers” or “No mammals have feathers.” However, when general knowledge is lacking, people may rely on retrieving examples to give their best guess at the answer. For example, to decide whether only mammals play, one could retrieve memories of playing animals and check to see if all of them are mammals. This strategy would be effective under the assumption that counterexamples would come to one’s notice if they existed (see Gentner & Collins, 1981). However, even that strategy would not work for properties that are not normally noticed and encoded into exemplar memory, e.g., “All squirrels breathe.” Although we have seen hundreds of squirrels, we don’t recall ever noticing that they were or weren’t breathing. Our strength of belief in this proposition probably derives from the Quillian-like inference that all mammals breathe air, squirrels are mammals, hence they breathe.
This discussion is consistent with a number of recent conclusions from the experimental literature on category learning that multiple systems are involved in learning categories, depending on the type of category and learning procedure (e.g., Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Nosofsky, Palmeri, & McKinley, 1994; Poldrack et al., 2001). More generally, Murphy (2002) concluded after an extensive review of the concepts literature that concepts are something of a mess. He pointed out that there are many different means to accomplish the tasks we refer to as conceptual, and it seems likely that all those means are used at one time or another (see also Hampton, 2010). The present research provides an example of this state of affairs even within a circumscribed topic, where exemplar use, feature matching, spatial strategies, and spreading activation across associations all appear to have been used, depending on what information was presented. Indeed, Smith (1978, p. 35) noted that feature comparison and learned associations both might underlie performance, “for the issue is not really one of a dichotomy.”
The Rogers and McClelland (2004) approach to semantic memory did fairly well in the experiment that was most similar to its model domain (see Discussion of Experiment 2), with object categories that were associated to features. Rogers and McClelland note that their model is intended to capture the long-term representation of semantic knowledge. They explicitly refer to other components that will be necessary for a complete theory, such as episodic memory needed to encode newly learned facts. Their theory was not intended to learn paired associates of the sort tested in Experiment 4. Their model also does not have a reasoning component, which could be necessary for novel induction questions. Such a component could act on their semantic representations. In short, we believe that their model has considerable promise as a representation of semantic information in long-term memory but that other processes will be involved in explaining all the tasks that are tested in semantic memory research.
Limitations
An experimental study of this sort can allow the manipulation of variables that are not easily controlled with natural materials. But such studies also are unlike actual semantic memory in a number of respects, such as having smaller, more recently learned networks that are semantically reduced compared to real concepts. One potentially important difference is that semantic organization may take place over multiple exposures to material over a very long time frame. Rogers and McClelland (2004) emphasize this aspect and contrast their model of semantic learning with a hippocampal-based system of episodic memory. This suggests that an important extension of our work might be to use a larger network learned over days and see how retrieval of information changes as it becomes more entrenched.
Our own intuition, however, is not that the distance effects that were absent from Experiments 2 and 3 will appear in entrenched categories. Inference through the hierarchy is what one does when one has not encoded the specific facts well enough to directly retrieve them (Logan, 1988). As marine biologists become more and more familiar with killer whales, we don’t think that they rely on inference to decide whether they breathe air or are animals. Research on visual categorization into familiar categories suggests that people classify objects directly into superordinates like animal or vehicle, rather than using inference up the taxonomy after identifying the object as a sparrow or truck (Mack & Palmeri, 2011; Murphy & Brownell, 1985). Of course, that is not to say that there will be no difference between retrieving newly learned and entrenched information from memory; there well may be. Our guess is that, rather than showing a positive distance effect, the present effects would flatten out with practice, as people get faster and faster at retrieving the information from memory.
Experimental studies using constructed categories are certainly not the only way to study semantic memory. Studies of semantic memory using natural categories should continue, perhaps in combination with experimentally controlled materials (as in Smith et al.’s, 1972 study).
Conclusion
Even taking into account the diversity of ways that hierarchical information might be encoded and retrieved, we did not find that the traditional Quillian hierarchy was the favored method. Instead, it appeared to be used only when other sources of information and retrieval strategies were entirely removed. Therefore, we suspect that in everyday life, such a model of hierarchical concepts is probably not the default way that information is retrieved from semantic memory.
Highlights.
Four experiments examine the classic problem of how semantic memory is structured.
Subjects learned novel hierarchies, eliminating stubborn problems of confounding variables.
Results gave little support for the Collins & Quillian network-inference model.
Results were consistent with feature-based models, including recent connectionist models.
Acknowledgments
We thank Rebecca Bainbridge for her help in collecting and analyzing data and the Concats Lab Meeting for helpful comments.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Recall that subjects with missing cells were excluded from the RT analysis. We included all subjects in the accuracy analysis, since errors are not missing data there. However, the interaction with form was much stronger in the accuracy data, apparently reflecting a number of subjects in Form B who did not learn the taxonomy well or who reversed left and right. Therefore, the RT data probably are a better reflection of memory retrieval by people who successfully learned the categories.
Indeed, a reading of the literature suggests that no account of false items has been generally accepted. Different kinds of false items may be answered in different ways (e.g., “close” items by a search for contradiction, and “distant” items by similarity judgment). In our data, the false items tended to show similar effects as the true items, though often weaker.
Contributor Information
Gregory L. Murphy, New York University
James A. Hampton, City University
Goran S. Milovanovic, University of Belgrade
References
- Anderson JR. Arguments concerning representations for mental imagery. Psychological Review. 1978;85:249–277. [Google Scholar]
- Ashby FG, Alfonso-Reese LA, Turken AU, Waldron EM. A neuropsychological theory of multiple systems in category learning. Psychological Review. 1998;105:442–481. doi: 10.1037/0033-295x.105.3.442. [DOI] [PubMed] [Google Scholar]
- Ashcraft MH, Radvansky GA. Cognition. 5th ed. Boston: Prentice-Hall; 2010. [Google Scholar]
- Chang T. Semantic memory: Facts and models. Psychological Bulletin. 1986;99:199–220. [Google Scholar]
- Close J, Pothos EM. “Object categorization: Reversals and explanations of the basic-level advantage” (Rogers & Patterson, 2007): A simplicity account. Quarterly Journal of Experimental Psychology. doi: 10.1080/17470218.2012.660963. (in press) [DOI] [PubMed] [Google Scholar]
- Collins AM, Loftus EF. A spreading-activation theory of semantic processing. Psychological Review. 1975;82:407–428. [Google Scholar]
- Collins AM, Quillian MR. Retrieval time from semantic memory. Journal of Verbal Learning and Verbal Behavior. 1969;8:241–248. [Google Scholar]
- Gentner D, Collins A. Studies of inference from lack of knowledge. Memory & Cognition. 1981;9:434–443. doi: 10.3758/bf03197569. [DOI] [PubMed] [Google Scholar]
- Hampton JA. Polymorphous concepts in semantic memory. Journal of Verbal Learning and Verbal Behavior. 1979;18:441–461. [Google Scholar]
- Hampton JA. A demonstration of intransitivity in natural categories. Cognition. 1982;12:151–164. doi: 10.1016/0010-0277(82)90010-5. [DOI] [PubMed] [Google Scholar]
- Hampton JA. Associative and similarity-based processes in categorization decisions. Memory & Cognition. 1997;25:625–640. doi: 10.3758/bf03211304. [DOI] [PubMed] [Google Scholar]
- Hampton JA. Similarity-based categorization and fuzziness of natural categories. Cognition. 1998;65:137–165. doi: 10.1016/s0010-0277(97)00042-5. [DOI] [PubMed] [Google Scholar]
- Hampton JA. Concepts in human adults. In: Mareschal D, Quinn P, Lea SEG, editors. The making of human concepts. Oxford: Oxford University Press; 2010. pp. 293–311. [Google Scholar]
- Holyoak KJ, Glass AL. The role of contradictions and counterexamples in the rejection of false sentences. Journal of Verbal Learning and Verbal Behavior. 1975;14:215–239. [Google Scholar]
- Kounios J, Osman AM, Meyer DE. Structure and process in semantic memory: New evidence based on speed–accuracy decomposition. Journal of Experimental Psychology: General. 1987;116:3–25. doi: 10.1037//0096-3445.116.1.3. [DOI] [PubMed] [Google Scholar]
- Linnaeus C. Systema naturae per regna tria naturae, secundum classes, ordines, genera, species, cum characteribus, differentiis, synonymis, locis. 10th ed. Vol. 1. Holmiae: Impensis Direct. Laurentii Salvii; 1758. [Coroli Linnaei] [Google Scholar]
- Lindsay PH, Norman DA. Human information processing: An introduction to psychology. New York: Academic Press; 1972. [Google Scholar]
- Logan GD. Toward an instance theory of automatization. Psychological Review. 1988;95:492–527. [Google Scholar]
- Mack ML, Palmeri TJ. The timing of visual object categorization. Frontiers in Psychology. 2011;2(165) doi: 10.3389/fpsyg.2011.00165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malt BC, Smith EE. The role of familiarity in determining typicality. Memory & Cognition. 1982;10:69–75. doi: 10.3758/bf03197627. [DOI] [PubMed] [Google Scholar]
- Markman EM, Callanan MA. An analysis of hierarchical classification. In: Sternberg R, editor. Advances in the psychology of human intelligence. vol. 2. Hillsdale, NJ: Erlbaum; 1984. pp. 325–365. [Google Scholar]
- McCloskey M. The stimulus familiarity problem in semantic memory research. Journal of Verbal Learning and Verbal Behavior. 1980;19:485–502. [Google Scholar]
- McCloskey M, Glucksberg S. Decision processes in verifying category membership statements: Implications for models of semantic memory. Cognitive Psychology. 1979;11:1–37. [Google Scholar]
- Medin DL, Schaffer MM. Context theory of classification learning. Psychological Review. 1978;85:207–238. [Google Scholar]
- Moss HE, Ostrin RK, Tyler LK, Marslen-Wilson WD. Accessing different types of lexical semantic information: Evidence from priming. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1995;21:863–883. [Google Scholar]
- Murphy GL. The big book of concepts. Cambridge, MA: MIT Press; 2002. [Google Scholar]
- Murphy GL, Brownell HH. Category differentiation in object recognition: Typicality constraints on the basic category advantage. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1985;11:70–84. doi: 10.1037//0278-7393.11.1.70. [DOI] [PubMed] [Google Scholar]
- Murphy GL, Smith EE. Basic level superiority in picture categorization. Journal of Verbal Learning and Verbal Behavior. 1982;21:1–20. [Google Scholar]
- Nosofsky RM, Palmeri TJ, McKinley SC. Rule-plus-exception model of classification learning. Psychological Review. 1994;101:53–79. doi: 10.1037/0033-295x.101.1.53. [DOI] [PubMed] [Google Scholar]
- Quillian MR. Semantic memory. In: Minsky M, editor. Semantic information processing. Cambridge, MA: MIT Press; 1968. pp. 227–270. [Google Scholar]
- Poldrack RA, Clark J, Paré-Blagoev EJ, Shohamy D, Creso Moyano J, Myers C, Gluck MA. Interactive memory systems in the human brain. Nature. 2001;414:546–550. doi: 10.1038/35107080. [DOI] [PubMed] [Google Scholar]
- Rips LJ, Shoben EJ, Smith EE. Semantic distance and the verification of semantic relations. Journal of Verbal Learning and Verbal Behavior. 1973;12:1–20. [Google Scholar]
- Rogers TT, McClelland JL. Semantic cognition: A parallel distributed processing approach. Cambridge, MA: MIT Press; 2004. [DOI] [PubMed] [Google Scholar]
- Rosch EH. On the internal structure of perceptual and semantic categories. In: Moore TE, editor. Cognitive development and the acquisition of language. New York: Academic Press; 1973. pp. 111–144. [Google Scholar]
- Rosch E. Principles of categorization. In: Rosch E, Lloyd BB, editors. Cognition and categorization. Hillsdale, NJ: Erlbaum; 1978. pp. 27–48. [Google Scholar]
- Rosch E, Mervis CB. Family resemblance: Studies in the internal structure of categories. Cognitive Psychology. 1975;7:573–605. [Google Scholar]
- Rosch E, Mervis CB, Gray W, Johnson D, Boyes-Braem P. Basic objects in natural categories. Cognitive Psychology. 1976;8:382–439. [Google Scholar]
- Shafto P, Kemp C, Mansinghka V, Gordon M, Tenenbaum JB. Learning cross-cutting systems of categories. In: Sun R, editor. Proceedings of the 28th Annual Conference of the Cognitive Science Society. Mahwah, NJ: Erlbaum; 2006. pp. 2146–2151. [Google Scholar]
- Smith EE. Theories of semantic memory. In: Estes WK, editor. Handbook of learning and cognitive processes. Vol. 6. Potomac, MD: Erlbaum; 1978. pp. 1–56. [Google Scholar]
- Smith EE, Haviland SE, Buckley PB, Sack M. Retrieval of artificial facts from long-term memory. Journal of Verbal Learning and Verbal Behavior. 1972;11:583–593. [Google Scholar]
- Smith EE, Rips LJ, Shoben EJ. Semantic memory and psychological semantics. In: Bower GH, editor. The psychology of learning and motivation. vol. 8. New York: Academic Press; 1974. pp. 1–45. [Google Scholar]
- Smith JD, Minda JP. Prototypes in the mist: The early epochs of category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1998;24:1411–1436. [Google Scholar]
- Tenenbaum JB. Bayesian modeling of human concept learning. Advances in Neural Information Processing Systems. 1999;11:59–68. [Google Scholar]