A high-performance computing toolset for relatedness and principal component analysis of SNP data

Abstract

Summary: Genome-wide association studies are widely used to investigate the genetic basis of diseases and traits, but they pose many computational challenges. We developed gdsfmt and SNPRelate (R packages for multi-core symmetric multiprocessing computer architectures) to accelerate two key computations on SNP data: principal component analysis (PCA) and relatedness analysis using identity-by-descent measures. The kernels of our algorithms are written in C/C++ and highly optimized. Benchmarks show the uniprocessor implementations of PCA and identity-by-descent are ∼8–50 times faster than the implementations provided in the popular EIGENSTRAT (v3.0) and PLINK (v1.07) programs, respectively, and can be sped up to 30–300-fold by using eight cores. SNPRelate can analyse tens of thousands of samples with millions of SNPs. For example, our package was used to perform PCA on 55 324 subjects from the ‘Gene-Environment Association Studies’ consortium studies.

Availability and implementation: gdsfmt and SNPRelate are available from R CRAN (http://cran.r-project.org), including a vignette. A tutorial can be found at https://www.genevastudy.org/Accomplishments/software.

Contact: zhengx@u.washington.edu

1 INTRODUCTION

Genome-wide association studies (GWAS) are widely used to investigate the genetic basis of many complex diseases and traits, but the large volumes of data generated in chip- and sequencing-based GWAS from thousands of study samples and millions of SNPs pose significant analytical and computational challenges. One important challenge is the inflated false-positive associations that arise in GWAS results when population structure and cryptic relatedness exist (Cardon and Palmer, 2003; Choi et al., 2009). These challenges can be addressed by using principal component analysis (PCA) to detect and correct for population structure (Price et al., 2006) and identity-by-descent (IBD) methods to identify the degree of relatedness between each pair of study samples. For both methods, it is suggested to use a pruned set of SNPs, which are in approximate linkage equilibrium with each other to avoid the strong influence of SNP clusters (Laurie et al., 2010). However, the computational burden associated with these methods is especially evident with large sample and SNP sizes and requires efficient numerical implementation and memory management, especially as chip arrays increase in size and sequencing data is used to call variants. For example, the 1000 Genomes Project identified ∼15 million SNP loci from whole-genome sequencing technologies recently (1000 Genomes Project Consortium, 2010).

R is one of the most popular statistical programming environment, but it is not typically optimized for high performance or parallel computing, which would ease the burden of large-scale SNP-based GWAS calculations. To overcome these limitations, we have initiated a project named CoreArray (http://corearray.sourceforge.net/) that includes two R packages: gdsfmt to provide efficient, platform-independent memory and file management for genome-wide numerical data, and SNPRelate to solve large-scale, numerically intensive GWAS calculations (i.e. PCA and IBD) on multi-core symmetric multiprocessing computer architectures.

2 FEATURES

To support efficient memory management for genome-wide numerical data, gdsfmt provides the genomic data structure (GDS) file format for array-oriented data. In this format, each byte encodes up to four SNP genotypes, thereby reducing file size and access time. During the process of scanning SNP profiles, operations on four genotypes may be performed simultaneously. The GDS format supports data blocking so that only the subset of data that is being processed needs to reside in memory, and it is also designed for efficient random access to large datasets. Although SNPRelate functions operate only on GDS-format data files, functions to reformat data from PLINK, sequencing Variant Call Format, NetCDF and other data files, are provided by our packages (Danecek et al., 2011; Laurie et al., 2010; Purcell et al., 2007).

SNPRelate provides computationally efficient functions for PCA and IBD relatedness analysis on GDS genotype files. The calculations of the genetic covariance matrix and pairwise IBD coefficients are split into non-overlapping parts and assigned to multiple cores for performance acceleration, as shown in Figure 1. The functions in SNPRelate for PCA include the basic calculations of sample and SNP eigenvectors, as well as useful accessory functions. The correlation between sample eigenvectors and observed allelic dosage can be used to evaluate the genome-wide distribution of SNP effects on each eigenvector. The SNP eigenvectors can be used to calculate the sample eigenvectors of a new set of samples, which is useful in studies with substantial relatedness (Zhu et al., 2008).

Fig. 1.

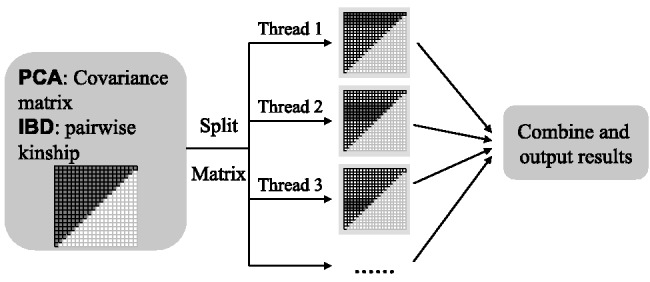
Flowchart of parallel computing for PCA and IBD analysis

For relatedness analysis, IBD estimation in SNPRelate can be done by either the method of moments (MoM) (Purcell et al., 2007) or maximum likelihood estimation (MLE) (Choi et al., 2009; Milligan, 2003) through identity by state. Our experience shows that MLE is significantly more computationally intensive than MoM for large-scale data analysis, although MLE estimates are usually more reliable than MoM. Additionally, the functions for linkage disequilibrium pruning generate a pruned subset of SNPs that are in approximate linkage equilibrium with each other, to avoid the strong influence of SNP clusters in PCA and IBD analysis. An actual kinship matrix of individuals can be estimated by either method, which could be used in downstream association analyses (Price et al., 2010).

Both R packages are written in C/C++, use the POSIX threads library for shared memory parallel computing on Unix-like systems and have an R interface in which the kernel has been highly optimized by blocking the computations to exploit the high-speed cache memory. The algorithms are optimized to load genotypes block by block, with no limit to the number of SNPs. The algorithms are limited only by the size of the main memory, which is accessed by the parallel threads, and holds either the genetic covariance matrix or IBD coefficient matrix.

GDS is also used by an R/Bioconductor package GWASTools as one of its data storage formats (Gogarten et al., 2012). GWASTools provides many functions for quality control and analysis of GWAS, including statistics by SNP or scan, batch quality, chromosome anomalies, association tests, etc.

3 PERFORMANCE

We illustrate the performance of SNPRelate using small, medium and large test datasets. The small and medium sets were constructed from simulated data and contain 500 and 5000 samples with 100 K SNP markers, respectively. The large set consists of 55 324 subjects selected from 16 projects of the ‘Gene-Environment Association Studies’ (GENEVA) consortium (Cornelis et al., 2010). We compared the run times of SNPRelate with EIGENSTRAT (v3.0) and PLINK (v1.07) for PCA and IBD estimation, respectively. The implementations were benchmarked on a system with two quad-core Intel processors running at 2.27 GHz and 32 GB RAM and running Linux Fedora 10.

As shown in Table 1, the uniprocessor implementations of PCA and IBD in SNPRelate are ∼8–50 times faster than the implementations provided in EIGENSTRAT and PLINK, respectively. When the SNPRelate algorithms were run using eight cores, the performance improvement ranged from ∼30 to 300. The SNPRelate PCA was conducted on the large dataset (n = 55 324 subjects with ∼310 K selected SNP markers). It took ∼64 h to compute the genetic covariance matrix (55 K-by-55 K) when eight cores were used, and ∼9 days to calculate eigenvalues and eigenvectors using the uniprocessor version of LAPACK in R. The analyses on the small- and medium-size datasets required <1 GB of memory, and PCA on ∼55 K subjects required ∼32 GB, as the genetic covariance matrix is stored in the main memory shared by threads. An improvement on running time for PCA is to use a multi-threaded version of BLAS to perform the calculation of eigenvalues and eigenvectors instead of the default uniprocessor one. Although SNPRelate is much faster than EIGENSTRAT for PCA or PLINK for IBD estimation using MoM, the results are numerically the same (i.e. identical accuracy).

Table 1.

Comparison of run-times (seconds and minutes) for SNPRelate, EIGENSTRAT and PLINK on a Linux system with two quad-core Intel processors (2.27 GHz) and 32 GB RAM

Number of cores	Small seta			Medium seta
Method	1	4	8	1	4	8
PCA
SNPRelate	11 s+	5 s+	3 s+	20 m+	8 m+	5 m+
	1 sb	1 sb	1 sb	12 mb	12 mb	12 mb
EIGENSTRAT	90 sc	—	—	710 mc	—	—
MoM for IBD analysis
SNPRelate	19 s	6 s	4 s	30 m	8 m	5 m
PLINK	980 s	—	—	1630 m	—	—

^aSimulated 500 (small set) and 5000 (medium set) samples with 100 K SNPs.

^bCalls the uniprocessor version of LAPACK in R to compute the eigenvalues and eigenvectors, taking 1 s and 12 m for the small and medium set, respectively.

^cIncludes the computation time of calculating the eigenvalues and eigenvectors.