Sensitivity analysis for plane orientation in three-dimensional cephalometric analysis based on superimposition of serial cone beam computed tomography images

Abstract

Objectives

The purpose of this study was to evaluate the potential errors associated with superimposition of serial cone beam CT (CBCT) images utilizing reference planes based on cranial base landmarks using a sensitivity analysis.

Methods

CBCT images from 62 patients participating in a maxillary expansion clinical trial were analysed. The left and right auditory external meatus (AEM), dorsum foramen magnum (DFM) and the midpoint between the left and right foramen spinosum (ELSA) were used to define a three-dimensional (3D) anatomical reference co-ordinate system. Intraclass correlation coefficients for all four landmarks were obtained. Transformation of the reference system was carried out using the four landmarks and mathematical comparison of values.

Results

Excellent intrareliability values for each dimension were obtained for each landmark. Evaluation of the method to transform the co-ordinate system was first done by comparing interlandmark distances before and after transformations, giving errors in lengths in the order of 10–14% (software rounding error). A sensitivity evaluation was performed by adding 0.25 mm, 0.5 mm and 1 mm error in one axis of the ELSA. A positioning error of 0.25 mm in the ELSA can produce up to 1.0 mm error in other cranial base landmark co-ordinates. These errors could be magnified to distant landmarks where in some cases menton and infraorbital landmarks were displaced 4–6 mm.

Conclusions

Minor variations in location of the ELSA, both the AEM and the DFM landmarks produce large and potentially clinically significant uncertainty in co-ordinate system alignment.

Introduction

In traditional two-dimensional (2D) cephalometric analyses, superimposition of cranial base structures is a method used to show changes over time associated with orthodontic treatment and growth. Although this method has been widely used, it presents limitations, such as overestimating changes in one direction compared with others depending on which structures it superimposes.^1,2 In traditional imaging, superimposition is performed using the anterior cranial base, which still presents minor variations affecting values of growth and treatment changes.² It has even been concluded that errors associated with this type of superimposition are large enough to have an effect on the interpretation of data.³ Furthermore 2D imaging does not represent the entirety of a three-dimensional (3D) structure. It has been stated that much information is lost when 3D structures are assessed through 2D methodologies.⁴

With the availability of cone beam CT (CBCT), many cephalometry-related limitations have been addressed.⁵ This technology is relatively new in the orthodontic field. Reliable and accurate landmark-based superimposition techniques for evaluating change over time have not been established. The establishment of a precise and reliable instrument or methodology to analyse images produced by 3D imaging would provide clinicians with new possibilities in determining the structural changes produced by growth and orthodontic treatment.^6,7

A possible method to use CBCT images in determining changes after treatment or growth is by superimposing images.^4,8–10 Oliveira et al¹¹ state that this is challenging because of the difficulty of selecting stable areas or structures as registration points or marks that would not change during orthodontic treatment. The reliability of many 3D-determined craniofacial landmarks has been determined,^12,13 but the reliability and accuracy of 3D superimposition of serial CBCT images using cranial base landmarks where change of structures can be obtained in terms of different axis in space (x, y and z) have not been determined.

The purpose of this study is to evaluate potential errors associated with superimposition of serial CBCT images utilizing reference planes based on cranial base landmarks. The potential impact of errors in cranial base landmark identification on assessment of the relative position of distant landmarks will be assessed with a sensitivity analysis based on measurement uncertainty.

Materials and methods

Determining a standardized plane orientation

CBCT volumetric data (NewTom 3G Volumetric Scanner, Aperio, Verona, Italy) taken at 110 kV, 6.19 mAs and 8 mm aluminium filtration from 62 patients participating in a maxillary expansion clinical trial were used for the present analysis. These images were taken using the 12 inch detector field at baseline (T1) before any treatment was carried out on the patient, at 6 months (T2) and at 12 months (T3). Ethics approval was obtained from the Health Research Ethics Board at the University of Alberta.

Images were obtained and converted to Digital Imaging and Communications in Medicine (DICOM) format using NewTom software version 2.04 (Aperio) to a voxel size of 0.25 mm. Using AMIRA software (Mercury Computer Systems, Berlin, Germany), the DICOM format images were rendered into a volumetric image using 512 × 512 matrices giving a range of 400–420 DICOM slices. Sagittal, axial and coronal volumetric slices as well as the 3D image reconstruction were used to determine landmark positions.

Four landmarks were required to define a 3D anatomical reference co-ordinate system. The left and right auditory external meatus (AEM) and the dorsum foramen magnum (DFM) were selected based on the position and early formation in skeletal growth as it has been reported that most cranial base growth (> 85%) occurs by 5 years of age, presenting minor changes after this age.^14–16 The fourth point, ELSA, is defined in a previous publication as the midpoint between the left and right foramen spinosum.¹⁷ ELSA was selected as the origin of the new Cartesian co-ordinate system. From the origin, 3D positional co-ordinates for AEM left (AEML), AEM right (AEMR) and DFM were determined. Intrareliability values were determined using the intraclass correlation coefficient (ICC)^18,19 for all four landmarks, repeating the process three times for each image.

Landmarks used in the present study are defined in Table 1. The principal investigator located the landmarks on each image three times. Spherical markers of 0.5 mm diameter were placed indicating the position of the landmark, and the software used the centre of these spherical markers as co-ordinates. Both AEMR and AEML lie in the xy-plane and thus have a zero z-co-ordinate and DFM lies in the yz-plane and thus has a zero x-co-ordinate.

Table 1. Definition of landmarks.

Foramen spinosum (FS)	Geometric centre of smallest circumference with defined borders viewed in axial view on the foramen spinosum
ELSA	Midpoint between line connecting both foramen spinosum landmarks
Auditory external meatus (AEM)	Point located in the most outer posterior surface of the AEM (where the curvature starts)
Dorsum foramen magnum (DFM)	Point located in the most posterior border of the foramen magnum
Infraorbital (InfraO)	Centre of infraorbital foramen outer border
Mental (Me)	Centre of mental foramen outer border

Co-ordinate transformation procedure

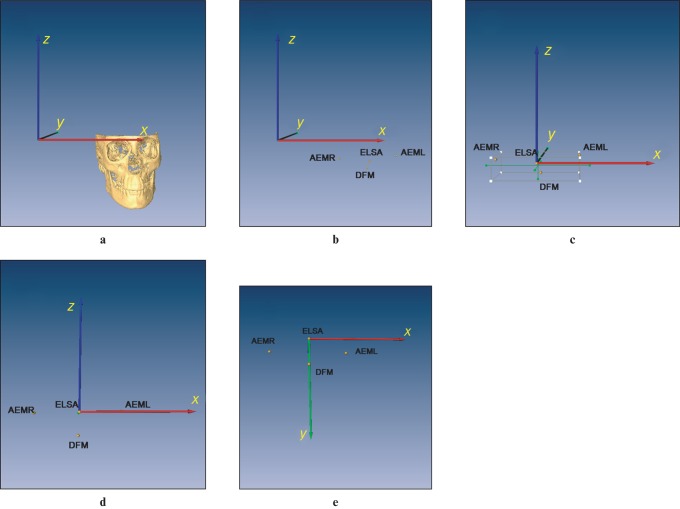
To transform all global landmark co-ordinates to an ELSA co-ordinate system, the vector describing the position of ELSA in the AMIRA co-ordinate system was subtracted from all anatomical landmarks, thus zeroing the co-ordinates about ELSA (Figure 1a–c).

Figure 1.

Co-ordinate system transformation sequence. (a) Three-dimensional reconstruction of the image with predetermined global co-ordinate system of AMIRA software. (b) Location of four landmarks to create new co-ordinate system. (c) Translation of the centre of global co-ordinate system to ELSA. (d) Determination of new xy-plane using ELSA, AEMR and AEML. (e) Determination of new yz-plane using ELSA and DFM. AEM, auditory external meatus; DFM, dorsum foramen magnum; ELSA, midpoint between the left and right foramen spinosum; L, left; R, right

Co-ordinate system transformations were performed in two steps. The co-ordinate system was constructed using two planes defined by anatomical landmarks. The first, which represents a new xy-plane, was defined using both the AEM and the ELSA; all three taken with respect to the ELSA co-ordinate system. The second was defined as a new yz-plane formed by the ELSA and DFM perpendicular to the new xy-plane (Figure 1d,e).

In this set of transformations, left and right AEM co-ordinates had zero z-component as they lie in the x″y″-plane. The second transformation is a rotation of the x″y″-plane defined in the above steps to set the y″z″-plane in which lies the DFM anatomical landmark. After this transformation, the DFM had zero x-component. (A detailed description of the transformation process is given in the Appendix.)

Results

Determination of the standardized reference system

Cartesian co-ordinates for the ELSA, AEMR, AEML and DFM were recorded in a datasheet for 62 subjects, each measured 3 times. Intrareliability values for each dimension were obtained, with the lowest value being 0.965 in the x-axis for AEML.

Once landmarks were located, an axial–horizontal plane (xy-plane) was determined using both AEM points and the ELSA as described in the previous section. Then a sagittal–vertical plane (yz-plane) was determined perpendicular to the axial–horizontal plane and passing through the ELSA and DFM.

Effect of plane orientation method

Evaluation of the method to translate the co-ordinate system was first done by comparing interlandmark distances before- and after-transformation using MathCAD^TM (Parametric Technology, Needham, MA). Lengths were considered to be the same post transformation, giving errors in the order of 10–14% resulting from significant digit calculations. In Table 2, this is reported as a 0.00% difference in length of transformed data without error.

Table 2. Co-ordinates of anatomical positions with and without 0.25 mm imposed offset and original lengths (L1 and L2) at times 1 (T1) and 2 (T2) and length error for each landmark with the respective imposed error (mm).

		T1			T2			Original length		% Error with original length T1
		x	y	z	x	y	z	T1	T2
Original data	ELSA	195.84	142.88	−87.84	201.58	124.59	−85.47
	AEML	252.42	159.31	−82.59	254.72	138.14	−75.61	59.15	55.72
	AEMR	141.82	154.65	−86.68	142.52	137.89	−91.26	55.30	60.82
	DFM	193.97	188.88	−105.73	203.73	171.75	−103.39	49.39	50.50
								With respect to ELSA
Transformed data	ELSA	0.00	0.00	0.00	0.00	0.00	0.00
	AEML	57.58	13.54	0.00	54.10	13.34	0.00	59.15	55.72	0.00
	AEMR	−53.19	15.15	0.00	−59.19	13.99	0.00	55.30	60.82	0.00
	DFM	0.00	41.04	−27.48	0.00	43.22	−26.12	49.39	50.50	0.00
Transformed data with 0.25 mm error added to x-value of ELSA at T1	ELSA	0.00	0.00	0.00	0.00	0.00	0.00
	AEML	57.76	14.52	0.00	54.10	13.34	0.00	59.56	55.72	0.69
	AEMR	−53.01	15.36	0.00	−59.19	13.99	0.00	55.19	60.82	−0.20
	DFM	0.00	41.86	−27.24	0.00	43.22	−26.12	49.94	50.51	1.12

AEM, auditory external meatus; DFM, dorsum foramen magnum; ELSA, midpoint between the left and right foramen spinosum; L, left; R, right

To evaluate the effect of user point selection error during landmark measurements, a sensitivity analysis of the method to measurement uncertainty was performed. AMIRA image resolution is 0.25 mm, which is thus the smallest measurement uncertainty. Imposing this error to the x-co-ordinate of ELSA as seen in Table 2 (from 195.84 mm to 196.09 mm), it was determined that this measurement error led to an error in length measurements for the other three landmarks used ranging from 0.01% to 1.12%. These findings are independent of the co-ordinate transformation.

A final sensitivity evaluation was performed to assess the effect on landmark position measurement errors in the ELSA co-ordinate system. This was done by adding 0.25 mm, 0.5 mm and 1 mm of error to one axis of the ELSA in the AMIRA co-ordinate system. It can be seen in Table 3 that there are position errors in the other three landmarks used for the reference system. A positioning error of 0.25 mm in the ELSA can produce up to 1.0 mm error (AEML y-axis) in other cranial base landmark co-ordinates. This error level increases as the imposed error in ELSA co-ordinate values increases, reaching approximately 1.9 mm (AEMR y-axis) for an imposed error of 1 mm in the x-axis of the ELSA. It was noted that as the imposed error increases, the error in landmark location increases and this increase is not directly proportional. It is also noted that the imposed error can cause non-negligible random errors in different axes.

Table 3. Error in each co-ordinate position caused by 0.25, 0.5 and 1 mm of error imposed on the x-axis of ELSA in T1 (mm).

	T1
Landmarks	x	y	z	x	y	z
No error
ELSA	0.00	0.00	0.00
AEML	57.58	13.54	0.00
AEMR	−53.19	15.15	0.00
DFM	0.00	41.04	−27.48	Error in mm with respect to no error data
0.25 mm error
ELSA	0.00	0.00	0.00
AEML	57.76	14.52	0.00	0.19	0.97	0.00
AEMR	−53.01	15.36	0.00	0.18	0.21	0.00
DFM	0.00	41.86	−27.24	0.00	0.82	0.24
0.5 mm error
ELSA	0.00	0.00	0.00
AEML	57.93	14.85	0.00	0.35	1.31	0.00
AEMR	−52.85	15.03	0.00	0.34	0.12	0.00
DFM	0.00	41.86	−27.22	0.00	0.82	0.26
1 mm error
ELSA	0.00	0.00	0.00
AEML	56.93	12.90	0.00	0.65	0.65	0.00
AEMR	−53.77	17.04	0.00	0.58	1.89	0.00
DFM	0.00	41.89	−27.30	0.00	0.85	0.18

AEM, auditory external meatus; DFM, dorsum foramen magnum; ELSA, midpoint between the left and right foramen spinosum; L, left; R, right

The effect of the transformation of the co-ordinate system was assessed by analysing the CBCT images of all 62 patients taken at baseline (T1), 6 months (T2) and 12 months (T3) measured 3 times each. In Table 4 it can be seen that large discrepancies exist between raw and transformed data mean differences, in some cases varying by approximately 3 mm.

Table 4. Mean difference of raw data and transformed data.

		T1				T2				T3
		Raw data		Transformed data		Raw data		Transformed data		Raw data		Transformed data
Landmarks	Axes	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
FSL	x	0.38	0.35	0.44	0.26	0.46	0.63	0.54	0.39	0.42	0.46	0.59	0.38
	y	0.44	0.40	0.68	0.37	0.49	0.44	0.81	0.50	0.42	0.40	0.78	0.49
	z	0.47	0.43	0.53	0.32	0.58	0.49	0.54	0.33	0.54	0.42	0.53	0.32
FSR	x	0.35	0.25	0.51	0.29	0.42	0.29	0.52	0.32	0.48	0.36	0.58	0.31
	y	0.53	0.61	0.63	0.35	0.48	0.59	0.75	0.57	0.52	0.53	0.73	0.38
	z	0.39	0.39	0.47	0.31	0.40	0.38	0.53	0.26	0.48	0.45	0.52	0.31
ELSA	x	0.46	0.29	0.00	0.00	0.51	0.29	0.00	0.00	0.52	0.32	0.00	0.00
	y	0.53	0.38	0.00	0.00	0.53	0.36	0.00	0.00	0.51	0.38	0.00	0.00
	z	0.46	0.33	0.00	0.00	0.48	0.36	0.00	0.00	0.53	0.30	0.00	0.00
AEML	x	2.14	1.69	2.15	1.62	2.11	2.07	2.20	2.11	2.21	1.62	2.20	1.48
	y	1.15	0.76	1.59	0.99	1.11	0.84	1.61	0.91	1.11	0.69	1.53	0.96
	z	0.61	0.63	0.00	0.00	0.47	0.61	0.00	0.00	0.51	0.44	0.00	0.00
AEMR	x	1.79	1.25	1.75	1.26	1.81	1.67	1.85	1.64	1.52	1.17	1.65	1.18
	y	0.84	0.66	1.28	0.75	0.88	0.81	1.53	1.02	0.87	0.56	1.45	0.76
	z	0.47	0.48	0.00	0.00	0.46	0.51	0.00	0.00	0.43	0.36	0.00	0.00
DFM	x	0.56	0.28	0.00	0.00	0.69	0.42	0.00	0.00	0.62	0.37	0.00	0.00
	y	0.53	0.36	1.59	1.29	0.55	0.35	1.63	1.00	0.63	0.57	1.46	0.92
	z	0.61	0.46	1.86	1.46	0.59	0.46	1.81	1.16	0.63	0.49	1.57	0.93
InfraOL	x	0.59	0.60	1.56	0.90	0.46	0.41	1.70	1.03	0.47	0.36	1.45	1.00
	y	0.58	0.53	1.14	0.82	0.57	0.46	0.96	0.58	0.85	1.31	1.29	1.33
	z	0.40	0.34	3.21	2.22	0.29	0.42	3.19	2.04	0.44	0.66	3.16	1.61
InfraOR	x	0.41	0.29	1.39	0.80	0.38	0.27	1.67	1.01	0.41	0.28	1.53	0.95
	y	0.60	0.46	1.08	0.69	0.68	0.51	1.09	0.71	0.65	0.50	1.04	0.58
	z	0.30	0.31	3.29	2.43	0.41	0.64	3.29	1.99	0.34	0.28	3.06	1.48
MeL	x	0.27	0.25	1.68	0.99	0.30	0.24	1.94	1.06	0.29	0.22	1.72	1.12
	y	0.21	0.28	2.57	2.21	0.24	0.29	2.60	1.87	0.24	0.23	2.29	1.34
	z	0.32	0.21	3.50	2.50	0.37	0.32	3.41	2.27	0.32	0.23	3.21	1.65
MeR	x	0.27	0.18	1.68	0.93	0.22	0.16	1.87	1.16	0.28	0.16	1.70	1.15
	y	0.17	0.23	2.57	2.09	0.16	0.18	2.75	1.84	0.20	0.27	2.40	1.34
	z	0.27	0.19	3.52	2.62	0.25	0.15	3.36	2.24	0.31	0.22	3.17	1.59

AEM, auditory external meatus; DFM, dorsum foramen magnum; ELSA, midpoint between the left and right foramen spinosum; FS, foramen spinosum; Me, mental; InfraO, infraorbital; L, left; R, right

The values from Table 4 were obtained by locating the landmarks 3 times on each image of 62 patients (each patient had images taken at baseline, 6 months and 12 months). These landmarks were located in AMIRA and the raw co-ordinate data of the landmarks (with respect to the AMIRA standard reference system) were obtained. Mean differences from the three trials for each axis of each landmark were obtained and averaged.

The equation used to obtain the raw data is

(1)

where M1, M2 and M3 are each trial's measured image and M is the mean measurement difference. This calculation was carried out for each co-ordinate axis and each image time.

Raw data were later transformed to the standardized ELSA co-ordinate system using the ELSA as reference (0,0,0), the AEM as (x,y,0) and the DFM as (0,y,z). These new values were later used to obtain the mean measurement differences for the three trials, for each axis of each landmark and then averaged. The same calculations as Equation (1) were performed.

The next step was to find the differences between time points in the transformed data. Since the points measured (infraorbital left and right, and menton left and right) were expected to maintain stability or vary mildly between the time of measurements (6 months and 1 year), it was expected that these points would not present big differences. Table 5 presents the average mean differences obtained in the differences found among the three measurement trial transformations and it can be noted that the values obtained presented excessive standard deviations as well as minimum and maximum values, amounting to as much as 25 mm in some cases.

Table 5. Average of differences among time points of transformed data.

		T2–T1				T3–T1				T3–T2
Landmarks	Axes	Mean	SD	Min.	Max.	Mean	SD	Min.	Max.	Mean	SD	Min.	Max.
FSL	x	0.14	0.41	−0.68	0.96	0.17	0.65	−1.40	2.35	0.02	0.59	−1.69	2.32
	y	0.20	0.58	−1.27	1.33	0.07	0.77	−2.07	2.08	−0.13	0.84	−2.28	2.07
	z	−0.02	0.51	−1.09	1.06	0.01	0.49	−1.06	1.59	0.03	0.59	−1.13	1.77
FSR	x	−0.11	0.54	−1.47	1.23	−0.18	0.62	−2.19	0.93	−0.07	0.58	−1.36	1.31
	y	−0.15	0.63	−1.33	1.31	−0.07	0.70	−1.61	1.66	0.08	0.63	−1.41	1.63
	z	−0.17	0.53	−1.79	0.94	−0.04	0.58	−1.97	0.97	0.13	0.64	−2.11	1.47
ELSA	x	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	y	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	z	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
AEML	x	0.32	2.00	−5.16	5.78	0.61	1.91	−3.24	6.14	0.30	1.92	−4.71	5.96
	y	0.27	1.24	−1.91	4.43	0.32	1.50	−2.92	3.84	0.04	1.78	−6.14	3.94
	z	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
AEMR	x	0.18	1.71	−4.76	4.02	0.02	1.62	−4.65	4.47	−0.16	1.72	−5.16	5.22
	y	−0.17	1.40	−3.36	3.17	−0.08	1.80	−6.58	2.93	0.08	1.42	−3.23	3.38
	z	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
DFM	x	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	y	0.85	1.99	−1.79	10.33	0.48	2.13	−4.76	5.43	−0.36	1.99	−6.67	3.42
	z	0.98	1.85	−3.06	5.08	0.51	2.25	−4.74	6.68	−0.48	2.22	−7.27	4.65
InfraOL	x	0.85	1.86	−3.49	5.60	0.69	2.03	−4.15	5.68	−0.17	1.79	−4.83	2.95
	y	−0.31	1.28	−3.01	2.46	−0.69	1.73	−8.07	2.89	−0.39	1.90	−10.18	2.77
	z	−1.84	3.33	−8.58	5.05	−1.14	4.14	−9.45	9.62	0.70	3.86	−9.34	13.99
InfraOR	x	−0.26	1.69	−4.61	3.96	−0.33	1.82	−4.68	3.56	−0.07	1.66	−3.20	3.68
	y	−0.76	1.19	−3.55	3.29	−0.65	1.22	−3.07	2.74	0.10	1.09	−1.85	4.32
	z	−2.00	3.33	−9.20	4.98	−1.23	4.17	−11.33	8.77	0.77	4.17	−10.78	14.05
MeL	x	0.77	1.88	−3.19	4.71	0.60	1.90	−3.62	5.49	−0.18	1.91	−4.70	4.04
	y	1.13	3.07	−5.09	10.49	−0.10	3.55	−8.99	7.96	−1.23	3.46	−12.14	7.64
	z	−2.95	3.48	−10.93	4.44	−2.39	4.45	−12.46	13.03	0.56	4.51	−10.36	17.18
MeR	x	0.65	1.94	−3.27	5.78	0.33	1.89	−3.69	5.84	−0.32	1.79	−4.35	3.81
	y	0.75	3.08	−4.90	10.17	−0.25	3.50	−9.21	7.53	−1.00	3.34	−12.88	7.09
	z	−3.12	3.60	−12.25	5.06	−2.56	4.61	−12.98	13.15	0.56	4.75	−10.74	17.05

AEM, auditory external meatus; DFM, dorsum foramen magnum; ELSA, midpoint between the left and right foramen spinosum; FS, foramen spinosum; Me, mental; InfraO, infraorbital; L, left; R, right

The values shown in Table 5 were obtained by taking the image co-ordinates at baseline, 6 months and 12 months of 62 patients and performing the transformation. Differences among time points for each series of images were calculated and averaged, as follows:

(2)

where a, b and c refer to the measurement trial. This was done for each axis co-ordinate.

Discussion

CBCT 3D imaging is a new type of auxiliary examination recently applied in orthodontics; however, no validated method of describing change over time exists. The establishment of a simple, precise and reliable instrument to analyse changes within an individual over time is needed for assessment of growth and treatment outcomes. It has been demonstrated that cranial base landmarks can be identified from CBCT with very good reliability. These landmarks are located in anatomically stable structures that should not be subject to growth^14–16 or treatment effects as by age 5 > 85% of growth is completed in this area.¹⁵ Furthermore, landmarks are available in different planes of space and therefore provide potential for a 3D landmark-based superimposition technique.

For the present analysis, ELSA was chosen as the origin to the co-ordinate system. It is constructed as the midpoint between the left and right foramen spinosum.¹⁷ To establish 3D reference planes three additional non-planar reliable cranial base landmarks are required. Left and right superior–lateral borders of the AEM and the DFM were chosen as they are anatomical structures located in the cranial base area and in relative correct positions for determining orientation of planes. The reference plane system eliminates the effect of head positioning during image acquisition.

The ELSA, both AEM and the DFM are used to form the xy-plane and zy-plane. It should be noted that for the xy-plane both AEM are used and intrareliability for the y- and z-axis is expected to be greater than that of the x-axis as the AEM is located in a cylinder-type structure and determining the x-axis location can present some difficulty as it lies along the cylinder long axis. In the case of the zy-plane, DFM is used and all co-ordinates were expected to have excellent intrareliability.

As viewed in the results, landmarks forming the standardized reference system all present excellent intrareliability in all axes. To verify if there were any discrepancies between length measures between raw data and transformed data, lengths were determined with respect to the centre of the reference system (ELSA) to the other three points forming the co-ordinate system. It was found that values were almost identical. When integrating a 0.25 mm error into one of the axes of the ELSA, the lengths did present changes of about 1% to the DFM, which is the farthest point from the ELSA. This 1% was 0.6 mm of difference between the original data and the transformed data; thus we could interpret that, for a distance of approximately 40 mm, marker uncertainty could cause an error margin of ± 0.6 mm. This effect is amplified further away from the origin. This should be viewed with caution because as a 0.25 mm error is integrated into one axis of a landmark, there can be other errors in another axis and even in other landmarks which can increase or cancel the error.

When analysing values obtained in co-ordinates when errors were intentionally introduced in one axis of the ELSA, differences were found in the co-ordinates of the other three landmarks with respect to the ELSA. By adding a 0.25 mm error in the x-axis of the ELSA, one landmark (AEML) presented a 1 mm difference from the original value in the y-axis. When incorporating an error of 1 mm to the x-axis in the ELSA, the AEMR presented a 1.9 mm error in the y-axis. These values can be considered large depending on the area of analysis. For example, if these differences were present on the teeth, since movements of teeth are small in value, this could cause misinterpretations. This shows that even if all these points present excellent intraexaminer reliability, a difference in the order of 0.25 mm, which is the accuracy of the images, can lead to displacement errors when determining the standardization of a reference system. It should also be noted that each individual landmark will have landmark measurement uncertainty and potential error in each co-ordinate. Errors may be cumulative or cancel out or be amplified at landmarks further away from the origin, leading to uncertainty about this method.

To determine if the transformations potentially produce clinically relevant superimposition error, four reference points located a maximum distance from the cranial base reference system were analysed. The left and right infraorbital foramina were chosen to represent the maxilla and the left and right mental foramina were chosen to represent the mandible. The nerve foramen location should be minimally affected by growth and dental treatment.

Repeated application of the transformation process resulted in large deviations (2–3 mm in some axis) in infraorbital and mental nerve foramen locations when compared with the raw data mean differences, as seen in Table 4. When landmark locations were averaged over three repeated transformations in an attempt to minimize repeated measurement errors, differences between raw and transformed data were still high.

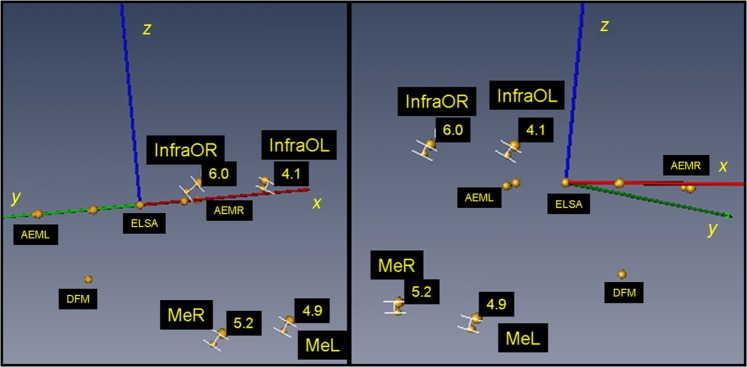
When the potential envelope of error for the reference plane system produced by the compounding error of the landmarks defining the reference points was applied using mathematical transformation, the error in locating distant landmarks was as high as 25 mm (e.g. Menton Right (MeR) z-axis minimum −10.74 mm; maximum 17.05 mm). An example of the potential discrepancy is shown in Figure 2, where two images (baseline and 6 months) of a non-treated patient were superimposed using the standardized reference system and viewing the displacements of both the infraorbital and the mental landmarks. The four points (ELSA, AEML, AEMR and DFM) used for the reference system were nearly overlapping (largest difference of 0.7 mm in the x-axis for AEMR). The potential displacement for the co-ordinates of these four landmarks ranged from 4 mm to 6 mm. The change in linear distance from the ELSA to the same landmarks varied from 1.4 mm to 2.3 mm, which could be considered to change because of growth of the individual.

Figure 2.

Superimposition of T1 and T2 of a non-treated patient on the standardized reference system. It can be seen that infraorbital and mental landmarks are displaced by 4.1–6.0 mm. AEM, auditory external meatus; DFM, dorsum foramen magnum; ELSA, midpoint between the left and right foramen spinosum; Me, mental; InfraO, infraorbital; L, left; R, right

This sensitivity analysis clearly demonstrated that 3D superimposition of serial CBCT images using four cranial base landmarks is not an appropriate approach. Although individual cranial base reference points had an excellent level of reliability, the small envelope of error for the individual landmarks had a compound effect in establishing the 3D superimposition reference planes. A potential alternative technique for CBCT image superimposition is best-fit analysis of multiple cranial base landmarks and computer-aided superimposition based on best fit of object shapes in the cranial base.²⁰ An optimization analysis is another alternative to use when trying to determine a standard reference system based on specific landmarks. Future research is needed to critically evaluate the errors associated with these alternative techniques.

In conclusion the ELSA, both AEM and the DFM points present excellent intrareliability when located on 3D images. Minor variations in location of these landmarks produce unacceptable uncertainty in co-ordinate system alignment. The potential error associated with location of distant landmarks is unacceptable for analysis of growth and treatment changes.

Appendix

Co-ordinate transformation procedure

The following section describes the procedure used to transform anatomical landmark positions for repeated images of individual patients into a single co-ordinate system.

A step-by-step procedure is outlined. Many of the steps could be done simultaneously; however, for clarity, a full breakdown of the process is provided. To transform all global landmark co-ordinates to an ELSA co-ordinate system, the vector describing the position of the ELSA in the AMIRA co-ordinate system must be subtracted from all anatomical landmarks. If there are n anatomical landmarks, the co-ordinate translation can be described as

(1)

where subscript i refers to the AMIRA co-ordinate system and i′ refers to the ELSA co-ordinate system. 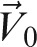is the co-ordinate vector of point ELSA in the AMIRA co-ordinate system.

Co-ordinate system transformations were performed in two steps. The co-ordinate system was constructed using two planes defined by anatomical landmarks. The first, which represents a new x″y″-plane, was defined using both AEM and ELSA, all three taken with respect to the ELSA co-ordinate system.

Vectors from the ELSA to AEML and AEMR were defined for simplicity sake as V_aeml and V_aemr, respectively. Their unit directional vectors are defined as V_aemlu and V_aemru, and are found by dividing the vector by its magnitude such that:

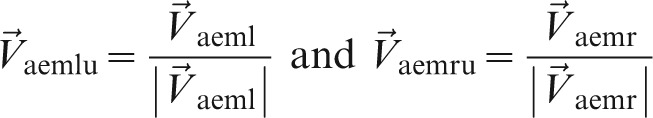(2)

The cross-product of both vectors is used to define a vector perpendicular to the plane defined by the two vectors. It was desirable to define a vector that would be principally orientated in the original z-direction; therefore based on their anatomical position, the following cross-product was performed to define a new z-axis, z′, with unit directional vector, 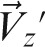, as

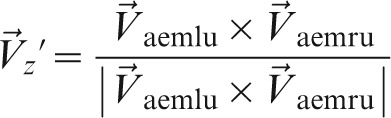(3)

An intermediate x-axis, x′, with unit directional vector, 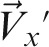, was defined using vector V_aemlu such that

(4)

An intermediate y-axis, y′, with unit directional vector, , was defined using the cross-product of the unit directional vector of z′ and x′, such that

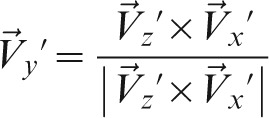(5)

The first transformation matrix was defined as

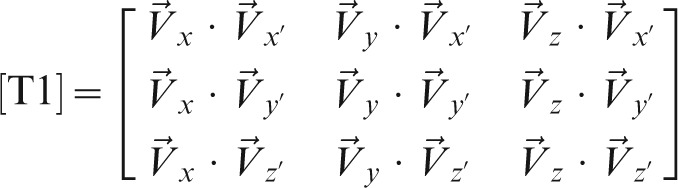(6)

where 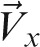, , 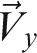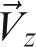are the unit directional vectors of the original global (AMIRA) co-ordinate system, defined as

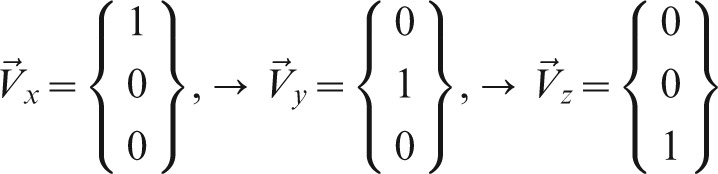(7)

The dot product of the vectors is performed in the transformation matrix of Equation (6) defining directional cosines of each component of the transformation.

New vectors for AEM left and right, as well as the DFM, defined using superscript (double prime), are found as

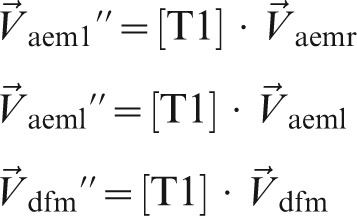(8)

In this first set of transformations, left and right AEM co-ordinates will have zero z-component as they lie in the x″y″-plane.

The second transformation is a rotation of the x″y″-plane defined in the above steps to set the y″z″-plane in which lies the DFM anatomical landmark. After this transformation, the DFM will have zero x-component. This is a simple 2D transformation, defined as

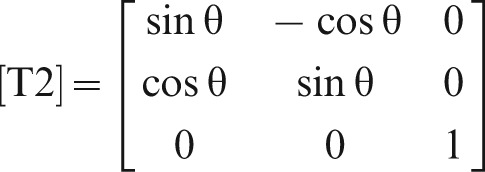(9)

where the angle θ is defined using the co-ordinates of the DFM

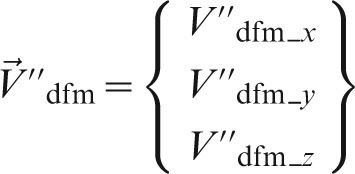(10)

where the subscripts x, y, z indicate the axis co-ordinate, and

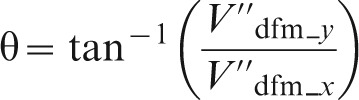(11)

New vectors for the AEM left and right, as well as the DFM, defined using superscript 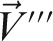(triple prime), are found as

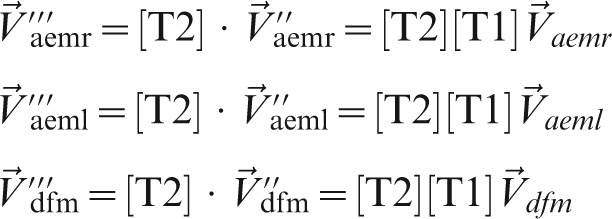(12)

This set of transformations can be applied to any anatomical co-ordinate, such that

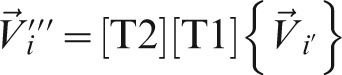(13)

where i is any of the n anatomical landmarks. For the following sections, the Cartesian co-ordinate system defined by the x″y″z″-axes is referred to as the standardized xyz ELSA co-ordinate system.