Uphill Sodium Transport Driven by an Inward Calcium Gradient in Heart Muscle

Abstract

Heart cells were loaded with sodium by treatment with toxic doses of acetyl strophanthidin. After this treatment, an increase in extracellular calcium resulted in a transient net outward sodium flux against its electrochemical gradient and in net cellular uptake of calcium. It is concluded that the free energy for the net outward sodium movement was derived from the increased calcium gradient and that these ion movements took place through the sodium-calcium exchange. While in the normal physiological state the sodium-calcium exchange produces calcium extrusion from the cell, these experiments demonstrate its reversibility.

There exists, in a variety of cells, a coupled exchange of sodium for calcium (1). This exchange is thought to provide a mechanism for the outward transport of calcium that enters cardiac cells by electrodiffusion (2). Moreover, the immediate energy source for this calcium transport is thought to be the large electrochemical gradient for sodium. It is conceivable that sodium-calcium exchange can reverse its direction and transport sodium out of the cell (against its electrochemical gradient) at the expense of free energy contained in the calcium gradient (3, 4). The exchange may be represented by a single hypothetical electrochemical transport reaction

$$n{\text{Na}}_{\text{i}}^{+}+1{\text{Ca}}_{\text{o}}^{2+}\stackrel{\text{membrane}}{\rightleftharpoons }n{\text{Na}}_{\text{o}}^{+}+1{\text{Ca}}_{\text{o}}^{2+}$$

where n is the stoichiometric coefficient and the subscripts i and o respectively refer to the cell interior and exterior. At equilibrium there is no net ion movement through the exchange and

$$n\mathrm{\Delta }{\stackrel{\sim }{\mu }}_{\text{i}-\text{o}}^{\text{Na}}=\mathrm{\Delta }{\stackrel{\sim }{\mu }}_{\text{i}-\text{o}}^{\text{Ca}}$$

where in each phase the electrochemical potential μ̃^j = μ^j + ZFψ (5); μ^jis the chemical potential of species j; Z, F, and ψ are the valence of j, the faraday, and the electric potential, respectively; and Δμ̃_i-o is the electrochemical potential difference between the cell interior and exterior, that is, $\mathrm{\Delta }{\stackrel{\sim }{\mu }}_{\text{i}-\text{o}}^j={\stackrel{\sim }{\mu }}_{\text{i}}^j-{\stackrel{\sim }{\mu }}_{\text{o}}^j$. With complete inhibition of the sodium pump, increasing Ca_o so that $\mathrm{\Delta }{\stackrel{\sim }{\mu }}_{\text{i}-\text{o}}^{\text{Ca}}$ exceeds $n\mathrm{\Delta }{\stackrel{\sim }{\mu }}_{\text{i}-\text{o}}^{\text{Na}}$ should produce net movement of sodium out of a cell against its own gradient and simultaneous entry of calcium down its gradient through the exchange. As this occurs, differences between $\mathrm{\Delta }{\stackrel{\sim }{\mu }}_{\text{i}-\text{o}}^{\text{Ca}}$ and $n\mathrm{\Delta }{\stackrel{\sim }{\mu }}_{\text{i}-\text{o}}^{\text{Na}}$ will tend to dissipate and movement of ions through the exchange will cease as a new equilibrium is approached. According to this hypothesis the driving force for ion movement through the exchange is measured by the difference $n\mathrm{\Delta }{\stackrel{\sim }{\mu }}_{\text{i}-\text{o}}^{\text{Na}}-\mathrm{\Delta }{\stackrel{\sim }{\mu }}_{\text{i}-\text{o}}^{\text{Ca}}$.

In this report we demonstrate that in heart cells inhibition of the sodium pump leads, as expected, to accumulation of sodium, which can be transiently reversed (against its electrochemical gradient) by significantly increasing external calcium. We use these observations to obtain preliminary estimates of n.

We first measured apparent intracellular sodium and potassium contents in rabbit ventricular myocardium. Rabbit hearts were rapidly excised from heparinized New Zealand White rabbits (3 to 5 kg) that had been anesthesized with sodium pentobarbital (50 mg/kg). The hearts were perfused at room temperature (20° to 23°C) in retrograde fashion through the aorta at approximately 1.5 ml g⁻¹ min⁻¹ with a modified Tyrode solution consisting of 118 mM NaCl, 5 mM KCl, 1 mM KCoEDTA, 1.0 mM MgCl₂, 0.4 mM NaH₂PO₄·H₂O, 24.0 mM NaHCO₃, and 1.5 mM CaCl₂. After 1 hour of perfusion the hearts were cut down; the ventricles were cut into three parts, dried for 24 hours at 100°C in platinum crucibles, and reweighed. From the difference in blotted and dried weight the water content was obtained. The pieces of dried ventricular tissue were ashed at 520°C for 24 hours and the ash dissolved in 0.1N HCl. The volume was made up to 10 ml and sodium, potassium, cobalt, and calcium in the samples were measured by conventional atomic absorption spectrophotometry (Perkin-Elmer model 360). Apparent extracellular water was calculated from the distribution of CoEDTA (6). Apparent intracellular sodium, potassium, and calcium content was calculated by deducting the apparent extracellular ion content from the total ion content. The ion contents of each heart were obtained by summing the contents in each tissue slice. Measurements on a particular slice were rejected if they were more than 2 standard deviations outside the mean for the whole heart. The apparent intracellular sodium content was 15.1 ± 3.4 mmole per kilogram of cell H₂O [mean ± standard error (S.E.); N = 3 hearts] and the potassium content was 132.5 ± 4.8 mmole/kg (N = 3).

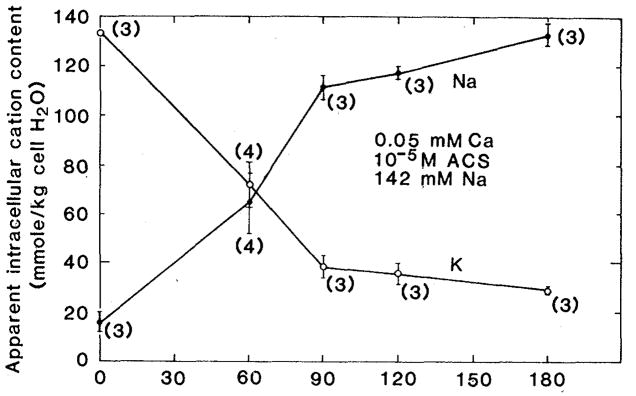
We next perfused rabbit hearts that had been equilibrated for 1 hour in standard Tyrode solution with a modified Tyrode solution in which the calcium concentration was reduced from a nominal value of 1.5 × 10⁻³M to 5 × 10⁻⁵M and to which acetyl strophanthidin (ACS) had been added at a concentration of 10⁻⁵M, sufficient to block the sodium pump. Figure 1 shows the resulting time course of intracellular sodium accumulation and potassium loss. During these ion content changes the sum (sodium content plus potassium content) remains approximately constant, as does the apparent intracellular H₂O.

Fig. 1.

Effect of 10⁻⁵M ACS on cation content in Langendorf perfused ventricular myocardium. The modified Tyrode perfusate contained 0.05 mM calcium. (●) Apparent intracellular sodium content; (○) apparent intracellular potassium content. Each point is represented by the mean ± standard error. The number of hearts contributing to each point is shown in parentheses.

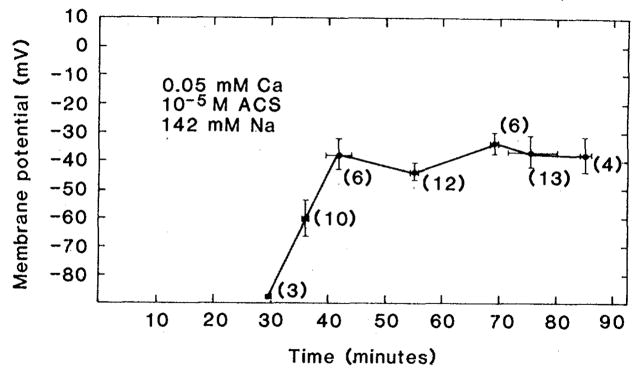
The time course of membrane potential change was measured with glass micropipettes filled with 3M KCl and with a resistance of 5 to 20 megohms. Multiple stable impalements were obtained from the surface of perfused ventricles during 90 minutes of exposure to 10⁻⁵M calcium. The results of this experiment are shown in Fig. 2. There is a progressive tendency for the cells to depolarize to values that lie between −30 and −40 mV. No impalements showed potentials positive to −10 mV. Thus sodium accumulation during 90 minutes of ACS application is in the direction of dissipation of the inwardly directed electrochemical gradient for sodium.

Fig. 2.

Effect of 10⁻⁵M ACS on membrane potential in Langendorf hearts treated in the manner described in the legend of Fig. 1. Each point represents the mean ± standard error of the number of impalements shown in parentheses. For the first 25 minutes it was not possible to obtain stable recordings because of excessive movement of the preparation.

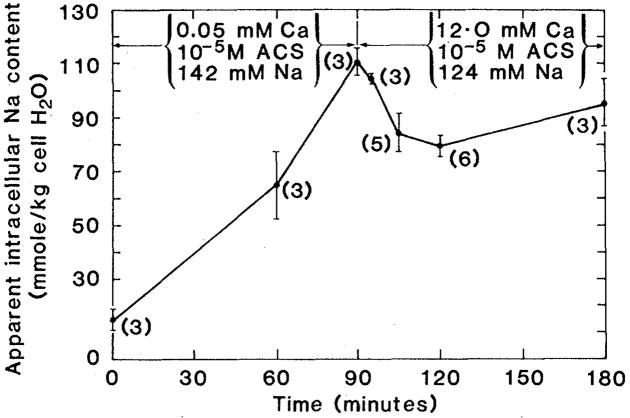
After 90 minutes of exposure to 10⁻⁵M ACS and 5 × 10⁻⁵M calcium, the external calcium concentration was increased to 12.0 mM. In order to retain osmotic balance, the sodium concentration was reduced from 142 to 124 mM. At this time the apparent intracellular sodium content was 111.2 ± 4.2 mmole/kg (N = 3) and the membrane potential was always negative. Since the intracellular sodium activity coefficient is unlikely to exceed the extracellular one, we may safely conclude that at the time of high calcium intervention the electrochemical sodium gradient was still inwardly directed. Within 5 minutes (Fig. 3) intracellular sodium content fell to 104.7 ± 1.5 mmole/kg (mean ± S.E.; N = 3) and within 15 minutes to 84.1 ± 7.0 mmole/kg (N = 5). This transient loss of sodium was highly significant (P ≤ 0.05) with slow reaccumulation of sodium beginning 30 minutes after high calcium intervention.

Fig. 3.

Effect on sodium content of increasing external calcium from 0.05 to 12.0 mM in ACS-intoxicated ventricular myocardium. Each point represents the mean ± standard error of the number of hearts shown in parentheses.

Apparent intracellular calcium increased after high calcium intervention. After 5 minutes it was 6.16 ± 0.56 mmole/kg (mean ± S.E.; N = 3) and after 15 minutes 13.08 ± 2.2 mmole/kg (N = 4). This represents a significant (P ≤ 0.05) accumulation (6.9 mmole/kg) of intracellular calcium between 5 and 15 minutes. Since extracellular calcium is unlikely to change after the first 5 minutes, the change in apparent intracellular calcium content should represent the true intracellular accumulation of calcium. During the same 10-minute period there was a sodium loss of 20.6 mmole/kg. The ratio of this sodium loss to the calcium accumulation is 3.0. Given that independent passive fluxes are not significant, sodium extrusion through sodium-calcium exchange driven by the calcium gradient would have a stoichiometric coefficient of 3.0. This is in agreement with the ratio estimated with a sarcolemmal vesicle preparation by Pitts (7). Any simultaneous inward electrodiffusive movement of both sodium and calcium must lead to underestimation of the stoichiometric coefficient for the sodium-calcium exchange; our value of 3.0 must therefore be a minimum.

The net loss of sodium can be attributed wholly to sodium-calcium exchange only if there is no transport through Na⁺ + K⁺–stimulated adenosinetriphosphatase. After the hearts were treated for 90 minutes with 10⁻⁵M ACS and 5 × 10⁻⁵ M calcium, the potassium content was 38.4 ± 3.6 mmole/kg (mean ± S.E.; N = 3). Fifteen minutes after the high calcium intervention the intracellular potassium content was 52.2 ± 5.9 mmole/kg (N = 6). This accumulation of intracellular potassium was not statistically significant (Student’s t-test; P ≤ 0.05). However, a small but real gain in potassium upon high calcium intervention would, owing to the relatively few inherently scattered determinations, be expected to remain statistically insignificant. Stimulation of either sodium-potassium exchange or an electrogenic sodium-calcium exchange and attendant membrane polarization sufficient to produce an inward electrochemical gradient for K⁺ would lead to net K⁺ accumulation. We therefore propose that the observed potassium accumulation is real. Sodium-potassium exchange is unlikely to be the source of this accumulation because the entire experiment was conducted in the presence of high levels of ACS. Moreover, there is no precedent for the view that calcium is capable of reactivating the sodium-potassium exchange. Increased inhibition of Na⁺ + K⁺–adenosinetriphosphatase due to high Ca_i has been reported (8) and may be expected in this preparation owing to the measured calcium accumulation accompanying the sodium loss. Although we were not able to measure E_m during the contracture that developed in high Ca_o, we believe that the potassium accumulation resulted from membrane polarization. In the absence of sodium-potassium exchange, the most likely source of this polarization is stimulated electrogenic sodium-calcium exchange.

We conclude that the step increase in the calcium gradient at 90 minutes was the source of free energy for the observed sodium transport. Since it does not seem possible that an increase in external calcium could make the membrane potential so positive that net outward electrodiffusion of sodium would occur, we consider that the sodium extrusion is coupled to calcium influx through the sodium-calcium exchange system. Because it appears that at least three Na⁺ must exchange for each Ca²⁺, Na⁺ extrusion should be accompanied by increased membrane polarization.

Since a diffusional barrier may have limited efflux rates and our observations were not made at very short intervals, we cannot calculate the initial rate of exchange. However, the parameter 3Δμ̃_Na − Δμ̃_Ca, which varies during an action potential, governs the direction of the sodium-calcium exchange. Thus the exchanger may make some contribution to the shape of the cardiac action potential if the stoichiometry is anything other than two Na⁺ to one Ca²⁺. Current contributions during cardiac action potentials by the exchangers, as proposed for the sodium-calcium exchange by Mullins (4) and for the Na/K exchange by Chapman et al. (9), should be considered.