Using the time-to-event continual reassessment method in the presence of partial orders

Abstract

The time-to-event continual reassessment method (TITE-CRM) was proposed to handle the problem of long trial duration in Phase 1 trials as a result of late-onset toxicities. Here, we implement the TITE-CRM in dose–finding trials of combinations of agents. When studying multiple agents, monotonicity of the dose-toxicity curve is not clearly defined. Therefore, the toxicity probabilities follow a partial order, meaning that there are pairs of treatments for which the ordering of the toxicity probabilities is not known at the start of the trial. A CRM design for partially ordered trials (PO-CRM) was recently proposed. Simulation studies show that extending the TITE-CRM to the partial order setting produces results similar to those of the PO-CRM in terms of maximum tolerated dose recommendation yet reduces the duration of the trial.

1. Introduction

The continual reassessment method (CRM), introduced by O'Quigley, Pepe, and Fisher [1], is a design with which to carry out and analyze dose-finding studies in oncology. One purpose of these trials is to estimate the maximum tolerated dose (MTD), which is defined as the highest dose that can be administered with a `tolerable' level of toxicity. This `tolerable' level is based upon the probability that a patient in the trial experiences a dose-limiting toxicity (DLT), which is typically defined by side effects that are considered severe and, in certain cases, potentially life threatening. The CRM is based on the use of a simple working model and sequential updating of the dose-toxicity relationship to estimate the dose level at which to treat the next available patient. Suppose we have a discrete set of available doses, d₁, …, d_k. The usual CRM begins by assuming a simplified working dose-toxicity curve,ψ(d_i, a), that is monotonic in both dose level, d_i, and the parameter, a, for instance, the power model or logistic curve. After having included j subjects, an estimate, ${\widehat{a}}_j$, for the parameter a can be generated through a Bayesian framework or maximum likelihood estimation. Once ${\widehat{a}}_j$ is calculated, the dose given to the (j + 1)th patient is the level, d_i, that minimizes some measure of distance, such as Euclidean distance, between ψ(d_i, ${\widehat{a}}_j$) and the target probability of DLT, θ The procedure continues until some predetermined sample size of n patients is exhausted or a stopping rule takes effect.

The CRM does not incorporate censored subjects; that is, subjects without toxicity who have not reached the end of their observation period do not contribute to estimation of the MTD until they are fully observed. In the presence of partially observed subjects, it has been suggested that the newest subject be enrolled on the current estimate of the MTD rather than delaying enrollment. This allocation scheme is flawed in that it disregards the partial information accumulated on censored subjects. Thus, completed trials can be considerably long in duration. For instance, suppose a DLT is being defined by a patient experiencing a grade 3 or higher toxicity in the first month of the patient being enrolled in a study. It is possible that patients could experience a grade 3 or grade 4 toxic response beyond the first month and thus not be considered dose-limiting because toxicity occurred outside of the observation period. If the duration of observation had been longer than 1 month, these observed toxicities would have impacted dose escalation throughout the trial.

Cheung and Chappell [2] introduced the time-to-event CRM (TITE-CRM) in an attempt to utilize information from partially observed subjects throughout the trial. In the absence of toxic response, this extension of the CRM weights each entered patient by the proportion of the full observation period that he or she has been observed. Therefore, a patient that has experienced a DLT provides complete information and is fully weighted. Suppose that the binary indicator Y_j takes value 1 in the case of a DLT for the j th entered subject and 0 otherwise. The dose for the j th entered subject X_j, j = 1, …, n can be thought of as random, taking values x_j = {d₁, …, d_k}. The TITE-CRM considers a weighted dose-response model ϕ(d_i, w, a) that is monotone, increasing in w with marginal constraints ϕ(d_i, 0, a) = 0 and ϕ(d_i; 1; a) = ψ(d_i, 1, a) for all d_i and for all d_i and a. The weight, w, is a function of the time-to-event of each patient and has a linear association with the dose-toxicity model ψ so that ϕ(d,w,a) = wψ(d,a),for 0 ≤ w ≤ 1. Using this model, after the inclusion of j patients into the study, we have data in the form Ωj = {x₁, y₁, w₁, …, x_j, y_j, w_j}. A weighted likelihood

$$\tilde{L}(a\mid {\Omega }_j)=\prod _{\ell =1}^j{\varphi }^{y_{\ell }}(x_{\ell },w_{\ell },a){\{1-\varphi (x_{\ell },w_{\ell },a)\}}^{(1-y_{\ell })}$$

is used to generate an estimate, ${\widehat{a}}_j$ on the basis of the posterior mean of a, whereby the dose given to the next enrolled patient is based on the minimization of

$$\Delta \left(\psi (d_i,{\widehat{a}}_j),\theta \right)=\mid \psi (d_i,{\widehat{a}}_j)-\theta \mid ,i=1,\dots ,k.$$ (1)

When a new patient is to be enrolled, the TITE-CRM allows for the toxicity information of patients to contribute to dose recommendation before they have been fully followed.

The weight function represents the amount of information available from a patient when a new patient is to be enrolled in the study. Suppose that each patient is followed up to a fixed time T and that U_j is the time-to-toxicity of patient j . Then, for u ≤ T,

$$\mathrm{Pr}(U_j\le u)=\mathrm{Pr}(U_j\le u\mid U_j\le T)\mathrm{Pr}(U_j\le T)$$ (2)

$$\equiv w(u;T)\psi (d_i,a).$$ (3)

The weight w can be thought of as the conditional distribution at time u, and the dose-response curve ψ can be identified with the distribution function of U_j at time T . Cheung and Chappell [2] utilize the simple linear weight function

$$w(u;T)=\frac{u}{T}.$$ (4)

and show that the TITE-CRM is consistent under conditions that do not depend on the time-to-toxicity distribution. Further, it assumed that the number of incomplete observations is small when compared with the number, j, of enrolled patients. Simulation results point towards the adequacy of a linear weight function in many cases.

Cheung and Chappell [2] also mention adaptive weights that are a functional form of the weight function determined by the accrued observations such as

$$w(u;T)=\frac{k}{z+1}+\frac{1}{z+1}\left(\frac{u-t_{\left(k\right)}}{t_{(k-1)}-t_{\left(k\right)}}\right)$$

where z is the total number of toxicities observed, 0 ≡ t₍₀₎ < t₍₁₎ ≤ … ≤ t_(z) < t_(z+1) ≡ T are the ordered failure times and, k = max_0≤j≤z{j : u ≥ t_(j)}. If a toxic response is observed at a time that is less than half of the full observation period, then this weight function will give a smaller weight for each fixed u than will weight function (4). However, if toxicities tend to occur in the latter part of the observation period, a smaller weight will be given to those who have been enrolled in the trial for only a brief amount of time. Cheung and Chappell [2] appeal to the simple, but adequate, choice of a linear weight function (4).

An assumption that is accepted in much of the statistical methodology underlying Phase 1 trial design, including the TITE-CRM, is that of a monotonic dose-toxicity curve; that is, the ordering of the probability of toxicity between any two doses is known, and the higher dose corresponds to a greater probability of toxicity. For single-agent trials, the assumption of this `simple order' is valid. When studying multiple agents, some of the orderings between doses are known, whereas others are not, resulting in a partial ordering. In this article, we extend the TITE-CRM to Phase 1 trials in which the ordering is not fully known. Section 2 gives an example of a partially ordered trial, reviews the continual reassessment method for partial ordering (PO-CRM) [3, 4], and presents the models and inference associated with an extension of TITE-CRM to partially ordered trials. Section 3 provides simulation results that investigate the operating characteristics of the method. We conclude this article with some discussion on the implications of this TITE-CRM extension to Phase 1 trials of combinations of agents.

2. Problem of partial ordering

In trials combining more than one agent, the ordering of the toxicity probabilities between some combinations is not known prior to the study. This is clearly seen in the simplest case where we have two drugs at two levels. Suppose that the second level corresponds to an increase in one of the drugs but a decrease in the other. Then, the ordering of the toxic probabilities is not known. Returning to multiple combinations and drug levels, some of the orderings between doses are known, whereas others are not. As a result, the most `appropriate' dose to which the trial should escalate could consist of more than one treatment combination. When combinations chosen for investigation follow a partial order, each combination has associated with it a set of `possible escalation combinations'. For example, suppose it is known that combinations d₂ and d₃ are both more toxic than dose d₁, but it is unknown whether d₂ is more or less toxic than d₃. If combination d₁ is deemed `safe', then the trial could proceed by assigning the next cohort of patients to either d₂ or d₃.

Consider the dose-escalation clinical study, discussed in Ranson et al. [5], evaluating the safety and tolerability of lomeguatrib in combination with temozolomide among patients with advanced solid tumors. DLT was defined as any of the following: (i) a grade 4 neutropenia lasting longer than 5 days; (ii) a grade 4 thrombocytopenia lasting more than 5 days; (iii) a grade 3 or 4 nonhematologic toxicity grade; or (iv) any drug-related death. Lomeguatrib was initially fixed at 10 mg/m²/day, and temozolomide was administered in escalating doses from 50, 75, 100, 125, and 150 mg/m²/day to a maximal dose of 175 mg/kg. The dosage of lomeguatrib was then escalated from 10 to 20 to 40 mg/m²/day, and temozolomide was de-escalated to 125 mg/m²/day. Therefore, the trial investigates the eight drug combinations given in Table I.

Table I.

Drug combinations used in Phase 1 trial of lomeguatrib and temozolomide.

	Dosage
Agent	d 1	d 2	d 3	d 4	d 5	d 6	d 7	d 8
Lomeguatrib (mg/m2/day)	10	10	10	10	10	10	20	40
Temozolomide (mg/m2/day)	50	75	100	125	150	175	125	125

The ordering between some of the combinations is unknown. Combination d₂ has a greater dose of temozolomide and the same dose of lomeguatrib as d₁, so that the toxicity ordering between doses d₂ and d₁ is known. Denoting the probability of a DLT at combination d_i by R(d_i), it is known that R(d₁) ≤ R(d₂). The ordering for combinations d₆ and d₇ is not known, however, asd₆ has a greater dose of temozolomide but a lower dose of lomeguatrib than d₇. If we continue to assess the known and unknown toxicity order relationships in this way, it is straightforward to determine that the following order relationships are known: (i) R(d₁) ≤ R(d₂) ≤ R(d₃) ≤ R(d₄) ≤ R(d₅) ≤ R(d₆); (ii) R(d₅) ≤ R(d₆); and (iii) R(d₇) ≤ R(d₈). Taking into account the subset of drug combinations for which we know the toxicity order, we aim to formulate the possible orderings of the toxicity profile. In the presence of partial orders, we want to consider all possible simple orders of the toxicity probabilities that are consistent with the partial order. For instance, the simple order

$$R\left(d_1\right)\le R\left(d_2\right)\le R\left(d_3\right)\le R\left(d_4\right)\le R\left(d_7\right)\le R\left(d_5\right)\le R\left(d_6\right)\le R\left(d_8\right)$$

is one possible ordering of the probabilities based on the known and unknown toxicity relationships among the combinations. In the Ranson et al. [5] example, the trial requires the investigation of the six simple orders given in Table II. In the table, we suppress the `R(·)' notation and just display the number associated with each combination.

Table II.

Six possible simple orders of toxicity probabilities.

Ordering	Simple order
m = 1	1 – 2 – 3 – 4 – 5 – 7 – 6 – 8
m = 2	1 – 2 – 3 – 4 – 5 – 7 – 6 – 8
m = 3	1 – 2 – 3 – 4 – 5 – 7 – 8 – 6
m = 4	1 – 2 – 3 – 4 – 7 – 5 – 6 – 8
m = 5	1 – 2 – 3 – 4 – 7 – 5 – 8 – 6
m = 6	1 – 2 – 3 – 4 – 7 – 8 – 5 – 6

2.1. Models and inference for partial ordering

Wages, Conaway and O'Quigley [3] proposed a method for Phase 1 trials involving partial orders. Suppose there are M possible simple orders for the toxicity probabilities associated with the treatment combinations. For a particular ordering, m,m = 1, …, M, we model the toxicity probability R(d_i) using a class of models via

$$R\left(d_i\right)={\psi }_m(d_i,a)i=1,\dots ,k;m=1,\dots ,M$$ (5)

for some working dose–toxicity model ψ_m(d_i, a) and a ∈ A. There is a wide variety of choices for potential working models but the power parameter model given by

$${\psi }_m(d_i,a)={\alpha }_{mi}^{\exp \left(a\right)},i=1,\dots ,k$$ (6)

has shown itself to work well in practice. Here, A = (−∞,∞) and 0 < α_m1 < … < α_mk < 1 is the skeleton representing the prior estimates of the toxicity probabilities. Further, we can allow M to be described by a set of prior probabilities p(m) = {p(1), …, p(M)}, where p(m) ≥ 0 and where Σ_m p(m) = 1. In the simplest case where each possible order is weighted equally, we would use p(m) = 1/M. The dose for the j th entered subject, X_j, is a random variable taking values x_j ∈ {d₁, …, d_k}; j = 1, …, n. After inclusion of the first j patients into the trial, we have data in the form of Ω_j = {x₁, y₁, …, x_j, y_j}. If the data are to be analyzed under ordering m, then the likelihood can be written as

$$L_m(a\mid {\Omega }_j)=\prod _{\ell =1}^j{\psi }_m^{y_{\ell }}(x_{\ell },a){\{1-{\psi }_m(x_{\ell },a)\}}^{(1-y_{\ell })}.$$ (7)

Under ordering m, we obtain a summary value of the parameter a, in particular the posterior mean, and we refer to this as ${\widehat{a}}_{mj}$. Given the value of ${\widehat{a}}_{mj}$ under ordering m, we have an estimate of the probability of toxicity at each dose level d_i via: $\widehat{R}\left(d_i\right)={\psi }_m(d_i,{\widehat{a}}_{mj})$, (i = 1, …, k). On the basis of this formula and having taken some value for m, we determine the dose to be given to the (j + 1)th patient, x_j+1. Thus, we need some value for m, and we make use of the posterior probabilities of the ordering given the data Ω_j. Denoting these posterior probabilities by π(m|Ω_j) then,

$$\pi (m\mid {\Omega }_j)=\frac{p\left(m\right){\int }_A{L}_m(a\mid {\Omega }_j)g\left(a\right)\mathrm{d}a}{\sum _{m=1}^{M}p\left(m\right){\int }_A{L}_m(a\mid {\Omega }_j)g\left(a\right)\mathrm{d}a},$$

where g(a) is the prior distribution on the parameter a. The estimated values of π(m|Ω_j) can aid us in deciding between models. Wages et al. [3] propose an escalation method that begins by selecting the ordering with the largest posterior probability π(m|Ω_j). In the event that two or more orderings have the same posterior probability, we will randomly select one of those orderings. If we use h to denote the chosen ordering, then we use the estimate ${\widehat{a}}_{hj}$ to estimate the toxicity probabilities for each combination under ordering h, $\widehat{R}\left(d_i\right)={\psi }_h(d_i,{\widehat{a}}_{hj})$, i = 1, …, k. We then allocate the next patient to the dose combination with the estimated toxicity probability closest to the target.

2.2. Time-to-event continual reassessment method in partially ordered trials

Here, we extend the PO-CRM by considering a class of weighted dose–response models, ϕ_m(d_i, w, a) = wψ_m(d_i, a) m = 1, …, M, i = 1 …, k, where w is a monotone increasing function of the patient's follow-up. In the Bayesian framework, we assign a prior probability distribution g(a) for the parameter a and a prior probability p(m) to each ordering. In order to get the trial underway, we will choose the ordering with the largest prior probability, p(m), among the M orderings. If several, or all, of the orderings have the same prior probability, then we will choose at random from these orderings. Given the starting ordering, the investigators then choose the starting dose, d_i. In order to establish running estimates of the probability of toxicity at the available treatment combinations, we need an expression for the weighted likelihood for the parameter a. Under ordering m, we give the weighted likelihood by

$${\tilde{L}}_m(a\mid {\Omega }_j)=\prod _{\ell =1}^j{\varphi }_m^{y_{\ell }}(x_{\ell },w_{\ell },a){\{1-{\varphi }_m(x_{\ell },w_{\ell },a)\}}^{(1-y_{\ell })}$$ (8)

which, for each ordering, we can use in order to generate a summary value, ${\widehat{a}}_{mj}$, for a. Given the set Ω_j and the likelihood, we give the posterior density for a by

$${\tilde{f}}_m(a\mid {\Omega }_j)=\frac{{\tilde{L}}_m(a\mid {\Omega }_j)g\left(a\right)}{{\int }_A{\tilde{L}}_m(a\mid {\Omega }_j)g\left(a\right)\mathrm{d}a}.$$

Once again, we can use this information to establish the posterior probabilities of the orderings given the data as

$$\tilde{\pi }(m\mid {\Omega }_j)=\frac{p\left(m\right){\int }_A{\tilde{L}}_m(a\mid {\Omega }_j)g\left(a\right)\mathrm{d}a}{\sum _{m=1}^{M}p\left(m\right){\int }_A{\tilde{L}}_m(a\mid {\Omega }_j)g\left(a\right)\mathrm{d}a}.$$

When a new patient is to be enrolled, we choose a single ordering, h, with the largest posterior probability. Given the ordering h and the working model, ψ_h(d_i, a), we can generate toxicity probability estimates at each level. After having included the j th subject, we can compute the posterior probability of a DLT for d_i so that

$$\widehat{R}\left(d_i\right)={\psi }_h(d_i,{\widehat{a}}_{hj});{\widehat{a}}_h={\int }_{A}a{\tilde{f}}_h(a\mid {\Omega }_j)\mathrm{d}a.$$ (9)

The treatment combination x_j+1 ∈ {d₁, …, d_k} assigned to the (j + 1)th included patient is the dose, d_i, such that (1) is a minimum.

3. Simulations

3.1. A single trial

To illustrate the proposed method, consider the example given in Section 2 involving k = 8 treatment combinations, d₁, …, d₈. The partial order associated with this trial has associated with it six possible simple orders. Suppose the true toxicity probabilities are R(d₁) = 0.02, R(d₂) = 0.05, R(d₃) = 0.10, R(d₄ = 0.20, R(d₅) = 0.30, R(d₆) = 0.50, R(d₇) = 0.70, and R(d₈) = 0.80, which corresponds to ordering m = 1 being the true dose–toxicity order. The targeted toxicity probability is θ = 0.20, indicating that d₄ gives the `correct' treatment combination for the MTD. As in Cheung and Chappell [2], we defined the MTD with respect to a 6-month follow-up period with one patient being enrolled every 0.5 month. We implemented the systematic approach of Lee and Cheung [6] in order to establish the skeleton for the monotonic order m = 1. Implementing the model calibration algorithm of [6], with a half-width value of δ = 0.06, yielded the values given in the first line of Table III. We adjusted the position of these values to correspond to each of the six possible orders consistent with the partial ordering, and we give these in the remainder of Table III.

Table III.

Working model for six simple orders.

	Treatment combinations
Model	d 1	d 2	d 3	d 4	d 5	d 6	d 7	d 8
m = 1	0.01	0.03	0.10	0.20	0.33	0.47	0.60	0.70
m = 2	0.01	0.03	0.10	0.20	0.33	0.60	0.47	0.70
m = 3	0.01	0.03	0.10	0.20	0.33	0.70	0.47	0.60
m = 4	0.01	0.03	0.10	0.20	0.47	0.60	0.33	0.70
m = 5	0.01	0.03	0.10	0.20	0.47	0.70	0.33	0.60
m = 6	0.01	0.03	0.10	0.20	0.60	0.70	0.33	0.47

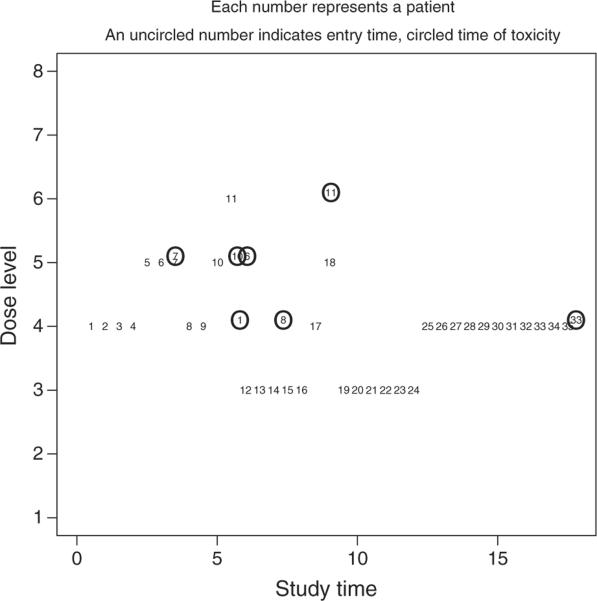
For each ordering, we implemented a normal prior, g(a), with mean 0 and variance 1.34, on the parameter a, as in O'Quigley and Shen [7]. Before entering the first patient, we chose an ordering by randomly selecting a value from 1 to 6, with each value weighted according to the prior probabilities, p(m), on the ordering. We assumed that, a priori, we believe that each of the six simple orders was equally likely and took p(m) = 1/6. Getting the trial underway, we randomly selected ordering 1, which corresponds to d₁ → d₂ → d₃ → d₄ → d₅ → d₆ → d₇ → d₈. Within this ordering, we treated the first entered patient at a level α_1i as close as possible to the target toxicity rate, θ = 0.20, which, for m = 1, is dose d₄. Figure 1 summarizes the responses from a simulated trial of 35 patients. We indicate the point at which a patient enters the trial by an uncircled patient number. We represent the point in the trial at which a patient suffers DLT by a circled patient number. For instance, patient 8 enters the trial at month (i.e., study time) 4 and experiences DLT at month 7.5. We can see that, after we obtain DLT information for patients 1, 6, and 10 at approximately month 6, the method de-escalates to a lower level. Conversely, in the absence of DLT information (patients 19 through 24), the method escalates and ultimately settles on d₄, which we choose as the MTD combination at the conclusion of the trial.

Figure 1.

A simulated trial using the TITE-CRM for partial orders.

3.2. Setup

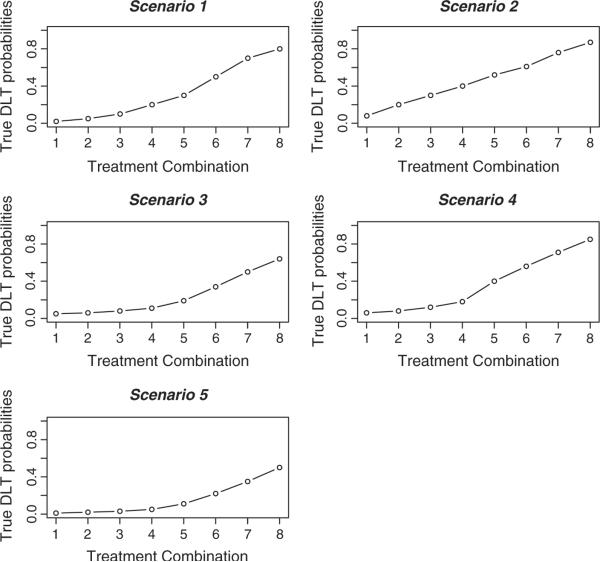
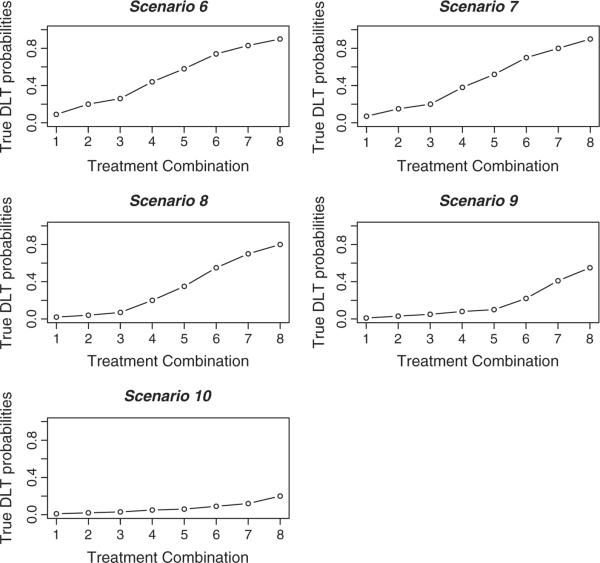
In this section, we examine the TITE-CRM for partial orders across 10 different toxicity scenarios. We provide the true toxicity probabilities for each of these scenarios in the lines labeled R(d_i) in Tables IV and V as well as graphically illustrated in Figures 2 and 3. In each scenario, the starting dose was that believed to be the `best' dose, according to which skeleton value was closest to the target toxicity probability of 0.20 within the ordering that we initially selected. For scenarios 1–5, in each trial, we followed patients for 6 months, and a new patient was accrued either on a fixed scheme of every 0.5 month or according to a Poisson process with a rate of one patient per 0.5 month. For scenarios 6–10, in each trial, we followed patients for 8 months, and a new patient was accrued either on a fixed scheme of every 1 month or according to a Poisson process with a rate of one patient per month. Before entering the first patient, we chose an ordering by randomly selecting a value from 1 to 6 with each value weighted according to the prior probabilities, p(m), on the ordering. In each set of 1000 simulated trials, we believe that each of the six simple orders is equally likely and took p(m) = 1/6. The sample size in each simulated trial was n = 35 and n = 30 patients for scenarios 1–5 and 6–10, respectively. For the first five toxicity scenarios, we modeled the probability of dose-limiting toxic response via the power parameter model, with the skeletons given in Table III. For scenarios 6–10, we used a different working model. We again utilized the approach of Lee and Cheung [6] using a half-width value of δ = 0.05 and a prior MTD at level 3. Again, this algorithm yielded the skeleton values for the ordering m = 1, and these values were adjusted to correspond to each of the six possible orderings. For each ordering, we implemented a normal prior N(0, 1.34) on the parameter a. In each of the 10 toxicity scenarios, we generated the failure times of the patients under either a conditionally uniform model or a Weibull model. For the conditionally uniform model, if a patient experienced toxic side effects, we uniformly generated a failure time on the interval (0, 6) for the first five scenarios. Similarly, we performed this on the interval (0, 8) for scenarios 6–10. For the Weibull model, we fixed the shape parameter at a value of 4, as in Cheung and Chappell [2], and we chose the scale parameters so that the cumulative distribution function at time T = 6 (or T = 8) would be the probability of toxicity. Cheung and Chappell [2] used both of these failure time models. Therefore, for each scenario, we investigated four different applications of the TITE-CRM for partial orders (PO-TITE) design:

1. PO-TITE (A): we enrolled patients after a fixed time interval, and we generated the patients' failure times under a conditionally uniform model.

2. PO-TITE (B): we enrolled patients according to a Poisson process, and we generated the patients' failure times under a conditionally uniform model.

3. PO-TITE (C): we enrolled patients after a fixed time interval, and we generated the patients' failure times under a Weibull model.

4. PO-TITE (D): we enrolled patients according to a Poisson process, and we generated the patients' failure times under a Weibull model.

We compared each of these applications with the CRM for partial orders (PO-CRM) of Wages et al. [3] in terms of the distribution of MTD recommendation and overall trial duration. Like the CRM, the PO-CRM does not allow for the toxicity information of patients to contribute to dose recommendation until they have been fully followed. We also compare our simulation results against the TITE-CRM for a fully known ordering (denoted in the simulation tables as TITE) in order to provide a benchmark of how well the proposed design is performing. For the TITE simulations under a known ordering, we used a fixed accrual scheme, and we generated the patient failure times under the conditionally uniform model. We simulated these results using the titesim function in R package dfcrm [8, 9]. It is unreasonable to expect an approach for a partially known toxicity order to perform as well as one that assumes a fully known order in all scenarios. However, the proposed method reduces to the TITE-CRM when the toxicity ordering is fully known, so a direct comparison is useful in measuring how much information is lost as a result of not having a fully known order.

Table IV.

Percentage of MTD recommendation and expected trial duration (in months) for the PO-CRM and the TTTE-CRM for partial orders for scenarios 1–5 based on 1000 simulated trials.

Scenario		d 1	d 2	d 3	d 4	d 5	d 6	d 7	d 8	Duration
1	R(di)	0.02	0.05	0.10	0.20	0.30	0.50	0.70	0.80
	TITE	0.00	0.01	0.22	0.58	0.18	0.01	0.00	0.00	23.50
	PO-CRM	0.00	0.02	0.25	0.56	0.16	0.01	0.00	0.00	210
	PO-TITE A	0.00	0.01	0.27	0.56	0.14	0.02	0.00	0.00	23.50
	PO-TITE B	0.00	0.01	0.24	0.55	0.17	0.01	0.01	0.00	23.54
	PO-TITE C	0.00	0.02	0.35	0.53	0.10	0.02	0.00	0.00	23.50
	PO-TITE D	0.00	0.03	0.32	0.53	0.10	0.02	0.00	0.00	23.40
2	R(di)	0.08	0.20	0.30	0.40	0.52	0.61	0.76	0.87
	TITE	0.12	0.56	0.30	0.02	0.00	0.00	0.00	0.00	23.50
	PO-CRM	0.18	0.54	0.26	0.02	0.00	0.00	0.00	0.00	210
	PO-TITE A	0.15	0.54	0.28	0.03	0.00	0.00	0.00	0.00	23.50
	PO-TITE B	0.17	0.55	0.24	0.03	0.00	0.00	0.00	0.00	23.51
	PO-TITE C	0.18	0.52	0.27	0.03	0.00	0.00	0.00	0.00	23.50
	PO-TITE D	0.20	0.52	0.23	0.04	0.01	0.00	0.00	0.00	23.52
3	R(di)	0.05	0.06	0.08	0.11	0.19	0.34	0.50	0.64
	TITE	0.00	0.01	0.04	0.26	0.55	0.15	0.00	0.00	23.50
	PO-CRM	0.00	0.01	0.05	0.31	0.46	0.10	0.07	0.00	210
	PO-TITE A	0.00	0.01	0.07	0.32	0.43	0.09	0.08	0.00	23.50
	PO-TITE B	0.00	0.01	0.06	0.35	0.42	0.10	0.06	0.00	23.54
	PO-TITE C	0.00	0.00	0.05	0.35	0.46	0.08	0.05	0.00	23.50
	PO-TITE D	0.00	0.00	0.05	0.41	0.43	0.06	0.05	0.00	23.41
4	R(di)	0.20	0.30	0.38	0.45	0.56	0.62	0.75	0.90
	TITE	0.71	0.25	0.04	0.01	0.00	0.00	0.00	0.00	23.50
	PO-CRM	0.69	0.25	0.06	0.00	0.00	0.00	0.00	0.00	210
	PO-TITE A	0.67	0.28	0.05	0.00	0.00	0.00	0.00	0.00	23.50
	PO-TITE B	0.68	0.27	0.05	0.00	0.00	0.00	0.00	0.00	23.50
	PO-TITE C	0.59	0.30	0.10	0.01	0.00	0.00	0.00	0.00	23.50
	PO-TITE D	0.58	0.33	0.09	0.01	0.00	0.05	0.00	0.00	23.52
5	R(di)	0.01	0.02	0.03	0.05	0.11	0.20	0.35	0.50
	TITE	0.00	0.00	0.00	0.02	0.34	0.54	0.11	0.00	23.50
	PO-CRM	0.00	0.00	0.00	0.04	0.33	0.39	0.22	0.01	210
	PO-TITE A	0.00	0.00	0.00	0.04	0.36	0.36	0.22	0.02	23.50
	PO-TITE B	0.00	0.00	0.00	0.05	0.34	0.37	0.22	0.04	23.46
	PO-TITE C	0.00	0.00	0.00	0.06	0.34	0.36	0.22	0.01	23.50
	PO-TITE D	0.00	0.00	0.00	0.04	0.39	0.37	0.20	0.01	23.53

The MTD combinations are indicated in bold type.

Table V.

Percentage of MTD recommendation and expected trial duration (in months) for the PO-CRM and the TITE-CRM for partial orders for scenarios 6–10 based on 1000 simulated trials.

Scenario		d 1	d 2	d 3	d 4	d 5	d 6	d 7	d 8	Duration
6	R(di)	0.09	0.20	0.26	0.44	0.58	0.74	0.83	0.90
	TITE	0.14	0.51	0.32	0.03	0.00	0.00	0.00	0.00	38.00
	PO-CRM	0.18	0.48	0.32	0.02	0.00	0.00	0.00	0.00	240
	PO-TITE A	0.18	0.49	0.30	0.03	0.00	0.00	0.00	0.00	38.00
	PO-TITE B	0.20	0.46	0.31	0.03	0.00	0.00	0.00	0.00	38.07
	PO-TITE C	0.20	0.49	0.28	0.03	0.00	0.00	0.00	0.00	38.00
	PO-TITE D	0.20	0.50	0.27	0.02	0.01	0.00	0.00	0.00	37.94
7	R(di)	0.07	0.15	0.20	0.38	0.52	0.70	0.80	0.90
	TITE	0.04	0.32	0.51	0.12	0.00	0.00	0.00	0.00	38.00
	PO-CRM	0.07	0.36	0.48	0.09	0.00	0.00	0.00	0.00	240
	PO-TITE A	0.06	0.36	0.45	0.13	0.00	0.00	0.00	0.00	38.00
	PO-TITE B	0.05	0.35	0.46	0.14	0.00	0.00	0.00	0.00	37.89
	PO-TITE C	0.07	0.38	0.44	0.11	0.00	0.00	0.00	0.00	38.00
	PO-TITE D	0.09	0.33	0.46	0.11	0.02	0.00	0.00	0.00	38.09
8	R(di)	0.02	0.04	0.07	0.20	0.35	0.55	0.70	0.80
	TITE	0.00	0.01	0.20	0.62	0.17	0.00	0.00	0.00	38.00
	PO-CRM	0.00	0.01	0.24	0.60	0.13	0.03	0.00	0.00	240
	PO-TITE A	0.00	0.01	0.24	0.59	0.13	0.03	0.00	0.00	38.00
	PO-TITE B	0.00	0.02	0.22	0.57	0.14	0.03	0.01	0.00	38.01
	PO-TITE C	0.00	0.02	0.26	0.58	0.12	0.01	0.01	0.00	38.00
	PO-TITE D	0.00	0.01	0.25	0.59	0.12	0.03	0.00	0.00	37.90
9	R(di)	0.01	0.03	0.05	0.08	0.10	0.20	0.41	0.55
	TITE	0.00	0.00	0.02	0.06	0.33	0.52	0.07	0.00	38.00
	PO-CRM	0.00	0.00	0.02	0.07	0.32	0.39	0.20	0.00	240
	PO-TITE A	0.00	0.00	0.01	0.12	0.35	0.35	0.17	0.00	38.00
	PO-TITE B	0.00	0.00	0.01	0.12	0.33	0.35	0.18	0.01	37.90
	PO-TITE C	0.00	0.00	0.01	0.10	0.40	0.35	0.13	0.01	38.00
	PO-TITE D	0.00	0.00	0.01	0.13	0.40	0.38	0.08	0.00	37.98
10	R(di)	0.01	0.02	0.03	0.05	0.06	0.09	0.12	0.20
	TITE	0.00	0.00	0.00	0.02	0.05	0.21	0.28	0.44	38.00
	PO-CRM	0.00	0.00	0.00	0.00	0.05	0.25	0.26	0.44	240
	PO-TITE A	0.00	0.00	0.00	0.02	0.07	0.22	0.22	0.47	38.00
	PO-TITE B	0.00	0.00	0.00	0.02	0.08	0.21	0.22	0.46	38.05
	PO-TITE C	0.00	0.00	0.00	0.02	0.07	0.16	0.28	0.47	38.00
	PO-TITE D	0.00	0.00	0.00	0.03	0.06	0.19	0.25	0.47	37.87

The MTD combinations are indicated in bold type.

Figure 2.

The true dose–toxicity relationships for scenarios 1–5.

Figure 3.

The true dose–toxicity relationships for scenarios 6–10.

3.3. Results

The percentage of simulated trials that each dose was recommended as the MTD for each application of the method in each of the 10 toxicity scenarios is shown in Tables IV and V. These tables also show the duration of trials across each of the scenarios. Through examination of Tables IV and V, it is evident that the PO-TITE design is having a significant impact on the reduction of trial duration in each of the four applications when compared with PO-CRM. This reduction was consistent across each of the 10 toxicity scenarios. For scenarios 1–5, the trial duration under each of the PO-TITE applications was consistently around 23.5 months, as compared with 210 months when only completely observed subjects contributed to dose recommendation. For scenarios 6–10, these values were approximately 38 and 240 months for the PO-TITE applications and PO-CRM, respectively.

The PO-CRM and the PO-TITE designs are comparable in terms of the percentage of trials each method correctly recommends the true MTD combination, henceforth referred to as percentage of correct selection (PCS). In scenario 1, each of the four PO-TITE applications, as well as the PO-CRM, has a PCS between 53% and 56%. Each of the five approaches has nearly identical performances in scenarios 2 and 3 as well. Scenario 4 contains the largest discrepancy between the smallest PCS and the largest PCS among the five approaches presented. PO-CRM performs better in this scenario, with a PCS of 69% compared with 58% for the poorest performing PO-TITE (D). Even though the PO-CRM outperforms the PO-TITE design in this scenario in terms of PCS, each of the PO-TITE applications recommend the MTD or a neighboring combination in a high percentage of trials while significantly reducing trial duration. Even in cases where the methods perform less well, they are recommending the MTD combination and a neighboring dose in a large percentage of trials. For instance, in scenario 5, in 95% of the simulated trials, PO-TITE (A) identifies treatments as the MTD that have toxicity probabilities between 0.11 and 0.35. Similarly, 93% of the time, PO-TITE (C) the method recommends the MTD to be a treatment with toxicity probability in the same range. For scenarios 6–10, we changed the observation window to T = 8 months and the accrual rate to one patient per month. The conclusions of scenarios 1–5 regarding PCS hold for these five scenarios as well. For each scheme, the four PO-TITE applications yield a PCS quite close to that of PO-CRM, indicating that we do not sacrifice performance when attempting to deal with the problem of long trial duration in partially ordered Phase 1 trials. Tables IV and V also present PCS results for the TITE-CRM for a fully known ordering (TITE). In some of the scenarios (i.e., 1, 2, 6, 8, and 10), the partially ordered methods result in a PCS that is very close to that of the TITE. This is an indication that not much information is being lost as a result of not having a fully known ordering. In other cases (i.e., 3, 5, and 9), the gap between the PCS of partial order approaches and the TITE is wider, although the partial order designs are still performing quite well. These gaps are not unexpected in that we would not expect a design for partial order to perform as well or nearly as well as a design for a fully known order in every instance. However, in general, MTD prediction based on the fully known ordering yields only a small gain relative to MTD prediction based on partially ordered methods. Overall, the simulation results of Tables IV and V indicate that the PO-TITE is performing well in terms of correctly recommending the combinations at and around the MTD, while also significantly reducing the duration of the trial, for the set of 10 scenarios considered. The partially ordered designs presented were also similar in regards to the percentages of in-trial patient allocation, although we do not present the results here for the sake of brevity.

4. Concluding remarks

The goal of the design presented in this article was to decrease the overall duration of Phase 1 clinical trials combining more than one agent. These trials usually involve a partially ordered dose–toxicity profile. Therefore, we showed how the TITE-CRM can be utilized in the presence of partial orders by extending the PO-CRM design of Wages, Conaway, and O'Quigley [3]. We examined the performance of a TITE-CRM design for partial orders, in terms of reducing the overall trial duration, correctly recommending the true MTD combination, and treating patients at and around the MTD combination. We then compared this performance with the PO-CRM. Overall, each of the four TITE applications were competitive with the PO-CRM in terms of PCS in the 10 toxicity scenarios presented. However, the PO-TITE design significantly reduced the overall trial duration. We recognize that this is only a snapshot comparison due to the amount of scenarios considered. Obviously, it is not possible to look at all situations, but the probabilities chosen reflect a somewhat wide range of toxicity scenarios. It is clear that the TITE-CRM, even in the presence of partial orders, does not sacrifice estimation accuracy as a result of shortening the trial duration.