A method for computing association rate constants of atomistically represented proteins under macromolecular crowding

Abstract

In cellular environments, two protein molecules on their way to form a specific complex encounter many bystander macromolecules. The latter molecules, or crowders, affect both the energetics of the interaction between the test molecules and the dynamics of their relative motion. In earlier work (Zhou and Szabo 1991 J. Chem. Phys. 95 5948-52), it has been shown that, in modeling the association kinetics of the test molecules, the presence of crowders can be accounted for by their energetic and dynamic effects. The recent development of the transient-complex theory for protein association in dilute solutions makes it possible to easily incorporate the energetic and dynamic effects of crowders. The transient complex refers to a late on-pathway intermediate, in which the two protein molecules have near-native relative separation and orientation but have yet to form the many short-range specific interactions of the native complex. The transient-complex theory predicts the association rate constant as k_a = k_a0exp (−ΔG_el*/k_BT), where k_a0 is the “basal” rate constant for reaching the transient complex by unbiased diffusion, and the Boltzmann factors captures the influence of long-range electrostatic interactions between the protein molecules. Crowders slow down the diffusion, therefore reducing the basal rate constant (to k_ac0), and induce an effective interaction energy ΔG_c. We show that the latter interaction energy for atomistic proteins in the presence of spherical crowders is “long”-ranged, allowing the association rate constant under crowding to be computed as k_ac = k_ac0exp[−(ΔG_el* + ΔG_c*)/k_BT]. Applications demonstrate that this computational method allows for realistic modeling of protein association kinetics under crowding.

1. Introduction

Protein association is at the center of essentially all cellular processes. Often, as in protein synthesis, protein association is under kinetic control, rather than thermodynamic control. The association rate constants of many protein pairs have been measured in dilute solutions. Recently there has been great progress in computing these rate constants using realistically represented protein molecules [1–3]. However, macromolecular crowding in cellular environments is expected to significantly affect association kinetics [4]. In particular, relative to dilute solutions, translational diffusion of protein molecules in cell cytoplasm and in mimetic environments is slowed by a few-fold [5, 6]. Theoretical consideration also suggests that crowding may induce an effective interaction between two protein molecules on their way to form a complex [4, 7]. Recognizing potential differences between cellular environments and dilute solutions, kinetic measurements have been reported for protein association inside cells and in mimetic environments [8–14]. To enable quantitative comparison with these measurements, here we present a method for computing protein association rate constants under crowded conditions.

The problem of protein association under crowding has been addressed by simulation and theoretical studies of simple model systems [15–23]. In these studies, the proteins are modeled as spheres. One early study [16] showed that the effects of crowders on the association kinetics of test proteins can be accounted for by including the influences of the crowders on the relative diffusion constant and the interaction energy of the test proteins. This finding presents a powerful strategy to model the effects of crowding on protein association kinetics, which we exploit here.

To explore how macromolecular crowding affects the diffusional dynamics of test proteins, sophisticated Brownian dynamics simulations have been carried out, even with proteins represented at the residue or sub-residue level and with protein compositions mimicking that of the Escherichia colicytoplasm [24–26]. The need for fine-tuning interaction energy parameters and deciding on an appropriate protocol for treating hydrodynamic interactions seem to hamper the ability of these simulations to predict the diffusion constants of test proteins in crowded conditions. On the other hand, there is a long history of theories for predicting the tracer diffusion constants in concentrated suspensions of hard-sphere particles. The most rigorous seems to be the theory of Tokuyama and Oppenheim [27], which predicts a 5-fold slowing down in tracer diffusion at a volume fraction of 0.3 and fits experimental data well for globular proteins like hemoglobin in red blood cells and in concentrated solutions [5].

It is essential to recognize that the native complexes formed by protein association are stereospecific [28]. Relative to the association in spherical models, the stereospecificity reduces the basal rate constant, i.e., the rate constant when the interaction (either direct or induced by crowders) between the protein molecules is switched off, by as much as five orders of magnitude [2, 29]. At the same time, the stereospecificity allows the rate constant to be sensitive to the presence of a long-range interaction [28]. In a spherical model, strong attractive interactions can enhance the rate constant by at most a few-fold, but for stereospecific association, long-range electrostatic attraction between the protein molecules can enhance the rate constant by up to four orders of magnitude [2, 3, 30]. According to the recently developed transient-complex theory, the rate constant for protein association in dilute solutions can be calculated as [2, 29]

$$k_a=k_{a0}\text{exp}(-\Delta G_{el}^{\ast }∕k_{B}T)$$ (1)

where k_a0 is the basal rate constant, ΔG_el is the electrostatic interaction between the protein molecules and “*” means that the calculation is to be done within the so-called transient complex, k_B is Boltzmann's constant, and T is the absolute temperature. The transient complex is a late on-pathway intermediate, in which the two protein molecules have near-native relative separation and orientation but have yet to form the many short-range specific interactions of the native complex.

Here we extend the transient-complex theory to protein association under crowded conditions. Based on our previous studies [16, 17], we propose that, under crowding, the association rate constant can be calculated as

$$k_{ac}=k_{ac0}\text{exp}[-(\Delta G_{el}^{\ast }+\Delta G_c^{\ast })∕k_{B}T]$$ (2)

where k_ac0 is the modified basal rate constant due to the slowing down of relative diffusion by crowders, and ΔG_c is a crowder-induced effective interaction energy between the protein molecules. Below we give justification for (2), describe its implementation, and present illustrative applications.

2. Computational details

2.1 Implementation of the transient-complex theory

The transient-complex theory for calculating protein association rate constants [29] has been automated and implemented into a web server called TransComp (http://pipe. sc.fsu.edu/transcomp) [2]. The input is the all-atom structure of the native complex, plus the partial charges and radii of the atoms (for calculating the electrostatic contribution to the rate constant).

A TransComp rate calculation consists of three steps. The first is to locate the transient complex, by sampling the configurations of a protein pair in the 6-dimensional space of relative translation and rotation. The 6 coordinates are defined as follows. From the collection of interface atoms in the native complex, the center and the least-squares plane are calculated. The interface center is marked as the binding-site center on each subunit, and a unit vector e that starts from the interface center and is normal to the least-squares plane is body-fixed on the second subunit. In any configuration of the protein pair, the displacement vector r between the binding-site centers of the two subunits defines the 3 degrees of freedom in relative translation; the unit vector e and the rotation angle χ of the second subunit around this unit vector define the 3 degrees of freedom in relative rotation. For any sampled configuration, which is free of steric clash between the subunits, the number, N_c, of contacts between representative interface atoms (which are at a minimum of 3.5 Å apart) is calculated. The sharp transition from the bound region, characterized by high N_c values but small freedom in χ, and the unbound region, characterized by low N_c values but large freedom in χ, defines the transient complex. Specifically, the dependence of N_c on the χ standard deviation σ_χ, which measures the freedom in χ, is fitted to a function used for analyzing protein denaturation data, and the mid-point of the transition, where N_c is denoted as N_c*, identifies the transient complex.

Once the transient complex is identified, the basal rate constant k_a0 for reaching it by unbiased diffusion is obtained from Brownian dynamics simulations, essentially with an absorbing boundary condition imposed at N_c = N_c* [31]. Finally, the electrostatic interaction energy ΔG_el* is calculated by solving the full, nonlinear Poisson-Boltzmann equation by the APBS program [32]; 100 configurations from the transient-complex are used to obtain an average value.

2.2 Calculation of ΔG_c

The crowder-induced interaction energy ΔG_c between two protein molecules can be calculated as the difference between two transfer free energies. The first is for transferring the pair of protein molecules in its given configuration from a dilute solution to a crowded solution; the second is the sum of the transfer free energies for the two separate protein molecules [4, 33]. If the effective interaction energy between a test protein (or a protein pair) and the crowders is U(R,Ω), where R and Ω represent the position and orientation, respectively, of the test protein, then the transfer free energy μ is

$$\text{exp}=(-\mu ∕k_{B}T)=<\text{exp}[-U\left(R,\Omega \right)∕k_{B}T]>$$ (3)

where < … > means averaging over the position and orientation of the test protein and over the configurations of the crowders.

2.2.1 The particle insertion method

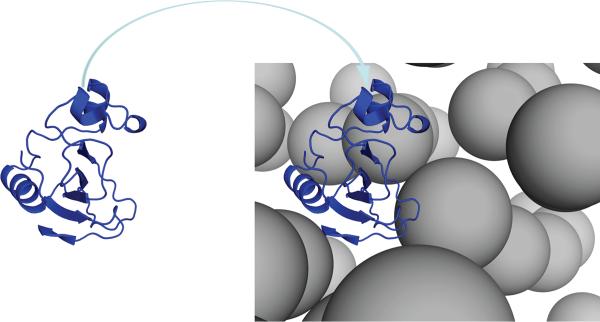
We focus on the excluded-volume type of interaction between crowders and test proteins. This means that U(R,Ω) is 0 when the test protein does not clash with crowders and is infinite when clash occurs (figure 1). Then exp[−U(R,Ω)/k_BT] is either 1 or 0, and the average on the right-hand side of (3) is the clash-free, or allowed fraction of attempts to insert the test protein into the crowded solution. Previously we designed an algorithm to speed up the calculation of the allowed fraction of insertion [33]. This, referred to as the insertion method, is used here for calculating some of the ΔG_c results.

Figure 1.

Illustration of the insertion method. Each protein conformation is placed in the crowded solution, and the interaction energy with the crowders is calculated. The Boltzmann average then gives the transfer free energy.

The test proteins in the present study are represented at the all-atom level. The crowders are modeled as spherical particles with varying radii and volume fractions. The configurations of the crowders are generated from simulations following a protocol described previously [33]. The simulation box is a cube with side length 1000 Å, with periodic boundary condition imposed. If the simulation box contains a total of N crowders with radius R_c (in units of Å), then the crowder volume fraction ϕ is $4\pi R_c^{3}N∕3\times {10}^9$. We choose ϕ values up to 0.43, which cover cellular crowding levels. The precise ϕ values are determined by the discrete values of N.

2.2.2 The generalized fundamental measure theory

We also developed an alternative, faster way of calculating the transfer free energy [34]. This is referred to as the generalized fundamental measure theory (GFMT) and predicts the transfer free energy as

$$\mu ={\Pi }_c{\nu }_p+{\gamma }_c{s}_p+{\kappa }_c{l}_p-k_{B}T\text{ln}(1-\varphi )$$ (4)

where v_p, s_p, and l_p are the volume, surface area, and linear size, respectively, of the test protein; and Π_c, γ_c, and κ_c are the osmotic pressure, surface tension, and bending rigidity, respectively, of the crowded solution. The latter crowder-only quantities are determined by the volume, surface area, and radius of the crowders. The geometric quantities v_p, s_p, and l_p of the test protein are essentially defined by its crowder-excluded surface (represented at the all-atom level), which depends on the crowder radius.

We have shown that the GFMT results are very close to those obtained by the insertion method for the effects of crowding on protein folding and binding stability [34]. Below we will further show that the GFMT is also very accurate for predicting the effects of crowding on protein association kinetics, which involve protein molecules at various separations.

3. Results

As test proteins, we study three systems (figure 2): a pair of spherical particles; the barnase-barstar pair; and the TEM1-BLIP pair. The effects of crowding on the association kinetics of the latter two systems have been investigated in recent experimental studies [8–10, 12–14].

Figure 2.

Systems studied. (a) A model consisting of two spherical particles. (b) barnase-barstar complex. (c) TEM1-BLIP complex.

3.1 Spherical test proteins

A pair of spheres, originally introduced by Smoluchowski [35] as a model for the kinetics of colloid coagulation, has often been used as a model for protein association, including for studying the effects of crowding. However, the lack of stereospecificity makes it a poor model [28]. Nevertheless the spherical model is useful for illustrating our strategy for treating crowding.

Throughout the present study, we focus on the diffusion-limited regime, where association occurs as soon as the reactant molecules reach the transient complex by diffusion. For the spherical model, the transient complex occurs at the contact distance; the Smoluchowski result for the association rate constant a dilute solution is

$$k_a=8\pi D{R}_p$$ (5)

where D is the relative diffusion constant of the spherical reactant particles, and R_p is their radius.

A crowded solution affects the thermodynamics of the reactant pair, by inducing an effective interaction energy ΔG_c, and the motional dynamics, by a reduction of the relative diffusion constant (to D_c). For the present case, ΔG_c only depends on the inter-reactant center-to-center distance s, or, equivalently, the closest surface-to-surface distance r = s − 2R_p. The association rate constant can then be calculated according to the Debye formula [36]:

$$k_{ac}=8\pi D_c{R}_p^{\prime }$$ (6)

where

$$R_p^{\prime }=\frac{2}{{\int }_0^{\infty }dr{(r+2R_p)}^{-2}\text{exp}[\Delta G_c\left(r\right)∕k_{B}T]}$$ (7)

Equation (6) shows that the two effects of crowding are separable. The slowing down of the reactant relative diffusion will always decrease the association rate constant whereas the effect of the crowder-induced interaction energy will depend on the sign of ΔG_c. An attractive interaction (i.e., ΔG_c < 0) will result in $R_p^{\prime }>R_p$ and hence an increase in k_ac while a repulsive interaction has the opposite effect.

If R_p = R_c, then both the reactant molecules and the crowders can be considered as part of a single-species hard-sphere suspension. In that case the crowder-induced interaction energy ΔG_c(r) is directly related to the pair distribution function g(r) [16]:

$$g\left(r\right)=\text{exp}[-\Delta G_c\left(r\right)∕k_{B}T]$$ (8)

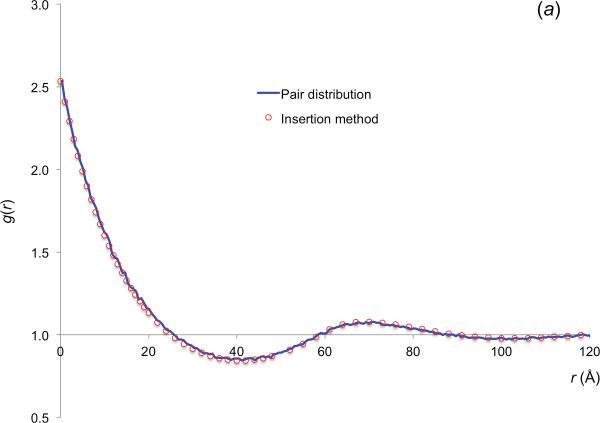
In figure 3a we display the g(r) result predicted from ΔG_c(r), obtained by the insertion method for R_p = R_c = 30 Å and ϕ = 0.3061, and the g(r) result directly calculated from binning the number of crowder pairs at varying distances. The close agreement demonstrates the reliability of the insertion method. As is well known, the pair distribution function at high ϕ oscillates around a value of 1, reflecting the layered structure of other hard spheres around a given hard sphere. The peaks occur at inter-reactant distances which are roughly multiples of the crowder diameter, followed by troughs at an additional distance equal to the crowder radius. A complementary perspective is offered by the insertion method. When a reactant molecule is inserted into the crowders, the volume of the reactant molecule plus a spherical shell with thickness R_c is excluded from the crowders. For two reactant molecules at contact, the extra excluded volumes of the two molecules overlap. Therefore the total excluded volume is reduced when the reactant molecules are brought from an infinite separation to the contact distance, making it easier to insert in the latter situation. This results in a negative ΔG_c(r) value, or equivalently, a greater than 1 g(r) value, at r = 0.

Figure 3.

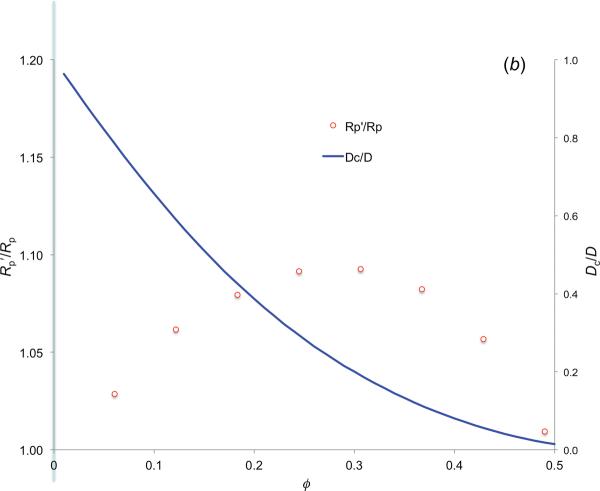
Results for R_p = R_c = 30 Å. (a) Comparison of the pair distribution function calculated from binning the number of pairs at various distances and that predicted from the insertion method. ϕ = 0.3061. (b) The effect of the crowder-induced interaction energy on the association rate constant of the spherical model and the reduction of the relative diffusion constant of the reactant particles by crowding.

The effect of the ΔG_c(r) on the association rate constant is contained in $R_p^{\prime }∕R_p$. This ratio is shown in figure 3b. The deviation of $R_p^{\prime }∕R_p$ from 1 is very small, no more than 10%, at any crowder volume fraction. At small ϕ, $R_p^{\prime }∕R_p$ increases with increasing ϕ, corresponding to the increasing difficulty of inserting a reactant pair at contact into denser crowders. As ϕ further increases, $R_p^{\prime }∕R_p$ decreases back to 1, reflecting the oscillatory nature of ΔG_c(r) at high ϕ. The weak effect of the interaction energy on $R_p^{\prime }∕R_p$ is a general result of the Debye formula, and is one of the limitations of the spherical model [28].

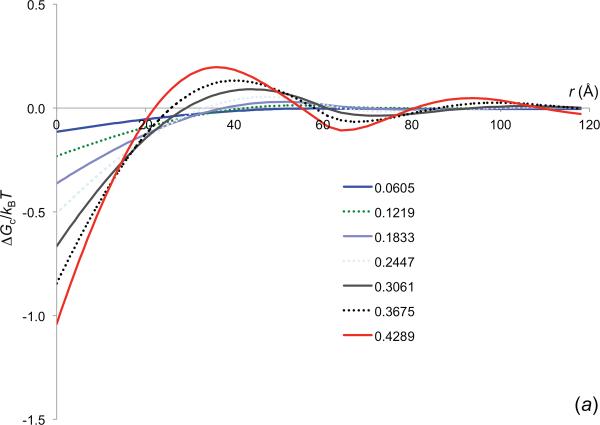
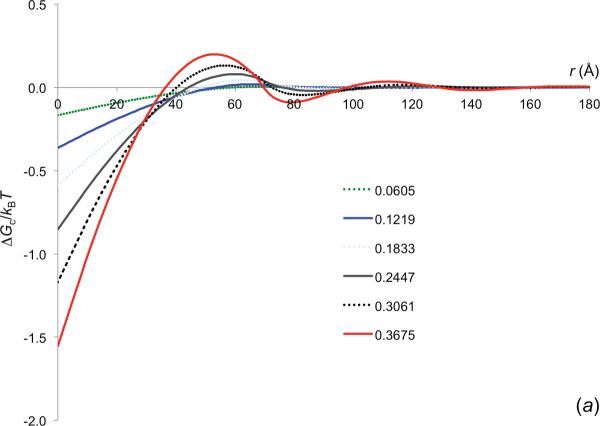
When the reactant molecules and the crowders have different radii, one could in principle obtain ΔG_c(r) from the pair distribution function of the reactant molecules present at infinite dilution within the crowders. However, the infinite dilution makes the pair distribution difficult to determine. On the other hand, our insertion method works equally well when the reactant molecules have a radius different from that of the crowders. In figure 4a we display the ΔG_c(r) results for R_p = 15 Å and R_c = 30 Å, at increasing crowder volume fractions. Note that, with increasing ϕ, ΔG_c(r) increases its value at the contact distance and becomes more and more oscillatory. These are similar to the results in figure 3 for R_p = 30 Å.

Figure 4.

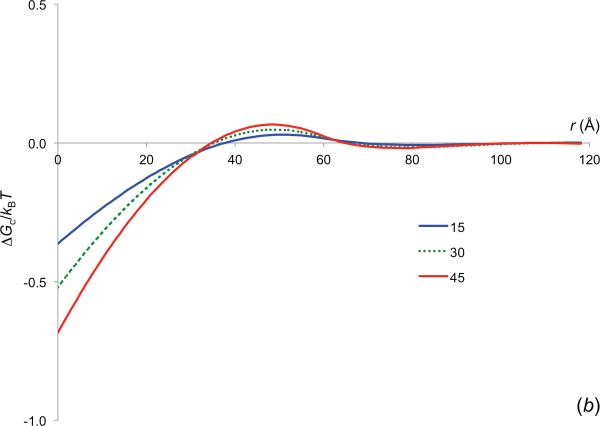
The effective interaction energy of the spherical reactants induced by crowders with R_c = 30 Å. (a) ϕ dependence of ΔG_c. R_p = 15 Å. (b) R_p dependence of ΔG_c. ϕ = 0.2447.

In figure 4b we display the ΔG_c(r) results for reactant molecules with increasing R_p, inside crowders with R_c = 30 Å and ϕ = 0.2447. As to be expected, the amplitude of ΔG_c(r) increases with increasing R_p, since it is harder to insert larger reactant molecules into the crowders than to insert smaller reactant molecules.

In addition to inducing an effective interaction energy ΔG_c(r), the crowders slows down the relative diffusion constant. When R_p = R_c, we can use the theory of Tokuyama and Oppenheim [27], which predicts

$$\frac{D_c}{D}=\frac{1-9\varphi ∕32}{1+L_1\left(\varphi \right)+L_2\left(\varphi \right)}$$ (9)

where

$$L_1\left(\varphi \right)=\frac{\varphi ∕{\varphi }_0}{{(1-\varphi ∕{\varphi }_0)}^2}$$ (10a)

with ϕ₀ = 0.57185, and

$$\begin{array}{cc}\hfill & L_2\left(\varphi \right)=\frac{2b_2^1}{1-b_1}-\frac{b_2}{1+2b_2}+[\frac{2b_1{b}_2}{1-b_1+b_2}\phantom{]}\hfill \\ \hfill & \times \left(1-\frac{6b_1{b}_2}{1-b_1+b_2+4b_1{b}_2}+\frac{2b_1{b}_2}{1-b_1+b_2+2b_1{b}_2}\right)\hfill \\ \hfill & +\frac{b_1{b}_2^2}{(1+b_2)(1-b_1+b_2)}(1+\frac{3b_1{b}_2^2}{(1+b_2)(1-b_1+b_2)-2b_1{b}_2^2}\phantom{)}\hfill \\ \hfill & -\phantom{[}\phantom{(}\frac{b_1{b}_2^2}{(1+b_2)(1-b_1+b_2)-b_1{b}_2^2})]\hfill \end{array}$$ (10b)

with b₁ = (9ϕ/8)^1/2 and b₂ = 11ϕ/16. The results for D_c/D at ϕ up to 0.5 are shown in figure 3b. As noted in the Introduction, the Tokuyama-Oppenheim theory predicts a 5-fold reduction in the diffusion constant at ϕ = 0.3. The reduction increases to 12.4-fold at ϕ = 0.4. Given that crowding results in just a minimal increase in $R_p^{\prime }$, the overall effect of crowding on the association rate constant of the spherical model is a decrease that essentially parallels that of the diffusion constant. The same conclusion holds when the reactant radius is different from the crowder radius, and is different from that for atomistically represented proteins, as we now show.

3.2 Barnase-barstar pair

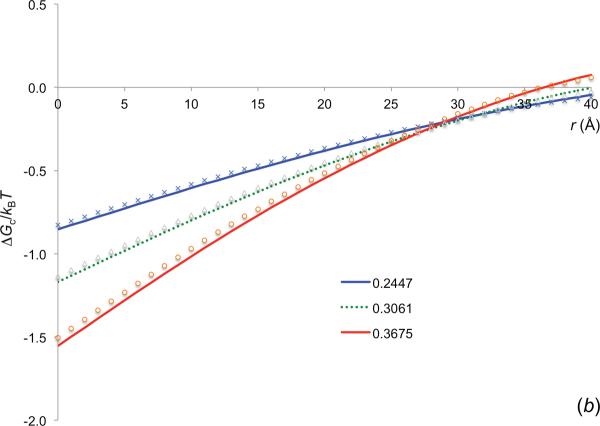
Using the insertion method, we obtained the crowder-induced interaction energy between barnase and barstar at various separations along the normal of the least-squares plane of the interface atoms. The results for inserting into crowders with R_c = 30 Å and 6 crowder volume fractions are shown in figure 5a. They are qualitatively similar to those in figure 4a for a pair of spherical reactant molecules with R_p = 15 Å. The magnitude of ΔG_c for the barnase-barstar pair is higher than for the spherical model. For example, at ϕ = 0.3061, ΔG_c is −1.2k_BT for the barnase-barstar native complex, but −0.7k_BT for the spherical contact pair. The difference can be attributed to the fact that the two protein molecules bury more surface areas than two tangent spheres. At high ϕ, the r dependence of ΔG_c for the barnase-barstar pair is also oscillatory, again reflecting the layered structure of the crowders around each reactant molecule. The oscillations start at r equal to the crowder diameter and have relatively small amplitudes. The weak interaction at such a long distance is not expected to have a significant biasing effect on the relative diffusion of the protein molecules, but as we suggest below, the crowder-induced interaction energy closer in will speed up the diffusional approach toward each other.

Figure 5.

The effective interaction energy of the barnase-barstar pair induced by crowders with R_c = 30 Å. The two protein molecules are moved along the normal of the least-squares plane of the interface atoms, (a) ϕ dependence of ΔG_c, calculated by the insertion method, (b) Comparison of the ΔG_c results obtained by the insertion method (curves) and predicted by the GMFT (symbols).

We previously developed an alternative, faster method for calculating ΔG_c, in the form of a generalized fundamental measure theory (GFMT) [34]. In figure 5b we show that, for r close to the crowder diameter, the GFMT results agree closely with the results obtained by the insertion method. At larger distances, the GFMT breaks down, but, as just noted, at such distances the effective interaction between the protein molecules is so weak as not to affect their relative diffusion. This means that we can use the GFMT for calculating the crowder-induced interaction energy in modeling the effects of crowding on protein association kinetics.

In our transient-complex theory for protein association [29, 37] (figure 6), we envision that, by translational and rotational diffusion, two protein molecules approach each other to form an intermediate with near-native relative orientation. From this transient complex, the protein molecules undergo further tightening and conformational rearrangement, leading to the native complex. When the second step is fast (relative to the dissociation of the transient complex), the overall process is rate-limited by the first, diffusional step, and the association rate constant can be calculated by (1). The validity of this equation depends on two conditions. First, the complex formed is stereospecific. In particular, it does not work for a spherical model. Indeed, for that case the Debye formula, (7), predicts a very different kind of dependence on the interaction energy. Second, the interaction energy that appears in the Boltzmann factor of (1) has to be long-ranged. For protein association in a dilute solution, the only long-ranged interaction is the electrostatic type. Short-range interactions cannot influence the diffusional approach to the transient complex (though they help determine the location of the transient complex and hence the basal rate constant k_a0).

Figure 6.

A schematic representation of the association process. Two protein molecules, represented by their electrostatic surfaces, diffuse to form the transient complex. Further tightening and rearrangement then lead to the native complex.

Now let us examine potential effects of the crowders on the association rate constant. As with spherical reactants, the crowders will slow down the relative diffusion of the protein molecules, resulting in a reduction of the basal rate constant. The basal rate constant for stereospecific complex formation depends on both the relative diffusion constant and on the rotational diffusion constants of the two reactant molecules; crowding reduces both, but to a somewhat lesser extent for the latter [10]. To a good approximation the slowing down of the relative diffusion translates to a reduction in the basal rate constant by the same factor.

The crowders could also possibly affect the location of the transient complex. In our view, the transient complex is dictated by the structure of the native complex. As long as the crowders do not change the structure of the native, which seems to be a safe assumption, the location of the transient complex is not likely to be significantly affected by the crowders. A recent experimental study involving many mutants of the TEM1-BLIP complex showed that the transient complex is unchanged by crowding [14].

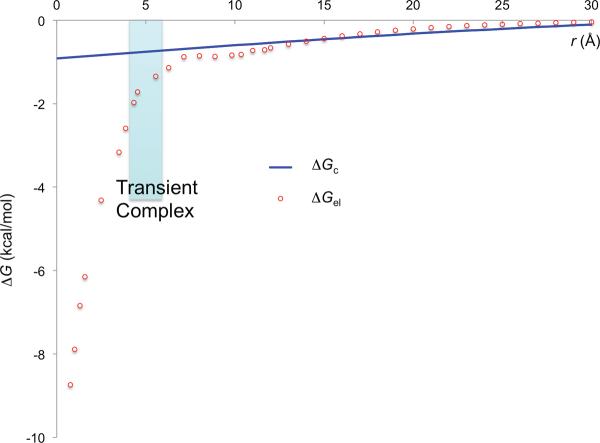
Finally the crowders can induce an effective interaction between the protein molecules on their way toward the transient complex, as figure 5 demonstrates. This crowder-induced interaction can be characterized as long-ranged, as a comparison of its dependence to that of the electrostatic interaction energy, a bona fide long-range force, shows (figure 7). Therefore the effect of the crowder-induced interaction energy ΔG_c on the association rate constant can be captured by an enhancement factor given by the Boltzmann factor exp (−ΔG_c*/k_BT), where ΔG_c* is the crowder-induced interaction energy for the transient complex. Combined with the effect on the basal rate constant, we obtain (2) for the association rate constant under crowding.

Figure 7.

Comparison of the r dependences of ΔG_el and ΔG_c for the barnase-barstar pair. The two protein molecules are moved along the normal of the least-squares plane of the interface atoms. For calculating ΔG_el, the configurations with 2 Å ≤ r ≤ 7 Å were rotated slightly to avoid clashes between the protein molecules; ionic strength = 150 mM. The shaded region corresponds to the range of r sampled by the transient complex.

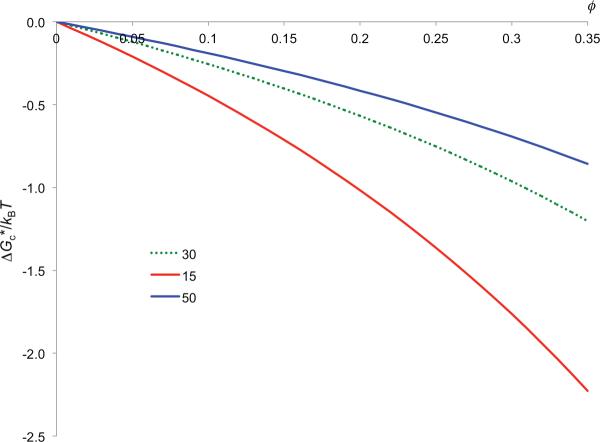
We generated the transient-complex ensemble for the barnase-barstar pair, and then applied the GFMT to calculate ΔG_c*. The transient-complex ensemble has separations of 4.7 ± 0.7 Å (mean ± standard deviation), and rotations of −3° ± 14° between the two protein molecules. The basal rate constant in a dilute solution is 9.2×10⁴ M⁻¹s⁻¹. With ΔG_el* = −2.9 kcal/mol at an ionic strength of 150 mM, (1) then predicts a rate constant of 1.3×10⁷ M⁻¹s⁻¹, in reasonable agreement with the experimental value of 7.8×10⁷ M⁻¹s⁻¹ [38]. In figure 8 we present ΔG_c* as a function of ϕ for the crowder radius at 15, 30, and 50 Å. For ϕ = 0.3 and R_p = 15 Å, ΔG_c* has a value of −1.8k_BT, which leads to a rate enhancement of 5.8-fold. This is offset by a ~5-fold reduction in the basal rate constant due to the slowing down of relative diffusion by crowding. The net effect of crowding is thus nearly null, in line with recent experimental results in cells and in crowded conditions [8–14].

Figure 8.

ϕ dependence of ΔG_c* for the barnase-barstar pair at three R_c values.

3.3 TEM1-BLIP pair

Recently we used the computational method illustrated above for the barnase-barstar pair to the association of another pair of proteins, TEM1 and BLIP [14]. At ϕ = 0.3, ΔG_c* has values of −3.3k_BT and −1.2k_BT, respectively, for R_p = 15 and 30 Å. These values are somewhat larger than those for the barnase-barstar pair, reflecting the larger sizes of the TEM1 and BLIP molecules (see figure 2b,c). Again, the crowder-induced interaction between the protein molecules results in a rate enhancement (3.3-fold for ϕ = 0.3 and R_p = 30 Å) that nearly offsets the effect of the slowing down of relative diffusion by crowding (~5 fold). In line with this prediction, the TEM1-BLIP association rate constant measured in 4–12% PEG 20 and 15% dextran 40 was (1.1 – 1.9)×10⁶ M⁻¹s⁻¹, nearly the same as the value of 1.1×10⁶ M⁻¹s⁻¹ measured in buffer [14].

4. Discussion

We have presented a computational method for calculating protein association rate constants under crowded conditions. The strategy for modeling the effects of crowding follows the postprocessing approach that we introduced previously for computing the effects of crowding on the thermodynamics and kinetics of protein folding and conformational transitions and the thermodynamics of protein association [33, 34, 39–42]. In the postprocessing approach, instead of simulating a biochemical reaction (e.g., protein association) in the presence of crowders, we calculate the changes in the free energies of the end states (the unbound state and transient complex in the case of protein association). We thus avoid simulating rare transitions between end states under crowded conditions. These transitions would be computationally demanding even without crowders. By the postprocessing strategy, we can afford to represent the proteins molecules (and even the crowders) at the all-atom level.

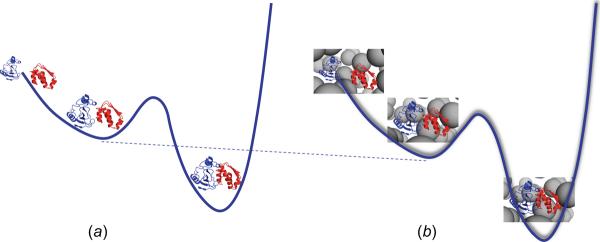
According to the transient-complex theory [29, 37], to form a stereospecific complex, two protein molecules, via translational and rotational diffusion, first approach each other to form a transient complex with near-native relative orientation. This diffusional process may be biased by long-range electrostatic attraction, correspondingly to moving on a down-hill energy surface (figure 9a). From the transient complex, the two molecules further tighten their interactions, which may involve a free-energy barrier, leading to the native complex. In a crowded solution, the crowders induce an effective interaction, which may further tilt the down-hill energy surface (figure 9b). However, the crowders also retard the diffusional process, thereby the effective friction on the path to the transient complex is increased. The two effects of crowding oppose each other, resulting in a very modest overall contribution. This explains recent experimental results for protein association in cells and in crowded solutions [8–14].

Figure 9.

Schemes of protein association in (a) dilute and (b) crowded solutions. In (a) the down-hill energy surface arises from electrostatic attraction between the protein molecules. In (b) the crowder-induced interaction energy further tilts the energy surface, but the crowders also effectively increase the friction (indicated by shading) on the path to the transient complex.

The limitations of the spherical model of protein association have been noted previously [28]. Here in the context of modeling crowding effects, we find that the spherical model predicts qualitatively incorrect results. According to the spherical model, the crowder-induced interaction has little effect on the association rate constant, and hence retardation of relative diffusion by crowding leads to a significant reduction in the association rate constant. In contrast, in an atomistic representation of the protein molecules, the crowder-induced interaction contributes a significant rate enhancement, which largely offsets the effect of the slow down in relative diffusion. To account for the stereospecificity of native complexes, some have used a reduction in the probability of forming the native complex while two spherical reactants are in contact. While this fix can produce the reduction in the magnitude of the association rate constant due to the stereospecificity, the predicted effects of crowding will still be incorrect, because the fix does not affect the diffusional approach to form the contact pair.

While the effects treated in the present study are essential, crowders may have other contributions. In addition to the excluded-volume interactions considered here, crowders may have soft interactions with the test proteins. This will change the magnitude and even sign of ΔG_c. Whether the additional contributions to ΔG_c are long-ranged is unknown and will critically determine how they contribute to the association rate constant. If the additional contributions are short-ranged, then they will have very little effect on the association rate constant. In contrast, if they are long-ranged, their effect will amount to an additional Boltzmann factor in (2).

The crowders could also perturb the electrostatic interactions between the test proteins by changing the dielectric environment. Previous studies have suggested that the dielectric constant in a crowded solution is moderated from a value of 78.5 for water at room temperature [43, 44]. If this is the case, then the electrostatic attraction between the test proteins will be strengthened. For example, upon changing the dielectric constant from 78.5 to 55, the electrostatic interaction energy in the transient complex of the barnase-barstar pair changes from −2.9 kcal/mol to −3.4 kcal/mol, resulting in a 3.4-fold increase in the rate constant. Additional computational and experimental studies will be needed to further quantify the contributions of crowders on protein association rate constants.

Technically, in the present treatment of protein association under crowding, the reactant protein molecules are present at infinite dilution. Even a protein concentration of 1 mM, which is much higher than concentrations of most individual protein species in either intracellular or extracellular spaces (as well as those typically used in kinetic measurements), corresponds to a volume fraction of just ~0.01. So our treatment applies to all these typical situations. The high total concentration of macromolecules in cellular environments comes mostly from the accumulation of many species. An exception is hemoglobin, which is present in red blood cells at high concentrations (ϕ ~ 0.3 [5]) and has mutant forms that can polymerize into long fibers. Protein association under such a “self-crowding” condition has been studied theoretically and by Brownian dynamics simulations [18, 22, 23].

We have not explicitly included hydrodynamic interaction (HI) in considering the relative diffusion of the reactant molecules. In dilute solutions, HI between the reactant molecules reduces the relative diffusion coefficient in a distance-dependent manner. As a result, diffusion-limited association rate constants are reduced by 20–50% according to theoretical calculations and Brownian dynamics simulations [45–48]. The effect of HI can thus be accounted for by slightly reducing the relative diffusion constant in our treatment. When crowders are present, they introduce additional HIs, which partly account for the slowing down in the relative diffusion of the reactant molecules at large distances; this is accounted for in our treatment by the change in relative diffusion constant from D to D_c. At shorter distances, the HI-induced decrease in the relative diffusion coefficient is probably not as strong as in the counterpart under dilute conditions. In short, the effects of HIs are probably to reduce D by 20–50% and D_c by a somewhat less amount. These effects result in just a very modest modification (e.g., ~10% increase) in k_ac0/k_a0.