A 3D glass optrode array for optical neural stimulation

Abstract

This paper presents optical characterization of a first-generation SiO₂ optrode array as a set of penetrating waveguides for both optogenetic and infrared (IR) neural stimulation. Fused silica and quartz discs of 3-mm thickness and 50-mm diameter were micromachined to yield 10 × 10 arrays of up to 2-mm long optrodes at a 400-μm pitch; array size, length and spacing may be varied along with the width and tip angle. Light delivery and loss mechanisms through these glass optrodes were characterized. Light in-coupling techniques include using optical fibers and collimated beams. Losses involve Fresnel reflection, coupling, scattering and total internal reflection in the tips. Transmission efficiency was constant in the visible and near-IR range, with the highest value measured as 71% using a 50-μm multi-mode in-coupling fiber butt-coupled to the backplane of the device. Transmittance and output beam profiles of optrodes with different geometries was investigated. Length and tip angle do not affect the amount of output power, but optrode width and tip angle influence the beam size and divergence independently. Finally, array insertion in tissue was performed to demonstrate its robustness for optical access in deep tissue.

1. Introduction

Optical methods are well established in the fields of neuroscience, medical imaging and diagnostics, etc. Optogenetics, for example, despite being a nascent field of study, was named the “Method of the Year 2010” by Nature Methods. Optogenetics is an approach to trigger gain or loss of function of explicit events in specific cells in tissue with temporal precision in the millisecond-scale, which is achieved through the use of light-sensitive control tools that may be targeted by gene delivery [1]. The control tools are mainly light-gated ion channels in the microbial opsin family; microbial opsins characterized for optogenetics include channelrodopsin-2 (ChR2; responsive to blue light for neuronal excitation), halorhodopsin (NpHR; responsive to yellow light for inhibition), channelrhodopsin from Volvox carteri (VChR; activated by green light), and ChR2 chimeras [2–5]. Optogenetics was first demonstrated using ChR2 in scattered hippocampal neurons in mammalian brain; non-invasive delivery of brief pulses of blue light prompted neuronal depolarization at the resolution of single spikes [6]. Similar experiments validating optogenetic induction of action potentials and control of synaptic transmission followed [7–9].

A method of optical excitation without requiring genetic manipulation is infrared neural stimulation (INS), where IR is applied as input energy. Like all other optical stimulation techniques, INS does not produce signal artifacts in electrical recordings due to the absence of direct charge injection [10]. Nerve stimulation with infrared light at 1064 nm was demonstrated in Aplysia in 1971 [11], but INS was first systematically analyzed in 2005 using rat sciatic nerve [10, 12]. In these experiments, a laser-coupled 600-μm optical fiber emitted a pulsed laser beam on a single spot on the sciatic nerve surface. Stimulation and ablation fluence thresholds were determined for several wavelengths between 2.1 and 6.1 μm; wavelengths with lower absorption coefficients had larger safety margins, while those having high absorption only stimulated at energies above the damage threshold. Other applications (e.g., stimulation of the cochlea, embryonic heart pacing) emerged using non-contact delivery of pulsed light via fibers as well [13–16]. Wavelengths of ∼1.87 and 2.12 μm, which exhibit similar absorption characteristics, have been extensively used across different applications, but other types of tissue may require different wavelengths for optimal stimulation such that the optical penetration depth is matched to the targeted excitable tissue. INS is believed to act via the induction of a spatio-temporal heat gradient in tissue [17], although the underlying physiological mechanism is still under investigation [18]. Infared-triggered temperature changes have been demonstrated to activate thermal transient receptor potential (TRP) ion channels [19], which can be genetically targeted to perform thermogenetic stimulation (similar to rhodopsins for optogenetic stimulation); these TRP channels are ∼ 1000× more sensitive than optogenetic tools (i.e., lower expression levels required) and have mainly been useful in the study of the relationship between specific neuronal activation to behavioral outputs in fruit flies, which does not require high temporal resolution [20–22].

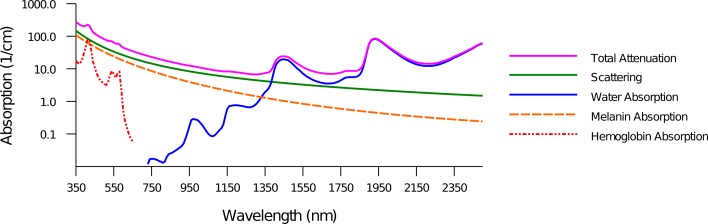
For highly effective optical stimulation, development of light delivery techniques is necessary to further effect deep tissue targets, utilize lower input energy and provide different spatio-temporal activation patterns; likely solutions include tissue penetration and use of more than one light guide or source during stimulation. In separate studies, light from an Argon laser projected through a digital micro-mirror device (DMD) and an array of high power micro light-emitting diodes (micro-LED) generated patterned excitation of neuronal slices expressing ChR2 [23, 24]. Still, these patterns were incident on the sample surface. The intrinsic tissue absorption and scattering limit light penetration to ∼1 mm and require higher energies at the surface to maintain threshold stimulation levels within the target volume underneath. Research with the mammalian brain with illumination at λ = 473 on the brain surface from a 100-μm fiber of 0.22 NA estimates that the irradiance decreases rapidly to 10% of the value on the surface within only 300 μm depth [25]. Fig. 1 plots a typical tissue attenuation spectrum, which is the combined scattering and absorption. Scattering is typically described by a combination of Rayleigh and Mie scattering; Rayleigh scattering scales as 1/λ⁴, while the scaling of Mie scattering is generally inverse with wavelength, with the power determined by the effective particle size. Tissue absorption is dominated by amino acids, nucleic acids, and fats below 450-nm wavelength, while absorption is dominated by (oxy)hemoglobin and melanin between 450 and 700 nm; beyond about 1400 nm, the dominant chromophore is water [26]. Overall, scattering dictates the light transport for wavelengths in the visible range, while water absorption prevails in the infrared. Although wavelengths in the near-IR window of 650–950 nm have been used in imaging to reach centimeters below the tissue surface due to very low absorption, the dominant scattering effect makes the detected signal at those depths very weak; spatial and temporal information about tissue activity and composition can still be determined as the techinique relies on variations in absorption and scattering within the volume [27]. This method, which is statistically modeled as a diffusion process, cannot be applied in optical stimulation mainly due to two reasons: (1) the wavelength range is not suitable for either optogenetics and INS, and (2) most results are gathered from scattering data whereas the intensity of light concentrated in a defined area is of interest in optical stimulation. Indeed, higher light intensity incident on cells expressing channelrhodopsin variants result in higher levels of action potential recordings [5]. Results of extraneural INS also reveal that effective stimulation in tissue requires wavelengths at relative valleys of the absorption spectrum; wavelengths having approximately zero penetration depths easily created nerve damage with threshold stimulation fluence, and wavelengths with very low absorption (i.e., absolute valleys in the spectrum) will likely fail to deliver sufficient amounts of energy to evoke a response [12].

Fig. 1.

Tissue attenuation spectrum. Light transport of wavelengths in the visible range is more strongly affected by scattering, while absorption is dominant in the infrared. Penetration depth (i.e., depth where intensity falls to 1/e of surface value) is limited to about 1 mm.

To circumvent tissue attenuation, penetrating optical probes have been designed. In the field of optogenetics, visible light has most commonly been delivered in vivo via a single laser-coupled optical fiber [28]. A 200-μm multimode fiber inserted through a cannula guide has been used for photostimulation of deep brain structures in freely moving mice [29–31]. For simultaneous awake stimulation and recording, an optical fiber through a zirconia ferrule was attached to a microwire array [32]. Similar commercially available optical probe packages, such as those from NeuroNexus (50 or 105-μm core fiber attached to a linear silicon probe with 16 electrical recording sites) [33], and an optetrode consisting of four microwires surrounding a multimode optical fiber [34] were also utilized successfully. Use of tapered optical fibers has been reported as well. A sharpened 50-μm fiber coated with gold was inserted in mouse brain slices to trigger localized epileptiform events; the same optrode was later integrated into a recording silicon multi-electrode array, replacing the center electrode for optical excitation of cells in a single cortical site [35, 36]. To provide 2D spatio-temporal control over multiple sites, tapered fibers were glued to a linear array of 4 or 8 commercially available planar silicon probes [37], which are an alternative to tungsten electrodes utilized in similar studies [38]. Experiments with ChR2-transfected rat hippocampus using these 2D arrays demonstrated multiple local stimulation with extensive recording of neurons. Optical and spatiotemporal stimulation characteristics of a 2D array of diode-coupled 50-μm tapered fibers in freely moving rat was presented as well [39]. Multi-site stimulation using a microfabricated multiwaveguide probe has also been proposed [40]. The device consists of parallel independent single-mode rectangular waveguides of silicon oxynitride core and oxide cladding that converge into a single probe; the paths end at different target depths along the probe axis and side-fires using a corner aluminum mirror. Transmission efficiencies are in the range of 23 to 33% as determined from bench testing.

For INS, a microfabricated 3D silicon waveguide array has been characterized [41, 42]. The 10 × 10 array has tapered microneedles with lengths varying in one direction from 0.5 mm to 1.5 mm in a 400-μm pitch. Its architecture provides intrafascicular access across the width and depth of the peripheral nerve. Light input from an optical fiber was coupled to the backside and output was recorded from the tips. Normalized output power ranged from 0.23 to 0.35 with longer optrodes performing at higher efficiencies; output beams had a nominal beam width and far-field full-angle divergence of 55 μm and 17°, respectively [41]. Despite the low efficiency, optrodes were able to stimulate responses in cat sciatic nerve [43]. Different optrodes activated different muscles and exhibited selectivity between different muscles innervated by different nerve branches (e.g. tibialis anterior and gastrocnemius (MG/LG)), between different muscles innervated by the same nerve branch (e.g. MG/LG and soleus (SOL) from the tibial nerve) and between presumed same nerve fascicle (e.g. MG and SOL). Comparable within-branch selectivity has not been reported for extraneural INS.

In this paper, we present a first-generation 3D glass penetrating waveguide array, which can be used for both optogenetics and INS for high-channel count patterned stimulation of independent neuron subpopulations. Two-level stimulation and flood illumination of multiple optrodes with overlapping output beams to effect a wider plane in tissue is possible as well. With these SiO₂ optrode arrays, nearly all modes of optical excitation (e.g., visible, infrared, multi-photon excitation) can be achieved with the penetration depth determined by the optrode length and not by wavelength. The device has application in basic and applied neuroscience research (e.g., studying information processing, neural control prosthetics), as well as in highly selective photodynamic therapy and deep tissue imaging for diagnostics and therapy. Detailed characterization of the optrode array is reported in this work. Note that optrode design features such as length, width, tip angle and spacing can be modified to suit a specific application.

2. Glass optrode array

The SiO₂ optrode array described in this paper consists of waveguide probes of constant length in a 10 × 10 grid with a 400-μm pitch. The optrodes, which have been fabricated in lengths ranging from 0.5 to 2-mm, are rectangular columns with pyramidal tips. The array is set upon a 1-mm thick backplane. Fig. 2 shows scanning electron micrographs of the glass array. Each optrode receives light from an aligned light source (e.g., edge-coupled optical fiber, collimated beam) to the backside; optrode tips emit light that is locally delivered to tissue. The backplane in between optrodes may also allow light to pass through for shallower targets.

Fig. 2.

SEM image of a 3D optrode array made from glass. (a) 10×10 rows of 1.5-mm long and 150-μm wide optrodes. (b) Profile of optrode geometry. (c) Definition of optrode sections along path of light propagation: 1-mm backplane, base extending 100 μm into straight-edge shank and 120-μm long linearly tapered tip.

2.1. Fabrication

Fabrication of these 3D glass arrays rely heavily on bulk-micromachining. Glass (fused silica or quartz) wafers with 3-mm thickness and 50-mm diameter are used as substrates; such material allows transmission of wavelengths both within the visible spectrum and the near-IR range. One wafer yields 23 arrays.

2.1.1. Tip formation

The tips were formed using a Disco DAD 640 dicing saw with a bevel blade. The blade is essentially a v-shaped blade with its vertex clipped into a flat that separates the bevels. The angle of the bevel defines the tip taper angle (i.e., angle of taper with respect to the optical axis). Shallow cuts spaced 400 μm apart (i.e. optrode spacing) were made on the wafer surface in orthogonal directions; each cut creates a face of the pyramidal tip on two adjacent optrodes. Fig. 3 shows the initial array structure after bevel dicing. Here, each face of the pyramidal tip tapers off at 45°.

Fig. 3.

Array after bevel dicing (a) to form pyramidal tips (b).

Note that the tips of these glass optrodes were shaped with dicing rather than the etching technique in silicon optrodes fabrication [41, 44]. Etching silicon can be a diffusion-limited process; as the etching reaction proceeds, the byproducts impede the etchant interaction with the shank surface within the array such that the more exposed column tips are preferentially etched. In glass however, the much slower etch rate (one-tenth of the Si etch rate) creates a reaction-limited process that uniformly etches the optrode along its length and thus does not sharpen the tips.

2.1.2. Shank dicing

The shanks were then defined by column dicing; deep kerfs were made in between the pyramids to create rectangular pillars. An extra row on all sides of each array is placed to maintain uniformity in optrode geometry within the 10×10 grid during subsequent wet etching. The average column width after dicing was 240±15μm. The resulting optrode architecture consists of a pyramid atop a rectangular shank, as pictured in Fig. 4.

Fig. 4.

Shank formation. Array after column dicing (a) has optrodes with pyramidal tips atop rectangular shanks (b). Array after etching (c) has thinner optrodes with the same shape as before.

2.1.3. Etching

Etching the arrays thins the shanks. The dynamic etching technique of the Utah Electrode Array was adapted [44]. The glass wafer was secured with wax onto a Teflon sheet, which was screwed on a Teflon base plate. The wafer was then immersed with columns facing down into 1500 ml of 49% HF; the wafer was rotated clockwise at (22 rpm) at the same time a magnetic stirrer in the solution was propelled counter-clockwise (500 rpm). The stirring action allow the continuous, aggresive etching of the high aspect ratio optrodes that minimizes surface scalloping by preventing the accumulation of the byproducts that tend to precipitate on the sidewalls. The etch rate is about 2.5 μm/min at room temperature. Fig. 4(a) shows the thinned optrodes having the same shape as before etching.

2.1.4. Annealing

The wafer was annealed at 1150°C for 6 hours to further reduce surface roughness of the shanks that resulted from both dicing and etching [45]. Surface roughness must be minimized to avoid significant scattering loss for light transmission. Annealing also relieves internal stresses in the glass. Fig. 5 shows a sample glass surface before and after annealing; etching produces the scalloping, which is greatly reduced by subjecting the arrays to the anneal temperature at extended hold times. The resulting RMS surface roughness was measured by atomic force microscopy (AFM) as 22 nm.

Fig. 5.

Side-by-side comparison of same glass surface after dicing and HF wet etching (a), and subsequently after annealing (b) to reduce surface roughness. RMS surface roughness after annealing is measured as 22 nm by AFM.

2.1.5. Singulation

The extra rows acting as sacrificial features were diced out using a resin blade to yield 10 × 10 arrays. Individual arrays were finally separated from the wafer by dicing through the backside. Fig. 2(a) shows a singulated array.

3. Theoretical loss mechanisms

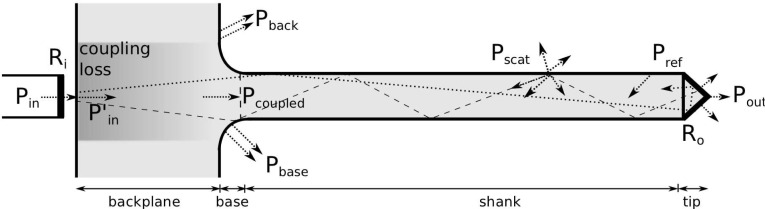
System losses in the optrode are expected to include Fresnel reflectance (R), coupling, back-reflection and scattering. Reflection inside the optrode tips is suspected to be the dominant loss mechanism, especially since the tapered tip of silicon optrodes has been determined as the major contributor of loss in silicon arrays [41]. Fig. 6 shows where each type of loss occurs. The source power P_in reduces to P′_in by the transmittance Ti = (1 − R_i) upon entering the glass backplane. The power exiting the optrode tips is P_out. P_back and P_base are radiation losses that constitute part of the coupling loss; the power coupled into the shanks is P_coupled. P_ref is the lump sum of reflected power towards the source from all sections within the device, while P_scat is the scattering loss due to the sidewall roughness. Absorption loss is assumed negligible. The variables are related through

$$P_{\mathit{in}}\times \left(1-R_{\text{i}}\right)=P_{\mathit{in}}^{\prime }+P_{\mathit{back}}+P_{\mathit{base}}+P_{\mathit{out}}+P_{\mathit{ref}}+P_{\mathit{scat}}.$$

The glass optrodes do not suffer from radiation loss through the shanks unlike tapered silicon optrodes [41]. Consequently, glass optrodes of different lengths are expected to exhibit the same transmission efficiency because there is no taper slope difference to consider.

Fig. 6.

Loss mechanisms within the glass optrode include Fresnel reflectance (R_i/o), coupling, backreflection and scattering.

3.1. Fresnel reflections

Refractive index contrast between the array and the surrounding medium (e.g., air, tissue) results in Fresnel reflection at the optrode backside and tip (i.e., input and output interfaces). Table 1 lists relevant refractive indices (n) at visible and near-IR wavelengths. Although an in-coupling optical fiber closely matches the index of the glass array, it leaves an air gap junction with the array backside during edge-coupling; the gap forms a double interface that suffers from a larger Fresnel reflection loss. Table 2 shows approximate reflectance values as computed from

$$R={\left(\frac{n_1-n_2}{n_1+n_2}\right)}^2$$ (1)

and

$$R_{\text{eff}}=1-\left(1-R_1\right)\left(1-R_2\right)=R_1+R_2-R_1{R}_2$$

for single and double interfaces, respectively. Variables n₁ and n₂ are the refractive indices on either side of the interfaces, while R₁ and R₂ are determined from Eq. 1. As computed, the loss due to Fresnel reflection is relatively small and may further be reduced with the use of index matching fluid at the input side to fill the air gap.

Table 1.

Refractive Indices at Visible and Near-IR Wavelengths.

Material	nvisible	nnear–IR	Reference
Air	1.00	1.00
Fused silica (optrode/fiber)	1.46	1.44	[46]
Quartz (optrode)	1.54	1.52	[46]
Index matching fluid	1.45	1.44	[47]
Tissue	1.36	1.36	[48]

Table 2.

Nominal Reflectance at Interfaces

Interface	Reflectance (R)	Transmittance (1-R)
Fiber - Air - Optrode	0.065	0.935
Fiber - Index fluid - Optrode	0.001	0.999
Optrode - Tissue	0.004	0.996
Optrode - Air	0.034	0.966

3.2. Coupling loss

Mismatch and misalignment between the optical source and the optrode waveguide result in coupling losses. Mismatch is considered an intrinsic loss caused by differences in core cross-sectional area (A) and numerical aperture (NA); the coupling efficiency (η) accounting for these losses are presented in most textbooks in fiber optics [49]. For a fiber coupled to an optrode for instance,

$${\eta }_A=\frac{A_O}{A_F}$$ (2)

and

$${\eta }_{\text{NA}}={\left(\frac{{\text{NA}}_{\text{O}}}{{\text{NA}}_{\text{F}}}\right)}^2,$$ (3)

where the subscripts O and F indicate the optrode and fiber, respectively. Misalignment arises as an extrinsic loss from lateral and angular displacement as well as end separation. Using lenses may couple more light into the optrode, but bench testing results in this paper were extracted by direct-coupling the source to the optrode for simplicity.

3.3. Scattering

Surface scattering may also contribute to transmission losses within the optrode. The amplitude and the spatial periodicity of the sidewall roughness after dicing and etching cannot be completely eliminated by annealing and thus may attenuate guided mode propagation due to light scattering. The concept of total integrated scatter (TIS) mathematically models the total amount of light scattered by a surface from a single reflection as [50]

$$\mathit{TIS}=R\left\{1-\mathit{exp}\left[-{\left(\frac{4\pi \sigma \cdot \mathit{cos}\left({\theta }_i\right)}{\lambda }\right)}^2\right]\right\},$$ (4)

where R is the theoretical surface reflectance (100% under total internal reflection conditions), σ is the RMS surface roughness, θ_i is the incidence angle of the ray with respect to the normal of the surface, and λ is the wavelength. This equation suggests that: reflective surfaces inherently scatter more light, shorter wavelengths scatter more than longer wavelengths, and maximum scattering occurs when light strikes the surface at normal incidence.

TIS will accumulate based on the total number of reflections experienced during propagation, which may be estimated for a meridional ray in a straight waveguide as

$$N_R=\frac{L}{t\cdot \mathit{cot}\left({\theta }_m\right)},$$ (5)

where L is the length of the waveguide, t is its thickness, and θ_m = 90° − θ_i is the ray propagation angle with respect to the optical axis. For a ∼100 micron-sized waveguide, the number of reflections is limited; smooth sidewalls then contribute to little surface scattering. However, when inserted into tissue, inhomogeneity at the optrode-tissue interface will contribute to additional scattering loss.

3.4. Total internal reflection in the tips

With the use of smaller fibers from which a large fraction of the light will be coupled into the shank, backreflected power is expected to come from the tips (additional backreflection will result from the backplane and the base when using larger diameter beams). Due to the tapered geometry of the tips, not all rays will be able to exit and instead reflect back towards the source. The angle of total internal reflection (TIR) for the glass-air interface is about 40°.

4. Optical characterization results and discussion

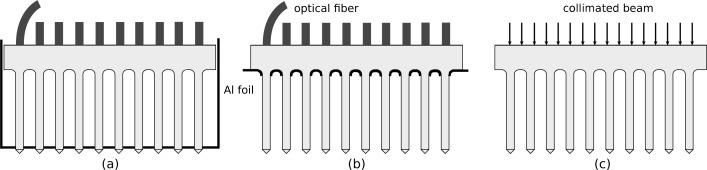
Output from the optrode tips was measured and profiled in air. In most measurements, a single bare fiber was mechanically aligned to the array backside through an intervening medium of n ≈ 1.45; the matching index medium eliminates the air gap (i.e., reflection losses) resulting from the fiber being only in contact with (i.e., not attached to) the array. The fiber is moved from one optrode to the next across the array, with the optrode tips inserted through aluminum foil, as shown in Fig. 7(a); the foil blocks radiation and scattering from the shank, base and backplane. Fig. 7(b) is a similar setup, except the foil is brought up to the backplane to expose the shanks during the measurements; this allows collection of any scattered light from the shank. Power from collimated beams was also coupled into the optrode shanks, but transmission through the backplane in between optrodes was assessed by removing the foil, as illustrated in Fig. 7(c). Three fiber-coupled lasers at wavelengths 640 nm, 1550 nm and 1875 nm, and a white light source provided the optical input. Planar photodetectors, an integrating sphere or a beam profiler collected the output in various experimental setups. Output power is normalized with respect to the power of the beam incident on the optrode backside.

Fig. 7.

Experimental Setup. (a) Determining output power and beam profile from optrode tips using in-coupling fibers. (b) Determining output power from optrode shanks and tips using in-coupling fibers to estimate shank losses. (c) Measuring transmission through optrode tips and array backplane using a collimated beam.

4.1. Coupling from different fiber sizes

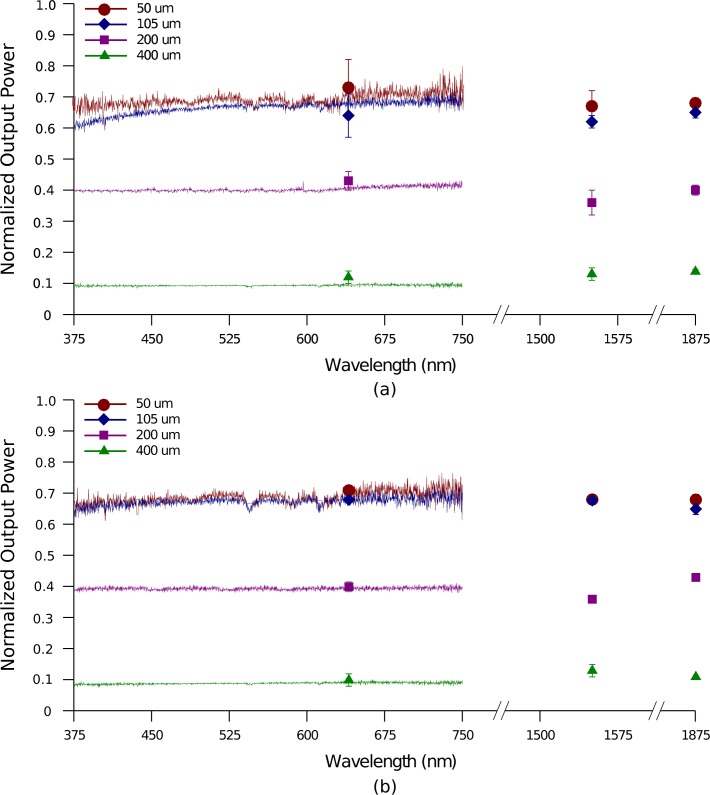
Fused silica fibers with 0.22 NA and core diameters 50, 105, 200 and 400μm coupled the optical source to optrodes having 150-μm wide, 1.5-mm long shanks and 45° tip taper. The setup in Fig. 7(a) was first utilized. Transmission about the visible spectrum (e.g., 375 – 750 nm) through the optrodes was quantified by using a broadband light source as input and an integrating sphere attached to a spectrometer as readout interface. Discrete wavelengths were also transmitted and the power emitted by the optrode tip was measured with corresponding photodetectors positioned normal to the optrode shank. Fig. 8 plots the resulting normalized output power from the tips with using different in-coupling fibers. The highest transmission attained is about 71% for fiber sizes less than the shank cross-sectional area. The scaling down of the output power with larger fibers follows the fraction of Eq. 2, which puts a limit on the amount of power coupled into the shanks from the incident beam. The optrode arrays transmit the spectrum from visible to near-IR approximately with the same efficiency. Note that optrodes implanted in tissue are likely to exhibit a slightly higher efficiency as the lower refractive index mismatch causes a decrease in output Fresnel reflectance and an increase in the critical angle to allow more power to exit out the tips.

Fig. 8.

Transmission of a broadband light source and several discrete wavelengths through the optrodes (150-μm wide, 1.5-mm long shanks and 45° tip taper). In-coupling fibers of different core sizes with 0.22 NA were used. Optrode output from only the tips (a) and from both shanks and tips (b) was measured relative to power from fiber.

Normalized output power from both optrode shanks and tips are plotted in Fig. 7(b) to determine shank losses from either radiation or scattering; any additional power measured in this configuration with respect to the results in Fig. 8(a) constitutes the shank loss. Comparison reveals that the difference between the data points of Fig. 8(a) and (b) is 0.002 (on the 0 to 1 scale) on average, suggesting negligible radiation and scattering from the optrode shanks. Radiation from the shanks is not expected since the shanks are not tapered; scattering is established as an insignificant loss, especially upon consideration of the optrode lengths in use (i.e., less than 1 cm propagation).

4.2. Illumination with a collimated beam

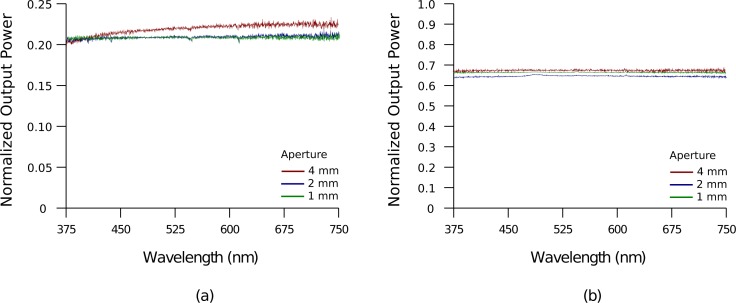
Instead of delivering light in smaller beams via fibers, a 4-mm wide collimated beam was used to shine light on the entire array backside in the setup of Fig. 7(a) to evaluate potential use of flood illumination with matrix switching (e.g, DMD, LCD) [51, 52]. To simplify testing, apertures were used to allow light through a localized area. Fig. 9(a) shows the power of the visible spectrum from the optrode tips normalized to the power of the beam out of the aperture as measured with an integrating sphere; the 2-mm aperture coupled light into 25 optrodes, while only 4 optrodes were illuminated with the use of a 1-mm aperture. Regardless of how many optrodes were illuminated, the efficiency remains the same. Note that if there were only one flood light as source, and optrodes were selected for transmission using a spatial light modulator, the efficiency would be the same except that the total output power would be less due to parts of the input beam being blocked.

Fig. 9.

Transmission of a broadband light source through optrodes (150-μm wide, 1.5-mm long shanks and 45° tip taper). A 4-mm wide collimated beam was used as input and restricted with apertures of different diameters. Light from optrode tips (a) and through backplane (b) were measured relative to the beam power through the aperture.

Due to interest in multilevel excitation, the transmission through the backplane was measured as it may deposit light in a shallow region of tissue near the surface. Fig. 9(b) plots the normalized transmitted power from the backplane alone, which was calculated by measuring the output power using the setup of Fig. 7(c) (i.e., array without blocker foil) and substracting the results of Fig. 9(a). Since light scattering from the shanks is negligible, as verified by the results in section 4.1, the additional power detected when the foil is removed is due almost entirely to transmission through the backplane. More power passes through the backplane than the tips as the interstitial space of the backplane occupies a greater area in the array. Futhermore, TIR does not occur at the backplane-air interface.

4.3. Transmission vs. optrode geometry

Geometrical features of a single optrode are its width, length and tip taper angle. To test the effect of the optrode geometry on its transmission, the setup in Fig. 7(a) was utilized with a 50-μm fiber coupling the white light source or single wavelength lasers to the optrodes. From the results discussed in section 4.1, it is evident that a change in the shank width, much like a change in fiber size, will scale the normalized output power from the tips according to Eq. 2. Thus, less power can be coupled into a narrower optrode shank and less output power will be measured consequently. For shanks having larger cross-sectional areas than the fiber core, output power is the same; for instance, a 95-μm wide optrode outputs the same amount of power as a 150-μm wide shank when using a 50-μm in-coupling fiber, as shown in Fig. 10 On the other hand, shank length does not affect transmission efficiency, as corroborated by the results in Fig. 10; this also supports the absence of scattering within and radiation out of the optrode shanks. Optrodes with a 45° tip taper of lengths (L) 0.5, 1.0, 1.5 and 2.0 mm were used. The normalized output power remains constant with varying optrode length because the shanks are straight and retain total internal reflection with negligible losses; this characteristic is contrary to that of tapered silicon optrode shanks, where the length defines the taper and ultimately determines the efficiency [41]. Lastly, the influence of the tip taper angle (θ) on the output power was observed. Fig. 11 shows tips with a taper angle of 45° and 30°. There was no conclusive difference between the results from 30° and the 45° tips. Although more rays theoretically undergo TIR in the sharper 30° tips, not all of these rays contribute to losses; some rays instead refract out through side firing as discussed in section 4.5.

Fig. 10.

Transmission of a broadband light source and several discrete wavelengths through the optrodes of varying length L, tip taper angle θ and width W. 50-μm core in-coupling fiber with 0.22 NA was used. Output from optrode tips were measured relative to power from fiber.

Fig. 11.

Optrode tips with 45° (a) and 30° (b) taper angle with respect to the the progation direction (i.e., vertical axis). Shank width is 150 μm.

The results, along with those presented in section 4.5, suggests that the optrode width, length and tip taper angle are independent variables that may be customized during the fabrication process in order to manipulate optical characteristics of the optrode.

4.4. Identifying system losses

From the results of the previous sections, loss at the input side is almost entirely due to coupling. Still, 30% of the input power is not transmitted out of the tips when coupling from fibers smaller than the shank cross-sectional area; this is true whether the array used for measurement is poked through foil or not. This loss is then due to scattering from the shank and/or TIR in the tip.

The experimental results indicate that scattering in the shank is an insignificant source of loss for the glass optrode. This is supported by considering Eq. 4. Based upon the NA of the fibers used, the largest ray angle with respect to the optical axis is θ_m ∼ 9°. Given the dimensions of the optrodes (i.e, width and length), the distance between reflections is about 1 mm for the 150 μm wide shank and 600 μm for the 95 μm shank; therefore, at most three reflections may occur inside the optrode shank. The surface roughness of the optrode measured by the AFM is 22 nm, which is relatively smooth for optogenetics and INS wavelengths according to the Rayleigh scattering criterion σ < λ/(8cosθ_i). With this σ value, the total integrated scatter (TIS) associated with a ray striking the shank sidewall is 0.8% (assuming a wavelength λ = 475 nm and θ_i = 81°). The estimated maximum scattering loss from the shank is then about 2–3%, which is greater than the experimental estimates. The conclusion is that the dominant loss mechanism is the loss of rays transmitting through the tips due to TIR.

4.5. Beam profiling

Output beam profiles were obtained to determine the effective spot size, divergence and excitation volume of the light from the optrode tips. Profiles were taken from three sets of optrodes, which differ in width (i.e., 95 or 150 μm) and/or tip taper angle (i.e., 45 or 30°). Tables 3 and 4 shows values of parameters characterizing the profiles, which includes the beam width (2W₀) at 13.5 % of peak power, far-field full divergence angle (ϕ) and Rayleigh distance (z_R). Fibers of different core sizes with 0.22 NA were used to couple IR (1550 nm) and red (640 nm) light into the optrode backside.

Table 3.

Output beam width (2W₀) in μm at 13.5 % of peak power for different optrode geometries (tip taper angle of 45° or 30° and shank width of 95 μm or 150 μm) at two wavelengths (IR and visible). In-coupling fibers of various core diameters (d_f) were used.

df (μm)	Optrode 2W0
	λ = 1550 nm			λ = 640 nm
	45°	45°	30°	45°	45°	30°
	95μm	150μm	150μm	95μm	150μm	150μm
50	60	123	118	62	127	119
105	68	122	124	62	125	113
200	73	136	123	63	137	127
400	81	145	123	88	144	121

Table 4.

Output beam far-field full angle divergence (ϕ) in ° and Rayleigh range (z_R) in μm for different optrode geometries (tip taper angle of 45° or 30° and shank width of 95 μm or 150 μm) at two wavelengths (IR and visible). In-coupling fibers of various core diameters (d_f) were used.

df (μm)	Optrode ϕ(zR)
	λ = 1550 nm			λ = 640 nm
	45°	45°	30°	45°	45°	30°
	95μm	150μm	150μm	95μm	150μm	150μm
50	13.7 (245)	16.1 (438)	56.6 (119)	16.5 (220)	17.5 (413)	61.3 (111)
105	15.8 (255)	15.5 (462)	55.9 (128)	18.9 (194)	18.7 (388)	57.0 (113)
200	16.2 (257)	20.0 (390)	69.1 (102)	19.2 (188)	21.0 (372)	76.5 (95)
400	19.9 (233)	20.7 (404)	83.0 (85)	22.7 (224)	22.9 (361)	102.7 (68)

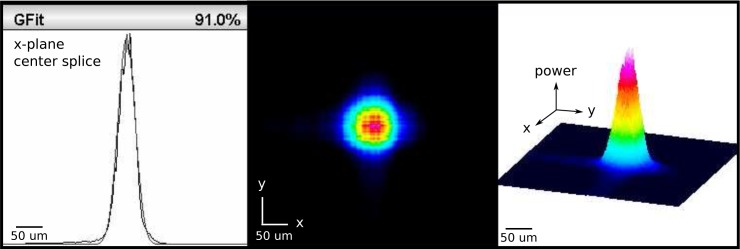
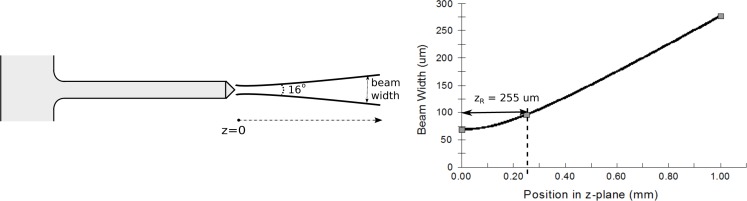
Output beams take a near-Gaussian form much like the power profile shown in Fig. 12 measured from a 150-μm wide optrode with 45° tip taper angle using a 105-μm in-coupling fiber. The optrode width appreciably affects the output beamwidth, which does not change significantly with tip angle and input wavelength. On the other hand, the output divergence is consistent regardless of optrode width, but significantly changes with the tip taper angle. The spatial divergence of the same optrode used in Fig. 12 is plotted against the propagation distance along the z-plane in Fig. 13; an optrode of the same width but having a 30° tip angle diverges 40° more. An advantage of having the ϕ = 56° full angle divergence instead of 16° is that light can be delivered to a continuous plane at about 150 μm depth from the tip when a block of optrodes in the array is excited. A lower tip taper angle causes more rays to undergo TIR, and these reflections most likely strike opposite faces of the tip that lead to a greater occurrence of side-firing and hence the higher divergence observed. It then follows that the Rayleigh distance for the 30° tip is much shorter. The Rayleigh distance represents the distance over which the beam width increases by a factor 2, and, along with the beam width, roughly defines the volume of maximum energy deposition into the tissue (provided that z_R is smaller than the tissue attenuation length). Because the optrode width only influences the beam width and the tip taper angle only modifies the divergence of the beam exiting the tips, these two geometric parameters can be set independently of each other to get the desired output beam profile. Note that this characteristic is not applicable to the Si optrode as its width and taper are concurrently set by the etching process [41].

Fig. 12.

Beam profile from 150-μm wide optrode with 45° tip taper angle using a 105-μm in-coupling fiber. Power is relative to peak.

Fig. 13.

Changes in beam width with propagation distance from 150-μm wide optrodes with 45° tapered tips; λ =1550 nm was coupled to a 105-μm in-coupling fiber of 0.22 NA.

When comparing the divergence of the IR and red beams, the divergence is slightly increased for red. The slightly higher refractive index of glass at shorter wavelengths may explain this observation; the higher refractive index at the input side accompanies a higher angle of refraction at the output. In tissue, the beam divergence is expected to be smaller according to Snell’s law for both visible and near-IR wavelengths because the refractive index on the output side increases to n = 1.34. In addition, the critical angle increases and the output of an optrode with 30° tip taper may due to light refracted through the first interface, instead of side-firing through the second interface due to TIR at the first. Consequently, the beam width may be smaller.

5. Optrode insertion in tissue

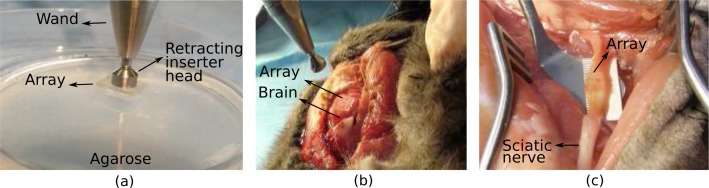
The feasibility of using glass optrode arrays for tissue penetration was tested, but only the ease of implantation and durability of the arrays were examined (i.e., tissue trauma has not been studied with histological data). Three arrays, consisting of 150-μm wide and 1.5-mm long optrodes with 45° tips, were tested in 2% agarose; the same arrays were later inserted post mortem in cat brain (dura removed) and sciatic nerve. Each insertion was repeated at least three times. To begin, the array was rested on the surface of the tissue with the tips facing down. Next, a pneumatic wand inserter was positioned against the optrode backside, where an impulse of force was exerted depending on the desired insertion depth (e.g, 1.5 mm in this case). Fig. 14 illustrates the wand, insertion setup and the implanted arrays. The arrays penetrated the brain and sciative nerve smoothly. However, the curvature of the brain caused difficulty in setting the array in position immediately. In addition, a mechanical support (e.g., ruler) underneath the sciatic nerve was needed to keep the nerve in place during insertion. The arrays were then removed and inspected; the backplane did not fracture and all 100 optrodes were intact after all tests. Overall, all arrays were able to withstand the impact of insertion into tissue.

Fig. 14.

A pneumatic wand inserter was used to fully implant the optrode arrays into 2% agarose (a), cat brain (b) and cat sciatic nerve (c). Arrays were intially rested on top of the tissue with the tips facing down; optrodes smoothly penetrated tissue. Optrodes are 150-μm wide and 1.5-mm long with 45° tips

6. Conclusion

First-generation penetrating glass waveguide arrays for optical stimulation (e.g., optogenetics, INS) have been designed and tested. SiO₂ wafers were used to fabricate a set of arbitrarily-sized (e.g., 10 × 10) arrays by dicing, etching and annealing. Optrode spacing, length, width and tip angle may be independently altered to obtain varying spatial resolution, depth access, output beam width and output divergence, respectively. Output power was measured from the optrode tips; fibers of different core sizes were coupled one at a time to an optrode. Input Fresnel loss with a butt-coupled fiber is computed as 6.5%, but may be eliminated with an index-matching medium. The maximum transmission efficiency obtained was approximately constant at 70% with a 50-μm or 100-μm fiber for wavelengths in the visible spectrum, at 1550 nm, and at 1875 nm. About the same level of output power was measured for varying optrode length and tip taper angle. The decrease in output power with larger fibers follows the limit imposed by coupling efficiency due to area mismatch. As an alternative to in-coupling fibers, a 4-mm collimated beam of white light was used as input to determine the feasibility of implementing flood illumination with optrode selective switching. Applying the same 4-mm beam, transmission through the base was also tested, where majority of the light incident on the array backside passes through.

Shank losses were trivial compared to coupling. Taper losses are not present in the optrode shank, while scattering is considered insignificant because light travels at a grazing incidence along a relatively smooth shank. With an input fiber smaller than the optrode shank, the majority of system loss is determined to come from the tips, where total internal reflection towards the source dominates over Fresnel loss and scattering. However, total internal reflection may also lead to side-firing in less tapered tips such that a wider output beam divergence is observed. The beam divergence is much greater for 30° tips, while the beam width is proportional to the shank width regardless of tip angle. Using a 105-μm fiber, a 150-μm wide optrode with a 45° tip taper emits a λ = 1550 nm beam with 122 μm diameter and 16° far-field full angle divergence.

Repeated optrode insertion in brain and nerve tissue demonstrated the suitability of the arrays as a neural interface in terms of depth access and durability. The current efficiency of these glass arrays does not leave much room for improvement, except to possibly modify the tip shape and apply an anti-reflection layer to the tip surfaces to reduce Fresnel losses.