Abstract
The structural anisotropy of biological tissues can be quantified using polarized light imaging in terms of birefringence; however, birefringence varies axially in anisotropic layered tissues. This may present ambiguity in result interpretation for techniques whose birefringence results are averaged over the sampling volume. To explore this issue, we extended the polarization sensitive Monte Carlo code to model bi-layered turbid media with varying uniaxial birefringence in the two layers. Our findings demonstrate that the asymmetry degree (ASD) between the off-diagonal Mueller matrix elements of heterogeneously birefringent samples is higher than the homogenously birefringent (uniaxial) samples with the same effective retardance (magnitude and orientation). We experimentally verified the validity of ASD as a birefringence heterogeneity measure by performing polarized light measurements of bi-layered elastic and scattering polyacrylamide phantoms.
OCIS codes: (170.3660) Light propagation in tissues, (110.0113) Imaging through turbid media, (260.1440) Birefringence, (260.5430) Polarization
1. Introduction
Diseases such as cancer, myocardium infarction and bladder obstruction involve microstructural alterations in the biological tissues [1–4]. One of these microstructural characteristics is anisotropy caused by fiber (and/or cellular) alignment which can be quantified as birefringence [5]. Birefringence is usually derived from the tissue’s Mueller matrix and polarimetric measurements [3,4,6–10]. But tissue properties, including birefringence, may be spatially varying; in particular, layered tissue often exhibits depth-dependent properties in its different layers. Thus, the Mueller matrix measured via polarized light imaging contains contribution from the entire sampling volume, and the derived birefringence is the effective value. However, as revealed by microscopy studies, biological tissues are often composed of layers with different anisotropy [11,12]. The question then becomes whether the derived anisotropy metrics arise from a homogeneously anisotropic (uniaxial) material, or instead represent an effective average from a heterogeneously anisotropic one. One approach to resolve this ambiguity altogether is to perform depth-resolved acquisition of polarimetric data and from there derive the birefringence information of the different layers. Several groups have demonstrated Mueller matrix measurement of different tissues using polarization sensitive optical coherence tomography (PS-OCT) [13–15]. Although this technique has been used to map the birefringence values in the 3D structure of various tissues, it suffers from low penetration depth. A similar drawback is encountered in depth-resolved linear and non-linear microscopies with polarization-sensing capabilities [16].
While the depth resolve techniques can determine the birefringence magnitude and the orientations projected in the imaging plane within their axial resolution limit, the Mueller matrix itself obtained from the polarimetric depth-averaged measurements contains a lot of information, including potentially an answer to the above homogenous versus heterogeneous question. The depth averaged Mueller matrix can be experimentally measured in biological tissues both in transmission and backscattering mode [17]. Depending on the tissue’s optical properties (absorption, scattering magnitude and anisotropy) and the detection angle, the Mueller matrix can be representative of few millimeters deep into the tissue [3,17,18]. Of great importance is the cumulative phase retardance δ ( = 2π·Δn·d/λ) which is proportional to the birefringence Δn and the average pathlength of photons d at wavelength λ. Retardance can be found from polar decomposition of Mueller matrix. In polar decomposition, Mueller matrix of the tissue is represented as a product of an equivalent retarder MR, diattenuator MD and depolarizer MΔ [19]:
| (1) |
From the retarder matrix MR, the retardance magnitude δ can be derived as a measure of tissue anisotropy [1–4,19]:
| (2) |
As mentioned above, the underlying causes of the polar decomposition derived effective retardance are ambiguous, in that different combinations of δs from different depths are possible that yield similar results. The matrix MR can be further decomposed to a linear part and a circular part [20,21]. From the linear part MLR, the retardance orientation (slow axis) can be obtained as [2,3]:
| (3) |
θ can be regarded as the anisotropy direction if the turbid media is homogenously birefringent (in this paper we assume positive birefringence and thus θ is the extraordinary axis as well [20]). Another parameter derived from polar decomposition is the retardance ellipticity which may give an indication of birefringence (in)homogeneity [3,20,21]. However, without resorting to polar decomposition analysis and assumptions, we note that the Mueller matrix itself possesses interesting symmetry properties, depending on the sample’s composition and structure, and thus may shed light on the tissue birefringence (in)homogeneity problem. For example, several studies have shown that the images of off-diagonal elements of the non-birefringent homogenous scattering media Mueller matrix are symmetric, in both transmission and backscattering [22–27]. These symmetric properties have been studied by polarization-sensitive Monte Carlo (MC) simulations and observed experimentally from Mueller matrices acquired from scattering liquid phantoms using polarized light imaging [11,27]. Further, Mueller matrix of a non-scattering retarder is symmetric too, so it remains to be seen how these symmetries combine when one deals with a complex material such as tissue that exhibits both turbid and birefringent properties, and whether inhomogeneities in the latter can be ascertained.
In this paper, we derive the symmetry properties of the transmission Muller matrix of birefringent turbid media, and show that it does indeed exhibit symmetric properties. Next, we extend our polarization sensitive Monte Carlo (PolMC) code to model bi-layered anisotropic media with arbitrary anisotropy values and directions in the layers, to examine the heterogeneous birefringence case. To simplify the problem, in this paper we limit the numbers of the layers to two, and investigate the Mueller matrix properties of these bi-layered birefringent turbid media. From the simulation results, we demonstrate how heterogeneity affects the Mueller matrix elements and their symmetry patterns. Moreover, we define a symmetry metric to quantify the uniformity of birefringence in bi-layered anisotropic turbid media. Finally, we validate the simulation results with experimental images of Mueller matrices measured in transmission geometry from anisotropic (both homogenous and heterogeneous) bi-layered scattering polyacrylamide phantoms.
2. Mueller matrix of turbid homogenous (uniaxial) birefringent media from polarization sensitive Monte Carlo simulations
Recently, a polarization-sensitive Monte Carlo (PolMC) code has been developed by Wood et al. which can simulate photon propagation in birefringent and chiral turbid media [28,29]. We use this simulation platform to examine the symmetries of the Mueller matrix from homogenous anisotropic turbid media, to be followed by extended PolMC simulations of heterogeneous bi-layered anisotropic media (different anisotropy orientations in the two layers). PolMC prediction will be validated experimentally with Mueller matrix measurements in scattering birefringent phantoms.
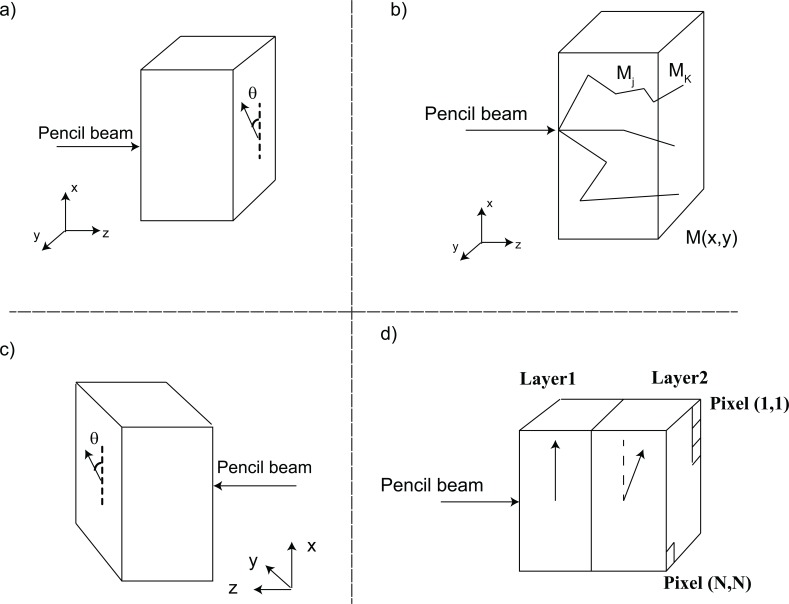
First, we analyze the symmetry properties of the Mueller matrix of a homogenously birefringent turbid media as is calculated from Monte Carlo. We model the uniaxial birefringent and turbid medium as a box with ordinary refractive index no, extraordinary refractive index ne = no + Δn (with Δn being the birefringence magnitude) and extraordinary axis θ relative to the x axis as shown in Fig. 1a ). Let us denote the forward transmission Mueller matrix at the detection facet by M(x, y), as depicted in Fig. 1b).
Fig. 1.
Simulation geometry in PolMC and its implementation for a 2-layer turbid (in)homogeneously birefringent media. (a) The problem geometry for simulating a box of homogenous birefringent (uniaxial) turbid media in PolMC. Anisotropy axis is shown by an arrow at an angle θ from x axis. (b) Monte Carlo calculation steps of Mueller matrix M(x,y). Mj is the Mueller matrix between two scattering events. Mk is the Mueller matrix of each trajectory k. (c) The problem’s geometry and reference frame in Eq. (14), because the transmission Mueller matrix is the same in both (a) and (c), Eq. (14) can be rewritten as Eq. (15). (d) Bi-layered anisotropic media simulated in PolMC; both layers have the same thickness and same birefringence magnitude but different orientations relative to each other.
To calculate M, many photons with different polarizations are propagated in the turbid media. Depending on the medium’s optical properties (scattering and absorption coefficients), photons are scattered and propagated along different trajectories as per standard MC modeling [28–30]. The scattering events are incoherent and not correlated, therefore, M(x,y) is the sum of the Mueller matrices of all the trajectories:
| (4) |
where k is the index of each individual trajectory. Mk(x,y) will be proportional to the product of Mueller matrices Mj of consecutive scattering events in each trajectory k:
| (5) |
where (r,ξ,ϕ) denotes the polar coordinate system and Nj is the number of scattering events in the trajectory k. For notational simplicity, we will write Mj(r,ξ,ϕ) as Mj. The symmetry properties of Mj, the Mueller matrix between two scattering events, will influence the symmetry properties of Mk the Mueller matrix of that particular path, and thus the final sample Mueller matrix M(x,y). Mj itself can be represented as a product of Mueller matrices which account for different optical effects acting on photons. Upon each scattering, the photon’s reference frame is changed to the scattering plane (rotation of ζj degrees), and the single scattering Mueller matrix is applied [28–32]. To incorporate birefringence after each scattering event, the reference frame of the photons is rotated by βj degrees, for the parallel polarization of the photon to be parallel with the direction of maximum refractive index (which is the projection of orientation θ in the plane perpendicular to the propagation direction), as described in detail in Wood et al. [28]. Accounting for both effects, the total Mj in the global coordinate (lab’s reference) frame can be written as
| (6) |
where Μδ(gj) is the retardance Mueller matrix and has the form [20]
| (7) |
gj = π.Δn(ϕj).dz/λ is half the retardance over the short pathlength dz between the two scattering events and Δn(ϕ) is the difference between the refractive indices seen by the photon calculated as [28]
| (8) |
where ϕj is the angle between the photon propagation direction after the scattering event j and the extraordinary axis. The total retardance δ of the medium is the accumulation of the retardances 2gj over the whole pathlength along the trajectory k. R (βj) and R (ζj) are the rotation matrices which rotate the photon reference frames and can be written as (with α representing βj or ζj) [20]
| (9) |
Scatterers in homogenous turbid media can often be identical spherical particles, hence, Ms(ψ) can be the single scattering Mueller matrix for a spherical scatterer, with ψj being the angle of the scattering. It can be written as
| (10) |
and its a, b, c, and d elements are calculated from Mie theory [23]. Thus knowing the form of the rotation, retardance and scattering matrices as per Eqs. (8)–(10), we can find the symmetric properties of the Mueller matrix Mj. Following the approach presented by Rakovic et al. [24], we should find a projection matrix P which reveals the symmetry properties of the matrices in Eqs. (8)–(10). Let us define the diagonal matrix P as
| (11) |
and P2 = I being the identity matrix. With direct calculation, it can be shown that
| (12) |
where Mt is the transpose of M. From matrix product properties transpose(A × B) = transpose(B) × transpose(A), then plugging Eq. (12) into Eq. (6) results in
| (13) |
On the other hand, plugging Eqs. (8)–(10) into Eqs. (6) and (13), it can be shown that the order of the multiplication in Eq. (6) is not important; that is the order of applying scattering or retardation over short pathlength dz will not change the total result on the photon. Therefore, Eq. (13) can be rewritten as
| (14) |
| (15) |
The reverse order of the multiplication in Eq. (15) is equal to a change of reference from (x,y,z) to (x,-y,-z), changing the extraordinary axis from θ in the old coordinate to θ in the new coordinate and switching the input/output plane as shown in Fig. 1.c relative to Fig. 1.a). Both these configurations result in the same forward Mueller matrix M(x,y). Hence, in a homogenously birefringent medium, the reverse order of the events in each trajectory is the same as the regular order and Eq. (15) can be rewritten as
| (16) |
Equation (16) reveals the symmetric properties of Mk along each trajectory k and dictates its general form. The general form of Mk that satisfies Eq. (16) is
| (17) |
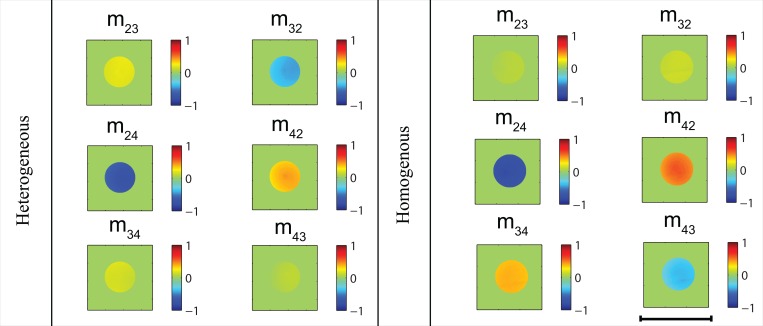
As can be seen, the off-diagonal elements in Eq. (17) exhibit certain symmetries (Mk12 = Mk21; Mk13 = Mk31; Mk23 = Mk32; Mk14 = -Mk41; Mk24 = -Mk42; Mk34 = -Mk43). The above form holds for the matrix M(x,y) as well, since it is the summation of all the Mks (all the trajectories). Therefore, the symmetry in Eq. (17) will be evident in terms of the symmetry in the images of the off-diagonal elements of M(x,y), denoted in the text by Mij(i≠j). For example, images of elements M23 and M32 are positively correlated. Similarly, the spatial patterns in the elements M24 and M42 or M34 and M43 are negatively correlated. These symmetry properties thus describe the Mueller matrix of homogenously birefringent turbid media.
When we proceed to the more difficult case of heterogeneity in birefringence, the order of the multiplication will determine the final outcome, and hence the inhomogeneous matrix Mk will not follow the form of Eq. (17). As such, the symmetry properties of M(x,y) can be used as metrics for identifying axial birefringence heterogeneity in the material. Mueller matrix of a pure retarder has non-zero values for the 9 lower right corner elements [20]; as such, these elements are more correlated to birefringence even in a turbid medium. In fact, the asymmetry between the 6 off-diagonal elements in the lower right corner of the Mueller matrix can be a measure of birefringence heterogeneity in a turbid medium (with homogenous optical properties). Thus, we will use the asymmetry between the images of elements (M24,M42),(M34,M43) and(M23,M32) to detect the heterogeneity in birefringence, as described in the next section.
3. Mueller matrix of turbid heterogeneous (bi-layered) birefringent media from polarization sensitive Monte Carlo simulations
We now modify the above PolMC code [28] to enable simulation of bi-layered anisotropic turbid media. In the new code, each of the layers in the structure can have arbitrary uniaxial birefringence (magnitude and direction). For this study, we simulate bi-layered cubes of 2cm × 2cm × 2cm in dimensions; the two layers have the same thickness and optical properties (e.g., composed of homogenous uniform scattering microspheres, with typical tissue-like scattering properties); also no optical activity is assumed for simplicity [33–35]. For biomedical relevance, we mimic the kidney’s reduced scattering coefficient, reported in Alali et al. [17]. Optical thickness equal to 2 mm of kidney tissue was chosen for the simulations, by setting the phantoms total thickness to 2 cm and its scattering coefficient to 6 cm−1 [17]. The absorption level was minimal, equal to water absorption at 635 nm [28]. The scatterers were modeled to be polystyrene beads with 1.2 μm diameter and refractive index of 1.59, to facilitate comparison with subsequent experiments.
The geometry of the bi-layered problem simulated with the extended version of PolMC is sketched in Fig. 1.d. As illustrated, the two layers can have different properties such as different anisotropy directions. A polarized pencil beam (~3 × 108 photons) was shone on the center of the layer 1 and the polarization state of the photons at each pixel of the external facet (in transmission mode) of the layer 2 are tabulated. The sample was illuminated with 4 different incident polarizations (linear at 0°, linear at 90°, linear at 45° and right circular) and for each case, the number of the photons with 4 different polarizations (linear at 0°, linear at 90°, linear at 45° and right circular) were counted. From these 16 outcomes, Mueller matrix of the sample in transmission mode M(x,y) was calculated, as described by several authors [21,29]. For these simulations, the magnitude of the birefringence in the two layers was kept same but the relative orientation was varied.
Prior to performing the Mueller matrix symmetry analysis suggested by Eq. (16), the obtained Mueller matrix was subjected to polar decomposition to determine the effective retardance δeff, and orientation θeff [1–4,7–10,19]. To investigate the effect of heterogeneity, equivalent homogenous (EH) samples (same magnitude and orientation of birefringence in the two layers) resulting in the same value of δeff and θeff were simulated in the new PolMC code. Each of the layers in the homogenous samples has the same anisotropy direction θeff, and half of the effective retardance value δeff/2. These simulations will thus highlight the differences in Mueller matrices of homogenous and heterogeneous samples as a function of birefringence orientation difference in the two layers. We are expecting the homogenous birefringent sample to show higher degree of symmetry between their off-diagonal Mueller matrix elements (as per Eq. (17)) compared to axially heterogeneous birefringent samples. To quantify the symmetries in equivalent homogenous (EH) and heterogeneous samples, we define the asymmetry degrees (ASD) based on Eq. (17), as the sum of normalized differences (or sums if there is a sign change) between the off-diagonal elements - excluding those of the first column and row because of their lower values as mentioned before—as follows:
| (18) |
with
| (19) |
where mij is defined as the off-diagonal Mueller matrix element Mij normalized by M11, xi and yj are the spatial position and N is the number of the pixels in each dimension of the element’s image. Normalization of mij with respect to its maximum in the defining equations above will help quantify the difference in the spatial profile (patterns) in the image, rather than the differences in the magnitude of the off-diagonal elements. The ASD metric will give an indication of the sample’s axial heterogeneity in comparison to its EH counterpart.
In general, we expect ASD values to increase as we proceed from birefringently homogeneous to heterogeneous samples. However, it is important to note that ASD will vary even among different homogenous samples, for example depending on birefringence orientation or sample turbidity. In another words, two homogenous samples with different δeff and θeff will have different ASD values. For example, if the values of the elements in the Mueller matrix of a pure retarder with retardance δeff and orientation θeff are large, then the symmetry in Eq. (16) will be more manifest, yielding lower ASD [21]. Otherwise, owing to relatively small magnitude of the off-diagonal elements of a pure scatterer, the spatial symmetry in the images will be less and the total ASDs will be higher. Thus, heterogeneity can be best gauged by comparing the unknown sample’s ASD to its equivalent homogenous ASD (ASDEH). Moreover, depending on the values of δeff and θeff, different axial heterogeneities will yield different deviations from the corresponding ASDEH.
4. Simulation results
4.1. Modeling heterogeneous anisotropic samples and their equivalent homogenous (EH) counterparts
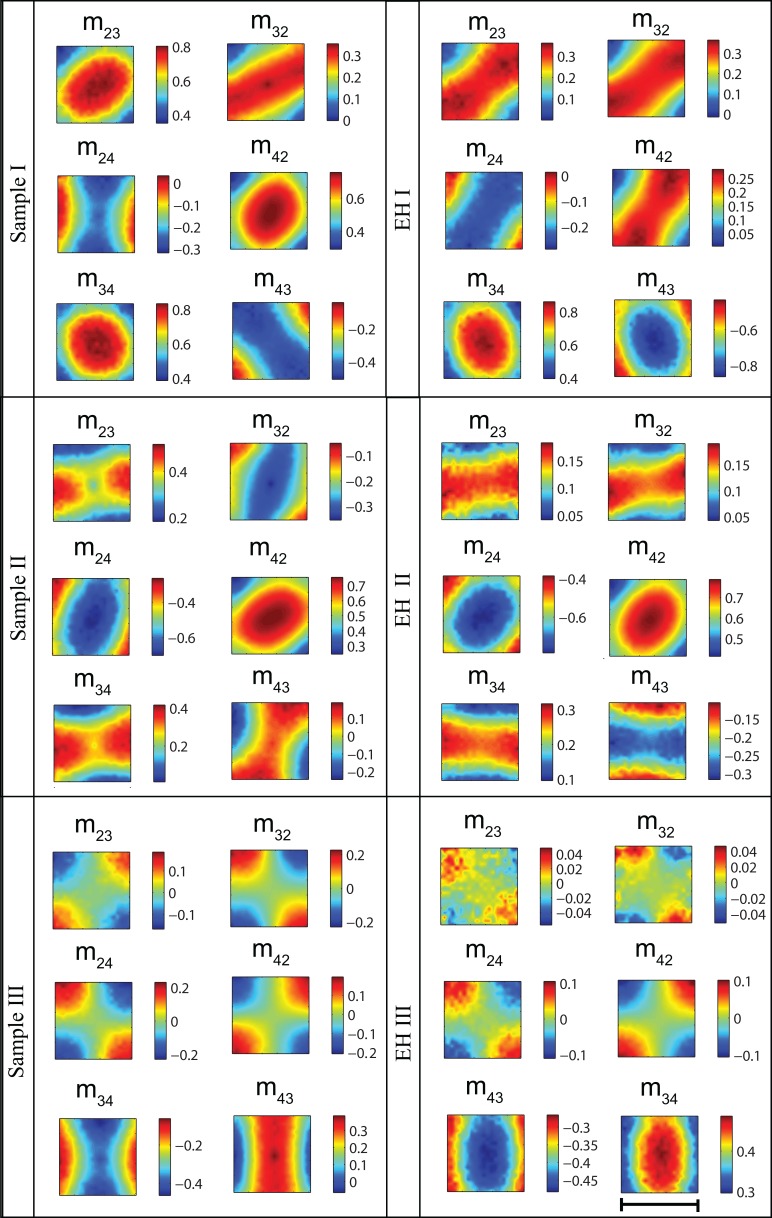
Using Monte Carlo simulations, we investigate how varying birefringence direction with depth will change the ASD in a bi-layer turbid system compared to a uni-directional ASDEH For this initial study, we chose to examine the effects of direction change only; the possible parameter space to explore is simply too large (orientation and magnitude values and their changes, varying layer thicknesses, varying optical properties in the layers, etc), so we start with simple, and biologically relevant, case of depth-dependent anisotropy axis change. The modeled samples I, II and III have the same constant birefringence magnitude and orientation in the first layer, but a different orientation relative to the first one (equal to 30°, 60° and 90°) in the second layer. Table 1 shows the birefringence magnitude and orientation of the two layers in sample I, II and III. Also shown are the δeff and θeff values derived from polar decomposition of the PolMC-generated Mueller matrix. δeff and θeff listed in Table 1 are the mean value of the images (δeff (x,y) and θeff(x,y)) obtained from polar decomposition.
Table 1. Birefringence magnitude and orientation in each layer of the heterogeneous samples and the bi-layered sample’s effective retardance magnitude and orientation calculated from polar decomposition.
| Sample | Δn1 | Δn2 | θ1(ο) | θ2(ο) | δeff(ο) | θeff(ο) |
|---|---|---|---|---|---|---|
| I | 1.15 × 10−5 | 1.15 × 10−5 | 0 | 30 | 108 ± 3 | 8 ± 1 |
| II | 1.15 × 10−5 | 1.15 × 10−5 | 0 | 60 | 59 ± 4 | 32 ± 3 |
| III | 1.15 × 10−5 | 1.15 × 10−5 | 0 | 90 | 23 ± 4 | 90 ± 5 |
Based on the derived δeff and θeff from these birefringently heterogeneous samples, the next task was to generate Mueller matrices for EH samples (homogenously birefringent samples) which exhibit the same δeff and θeff. Obviously, the birefringence orientation in both layers of an EH sample should be equal to θeff. But choosing the appropriate birefringence Δn value is not trivial, since the samples are turbid and the overall pathlength is not known before simulations. So we ran several PolMC simulations, with birefringence orientation θeff and different birefringence magnitudes Δn. After some trial and error, the parameter values for the three EH samples (to match the heterogeneous samples I-III) were selected, as shown in Table 2 (compare its last two columns with those in Table 1). We now have the PolMC-generated Mueller matrices for the three heterogeneous samples and their EH counterparts, and can proceed with ASD analysis (Eqs. (15)–(17)).
Table 2. Birefringence magnitude and orientation in each layer of the equivalent homogenous samples and the bi-layered sample’s effective retardance magnitude and orientation calculated from polar decomposition.
| Samples | Δn | θ(ο) | δeff(ο) | θeff(ο) |
|---|---|---|---|---|
| EH I | 9.4 × 10−6 | 7 | 106 ± 3 | 7 |
| EH II | 5.53 × 10−6 | 35 | 63 ± 4 | 35 |
| EH III | 2.7 × 10−6 | 90 | 23 ± 4 | 90 |
4-2. Symmetry analysis of the Mueller matrix images
Figure 2 demonstrates the images of the off-diagonal Mueller matrix elements (normalized to M11) of the sample I-III and their respective EHs respectively. As seen, the homogenous samples follow the symmetry patterns predicted in Eq. (17); however, as mentioned previously the symmetries are different among EHs. To quantify the symmetry of these Mueller matrix elements, we calculated ASD numbers from Eqs. (18)–(19) (Table 3 ).
Fig. 2.
Simulation results of extended PolMC. Images of the Mueller matrices’ off-diagonal elements (normalized to M11) of samples I, II, and III and their equivalent homogenous samples which result in the same value of effective retardance magnitude and orientation. The color bar shows the relative values of the element in x and y direction. The scale bar is 2 cm. Thickness of all the layers is 1 cm and the media’s scattering coefficient is 6 cm−1. Anisotropy properties of the samples can be found in Tables 1 and 2.
Table 3. Asymmetry degrees of the axially heterogeneous samples and their EH counterparts.
| Sample | Sample’s ASD | EH’s ASD |
|---|---|---|
| I | 0.0084 | 0.0014 |
| II | 0.0429 | 0.0017 |
| III | 0.0902 | 0.0354 |
It can be concluded from Table 3 that the heterogeneous anisotropic samples show higher ASDs compare to their EHs. In another words, axial change in the extraordinary axis direction reduces the symmetry and increases the ASD, relative to a homogenous sample with the same effective retardance and orientation. Therefore, ASD of the Mueller matrix can be used as a metric to identify axial heterogeneity of anisotropy in turbid media. However, this measure is relative and should be used cautiously in light of the following considerations.
The spatial profile of effective retardance and orientation that are calculated from polar decomposition are not uniform over all the pixels, so their values are presented in terms of mean and standard deviation in Tables 1 and 2. As such, it is very difficult to simulate an EH sample which result in the exact desired image of effective retardance and orientation (equal to those of the heterogeneous sample). That’s why the mean values of the retardance and orientation of the samples and their EHs, listed in Tables 1 and 2, are close but slightly different. As mentioned before, homogenous variations in effective retardance and orientation leads to deviation in ASD numbers as well. For instance, uniform axial changes of ± 10% in δeff and θeff in the homogenous sample EH II causes a ΔASDEH of ~15%. Given this uncertainty in ASDEH, for a sample with effective values of δeff and θeff to be classified as heterogeneous, its ASD should obey the condition: (ASDSample- |ΔASDEH|) /ASDEH> 1. This condition will ensure that the ASD difference between the sample and its EH arises solely from heterogeneity. For example, the large difference between the ASDs in sample II and EH II, is due to heterogeneity and not from homogenous variations in δeff and θeff. This condition holds for samples I-III verifying their heterogeneity.
An additional important point to note is that the relative ratios of the ASDsample/ASDEH are different for each case and cannot be regarded as a measure of higher or lower heterogeneity. For example, ASDsample/ASDEH of sample II is about 8 times that of sample III, while the heterogeneity (in this case change of anisotropy axis) is larger in sample III.
Therefore, the heterogeneity strength cannot be inferred unless a look up table of heterogeneous samples ASD with the equal value of δeff and θeff are prepared. Generating such a table requires high computational power to run the PolMC code many times.
As will be discusses in the next section, ASD can be used in polarized light imaging to identify axial change of anisotropy. However, experimental availability of EH samples is challenging. In practice for biomedical diagnosis, one possibility would be to measure ASD of the normal and abnormal birefringent tissue, to detect axial change of fiber orientation in the latter. Yet to characterize the strength of orientation change, careful MC simulations (with the tissue’s optical properties) should complement the experiment. Finally, ASD can be used to better interpret the results of depth resolved techniques which use Mueller matrix imaging. For example, the depth resolved birefringence map obtained by PS-OCT is limited to the OCT axial resolution and ASD can be used to identify sub-resolution heterogeneity/homogeneity of the detected birefringence at each depth in the tissue.
5. Experimental validation with turbid birefringent phantoms
To validate the simulation results experimentally, we used elastic polyacrylamide phantoms with controlled scattering properties (through addition of polystyrene beads) [28,35]. On average, these phantoms exhibit birefringence on the order of 1 × 10−5 per 1 mm of stretch [28]. To make a bi-layered anisotropic media, two identical slabs (6 cm × 4 cm × 1 cm) of polyacrylamide were fabricated, following the recipe explained in [35]. The phantoms’ scattering coefficient was set to 6 cm−1, by adding polystyrene beads of 1.2 μm size and of refractive index of 1.59 using Mie theory [22,36].
Each slab was placed into a custom made puller (Fig. 3 ). The introduced strain induces a birefringence with the extraordinary axis along the stretching direction. To enable change of birefringence orientation, the pullers were made to rotate freely around their centers, as illustrated in Fig. 3. Each phantom was characterized using transmission mode polarized light imaging method described in [17]. From there the Mueller matrix elements and its effective retardance magnitude and orientation were calculated. The stretch and rotation angle of each phantom was modified to achieve the simulation parameters of the individual layers of sample II of Table 1. Experimental measurement values are listed in Table 4 .
Fig. 3.
Experimental set up for heterogeneous anisotropy test. (a) Custom made gel puller with the phantom inside it; the anisotropy axis is in the pulling direction. (b) Heterogeneously birefringent bi-layered phantoms made from two phantoms, each in a gel puller, with different orientation labeled by yellow arrows.
Table 4. Anisotropy properties of the layers in of the samples heterogeneous and its EH polyacrylamide phantoms, their effective values of retardance and slow axes and their ASD.
|
Phantoms |
δ1(ο) |
δ2(ο) |
θ1(ο) |
θ2(ο) |
δeff(ο) |
θeff(ο) |
ASD |
|---|---|---|---|---|---|---|---|
| Heterogeneous | 60 ± 3 | 66 ± 2 | 0 | 60 ± 2 | 62 ± 4 | 35 ± 1 | 43.3870 |
| EH | 27 ± 2 | 33 ± 2 | 31 ± 1 | 31 ± 1 | 60 ± 5 | 31 ± 1 | 3.4808 |
To make the heterogeneous bi-layered medium, the two phantoms in the pullers were placed against each other as depicted in Fig. 3(b). Following the same procedure, the sample EH II was made by changing the stretches in the two phantoms (till each yields half of the retardance δeff) and rotating their orientation (till it is equal to θeff). The properties of each slab and the effective retardance and orientation of the two layers together, found from polar decomposition, are listed in Table 4. As seen, the heterogeneous sample and its EH have a difference of about 20% in the experimental values of δeff and θeff . This is the closest we could achieve with this phantom system. Our simulation results indicate that 20% homogenous change in δeff and θeff will result in ΔASDEH < 25%.
The off-diagonal normalized elements of the Mueller matrix of the two bi-layered phantom samples are shown in Fig. 4 . The relation between the images of the respective off-diagonal elements of the phantoms in Fig. 4. agrees well with those of the Monte Carlo simulations for sample II, shown in Fig. 2. However, the experimental results show higher asymmetry than the Monte Carlo simulations in both heterogeneous sample and its EH. This is most likely due to noise: experiments with layered scattering polyacrylamide phantoms of controlled and variable birefringence are challenging and prone to many errors. For example, these phantoms dehydrate slightly with time and as a result their birefringence increases over the course of the experiment. Therefore, there might be a slight change of retardance in the layers from the time that we characterize them individually to the time we measure them together.
Fig. 4.
Mueller matrix elements obtained from polarized light imaging experiment. Experimental images of the Mueller matrix’s off-diagonal elements (normalized to M11) of sample II and its EH. The color shows the relative values of the element in x and y direction. The images were filtered using intensity threshold filter to highlight the higher SNR regions and therefore the images are comparable to the central part of the PolMC predictions in the middle row in Fig. 2. The scale is 2 cm. Thickness of all the layers is 1 cm and the media’s scattering coefficient is 6 cm−1. Anisotropy properties of the samples can be found in Table 4.
The ASD numbers of the bi-layered phantoms, calculated from the images in Fig. 4 are listed in Table 4. As expected from the simulations, the experiments now confirm that the heterogeneous sample’s ASD is higher than its EH’s ASD. The measured ASD ratio is less than Monte Carlo predictions, largely due to experimental challenges with this phantom system. Nevertheless, the experimental ratio is large enough to satisfy our suggested condition: (ASDSample- ΔASDEH) /ASDEH> 1, and is consistent with MC. Hence, experiments and MC simulation agree in the trends and both give farther credence to the proposed Mueller matrix asymmetry formalism for detecting and quantifying axial birefringence heterogeneity.
6. Conclusion
In this paper, we have developed a protocol to detect depth-dependent heterogeneity in birefringent turbid media using polarized light imaging. Employing polarization sensitive Monte Carlo simulation, we showed that forward Mueller matrix of a homogenous birefringent turbid medium has symmetric properties about its diagonal. To further examine Mueller matrix symmetry, the polarization sensitive Monte Carlo code was extended to model bi-layered anisotropic media with different anisotropy orientation in each layer. Our simulations show that symmetry between off-diagonal elements of the Mueller matrix can be used as a metric to identify birefringence heterogeneity of a turbid bi-layered medium. To quantify these trends, a metric called asymmetry degree (ASD) was defined from the symmetry between the 6 lower right off-diagonal elements of the Mueller matrix. Based on our results, the procedure to detect birefringence heterogeneity is to first, calculate the effective retardance magnitude and orientation of the sample using polar decomposition; then, to simulate an equivalent homogenous (EH) sample which exhibit the same effective retardance and orientation (from polar decomposition); lastly, to compare the ASD of the unknown sample with its EH’s ASD. Our simulations show that ASD values are larger in heterogeneous samples compared to their EHs. We verified these ASD trends experimentally using polarized light imaging of bi-layered elastic polyacrylamide phantoms. The ASD metric developed in this paper and the procedure of using it for identifying axial heterogeneity of birefringence in turbid media may provide new criteria of characterizing biological tissues with different anisotropic layers.
References and links
- 1.Wood M. F. G., Ghosh N., Wallenburg M. A., Li S. H., Weisel R. D., Wilson B. C., Li R. K., Vitkin I. A., “Polarization birefringence measurements for characterizing the myocardium, including healthy, infarcted, and stem-cell-regenerated tissues,” J. Biomed. Opt. 15(4), 047009 (2010). 10.1117/1.3469844 [DOI] [PubMed] [Google Scholar]
- 2.Wallenburg M. A., Pop M., Wood M. F. G., Ghosh N., Wright G. A., Vitkin I. A., “Comparison of optical polarimetry and diffusion tensor MR imaging for assessing myocardial anisotropy,” J. Innovative Opt. Health Sci. 03(02), 109–121 (2010). 10.1142/S1793545810000976 [DOI] [Google Scholar]
- 3.Alali S., Aitken K., Shröder A., Bagli D., Vitkin I. A., “Optical assessment of tissue anisotropy in ex vivo distended rat bladders,” J. Biomed. Opt. 17(8), 086010 (2012). 10.1117/1.JBO.17.8.086010 [DOI] [PubMed] [Google Scholar]
- 4.Wood M. F. G., Ghosh N., Moriyama E. H., Wilson B. C., Vitkin I. A., “Proof-of-principle demonstration of a Mueller matrix decomposition method for polarized light tissue characterization in vivo,” J. Biomed. Opt. 14(1), 014029 (2009). 10.1117/1.3065545 [DOI] [PubMed] [Google Scholar]
- 5.Courtney T., Sacks M. S., Stankus J., Guan J., Wagner W. R., “Design and analysis of tissue engineering scaffolds that mimic soft tissue mechanical anisotropy,” Biomaterials 27(19), 3631–3638 (2006). [DOI] [PubMed] [Google Scholar]
- 6.Manhas S., Swami M. K., Buddhiwant P., Ghosh N., Gupta P. K., Singh J., “Mueller matrix approach for determination of optical rotation in chiral turbid media in backscattering geometry,” Opt. Express 14(1), 190–202 (2006). 10.1364/OPEX.14.000190 [DOI] [PubMed] [Google Scholar]
- 7.Ghosh N., Wood M. F., Vitkin I. A., “Mueller matrix decomposition for extraction of individual polarization parameters from complex turbid media exhibiting multiple scattering, optical activity, and linear birefringence,” J. Biomed. Opt. 13(4), 044036 (2008). 10.1117/1.2960934 [DOI] [PubMed] [Google Scholar]
- 8.Ghosh N., Wood M. F. G., Li S. H., Weisel R. D., Wilson B. C., Li R. K., Vitkin I. A., “Mueller matrix decomposition for polarized light assessment of biological tissues,” J Biophotonics 2(3), 145–156 (2009). 10.1002/jbio.200810040 [DOI] [PubMed] [Google Scholar]
- 9.Li X., Yao G., “Mueller matrix decomposition of diffuse reflectance imaging in skeletal muscle,” Appl. Opt. 48(14), 2625–2631 (2009). 10.1364/AO.48.002625 [DOI] [PubMed] [Google Scholar]
- 10.Ghosh N., Wood M. F. G., Vitkin I. A., “Influence of the order of the constituent basis matrices on the Mueller matrix decomposition-derived polarization parameters in complex turbid media such as biological tissues,” Opt. Commun. 283(6), 1200–1208 (2010). 10.1016/j.optcom.2009.10.111 [DOI] [Google Scholar]
- 11.Gilbert T. W., Wognum S., Joyce E. M., Freytes D. O., Sacks M. S., Badylak S. F., “Collagen fiber alignment and biaxial mechanical behavior of porcine urinary bladder derived extracellular matrix,” Biomaterials 29(36), 4775–4782 (2008). 10.1016/j.biomaterials.2008.08.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Costa K. D., Lee E. J., Holmes J. W., “Creating alignment and anisotropy in engineered heart tissue: role of boundary conditions in a model three-dimensional culture system,” Tissue Eng. 9(4), 567–577 (2003). 10.1089/107632703768247278 [DOI] [PubMed] [Google Scholar]
- 13.de Boer J. F., Milner T. E., van Gemert M. J. C., Nelson J. S., “Two-dimensional birefringence imaging in biological tissue by polarization-sensitive optical coherence tomography,” Opt. Lett. 22(12), 934–936 (1997). 10.1364/OL.22.000934 [DOI] [PubMed] [Google Scholar]
- 14.Jiao S., Wang L. V., “Two-dimensional depth-resolved Mueller matrix of biological tissue measured with double-beam polarization-sensitive optical coherence tomography,” Opt. Lett. 27(2), 101–103 (2002). 10.1364/OL.27.000101 [DOI] [PubMed] [Google Scholar]
- 15.Götzinger E., Pircher M., Baumann B., Ahlers C., Geitzenauer W., Schmidt-Erfurth U., Hitzenberger C. K., “Three-dimensional polarization sensitive OCT imaging and interactive display of the human retina,” Opt. Express 17(5), 4151–4165 (2009). 10.1364/OE.17.004151 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Brasselet S., “Polarization-resolved nonlinear microscopy: application to structural molecular and biological imaging,” Adv. Opt. Photonics 3(3), 205–271 (2011). 10.1364/AOP.3.000205 [DOI] [Google Scholar]
- 17.Alali S., Ahmad M., Kim A., Vurgun N., Wood M. F. G., Vitkin I. A., “Quantitative correlation between light depolarization and transport albedo of various porcine tissues,” J. Biomed. Opt. 17(4), 045004 (2012). 10.1117/1.JBO.17.4.045004 [DOI] [PubMed] [Google Scholar]
- 18.Guo X., Wood M. F. G., Vitkin I. A., “A Monte Carlo study of penetration depth and sampling volume in of polarized light in turbid media,” Opt. Commun. 281(3), 380–387 (2008). 10.1016/j.optcom.2007.09.043 [DOI] [Google Scholar]
- 19.Lu S., Chipman R. A., “Interpretation of Mueller matrices based on polar decomposition,” J. Opt. Soc. Am. A 13(5), 1106–1113 (1996). 10.1364/JOSAA.13.001106 [DOI] [Google Scholar]
- 20.D. Goldstein, Polarized Light, 2nd ed. (Marcel Dekker, New York, 2003). [Google Scholar]
- 21.R. A. Chipman, Handbook of Optics, 2nd ed., M. Bass, ed. (McGraw-Hill, New York, 1994) [Google Scholar]
- 22.H. C. V. de Hulst, Light Scattering by Small Particles (Dover, New York (1981) [Google Scholar]
- 23.C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles (Wiley, New York, 1998). [Google Scholar]
- 24.Raković M. J., Kattawar G. W., Mehruűbeoğlu M. B., Cameron B. D., Wang L. V., Rastegar S., Coté G. L., “Light backscattering polarization patterns from turbid media: theory and experiment,” Appl. Opt. 38(15), 3399–3408 (1999). 10.1364/AO.38.003399 [DOI] [PubMed] [Google Scholar]
- 25.Brown A. J., Xie Y., “Symmetry relations revealed in Mueller matrix hemispherical maps,” J. Quant. Spectrosc. Radiat. Transf. 113(8), 644–651 (2012). 10.1016/j.jqsrt.2012.01.008 [DOI] [Google Scholar]
- 26.Fallet C., Novikova T., Foldyna M., Manhas S., Ibrahim B. H., De Martino A., “Overlay measurements by Mueller polarimetry in back focal plane,” J. Micro/Nanolithogr. MEMS MOEMS 10(3), 033017 (2011). [Google Scholar]
- 27.Cheng X., Wang X., “Numerical study of the characterization of forward scattering Mueller matrix patterns of turbid media with triple forward scattering assumption,” Optik (Stuttg.) 121(10), 872–875 (2010). 10.1016/j.ijleo.2008.09.038 [DOI] [Google Scholar]
- 28.Wood M. F. G., Guo X., Vitkin I. A., “Polarized light propagation in multiply scattering media exhibiting both linear birefringence and optical activity: Monte Carlo model and experimental methodology,” J. Biomed. Opt. 12(1), 014029 (2007). 10.1117/1.2434980 [DOI] [PubMed] [Google Scholar]
- 29.Ghosh N., Wood M. F. G., Vitkin I. A., “Polarimetry in turbid, birefringent, optically active media: a Monte Carlo study of Mueller matrix decomposition in the backscattering geometry,” J. Appl. Phys. 105(10), 102023 (2009). 10.1063/1.3116129 [DOI] [Google Scholar]
- 30.Côté D., Vitkin I. A., “Robust concentration determination of optically active molecules in turbid media with validated three-dimensional polarization sensitive Monte Carlo calculations,” Opt. Express 13(1), 148–163 (2005). 10.1364/OPEX.13.000148 [DOI] [PubMed] [Google Scholar]
- 31.Wang X., Wang L. V., “Propagation of polarized light in birefringent turbid media: a Monte Carlo study,” J. Biomed. Opt. 7(3), 279–290 (2002). 10.1117/1.1483315 [DOI] [PubMed] [Google Scholar]
- 32.Ramella-Roman J. C., Prahl S. A., Jacques S. L., “Three Monte Carlo programs of polarized light transport into scattering media: part I,” Opt. Express 13(12), 4420–4438 (2005). 10.1364/OPEX.13.004420 [DOI] [PubMed] [Google Scholar]
- 33.Côté D., Vitkin I. A., “Balanced detection for low-noise precision polarimetric measurements of optically active, multiply scattering tissue phantoms,” J. Biomed. Opt. 9(1), 213–220 (2004). 10.1117/1.1629683 [DOI] [PubMed] [Google Scholar]
- 34.Hadley K. C., Vitkin I. A., “Optical rotation and linear and circular depolarization rates in diffusively scattered light from chiral, racemic, and achiral turbid media,” J. Biomed. Opt. 7(3), 291–299 (2002). 10.1117/1.1483880 [DOI] [PubMed] [Google Scholar]
- 35.Surowiec A., Shrivastava P. N., Astrahan M., Petrovich Z., “Utilization of a multilayer polyacrylamide phantom for evaluation of hyperthermia applicators,” Int. J. Hyperthermia 8(6), 795–807 (1992). 10.3109/02656739209005027 [DOI] [PubMed] [Google Scholar]
- 36.S. Prahl, “Mie Scattering Calculator,” http://omlc.ogi.edu/calc/mie_calc.html