COMPARISON OF SPARSE CODING AND KERNEL METHODS FOR HISTOPATHOLOGICAL CLASSIFICATION OF GLIOBASTOMA MULTIFORME

Abstract

This paper compares performance of redundant representation and sparse coding against classical kernel methods for classifying histological sections. Sparse coding has been proven to be an effective technique for restoration, and has recently been extended to classification. The main issue with classification of histology sections is inherent heterogeneity as a result of technical and biological variations. Technical variations originate from sample preparation, fixation, and staining from multiple laboratories, where biological variations originate from tissue content. Image patches are represented with invariant features at local and global scales, where local refers to responses measured with Laplacian of Gaussians, and global refers to measurements in the color space. Experiments are designed to learn dictionaries, through sparse coding, and to train classifiers through kernel methods with normal, necorotic, apoptotic, and tumor with with characteristics of high cellularity. Two different kernel methods of support vector machine (SVM) and kernel discriminant analysis (KDA) are used for comparative analysis. Preliminary investigation on histological samples of Glioblastoma multiforme (GBM) indicates that kernel methods perform as good if not better than sparse coding with redundant representation.

1. INTRODUCTION

Histological sections, typically stained by haematoxylin and eosin (H&E), are widely used in cancer diagnosis, prognosis, and theranostics. In a clinical setting, pathologists examine cellular morphology and tissue organization of a stained histological section under a microscope, and make judgments based on their prior knowledge. However, such a subjective evaluation may lead to considerable variability [1]. Moreover, vast amounts of data generated by pathology laboratories at a regular basis also create a demand for the development of quantitative histopathological analysis. Therefore, an automated system can serve as a diagnostic aid to pathologists. One of the critical issues in building an automated diagnostic system has to do with the variations associated with sample preparation (e.g., fixative and staining) that originate from different clinical protocol. For example, our data set includes samples that have been frozen and then stained, and those that have been paraffin embedded and then stained. Furthermore, the visualized color representation is highly variable as a result of technical and biological variations. Technical variations originate from fixation and variabilities in the amount of stain that is utilized. On the other hand, biological variations originates from sample type, tissue location, and the health of the tissue. For example, when cells go through apoptosis, they can release some of their protein contents into the nearby region, and as a result, increase increase the pink content locally. Therefore, the main motivation for sparse coding and redundant representation has been to capture a rich dictionary where classification error is measured as the reconstruction error. However, such a method needs to be compared with the classical methods, such as linear or kernel methods.

Over the past two decades, much research has been conducted for automated histological image analysis [2]. Nakazato et al. developed a method for nuclear grading of primary pulmonary adenocarcinomas based on the correlation between nuclear size and prognosis [3]. Tambasco et al. graded tumor by quantifying degree of architectural irregularity and complexity of histological structures based on fractal dimension [4]. Wittke et al. classified prostate carcinoma by combining morphological characteristics with Euler number. Wang et al. detected and classified follicular lesions of thyroid based on nuclear structure, which is characterized by shape and texture features [5]. A simple voting strategy coupled with support vector machine is used for classification. Tabesh et al. aggregated color, texture, and morphometric features at the global and object levels for classification of histological images [6]. The performance of several existing classifiers coupled with feature selection strategies are evaluated. Doyle et al. developed a multiscale scheme for detection of prostate cancer on high resolution [7] images, where a pixel-wise Bayesian classification is performed at each image scale while an AdaBoost classifier combines discriminating features in a hierarchal manner. Monaco et al. [8] proposed an efficient high throughput screening of prostate cancer using probabilistic pairwise Markov models. Bhagavatula et al. defined a set of histopathology specific vocabularies for region-based segmentation, which is realized through neural networks [9].

Recent advances on the analysis of histological image data hold great promise for large-scale use in advanced cancer diagnosis, prognosis and theranostics. There is a rapidly growing interest in the development of appropriate technology to address the processing and analysis issues associated with it, including (i) large dimension of the digitized samples, (ii) artifacts introduced during sample preparation, (iii) variations in fixation and staining across different laboratories, and (iv) variations in phenotypic signature across different samples. Here, we investigate emerging methods in dictionary learning and sparse coding, which has been widely applied for image reconstruction and classification [10, 11]. The rest of the this paper is organized as follows. Section 2 describes computational steps and the detailed implementation. Section 3 discusses the preliminary results of application of sparse coding for classification. Section 4 concludes the paper.

2. TECHNICAL APPROACH

Steps for classification of histological images are summarized as follows. First, we represent local patches by aggregating invariant features at the global and object levels. Then, class-specific dictionaries are learned for each class through sparse coding by iteratively removing shared elements among dictionaries. Finally, classification of histological patches are performed by comparing the error in sparse constrained reconstruction against all dictionaries.

2.1. Histological characterization of tumors

Biological samples have little inherent contrast in the light microscope, and, therefore, enzymatic staining is used to give both contrast to the tissue as well as highlighting particular features of interest through bright field microscopy. Haematoxylin and eosin (H&E stain) is the most commonly used light microscopical stain in histology, where haematoxylin stains nuclei as blue, and eosin stains all protein components as pink [12].

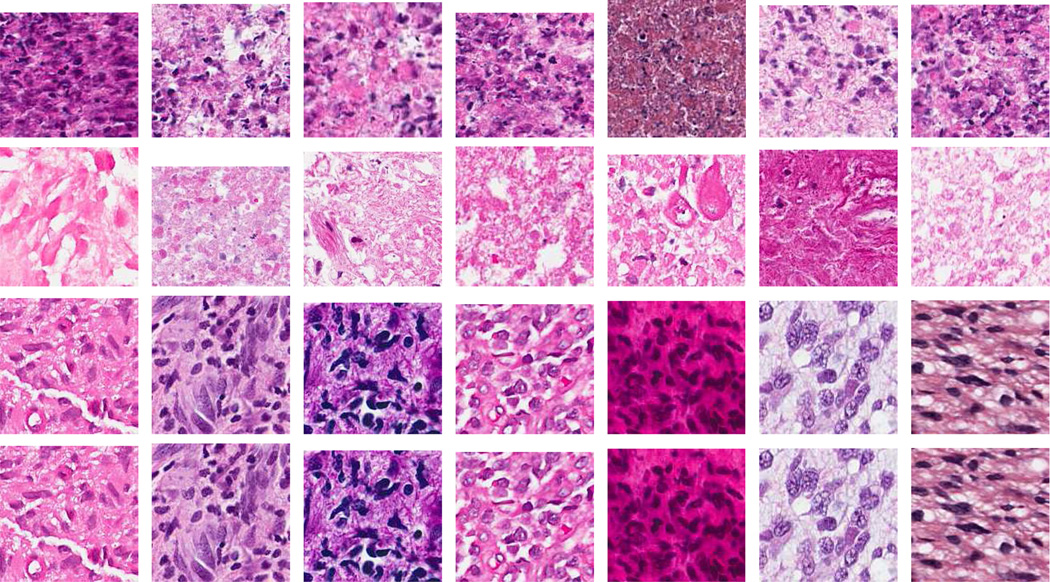
Tumors have characteristics that allow pathologists to determine their grade, predict their prognosis, and allow the medical team to determine the theranostics. While detailed morphometric analysis is one facet of diagnostic capability, global description of tissue sections in terms of the rate of high cellularity, apoptotic, and necrotic is pathologically important. Here, we focus on classification of tumors associated with Glioblastoma multiforme (GBM), which is the most aggressive type of primary brain tumor in human. Three different histopathological classes of GBM are apoptosis, necrosis and high-cellularity as shown in Fig. 1, which is a small sample of the training set that have been annotated by a pathologist. The significance of this training set is that there is a significant heterogeneity in the sample signature as a result technical variation in sample preparation. It is an issue that we aim to investigate through the sparse dictionary model.

Fig. 1.

Four classes of patch-level histology from Glioblastoma multiforme (GBM), which is the one of the most aggressive type of primary brain tumor: first row - apoptotic regions, second row - necrotic regions, third row - high cellularity regions, and fourth row - normal regions. Note that there is a significant amount of heterogeneity in the signature of these samples, which originate from variations in sample preparation among multiple clinics.

Apoptosis is the process of programmed (e.g., normal) cell death, which can be induced through various chemotherapeutic agents, ultraviolet and γ-irradiation, heat, osmotic imbalance, and high calcium [13]. During apoptosis, individual cells are triggered to undergo self-destruction in a manner that will neither injure neighboring cells nor elicit any inflammatory reaction, therefore, only scattered cells are involved. Cell changes in morphology caused by apoptosis include blebbing, loss of cell membrane asymmetry and attachment, cell shrinkage, nuclear fragmentation, chromatin condensation, and chromosomal DNA fragmentation. Necrosis is the premature death of cells and tissue induced by external injuries, such as infection, toxins, or trauma. Unlike apoptosis, necrosis leads to a destruction of a large group of cells in the same area. In necrosis, the chromatin is never marginated, but unevenly distributed as clumps that are irregular and poorly defined. Moreover, there is no nuclear fragmentation, cellular shrinking, or “body” formation in necrosis. Our objective is to detect and classify the apoptosis, necrosis and high-cellularity regions in samples that have been prepared at different clinical centers.

2.2. Representation

Each image patch of 40-by-40 pixels, at 10X magnification, is represented with global and local invariant features. Global features refers to basic statistics in the color space (e.g., RGB), which consists of six features (mean and variance in each of the color space). Other representations, such as HSV, did not improve performance of the classifier. Local representation is based on Laplacian of Gaussian (LoG) blob detector at multiple scales, which is applied on a gray scale images constructed from the ratio of the blue to red and green channels (e.g., $\frac{B}{R+G}$). This ratio image highlights chromatin contents, which reduces expensive and higher dimensional representation of image patches from the RGB space. The local representation can be computed by the direct convolution of the second derivative of the Gaussian kernel with the ratio image or by the difference of two Gaussians for improved performance [14]. The kernel response is measured at four scales (e.g., σ = 1, 2, 3, 4), and at each statistics of filter response (e.g., mean and variance) are computed for each local patch. The main rationale is that apoptotic regions should have a high filter response at lower scales of the LoG filter, while tumor regions should have higher filter response at higher scales of the LoG filter. We have also experimented with the distribution of the LoG response; however, this represention did not improve the classifier performance. The above representation is normalized for zero mean and variance of one.

2.3. Dictionary learning and sparse coding

In recent years, sparse representations has proven to be very effective for image reconstruction and classification [10]. The assumption is that the images can be well approximated by a linear combination of a few elements of some redundant basis, which are called dictionaries [11]. The basic ideas of dictionary learning and sparse coding are summarized as follows.

In sparse coding, a signal is represented as a linear combination of a few elements of a given dictionary. Given a signal x ∈ ℝⁿ and a dictionary D ∈ ℝ^n×k, the sparse representation problem can be stated as min_a ‖a‖₀, s.t. x = Da, where ‖a‖₀ is the number of non-zero elements. An alternative is to solve the unconstrained problem, ${\text{min}}_{\mathbf{a}}{\Vert \mathbf{x}-\mathbf{\text{Da}}\Vert }_2^2+\lambda {\Vert \mathbf{a}\Vert }_1$, where λ is a parameter that balances the tradeoff between reconstruction error and sparsity induced by ‖a‖₁. Given a set of signals {x_i}_{i=1, …, m} in ℝⁿ, the dictionary D is learned by optimizing

$$\underset{\mathbf{D},\{{\mathbf{a}}_i\}i=1,\dots ,m}{\text{min}}{\displaystyle \sum _{i=1}^m}{\Vert {\mathbf{x}}_i-{\mathbf{\text{Da}}}_i\Vert }_2^2+\lambda {\Vert {\mathbf{a}}_i\Vert }_1$$ (1)

with constrains that elements have norm less than one. This optimization problem is solved using an iterative approach that is composed of two convex steps: the sparse coding step on a fixed D and the dictionary update step on fixed a.

Eq. (1) provides a solution for dictionary learning within each class. Given a signal x, the sparse constrained reconstruction error can be measured as $\mathrm{ℛ̂}(\mathbf{x},\mathbf{D})={\text{min}}_{\mathbf{a}}{\Vert \mathbf{x}-\mathbf{\text{Da}}\Vert }_2^2+\lambda {\Vert \mathbf{a}\Vert }_1$. Optimizing ${\text{min}}_{i=1}^C\mathrm{ℛ̂}(\mathbf{x},{\mathbf{D}}_i)$ leads to predicted class label of x, where C is the number of classes. However, the dictionaries so-obtained may not provide enough discriminating power due to the potential sharing elements among dictionaries. Ramirez et al. [11] proposed an improved optimization by adding a dictionary incoherence term as follows:

$$\begin{array}{cc}\underset{{\{{\mathbf{D}}_i,{\mathbf{A}}_i\}}_{i=1,\dots ,C}}{\text{min}}\hfill & {\displaystyle \sum _{i=1}^C}\{{\Vert {\mathbf{X}}_i-{\mathbf{D}}_i{\mathbf{A}}_i\Vert }_2^2+\lambda {\displaystyle \sum _{j=1}^{m_i}}{\Vert {\mathbf{a}}_i^j\Vert }_1\}+\eta {\displaystyle \sum _{i\ne j}}{\Vert {\mathbf{D}}_i^T{\mathbf{D}}_j\Vert }_F^2\hfill \end{array}$$ (2)

The solution of this optimization problem can be estimated by iteratively removing certain percentage of shared elements from each library. Given a signal x, optimizing ${\text{min}}_{i=1}^C\mathrm{ℛ̂}(\mathbf{x},{\mathbf{D}}_i)$ with the dictionaries learned from Eq. (2) leads to predicted class label of x, where C is the number of classes.

2.4. Classification with kernel-based methods

Kernel methods, such as support vector machine (SVM) and kernel discriminant analysis (KDA), represent powerful baseline methods for comparative analysis. The main motivation of kernel methods is that the data may not be linearly separable in the original space; however, by mapping them into a much higher dimensional space, improved class separation is revealed. These methods use a variety of kernel functions to operate in a higher dimensional space by computing the inner products in that space. For example, SVM constructs a hyperplane or set of hyperplanes in a high or infinite dimensional space for classification. Ideally, good separation is achieved by the hyperplane that has the largest distance to the nearest training data of any class, which is referred to as the functional margin. A modified maximum margin (soft margin) method is further suggested to allow for mislabeled training data [15]. KDA is a another kernel methods that essentially combines KPCA and linear discriminant analysis (LDA) [16, ?, ?]. The first step is to construct a similarity matrix from the training data, which is computed through a weighted Gaussian function such as $K=e\left(\frac{-A^2}{\sigma }\right)$. In addition, the rank of the kernel matrix can be large and the first T eigenvectors corresponding to the largest T eigenvalues are selected. Therefore, parameters σ and T are empirically determined for a range of values.

3. EXPERIMENTAL RESULTS

The dataset consists of 61 images of varying sizes that have been collected from the NIH repository of The Cancer Genome Atlas. Two experiments were designed with and without normal tissue, however, in both cases, necrotic (16 images), apoptotic (16 images), and tumor (22 images) patches are annotated by the pathologist. Pixels that are close to the image boundary are removed from the analysis due to the edge effect. A total of 20, 000 pixels are selected as a library for evaluating each classifier, where each class has 5000 pixels, and images in the same class have approximately the same number of representative data points. The computational modules are implemented in MATLAB and integrated with other toolboxes for solving optimization problems of sparse coding and dictionary learning. Table 1 summarizes classification results using leave-one-out policy.

Table 1.

Comparison of classification performance of algorithms: Sparse (classification algorithm based on dictionary learning and sparse coding), KDA (Kernel Discriminant Analysis), and SVM with linear, quadratic, rbf (Gaussian radial basis function) and polynomial kernels. All units are in %.

	Sparse	KDA	SVM linear	SVM quad	SVM rbf	SVM poly
3-class	90.05	99.12	94.27	91.89	91.44	88.22
4-class	85.87	78.65	90.03	83.47	81.84	82.58

The rationale for adding the normal class is that these patches may come from the Gray matter; therefore, morphology of the larger neurons may be interpreted as tumor regions. However, there was a very little impact by introducing this class. Our analysis also indicates sparse coding and redundant representation did not advance classification accuracy. However, KDA seems to outperform SVM. This is potentially due to the fact that KDA also does dimensionality reduction; therefore, by denoising and removing outliers, an improved performance is achieved. In another experiment, we removed all but one training sample that contained tumor cells with low chromaticity. As a result, most of the classifiers under-performed, which emphacises the need for adequate training data. However, KDA can be difficult to train for a very large training dataset and empirical evaluation of the parameter space (e.g., σ and T) can be expensive.

4. CONCLUSIONS

In this paper, we presented an approach for automatic classification of tissue histology based on dictionary learning and sparse coding, and compared it with the traditional kernel methods. Histological images are processed and represented by a number of invariant features at the global and object levels. Class-specific dictionaries are then learned for each class through sparse coding by iteratively removing shared elements among dictionaries. Classification of each patch is performed by comparing the error in the sparse reconstruction among all dictionaries. The classifier performance was then compared with two kernel methods of SVM and KDA. The training data were selected to represent inherent heterogeneity that is present from multiple laboratories. Preliminary data indicates the kernel methods tend to perform better than sparse coding. Our current efforts are to construct a larger training set and to classify the entire tissue section for a larger database.