Appropriateness of the probability approach with a nutrient status biomarker to assess population inadequacy: a study using vitamin D

Abstract

Background: There are questions about the appropriate method for the accurate estimation of the population prevalence of nutrient inadequacy on the basis of a biomarker of nutrient status (BNS).

Objective: We determined the applicability of a statistical probability method to a BNS, specifically serum 25-hydroxyvitamin D [25(OH)D]. The ability to meet required statistical assumptions was the central focus.

Design: Data on serum 25(OH)D concentrations in adults aged 19–70 y from the 2005–2006 NHANES were used (n = 3871). An Institute of Medicine report provided reference values. We analyzed key assumptions of symmetry, differences in variance, and the independence of distributions. We also corrected observed distributions for within-person variability (WPV). Estimates of vitamin D inadequacy were determined.

Results: We showed that the BNS [serum 25(OH)D] met the criteria to use the method for the estimation of the prevalence of inadequacy. The difference between observations corrected compared with uncorrected for WPV was small for serum 25(OH)D but, nonetheless, showed enhanced accuracy because of correction. The method estimated a 19% prevalence of inadequacy in this sample, whereas misclassification inherent in the use of the more traditional 97.5th percentile high-end cutoff inflated the prevalence of inadequacy (36%).

Conclusions: When the prevalence of nutrient inadequacy for a population is estimated by using serum 25(OH)D as an example of a BNS, a statistical probability method is appropriate and more accurate in comparison with a high-end cutoff. Contrary to a common misunderstanding, the method does not overlook segments of the population. The accuracy of population estimates of inadequacy is enhanced by the correction of observed measures for WPV.

See corresponding editorial on page 1

INTRODUCTION

The ability to estimate the prevalence of nutrient inadequacy for a population group is an important component of public health policy. The estimation drives decisions about the adequacy of the food supply as well as activities for the maintenance of the health of the population. An accurate characterization of the prevalence of inadequacy is critical because the policy and program implications differ depending on the proportion of persons considered nutritionally inadequate.

For >50 y, the estimation of nutrient inadequacy has relied primarily on measures of intake for which observed nutrient intakes have been compared with nutrient-intake reference values. Over time, a statistically driven methodology known as the probability approach (1) has been developed to estimate the prevalence of inadequacy based on intake and has proven to be more accurate than the use of a so-called high-end cutoff (1–3), which is an approach that specifies risk of inadequacy when an intake is below the requirement of an upper percentile of the population, typically the 97.5th percentile.

There is increasing interest in the use of a biomarker of nutrient status (BNS)⁴ to derive the prevalence of inadequacy for a population group and, as underscored in a recent report from the Institute of Medicine (IOM) (4), in the assessment of whether the probability approach that is used with intake measures is applicable to BNSs. A BNS often provides information on whether a population has met physiologic requirements for the nutrient (5). When available, BNSs may offer advantages for the estimation of the prevalence of inadequacy compared with intake measures because they can reflect other information about status such as bioavailability and absorption. Moreover, BNSs can be objectively measured, whereas intakes are affected by biases common to self-reported data. To date, the application of BNSs for the estimation of inadequacy has mirrored the earlier history of the more commonly available nutrient intake measure whereby the high-end cutoff is used, and persons who fall below that measure are deemed to be inadequate, which is an approach known to inappropriately inflate prevalence estimates. However, unlike the evolving approach for intake measures, the use of BNSs has not readily incorporated newer methods for the estimation of the prevalence of nutrient inadequacy such as the probability approach. This failure is likely due to questions about the appropriateness of statistical methods developed for intake measures for use with BNSs as well as the lack of understanding of the principles surrounding the use of statistical probability and the improved accuracy of estimation afforded by the probability approach compared with the 97.5th percentile high-end cutoff approach.

The purpose of this analysis was to evaluate the applicability of the probability approach to a BNS. Serum 25-hydroxyvitamin D [25(OH)D], which is a BNS known to reflect the nutrient status of vitamin D and an identified subject for a test of the probability approach (4), was selected for this study. In addition, our work addresses several misunderstandings about the estimation of the prevalence of inadequacy using probability.

SUBJECTS AND METHODS

Analysis of probability approach

Details concerning the probability approach are available from several sources (1–3). In brief, the 2 essential data sets are 1) the distribution of measures of the BNS as observed in the population (ie, the observed distribution) and 2) the specification of a reference value distribution. For a BNS, the reference value can be identified as the healthy serum concentration, which is distributed around an average for a group. The probability approach originally developed for use with intake measures has been modified to make use of a shortcut that incorporates the average reference intake, which in the case of intake is the Estimated Average Requirement (EAR) (1, 6), and thus, it is also termed the EAR cutoff method. The shortcut is carried out mathematically by determining the proportion of the population below the average reference intake. The shortcut is used more commonly than the relatively complicated full probability approach and is the focus of this study. The shortcut relies on certain statistical assumptions about distributions of observed and reference values. Thus, to ensure the appropriateness of the application of the shortcut probability approach to a BNS, distributions of BNS reference and observed values must meet the following assumptions: 1) the reference distribution is at least symmetric if not normal, 2) the variance of the reference distribution is less than the variance of the observed distribution (expressed as the estimated usual intake), and 3) reference and observed distributions are independent (1, 3). In addition, it has been established that reference values are appropriately compared with observed measures corrected for within-person variability (WPV), which are referred to as usual measures (7–9).

The observed values used in this study to test the 3 statistical assumptions for serum 25(OH)D concentrations are from NHANES. Although outcomes related to the applicability of the probability approach to vitamin D intake are independent of those for BNSs and assumed to be consistent with the probability approach, we conducted the same analyses for vitamin D intake measures from NHANES to ensure that, as anticipated, the approach was applicable to the intake measure and to compare prevalence outcomes because of the likely differences between these 2 measures used for the estimation of prevalence. The 2005–2006 cycle from NHANES was selected because it is the only time period for which both serum 25(OH)D concentrations and vitamin D intakes (from food and supplements) have been released by the CDC. The IOM report on Dietary Reference Intakes for vitamin D (4) provided information on reference values for concentrations of serum 25(OH)D as well as vitamin D intake. Serum 25(OH)D is reported in nanomoles per liter (a nmol/L value is ∼2.5 times the amount in ng/mL). Vitamin D intake is reported in microgram amounts (1 μg is equivalent to 40 IU vitamin D).

Observed distributions for vitamin D

NHANES is a nationally representative, cross-sectional survey of the noninstitutionalized US population (10). The survey uses a complex, stratified, multistage probability cluster sampling design. The National Center for Health Statistics within CDC administers NHANES and obtains written informed consent from all participants or proxies. The examination response rate for the 2005–2006 cycle was 77% (unweighted) (11).

Survey personnel first interview participants in their homes during which interviewers collect information on demographic characteristics, dietary supplement use, and health-related issues. From 1 to 2 wk after the household interview, participants undergo a standardized physical examination and blood collection in a mobile examination center, and dietary recall information is collected. A second dietary recall is conducted via telephone 3–10 d after the first recall. Both recalls are collected by using the USDA's Automated Multiple Pass Method (12, 13).

To facilitate comparisons, only persons 19–70 y of age were included in this study because reference values for serum 25(OH)D concentrations do not vary by age or sex within this group (4). The initial sample, after the exclusion of individuals with missing survey weights, was 10,348 persons. We excluded persons younger than 19 y of age (n = 5101) or older than 70 y of age (n = 814). Participants who were missing both 24-h dietary recalls (n = 362) or missing the serum 25(OH)D measure (n = 413) were also excluded; persons with a single dietary recall were retained. The final analytic sample consisted of 3871 adults.

Serum 25(OH)D measurements were determined at the CDC by using a radioimmunoassay kit (DiaSorin). Adjustments recommended by the CDC (14) were made to the 2006 data for serum 25(OH)D concentrations because of quality control drifts noted by the CDC.

We calculated the observed mean vitamin D intake from food by averaging the 2 dietary recalls after adjustment for the covariates described in Statistical methods. A single recall was used if a second recall was not conducted. The average daily intake of vitamin D from dietary supplements was added to the average intake from foods. The dietary supplement questionnaire administered in the home determined the use of dietary supplements over the past 30 d (15). Product-label declarations were used to identify the presence and amount of vitamin D in identified supplements. As described elsewhere (16), the average daily intake of vitamin D from all dietary supplements was calculated by using the number of days of reported consumption of the supplement, the reported amount that respondents took per day, and the serving-size unit from the product label.

Reference distributions for vitamin D

We identified reference distributions by using information from the IOM report on Dietary Reference Intakes for vitamin D (4). The average reference serum 25(OH)D concentration for adults 19–70 y of age specified by the IOM was 40 nmol/L, and the 97.5th percentile reference value was identified as 50 nmol/L. Intake reference values were specified as 10 μg/d for the EAR and 15 μg/d for the 97.5th percentile (ie, the Recommended Dietary Allowance). The IOM report indicated a normal distribution for vitamin D reference values but did not provide variance measures. We calculated the variance for reference distributions by recalling that, for normal distributions, the 97.5th percentile equals the mean plus 2 SDs. Therefore, the variance is equal to the square of one-half of the difference between the 97.5th percentile and the mean of distributions.

Statistical methods

Analyses to produce means, variances, SEs of the mean, and percentiles for values not corrected for WPV were computed with the SAS System for Windows software (release 9.2; SAS Institute Inc). We incorporated NHANES survey specific weights to ensure national representation. For serum 25(OH)D, adjustments were made for season because of the ability of sun exposure to influence serum 25(OH)D concentrations, and the NHANES variable for time of year of data collection was used for this purpose. An initial analysis revealed that variables that reflect fasting state and time of day did not affect serum 25(OH)D concentrations, and thus, these possible adjustments were not incorporated. For intake, adjustments used were the day of week that the dietary recall was collected and sequence (ie, first or second recall).

The correction for WPV allows the observed distribution to reflect usual measures rather than a single observed measure, and the procedure uses measurements from participants with ≥2 observations to compute the variance of daily measurements around their mean (7–9). Biological measures may naturally vary within a normal range for an individual on a day-to-day basis, which causes variability within a person. Thus, a distribution on the basis of a single measurement will lead to an overestimate of the percentage of population above or below a set criterion because the distribution derived will be flatter and wider (ie, greater variability) than a distribution that is based on measures averaged over ≥2 observations, which reduces variability. The basis for correction for WPV rests on the understanding that the SD for observed values has 2 components (ie, the within-person SD and between-person SD), whereas the SD for the usual distribution reflects only between-person variability. Because the reference distribution also reflects only between-person variability, error components of the usual distribution and the reference distribution are more similar than are error components of the uncorrected observed and reference distributions (7, 8). We analyzed observed values for WPV and derived usual serum concentrations as well as usual intakes by correcting for WPV with the software PC-Side (version 1.01; Iowa State University), which is based on the Iowa State University method (17, 18). Observed values were adjusted for the covariates before correction for WPV. Because a replicate blood collection was not available for the NHANES 2005–2006, we used replicate estimates from a subsample of the NHANES 2001–2002 Second Day Exam public-use file (n = 469) to estimate WPV (19). We used this WPV value to correct single 2005–2006 serum 25(OH)D values. When we attempted to transform NHANES 2005–2006 data for serum 25(OH)D concentrations into the normal scale, we encountered difficulties because the serum data had been discretized before they were reported. Serum 25(OH)D concentrations were reported to the nearest 0.5 nmol/L, and this resulted in an observed distribution of concentrations with numerous peaks and valleys. For this reason, we added random normal noise with mean zero and very small variance to the serum measurements to smooth the empirical distribution and ease the process of normalization. This method was consistent with the accepted statistical procedure to improve properties of data without changing summary statistics (20). In the case of vitamin D intake, observed intakes of vitamin D from foods were also corrected for WPV, and the average daily intake of vitamin D from supplements was added to estimates (21, 22).

The PC-Side software produces all descriptive statistics for measures corrected for WPV, and these were used with serum reference values from the IOM (4) to identify the proportion below the average reference value of 40 nmol/L, which is a calculation that was shown to be equivalent to the determination of the prevalence by using the shortcut probability approach (1). The population percentage below the 97.5th percentile of the BNS reference-value distribution (ie, 50 nmol/L) was also determined to characterize the high-end cutoff approach. Similar estimates were made for intakes by using relevant IOM reference values.

Observed distributions for this study are referred to as either usual distributions (ie, observed values corrected for WPV) or uncorrected observed distributions. They may also be termed generally as observed values.

RESULTS

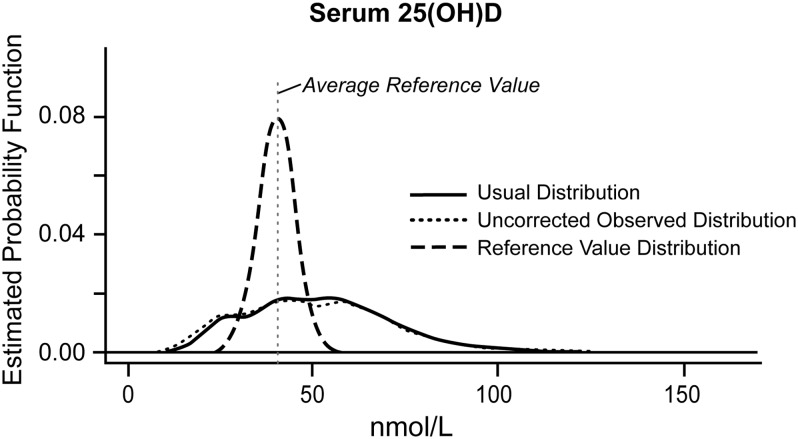
Results are presented in the context of the statistical assumptions for use of the shortcut probability approach with a BNS. The usual distribution, uncorrected observed distribution, and reference distribution for serum 25(OH)D concentrations are illustrated in Figure 1 for our sample of adults aged 19–70 y. The WPV analysis revealed that differences between the uncorrected observed distribution and the usual distribution were relatively small for serum 25(OH)D, although, as expected, the uncorrected observed distribution trended toward greater variability than the usual distribution did [SD: 23.7 compared with 21.4 nmol/L serum 25(OH)D]. Distributions and related SDs for vitamin D intake also showed greater variability for the uncorrected observed distributions as shown elsewhere (see Figure 1 under “Supplemental data” in the online issue).

FIGURE 1.

Usual, uncorrected observed, and reference distributions: serum 25(OH)D for adults aged 19–70 y in NHANES 2005–2006 (n = 3871). The usual distribution (SD: 21.4 nmol/L) was corrected for within-person variability and derived by using PC-Side software (version 1.01; Iowa State University). The uncorrected observed distribution (SD: 23.7 nmol/L) was derived with SAS System for Windows software (release 9.2; SAS Institute Inc) and was not corrected for within-person variability. The reference distribution was derived by using the mean (95th percentile) specified by the Institute of Medicine (5) with calculated SD = 5.0 nmol/L on the basis of normality. The x-axis indicates concentration values. The estimated probability function (y-axis) indicates the frequency of each concentration in the sample. 25(OH)D, 25-hydroxyvitamin D.

Overall, the distributions for serum 25(OH)D (Figure 1) satisfied statistical assumptions for the use of the shortcut probability approach with BNSs. First, as indicated by the IOM (4), the reference distribution was normal and symmetrical. Second, the variance of the observed distribution for serum 25(OH)D was larger than the variance of the reference distribution; specifically, the SD was 5.0 nmol/L for the reference distribution and 21.4 nmol/L for the estimated usual distribution. Measures of vitamin D intake also met statistical assumptions (see Figure 1 under “Supplemental data” in the online issue). Third, the assumption of independence between observed and reference values stands without empirical evidence because the correlation can be examined only if the healthy BNS concentration is known for each individual. In the absence of the ability to determine personal requirements, the long-standing assumption for intake, which has largely been untested, is that the amount of the vitamin consumed is unrelated to the amount needed by the individual (1). IOM committees that have been responsible for the development of dietary reference values have incorporated this assumption across a wide range of nutrients, with the exception of calories (6). The independence between observed serum 25(OH)D concentrations and reference values is also not testable, but importantly, the assumption has not been contradicted by available evidence. Current literature has suggested that the serum 25(OH)D concentrations observed in the population are primarily a function of vitamin D exposures, and there is no systematic evidence that persons with lower serum concentrations have lower needs (4).

With regard to estimates of vitamin D inadequacy, for adults aged 19–70 y in this sample, the shortcut probability approach calculated a 19% inadequacy on the basis of serum 25(OH)D, which is an estimate that is similar to that highlighted in the IOM report, which noted the percentage of persons below the average reference value in the absence of a confirmed statistical approach for the estimation of inadequacy (4). Our prevalence estimates varied little on the basis of age subgroup or sex within our sample (Table 1). The use of a 97.5th percentile high-end cutoff inflated estimates of inadequacy compared with those of the shortcut probability approach (Table 1), which increased the prevalence to 36% for adults aged 19–70 y with similar increases for age subgroups and sex groups. Finally, as expected, the estimation of the prevalence of inadequacy without correction for WPV, even when the shortcut probability approach was used, resulted in an inflated prevalence estimate. The increase was relatively small in the case of serum 25(OH)D, which reflected 1–4 percentage points depending on the age subgroup and sex (Table 1).

TABLE 1.

Prevalence of vitamin D inadequacy on the basis of serum 25(OH)D concentrations: comparisons of outcomes for adults aged 19–70 y in NHANES 2005–2006¹

	On the basis of the 97th percentile cutoff2	On the basis of the shortcut probability approach without correction for WPV3	On the basis of the shortcut probability approach with correction for WPV4
	%	%	%
Age
Total: 19–70 y (n = 3871)	36 ± 0.7	22 ± 0.7	19 ± 0.8
19–30 y (n = 1219)	36 ± 1.3	22 ± 1.2	19 ± 1.4
31–50 y (n = 1476)	36 ± 1.2	20 ± 1.0	19 ± 1.3
51–70 y (n = 1176)	36 ± 1.4	22 ± 1.2	20 ± 1.4
Sex
M (n = 1827)	35 ± 1.1	22 ± 1.0	18 ± 1.2
F (n = 2044)	37 ± 1.0	20 ± 0.9	20 ± 1.1

¹All values are prevalences ± SDs. Descriptive statistics were computed with SAS System for Windows software (release 9.2; SAS Institute Inc) and Iowa State University PC-Side software. Serum concentrations were adjusted for season. WPV, within-person variability; 25(OH)D, 25-hydroxyvitamin D.

²Estimates of inadequacy were inappropriately inflated because of misclassification (cutoff method). Serum concentrations were corrected for WPV.

³Estimates of inadequacy were inappropriately inflated because of the use of a probability approach without correction for WPV.

⁴Provides the most accurate estimate of inadequacy because of the use of the shortcut probability approach with WPV correction.

When vitamin D intake was used with the probability approach, the outcome was an estimate of 71% inadequacy. Prevalence estimates on the basis of intake may differ from those on the basis of a BNS for the same nutrient because measures may reflect different variables of status. Vitamin D offers a clear example of such a difference because UVB radiation as well as intake affects the BNS.

DISCUSSION

Application of the shortcut probability approach

The use of the shortcut probability approach with a BNS to estimate the prevalence of nutrient inadequacy cannot be fully appreciated without an understanding of the underlying framework of the approach. This framework has been described by others (1–3), and the discussion in the current article is brief to provide context for conclusions. A common point of confusion is how the determination of the proportion of individuals with observed measures below the average reference value comports mathematically with the application of statistical probability and, in turn, offers an accurate estimate of the prevalence of inadequacy.

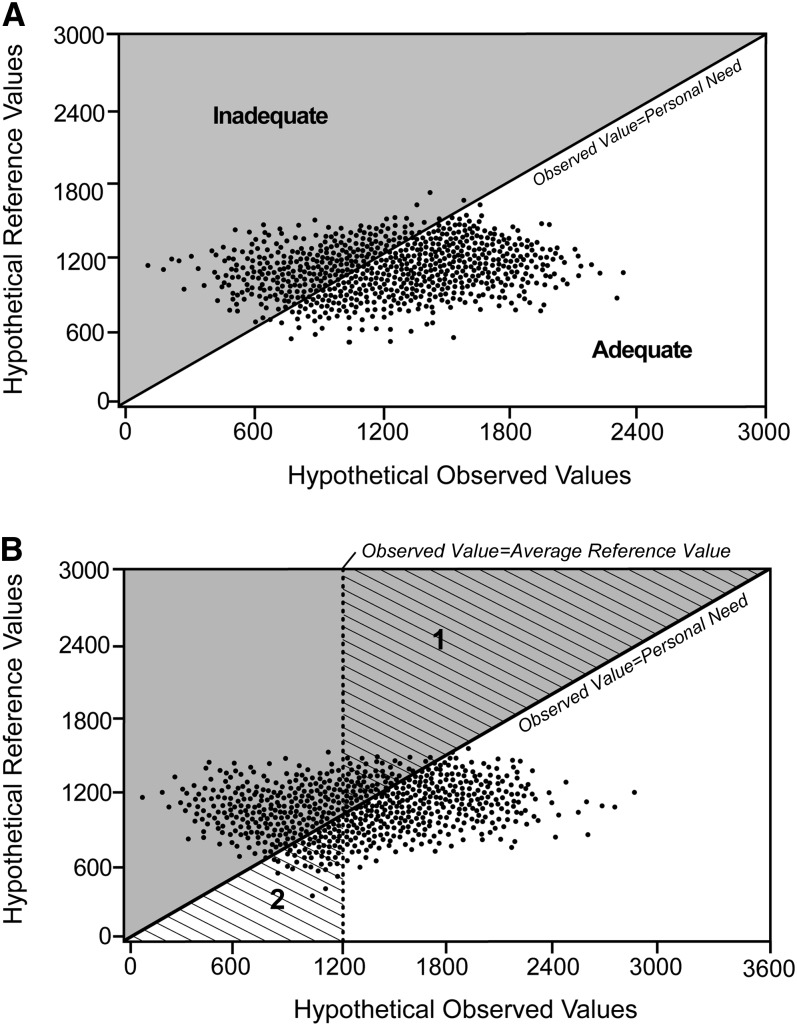
An estimation method is needed because, although we may know observed BNS concentrations of individuals, it is not possible to know the personal healthy BNS concentrations of individuals. If such knowledge were possible, a count as shown in Figure 2A would readily specify the prevalence of inadequacy. The 45° line reflects the point at which observed values of individuals match their personal needs relative to a BNS concentration. Persons on or below the 45° line are adequate for the nutrient. Persons above the diagonal line (shaded area) have observed values that are less than their personal needs and, therefore, experience inadequacy. The counting of the points above the diagonal line provides a precise prevalence of inadequacy.

FIGURE 2.

A: Hypothetical plot of individuals’ observed measure compared with individuals’ known personal requirements or BNS concentration for a nutrient. The line at the 45° angle reflects the point at which an observed value is equivalent to an individual's personal need. Persons above the 45° line (shaded area) are inadequate for a nutrient; persons below the 45° line are adequate for a nutrient. B: Illustration of mathematical equivalence between the number of persons below an average reference value and the number of persons who experienced inadequacy. The vertical line reflects the point at which an observed value is equivalent to a reference value (ie, 1200 units). The line at the 45° angle reflects the point at which an observed value is equivalent to an individual's personal need. Triangles 1 and 2 (diagonal hash lines) are bounded by the vertical line and the 45° line. The number of persons in triangle 2, which can be determined by readily available data, is equal to the number of persons in triangle 1, which is unknown. The numerical count for the gray shaded area to the left of the vertical line is known; the numerical count for triangle 2 (known) can be substituted for the count for triangle 1 in the gray shaded area. Modified from reference 2 and reproduced with permission from National Academies Press.

However, in the absence of knowing personal needs, the shortcut probability approach uses data that can be obtained about each individual's observed measures to provide an indirect count of persons above the 45° line shown in Figure 2A (ie, persons with observed values less than their personal needs). The ability to do so rests on meeting the 3 statistical assumptions. Thus, contrary to a common misunderstanding, the shortcut probability approach does not ignore persons between the average reference value and high-end 97.5th percentile cutoff. The indirect count is illustrated in Figure 2B. Two triangles (triangles 1 and 2) are identified with diagonal lines: These triangles are bounded by 1) a vertical line that reflects the point at which an observed value equals the average reference value and 2) a 45° line that reflects the point at which an observed value equals the individual's personal requirement or BNS concentration. As concerns the goal of counting persons above the 45° line, the points within triangle 1 are persons who must be included in the count for inadequacy, whereas persons in triangle 2 are not to be included in the count. Because of the data available, the number of observed values that are less than the average reference value can be readily counted (ie, persons to the left of the vertical line). However, this count inappropriately includes persons in triangle 2 while omitting persons in triangle 1. The solution rests with the fact that the number of persons in triangle 2 is virtually the same as the number in triangle 1 (1). Consequently, if, for counting purposes, we use the number of persons in triangle 2 as a stand-in for the number of persons in triangle 1, the count of persons with observed values less than the average reference value (ie, all persons to the left of the vertical line) is mathematically equivalent to the count of all persons above the 45° line. Hence, the shortcut probability approach uses the number of persons below the average reference value to specify the prevalence of nutrient inadequacy for a group.

Meeting statistical assumptions and enhancing accuracy

The statistical assumptions that were the basis for this study (ie, the reference distribution is symmetric, the variance of the reference distribution is less than the variance of observed distribution, and the reference and observed distributions are independent) have been considered in detail by Carriquiry (3), who used simulations to illustrate the importance of meeting the assumptions. When serum 25(OH)D concentrations were examined in our study, observed and reference distributions were shown to conform to the 3 statistical assumptions. Although the ability to quantitatively ascertain independence between the 2 types of distributions for serum 25(OH)D was not possible, the assumption was accepted in the absence of evidence to the contrary, which was similar to applications with intake data. Future research should continue to explore this assumption across the range of BNSs because each BNS reflects a unique underlying biological status. For example, we need to clarify what, if any, role homeostatic mechanisms may play in the use of BNSs for the estimation of the prevalence of inadequacy. Although biological measures could be affected by homeostatic mechanisms that maintain an apparently healthy concentration even at the expense of body stores and other metabolic needs (eg, plasma retinol), measures that would be subject to such regulation may not be appropriate as BNSs because they may fail to serve as sensitive signals of nutrient status or mask the true status of the individual. In addition, there may be as yet unknown characteristics of BNSs that make them different from intake measures in ways that require adjustment of the shortcut probability approach.

In any case, the shortcut probability approach is more accurate than the use of the 97.5th percentile high-end cutoff when statistical assumptions are met because statistical probability eliminates the inherent misclassification (1, 2) caused by the inability of the cutoff approach to address the fact that personal needs vary, and virtually all (97.5%) of the population have needs below the cutoff. The cutoff approach results in a portion of persons with adequate status who are misclassified as inadequate and, in turn, overestimates the true magnitude of the inadequacy. This inflation of prevalence estimates was examined in detail in a seminal 1986 report that showed that the overestimation could range from 4.2% to 75.2% of 3 nutrients used as examples (2), depending on the nutrient and sex. In our sample, the shortcut probability approach estimated a vitamin D inadequacy of 19% on the basis of serum measures. In contrast, the 97.5th percentile high-end cutoff inflated prevalence estimates by 17 percentage points because of the misclassification, which resulted in an estimate of 36% inadequacy. Differences of this magnitude cannot be ignored, and continued use of the high-end cutoff for the assessment of the nutrient status of population groups is potentially misleading.

There was no expectation that prevalence estimates that were based on vitamin D intake would mirror those that were based on serum 25(OH)D because serum measures reflect total exposure, including contributions from sunlight, whereas intake reflects only diet (food and supplements). Moreover, BNSs are not subject to an underreporting bias, incomplete food composition data, or the effect of bioavailability. However, the notable difference of 52 percentage points in our sample of adults aged 19–70 y suggested that either there is a serious underreporting of foods that contain vitamin D, there are shortcomings in the food-composition database, or most likely, sun exposure, even if inadvertent, makes meaningful contributions to vitamin D status. BNSs for other nutrients may provide prevalence estimates more or less similar to those that are based on intake, depending on how status is defined for each nutrient.

Finally, the correction of observed values of a BNS for WPV results in a better representation of observed values than a single data point. This procedure ensures additional accuracy in prevalence estimates. In the case of serum 25(OH)D, WPV was relatively low. However, other researches have shown greater day-to-day variability in biological measures for nutrients (23), and this variability would result in a greater inflation of estimates if values were uncorrected for WPV. Corrections for WPV have been incorporated regularly when intake measures serve as the basis for prevalence estimates, but the correction has not been commonly carried out for BNSs. Two recent reports from the CDC on serum 25(OH)D concentrations for the US population illustrated this point. One report issued in 2011 (24) did not correct for WPV and also used a high-end cutoff approach. The second report, which was made available in 2012, presented biochemical indicators from NHANES and reported percentages of persons below the serum 25(OH)D average reference value of 40 nmol/L but did not correct serum concentrations for WPV (25). Putting aside the use of the high-end cutoff approach in the 2011 report, the failure to correct for WPV in either report is concerning because a central goal for the estimation of nutrient inadequacy within a population group should be to ensure accuracy, even in the case of small levels of WPV that can be meaningful on a population basis.

This work supports the use of BNSs for nutrient assessment of population groups on the basis of a statistical probability rather than the 97.5th percentile high-end cutoff approach. In this way, estimates for the prevalence of nutrient inadequacy will take into account the variability in observed measures in individuals and in reference-value distributions. In turn, reports on the nutrient status of population groups may be closer to the reality of the number of persons who are inadequate and, thus, may better inform health providers and policy makers about the extent of interventions required. However, additional exploration of certain BNS issues is needed. It would be useful to specifically elucidate factors about BNSs, either as a single measure or as like-groups of BNSs, that may impact conformity with the 3 statistical assumptions, including the independence between observed and healthy reference concentrations and the extent to which homeostatic mechanisms affect the ability of a biological measure to serve as a BNS. A focus on correction of WPV is warranted as well as research to clarify the nature of WPV for BNSs.