A Novel Approach for Choosing Summary Statistics in Approximate Bayesian Computation

Abstract

The choice of summary statistics is a crucial step in approximate Bayesian computation (ABC). Since statistics are often not sufficient, this choice involves a trade-off between loss of information and reduction of dimensionality. The latter may increase the efficiency of ABC. Here, we propose an approach for choosing summary statistics based on boosting, a technique from the machine-learning literature. We consider different types of boosting and compare them to partial least-squares regression as an alternative. To mitigate the lack of sufficiency, we also propose an approach for choosing summary statistics locally, in the putative neighborhood of the true parameter value. We study a demographic model motivated by the reintroduction of Alpine ibex (Capra ibex) into the Swiss Alps. The parameters of interest are the mean and standard deviation across microsatellites of the scaled ancestral mutation rate (θ_anc = 4N_eu) and the proportion of males obtaining access to matings per breeding season (ω). By simulation, we assess the properties of the posterior distribution obtained with the various methods. According to our criteria, ABC with summary statistics chosen locally via boosting with the L₂-loss performs best. Applying that method to the ibex data, we estimate ${\widehat{\theta }}_{\text{anc}}\approx \text{1.288}$ and find that most of the variation across loci of the ancestral mutation rate u is between 7.7 × 10⁻⁴ and 3.5 × 10⁻³ per locus per generation. The proportion of males with access to matings is estimated as $\widehat{\omega }\approx \text{0.21}$, which is in good agreement with recent independent estimates.

UNDERSTANDING the mechanisms leading to observed patterns of genetic diversity has been a central objective since the beginnings of population genetics (Fisher 1922; Haldane 1932; Wright 1951; Charlesworth and Charlesworth 2010). Three recent trends keep advancing this undertaking: (1) molecular data are becoming available at an ever higher pace (Rosenberg et al. 2002; Frazer et al. 2007), (2) new theory continues to be developed, and (3) increased computational power allows solution of problems that were intractable just a few years ago. In parallel, the focus has shifted to inference under complex models (e.g., Fagundes et al. 2007; Blum and Jakobsson 2011) and to the joint estimation of parameters (e.g., Williamson et al. 2005). Usually, these models are stochastic. The increasing complexity of models is justified by the underlying processes like inheritance, mutation, modes of reproduction, and spatial subdivision. On the other hand, complex models are often not amenable to inference based on exact analytical results. Instead, approximate methods such as Markov chain Monte Carlo (MCMC) (Gelman et al. 2004) or approximate Bayesian computation (ABC) (Marjoram and Tavaré 2006) are used. These approximate methods address different issues in inference and the choice therefore depends on the specific problem. A significant part of research in the field is currently devoted to the refinement and development of such methods. ABC is a Monte Carlo method of inference that emerged from the confrontation with models for which the evaluation of the likelihood is computationally prohibitive or impossible (Fu and Li 1997; Tavaré et al. 1997; Weiss and Von Haeseler 1998; Pritchard et al. 1999; Beaumont et al. 2002). ABC may be viewed as a class of rejection algorithms (Marjoram et al. 2003; Marjoram and Tavaré 2006), where the full data are projected to a lower-dimensional set of summary statistics. Here, we propose an approach for choosing summary statistics based on boosting (see below), and we apply it to the estimation of the mean and variance across microsatellites of the scaled ancestral mutation rate and of the mating skew in Alpine ibex (Capra ibex). We further show that focusing the choice of statistics on the putative neighborhood of the true parameter value improves estimation in this context.

The principle of ABC is to first simulate data under the model of interest and then accept simulations that produced data close to the observation. Parameter values belonging to accepted simulations yield an approximation to the posterior distribution, without the need to explicitly calculate the likelihood. The full data are usually compressed to summary statistics to reduce the number of dimensions. Formally, the posterior distribution of interest is given by

$$\pi \left(\mathbf{\phi }|D\right)=\frac{\pi \left(D|\mathbf{\phi }\right)\pi \left(\mathbf{\phi }\right)}{\pi \left(D\right)}=\frac{\pi \left(D|\mathbf{\phi }\right)\pi \left(\mathbf{\phi }\right)}{{\displaystyle {\int }_{\text{Φ}}\pi \left(D|\mathbf{\phi }\right)\pi \left(\mathbf{\phi }\right)d\mathbf{\phi }}},$$ (1)

where φ is a vector of parameters living in space Φ, D denotes the observed data, π(φ) the prior distribution, and π(D|φ) the likelihood. With ABC, (1) is approximated by

$${\pi }_{\epsilon }\left(\mathbf{\phi }|s\right)\propto \pi \left(\rho \left(s\prime ,s\right)\le {\delta }_{\epsilon }|\mathbf{\phi }\right)\pi \left(\mathbf{\phi }\right),$$ (2)

where s and s′ are abbreviations for realizations of S(D) and S(D′), respectively, and S is a function generating a q-dimensional vector of summary statistics calculated from the full data. The prime denotes simulated points, in contrast to quantities related to the observed data. Further, ρ(⋅) is a distance metric and δ_ε the rejection tolerance in that metric space, such that on average a proportion ε of all simulated points is accepted. ABC, its position in the ensemble of model-based inference methods, and its application in evolutionary genetics are reviewed in Marjoram et al. (2003), Beaumont and Rannala (2004), Marjoram and Tavaré (2006), Beaumont (2010), Bertorelle et al. (2010), and Csilléry et al. (2010). Although the origin of ABC is generally assigned to Fu and Li (1997), Tavaré et al. (1997), and Pritchard et al. (1999), some aspects, such as the summary description of the full data, inference for implicit stochastic models, and algorithms directly sampling from the posterior distribution, trace farther back (e.g., Diggle 1979; Diggle and Gratton 1984; Rubin 1984).

A fundamental issue with the basic ABC rejection algorithm (e.g., Marjoram et al. 2003) is its inefficiency: A large number of simulations are needed to obtain a satisfactory number of accepted runs. This problem becomes worse as the number of summary statistics increases and is known as the curse of dimensionality. Three solutions have been proposed: (1) more efficient algorithms combining ABC with principles of MCMC (e.g., Marjoram et al. 2003; Wegmann et al. 2009) or sequential Monte Carlo (e.g., Sisson et al. 2007, 2009; Beaumont et al. 2009; Toni et al. 2009); (2) fitting a statistical model to describe the relationship of parameters and summary statistics after the rejection step, allowing for a larger tolerance δ_ε (Beaumont et al. 2002; Blum and François 2010; Leuenberger and Wegmann 2010); and (3) reduction of dimensions by sophisticated choice of summary statistics (e.g., Joyce and Marjoram 2008; Wegmann et al. 2009). In this study, we focus on point 3, which involves two further issues. First, most summary statistics used in evolutionary genetics are not sufficient. A summary statistic S(D) is sufficient for parameter φ if the conditional probability distribution of the full data D, given S(D) and φ, does not depend on φ, i.e., if

$$\pi \left(D=d|S\left(D\right)=s,\mathit{\phi }\right)=\pi \left(D=d|S\left(D\right)=s\right).$$ (3)

In other words, a statistic is sufficient for a parameter of interest, if it contains all the information on that parameter that can possibly be extracted from the full data (e.g., Shao 2003). Second, the choice of summary statistics implies the choice of a suitable metric ρ(⋅) to measure the “closeness” of simulations to observation (except for the nongeneric case ε = 0 in which no metric needs to be defined). The Euclidean distance (or a weighted version, e.g., Hamilton et al. 2005) has been used in most applications, but it is not obvious why this should be optimal. By “optimal” we mean that the resulting posterior estimate performs best in terms of an error criterion (or a set of criteria). The Euclidean distance is a scale-dependent measure of distance—changing the scale of measurement changes the results. Since this scale is determined by the summary statistics, the choice of summary statistics has implications for the choice of the metric. For these reasons, the choice of summary statistics should aim at reducing the dimensions, but also at extracting (combinations of) statistics that contain the essential information about the parameters of interest. This task is reminiscent of the classical problem of variable selection in statistics and machine learning (Hastie et al. 2011), and it is of principal interest here.

The choice of summary statistics in ABC has become a focus of research only recently. Joyce and Marjoram (2008) proposed a sequential scheme based on the principle of approximate sufficiency. Statistics are included if their effect on the posterior distribution is larger than some threshold. Their approach seems demanding to implement, and it is not obvious how to define an optimal threshold. Wegmann et al. (2009) suggested partial least-squares (PLS) regression as an alternative. In this context, PLS regression seeks linear combinations of the original summary statistics that are maximally decorrelated and, at the same time, have high correlation with the parameters (Hastie et al. 2011). A reduction in dimensions is achieved by choosing only the first r PLS components, where r is determined via cross-validation. PLS is one of several approaches for variable selection, but it is an open question how it compares to alternative methods in any specific ABC setting. Moreover, the optimal choice of summary statistics may depend on the location of the true (but unknown) parameter values. By definition, this is to be expected whenever the summary statistics are not sufficient, because then the information extracted from the full data by the summary statistics depends on the parameter value (see Equation 3). It is therefore not obvious why methods that assess the relation between statistics and parameters on a global scale should be optimal. Instead, focusing on the correlation only in the (supposed) neighborhood of the true parameter values might be preferable. The issue is that this neighborhood is not known in advance—if we could choose an arbitrarily small neighborhood around the truth, our inference problem would be solved and we would not need ABC or any other approximate method. However, the neighborhood may be established approximately, as we will argue later. The idea of focusing the choice of summary statistics on some local optimization has also been followed by Nunes and Balding (2010) and Fearnhead and Prangle (2012). Nunes and Balding (2010) proposed using a minimum-entropy algorithm to identify the neighborhood of the true value and then chose the set of summary statistics that minimized the mean squared error across a test data set. Fearnhead and Prangle (2012), on the other hand, first proved that, for a given loss function, an optimal summary statistic may be defined. For example, when the quadratic loss is used to quantify the cost of an error, the optimal summary statistic is the posterior mean. Since the latter is not available a priori, the authors devised a heuristic to estimate it and were able to show good performance of their approach. The choice of the optimization criterion may include a more local or a global focus on the parameter range. Different criteria will lead to different optimal summary statistics. The approaches by Nunes and Balding (2010) and Fearnhead and Prangle (2012), and the one we take here, have in common that they employ a two-step procedure, first defining “locality” and then using standard methods from statistics or machine learning to select summary statistics in this restricted range. They differ in the details of these two steps (see Discussion).

Here, we propose a novel approach for choosing summary statistics in ABC. It is based on boosting, a method developed in machine learning to establish the relationship between predictors and response variables in complex models (Schapire 1990; Freund 1995; Freund and Schapire 1996, 1999). Given some training data, the idea of boosting is to iteratively train a function that describes this relationship. At each iteration, the training data are reweighted according to the current prediction error (loss), and the function is updated according to an optimization rule. It has been argued that boosting is relatively robust to overfitting (Friedman et al. 2000), which would be an advantage with regard to high-dimensional problems as encountered in ABC. Different flavors of boosting exist, depending on assumptions about the error distribution, the loss function, and the learning procedure. In a simulation study, we compare the performance of ABC with three types of boosting to ABC with summary statistics chosen via PLS and to ABC with all candidate statistics. We further suggest an approach for choosing summary statistics locally and compare the local variants of the various methods to their global versions. Throughout, we study a model that is motivated by the reintroduction of Alpine ibex into the Swiss Alps. The parameters of interest are the mean and standard deviation across microsatellites of the scaled ancestral mutation rate and the proportion of males that obtain access to matings per breeding season. This model is used first in the simulation study for inference on synthetic data and assessment of performance. Later, we apply the best method to infer posterior distributions given genetic data from Alpine ibex. It is not our goal to compare all the approaches recently proposed for choosing summary statistics in ABC. This would reach beyond the scope of this article, but provides a perspective for future research. Recently, Blum et al. (2012) carried out a comparative study of the various approaches and found that, for an example similar to our context, PLS performed slightly better than approximate sufficiency (Joyce and Marjoram 2008), but worse than a number of alternative approaches including the posterior loss method (Fearnhead and Prangle 2012) and the two-stage minimum entropy procedure (Nunes and Balding 2010). Nevertheless, PLS has been widely used in recent applications and we have therefore focused on comparing our approach to PLS.

We start by describing the ibex model and its parameters. We then present an ABC algorithm that includes a step for choosing summary statistics. Later, we describe the boosting approach for choosing the statistics and we suggest how to focus this choice on the putative neighborhood of the true parameter value. Comparing different versions of boosting among each other and with PLS, we conclude that boosting with the L₂-loss restricted to the vicinity of the true parameter performs best, given our criteria. However, the difference from the next best methods (local boosting with the L₁-loss and local PLS) is small.

Model and Parameters

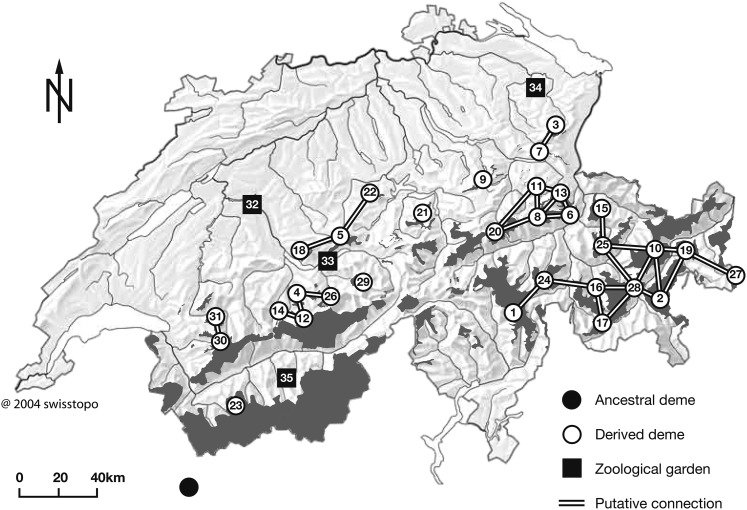
We study a neutral model of a spatially structured population with genetic drift, mutation, and migration. The demography includes admixture, subdivision, and changes in population size. This model is motivated by the recent history of Alpine ibex and their reintroduction into the Swiss Alps (Figures 1 and 2). By the beginning of the 18th century, Alpine ibex had been extinct except for ∼100 individuals in the Gran Paradiso area in Northern Italy (Figure 1). At the beginning of the 20th century, a schedule was set up to reestablish former demes in Switzerland (Couturier 1962; Stuwe and Nievergelt 1991; Scribner and Stuwe 1994; Maudet et al. 2002). The reintroduction has been documented in great detail by game keepers and authorities. We could reconstruct for 35 demes their census sizes between 1906 and 2006 (Supporting Information, File S2, census sizes) and the number of females and males transferred between them, as well as the times of these founder/admixture events (File S3, transfers). Inference on mutation and migration can therefore be done conditional on this information. The signal for this inference comes from the distribution of allele frequencies across loci and across demes.

Figure 1.

Location of Alpine ibex demes in the Swiss Alps. The parts with dark shading represent areas inhabited by ibex. The ancestral deme is located in the Gran Paradiso area in Northern Italy, close to the Swiss border. The two demes in the zoological gardens 33 and 34 were first established from the ancestral one. Further demes, including the two in zoological gardens 32 and 35, were derived from demes 33 and 34. Putative connections indicate the pairs of demes for which migration is considered possible. For a detailed record of the demography and the genealogy of demes see Figure S1 and File S3. For deme names see Table S1. The map was obtained via the Swiss Federal Office for the Environment (FOEN) and modified with permission.

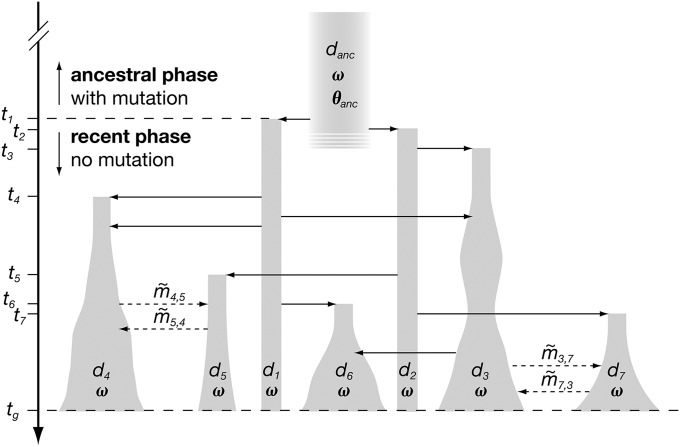
Figure 2.

Schematic representation of the demographic model motivated by the reintroduction of Alpine ibex into the Swiss Alps. Shaded shapes represent demes, indexed by d_i, and the width of the shapes reflects the census size. Time goes forward from top to bottom, and the point in time when deme d_i is established is shown as t_i; t_g is the time of genetic sampling. The total time is split by t₁ into an ancestral phase with mutation and a recent phase for which mutation is ignored (see text for details). Solid horizontal arrows represent founder/admixture events and dashed arrows migration. The parameters are (1) the scaled mutation rate in the ancestral deme, θ_anc = 4N_eu; (2) the proportion of males getting access to matings, ω; and (3) forward migration rates between putatively connected demes, ${\tilde{m}}_{i,j}$. The actual model considered in the study contains 35 derived demes (Figure 1 and Table S1). The exact demography is reported in Figure S1 and File S3, transfers.

We constructed a forward-in-time model starting with an ancestral gene pool d_anc of unknown effective size, N_e, representing the Gran Paradiso ibex deme. At times t₁ and t₂, two demes, d₁ and d₂, are derived from the ancestral gene pool. They represent the breeding stocks that were established in two zoological gardens in Switzerland in 1906 and 1911 (Figure 1) (Stuwe and Nievergelt 1991). Further demes are then derived from these. We let t_i be the time at which deme d_i is established. Once a derived deme has been established, it may contribute to the foundation of additional demes. The sizes of derived demes follow the observed census size trajectories (File S2, census sizes). We interpolated missing values linearly, if the gap was only 1 year, or exponentially, if values for ≥2 successive years were missing. Derived demes may exchange migrants if they are connected. This depends on information obtained from game keepers and on geography (Figure 1). Given a pair of connected demes d_i and d_j, we define the forward migration rates, ${\tilde{m}}_{i,j}$ and ${\tilde{m}}_{j,i}$. More precisely, ${\tilde{m}}_{i,j}$ is the proportion of potential emigrants (see File S1) in deme d_i that migrate to deme d_j per year. We assume that ${\tilde{m}}_{i,j}$ is constant over time and the same for females and males. Migration is included in the model, although we do not estimate migration rates in this article, but in a related article (S. Aeschbacher, A. Futschik, and M. A. Beaumont, unpublished results). Here, we restrict our attention to the ancestral mutation rate and the proportion of males getting access to matings, marginal to the migration rates (see below). Estimating migration rates comes with additional complications that go beyond the focus of this article. A schematic representation of the model is given in Figure 2. When modeling migration, reproduction, and founder events, we take into account the age structure of the population (see File S1 for details).

Population history is split into two phases. The first started at some unknown point in the past and ended at t_i = 1906, when the first ibex were brought from Gran Paradiso (d_anc) to d₁. For this ancestral phase, we assume constant, but unknown effective size N_e and mutation following the single stepwise model (Ohta and Kimura 1973) at a rate u per locus and generation. Accordingly, we define the scaled mutation rate in the ancestral deme as θ_anc = 4N_eu. Mutation rates may vary among microsatellites for several reasons (Estoup and Cornuet 1999). To account for this, we use a hierarchical model, assuming that θ_anc is normally distributed across loci on the log₁₀-scale with mean ${\mu }_{{\theta }_{\text{anc}}}$ and standard deviation ${\sigma }_{{\theta }_{\text{anc}}}$. In our case, ${\mu }_{{\theta }_{\text{anc}}}$ and ${\sigma }_{{\theta }_{\text{anc}}}$ are the hyperparameters (Gelman et al. 2004) of interest. We assume that N_e is the same for all loci, so that variance in θ_anc can be attributed to u exclusively. In principle, variation in diversity across loci could also be due to selection at linked genes (Maynard Smith and Haigh 1974; Charlesworth et al. 1993; Barton 2000), rather than variable mutation rates. Most likely, we cannot distinguish these alternatives with our data. The second, recent phase started at time t₁ and went up to the time of genetic sampling, t_g = 2006. During this phase, the numbers of males and females transferred at founder/admixture events and census population sizes are known and accounted for. Mutation is neglected, since, in the case of ibex, this phase spans only ∼11 generations at most (Stuwe and Grodinsky 1987). At the transition from the ancestral to the recent phase, genotypes of the founder individuals introduced to demes d₁ and d₂ are sampled at random from the ancestral deme, d_anc. At the end of the recent phase (t_g), genetic samples are taken according to the sampling scheme under which the real data were obtained. Of the total 35 demes, 31 were sampled (Table S1).

In Alpine ibex, male reproductive success is highly skewed toward dominant males. Dominance is correlated with male age (Willisch et al. 2012), and ranks are established during summer. Only a small proportion of males obtain access to matings during the rut in winter (Aeschbacher 1978; Stuwe and Grodinsky 1987; Scribner and Stuwe 1994; Willisch and Neuhaus 2009; Willisch et al. 2012). To take this into account, we introduce the proportion of males obtaining access to matings, ω, as a parameter. It is defined relative to the number of potentially reproducing males (and therefore conditional on male age; see File S1) and has an impact on the strength of genetic drift. For simplicity, we assume that ω is the same in all demes and independent of deme size and time.

In principle, we want to infer the joint posterior distribution $\pi \left(\tilde{m},\mathbf{\alpha }|D\right)$, where $\alpha =\left({\mu }_{{\theta }_{\text{anc}}},{\sigma }_{{\theta }_{\text{anc}}},\omega \right)$ and $\tilde{m}=\left\{{\tilde{m}}_{i,j}:i\ne j,i\in {\mathcal{J}}_m,j\in {\mathcal{J}}_m\right\}$, with ${\mathcal{J}}_m$ denoting the set of all demes connected via migration to at least one other deme (Figure 1). This is a complex problem because there are many parameters and even more candidate summary statistics; the curse of dimensionality is severe. Targeting the joint posterior with ABC naively would give a result, but it would be hard to assess its validity. It is more promising to address intermediate steps and assess them one by one. A first step is to focus on a subset of parameters and marginalize over the others. By marginalizing we mean that the joint posterior distribution is integrated with respect to the parameters that are not of interest. In our case, we may focus on α and integrate over the migration rates $\tilde{\mathbf{m}}$ where they have prior support (Table 1). In practice, marginal posteriors can be targeted directly with ABC—without the need to compute the joint likelihood explicitly and integrate over it (see below). A second step is to clarify what summary statistics should be chosen for the subset of focal parameters (α). A third one is to deal with the curse of dimensionality related to estimating $\tilde{\mathbf{m}}$. In this article, we deal with steps one and two: We aim at estimating α marginally to $\tilde{\mathbf{m}}$ and we seek a good method for choosing summary statistics with respect to α. The third step—estimating $\tilde{\mathbf{m}}$ and dealing with its high dimensionality—is treated separately (S. Aeschbacher, A. Futschik, and M. A. Beaumont, unpublished results). Note that this division of the problem implies the assumption that priors of the migration rates and male mating success are independent. We make this assumption partly for convenience and partly because we are not aware of any study that has shown a relation between the two in Alpine ibex. The division into two steps also requires that the set of all summary statistics (S) can be split into two subsets, such that the first (S_α) contains most of the information on α, whereas the second $\left(S_{\tilde{\mathbf{m}}}\right)$ contains most of the information on $\tilde{\mathbf{m}}$. Moreover, S_α should not be affected much by $\tilde{\mathbf{m}}$. As shown in the Appendix, the results are not much affected in such a situation while the computational burden decreases significantly. The arguments in the Appendix rely on the notions of approximate sufficiency and approximate ancillarity.

Table 1. Parameters and prior distributions.

Parameter	Description	Prior distribution
θanc,l	Scaled ancestral mutation rate at locus l, 4Neu	${\text{log}}_{10}\left({\theta }_{\text{anc},l}\right)\sim N\left({\mu }_{{\theta }_{\text{anc}}},{\sigma }_{{\theta }_{\text{anc}}}^2\right)$a
${\mu }_{{\theta }_{\text{anc}}}$	Mean across loci of θanc,l (on log10-scale)	${\mu }_{{\theta }_{\text{anc}}}\sim N\left(0.5,1\right)$
${\sigma }_{{\theta }_{\text{anc}}}$	Standard deviation across loci of θanc,l (on log10-scale)	${\sigma }_{{\theta }_{\text{anc}}}\sim {\text{log}}_{10}$-uniform in [0.01, 1]
ω	Proportion of mature males with access to matings	ω ∼ log10-uniform in [0.01, 1]
${\tilde{m}}_{i,j}$b	Forward migration rate per year from deme i to deme j	${\tilde{m}}_{i,j}\sim {\text{log}}_{10}$-uniform in [10−3.5, 10−0.5]

^aN(μ, σ²), normal distribution with mean μ and variance σ².

^bAlthough migration rates are not estimated here, they are drawn from the prior in all simulations (see main text).

Methods

The joint posterior distribution of our model may be factorized as

$$\pi \left(\tilde{m},\alpha |D\right)=\pi \left(\tilde{m}|\alpha ,D\right)\pi \left(\alpha |D\right).$$ (4)

As mentioned, here we target only the marginal posterior of α, which is formally obtained as

$$\pi \left(\alpha |D\right)={\displaystyle {\int }_{\mathrm{ℳ}}\pi \left(\tilde{m},\alpha |D\right)d\tilde{m}},$$ (5)

where ℳ is the domain of possible values for $\tilde{m}$. By the nature of our problem, $\pi \left(\tilde{m},\alpha |D\right)$ is not available. However, with ABC we may target (5) directly by sampling from π_ε(α|s_α = S_α(D)), where we assume that S_α is a subset of summary statistics approximately sufficient for estimating α (Appendix). Note that S_α may not be sufficient to estimate the joint posterior (4), however (Raiffa and Schlaifer 1968). The following standard ABC algorithm provides an approximation to π(α|s_α) (e.g., Marjoram et al. 2003):

Algorithm A

• A1. Calculate summary statistics s_α = S_α(D) from observed data.

• A2. For t = 1 to t = N,

  • i.Sample $\left({{\alpha }^{\prime }}_t,{{\tilde{m}}^{\prime }}_t\right)$ from $\pi \left(\alpha ,\tilde{m}\right)=\pi \left(\alpha \right)\pi \left(\tilde{m}\right)$.
  • ii.Simulate data ${D^{\prime }}_t$ (at all loci and for all demes) from $\pi \left(D|{{\alpha }^{\prime }}_{\mathit{t}},\hspace{0.17em}{{\tilde{m}}^{\prime }}_t\right)$.
  • iii.Calculate ${{\mathbf{s}}^{\prime }}_{\alpha ,t}=S_{\mathbf{\alpha }}\left({D^{\prime }}_t\right)$ from simulated data.

• A3. Scale s_α and ${{\mathbf{s}}^{\prime }}_{\alpha ,t}$ (t = 1, … , N) appropriately.

• A4. For each t, accept ${{\alpha }^{\prime }}_t$ if $\rho \left({s^{\prime }}_{\alpha ,t},s_{\mathbf{\alpha }}\right)\le {\delta }_{\epsilon }$, using scaled summary statistics from A3.

• A5. Estimate the posterior density π_ε(α|s_α) from the εN accepted points $\langle {s^{\prime }}_{\alpha ,t},{{\alpha }^{\prime }}_t\rangle$.

Step A2 may be easily parallelized on a cluster computer. In doing so, one needs to store $\langle {s^{\prime }}_{\alpha ,t},\hspace{0.17em}{{\alpha }^{\prime }}_t\rangle$. Step A5 may include postrejection adjustment via regression (Beaumont et al. 2002; Blum and François 2010; Leuenberger and Wegmann 2010) and scaling of parameters. In general, the set of well-chosen, informative summary statistics S_α is not known in advance. Instead, a set of candidate statistics S (chosen based on intuition or analogy to simpler models) may be available. Therefore, we propose algorithm B—a modified version of algorithm A—that includes an additional step for the empirical choice of summary statistics S_α informative on α given a set of candidate statistics, S (for similar approaches, see Hamilton et al. 2005; Wegmann et al. 2009):

Algorithm B

• B1. Calculate candidate summary statistics s = S(D) from observed data.

• B2. For t = 1 to t = N,

  • i.Sample $\left({{\alpha }^{\prime }}_t,{{\tilde{m}}^{\prime }}_t\right)$ from $\pi \left(\alpha ,\tilde{m}\right)=\pi \left(\alpha \right)\pi \left(\tilde{m}\right)$.
  • ii.Simulate data ${D^{\prime }}_t$ (at all loci and for all demes) from $\pi \left(D{|{\alpha }^{\prime }}_t,{{\tilde{m}}^{\prime }}_t\right)$.
  • iii.Calculate candidate summary statistics ${s^{\prime }}_t=S\left({D^{\prime }}_t\right)$ from simulated data.

• B3. Sample without replacement n ≤ N simulated pairs $\langle {s^{\prime }}_t,{{\alpha }^{\prime }}_t\rangle$, denote them by $\langle {{\mathbf{s}}^{\prime }}_{t*},{{\mathbf{\alpha }}^{\prime }}_{t*}\rangle$, and use them as a training data set to choose informative statistics S_α.

• B4. According to B3, obtain s_α from s; for t = 1 to t = N, obtain ${s^{\prime }}_{\alpha ,t}$ from ${s^{\prime }}_t$.

• B5. Scale s_α and ${s^{\prime }}_{\alpha ,t}$ (t = 1, … , N) appropriately.

• B6. For each t, accept ${{\alpha }^{\prime }}_t$ if $\rho \left({s^{\prime }}_{\alpha ,t},s_{\mathbf{\alpha }}\right)\le {\delta }_{\epsilon }$, using scaled summary statistics from B5.

• B7. Estimate the posterior density π_ε(α|s_α) from the εN accepted points $\langle {{\mathbf{S}}^{\prime }}_{\alpha ,t},{{\alpha }^{\prime }}_t\rangle$.

Note that S_α in steps B3 and B4 may be either a subset of S or some function (e.g., a linear combination) of S (details of implementation given below). In the following, we describe a novel approach based on boosting and recently proposed by Lin et al. (2011) for the choice of S_α in B3.

Choice of summary statistics via boosting

Boosting is a collective term for meta-algorithms originally developed for supervised learning in classification problems (Schapire 1990; Freund 1995). Later, versions for regression (Friedman et al. 2000) and other contexts were developed (Bühlmann and Hothorn 2007 and references therein). Assume a set of n observations indexed by i and associated with a one-dimensional response Y_i. For (binary) classification, Y_i ∈ {0, 1}, but in a regression context, Y_i may be continuous in ℝ. Further, each observation is associated with a vector of q predictors $X_i=\left(X_i^{\left(1\right)},\dots ,X_i^{\left(q\right)}\right)$. Given a training data set {〈X₁, Y₁〉, … , 〈X_n, Y_n〉}, the task of a boosting algorithm is to learn a function F(X) that predicts Y. Boosting was invented to deal with cases where the relationship between predictors and response is potentially complex, for example, nonlinear (Schapire 1990; Freund 1995; Freund and Schapire 1996, 1999). Establishing the relationship between predictors and response, and weighting predictors according to their importance, directly relates to the problem of choosing summary statistics in ABC: Given candidate statistics S, we want to find a subset or combination of statistics $S_{{\alpha }^{\left(k\right)}}$ informative for the kth parameter α^(k) in α, for every k. Taking the set of simulated pairs $\langle {{\mathbf{s}}^{\prime }}_t,f\left({{\alpha }^{\prime }}_t\right)\rangle$ (t = 1, … , N) from step B3 of algorithm B as a training data set, this may be achieved by boosting. For this purpose, we interpret the summary statistics S as predictors X and the parameters α^(k) as the response Y. Note that we use $f\left({{\alpha }^{\prime }}_t\right)$ to be generic in the sense that the response might actually be a function—such as a discretization step (see below)—of ${{\alpha }^{\prime }}_t$.

The principle of boosting is to iteratively apply a weak learner to the training data and then combine the ensemble of weak learners to construct a strong learner. While the weak learner predicts only slightly better than random guessing, the strong learner will usually be well correlated with the true Y. This is because the training data are reweighted after each step according to the current error, such that the next weak learner will focus on those observations that were particularly hard to assign. However, too strong a correlation will lead to overfitting, so that in practice one defines an upper limit for the number of iterations (see below). The behavior of the weak learner is described by the base procedure $\widehat{g}(\cdot )$, a real valued function. The final result (strong learner) is the desired function estimate $\widehat{F}(\cdot )$. Given a loss function L(⋅, ⋅) that quantifies the disagreement between Y and F(X), we want to estimate the function that minimizes the expected loss,

$$F*(\cdot )=\text{arg}\hspace{0.17em}{\text{min}}_{F(\cdot )}\mathbb{E}\left[L\left(Y,F\left(X\right)\right)\right].$$ (6)

This can be done by considering the empirical risk $n^{-1}{\displaystyle {\sum }_{i=1}^{n}L\left(Y_i,F\left(X_i\right)\right)}$ and pursuing iterative steepest descent in function space (Friedman 2001; Bühlmann and Hothorn 2007). The corresponding algorithm is given in the Appendix. The generic boosting estimator obtained from this algorithm is a sum of base procedure estimates,

$$\widehat{F}(\cdot )=\nu {\displaystyle \sum _{m=1}^{m_{\text{stop}}}{\widehat{g}}^{\left[m\right]}(\cdot )}.$$ (7)

Both ν and m_stop are tuning parameters that essentially control the overfitting behavior of the algorithm. Bühlmann and Hothorn (2007) argue that the learning rate ν is of minor importance as long as ν ≤ 0.1. The number of iterations, m_stop, however, should be chosen specifically in any application via cross-validation, bootstrapping, or some information criterion [e.g., Akaike’s information criterion (AIC)].

Base procedure:

Different versions of boosting are obtained depending on the base procedure $\widehat{g}(\cdot )$ and the loss function L(⋅, ⋅). Here, we let $\widehat{g}(\cdot )$ be a simple componentwise linear regression (Bühlmann and Hothorn 2007; see Appendix). With this choice, the boosting algorithm selects in every iteration only one predictor, namely the one that is most effective in reducing the current loss. For instance, with the L₂-loss (defined below), after each step, $\widehat{F}(\cdot )$ is updated linearly according to

$${\widehat{F}}^{\left[m\right]}\left(x\right)={\widehat{F}}^{\left[m-1\right]}\left(x\right)+\nu {\widehat{\lambda }}^{\left({\widehat{\zeta }}_m\right)}{x}^{\left({\widehat{\zeta }}_m\right)},$$ (8)

where ${\widehat{\zeta }}_m$ denotes the index of the predictor variable selected in iteration m. Accordingly, in iteration m only the $\widehat{\zeta }\text{th}$ component of the coefficient estimate ${\widehat{\lambda }}^{\left[m\right]}$ is updated. As m goes to infinity, $\widehat{F}(\cdot )$ converges to a least-squares solution. In practice, we stop at m_stop, and we denote the final vector of estimated coefficients as $\widehat{\lambda }={\widehat{\lambda }}^{\left[m_{\text{stop}}\right]}$. Recall that in our context, the predictor variables X correspond to the candidate summary statistics S. For each of the k parameters in α, we estimate one function ${\widehat{F}}^{\left[m_{\text{stop}}\right]}$ and use it to obtain new parameter-specific statistics $S_{{\alpha }^{\left(k\right)}}$.

Loss functions:

We employed boosting with three loss functions. The first two, L₁-loss and L₂-loss, are appropriate for a regression context with a continuous response Y ∈ ℝ. In this case, the parameters ${{\alpha }^{\prime }}_t$ are directly interpreted as y_i [i.e., $f\left({{\alpha }^{\prime }}_t\right)={{\alpha }^{\prime }}_t$]. The L₁-loss is given by

$$L_{L_1}\left(y,F\right)=|y-F|$$ (9)

and results in L₁Boosting. The L₂-loss is given by

$$L_{L_2}\left(y,F\right)=\frac{1}{2}|y-F^2|$$ (10)

and results in L₂Boosting. The scaling factor $\frac{1}{2}$ in (10) ensures that the negative gradient vector U in the functional gradient descent (FGD) algorithm (Appendix and File S1) equals the residuals (Bühlmann and Hothorn 2007). L₁-and L₂Boosting result in a fit of a linear regression, similarly to ordinary regression using the least absolute deviation (L₁-norm) or the least-squares criterion (L₂-norm), respectively. The difference, and a potential advantage of boosting, is that residuals are fitted multiple times depending on the importance of the components of X. Moreover, boosting is considered less prone to overfitting than ordinary L₁- or L₂-fitting (Bühlmann and Hothorn 2007). In general, the L₁-loss is more robust to outliers, but it may produce multiple, potentially unstable solutions. Using L₁- and L₂Boosting to choose summary statistics means assuming a linear relationship between summary statistics and parameters. This is a strong assumption and most likely not globally true. However, the advantage is that the resulting linear combination has only one dimension, such that the curse of dimensionality in ABC may be strongly reduced. Again, the approach using the L₁- or L₂-loss results in one linear combination ${\widehat{F}}^{\left[m_{\text{stop}}\right]}$ per parameter α^(k), such that $S_{{\alpha }^{\left(k\right)}}$ has only one component. These linear combinations may end up being correlated across parameters, especially if parameters are not identifiable, e.g., because they are confounded with each other.

To motivate the third loss function, we propose considering the choice of summary statistics as a classification problem. Imagine two classes of parameter values—say, high values in one class and low values in the other. We may ask what summary statistics are important to assign simulations to one of these two classes. With Y ∈ {0, 1} as the class label and p(x) := Pr[Y = 1|X = x], a natural choice is the negative binomial log-likelihood loss

$$L_{\text{log-lik}}\left(y,p\right)=-\left[y\hspace{0.17em}\text{log}\left(p\right)+\left(1-y\right)\text{log}\left(1-p\right)\right],$$ (11)

omitting the argument of p for ease of notation. If we parameterize p = e^F/(1 + e^F) so that we obtain F = log[p/(1 − p)] corresponding to the logit-transformation, the loss in (11) becomes

$$L_{\text{log-lik}}\left(y,F\right)=\text{log}\left[1+e^{-\left(2y-1\right)F}\right].$$ (12)

The corresponding boosting algorithm is called LogitBoost (or binomial boosting) (Bühlmann and Hothorn 2007). An advantage is that it does not assume a linear relationship between summary statistics and parameters, as is the case for L₁- and L₂Boosting. Instead, LogitBoost fits a logistic regression model, which might be more appropriate. On the other hand, it requires choosing a discretization procedure f(⋅) to map α_t ∈ ℝ to y ∈ {0, 1} (see below). Since such a choice is arbitrary, it would be problematic to use the resulting fit (a linear combination on the logit-scale) directly as $S_{{\alpha }^{\left(k\right)}}$. In practice, we instead assigned a candidate statistic S^(j) (j = 1, … , q) to $S_{{\alpha }^{\left(k\right)}}$ if the corresponding boosted coefficient ${\widehat{\lambda }}^{\left(j\right)}$ (cf. Equation 8) was different from zero and omitted it otherwise. Therefore, compared to L₁- and L₂Boosting, the reduction in dimensionality was on average lower, but the strong assumption of a linear relationship between α^(k) and $S_{{\alpha }^{\left(k\right)}}$ was avoided. Note that, in principle, nonlinear relationships may be fitted with the L₁- and L₂-loss, too (Friedman et al. 2000). In File S1 we provide explicit expressions for the population minimizers (Equation 6) and some more insight on the boosting algorithms under the three loss functions used here.

Partial least-squares regression:

Recently, Wegmann et al. (2009) proposed to choose summary statistics in ABC via PLS regression (e.g., Hastie et al. 2011 and references therein). PLS is related to principal component regression. But in addition to maximizing the variance of the predictors X, at the same time, it maximizes the correlation of X with the response Y. Applied to the choice of summary statistics, it therefore not only decorrelates the summary statistics, but also chooses them according to their relation to α. Hastie et al. (2011) argue that the first aspect dominates over the latter, however. The number r of PLS components to keep is usually determined based on some cross-validation procedure (see below). In the context of ABC, the r components are multiplied by the corresponding statistics S^(j) (j ≤ r) to obtain $S_{{\alpha }^{\left(k\right)}}$ (Wegmann et al. 2009).

Global vs. local choice

We have so far suggested that S_α is close to sufficient for estimating α. This will hardly be the case in practice. By definition, the optimal choice of S_α then depends on the unknown true parameter value(s). Ideally, we therefore want to focus the choice of S_α on the neighborhood of the truth. The latter is not known in practice. As a workaround, we propose to use the n simulated pairs $\langle {{\mathbf{s}}^{\prime }}_{t*},{{\mathbf{\alpha }}^{\prime }}_{t*}\rangle$ from step B3 in algorithm B and the observed summary statistics s to approximately establish this neighborhood as follows.

Local choice of summary statistics in B3:

1. Consider the n pairs $\langle {s^{\prime }}_{t*},{{\alpha }^{\prime }}_{t*}\rangle$ (t* = 1, … , n) from step B3 in algorithm B.

2. Mean center each component s′^(j) (j = 1, … , q) and scale it to have unit variance.

3. Rotate s′ using principal component analysis (PCA).

4. Apply the scaling from steps 2 and 3 to the observed summary statistics s.

5. Mean center the PCA-scaled summary statistics obtained in step 3, and scale them to have unit variance. Do the same for the PCA-scaled observed statistics obtained in step 4. Denote the results by ${\dot{\mathbf{s}}}^{\prime }$ and $\dot{\mathbf{s}}$, respectively.

6. For each t* ∈ n, compute the Euclidean distance ${\delta }_{t*}=\Vert {{\dot{\mathbf{s}}}^{\prime }}_{t*}-{\dot{\mathbf{s}}}_{t*}\Vert$.

7. Keep the n′ pairs $\langle {s^{\prime }}_{t**},{{\alpha }^{\prime }}_{t**}\rangle$ (t** = 1, … , n′) for which ${\delta }_{t*}\le z$, where z is some threshold.

8. Use the n′ points accepted in step 7 as a training set to choose statistics S_α with the desired method.

9. Continue with step B4 in algorithm B.

In step 2 above, the original summary statistics are brought to the same scale. Otherwise, summary statistics with a high variance would on average contribute relatively more to the Euclidean distance than summary statistics with a low variance. However, whether a simulated data point is far from or close to the target (s) in multidimensional space may depend not only on the distance along the dimension of each statistic, but also on the correlation among statistics. This can be accounted for by decorrelating the statistics, as is done by PCA in step 3. In combination with the Euclidean distance in step 6, the procedure above essentially uses the Mahalanobis distance as a metric (Mahalanobis 1936). Although we cannot prove the optimality of this approach, it seems to work well in our simulations. Note that in steps 8 and 9, the summary statistics are used on their original scale again. This is because we want our method for choosing parameter-specific combinations of statistics to use the information comprised in the difference in scale among the original statistics—even in the vicinity of s. The PCA scaling in step 5 is only used temporarily to determine δ_t* in step 6. Figure S2 visualizes the different scales and the effect of determining an approximate neighborhood around s.

The scheme just described may be combined with any of the methods for choosing summary statistics described above. In our case, we considered ABC with global and local versions of PLS (called pls.glob and pls.loc in the following), LogitBoost (lgb.glob and lgb.loc), L₁Boosting (l1b.glob and l1b.loc), and L₂Boosting (l2b.glob and l2b.loc). Moreover, we performed ABC with all candidate statistics S (all) as a reference.

Candidate summary statistics:

Our set S of candidate summary statistics consisted of the mean and standard devation across loci of the following statistics: the average within-deme variance of allele length, the average within-deme gene diversity (H₁), the average between-deme gene diversity (H₂), the total F_IS, the total F_ST, the total within-deme mean squared difference (MSD) in allele length (S₁), the total between-deme MSD in allele length (S₂), the total R_ST, and the number of allele types in the total population. This amounts to a total of 18 summary statistics. We computed H₁, H₂, F_IS, and F_ST according to Nei and Chesser (1983) and S₁, S₂, and R_ST according to Slatkin (1995). Note that all summary statistics are symmetrical with respect to the order of the loci, which is consistent with our hierarchical parameterization of the ancestral mutation rate.

Implementation:

Throughout, we used the prior distributions given in Table 1. In algorithm B, we performed N = 10⁶ simulations and in B2i we assumed that $\pi \left(\alpha ,\tilde{\mathbf{m}}\right)=\pi \left(\alpha \right)\pi \left(\tilde{\mathbf{m}}\right)$. In B3, we used n = 10⁴ simulations for the choice of summary statistics (in both the global and the local versions). Moreover, we first chose sets of summary statistics for each parameter separately and then took the union of the sets, i.e., $S_{\alpha }={\displaystyle {\cup }_k{S}_{{\alpha }^{\left(\mathit{k}\right)}}}$, where each $S_{{\alpha }^{\left(\mathit{k}\right)}}$ is chosen according to one of the methods proposed. This also applies to step 8 in the procedure for the local choice of summary statistics (see above). For the local choice, we kept the n′ = 1000 pairs closest to the observation s, and we used the pcrcomp function in R version 2.11 (R Development Core Team 2011) for PCA. Note that the set of the n′ simulations closest to s and, hence, z in step 7 of the procedure for the local choice were the same for all local methods compared. In B5, we mean centered the summary statistics and scaled them to have unit variance. In B6, we chose the Euclidean distance as metric ρ(⋅). In B7 we did postrejection adjustment with a weighted local-linear regression with weights from an Epanechnikov kernel (Beaumont et al. 2002), without additional scaling of parameters. For steps B6 and B7 we used the abc package (Csilléry et al. 2011) for R. We estimated the parameters and performed the linear regression on the same scale as the respective priors were defined.

For the PLS method, we used the pls package (Mevik and Wehrens 2007) for R and followed Wegmann et al. (2009, 2010). Specifically, we performed a Box–Cox transformation of the summary statistics prior to the PLS regression, and we chose the number of components to keep based on a plot of the root mean squared prediction error. We kept r = 10 components, both for pls.glob and pls.loc (Figure S3). For all methods based on boosting, we mean centered the summary statistics before boosting and used the glmboost function of the mboost package (Bühlmann and Hothorn 2007; Hothorn et al. 2010) for R. For the LogitBoost methods, we chose for each k the first and third quartiles of the sample of α^(k) drawn in step B3 of algorithm B3 as the centers of the two classes of parameter values. For lgb.glob, we then assigned the 500 α^(k)-values closest to the first quartile to the first class (y = 0) and the 500 values closest to the third quartile to the second class (y = 1). For lgb.loc, we analogously assigned the 100 α^(k)-values closest to the two quartiles to the two classes. For both lgb.glob and lgb.loc, we chose the optimal m_stop based on the AIC (Akaike 1974; Bühlmann and Hothorn 2007), but set an upper limit for m_stop of 500 iterations. For l1b.glob and l1b.loc, we chose m_stop via 10-fold cross-validation with the cvrisk function of the mboost package, setting an upper limit of 100. Finally, for l2b.glob and l2b.loc, we chose m_stop based on the AIC, with an upper limit of 100. Figure S4, Figure S5, and Figure S6 further illustrate the boosting procedure.

Simulation study and application to data

To assess the performance of the different methods for choosing summary statistics and to study the influence of the rejection tolerance ε, we carried out a simulation study. For each ε ∈ {0.001, 0.01, 0.1}, we simulated 500 test data sets with parameter values sampled from the prior distributions and then inferred the posterior distribution for each set. In the case of local choice of summary statistics, the procedure of defining informative summary statistics based on the candidate statistics was run for each test data set separately. For the global choice, it was run only once per method, because there is no dependence on the supposed true value. Similar to Wegmann et al. (2009), we used as a measure of accuracy of the marginal posterior distributions the root mean integrated squared error (RMISE), defined as ${\text{RMISE}}_k=\sqrt{{\displaystyle {\int }_{{\text{Φ}}^{\left(k\right)}}{\left({\mathbf{\phi }}^{\left(k\right)}-{\mu }_k\right)}^2\pi \left({\mathbf{\phi }}^{\left(k\right)}|s\right)d{\mathbf{\phi }}^{\left(k\right)}}}$, where μ_k is the true value of the kth component of the parameter vector φ and π(φ^(k)|s) is the corresponding estimated marginal posterior density. Recall that $\mathbf{\phi }=\alpha =\left({\mu }_{{\theta }_{\text{anc}}},{\sigma }_{{\theta }_{\text{anc}}},\omega \right)$ in our case. From this, we obtained the relative absolute RMISE (RARMISE) as RARMISE_k = RMISE_k/|μ_k|. We also computed the absolute error (AE_k) between three marginal posterior point estimates (mode, mean, and median) and μ_k. Dividing by |μ_k|, we obtained the relative absolute error (RAE_k). To directly compare the various methods to ABC with all summary statistics, we computed standardized variants of the RMISE and AE as follows: If $a_k^{\text{all}}$ is the measure of accuracy for ABC with all summary statistics, and ${a\mathrm{\ast }}_k$ is the one for ABC with the method of interest, the standardized measure was obtained as ${a\mathrm{\ast }}_k/a_k^{\text{all}}$. Importantly, we also assessed whether—across the 500 test data sets—the values obtained by evaluating the cumulative posterior distribution function at the respective true parameter value were uniformly distributed in [0, 1]. This indicates whether an inferred posterior distribution has converged to a distribution with correct coverage properties, given the respective computational constraints and summary statistics. We refer to this criterion as “coverage property” or “uniform distribution of posterior probabilities.” This approach has been motivated by Cook et al. (2006) and applied in previous ABC studies (e.g., Wegmann et al. 2009). Note that Cook et al. (2006) called these posterior probabilities “posterior quantiles,” which is somewhat misleading. We tested for a uniform distribution of the posterior probabilities, using a Kolmogorov–Smirnov test (Sokal and Rohlf 1981). Since 81 such tests had to be performed, it would at first glance seem appropriate to correct for multiple testing. However, we want to protect ourselves from keeping by mistake the null hypothesis of uniformly distributed posterior probabilities, rather than to avoid rejection of the null hypothesis in marginal cases. Therefore, correcting for multiple testing would be conservative in the wrong direction. As a measure of our skepticism against uniformly distributed posterior probabilities, we report the Kolmogorov–Smirnov distance

$${\text{KS}}_n=\underset{x}{\text{sup}}\left|F_n\left(x\right)-F\left(x\right)\right|,$$ (13)

where F_n(x) is the empirical distribution function of n identically and independently distributed observations x_i from a random variable X, and F(x) is the null distribution function (the uniform distribution between 0 and 1 in our case).

For the application to Alpine ibex, we used allele frequency and repeat length data from 37 putatively neutral microsatellites as described in Biebach and Keller (2009) (Figure 1 and Table S1). The data were provided to us by the authors. ABC simulations and inference were identical to those in the simulation study, with the same number of markers (see also File S1). The program called SPoCS that we wrote and used for simulation of the ibex scenario and a collection of R and shell scripts used for inference are available on the website http://pub.ist.ac.at/^∼saeschbacher/phd_e-sources/.

Results

Comparison of methods for choice of summary statistics

We have suggested boosting with componentwise linear regression as a base procedure for choosing summary statistics in ABC. Three loss functions were considered: the L₁- and the L₂-loss and the negative binomial log-likelihood. We have compared the performance of ABC with summary statistics chosen via different types of boosting to that of ABC with statistics chosen via PLS (Wegmann et al. 2009) and to that of ABC with all candidate summary statistics (Table 2). The RAE behaved similarly for the three point estimates (mode, mean, and median), but the mode was less reliable in cases where the posterior distributions did not have a unique mode (Figure S7). We decided to focus on the median. For assessment of the methods, we sought a low RARMISE and a low RAE of the median (RAE_median in the following), and we required that the distribution of posterior probabilities of the true value did not deviate from uniformity for any parameter.

Table 2. Accuracy of different methods for choosing summary statistics on a global scale.

Method	ε	Parameter	RARMISEa		RAEb mode		RAE mean		RAE median		${\text{KS}}_{\text{500}}$c	Cov. Pd
all	0.001	${\mu }_{{\theta }_{\text{anc}}}$	0.143	(0.147)	0.062	(0.074)	0.065	(0.075)	0.062	(0.075)	0.072	0.011*
		${\sigma }_{{\theta }_{\text{anc}}}$	0.452	(0.231)	0.269	(0.213)	0.269	(0.222)	0.265	(0.218)	0.034	0.610
		ω	0.446	(0.272)	0.221	(0.225)	0.215	(0.218)	0.219	(0.22)	0.027	0.859
	0.01	${\mu }_{{\theta }_{\text{anc}}}$	0.141	(0.145)	0.061	(0.072)	0.064	(0.074)	0.065	(0.075)	0.082	0.003*
		${\sigma }_{{\theta }_{\text{anc}}}$	0.466	(0.257)	0.299	(0.21)	0.286	(0.225)	0.282	(0.226)	0.019	0.992
		ω	0.432	(0.259)	0.233	(0.232)	0.226	(0.23)	0.232	(0.232)	0.026	0.880
	0.1	${\mu }_{{\theta }_{\text{anc}}}$	0.140	(0.134)	0.065	(0.075)	0.067	(0.078)	0.067	(0.075)	0.081	0.003*
		${\sigma }_{{\theta }_{\text{anc}}}$	0.463	(0.272)	0.324	(0.238)	0.306	(0.248)	0.296	(0.243)	0.032	0.677
		ω	0.431	(0.263)	0.234	(0.229)	0.228	(0.22)	0.226	(0.223)	0.038	0.482
pls.glob	0.001	${\mu }_{{\theta }_{\text{anc}}}$	0.171	(0.16)	0.077	(0.087)	0.083	(0.089)	0.081	(0.088)	0.038	0.466
		${\sigma }_{{\theta }_{\text{anc}}}$	0.488	(0.276)	0.291	(0.223)	0.289	(0.252)	0.276	(0.228)	0.024	0.936
		ω	0.451	(0.275)	0.238	(0.221)	0.234	(0.224)	0.237	(0.227)	0.022	0.969
	0.01	${\mu }_{{\theta }_{\text{anc}}}$	0.166	(0.152)	0.080	(0.09)	0.079	(0.09)	0.079	(0.089)	0.035	0.562
		${\sigma }_{{\theta }_{\text{anc}}}$	0.480	(0.291)	0.307	(0.223)	0.295	(0.268)	0.293	(0.242)	0.038	0.473
		ω	0.441	(0.262)	0.241	(0.234)	0.230	(0.225)	0.229	(0.226)	0.035	0.562
	0.1	${\mu }_{{\theta }_{\text{anc}}}$	0.171	(0.146)	0.083	(0.091)	0.086	(0.097)	0.087	(0.094)	0.037	0.497
		${\sigma }_{{\theta }_{\text{anc}}}$	0.469	(0.283)	0.319	(0.237)	0.307	(0.286)	0.310	(0.276)	0.056	0.089
		ω	0.433	(0.265)	0.240	(0.226)	0.234	(0.224)	0.234	(0.23)	0.049	0.178
lgb.glob	0.001	${\mu }_{{\theta }_{\text{anc}}}$	0.149	(0.152)	0.064	(0.074)	0.065	(0.076)	0.064	(0.074)	0.082	0.002*
		${\sigma }_{{\theta }_{\text{anc}}}$	0.435	(0.204)	0.270	(0.231)	0.261	(0.214)	0.247	(0.205)	0.038	0.466
		ω	0.456	(0.275)	0.235	(0.23)	0.230	(0.237)	0.232	(0.224)	0.025	0.913
	0.01	${\mu }_{{\theta }_{\text{anc}}}$	0.145	(0.15)	0.066	(0.076)	0.066	(0.078)	0.066	(0.076)	0.103	<0.001*
		${\sigma }_{{\theta }_{\text{anc}}}$	0.450	(0.223)	0.281	(0.215)	0.269	(0.217)	0.258	(0.209)	0.046	0.238
		ω	0.436	(0.27)	0.235	(0.234)	0.222	(0.223)	0.225	(0.228)	0.025	0.916
	0.1	${\mu }_{{\theta }_{\text{anc}}}$	0.147	(0.142)	0.068	(0.079)	0.067	(0.078)	0.069	(0.079)	0.135	<0.001*
		${\sigma }_{{\theta }_{\text{anc}}}$	0.471	(0.284)	0.288	(0.209)	0.301	(0.249)	0.271	(0.233)	0.054	0.103
		ω	0.427	(0.259)	0.232	(0.222)	0.225	(0.216)	0.228	(0.22)	0.042	0.329
l1b.glob	0.001	${\mu }_{{\theta }_{\text{anc}}}$	0.188	(0.178)	0.075	(0.087)	0.074	(0.087)	0.076	(0.088)	0.035	0.573
		${\sigma }_{{\theta }_{\text{anc}}}$	0.445	(0.202)	0.271	(0.236)	0.261	(0.232)	0.256	(0.216)	0.023	0.954
		ω	0.487	(0.297)	0.251	(0.259)	0.226	(0.227)	0.232	(0.226)	0.031	0.723
	0.01	${\mu }_{{\theta }_{\text{anc}}}$	0.178	(0.17)	0.075	(0.087)	0.075	(0.088)	0.075	(0.085)	0.031	0.711
		${\sigma }_{{\theta }_{\text{anc}}}$	0.463	(0.217)	0.288	(0.24)	0.271	(0.238)	0.259	(0.221)	0.029	0.805
		ω	0.468	(0.288)	0.255	(0.262)	0.228	(0.222)	0.235	(0.233)	0.034	0.595
	0.1	${\mu }_{{\theta }_{\text{anc}}}$	0.177	(0.173)	0.078	(0.092)	0.078	(0.094)	0.079	(0.094)	0.043	0.311
		${\sigma }_{{\theta }_{\text{anc}}}$	0.508	(0.299)	0.307	(0.21)	0.304	(0.269)	0.290	(0.248)	0.051	0.144
		ω	0.449	(0.272)	0.238	(0.241)	0.237	(0.222)	0.239	(0.227)	0.031	0.716
l2b.glob	0.001	${\mu }_{{\theta }_{\text{anc}}}$	0.183	(0.173)	0.075	(0.087)	0.074	(0.085)	0.074	(0.086)	0.029	0.794
		${\sigma }_{{\theta }_{\text{anc}}}$	0.441	(0.202)	0.273	(0.229)	0.257	(0.228)	0.254	(0.212)	0.028	0.828
		ω	0.487	(0.296)	0.251	(0.257)	0.231	(0.226)	0.234	(0.229)	0.033	0.648
	0.01	${\mu }_{{\theta }_{\text{anc}}}$	0.180	(0.173)	0.077	(0.087)	0.077	(0.088)	0.076	(0.087)	0.030	0.766
		${\sigma }_{{\theta }_{\text{anc}}}$	0.459	(0.213)	0.278	(0.242)	0.262	(0.235)	0.259	(0.214)	0.028	0.815
		ω	0.470	(0.288)	0.253	(0.26)	0.231	(0.221)	0.237	(0.229)	0.037	0.497
	0.1	${\mu }_{{\theta }_{\text{anc}}}$	0.176	(0.171)	0.080	(0.092)	0.080	(0.096)	0.080	(0.093)	0.041	0.365
		${\sigma }_{{\theta }_{\text{anc}}}$	0.503	(0.281)	0.300	(0.213)	0.297	(0.249)	0.283	(0.253)	0.052	0.139
		ω	0.445	(0.267)	0.240	(0.24)	0.239	(0.227)	0.236	(0.225)	0.030	0.755

RARMISE and RAE are given as the median across 500 independent estimations with true values drawn from the prior (median absolute deviation in parentheses). ${\sigma }_{{\theta }_{\text{anc}}}$ and ω were estimated on the log₁₀-scale. *P < 0.05 without correction for multiple testing; cf. Figure S8.

^aRelative absolute root mean integrated squared error (see text) with respect to the true value.

^bRelative absolute error with respect to the true value.

^cKolmogorov–Smirnov distance between empirical distribution of posterior probabilities of the true parameter and U(0, 1).

^dP-value from a Kolmogorov–Smirnov test.

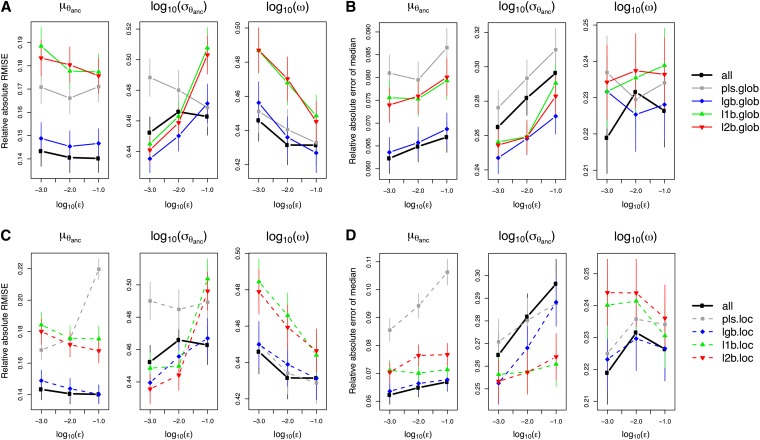
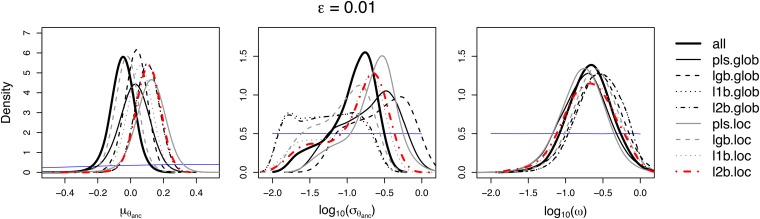
ABC with all summary statistics (all) and ABC with LogitBoost (lgb.glob) performed well in terms of RARMISE and RAE_median, especially when estimating ${\mu }_{{\theta }_{\text{anc}}}$ and ω (Figure 3, A and B). However, the posteriors of ${\mu }_{{\theta }_{\text{anc}}}$ inferred with all and lgb.glob tended to be biased (Kolmogorov–Smirnov distance and coverage P-value in Table 2).

Figure 3.

Accuracy of different methods for choosing summary statistics as a function of the acceptance rate (ε). (A and B) Results for different methods when applied to the whole parameter range (global choice). (C and D) The methods were applied only in the neighborhood of the (supposed) true value (local choice). The performance resulting from using all candidate summary statistics is shown for comparison in both rows. A and C show the root mean integrated squared error (RMISE), relative to the absolute true value. B and D give the absolute error of the posterior median, relative to the absolute true value. Plotted are the medians across n = 500 independent test estimations with true values drawn from the prior (error bars denote the $\text{median}\pm \text{MAD}/\sqrt{n}$, where MAD is the median absolute deviation).

Figure S8 implies that all yielded too narrow a posterior on average (U-shaped distribution of posterior probabilities of the true value), while lgb.glob tended to underestimate ${\mu }_{{\theta }_{\text{anc}}}$ (left-skewed distribution of posterior probabilities). This made us disfavor the methods all and lgb.glob. Throughout, ABC with L₁- and L₂Boosting on the global scale (l1b.glob and l2b.glob) performed very similarly in terms of RARMISE and RAE_median (Figure 3, A and B). Because the L₂-loss is in general more sensitive to outliers, similarity in performance of l1b.glob and l2b.glob suggests that there were no problems with outliers, i.e., no simulations producing extreme combinations of parameters and summary statistics. The accuracy of the pls.glob method was intermediate, except for the RAE_median of ${\mu }_{{\theta }_{\text{anc}}}$ and ${\sigma }_{{\theta }_{\text{anc}}}$, where pls.glob performed worst (Figure 3B). For all methods, the RARMISE and the RAE_median were considerably lower for ${\mu }_{{\theta }_{\text{anc}}}$ than for ${\sigma }_{{\theta }_{\text{anc}}}$ and ω. This implies that the latter two are more difficult to estimate with the data and model given here (see Figure S7). For an idea of how the data drive the parameter estimates, it is instructive to consider the correlation of individual summary statistics with the parameters (see Figure S11, Figure S12, and Figure S13).

The accuracy of estimation is expected to depend on the acceptance rate ε in a way determined by a trade-off between bias and variance (e.g., Beaumont et al. 2002). While the RAE measures only the error of the point estimator, the RARMISE is a joint measure of bias and variance across the whole posterior distribution. The variance may be assigned to different sources. A first component—call it simulation variance—is a consequence of the finite number N of simulations. The lower ε is, the fewer points are accepted in the rejection step (B6 of algorithm B, see above). Posterior densities estimated from fewer points will be less stable than those inferred from more points, i.e., show higher variance around the true posterior. A second variance component—the sampling variance—is due to the loss of information caused by using summary statistics that are not sufficient. To illustrate the trade-off between simulation and sampling variance, assume ε is fixed. If a large number of summary statistics are chosen, these may extract most of the information and thus limit the sampling variance. However, more summary statistics mean more dimensions and therefore a lower chance of accepting the same number of simulations than with fewer summary statistics and hence a higher simulation variance. In addition, accepting with δ_ε > 0—which is characteristic of ABC—will introduce a systematic bias if the multidimensional density is not symmetric on the chosen metric with respect to the observation s. On the other hand, increasing δ_ε reduces the simulation variance. Hence, there are in fact multiple trade-offs. It is not obvious in advance which one will dominate, and it is hard to make a prediction. This is reflected in our results: We found no uniform pattern for the dependence on ε of the RARMISE and the RAE_median. For instance, with l2b.glob the RARMISE increased as a function of ε for ${\sigma }_{{\theta }_{\text{anc}}}$, but decreased for ω (Figure 3A). Moreover, and typically for a trade-off, the relationship between accuracy and ε need not be monotonic (Figure 3) (cf. Beaumont et al. 2002).

Attempting to mitigate the lack of sufficiency, we have proposed to choose summary statistics locally—in the putative neighborhood of the true parameter values—rather than globally over the whole prior range. As expected, the local choice led to different combinations of statistics, and it had an effect on the scaling of the statistics for pls.loc, l1b.loc, and l2b.loc (Figure S14). However, the local versions of the different methods performed similarly to their global counterparts in terms of RARMISE and RAE_median (Table 3 and Figure 3). The only exception to this is PLS when estimating μ{_{θ_anc}}, where the local version (pls.loc) resulted in an estimation error that increased more strongly with ε compared to the global version (pls.glob). More importantly, however, the coverage properties of the posteriors for ${\mu }_{{\theta }_{\text{anc}}}$ deteriorated for pls.loc, l1b.loc, and l2b.loc (Table 3), compared to their global versions (Table 2). The effect was weakest for l2b.loc and in general increased as a function of ε. The pls.loc method tended to overestimate ${\mu }_{{\theta }_{\text{anc}}}$, while lgb.loc, l1b.loc, and l2b.loc tended to underestimate it (Figure S9).

Table 3. Accuracy of different methods for choosing summary statistics on a local scale.

Method	ε	Parameter	RARMISE		RAE mode		RAE mean		RAE median		KS500	Cov. P
pls.loc	0.001	${\mu }_{{\theta }_{\text{anc}}}$	0.168	(0.136)	0.081	(0.091)	0.088	(0.095)	0.086	(0.091)	0.043	0.314
		${\sigma }_{{\theta }_{\text{anc}}}$	0.490	(0.262)	0.283	(0.229)	0.277	(0.234)	0.271	(0.226)	0.043	0.314
		ω	0.450	(0.278)	0.232	(0.234)	0.225	(0.228)	0.225	(0.228)	0.031	0.723
	0.01	${\mu }_{{\theta }_{\text{anc}}}$	0.175	(0.126)	0.088	(0.094)	0.098	(0.103)	0.094	(0.099)	0.067	0.023*
		${\sigma }_{{\theta }_{\text{anc}}}$	0.485	(0.274)	0.287	(0.222)	0.287	(0.243)	0.280	(0.223)	0.046	0.232
		ω	0.434	(0.259)	0.240	(0.238)	0.235	(0.224)	0.236	(0.227)	0.033	0.655
	0.1	${\mu }_{{\theta }_{\text{anc}}}$	0.220	(0.147)	0.101	(0.103)	0.113	(0.108)	0.106	(0.104)	0.087	0.001*
		${\sigma }_{{\theta }_{\text{anc}}}$	0.489	(0.282)	0.294	(0.216)	0.275	(0.243)	0.288	(0.231)	0.057	0.078
		ω	0.429	(0.259)	0.239	(0.226)	0.239	(0.227)	0.234	(0.223)	0.045	0.273
lgb.loc	0.001	${\mu }_{{\theta }_{\text{anc}}}$	0.149	(0.151)	0.061	(0.074)	0.067	(0.081)	0.064	(0.077)	0.076	0.006*
		${\sigma }_{{\theta }_{\text{anc}}}$	0.440	(0.213)	0.271	(0.213)	0.259	(0.209)	0.253	(0.209)	0.037	0.500
		ω	0.450	(0.283)	0.229	(0.231)	0.223	(0.219)	0.223	(0.217)	0.029	0.794
	0.01	${\mu }_{{\theta }_{\text{anc}}}$	0.144	(0.147)	0.065	(0.074)	0.068	(0.078)	0.066	(0.077)	0.085	0.001*
		${\sigma }_{{\theta }_{\text{anc}}}$	0.456	(0.237)	0.292	(0.209)	0.277	(0.223)	0.268	(0.213)	0.035	0.576
		ω	0.439	(0.27)	0.235	(0.229)	0.228	(0.225)	0.230	(0.225)	0.027	0.862
	0.1	${\mu }_{{\theta }_{\text{anc}}}$	0.140	(0.133)	0.068	(0.077)	0.069	(0.078)	0.068	(0.078)	0.093	<0.001*
		${\sigma }_{{\theta }_{\text{anc}}}$	0.467	(0.275)	0.315	(0.233)	0.298	(0.24)	0.288	(0.234)	0.020	0.991
		ω	0.431	(0.264)	0.232	(0.22)	0.226	(0.219)	0.227	(0.222)	0.039	0.423
l1b.loc	0.001	${\mu }_{{\theta }_{\text{anc}}}$	0.184	(0.183)	0.070	(0.081)	0.070	(0.083)	0.071	(0.082)	0.059	0.062
		${\sigma }_{{\theta }_{\text{anc}}}$	0.449	(0.215)	0.263	(0.234)	0.254	(0.219)	0.256	(0.218)	0.034	0.610
		ω	0.484	(0.281)	0.246	(0.253)	0.232	(0.218)	0.240	(0.233)	0.034	0.610
	0.01	${\mu }_{{\theta }_{\text{anc}}}$	0.176	(0.18)	0.072	(0.081)	0.070	(0.083)	0.070	(0.082)	0.071	0.012*
		${\sigma }_{{\theta }_{\text{anc}}}$	0.450	(0.218)	0.268	(0.25)	0.263	(0.23)	0.257	(0.221)	0.033	0.651
		ω	0.466	(0.279)	0.255	(0.265)	0.234	(0.22)	0.241	(0.234)	0.029	0.791
	0.1	${\mu }_{{\theta }_{\text{anc}}}$	0.175	(0.181)	0.076	(0.092)	0.072	(0.084)	0.071	(0.085)	0.107	<0.001*
		${\sigma }_{{\theta }_{\text{anc}}}$	0.504	(0.276)	0.277	(0.234)	0.291	(0.251)	0.261	(0.227)	0.045	0.257
		ω	0.444	(0.267)	0.238	(0.236)	0.237	(0.227)	0.231	(0.225)	0.032	0.694
l2b.loc	0.001	${\mu }_{{\theta }_{\text{anc}}}$	0.180	(0.18)	0.071	(0.08)	0.074	(0.084)	0.070	(0.081)	0.043	0.314
		${\sigma }_{{\theta }_{\text{anc}}}$	0.436	(0.207)	0.249	(0.222)	0.251	(0.215)	0.253	(0.213)	0.030	0.759
		ω	0.479	(0.275)	0.257	(0.261)	0.233	(0.226)	0.244	(0.235)	0.037	0.500
	0.01	${\mu }_{{\theta }_{\text{anc}}}$	0.172	(0.173)	0.075	(0.085)	0.077	(0.087)	0.076	(0.087)	0.056	0.084
		${\sigma }_{{\theta }_{\text{anc}}}$	0.444	(0.211)	0.258	(0.246)	0.264	(0.225)	0.257	(0.215)	0.033	0.651
		ω	0.459	(0.276)	0.256	(0.276)	0.234	(0.228)	0.244	(0.236)	0.036	0.532
	0.1	${\mu }_{{\theta }_{\text{anc}}}$	0.168	(0.169)	0.077	(0.091)	0.076	(0.09)	0.077	(0.091)	0.128	<0.001*
		${\sigma }_{{\theta }_{\text{anc}}}$	0.496	(0.266)	0.277	(0.235)	0.289	(0.241)	0.264	(0.23)	0.044	0.284
		ω	0.446	(0.271)	0.239	(0.242)	0.237	(0.23)	0.236	(0.233)	0.035	0.579

Details are as in Table 2 (cf. Figure S9).

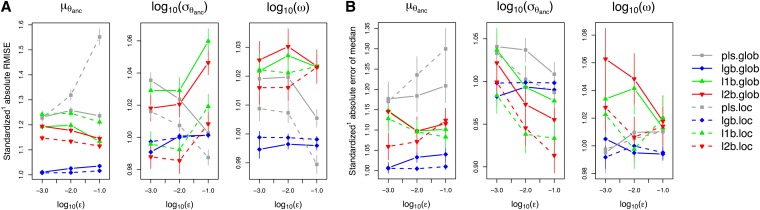
For direct comparison of methods, before averaging across test sets, we standardized the measures of accuracy relative to those obtained with all summary statistics (Figure 4). The only local method that, for all parameters, led to lower RARMISE and RAE_median than its global version was l2b.loc. In contrast, lgb.glob and lgb.loc performed very similarly; pls.loc did worse than pls.glob for ${\mu }_{{\theta }_{\text{anc}}}$, but better than pls.glob for ${\sigma }_{{\theta }_{\text{anc}}}$ and ω. Overall, we chose l2b.loc with ε = 0.01 as our favored method. This configuration provided good coverage for all parameters (Table 3). At the same time, it had lower RARMISE and RAE_median than pls.glob, the method that would also have had good coverage properties for ${\mu }_{{\theta }_{\text{anc}}}$. We disfavored all, lgb.glob, and lgb.loc due to their relatively weak coverage properties. Note that all methods compared in Figure 4 performed worse in terms of RARMISE and RAE_median than all when estimating ${\mu }_{{\theta }_{\text{anc}}}$. This might be due to the loss of information caused by leaving out some summary statistics. Apparently, this loss is not fully compensated in our setting by the potential gain from reducing the dimensions. In models with many more dimensions, this may be different.

Figure 4.

Standardized accuracy of different methods for choosing summary statistics as a function of the acceptance rate (ε). Standaridized¹ means that, before averaging across test sets, we divided the measures of accuracy for the respective method by the measure of accuracy obtained with all candidate summary statistics (this may change the relative order of methods compared to Figure 3, as the average of a ratio is generally not the same as the ratio of two averages). (A) Root mean integrated squared error (RMISE), relative to the RMISE obtained with all summary statistics. (B) Absolute error of the posterior median, relative to the one obtained with all summary statistics. Further details are as in Figure 3.

In summary, although performance in terms of RMISE and absolute error was only partially in favor of l2b.loc, we preferred this method based on its good coverage properties (Tables 2 and 3). Moreover, for ${\text{log}}_{10}\left({\sigma }_{{\theta }_{\text{anc}}}\right)$ and log₁₀(ω), the differences between methods measured by RMISE and absolute error were small compared to the error bars $\left(\pm \text{MAD}/\sqrt{n}\right)$, implying that too much weight should not be given to the respective rankings in Figures 3 and 4.

It is worth recalling some of the characteristics of the methods compared here. The pls method is the only one that involves decorrelation of the statistics. Apparently, this did not lead to a net improvement compared to the other methods. Although one explanation might be that the statistics were only weakly correlated, Figure S10 shows evidence of strong correlation among some statistics. Thus, it would appear that correlation among statistics does not substantially reduce efficiency (but this finding cannot be readily extrapolated to other settings, as we have used only a moderate number of summary statistics here). The reduction of dimensions is strongest with the l1b and l2b methods, since they result in one linear predictor per parameter. On the other hand, these methods assume a linear relationship between parameters and statistics. Since the latter was clearly not the case (e.g., Figure S11), it seems that the reduction of dimensions compensated for that assumption. This effect might be more pronounced in problems with many more statistics.

Application to Alpine ibex

Posterior distributions inferred for the ibex data with the various methods and ε = 0.01 are shown in Figure 5. The projection of some posterior density out of the prior support is not an artifact of kernel smoothing, but a consequence of regression adjustment. Leuenberger and Wegmann (2010) suggested a way of avoiding this problem. Since the effect is small—essentially absent for our favored method l2b.loc—we did not correct for this (cf. Figure S7). Moreover, the uniform distribution of posterior probabilities obtained with l2b.loc and ε = 0.01 (Figure S9) shows that the concerns that motivate the approach by Leuenberger and Wegmann (2010) do not apply in our case. Point estimates and 95% highest posterior density (HPD) intervals obtained with l2b.loc are given in Table 4. Recall that ${\mu }_{{\theta }_{\text{anc}}}$ and ${\sigma }_{{\theta }_{\text{anc}}}$ are hyperparameters of the distribution of ${\theta }_{\text{anc},l}$ across loci: ${\text{log}}_{10}\left({\theta }_{\text{anc},l}\right)\sim N\left({\mu }_{{\theta }_{\text{anc}}},{\sigma }_{{\theta }_{\text{anc}}}^2\right)$ (cf. Table 1). Inserting the estimates from Table 4, we obtained ${\text{log}}_{10}\left({\theta }_{\text{anc},l}\right)\sim N\left(0.110,\hspace{0.5em}{0.163}^2\right)$, which implies a mean ${\widehat{\theta }}_{\text{anc}}$ across loci of 1.288. The limits of the interval defined by ${\widehat{\mu }}_{{\theta }_{\text{anc}}}\hspace{0.5em}\pm 2{\widehat{\sigma }}_{{\theta }_{\text{anc}}}$ translate into (0.607, 2.735) on the scale of θ_anc. Remember that θ_anc = 4N_eu; it measures the total genetic diversity present in the ancestral deme at time t₁ = 1906 (Figure 2), i.e., at the start of the reintroduction phase. Although we were able to estimate θ_anc with relatively high precision, that does not immediately tell us about N_e or u without knowing one of the two. However, given some rough, independent estimates of N_e and u, we may assess whether our estimate ${\widehat{\theta }}_{\text{anc}}\approx 1.288$ is plausible. On the one hand, historical records of the census size of the ancestral Gran Paradiso deme are available. In combination with an estimate of the ratio of effective to census size, we may therefore obtain a rough estimate of N_e. Specifically, the census size of the Gran Paradiso deme (Figure 1) was estimated as <100 for the early 19th century (Stuwe and Nievergelt 1991; Scribner and Stuwe 1994), as 3000 for the early 20th century (Stuwe and Scribner 1989), and as 4000 for the year 1913 (Maudet et al. 2002). In addition, Scribner and Stuwe (1994) estimated for eight ibex demes in the Swiss Alps the effective population size from census estimates of the numbers of adult males and females. Their estimates of N_e were about one-third of the respective total census estimates. Together, these numbers suggest that a realistic range for the ancestral effective size N_e might be between 30 and 1300. On the other hand, estimates of the mutation rate u for microsatellites range from 10⁻⁴ to 10⁻² per locus and generation (Di Rienzo et al. 1998; Estoup and Angers 1998). Combining these two ranges results in θ_anc ranging from 1.2 × 10⁻² ≈ 10⁻² to 5.2 × 10 ≈ 10², suggesting that our estimate ${\widehat{\theta }}_{\text{anc}}\approx 1.288$ is plausible. Perhaps more interestingly, we may ask about the range across loci of u that is compatible with the range of ${\widehat{\theta }}_{\text{anc}}$ corresponding to ${\widehat{\mu }}_{{\theta }_{\text{anc}}}\hspace{0.5em}\pm \hspace{0.5em}2{\widehat{\sigma }}_{{\theta }_{\text{anc}}}$ (0.607, 2.735). The underlying assumption is that N_e is roughly the same for all loci, so that variation in ${\widehat{\theta }}_{\text{anc}}$ is exclusively due to variation of u across loci. Taking the geometric mean of the extremes from above, ${\widehat{N}}_{\text{e}}={\left(30\hspace{0.5em}\times \hspace{0.5em}1300\right)}^{1/2}\approx 197$, as a typical value, the corresponding interval for $\widehat{u}$ across loci is (7.7 × 10⁻⁴, 3.5 × 10⁻³). In other words, most of the variation in u across loci spans less than one order of magnitude.

Figure 5.

Marginal posterior distributions inferred from the Alpine ibex data. Posteriors obtained with tolerance ε = 0.01 and various methods for choosing summary statistics are compared. The dot-dashed red line corresponds to the method that performed best in the simulation study (I2b.loc; Tables 2 and 3 and Figures 3 and 4). Thin blue lines give the prior distribution (cf. Table 1). For pairwise joint posterior distributions, see Figure 6. Point estimates and 95% HPD intervals are given in Table 4.

Table 4. Posterior estimates for Alpine ibex data from ABC with summary statistics chosen locally via L₂Boosting and acceptance rate ε = 0.01.

Parameter	Mode	Mean	Median	95% HPDa interval
${\mu }_{{\theta }_{\text{anc}}}$	0.1089	0.1081	0.1101	(−0.0391, 0.2545)
${\text{log}}_{10}\left({\sigma }_{{\theta }_{\text{anc}}}\right)$	−0.6453	−0.8928	−0.7867	(−1.7615, −0.2613)
log10(ω)	−0.6159	−0.6933	−0.6824	(−1.33, −0.0294)

^aHighest posterior density.

The estimates for log₁₀(ω) from Table 4 imply a proportion of males obtaining access to matings of $\widehat{\omega }\approx 0.208$ or ∼21%. The 95% HPD interval for ω is (0.047, 0.934). An observational study in a free-ranging ibex deme suggested that ∼10% of males reproduced (Aeschbacher 1978). More recently, Willisch et al. (2012) conducted a behavioral and genetic study and reported paternity scores for males of different age classes. The weighted mean across age classes from this study is ∼14% successful males. Given the many factors that influence such estimates, our result of 21% seems in good agreement with these values, and our 95% HPD interval includes them. Two points are worth noting. First, our 95% HPD interval for ω seems large, which reflects the uncertainty involved in this parameter. Second, when estimating ω, we are essentially estimating the ratio of recent effective population size to census population size, $N_{\text{e}}^{\left(i\right)}/N$, where $N_{\text{e}}^{\left(i\right)}$ is the effective size of a derived deme d_i. This ratio may be smaller than one for many reasons—not just male mating access. Thus, we have strictly speaking estimated the strength of genetic drift due to deviations in reproduction from that in an idealized population. Nevertheless, the good agreement with the independent estimates of male mating access is striking.

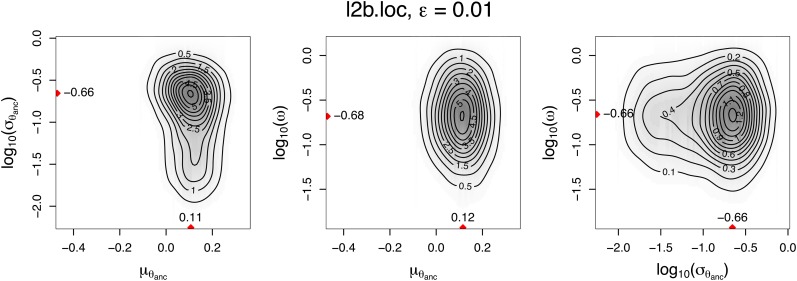
In Figure 6, we report pairwise joint posterior distributions for l2b.loc and ε = 0.01. The pairwise joint modes are close to the marginal point estimates in Table 4. Moreover, Figure 6 suggests no strong correlation among parameters.

Figure 6.

Pairwise joint posterior distributions given data observed in Alpine ibex, obtained with tolerance ε = 0.01 and summary statistics chosen locally via L₂Boosting (l2b.loc). Red triangles denote parameter values corresponding to the pairwise joint modes. Each time, the third parameter has been marginalized over.

Discussion

We have suggested three variants of boosting for the choice of summary statistics in ABC and compared them to each other, to PLS regression, and to ABC with all candidate summary statistics. Moreover, we proposed to choose summary statistics locally, in the putative neighborhood of the observed data. Overall, the mean of the ancestral mutation rate ${\mu }_{{\theta }_{\text{anc}}}$ was more precisely estimated than its standard deviation ${\sigma }_{{\theta }_{\text{anc}}}$ and the male mating access rate ω. In our context, ABC with summary statistics chosen locally via boosting with componentwise linear regression as a base procedure and the L₂-loss performed best in terms of accuracy (measured by RARMISE and RAE_median) and uniformity of posterior probabilities together. However, the difference between the methods was moderate and the ranking depended to some degree on our choice of criteria to assess performance. If the main interest had been in a small error of point estimates (low RAE_median), but less in good overall posterior properties (low RARMISE and uniform posterior probabilities of the true value) at the same time, boosting with the negative binomial log-likelihood loss and, somewhat surprisingly, ABC with all candidate statistics, would have been preferable to boosting with the L₁- and L₂-loss. Under this criterion (low RAE_median), the performance of the PLS method was intermediate when estimating ω, but inferior to that of any boosting approach when estimating ${\mu }_{{\theta }_{\text{anc}}}$ and ${\sigma }_{{\theta }_{\text{anc}}}$. In general, choosing summary statistics locally slightly improved the accuracy compared to the global choice, but it led to worse posterior coverage for ${\mu }_{{\theta }_{\text{anc}}}$. The local version of L₂Boosting with acceptance rate ε = 0.01 coped best with this trade-off.

Applying that method to Alpine ibex data, we estimated the mean across loci of the scaled ancestral mutation rate as ${\widehat{\theta }}_{\text{anc}}\approx 1.288$. The estimates for ${\sigma }_{{\theta }_{\text{anc}}}$ implied that most of the variation across loci of the mutation rate u was between 7.7 × 10⁻⁴ and 3.5 × 10⁻³. The proportion of males obtaining access to matings per breeding season was estimated as $\widehat{\omega }\approx 0.21$, which is in good agreement with recent independent estimates. This result suggests that the strong dominance hierarchy in Alpine ibex is reflected in overall genetic diversity and should therefore be considered an important factor in determining the strength of genetic drift.

It should be noted that the results we reported here about the choice of summary statistics are specific to the model, to the data, and, in particular, to the choice of criteria used to assess performance. Another method may perform better under a different setting, and this is most likely a general feature of inference with ABC (cf. Blum et al. 2012). For the various points where some choice must be made—summary statistics, metric, algorithm, and postrejection adjustment—by nature, no single strategy is best in every case. Rather, the focus should be on choosing the best strategy for a specific problem. In practice, this implies comparing alternatives and assessing performance in a simulation study. Along these lines, there is still scope for new ideas concerning the various choices in ABC (see Beaumont et al. 2010). In particular, the choice of the metric makes ABC a scale-dependent method. This applies both to the ABC algorithm in general and to our suggestion of choosing summary statistics in the putative neighborhood of the truth. One could, for instance, use the Mahalanobis instead of the Euclidean distance, but even this is based on an assumption that is not necessarily appropriate (multivariate normal distribution of variables). In a specific application, one metric may do better than another, but it may not be obvious why. Overall, this poses an open problem and motivates future research (Wilkinson 2008).

As more data become available and more complex models are justifiable, it will be necessary that methods of inference keep pace. In principle, ABC is scalable and able to face this challenge. The problems arise in practice, and the combination of approaches devised to tackle them is itself becoming intricate. Researchers may be interested in a single program that implements these approaches and allows for inference with limited effort needed for tuning, simulation, and cross-validation. However, such software runs the risk of being treated as a black box. This problem is not unique to ABC, but equally applies to other sophisticated approaches of inference, such as coalescent-based genealogy samplers (Kuhner 2009). In the context of ABC, rather than having a single piece of software, we find it more promising to combine separate pieces of software that each implement a specific step. The appropriate combination must be chosen specifically for any application. It will always be necessary to evaluate the performance of any ABC method through simulation-based studies. Such a modular approach has recently been fostered by the developers of ABCtoolbox (Wegmann et al. 2010) or the abc package for R (Csilléry et al. 2011). Here, we contribute to this by providing a flexible simulation program that readily integrates into any ABC procedure.

Recently, two interesting alternative approaches have been proposed for choosing summary statistics with a focus on the putative location of the true parameter value, rather than the whole prior range. Nunes and Balding (2010) suggest a two-step procedure. Starting with a set of candidate summary statistics, at a first stage, standard ABC is carried out for (possibly) all subsets of these statistics, and the subset resulting in the posterior distribution with the minimum entropy is chosen. This subset of statistics is used to determine the n′ simulations with the smallest Euclidean distance to the observation. At the second stage, the n′ data sets close to the putative truth are used as a training set to choose, again, among (possibly) all subsets of the original candidate statistics. Here, Nunes and Balding (2010) propose as an optimization criterion the average square root of the sum of squared errors, averaged over the training data sets.

Fearnhead and Prangle (2012) follow the idea of optimizing the choice of summary statistics with respect to the accuracy of certain estimates of the parameters (e.g., a point estimate), rather than the full posterior distribution. For instance, if the goal is to minimize the quadratic loss between the point estimate and the true value, the authors prove that the posterior mean is the optimal summary statistic. Since the posterior mean is not available in advance, they propose to first conduct a pilot ABC study to determine the region of high posterior mass. For this region, they then draw parameters and simulate data to obtain training data sets. These are used in a third step to fit a linear regression with the parameters as responses and a vector-valued function of the original summary statistics as explanatory variables (allowing for nonlinear transformations of the original statistics). The linear fits are used as new summary statistics for the corresponding parameter. A final ABC run is then performed, with a prior restricted to the range established in the first step, and summary statistics chosen in the third step. Fearnhead and Prangle (2012) refer to this as semiautomatic and independent of the choice of statistics. However, as the authors note, it does depend on the initial choice of candidate statistics and on the choice of the vector-valued function. Moreover, if the (transposed) candidate statistics are uncorrelated, we suspect that their method would be equivalent to using the first component in a univariate PLS regression.

The approaches by Nunes and Balding (2010) and Fearnhead and Prangle (2012) and our local boosting procedures all consist of several steps, at least one being devoted to establishing the vicinity of the putative truth. While the method by Nunes and Balding (2010) and LogitBoost aim at choosing the “best subset” from a set of candidate statistics (without transforming them), the method by Fearnhead and Prangle (2012), PLS, and L₁- and L₂Boosting “construct” new summary statistics as functions of the original ones. The former has the advantage that the summary statistics conserve their interpretation, while the latter has the potential of better extracting and combining information contained partly in the various candidate statistics. The method by Nunes and Balding (2010) suffers from the fact that all subsets of candidate statistics must be explored, which is prohibitive in the case of large numbers of statistics. Here, boosting offers a potential advantage, because the functional gradient descent is a “greedy” algorithm (see Appendix). It does not explore all possible combinations of statistics, but in any iteration selects only one candidate statistic that improves an optimization criterion, given the current stage of the algorithm.

A direct comparison of all the recently proposed methods for the choice of statistics in ABC (e.g., Joyce and Marjoram 2008; Wegmann et al. 2009; Nunes and Balding 2010; Jung and Marjoram 2011; Fearnhead and Prangle 2012) seems due. Nunes and Balding (2010) and Blum et al. (2012) compare a subset of these methods for a simple toy model with mutation and recombination in a panmictic population (cf. Joyce and Marjoram 2008). Blum et al. (2012) also include two examples from epidemiological modeling and material science. Their main conclusion is that the best method depends on the model. Crucial aspects seem to be the number of parameters, the number of candidate summary statistics, and the degree of collinearity of the statistics. Importantly, the PLS method (Wegmann et al. 2009)—although widely used in recent ABC applications—has been shown not to be very efficient and our results are consistent with this. However, a comparison for a range of relevant population genetic models, including some with larger numbers of parameters, is currently missing.

The boosting approach proposed here should also be suitable for constructing summary statistics to perform model comparison with ABC (e.g., Fagundes et al. 2007; Blum and Jakobsson 2011). Despite recent criticism (Robert et al. 2011; but see Didelot et al. 2011), ABC-type model comparison remains an interesting option. By treating the model index as the single response, the algorithm proposed here might be used in this context.

Appendix

Modular Inference for High-Dimensional Problems Using ABC

Here, we explore how ABC can be applied to complex situations, where a modular structure of the inferential problem can be exploited. For this purpose, we assume that the parameter vector φ relevant to the problem can be split into two subvectors α and $\tilde{m}$ and that we have two corresponding vectors of summary statistics S_α and $S_{\tilde{m}}$, such that S_α contains most of the information on α, whereas $S_{\tilde{m}}$ contains most of the information on $\tilde{m}$. It turns out that the modular structure can be exploited in such a situation, to split a high-dimensional problem into subproblems involving only lower-dimensional summary statistics.

To make this precise, we adapt the concepts of approximate sufficiency (e.g., Le Cam 1964) and approximate ancillarity (Ghosh et al. 2010 and references therein). In the context of ABC, Joyce and Marjoram (2008) proposed an approach for choosing summary statistics based on approximate sufficiency.

In particular, we call S_α to be ε-sufficient for α with respect to $S_{\tilde{m}}$, if

$$\underset{\alpha }{\text{sup}}\text{ln}\hspace{0.17em}\pi \left(S_{\tilde{m}}|S_{\alpha },\tilde{m},\alpha \right)-\underset{\alpha }{\text{inf}}\text{ln}\hspace{0.17em}\pi \left(S_{\tilde{m}}|S_{\alpha },\tilde{m},\alpha \right)\le \epsilon$$ (A1)

for all $\tilde{m}$. We further define S_α to be δ-ancillary with respect to $\tilde{m}$, if

$$\underset{\tilde{m}}{\text{sup}}\text{ln}\hspace{0.17em}\pi \left(S_{\alpha }|\tilde{m},\alpha \right)-\underset{\tilde{m}}{\text{inf}}\text{ln}\hspace{0.17em}\pi \left(S_{\alpha }|\tilde{m},\alpha \right)<\delta$$ (A2)

for all α. Analogously, we define ε-sufficiency and δ-ancillarity for $S_{\tilde{m}}$ (note that ε and δ do not have the same meaning here as in the main text).

We first assume that S_α is ε-sufficient for α relative to $S_{\tilde{m}}$ and δ-ancillary with respect to $\tilde{m}$. Then,

$$\begin{array}{l}\pi \left(\alpha |S\right)={\displaystyle \int \pi \left(\tilde{m},\alpha |S\right)d\tilde{m}}\\ =\frac{{\displaystyle \int \pi \left(S_{\alpha },S_{\tilde{m}}|\tilde{m},\alpha \right)\pi \left(\alpha \right)\pi \left(\tilde{m}\right)d\tilde{m}}}{{\displaystyle \iint \pi \left(S_{\alpha },S_{\tilde{m}}|\tilde{m},\alpha \right)\pi \left(\alpha \right)\pi \left(\tilde{m}\right)d\tilde{m}\hspace{0.17em}d\alpha }}\\ =\frac{{\displaystyle \int \pi \left(S_{\alpha }|\tilde{m},\alpha \right)\pi \left(\alpha \right)\pi \left(S_{\tilde{m}}|S_{\alpha },\tilde{m},\alpha \right)\pi \left(\tilde{m}\right)d\tilde{m}}}{{\displaystyle \iint \pi \left(S_{\alpha }|\tilde{m},\alpha \right)\pi \left(\alpha \right)\pi \left(S_{\tilde{m}}|S_{\alpha },\tilde{m},\alpha \right)\pi \left(\tilde{m}\right)d\tilde{m}\hspace{0.17em}d\alpha }}\\ \le \frac{\pi \left(S_{\alpha }|\alpha \right)\pi \left(\alpha \right)e^{\delta }{\displaystyle \int {\text{sup}}_{\alpha }\pi \left(S_{\tilde{m}}|S_{\alpha },\tilde{m},\alpha \right)\pi \left(\tilde{m}\right)d\tilde{m}}}{e^{-\delta }{\displaystyle \int \pi \left(S_{\alpha }|\alpha \right)\pi \left(\alpha \right)d\alpha }{\displaystyle \int {\text{inf}}_{\mathit{\alpha }}\pi \left(S_{\tilde{m}}|S_{\alpha },\tilde{m},\alpha \right)\pi \left(\tilde{m}\right)d\tilde{m}}}\\ \le \pi \left(\alpha |S_{\alpha }\right)e^{2\delta +ϵ}.\end{array}$$ (A3)

A lower bound can be obtained in an analogous way, and we get

$$\pi \left(\alpha |S_{\alpha }\right)e^{-2\delta -ϵ}\le \pi \left(\alpha |S\right)\le \pi \left(\alpha |S_{\alpha }\right)e^{2\delta +ϵ}.$$ (A4)

If δ and ε are both small, a good approximation to the ABC-posterior π(α|S) can therefore be obtained by using only S_α.

Next, we look at the ABC posterior for $\tilde{m}$ given α, $\pi \left(\tilde{m}|\mathbf{\alpha },S_{\tilde{\mathbf{m}}}\right)$, and start with Equation 4,

$$\pi \left(\tilde{m},\alpha |S\right)=\pi \left(\tilde{m}|\alpha ,S\right)\pi \left(\alpha |S\right),$$ (A5)

and Equation 5,

$$\pi \left(\alpha |S\right)={\displaystyle \int \pi \left(\tilde{m},\alpha |S\right)d\tilde{m}},$$ (A6)

from the main text, replacing the full data D by the summary statistics S.

From (A6) it follows that a sample from the marginal posterior of α can be obtained by taking the α-components of a sample from the joint posterior of $\tilde{m}$ and α.

As shown above, π(α |S) can be replaced without much loss by π(α |S_α), if $S_{\tilde{m}}$ is not informative for α and S_α is not informative for $\tilde{m}$. We show that $\pi \left(\tilde{m}|\alpha ,S\right)=\pi \left(\tilde{m}|\alpha ,S_{\alpha },S_{\tilde{m}}\right)\approx \pi \left(\tilde{m}|\alpha ,S_{\tilde{m}}\right)$, given that $S_{\tilde{m}}$ is ε-sufficient for $\tilde{m}$:

$$\begin{array}{c}\pi \left(\tilde{m}|\alpha ,S_{\alpha },S_{\tilde{m}}\right)=\pi \left(S_{\alpha }|\alpha ,\tilde{m},S_{\tilde{m}}\right)\frac{\pi \left(\alpha ,\tilde{m},S_{\tilde{m}}\right)}{\pi \left(\alpha ,S_{\alpha },S_{\tilde{m}}\right)}\\ \le e^{\epsilon }\pi \left(S_{\alpha }|\alpha ,S_{\tilde{m}}\right)\frac{\pi \left(\alpha ,\tilde{m},S_{\tilde{m}}\right)}{\pi \left(\alpha ,S_{\alpha },S_{\tilde{m}}\right)}\\ =e^{ϵ}\pi \left(S_{\alpha }|\alpha ,S_{\tilde{m}}\right)\frac{\pi \left(\alpha ,\tilde{m},S_{\tilde{m}}\right)}{\pi (S_{\alpha }|\alpha ,S_{\tilde{m}})\pi \left(\alpha ,S_{\tilde{m}}\right)}\\ =e^{ϵ}\frac{\pi \left(\alpha ,\tilde{m},S_{\tilde{m}}\right)}{\pi \left(\alpha ,S_{\tilde{m}}\right)}\\ =e^{ϵ}\pi \left(\tilde{m}|\alpha ,S_{\tilde{m}}\right).\end{array}$$ (A7)

Together with an analogously obtained lower bound, we have that

$$e^{-\epsilon }\pi \left(\tilde{m}|\alpha ,S_{\tilde{m}}\right)\le \pi \left(\tilde{m}|\alpha ,S_{\alpha },S_{\tilde{m}}\right)\le e^{\epsilon }\pi \left(\tilde{m}|\alpha ,S_{\tilde{m}}\right)$$ (A8)

and again S_α can be omitted without much loss, if S_α does not provide much further information about $\tilde{m}$ given $S_{\tilde{m}}$.

To summarize, breaking up ABC into lower-dimensional modules with separate summary statistics can be shown to lead to good approximations, if S_α and $S_{\tilde{m}}$ are ε-sufficient with respect to each other for their respective parameters. Also, S_α should be δ-ancillary for $\tilde{m}$.

Functional Gradient Descent Boosting Algorithm

The general FGD algorithm for boosting, as given by Friedman (2001) and modified by Bühlmann and Hothorn (2007), is as follows.

FGD algorithm

• 1.Initialize ${\widehat{F}}^{\left[0\right]}(\cdot )\equiv \text{arg}\hspace{0.17em}{\text{min}}_c{n}^{-1}{\displaystyle {\sum }_{i=1}^{n}L\left(Y_i,c\right)}$, set m = 0.
• 2.
  Increase m by 1. Compute the negative gradient and evaluate at ${\widehat{F}}^{\left[m-1\right]}\left(X_i\right)$:

  $$U_i=-\frac{\partial }{\partial F}{L\left(Y_i,F\right)|}_{F={\widehat{F}}^{\left[m-1\right]}\left(X_i\right)}.$$
• 3.
  Fit the negative gradient vector (U₁, … , U_n) to (X₁, … , X_n) by the base procedure:

  $${\left(X_i,U_i\right)}_{i=1}^n\to {\widehat{g}}^{\left[m\right]}.$$
• 4.Update ${\widehat{F}}^{\left[m\right]}(\cdot )={\widehat{F}}^{\left[m-1\right]}(\cdot )+\nu {\widehat{g}}^{\left[m\right]}(\cdot )$, where ν is a step-length factor.
• 5.Iterate steps 2–4 until m = m_stop.

Here, ν and m_stop are tuning parameters discussed in the main text. The result of this algorithm is a linear combination $\widehat{F}(\cdot )$ of base procedure estimates, as shown in Equation 7 of the main text. In any specific version of boosting, the form of the initial function ${\widehat{F}}^{\left[0\right]}(\cdot )$ in step 1 and the negative gradient U_i in step 2 may be expressed explicitly according to the loss function L(⋅, ⋅) (see File S1).

Base Procedure: Componentwise Linear Regression

We write the jth component of a vector v as v^(j). The following base procedure performs simple componentwise linear regression,

$$\begin{array}{l}\widehat{g}\left(X\right)={\widehat{\lambda }}^{\left(\widehat{\zeta }\right)}{X}^{\left(\widehat{\zeta }\right)},\\ {\widehat{\lambda }}^{\left(j\right)}=\frac{{\displaystyle {\sum }_{i=1}^n{X}^{\left(j\right)}{U}_i}}{{\displaystyle {\sum }_{i=1}^n{\left(X_i^{\left(j\right)}\right)}^2}},\\ \widehat{\zeta }=\text{arg}\hspace{0.17em}{\text{min}}_{1\le j\le p}{\displaystyle \sum _{i=1}^n{\left(U_i-{\widehat{\lambda }}^{\left(j\right)}{X}_i^{\left(j\right)}\right)}^2},\end{array}$$ (A9)

where $\widehat{g}(\cdot )$, X, and U_i are as in the FGD algorithm above. This base procedure selects the best variable in a simple linear model in the sense of ordinary least-squares fitting (Bühlmann and Hothorn 2007). To see this, note that ${\widehat{\lambda }}^{\left(j\right)}$ in (A9) is the ordinary least-squares solution of a linear regression $U_i=X_i^{\left(j\right)}{\lambda }^{\left(j\right)}$, in matrix form ${\widehat{\lambda }}^{\left(j\right)}={\left(X_i^{\left(j\right)\mathrm{\top }}{X}_i^{\left(j\right)}\right)}^{-1}{X}_i^{\left(j\right)\mathrm{\top }}{U}_i$. The choice of the loss functions enters indirectly via U_i (see File S1).