Indirect genetic effects and the genetic bases of social dominance: evidence from cattle

Abstract

Genetic studies of social behaviour have currently received new impetus from models including indirect genetic effects (IGEs) of social partners. This study aimed at investigating the contribution of conspecifics in social dominance, considered as response of dyadic interaction that is, winning (dominant individual) or losing (subordinate). A genetic correlation of −1 is expected between the attitude to win and the attitude to loose, and because a population always accounts for half winners and half losers, the heritability of the dominant status should be close to zero. Specifically, social dominance was studied in Aosta Chestnut and Aosta Black Pied (Bos taurus) breeds, alpine rustic cattle famous for traditional tournaments where pairs of cows assess dominant status in bloodless fights. The outcomes of 25 590 dyadic interactions performed by 8159 individuals in 11 years were analysed by applying a classical quantitative model and models including indirect effects. Data were analysed via Bayesian approach on a threshold trait. The assessment of variances revealed a genetic correlation of −0.976 between direct and indirect genetic components. The heritability measured on a liability scale was 0.122 for direct phenotype, but decreased to 0.014 when the total heritable variance (TBV) was considered. The trend of estimated breeding values showed that the total TBV was constant over the years, even though its direct component increased and the indirect part decreased. This result confirms the relevance of IGEs on social behaviour and the assumption that the mean individual social dominance cannot evolve within a population, due to the evolutionary constraints imposed by the ‘social environment'.

Introduction

Genetic investigations on behavioural traits are generally complicated by the strong influence of the environment (Boake et al., 2002), and studies on social behaviour are intricate because focal individuals constitute an environment effect for the conspecifics with whom they interact (that is, ‘interacting phenotypes' Moore et al., 1997). Moore et al., 1997 introduced the concept of ‘indirect genetic effects' (IGEs) as the part of the individual phenotype provided by the genes of interacting social partners. Moving from the work of Griffing (1967); Muir and Schinckel (2002), as well as Bijma et al. (2007a), observed that both permanent environmental and genetic parts of social traits can be considered to be a sum of direct and indirect components provided by focal individual and by interacting conspecifics, respectively. Social dominance is the relation of dominance/subordination established between the two individuals after agonistic interaction (Drews, 1993). In the assessment of hierarchies, a dominance relationship among the two conspecifics is usually established by the outcome of a contest, where the winner acquires a dominant status over the loser. Social dominance is therefore constituted by both the dominant status of the individual winner and the subordinate condition of loser conspecific (Moore et al., 2002). ‘To be a winner' and ‘not to be a loser' are two sides of the same coin, thus an individual providing the direct information ‘good at winning' also carries the information ‘bad at losing' as an indirect effect. The correlation among these two components arises from an evolutionary constraint (Arnold, 1992) in which any change in one of the two components necessarily leads to a modification equal in magnitude but opposite in verse. Direct and indirect effects should have equal variances and opposite covariances, thus the correlation is likely of attaining a level of −1 (Bijma, 2011; Wilson et al., 2011). Focusing on a population level, and considering that each win necessarily implies a loss, the average number of wins in a population cannot increase, and the heritability of the dominant status is expected to be close to zero. Empirical evidence of such assumptions have so far only been found in red deer (Cervus elaphus; Wilson et al., 2011). The present work aimed at improving the knowledge about genetics of social dominance by extending the study to cattle. Subjects of the study were Aosta Chestnut and Aosta Black Pied breeds (Bos taurus), two Alpine rustic cattle famous for traditional tournaments in which pairs of cows assess the respective dominant status in ritual bloodless fights (Mantovani et al., 2007; Sartori and Mantovani, 2010, 2012). The outcome (that is, win or defeat) of cow dyadic interactions was considered to be a phenotype aimed at investigating (i) the incidence of IGEs in social dominance, (ii) the magnitude of the relationship between direct and indirect effects, both genetic and environmental and (iii) the response of a population to a selection for dominance.

Materials and methods

Study subject and data set

Study subjects were the results of the traditional battle contest (Batailles de Reines) organized annually by farmer organizations within the Aosta region (North-West of Italy) as a revival of the agonistic interactions that naturally occur at pasture. Two autochthonous and genetically related breeds (Aosta Chestnut and Aosta Pie Black) are involved in the battle contest, for which an exhaustive description has been given elsewhere (Mantovani et al., 2007; Sartori and Mantovani, 2010). Briefly explained, the competitions consist of 20 preliminary tournaments per year in which participants are divided into three weight categories. Within each weight category cows take part in duels where the winner is allowed to proceed further in the challenge and the loser leaves the contest. The battle board has no seeds and the best qualified cows during the preliminary tournaments gain the right to take part in the yearly final competition. Each cow is allowed to compete in more than one preliminary tournament within a year. In the course of a tournament an individual can engage in up to seven encounters, depending on the number of participants (from 16 to 150 competitors within each category). From an ethical point of view, Batailles de Reines guarantee the welfare of animals, as cows are free to behave as they were under natural conditions (for example, an interaction may simply solve in a quick glance followed by a submissive posture of one the two contenders, without any physical contact). Small injuries as slight wounds in forehead seldom occur, but they are immediately treated by veterinarians.

All the fighting results achieved in the course of all the days of the competitions performed in 11 successive years of battle contests (from 2001 to 2011) were considered in the present study. Fighting records were collected by the farmers' association organizing the tournaments (‘Amis de Reines') and thus provided by the regional farmer association. Additional herd book information was made available by the national breeders organization. Raw data referring to each dyad encounter played within a day of tournament were edited and organized by choosing at random one player as the focal individual (that is, providing direct components to the phenotype) and the other as the opponent (that is, accounting for indirect effects). The outcome of the dyadic interaction was retained as a phenotype and expressed as a binary result (0/1), attaining a value of 0 if the focal individual was defeated, and 1 otherwise. In accordance with the rules of the tournaments, no intermediate situations such as ties were feasible. Information available for each dyadic encounter included: the day of the tournament, the weight category to which cows were referred, the moment of the battle within the tournament (that is, first round of fights, second round,… final round), the identity of the two contenders, individual weight and age at the moment of battle, and all the genealogical information included in the herd book. Dyadic interactions with unknown competitors or those lacking in pedigree data were discarded. After editing, a data set of 25 590 individual records belonging to 8159 cows was retained for subsequent analysis. The total number of animals in the pedigree file recovered from the breeders' database was 17 579. Table 1 summarizes these and other descriptive statistics for the final data set used, which included an average of 1271±180 participants to ‘Batailles de Reines' per year and 27.2±15.5 participants within a tournament. Outcome data referred to an average of 1.4±0.7 fights that a cow performed in the course of a day of a tournament (that is, each fight with a different competitor), increasing to 3.1±3.3 considering the whole data set.

Table 1. Descriptive statistics on the final data set from ‘Batailles de Reines' retained for analysis.

Item	Value
No. of records	25590
No. of participants (over the 11 years)	8159
No. of participants per year	1271±180
No. of participants within tournament	27.2±15.5
No. of participations/cow (over the 11 years)	2.3±1.9
No. of participations/cow within year	1.8±1.2
No. of competitors/cow (over the 11 years)	3.1±3.3
No. of competitors/cow within tournament	1.4±0.7
No. of animals in the pedigree file	17579
Age of participant, years	6.1±1.7
BW of participant, kg	555±63
BW category, kg
1 (heavy)	642±44
2 (medium)	550±20
3 (light)	499±22

Abbreviation: BW, body weight.

Data refer to 11 years of tournaments (that is, from 2001 to 2011).

Models and analysis

Each dyadic interaction entered the data set as a single record (that is, each member of a dyad was considered as either a focal individual or an opponent, and not vice versa in another record). This was done to avoid non-independent data. In order to carry out the analyses, dyadic interactions were retained within the data set only if the individual accounted as opponent had at least another observation as focal. Moreover, due to the number of years considered and because of possible participation of a cow in more than one competition per year repeated measurements of the same individuals were possible. Preliminary logistic analyses were performed on data (logistic procedure; SAS Institute, 2009) to retain non-genetic fixed factors for subsequent genetic analyses. After this preliminary analysis, the factors retained were: the year (11 levels), the day of tournament (21 levels from the 1st to the 21st day of battles for years 2001–2009, and 22 levels for years 2010 and 2011 due to an additional day of competition), the weight category (three levels), and the difference in age between the focal individual and the opponent expressed in categories (13 classes, where the central one refers to age differences equal to zero).

In the final models, considering a dyadic interaction k performed by a focal individual i vs opponent j, the outcome y_ijk, considered as binary (0 for defeat and 1 for win), was distributed as:

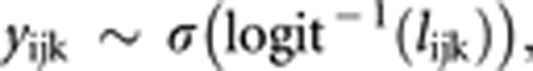where σ is a draw from a Bernoulli distribution with probability logit⁻¹(l_ijk), and l_ijk is the liability on logit scale of the event ‘i wins the contest', thus resulting as dominant. The l_ijk was predicted in a series of four different models accounting for the same fixed effects as above, but considering different partitioning of phenotypic and genetic variance, as suggested by recent literature (Arango et al., 2005; Muir, 2005; Chen et al., 2008; Wilson et al., 2009, 2011). Different models were as follows:

where ‘fixed' are the all fixed effects retained in the models, Pe_Di is the random permanent environmental effect, Pe_Cj is the random associative permanent environmental effect due to the interacting conspecifics, a_Di is the random direct additive genetic effect, a_Cj is the associative genetic component (that is, IGE) and e_ijk is the random residual component. Therefore, the first model (M1) included permanent environmental and additive genetic variances of the focal individual, as in classical quantitative analyses, while the subsequent models added alternatively the permanent environmental effect of the interacting conspecific (M2) or the additive associative components (IGE; M3) or both (M4).

In a matrix notation, the most complete model adopted (that is, M4) could be written as follows:

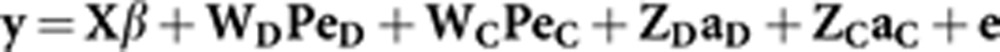where y is an N × 1 vector of observations, β is the vector of systematic fixed effects of order p, Pe_D is the vector of permanent environmental effects of order q, Pe_C is the vector of permanent environmental effects provided by the conspecifics with the same order of Pe_D, a_D is the vector of direct animal effects with order m, a_C is the vector of the additive associative effect with the same order as a_D, and e is the vector of residual effects. Furthermore, X, W_D, W_C, Z_D and Z_C are the corresponding incidence matrices with the appropriate dimensions.

The assumptions about the structures of (co)variance in the most complete model were:

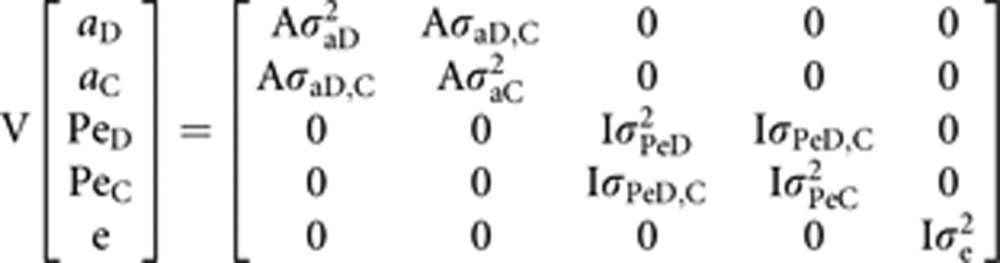where, σ²_PeD is the random permanent environmental effect, σ²_PeC is the random associative permanent environmental effect due to the interacting conspecifics, σ_PeD,C is the covariance between these two effects, σ²_aD is the random direct additive genetic effect, σ²_aC is the associative genetic component (that is, IGE), σ_aD,C is the covariance between the last two effects, σ²_e is the random residual variance, A the numerator relationship matrix and I an identity matrix.

Analyses of IGEs were carried out by applying the social competitive model with the categorical expression presented by Misztal and Rekaya, 2007 as an implementation of the competitive model for linear traits proposed by Muir and Schinckel, 2002 and further developed by Arango et al., 2005. The ‘variance partitioning approach' for direct and associative components described by Bijma et al. (2007a) was adopted, and dyadic phenotypes were treated as in Wilson et al. (2011). Data were analyzed via a Bayesian approach through the program ‘thrgibbs1f90' (Tsuruta and Misztal, 2006; Misztal, 2008), whereby the Gibbs sampling algorithm (Geman and Geman, 1984; Misztal, 2008) was applied to run analyses of single-trait threshold models for categorical data (Sorensen et al., 1995). Flat priors were used for systematic effects and dispersion parameters. The Gibbs sampler performed 990 000 iterations with a starting burn-in, which discarded 90 000 samples. Convergence was screened by graphical inspection, that is, drawing the plots of the sampled values vs performed iterations (Kass et al., 1998). The posterior mean of 3000 samples (that is, one every 300 samples of the remaining 900 000) was used as a point estimate of parameters under investigation. Lower and upper bounds of the 95% highest posterior probability density regions for permanent and additive effects were estimated from the Gibbs samples.

Heritability and genetic correlation estimates

Heritability components (h²) for the four models considered were estimated and compared. A direct heritability h²_D for social dominance was assessed for all the models as the ratio of the direct genetic variance σ²_aD and the total phenotypic variance σ²_P consisting in the sum of all estimated variance components, thus 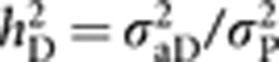. An associative heritability h²_c, arising from the proportion of the IGEs on the total phenotypic variance, that is, 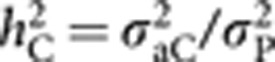, was assessed for models including IGEs, that is, M3 and M4, whereas a total heritable variance (TBV) h²_TOT, also known in the literature as τ² (Bijma et al., 2007a; Bijma, 2010) and consisting in the ratio of direct and associative genetic variances plus their correlation on the total phenotypic variance, h²_TOT=(σ²_aD+σ²_aC+2σ_aD,C)/σ²_P, was computed for all the four models. Genetic correlations between direct and associative genetic components were obtained for M3 and M4, whereas phenotypic correlations were estimated for all models except M1. The posterior means and the corresponding 95% highest posterior density intervals (HPD) were computed for all heritability estimates and correlations.

Model comparison

The predictive ability of four models was evaluated through a data-splitting or cross-validation approach based on posterior predictive distributions as proposed by Shao, 1993 and applied in Ramirez-Valverde et al., 2001. The splitting technique applied in this study consisted in creating a group of five different sub-data sets, each one retaining a randomly selected 75% of the animals with phenotypic recording (that is, the fighting cows). After editing, sub-data sets included an average of 13 610±236 fighting records performed by 5452±33 cows and referred to 14 063±81 animals in the pedigree (Table 2). Individual breeding values (that is, direct breeding values for models including associative effects, as M3 and M4) were then estimated by applying each of the four models described above to the five sub-data sets. Pearson product-moment correlation coefficients between cow estimated breeding values (EBV) for pairs of sub-data sets within each model were computed (correlation procedure; SAS Institute, 2009). An average of 2902±36 cows were shared by the considered pairs of data sets and used for correlation analysis, as well as the mean correlation obtained for each model were compared to analyze the stability of each model in predicting EBV.

Table 2. Posterior means and 95% highest posterior density intervals (HPD; in parenthesis) for each variance component other than the residual estimated with the four models considered in the study.

Variance componenta	Model
	M1	M2	M3	M4
σ2PeD	0.052 (0.017 to 0.086)	0.349 (0.302 to 0.395)	0.069 (0.033 to 0.105)	0.196 (0.144 to 0.249)
σ2PeC	—	0.358 (0.319 to 0.396)	—	0.127 (0.085 to 0.169)
σPeD,C	—	−0.351 (−0.387 to −0.315)	—	−0.150 (−0.188 to −0.113)
σ2aD	0.146 (0.111 to 0.181)	0.111 (0.079 to 0.143)	0.410 (0.360 to 0.461)	0.276 (0.222 to 0.329)
σ2aC	—	—	0.361 (0.320 to 0.401)	0.224 (0.178 to 0.27)
σaD,C	—	—	−0.383 (−0.421 to −0.344)	−0.243 (−0.284 to −0.201)

^aσ²_PeD is the random permanent environmental effect, σ²_PeC is the random associative permanent environmental effect due to the interacting conspecifics, σ_PeD,C is the correlation between these two effects, σ²_aD is the random direct additive genetic effect, σ²_aC is the associative genetic component (that is, IGE), σ_aD,C is the correlation between the last two effects.

Genetic trend of breeding values

EBV for direct, associative and total genetic components for fight outcome (0/1) assessed using the most complete model, that is, M4, were plotted to detect the variation over time of the average EBV of individuals born in the same year. The significance of the slope coefficient of regression from zero was tested (regression procedure; SAS Institute, 2009).

Results

Variance components

Table 2 portrays the posterior means and the corresponding 95% HPD intervals for variance components estimated on a liability scale. The permanent environmental variance (σ²_PeD) ranged from 0.052 (M1) to 0.358 (M2), whereas the additive genetic variance (σ²_aD) was always greater than the σ²_PeD, ranging from 0.111 (M2) to 0.410 (M3). When jointly assessed, direct and indirect (that is, associative) variances assumed distinct values, but 95% HPD estimates revealed some degree of overlapping (that is, from a 15% for 95% HPD of σ²_PeD and σ²_PeC in M4 to an 80% of overlapping for σ²_PeD and σ²_PeC in M2). Excluding the permanent environment in M2, all direct variances estimates resulted slightly greater of the corresponding indirect variance (Table 2). Greater values for direct and indirect variances of permanent, environmental and genetic effects were, respectively, achieved in M2 and M3, where they were the only effects for which the indirect component was assessed. Total breeding value (TBV; Bijma et al., 2007a) and total permanent environmental variance (here indicated as TPV), computed as the sum of direct and indirect components plus the double of their covariance, (that is, TBV=σ²_aD+σ²_aC +2σ_aD,C; TPV=σ²_PeD+σ²_PeC+2σ_PeD,C) dramatically decreased to values close to zero in all the cases in which they were calculated (that is, TBV=0.006 in M3 and 0.014 in M4; TPV=0.004 in M2 and 0.022 in M4; data not shown) due to the negative value of the covariance that ranged from −0.150 (σ_PeD,C, M4) to −0.383 (σ_aD,C, M3), suggesting a similar but opposite magnitude of direct and indirect components for fight outcome. The permanent environmental covariance of M2, the genetic covariance of M3 and the sum of permanent environmental and genetic covariance of M4 revealed similar estimates (that is, −0.351, −0.383 and −0.393, respectively), indicating that the global covariance between the direct and indirect effects of fight outcome was almost the same through different models.

Heritability and genetic correlation estimates

Heritability of all the components (Table 3) were measured on a liability scale as in Wilson et al. (2011). When assessed through a classical quantitative model, as in M1, only a direct heritability (h²_D) could be assessed, thus coinciding with the TBV (h²_TOT or τ²) of the trait. Heritability for fight outcome assumed a value of 0.122 in M1, with a 95% HPD ranging from 0.094 to 0.150. In M2, the split of the permanent environmental variance in its direct and indirect components did not cause great variations to direct heritability compared with M1, achieving a value of 0.099 (with a range of 0.073–0.125 for 95% HPD). Conversely, the introduction of IGEs in M3 and M4 led to a great increase of both direct and associative heritability. In these cases, the magnitude of direct heritability was greater than that of the associative heritability (that is, 0.381 and 0.265 of h²_D, in M3 and M4, respectively, vs 0.335 and 0.215 h²_C; Table 3). When only the genetic variance was split in direct and indirect components as in M3, heritability was greater (Table 3). A noteworthy reduction of the TBV to values close to zero was also observed in M3 and M4 (h²_TOT equal to 0.005 in M3 and to 0.014 in M4). This is consistent with the presence of a negative and opposite covariance between direct and indirect components in all the models in which they were assessed (Table 2). As expected, genetic correlations between direct and indirect genetic components were close to −1 (that is, −0.995 and −0.976 for M3 and M4, respectively). Furthermore, Pearson's product-moment correlations estimated between individual direct and indirect breeding values (EBVs) reached an average value of −0.997 in models in which they were assessed (data not shown). Phenotypic correlations ranged from −0.259 to −0.279 when computed (that is, in all models except for M1), and the values they assumed were close to Pearson's product-moment correlations between individual direct EBV and competitor indirect EBV of each analyzed dyadic interaction (average value of −0.278; data not shown).

Table 3. Posterior means and 95% highest posterior density intervals (HPD; in parenthesis) for heritability estimates, genetic and phenotypic correlations obtained with the four models considered in the study and mean correlation between individual EBVs obtained from five sub-dataset samples for each model.

Item	Model
	M1	M2	M3	M4
Heritabilitya
h2D	0.122 (0.094 to 0.150)	0.099 (0.073 to 0.125)	0.381 (0.330 to 0.433)	0.265 (0.214 to 0.317)
h2C	—	—	0.335 (0.297 to 0.737)	0.215 (0.172 to 0.259)
h2TOT	0.122 (0.094 to 0.150)	0.099 (0.073 to 0.125)	0.005 (−0.005 to 0.015)	0.014 (−0.006 to 0.033)
Correlationb
raD,C	—	—	−0.995 (−1.007 to −0.983)	−0.976(−1.018 to −0.938)
rPeD,C	—	−0.259 (−0.279 to −0.239)	−0.276(−0.296 to −0.256)	−0.279 (−0.298 to −0.260)
rEBVc	0.746	0.726	0.847	0.855

^ah²_D is the direct heritability for social dominance (measured as a ratio of direct variance on the total phenotype, as 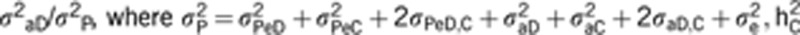is the indirect heritability 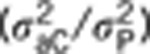, and h²_TOT is the TBV computed as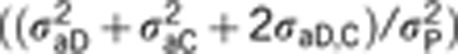

^br_aD,C is the genetic correlation for direct and indirect effects (that is, σ_aD,C/(σ²_aDσ²_aC)^0.5), r_PeD,C is the phenotypic correlation for the same components, calculated as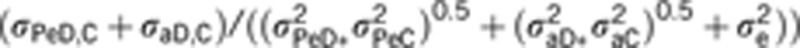

^cr_EBV is the average correlation between direct EBVs estimated from five sub-datasets (that is, 13 610±236 data) obtained after retaining about half of the dataset (that is, 5452±33 cows). ±Correlations were carried out on the EBV of individuals shared by each sub-dataset (that is, 2902±36 cows) and were averaged for each model.

Model comparison

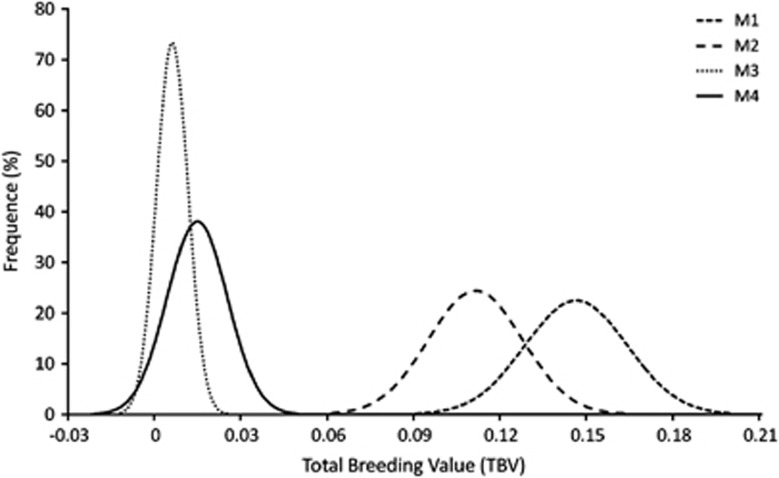
Pearson's product-moment correlations between individual EBVs (that is, direct breeding values for M3 and M4) shared by each one of the pairs of models drawn from the five focused sub-data sets (Table 3) was on average greater in models including IGEs (that is, 0.847 and 0.855 in M3 and M4, respectively; P<0.001) and lower when IGEs were not accounted for (0.746 and 0.726 in M1 and M2, respectively; P<0.001). The most complete model, including both indirect permanent environmental and genetic variances (that is, M4), therefore revealed the greatest predictive ability. This was also confirmed by plotting the estimated posterior density of TBV (Figure 1), in which a flatter distribution for TBV was observed when M1 and M2 where applied, that is, not accounting for IGEs. The thinnest distribution with values dispersed around a mean of zero was observed in M3 (Figure 1), that is, excluding the indirect permanent environmental variance. On the other hand, M4 showed a distribution around a zero mean, but slightly flatter than in M3. This could be probably due to the shift of part of indirect variance to the permanent environmental component, reducing the magnitude of the genetic variance partitioning.

Figure 1.

Posterior density for the estimated TBV computed for each of the four models (M1, M2, M3 and M4; details on models are provided within the text).

Genetic trends

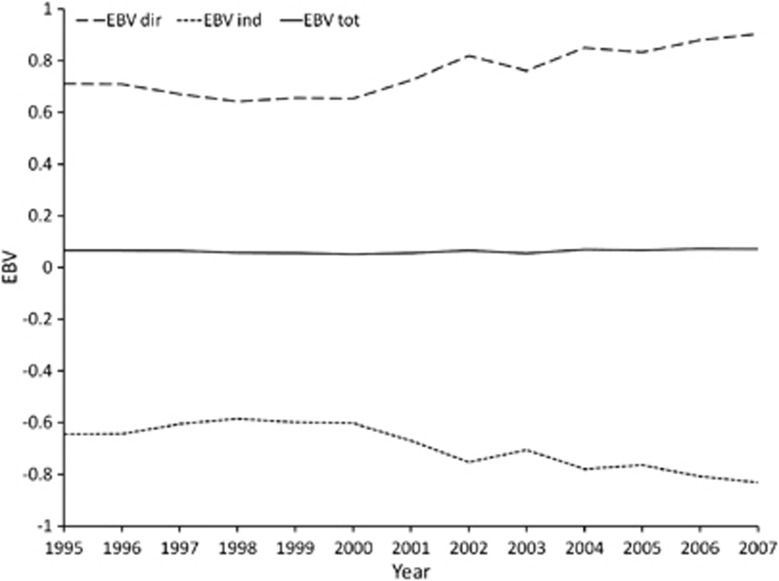
The variation of direct (EBV_dir), indirect (EBV_ind) and total (EBV_tot) breeding values of individuals born in a period of 12 years (from 1995 to 2007) and estimated through M4 is depicted in Figure 2. As the graph reveals, EBV_tot did not vary over time (the slope of the regression line assumed a value of 0.001, not statistically different from zero), consistently with the theoretical assumption that because each winner implies a loser, the average trait (that is, the fighting outcome) within a population cannot evolve (Wilson et al., 2011). Interestingly, despite the flat individual TBV over years, both direct and indirect components showed a slight but existing variation over time, with a slope of the regression line equal to 0.020 (P<0.001) for EBV_dir and −0.019 (P<0.001) for EBV_ind, respectively. Such a trend indicated that an empirical but existing positive selection for cows' fighting ability may have led to an increase in the ‘capability at winning' and to a correspondent increase in the ‘inability at losing'.

Figure 2.

Genetic trend of direct (EBV_dir), indirect (EBV_ind) and total (EBV_tot) breeding values of individuals born in a period of 12 years (from 1995 to 2007) and estimated through Model 4.

Discussion

A number of controversies and debates have characterized ‘social dominance' over the years. A strong debate occurred between the 80s and the 90s of the last century as regards the possibility that social dominance may be inherited. Barrette (1987) asserted that dominance cannot be inherited because it is not an individual trait but it is shared; moving from this statement a series of replies arose either to contradict (that is, Barrette; 1993) or to support it (that is, Capitanio, 1991; Moore, 1991). Some tools to resolve the controversy were offered by Drews (1993) who, after collecting different definitions and meanings of social dominance (that is, reproductive status, privileged role, priority in accessing resources, winning an agonistic contest), provided a synthesis defining social dominance as ‘an attribute of the pattern of repeated, agonistic interactions between two individuals, characterized by a consistent outcome in favour of the same dyad member and a default yielding response of its opponent rather than escalation. The status of the consistent winner is dominant and that of the loser subordinate'. Even though he provided a good key to talk about social dominance, Drews work did not, however, clarify if social dominance may evolve, and in which way. Some answers were given years later, when the new issues of ‘interacting phenotypes' and ‘IGEs' offered a number of good tools to approach social behaviour concerns, such as the question of social dominance (Moore et al., 1997; Moore et al., 2002; Wolf, 2003; Bijma et al., 2007a). Interacting phenotypes occur when social partners are both focal individual (that is, target of selection) and environment (that is, selective force) at the same time (Moore et al., 1997), and are therefore constituted by a sum of direct components (both genetic and permanent environmental) of the focal individual and indirect components (genetic, that is, IGEs, and permanent environmental as well) provided by conspecifics (Moore et al., 1997; Bijma et al., 2007a). The magnitude of the interaction between direct (D) and indirect (C) parts is quantified by estimators like the path coefficient ψ_D,C (Moore et al., 1997), the covariance direct-indirect genetic coefficient σ_aD,C (Bijma et al., 2007a), as σ_aD,C=ψ_DC σ²_aD (McGlothlin and Brodie, 2009); and the genetic correlation coefficient r_aD,C (that is, σ_aD,C/((σ²_aD*σ²_aD)^0.5), ranging from −1 to 1. Direct and indirect genetic components, as well as their covariance, represent the heritable quote of the trait variance (σ²_TBV; Bijma et al., 2007a) or total heritability of the trait or τ² (Bijma, 2010). Such assumptions make it possible to quantify the heritability of a trait dependent on the contribution of more than one individual. An estimation of heritability that accounts for the incidence of IGEs has been already assessed for social behaviours like chemical display (Drosophila melanogaster; Kent et al., 2008), and ant predator response (Poecilia reticulata; Bleakley and Brodie, 2009), as well as for other traits related to social behaviours (for example, survival, Ellen et al., 2007; and growth rate, Arango et al., 2005; Van Vleck et al., 2007). Concerning the focus of our study, social dominance is not only a trait that is influenced by the social environment, but it can exist only if there is a social environment (Moore et al., 2002). Interacting partners represent an absolute constraint for the manifestation of social dominance in the focal individual: a submissive or a dominant posture in the opponent leads to the expression of, respectively, a dominant or submissive posture in the focal individual, and vice versa (Moore et al., 1997; Moore et al., 2002). Moreover, the outcome of a hierarchical interaction is necessarily constituted by both the win of an individual (for example, the focal) and the defeat of the other (for example, the opponent). One of these two aspects, such as dominance/submissive postures, cannot exist without the other. Therefore, the magnitude of interaction coefficients, such as ψ_D,C or r_aD,C, must be maximum, and due to the opposite condition of the two individuals (that is, dominant vs subordinate; winner vs loser), it has to assume a negative sign. The genetic correlation of direct and indirect components of social dominance is, therefore, expected to be equal to −1, the greatest value that an evolutionary constraint may assume. Genetic correlations between direct and indirect effects we discovered for fighting outcome in cows offer empirical evidence for such an assumption, showing values very close to predicted (r_aD,C ranging from −0.995 to −0.976). Similar results were also found out by Wilson et al. (2011) for social dominance outcomes in red deer (Cervus elaphus), where r_aD,C reached a value of −0.913, and a similarly phenotypic correlation was assessed (r_PeD,C=−1.080). Conversely, phenotypic correlations we estimated were lower (that is, an average r_PeD,C of −0.271), but this could be attributable to the fact that individuals had more than one observation (that is, 2.3 on average), sometimes ending up as winners and other times as losers. At present, literature on this topic is very recent (for example, Bijma, 2011) and lacking in examples, and this is also because it is difficult to build up data sets with a feasible number of interactions. However, genetic correlations between direct and indirect components of traits related to social dominance assuming negative values were also obtained in deer mice (Peromyscus maniculatus) by Wilson et al. (2009), that reported a r_aD,C of −0.300 for the approach rate and a r_aD,C of −0.853 for mounting rate.

Furthermore, a genetic correlation of −1 implies that direct and indirect variances exhibit about the same magnitude and are opposite in sign with the related covariances (as demonstrated by Wilson et al., 2011). Thus, total variance (σ²_TBV), arising from the sum of the other components, as well as the total heritability τ² of the trait, is expected to be null. The σ²_TBV and τ² we estimated for fighting outcome confirmed this theory, assuming values close to zero. Similar values were also reported by Wilson et al. (2009, 2011), and provide a key to explaining how social dominance may be heritable and not evolve under positive selection (that is, focusing on a population, for each win (1) necessary corresponds a defeat (0) and vice versa, and the average phenotype is equal to 0.5). As already observed in Wilson et al. (2011), a ‘perfect negative correlation' between direct genetic components and IGEs produces a whole constraint on both the members in the pairs of opposite traits constituting social dominance, as the win/defeat rates or the occurrence of dominant/submissive postures. In spite of an absolute evolutionary constraint on the mean phenotype, a change and evolution of each trait constituting dominance is possible. If a positive selection for social dominance occurs, in the course of subsequent generations focal individuals will become increasingly ‘good at winning', and consequently increasingly ‘bad at losing'. A sort of ‘treadmill competition' (Wolf, 2003) has to take place, where each positive change of a trait is corresponded by a feedback in the antagonistic trait, and so the overall phenotype does not evolve. An empirical demonstration of such an assumption is difficult because of a number of generations and individuals under study are required (Wilson et al., 2011). First evidence of this was provided by Moore et al., 2002, who created lines of cockroaches (Nauphoeta cinerea) that were either highly selected or not for social status. However, an experimental manipulation was required, and observing the natural evolution of a population under positive selection for social dominance has not been possible till now. Traditional agonistic competitions of fighting cows in the North-West Alps provide a good subject for studies concerning social dominance and its evolution over time. Despite the lack of a planned selection for good fighters able to acquire higher social status and thus to win traditional competitions, an empirical selection for fighting ability (that is, the capability of winning a contest) has been carried out over the years, also due to a low but existing level of heritability for the trait (Mantovani et al., 2007; Sartori and Mantovani, 2010, 2012). Therefore, also the traits ‘good at winning' (another way of expressing fighting ability) and ‘bad at losing', that is, the two faces of social dominance, are expected to vary over time. A long term data set of 11 years of agonistic performance recordings (from 2001 to 2011) allowed us to provide the first evidence (that is, without laboratory manipulation) of a social dominance evolutionary pattern within a population under positive selection for the trait. Genetic trends for fighting outcome EBVs measured on individuals born in 12 subsequent years revealed that although the TBV (EBV_tot) did not vary over time as expected, both direct (EBV_dir) and indirect (EBV_ind) breeding values showed a slight but existing variation. Moreover, the equal and opposite coefficient of the regression line (0.020 and −0.019 for EBV_dir and EBV_ind, respectively) revealed that the same selective force produced an effect equal in magnitude but opposite in pairs of traits constituting social dominance, where an absolute negative evolutionary constraint is realized. Therefore, it is possible to observe that data on fighting cows pointed to a clear answer to the long-debated question about social dominance inheritance.

In addition, other than providing feasible explanations for issues concerning evolutionary theory, such as social dominance inheritance (for example, see Bijma, 2011), models including IGEs revealed a greater predictive ability in this study. Moreover, both 95% HPD and the posterior density distributions of the variance components estimated via Bayesian inference showed smaller ranges in the model accounting for IGEs than the classical quantitative model. However, accounting for the indirect genetic variance and not for an indirect permanent environment, results unfeasible when repeated individual measurements are considered. Therefore, the best model for evaluating social dominance, as well as other traits occurring in a social framework (Moore et al., 2002, Wolf, 2003; Bijma, 2010) should include the indirect variance components.

Such an approach has shown to be useful also in genetic investigations for social behaviours such as courtship (Miller and Moore, 2007), cooperation (Charmantier et al., 2007) and predator avoidance (Bleakley and Brodie, 2009). Moreover, in recent years animal breeding practices have also shown appreciable benefits when social components have been accounted for, especially in managing social species reared in the groups of conspecifics, such as hens or pigs (Bijma et al., 2007b; Van Vleck et al., 2007; Chen et al., 2008). All these studies have provided important evolutionary explanations for social dynamics when accounting for IGEs, thereby expanding the first dissertations on heritability estimates and evolutionary changes in the interacting phenotypes, as well as providing a sound approach in many theoretical and operative questions.

Conclusions

IGEs assessed on data from fighting cows allowed us to estimate direct and indirect variance components plus their correlation for social dominance, and to investigate the impact of selection on social dominance. Direct and indirect genetic components for social dominance revealed a negative correlation close to −1 as expected, realizing an absolute evolutionary constraint that does not allow a mean phenotype of social dominance to evolve. Total heritable variation for the trait was close to zero as expected, and direct and indirect variance components were similar in magnitude and opposite in sign covariance. Genetic trends carried out on EBVs for individuals born in 12 subsequent years revealed that, despite individual TBVs being kept constant over the years, direct and indirect breeding values changed. Particularly, they exhibit a slow but significant variation over time, equal in magnitude and opposite in sign. Therefore, according to this study, the question surrounding the possibility of ‘an inheritance for social dominance' has found a response under the approach of IGEs.

Data archiving

Data have been deposited at Dryad doi: 10.5061/dryad.pq742.

The authors declare no conflict of interest.