Inbreeding depression in self-incompatible North-American Arabidopsis lyrata: disentangling genomic and S-locus-specific genetic load

Abstract

Newly formed selfing lineages may express recessive genetic load and suffer inbreeding depression. This can have a genome-wide genetic basis, or be due to loci linked to genes under balancing selection. Understanding the genetic architecture of inbreeding depression is important in the context of the maintenance of self-incompatibility and understanding the evolutionary dynamics of S-alleles. We addressed this using North-American subspecies of Arabidopsis lyrata. This species is normally self-incompatible and outcrossing, but some populations have undergone a transition to selfing. The goals of this study were to: (1) quantify the strength of inbreeding depression in North-American populations of A. lyrata; and (2) disentangle the relative contribution of S-linked genetic load compared with overall inbreeding depression. We enforced selfing in self-incompatible plants with known S-locus genotype by treatment with CO₂, and compared the performance of selfed vs outcrossed progeny. We found significant inbreeding depression for germination rate (δ=0.33), survival rate to 4 weeks (δ=0.45) and early growth (δ=0.07), but not for flowering rate. For two out of four S-alleles in our design, we detected significant S-linked load reflected by an under-representation of S-locus homozygotes in selfed progeny. The presence or absence of S-linked load could not be explained by the dominance level of S-alleles. Instead, the random nature of the mutation process may explain differences in the recessive deleterious load among lineages.

Introduction

Although many plants and animals are capable of self-fertilisation (selfing), cross-fertilisation (outcrossing) is generally considered to be favored in the long term. Cross-fertilisation facilitates effective genomic recombination and hence provides a means to produce variable progeny and to break up linkage disequilibrium (Barton and Charlesworth, 1998). Despite the long-term benefits of outcrossing and abundance of mechanisms to promote it (Jarne and Charlesworth, 1993; Barrett, 2002), transitions from outcrossing to selfing are frequent across the plant kingdom (Barrett, 2002).

The transition to selfing can be explained by the associated short-term benefits. Selfers can reproduce even in scenarios where mates or pollinators are scarce (reproductive assurance). Moreover, selfers have an inherent transmission advantage over outcrossers. The short-term advantages of selfing can be offset by direct costs due to inbreeding depression, that is, the reduced fitness of selfed or inbred progeny compared with outcrossed progeny (Charlesworth and Charlesworth, 1987). It has been suggested that inbreeding depression due to expression of recessive mutational load forms an important barrier to the evolution of selfing in outcrossing species (Kondrashov, 1985; Lande and Schemske, 1985; Porcher and Lande, 2005).

Such mutational load can be caused by a genome-wide low frequency of recessive deleterious mutations (Charlesworth and Willis, 2009), but also by deleterious mutations linked to loci under balancing selection (Uyenoyama, 2005). The S-locus in plants is a classic example of such a locus. It confers self-incompatibility and generally consists of two tightly linked genes encoding a female and a male specificity, respectively. If these specificities match (for example, in the case of self-pollination), the pollen is rejected and cannot fertilise the ovule (reviewed by Charlesworth et al., 2005). The S-locus is under balancing selection with rare allele advantage (negative-frequency-dependent selection), which leads to high heterozygosity. Furthermore, recombination is suppressed in the S-locus region, as it would cause the male and female specificity to break up (reviewed in Charlesworth et al., 2005). The high heterozygosity due to balancing selection therefore extends to the genes surrounding the S-locus (Awadalla and Charlesworth, 1999; Kamau et al., 2007; Ruggiero et al., 2008), which likely helps to mask recessive deleterious mutations. Hence, genomic regions with alleles under balancing selection (for example, the S-locus or major histocompatibility complex) are expected to accumulate deleterious mutations (Uyenoyama, 2005; van Oosterhout, 2009).

Deleterious load linked to S-loci can be disentangled from genome wide load by generating S-locus homozygotes, for example by enforcing self-fertilisation of plants with known S-genotype. The resulting progeny are inbred across the whole genome and should suffer inbreeding depression due to increased homozygosity in general. A reduced performance of S-locus homozygotes relative to S-locus heterozygotes would then indicate specific S-linked load. Such load has been suggested to have a significant role in preventing breakdown of self-incompatibility (Porcher and Lande, 2005). In addition, S-linked load may have a role in shaping S-allele genealogies and have an effect on the frequency distribution of S-alleles in natural populations. Numerous studies have documented the existence of a mutational load in species with a genetic self-incompatibility system (for example, Stone, 2004; Busch, 2005; Glemin et al., 2006). However, only few studies have attempted to disentangle the S-linked genetic load from the background genomic load.

In systems with gametophytic self-incompatibility all individuals are heterozygous at the S-locus because pollen grains express their own haploid genotype. This means that any recessive load linked to the S-locus will always be masked. In contrast, in systems with sporophytic self-incompatibility, there is the potential for homozygotes to be formed. This is because the specificity of both pollen and stigma are determined by the diploid parental tissues and dominance interactions determine which alleles are expressed; recessive alleles could thus be present in homozygous form (for example, Prigoda et al., 2005; Llaurens et al., 2009a and references therein). There thus could be the potential for recessive alleles to purge their mutational load and so the purging history of particular alleles could depend on their position in the dominance hierarchy (Billiard et al., 2007; Llaurens et al., 2009b). However, few homozygotes have been observed in natural outcrossing populations, even for the single most recessive allele that has been found worldwide (S₁: Mable et al., 2003, 2005).

Genetic load linked to particular S-alleles in a gametophytic system was revealed in Solanum carolinense by increased frequency of aborted seeds after selfing and crossing of incompatible unrelated plants (Stone, 2004). In addition, S-locus homozygotes were under-represented in the viable progeny. A similar study in the same species found the opposite—that S-locus homozygotes were over-represented in selfed progeny—but revealed that homozygotes had reduced fitness in terms of growth (Mena-Ali et al., 2009). Both studies suggested that different S-alleles were associated with a different genetic load, depending on the evolutionary time for mutations to accumulate, or due to different purging histories.

In systems with sporophytic self-incompatibility characteristic of the Brassicaceae, genes coding for SI specificity in pollen (SCR: for S-locus cysteine rich) and pistils (SRK: for S-locus receptor kinase) are organised into self-recognition haplotypes, thought to be maintained intact due to rare or no recombination (Awadalla and Charlesworth, 1999). The effect of dominance on recessive mutational load has been considered in highly outcrossing populations after enforced selfing of self-incompatible individuals of Arabidopsis halleri (Llaurens et al., 2009b), which is a highly outcrossing species. Only the most dominant out of four S-haplotypes was associated with a significant S-linked genetic load. In progeny of crosses with the European subspecies A. lyrata (subsp. petraea), the most recessive S-haplotype had a transmission advantage over more dominant ones, which was attributed to selection at the gametic stage (Bechsgaard et al., 2004). An earlier study had found that forced self-pollinations led to considerable inbreeding depression (Karkkainen et al., 1999), suggesting that mutational load and potentially also segregation load helps to maintain SI and outcrossing in European A. lyrata.

The North-American subspecies of A. lyrata (subsp. lyrata) provides an excellent model to address the role of inbreeding depression in the evolution and maintenance of mating systems in plants with a sporophytic self-incompatibility system. It is outcrossing and self-incompatible throughout most of its range. However, there are natural populations in the Great Lakes region in which individuals occur that have become self-compatible (Mable et al., 2005; Mable and Adam, 2007). In some populations this breakdown of self-incompatibility has led to a complete transition to predominant inbreeding. This forms an interesting contrast with the European subspecies of A. lyrata (subsp. petraea), where a breakdown of self-incompatibility has not been documented. One would predict that this pattern could be associated with reduced inbreeding depression in North-American A. lyrata, either because an inherently lower genetic load may have facilitated the evolution of selfing, or as a consequence of purging following a period of inbreeding; two scenarios that are not mutually exclusive.

The first goal of this study was to assess inbreeding depression in a focal population of the North-American subspecies. To this end, we enforced selfing in normally self-incompatible plants with known S-locus genotype, and compared the performance (germination rates and growth) of selfed vs outcrossed progeny. Our second and main goal was to assess whether inbreeding depression could be partly attributed to deleterious mutations linked to the S-locus. For this purpose, we genotyped the selfed progeny based on parental S-locus genotypes and tested whether segregation of S-alleles in the selfed progeny deviated from Mendelian expectations (that is, if homozygotes were under-represented), and whether selfed progeny homozygous for the S-locus had reduced growth relative to heterozygotes. A third goal was to compare the relative effects of selfing and biparental inbreeding. For this, in addition to the enforced selfing, we crossed full siblings that despite their relatedness were cross-compatible due to their particular S-locus genotypes, and compared levels of inbreeding depression. According to theoretical expectations, biparental inbreeding through crosses between full siblings should result in inbreeding depression half of that of selfed progeny. Our findings improve our limited understanding of the causes and consequences of genetic load linked to S-loci.

Materials and methods

Plant material

In spring 2008, plants were raised in the greenhouse of the University of Amsterdam from seed batches collected in the summer of 2007. Seeds originated from two North-American populations of A. lyrata that have been described previously (Mable et al., 2005; Mable and Adam, 2007; Foxe et al., 2010): Pinery Provincial Park on Lake Huron (PIN: outcrossing (T_m=0.84), with self-incompatible individuals predominating) and Rondeau Provincial Park on Lake Erie (RON: inbreeding (T_m=0.28), with self-compatible individuals predominating). Reciprocal crosses were performed between three independent pairs of plants of which the S-locus genotype had been at least partly determined previously (see supporting information for details). This yielded three cohorts of F1 cross-progeny from three different parental backgrounds (PB), for some of which the S-locus genotype could be fully resolved based on the parental alleles (see supporting information). Two cohorts were derived from reciprocal crosses between self-incompatible plants from the PIN population (PB1: PIN 4-2 (S₁S_?) × PIN 16-2 (S₁S₃₉); PB2: PIN 12-3 (S_?S₂₃) × PIN 17-3 (S₃S₄₅)), while the third cohort was derived from a cross between a self-incompatible plant from the PIN population and a self-compatible plant from the RON population (PB3: PIN 12-3 (S_?S₂₃) × RON 19-3 (S₁S₁)). Besides analysis of S-linked load, the main purpose of the cross underlying PB3 was to allow assessment of biparental inbreeding depression relative to uniparental inbreeding depression due to selfing. It is expected that biparentally inbred progeny from full-sib matings should suffer inbreeding depression by half that of selfed progeny (Uyenoyama, 1986; Charlesworth and Charlesworth, 1987), but this has rarely been tested empirically. In a system with dominance, cross-compatible siblings can be generated by crossing a homozygote for the most recessive allele (S₁) with a plant that does not carry this allele. Therefore, we crossed the plant with the S_?S₂₃ S-genotype with an S₁S₁ homozygous parent from a selfing population (S₁S₁ homozygotes are rare in outcrossing populations).The resulting F1 progeny with S₁S_? and S₁S₂₃ are cross-compatible and hence allowed us to evaluate biparental inbreeding depression after full sib crossing.

Up to 10 F1 progeny per PB were raised in the greenhouse of the University of Glasgow and tested for self-incompatibility; all were found to be self-incompatible (no seed set after at least six manual self-pollinations performed on at least three different days). Thus, for PB3, even though one of the parents was self-compatible, F1 individuals were all self-incompatible.

Selection of F1 progeny for enforced self-pollination

Within each of the three parental backgrounds, we selected F1 progeny for which the S-locus genotype had been resolved (see supporting information), and generated enforced selfed progeny (Figure 1). In PB1, we selected three F1 plants with S-locus genotype S₁S₃₉ (two derived from the cross ♀ PIN 16-2 (S₁S₃₉) × ♂ PIN 4-2 (S₁S_?); one from the reciprocal cross). In PB2, we selected four F1 plants with genotype S₃S₂₃ (two from the cross between ♀ PIN 12-3 (S_?S₂₃) × ♂ PIN 17-3 (S₃S₄₅); two from the reciprocal cross). In PB3, we selected four F1 plants with genotype S₁S_? and four F1 plants with S₁S₂₃ (four from the cross between ♀ PIN 12-3 (S_?S₂₃) × ♂ RON 19-3 (S₁S₁), four from the reciprocal cross).

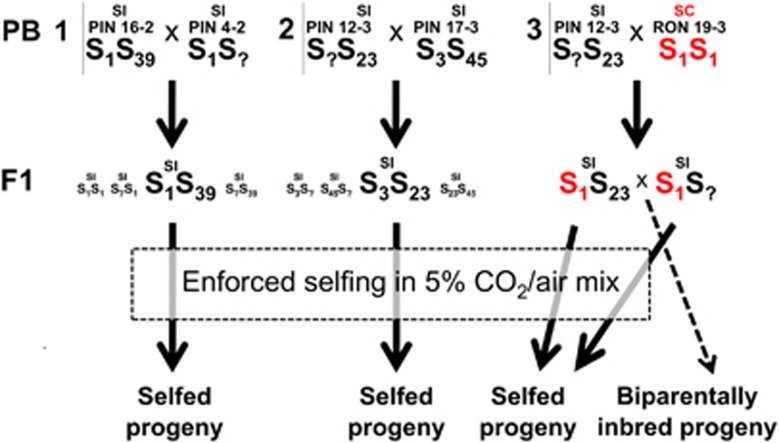
Figure 1.

Experimental design for generating outcross control seeds, selfed seeds and biparentally inbred seeds. Three crosses were performed between unrelated plants that were fully or partly genotyped for the S-locus to generate F1 cross-progeny with three different parental PB. In PB1 and PB2, the cross involved self-incompatible (SI) plants from the outcrossing population from Pinery Provincial Park (PIN). In PB3, a SI plant from PIN was crossed with a self-compatible (SC) plant from the inbreeding population from Rondeau Provincial Park (RON). A subset of the resulting F1 seeds were germinated and genotyped at SRK, which is the gene controlling female specificity (expected S-locus genotypes in the F1 are indicated), the remainder were kept to serve as control outcrossed seeds. F1 that could be unambiguously genotyped for the S-locus (larger font) were manually selfed in a CO₂-rich environment. In addition, in PB3 crosses were performed between two compatible F1-sibling SRK genotypes (S₁S₂₃ × S₁S_?) to generate biparentally inbred progeny. In PB3, the S₁ haplotype derived from the inbred parent is indicated in red. A full color version of this figure is available at the Heredity journal online.

Enforced selfing was done by manually self-pollinating young flowers (that is, <2 days since opening) and placing whole plants in a metal container with a transparent rubber-sealed lid. After closing the container, a 5% CO₂–air mixture was pumped into the container from a pressurised gas cylinder connected to it. This treatment compromises the self-incompatibility response in Brassicaceae (Nakanishi et al., 1969) and results in at least partial seed set in self-incompatible A. lyrata (Hoebe, 2009). Plants were left for 6–12 h in this CO₂ rich environment, after which they were placed back on open benches in the greenhouse. Depending on flower availability, 7–32 flowers were enforced self-pollinated per plant, which resulted in 12–142 seeds per plant. Selfed seeds derived from plants with the same parental background (that is, full siblings) and the same S-locus genotype were pooled to obtain the required numbers for evaluation of inbreeding depression.

Experimental design

For each of the three parental backgrounds, F1 cross-progeny (that is, seeds) were used as outcrossed control seeds (that is, these were full siblings of the plants that we used before to generate enforced selfed progeny). The maternal environment of these cross-progeny was not CO₂ enriched, as a previous study found that this can give problems due to inadvertent self-fertilisation. The same study also found no differences when comparing selfed progeny of a self-compatible plant generated in CO₂ enriched vs ambient conditions (Hoebe, 2009). For both PB1 and PB2, we planted 112 enforced selfed seeds (56 seeds derived from self-pollination of progeny resulting from the cross in one direction, and 56 seeds from the reciprocal cross) and 48 control seeds. Selfed and outcrossed control seeds were equally divided over eight 40-cell trays (four for PB1, four for PB2), so that each tray contained 28 selfed seeds and 12 control outcrossed seeds. Within PB3, enforced selfed seeds were divided in two subsets: one for the selfed progeny derived from the F1 plants with S-locus genotype S₁S₂₃ and one for those derived from the F1 plants with S₁S_?, as we had hoped we would be able to identify this unknown S_?-allele later. For each subset within PB3, we planted 96 enforced selfed seeds, 24 control seeds and 40 biparentally inbred seeds, divided over eight 40-cell trays (four for each subset), such that each tray contained 24 selfed seeds, 6 control outcrossed seeds and 10 biparentally inbred seeds. Positions were randomized within all 16 trays of the experiment. Seeds were sown in Levington S2+Sand mix (Scotts Professional, Ipswich, UK) on the 10 July 2009, and trays were placed in climate controlled incubators (16 h light at 20 °C: 8 h dark at 16 °C, with 80% relative humidity).

Measurements of life history traits

We monitored germination every Monday, Wednesday and Friday, and recorded the germination date in order to calculate time to germination for each plant, and to facilitate exact timing of later measurements. Plants that were chlorotic or did not develop true leaves after germination were recorded as such, and removed for DNA extraction. Two weeks after germination, we counted the number of leaves (cotyledons were counted as leaves for this purpose), and identified the three largest leaves. Using digital calipers, we then measured length and width of the blade of these three leaves. Leaf blade length was measured from the tip of the leaf to the point where the blade width was <1 mm on either side of the petiole. Leaf width was measured at the widest part of the leaf, perpendicular to the main leaf axis. In order to obtain a single non-quadratic estimate of the total leaf surface area of the three largest leaves, we took the square root of the products of length and width for each of the three measured leaves, and summed them. Four weeks after germination, we recorded whether plants had survived or not. For surviving plants, we repeated the measurements. Finally, we monitored plants regularly throughout the following year and for each surviving plant recorded whether it produced flowers or not. From these measurements and observations, we calculated the relative growth rate (RGR) in terms of increase in leaf number as: ln(leaf number_4weeks)−ln(leaf number_2weeks) and in terms of increase in leaf surface as ln(leaf surface_4weeks)−ln(leaf surface_2weeks). We also calculated germination rate (number of emerged seedlings/number of seeds sown), juvenile survival rate to 4 weeks (number of survived plants/number of seeds sown), and flowering rate (number of plants that flowered/number of plants surviving to 4 weeks).

DNA extraction and S-locus genotyping of selfed plants

After the second measurements (that is, 4 weeks after germination), tissue was collected from each of the experimental plants (enforced selfed progeny and F1 cross-progeny used as controls). Tissue was sent on ice to the John Innes Centre genome lab in Norwich for DNA extraction with the DNeasy96 Plant Kit (Qiagen Ltd, Crawley, UK). To genotype the S-locus of the selfed progeny, we used PCR with a general reverse primer (SLGR) and allele-specific forward primers (Supplementary Table S1) for the alleles identified in the F1 plants used to generate selfed seeds (Figure 1). Reactions of 10 μl contained 2.5 mℳ MgCl₂ (Invitrogen, Paisley, UK), 1 × PCR Buffer (Invitrogen), 0.2 mℳ dNTP (Invitrogen), 0.1 μℳ of allele-specific forward primer, 0.1 μℳ of general reverse primer (SLGR), 0.5 units of Taq polymerase (Invitrogen) and 0.5 μl of DNA template (∼50 ng/μl). PCR conditions were as follows: an initial cycle of denaturation at 94 °C for 3 min, annealing at 50 °C for 1 min, extension at 72 °C for 2 min, followed by 34 cycles of 94 °C for 30 s, 50 °C for 30 s, 72 °C for 2 min and a final elongation at 72 °C for 6 min. Genotypes were inferred based on electrophoresis on 2% agarose gels stained with ethidium bromide and a 100 bp size standard (Promega, Southampton, UK), evaluating presence or absence of a PCR product of the appropriate size. S-locus genotyping was performed at least twice by different persons and using different batches of chemicals.

Verification of pollen-contamination using microsatellites

Supposedly selfed seeds from the enforced selfings could actually have resulted from inadvertent cross-pollinations with pollen from other plants in the greenhouse. We genotyped seed parents and their progeny for microsatellites (PCR procedures outlined in Hoebe et al., 2009), and excluded progeny with unexpected alleles from further analyses: 12 selfed plants (11%) were excluded in PB1; none were excluded in PB2 (0%); and 6 selfed (7%) and 9 biparentally inbred plants (11%) were excluded in PB3.

Estimation and statistical analysis of genomic inbreeding depression

We calculated inbreeding depression (δ) as the relative reduction in fitness of selfed vs outbred progeny according to the formula δ=1− ω_selfed/ω_outcrossed, in which ω represents the fitness trait value under consideration. For traits where higher trait values are associated with decreased fitness (for example, time to germination), we used the formula δ=ω_selfed/ω_outcrossed−1. As F1 seeds retained for estimating ω_outcrossed in PB3 resulted from a cross between parents from different populations (inbreeding RON and outcrossing PIN), there is a potential issue of heterosis inflating the ω_outcrossed estimate, causing overestimation of overall genomic inbreeding depression. Therefore, although we chose two genetically similar populations (Foxe et al., 2010) our estimate of genomic inbreeding depression should be interpreted with care for PB3. However, the estimation of S-linked genetic load (see next paragraph) is not affected by these complications, as it was assessed within selfed families. In PB3 we also calculated inbreeding depression for biparentally inbred seeds, according to the same formulas (replacing ω_selfed with ω_{biparentally inbred}). We used Fisher's one-tailed exact tests (SPSS version 17.0, Statsoft Inc., Tulsa, OK, USA) to test whether germination rate, survival to 4 weeks of age and flowering rate were significantly reduced in selfed compared with outcrossed control seeds. In addition, in the plants derived from PB3, we tested whether biparentally inbred seeds performed worse than control seeds and whether selfed seeds performed worse than biparentally inbred seeds. We used analysis of variance (ANOVA) models to test the effect of pollination treatment (fixed effect: selfed, biparentally inbred, outcrossed) and parental background (fixed effect: PB1, PB2, PB3), and their interaction on time to germination, relative growth rate of leaf surface from 2 to 4 weeks of age, and increase in leaf number over the same time period.

Estimation and statistical analysis of S-linked genetic load in selfed progeny

In order to assess whether there was evidence of selection against individuals homozygous for particular S-alleles, we used an exact multinomial tests (SISA Exact Multinomial Test v2.2, available online from http://www.quantitativeskills.com/sisa/index.htm) to evaluate whether segregation of SRK alleles differed significantly from Mendelian expectations in each of the three selfed families (derived from S₁S₃₉ in PB1, from S₃S₂₃ in PB2 and from S₁S₂₃ in PB3). In addition, we compared the distribution of S-locus genotypes between germinated plants that did and did not survive the first 4 weeks (Fisher's exact test as implemented in SPSS 17.0 for Windows).

We also assessed if S-locus homozygotes performed worse in terms of juvenile growth (leaf formation and leaf increase from 2 to 4 weeks, both relative to control), by using one-way ANOVA models with S-locus genotype as a fixed effect (homozygous for first allele; heterozygous; homozygous for second allele). We used trait values of the selfed progeny scaled to that of the control outcross progeny in the same parental background (that is, we divided the trait values by the mean of the control) to facilitate comparisons between the parental backgrounds. Then we calculated inbreeding depression for growth attributable to each specific S-allele as δ_Sx-linked=1−(MeanRGR_SxSx)/(MeanRGR_SxSy), and performed power analyses to assess whether sample sizes in our experiment would have been sufficient to detect mild levels of such S-linked depression. We first calculated effect sizes (f) given the observed variance (MS_error) for given levels of S-linked inbreeding depression ranging from δ_S-linked=0.05–0.35 (that is, 5–35% fitness reduction of S-locus homozygotes relative to heterozygotes) within each parental background: 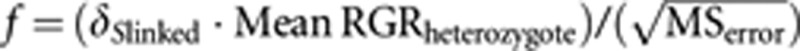. Then we used the software GPower (version 3.1.2;Faul et al., 2007) to calculate the minimum sample size needed to detect the given effect sizes with at least 80% power at a 5% rejection level (that is, β>0.80; α<0.05).

Results

Inbreeding depression for early life history traits

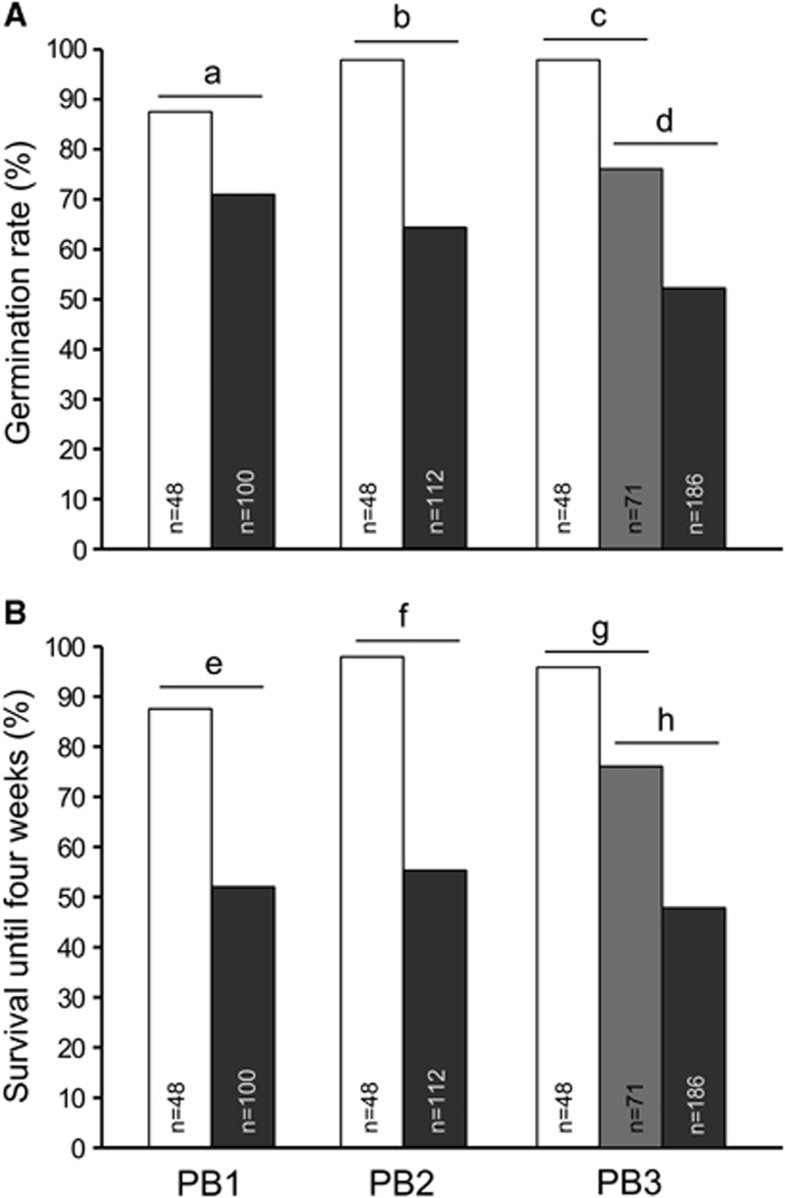
There was significant uniparental inbreeding depression for germination rate (number of emerged seedlings/number of seeds sown) at levels of δ_selfed=0.20, 0.33 and 0.47 for PB1, PB2 and PB3, respectively (Figure 2). Biparental inbreeding depression (only assessed in PB3) was also significant (δ_{biparentally inbred}=0.22) but significantly less than uniparental inbreeding depression (δ_selfed=0.47) (Figure 2).

Figure 2.

Early inbreeding depression for (A) germination rate (%) and (B) survival until 4 weeks (%). For each of three parental backgrounds (PB1–PB3), control outcrossed progeny (white bars) were compared with selfed progeny (dark grey bars), and for PB3 also to biparentally inbred progeny (light grey bars). Sample sizes (n) are indicated within each bar. Significance of differences among seed classes was assessed by one-sided Fisher's exact tests (letters a–h identify individual comparisons). All comparisons showed significant differences, with the following exact P-values: P_a=2.0 × 10⁻²; P_b=2.0 × 10⁻⁶; P_c=5.7 × 10⁻⁴; P_d=1.2 × 10⁻³; P_e=1.3 × 10⁻⁵; P_f=4.8 × 10⁻⁹; P_g=2.7 × 10⁻³; P_h=3.3 × 10⁻⁴.

Some of the seedlings carried clearly lethal malformations (mainly chlorotic colouring). Such malformations were most common in the selfed progeny of PB1 (18 out of 112 seedlings), less so in PB2 (6 out of 120 seedlings), and absent in PB3. As chlorotic seedlings do not survive the first weeks, the proportion of sowed seeds that germinated and survived to 4 weeks of age may more accurately reflect seedling establishment than germination rate alone. There was significant inbreeding depression for survival to 4 weeks (number of surviving plants/number of seeds sown) at levels of δ_selfed=0.42, 0.44 and 0.48, for PB1, PB2 and PB3, respectively. Biparental inbreeding depression in PB3 was significant (δ_{biparentally inbred}=0.21), but significantly less severe than uniparental inbreeding depression (δ_selfed=0.48) (Figure 2).

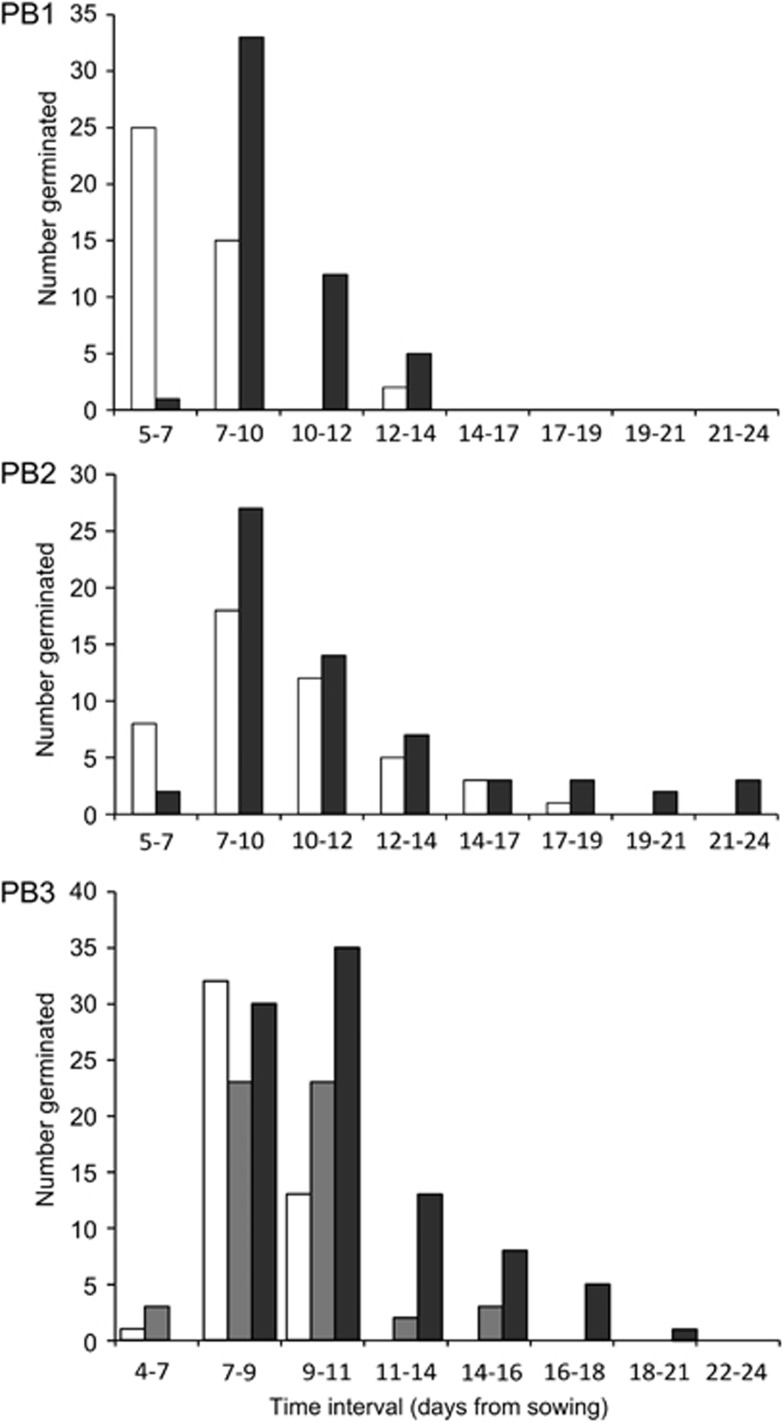
Even for those plants for which the seedlings established successfully (that is, those that survived until 4 weeks of age), selfed seeds took significantly longer to germinate than outcrossed control seeds (Figure 3, Table 1). The PB also had a significant effect on time to germination, but there was no significant interaction between pollination treatment and PB (Table 1).

Figure 3.

Delayed germination of inbred seeds. Histograms of time to germination for each of the three PBs (PB1–PB3). For each PB, control outcrossed progeny (white bars) were compared with selfed progeny (dark grey bars), and for PB3 also to biparentally inbred progeny (light grey bars). Germination was assessed on Mondays, Wednesdays and Fridays, which determined the time interval bins used to make the histograms.

Table 1. ANOVA testing the effects of Parental Background (PB: 1, 2 and 3), Pollination Treatment (PT: outcrossed vs selfed), and their interaction on time to germination and relative growth rate (leaf surface and number increase).

Variable	Factor	dffactor	F	Significance
Time to germination	PB	2	18.6	P<0.0005
MSerror=1.33, dferror=333	PT	1	41.4	P<0.0005
	PB*PT	2	0.49	P=0.613
RGR three largest leaves 2–4 weeks	PB	2	71.4	P<0.0005
MSerror=0.017, dferror=333	PT	1	17.5	P<0.0005
	PB*PT	2	0.132	P=0.877
Leaf number increase 2–4 weeks	PB	2	31.1	P<0.0005
MSerror=1.06, dferror=333	PT	1	16.6	P<0.0005
	PB*PT	2	11.2	P<0.0005

Abbreviations: df, degrees of freedom; MS, mean square; PB, parental background; PT, pollination treatment; RGR, relative growth rate.

Inbreeding depression for growth and flowering rate

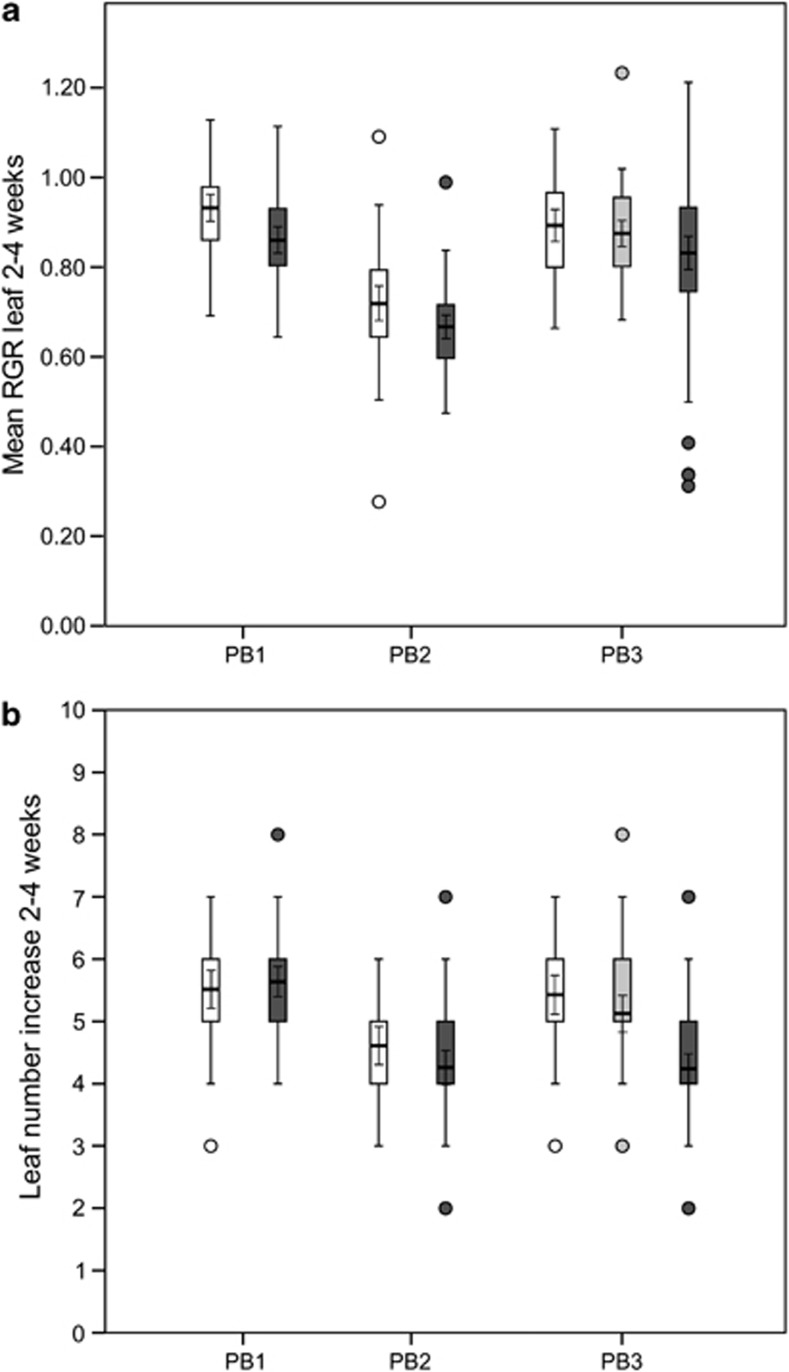
PB had a significant effect on the relative increase in leaf surface from 2 to 4 weeks of age (Table 1). Pollination treatment also had a significant effect (Table 1), indicating significant inbreeding depression, albeit of a very small magnitude (δ_selfed=0.068–0.077, see Figure 4). There was no interaction between PB and pollination treatment (Table 1). PB had a significant effect on the number of leaves formed in the period from 2 to 4 weeks of age (Table 1). Pollination treatment also had a significant effect (Table 1), indicating significant overall inbreeding depression. However, inbreeding depression was only of considerable magnitude in PB3 (δ=0.22), in contrast with PB1 and PB2 (δ=−0.02 and δ=0.08, respectively) (Figure 4), causing a significant interaction between PB and pollination treatment (Table 1).

Figure 4.

Inbreeding depression for early juvenile growth. Boxplots for relative leaf surface increase (RGR) from 2 to 4 weeks (a) and leaf number increase from 2 to 4 weeks (b) for each of three PB. For each PB, control outcrossed progeny (white bars) were compared with selfed progeny (dark grey bars), as well as to biparentally inbred progeny for PB3 (light grey bars). Boxes represent the interquartile range. Bold horizontal lines and associated error bars within boxes indicate mean and 95% confidence interval. Whiskers outside boxes indicate minimum and maximum observations, or 1.5 times the interquartile range when outliers were present. Outliers (circles) are defined as data points beyond 1.5 times the interquartile range.

For flowering we detected no inbreeding depression. Regardless of inbreeding, plants that survived to 4 weeks almost always succeeded to flower (percentages of plants that flowered ranged from 97 to 98% for selfed progeny vs 98–100% for control outcrossed plants; Fisher's exact tests: P>0.29).

S-locus-specific genetic load

We detected significant distortion from Mendelian segregation of S-alleles in the selfed seeds derived from PB1 and PB2 (Table 2). In PB1 (enforced selfed progeny of F1 plants with the S-locus genotype S₁S₃₉), this was due to significant under-representation of both homozygous classes (Table 2), consistent with very early acting inbreeding depression in the zygote (that is, during early embryo development). In PB2 (enforced selfed progeny of F1 plants with the S-locus genotype S₃S₂₃), the distortion was due to under-representation of S₃S₃ homozygotes (they were about as frequent as the homozygotes in the first parental background), but S₂₃S₂₃ homozygotes were over-represented (leaving relatively few heterozygotes, Table 2). In PB3, no significant distortion from Mendelian segregation was detected (Table 2).

Table 2. Segregation of S-haplotypes in relation to survival to 4 weeks of age in enforced selfed progeny derived from the three parental backgrounds.

	Survival		Total
	N	Y	O (E)
Selfed progeny PB1 (S1S39)
S1S1	1	3	4 (10)
S1S39	12	18	30 (20)
S39S39	3	3	6 (10)
Probability	0.762a		0.00654b
Selfed progeny PB2 (S3S23)
S3S3	1	7	8 (13)
S3S23	5	9	14 (26)
S23S23	9	21	30 (13)
Probability	0.577a		0.000003b
Selfed progeny PB3 (S1S23)
S1S1	1	8	9 (10.5)
S1S23	3	19	22 (21)
S23S23	1	10	11 (10.5)
Probability	1.00a		0.919b

Abbreviation: PB, parental background.

^aTo test whether there were differences in survival by genotype, we used Fisher's exact tests to compare the frequency distribution of S-locus genotypes among progeny that did not (N) and did (Y) survive to 4 weeks of age. The exact probability for the observed or a larger difference is given.

^bTo test for overall segregation distortion, we tested for deviations from expected Mendelian ratios (1:2:1) based on observed (O) and expected (E) genotype frequencies summed across both surviving and dead progeny. The exact multinomial probability for the observed or a larger deviation is given.

The chance of germinated seedlings to survive until 4 weeks did not depend on S-locus homozygosity in any of the parental backgrounds, as there were no significant differences between the distributions of homozygous and heterozygous S-locus genotypes for plants that either did or did not survive until 4 weeks of age (Table 2).

There was no S-linked inbreeding depression for juvenile growth traits, as there was no significant effect of S-locus genotype in any of the parental backgrounds, whether in terms of leaf formation from 2 to 4 weeks or increase in leaf surface area (Table 3). This lack of an effect was not simply due to low sample sizes. Owing to the relatively low variance around our growth estimates, we had reasonable power to detect even moderate inbreeding depression (Table 4). In PB1, a total sample size of N=9 (that is, three samples per genotype) would have given sufficient power to detect δ_S-linked=0.20 or more (Table 4). Hence, the power of our experiment (with N_S1S1=3, N_S39S39=3, N_S1S39=18) was at least comparable to this. Similarly, in PB2 and PB3, a total sample size of N=21 and N=24 would have given sufficient power to detect δ_S-linked=0.15 or more (Table 4). Even using more conservative variance estimates than those observed in our experiment, our sample sizes would have had reasonable power (close to 80%) to detect δ_S-linked>0.30 (Supplementary Table S2).

Table 3. Mean relative growth rates for S-locus homozygotes and heterozygotes within selfed progeny derived from three parental backgrounds (PB1–3).

Selfed progeny PB1 (S1S39)
Genotype	RGRa	s.d.	N	δS-linkedb
S1S1	0.890	0.158	3	0.101
S1S39	0.990	0.106	18	—
S39S39	0.925	0.080	3	0.066
ANOVA	df	MS	F	P
Genotype	2	0.021	1.33	0.286
Error	21	0.016
Selfed progeny PB2 (S3S23)
Genotype	RGRa	s.d.	N	δS-linkedb
S3S3	0.943	0.142	7	−0.036
S3S23	0.910	0.099	9	—
S23S23	0.991	0.152	21	−0.089
ANOVA	df	MS	F	P
Genotype	2	0.219	1.15	0.328
Error	34	0.019
Selfed progeny PB3 (S1S23)
Genotype	RGRa	s.d.	N	δS-linkedb
S1S1	0.996	0.125	8	0.069
S1S23	1.07	0.151	19	—
S23S23	0.982	0.305	10	0.082
ANOVA	df	MS	F	P
Genotype	2	0.032	0.807	0.455
Error	34	0.040

Abbreviations: df, degrees of freedom; MS, mean square; PB, parental background; RGR, relative growth rate; s.d., standard deviation.

For each S-locus genotype s.d. and sample size (N) are given, as well as an estimate of S-linked inbreeding depression (δ_S-linked) for S-locus homozygotes. Significance of differences among genotypes was evaluated by one-way ANOVA within each parental background.

^aRGR: Relative Growth Rate, calculated as the relative increase in leaf surface over 2 weeks: RGR_{2–4 weeks}=ln(leaf surface_{4 weeks})/ln(leaf surface_{2 weeks}).

^bDetectable δ_S-linked: δ_Sx-linked=1−(MeanRGR_SxSx)/(MeanRGR_SxSy).

Table 4. Power analysis inferring minimum sample sizes (N_min) needed to detect effect sizes given increasing levels of S-linked inbreeding depression (δ_S-linked) for relative growth rate in the three parental backgrounds (PB1–3).

	Detectable δS-linkeda	Effect sizeb	Nmin (actual power)c
Selfed progeny PB1 (S1S39)	0.05	0.450	51 (0.83)
MSerror=0.016	0.10	0.899	18 (0.88)
Neffectived=9	0.15	1.349	12 (0.95)
	0.20	1.799	9 (0.96)
	0.25	2.249	9 (1.00)
	0.30	2.698	6 (0.90)
	0.35	3.148	6 (0.96)
Selfed progeny PB2 (S3S23)	0.05	0.327	96 (0.81)
MSerror=0.019	0.10	0.654	27 (0.82)
Neffectived=21	0.15	0.981	15 (0.86)
	0.20	1.308	12 (0.93)
	0.25	1.635	9 (0.92)
	0.30	1.962	9 (0.98)
	0.35	2.289	6 (0.80)
Selfed progeny PB3 (S1S23)	0.05	0.268	138 (0.80)
MSerror=0.040	0.10	0.536	39 (0.83)
Neffectived=24	0.15	0.804	21 (0.87)
	0.20	1.071	12 (0.80)
	0.25	1.339	12 (0.94)
	0.30	1.607	9 (0.91)
	0.35	1.875	9 (0.97)

Abbreviations: MS, mean square; PB, parental background.

For each PB, the level of variance (MS_error) underlying the effect size calculation and the effective sample size (N_effective) was obtained from the analysis of variance presented in Table 3.

^aDetectable δ_S-linked: δ_Sx-linked=1−(MeanRGR_SxSx)/(MeanRGR_SxSy).

^bEffect size (f) standardized by MS_error: .

^cMinimum sample size (N_min) needed (rounded up to the nearest product of three) to achieve at least 80% power to detect the given effect size.

^dThe effective sample size was determined conservatively based on the sample size in the smallest genotype class: N_effective=N_{smallest genotype class} × number of genotype classes.

Discussion

Inbreeding depression is thought to have an important role in the evolution of mating systems, and form one of the main barriers to the evolution of selfing (Kondrashov, 1985; Lande and Schemske, 1985; Porcher and Lande, 2005). In self-incompatible plants, inbreeding depression could partly have a genome-wide basis (Charlesworth and Willis, 2009), and partly be due to recessive deleterious mutations linked to the S-locus (Uyenoyama, 2005). In this study, we show that enforced selfed progeny from normally self-incompatible North-American A. lyrata suffer considerable inbreeding depression (upto 0.5 cumulative across early life history stages). Following theoretical predictions, biparental inbreeding (through crossing full siblings) resulted in inbreeding depression about half of that due to selfing. The observed inbreeding depression due to enforced selfing could partly be attributed to S-linked genetic load, as some S-locus homozygotes had a segregation disadvantage in selfed progeny. Our results add to the limited body of empirical evidence for the existence of genetic load linked to genes under balancing selection.

Timing of inbreeding depression

Selfed seeds had reduced fitness compared with outcrossed seed owing to lower germination rates and seedling survival (Figure 2). Selfed seeds also took longer to germinate (Figure 3), which may have negative fitness consequences under natural conditions. There was a pattern of stronger inbreeding depression for early traits (δ=0.33 for germination rate and δ=0.45 for seedling survival, Figure 2) than for juvenile growth (δ=0.07, Figure 4). Although we did not assess later life history traits related to flowering in much detail, we found no inbreeding depression for flowering rate. It remains to be tested whether this pattern can be generalised across North-American populations, but it contrasts with patterns of inbreeding depression described for the European subspecies of A. lyrata, where the level of inbreeding depression was in fact higher for growth (around 0.4) and flowering rate (δ>0.75, Karkkainen et al., 1999). Differences in timing of inbreeding depression may have consequences for the efficiency of purging: genetic load expressed in early life history stages may be purged more easily than that in later life history stages (Husband and Schemske, 1996). It would therefore be interesting to make a comparison of inbreeding depression between more European and North-American populations of A. lyrata that takes into account the whole life history cycle and particularly also traits related to flowering.

The potential role of purging

Levels of inbreeding depression in selfed progeny were comparable across the different parental backgrounds, but highest in PB3 (Figures 2 and 4). Given the potential purging history in PB3 (F1 progeny derived from a cross between the outcrossing PIN and selfing RON population), this may seem surprising. The RON population has been predominantly inbreeding for at least several generations, with low outcrossing rates (T_m=0.29 in 2003 and T_m=0.28 in 2007), and characteristically low genetic diversity and heterozygosity (Mable et al., 2005; Foxe et al., 2010). Alternatively, heterotic effects in the F1 cross-progeny used as control could explain upward bias of the estimate of inbreeding depression in PB3, although PIN and RON are geographically and genetically similar based on analyses of microsatellites, nuclear DNA SNPs and chloroplast DNA (Hoebe et al., 2009; Foxe et al., 2010). Estimation of inbreeding depression in relation to outcrossing rates in multiple populations, ideally using within-population crosses as control would provide better insights into the potential role of purging throughout the North-American populations of A. lyrata.

Biparental inbreeding depression

Biparental inbreeding can be frequent in natural populations (Griffin and Eckert, 2003; Collin et al., 2009). For matings between full siblings, partners share half of their genome, so the level of biparental inbreeding depression is expected to be half of that due to selfing, which could help to purge the genetic load (Uyenoyama, 1986; Charlesworth and Charlesworth, 1987). Our results (δ_{biparentally inbred}=0.21 vs δ_selfed=0.48) followed these predictions remarkably well. This highlights that purging of deleterious load is possible even in systems with sporophytic self-incompatibility, where selfing is strictly prevented.

Experimental design considerations

Several approaches are possible to assess inbreeding depression and each of these has specific advantages and disadvantages (Fox, 2005; Kelly, 2005). Typically, cross-progeny are obtained by pollinating a seed parent with one or more presumably unrelated fathers. This has the disadvantage that outcrossed progeny (combining the genes of the seed parent with one or more unrelated pollen donors) will have a different genetic background than selfed progeny (which will only carry genes of the seed parent). Hence, each point estimate of inbreeding depression (within each family) can be biased upward (for example, if the cross combines favourable gene sets), or downward (for example, if the cross combines unfavourable gene sets, or if plants are crossed that are not entirely unrelated). Sufficient replication at the family level is therefore needed to obtain an unbiased overall estimate of inbreeding depression at the population level). However, replication can be impractical in labour intensive studies on S-linked load, and require alternative approaches to avoid bias due to differences in genetic background between self- and cross-progeny.

Therefore, we used F1 cross-progeny as base material for generating enforced selfed seeds, while keeping seeds from the F1 cross-progeny for use as the control outcross progeny. This ensures that selfed and outcrossed seeds have a comparable genetic background, even with low replication at the family level. Although it introduces a generational difference between selfed and control outcrossed progeny, it may be the best possible approach in cases where sufficient replication at the family level is impractical, such as in studies of S-linked load.

Potential bias of inbreeding depression estimates

Inbreeding depression estimates in general can be biased for several reasons. Firstly, plant performance is commonly assessed in a relatively benign environment. This could lead to under-estimation of the true level of inbreeding depression under natural conditions (Fox and Reed, 2011). A second potential source of bias is related to the artificial by-passing of the self-incompatibility system to generate selfed progeny. The problem is that reduced seed set can be both the result of incomplete bypassing of the self-incompatibility response, or due to inbreeding depression in the zygotic stage (leading to early seed abortion). Moreover, the maternal environment can also have negative effects on seed set unrelated to inbreeding depression. Therefore, the trait ‘seed set' cannot be used directly to estimate the level of inbreeding depression due to zygote abortion, particularly in systems with genetically controlled self-incompatibility. To get a better idea of the potential importance of zygote abortion, we counted the number of seeds with aberrant development as a crude estimate. We observed relatively few prematurely aborted seeds (upto 8.5%, Supplementary Table S3). The vast majority of selfed seeds were rather uniform in size, regularly shaped and had a regular yellow–brown seed coat characteristic of healthy seeds. This suggests only a minor role of early zygote abortion, although more detailed (microscopic) analysis of seed/zygote abortion would be needed to get a better idea of the importance of inbreeding depression during (early) zygote development.

Genetic load attributable to the S-locus

The overall inbreeding depression we observed (Figures 2 and 3) could be due to a combination of increased genome-wide homozygosity (Charlesworth and Charlesworth, 1987), and increased homozygosity at the S-locus and the region surrounding it. Using bud-pollination or pollination in a CO₂-enriched environment to by-pass the incompatibility response, two alternative approaches can be used to detect S-linked genetic load: (1) generating S-locus homozygotes through enforced crossing of unrelated individuals with an identical S-locus genotype or (2) generating enforced selfed progeny. For the former, the progeny are ‘inbred' for the S-locus, but not for the rest of the genome. A fitness reduction of these ‘incompatible cross-progeny' compared with normally crossed progeny can then be attributed to increased S-locus homozygosity. For the latter, progeny are inbred across the whole genome, after which S-linked load can be estimated by testing whether S-locus homozygotes have a reduced fitness compared with heterozygotes. This is the approach we used because earlier work had indicated that the S-linked load estimates from the enforced crossing of unrelated individuals approach may potentially be inflated (see supporting information). In general, our results indicated a segregation bias against S-locus homozygotes for two out of four S-alleles (for S₁ and S₃₉ in PB1, Table 2), but no S-locus-specific inbreeding depression for life history traits. The latter was not due to a lack of statistical power. With our sample sizes inbreeding depression for growth due to the S-locus as low as δ=0.15–0.20 would have been detectable with more than 80% power (see power analysis in Table 4). Even when conservatively assuming larger variances, our sample size would have allowed detection of levels of inbreeding depression for growth of δ>0.3 with more than 80% power (Supplementary Table S2). Our results are in line with a study on the closely related species A. halleri that also found that the level of inbreeding depression was trait dependent and varied among S-alleles (Llaurens et al., 2009b).

Dominance does not explain differences in genetic load among S-alleles

In sporophytic self-incompatibility systems, differences in dominance have been suggested as an explanation for differences in genetic load among S-alleles, predicting that more dominant S-alleles should have an increased load (Llaurens et al., 2009b). In A. halleri, indeed the most dominant haplotype (S15) was the only allele that carried a significant load, whereas no load was detected for more recessive haplotypes (S01 and S02) (Llaurens et al., 2009b). S01 is the most recessive haplotype in A. halleri (homologous to S₁ in our study). S02 is dominant only to S01, but not to any other known A. halleri S-haplotypes (Llaurens et al., 2009a), which is comparable to haplotype S₃ in our study. We found evidence for a genetic load for haplotype S₁ and S₃₉ on the basis of their segregation disadvantage in homozygous state (Table 2). The dominance level of S₃₉ has not been established, but S₁ is the most recessive allele known in A. lyrata. This indicates that factors other than dominance must have led to the accumulation of recessive deleterious load for the recessive S₁ allele.

The lack of evidence for a genetic load associated with S₂₃ in PB2 and PB3 (Tables 2 and 3) provides further indication that dominance is not the only factor explaining deleterious load. S₂₃ represents the most dominant allelic class in A. lyrata (Schierup et al., 2001; Prigoda et al., 2005). In fact, S₂₃ homozygotes were even over-represented in PB2. The latter could have three causes. First, S₃ alleles may have a deleterious load expressed in the gametic stage, giving S₃ a transmission disadvantage relative to S_23, but this is not suggested by the relatively high frequency (0.38) of S₃ in the PIN population (Mable et al., 2005). Secondly, S₂₃ could have a transmission advantage but this is not reflected in its low frequency (0.03) in PIN (Mable et al., 2005) or the fact that such a transmission advantage was not present in PB3. Alternatively, PCR amplification of S₃ may be suboptimal in the presence of S₂₃. That way, some of the S₃S₂₃ heterozygotes would appear as S₂₃S₂₃ homozygotes. The high load associated with the most recessive allele S₁, and the lack of evidence for a genetic load associated with the most dominant allele S₂₃, indicate that factors other than dominance underlie variation in S-linked genetic load in A. lyrata.

Alternative explanations for differences in genetic load among S-alleles

In gametophytic systems, there are no dominance interactions between S-alleles, so differences in genetic load between S-alleles can by definition not be explained by differences in purging history due to dominance. The few studies that have been performed so far, both in Solanum carolinense (Solanaceae), indeed found differences between S-haplotypes in the amount of genetic load (Stone, 2004; Mena-Ali et al., 2009). Stochastic differences due to the random nature of the mutation process have been suggested as an explanation for this pattern (Stone, 2004). In turn, differences in load can lead to differences in diversification rates of specificities, as lineages of specificities with a large mutational load are expected to diversify at a lower rate than specificities with a smaller load (Uyenoyama, 2003). Some (inconclusive) empirical evidence for this was found in S. carolinense, where three out of five alleles without a strong genetic load were part of a clade that exhibits strong diversification, and one out of two alleles with a strong load was positioned on a long terminal branch (Stone, 2004). In sporophytic systems, relationships among S-alleles normally have low bootstrap support (Prigoda et al., 2005; Tedder et al., 2011). Moreover, comprehensive sampling of alleles is difficult (for example, Mable et al., 2003) which may compromise robust interpretation of diversification patterns (for example if close relatives of some alleles have not been sampled). It is therefore hard to place our results in a phylogenetic context, and test whether alleles with larger mutational load are indeed characterised by longer branch lengths.

A phylogeny of SRK variation in A. lyrata (Prigoda et al., 2005) provides at least some indication of relative branch lengths for S₁ and S₃ (for S₂₃ and S₃₉ the phylogeny is not supported well enough). S₁ is the single most recessive allele, is found worldwide and has the deepest branch length because it has no close relatives. S₃, on the other hand, has a relatively short branch length and is part of a well-resolved clade with strong diversification (Prigoda et al., 2005). Therefore, the presence of a significant deleterious load for S₁ and absence of such a load for S₃ is in line with predictions that genetic load prevents the diversification of S-alleles, and causes longer branch lengths (Uyenoyama, 2003).

Overall, our results add to the growing body of evidence that alleles at a locus under balancing selection can build up a deleterious load (Stone, 2004; Llaurens et al., 2009b; Mena-Ali et al., 2009), as predicted by theory (Uyenoyama, 2005; van Oosterhout, 2009). As all studies so far, we found evidence for such a load for some, but not all alleles. In contrast to previous work in A. halleri, our results do not lend support to the theory that dominance explains differences in deleterious load among S-alleles (Llaurens et al., 2009b). Instead, these differences might be the result of the random nature of the mutation process (Stone, 2004). Assessment of genetic load targeting more S-alleles of known dominance level from well-sampled and well-resolved clades is needed to establish the relative importance of the different causes for accumulation of deleterious load linked to S-loci.

Data archiving

Data have been deposited at Dryad: http://dx.doi.org/10.5061/dryad.j44hf20s.

The authors declare no conflict of interest.