Multi-Reader ROC studies with Split-Plot Designs: A Comparison of Statistical Methods

Abstract

Rationale and Objectives

Multi-reader imaging trials often use a factorial design, where study patients undergo testing with all imaging modalities and readers interpret the results of all tests for all patients. A drawback of the design is the large number of interpretations required of each reader. Split-plot designs have been proposed as an alternative, in which one or a subset of readers interprets all images of a sample of patients, while other readers interpret the images of other samples of patients. In this paper we compare three methods of analysis for the split-plot design.

Materials and Methods

Three statistical methods are presented: Obuchowski-Rockette method modified for the split-plot design, a newly proposed marginal-mean ANOVA approach, and an extension of the three-sample U-statistic method. A simulation study using the Roe-Metz model was performed to compare the type I error rate, power and confidence interval coverage of the three test statistics.

Results

The type I error rates for all three methods are close to the nominal level but tend to be slightly conservative. The statistical power is nearly identical for the three methods. The coverage of 95% CIs fall close to the nominal coverage for small and large sample sizes.

Conclusions

The split-plot MRMC study design can be statistically efficient compared with the factorial design, reducing the number of interpretations required per reader. Three methods of analysis, shown to have nominal type I error rate, similar power, and nominal CI coverage, are available for this study design.

Introduction

In imaging clinical trials investigators often compare the accuracy of clinicians’ diagnostic interpretations of different imaging modalities, assessing the sensitivity, specificity, and/or receiver operating characteristic indices of the modalities [1–4]. In estimating the accuracy of mammography for detecting breast cancer, for example, mammograms are interpreted by trained radiologists who read the images to determine if suspicious lesions are present. It is well-known that there is variability between readers in their visual, cognitive, and perceptual abilities [4–7]; similarly, there is variability between patients in their anatomy, co-morbidities, and manifestation of disease. Thus, samples of both readers and patients are integral components in characterizing diagnostic test accuracy. The average accuracy of the readers is typically used as the measure of the test’s accuracy. There has been a great deal of methodology development for the estimation and comparison of diagnostic tests’ accuracy from multiple-reader studies [4,8–16].

Multi-reader imaging trials often use a factorial, or fully-crossed, design, where study patients undergo testing with all imaging modalities being compared, and study readers interpret the results of all of the tests for all patients. The rationale is that since both patients and readers introduce variability to the measurement of diagnostic accuracy, for comparing modalities variability from these sources can be reduced if study patients undergo all modalities and if study readers interpret all of the test results.

While the fully-crossed design is efficient in terms of the number of patients and readers required for the study, one drawback of the design is the number of interpretations required of each reader [17]. For a typical-sized study with 200 study patients and 2 modalities, each reader must interpret 400 images. If each test requires an average of 5 minutes to interpret, each study reader needs nearly a week to participate in the study. Some tests, such as CT colonoscopy, can take closer to 30 minutes to interpret (5 weeks of reading time).

When the number of interpretations per reader is a limiting factor in the execution of a trial, other study designs, such as the “hybrid” [17] or “mixed” [18] design, have been proposed, which are two different split-plot designs. In these designs one or a subset of readers interprets all of the images of a sample of patients, while other readers interpret all of the test results of other samples of patients. Compared to the factorial design, these designs can be more efficient for testing for a difference in modalities, with respect to the total number of reader interpretations, because they retain the reader and patient pairing across modalities while eliminating some of the positive correlations between readers. By reducing some of the between-reader correlations, these alternative study designs can reduce the overall numbers of interpretations needed per reader.

There are multiple statistical methods available for analyzing data from a fully-crossed multiple-reader multiple-case (MRMC) design [4, 8–16] but only a few papers discussing analysis of MRMC studies using other study designs [19–21]. In this paper we present three methods of analysis for the MRMC split-plot design: the OR method [9] modified for the split-plot design, a newly proposed marginal-mean ANOVA approach [21], and an extension of the three-sample U-statistic method [15, 20]. We perform a simulation study to compare the type I error rate, power and confidence interval coverage of three test statistics. The motivation for this study was an imaging trial assessing the accuracy of 36 readers who interpreted the mammograms of 200 patients without and with a computer aided detection (CAD) device. A four-block split-plot design was used such that each reader interpreted images from 50 patients. We present the trial in detail and analyze the results with the three test statistics. A discussion follows.

Methods

MRMC Split-Plot Study Design

Multi-reader multi-case (MRMC) trials are conducted to compare the diagnostic accuracy of two or more tests where the tests being studied require interpretation of cases by a trained reader. The primary goal of these studies is the comparison of the average accuracy of readers between the diagnostic tests. Common measures of test accuracy are sensitivity, specificity, and measures of accuracy from Receiver Operating Characteristic (ROC) curves [1–4]. In this paper we focus on the area under the ROC curve, AUC, but the methods are applicable to these other measures of test accuracy, as well.

Several MRMC study designs have been proposed [17], but the most common design to date is the fully-crossed design. In this design there are N_T total patients who have undergone each diagnostic test. J readers interpret all of the test results of the N_T patients (See Table 1). For a study comparing two diagnostic tests, there are 2×J×N_T reader interpretations.

Table 1.

Lay-Out of Fully-Crossed MRMC Study Design

	Reader 1		Reader 2 …		Reader J
	Test 1	Test 2	Test 1	Test 2	Test 1	Test 2
Patient 1	X111	X211	X121	X221	X1J1	X2J1
Patient 2	X112	X212	X122	X222	X1J2	X2J2
Patient 3	X113	X213	X123	X223	X1J3	X2J3
…
Patient NT	X11N	X21N	X12N	X22N	X1JN	X2JN

X_ijk denotes the test score assigned by the j-th reader to the k-th patient imaged with modality i.

The split-plot MRMC study design [18] was proposed to reduce the number of interpretations required from each reader. In this design readers interpret all of the test results from a patient, but each reader interprets just a subset of the total study patients. Thus, the pairing across modalities is present (each patient imaged with all modalities and each reader interpreting results from all modalities), but some of the positive correlations between readers that would be present in a fully-crossed design are eliminated, typically improving the statistical efficiency relative to the fully-crossed design with respect to total number of reader interpretations.

There are many possible configurations of the split-plot design, but in this paper we focus on balanced designs where the J readers and N_T patients are randomized to one of G blocks. In each block, the readers interpret all of the test results from the patients in that block. Table 2 illustrates the split-plot study design with G=3 blocks and two readers in each block (i.e. J=6). (Note that it can be shown that the design in Table 2 is a split-plot design with the reader and case combinations as the whole plots, test as the split-plot factor, and block as the between-whole-plots factor.)

Table 2.

Lay-out of Split-Plot MRMC Study Design with Three Blocks

Block 1		Block 2		Block 3
Reader 1	Reader 2
X1111, X2111	X1211, X2211
X1121, X2121	X1221, X2221
X1131, X2131	X1231, X2231
		Reader 3	Reader 4
		X1342, X2342	X1442, X2442
		X1352, X2352	X1452, X2452
		X1362, X2362	X1462, X2462
				Reader 5	Reader 6
				X1573, X2573	X1673, X2673
				X1583, X2583	X1683, X2683
				X1593, X2593	X1693, X2693

In a split-plot reader design with G blocks, J readers are randomized to a block and N_T patients are randomized to a block such that in each block there are J/G readers and N_T/G patients. In the 3-block split-plot design illustrated here, J=6 and N_T=9; thus, two readers are randomized to each of the three reader blocks and three patients are randomized to each of the three blocks.

X_ijkg denotes the test score assigned by the j-th reader in block g to the k-th patient in block g imaged with modality i.

To illustrate the efficiency gains possible with the split-plot design, we compared the efficiency of the 2-block split-plot design (J=6, N_T=120) to five alternatives: a 3-block split-plot design, a 4-block split-plot design, two fully-crossed designs (compared with the 2-block design, the Full-A study design has the same total number of readers, J, but half the total number of cases, N_T/2; and the Full-B study design has the same total number of readers and cases, J and N_T, respectively), and an unpaired reader study design (i.e. the readers are unpaired across modalities). In Table 3 we summarize the resource needs of the six study designs. From the table we can consider our ability to recruit the total number of readers, the cost of collecting the cases, the total number of interpretations required, and the total number of interpretations required per reader. The last two variables are likely to be proportional with total study time and time required per reader. The table also includes the statistical efficiency of each of the study designs relative to the 2-block study.

Table 3.

Resources Needed for Different Study Designs

Study Design	# readers, J	# patients*	Total # of image interpretations	# image interpretations per reader	Statistical Efficiency**
2-block split-plot	6 (3/block)	120 (30+30)	720	120	1.0
3-block split-plot	9 (3/block)	120 (20+20)	720	80	1.2
4-block split-plot	12 (3/block)	120 (15+15)	720	60	1.33
Fully-paired A	6	60 (30+30)	720	120	0.83
Fully-paired B	6	120 (60+60)	1440	240	1.16
Unpaired-reader	12	120 (60+60)	1440	120	0.90

^*Total sample size (number of non-diseased and diseased patients per block)

^**Statistical efficiency is defined as the variance of the two-block split plot design divided by the variance of the specified alternative design [19]. An efficiency >1 indicates that the variance of the 2- block split design is larger than the variance of the specified alternative design; an efficiency <1 indicates that the variance of the 2-block split design is smaller than the variance of the specified alternative. The calculations are based on the first set of model parameters in our simulation study (see Section 3).

We see that the 2-block split-plot study takes only a moderate hit in efficiency relative to the fully-crossed study design with the same number of readers and cases (Full-B). This moderate loss in efficiency comes at a savings of half the reading time of each reader. We also see that the 2-block split-plot study is more efficient than the fully-crossed study design with the same number of readings per reader and total readings (Full-A). Splitting the study into even more blocks (each with three readers) saves even more time per reader and the additional readers increase the efficiency. It is important to realize, however, that these results are only for one particular data structure; for other structures, gains can be less or greater with respect to total readings.

OR Test Statistic Modified for Split-Plot Design

Obuchowski and Rockette (OR) [9] developed a general linear model of the estimate of the ROC area for the i-th modality by reader j for a fully-crossed (i.e. factorial) design:

$${\widehat{\theta }}_{ij}={\tau }_i+{\text{R}}_j+{(\tau \text{R})}_{ij}+{\epsilon }_{ij},$$ [1]

where τ_i is the fixed effect of the ith modality, R_j is the random reader effect, and (τR)_ij is the random effect due to the interaction of modality and reader. The error term in Equation 1 is assumed to have a multivariate normal distribution with mean zero and covariance matrix defined as follows:

$$\text{E}({\epsilon }_{\text{ij}},{\epsilon }_{{\text{i}}^{\prime }{\text{j}}^{\prime }})=\begin{array}{ll}{{\sigma }_{\text{c}}}^2\hfill & \text{if}\text{i}={\text{i}}^{\prime }\text{and}\text{j}={\text{j}}^{\prime }\hfill \\ {cov}_1={{\sigma }_{\text{c}}}^2{\rho }_1\hfill & \text{if}\text{i}\ne {\text{i}}^{\prime }\text{and}\text{j}={\text{j}}^{\prime }\hfill \\ {cov}_2={{\sigma }_{\text{c}}}^2{\rho }_2\hfill & \text{if}\text{i}={\text{i}}^{\prime }\text{and}\text{j}\ne {\text{j}}^{\prime }\hfill \\ {cov}_3={{\sigma }_{\text{c}}}^2{\rho }_3\hfill & \text{if}\text{i}\ne {\text{i}}^{\prime }\text{and}\text{j}\ne {\text{j}}^{\prime }\text{.}\hfill \end{array}$$

ρ₁ denotes the correlation betweens errors corresponding to a reader reading the results of the same patients from different tests, ρ₂ denotes the correlation between different readers interpreting the same test, and ρ₃ denotes the correlation between different readers interpreting different tests.

The null and alternative hypotheses are

$$\begin{array}{l}{\text{H}}_{\text{o}}:{\tau }_1={\tau }_2,\\ {\text{H}}_{\text{A}}:{\tau }_1\ne {\tau }_2.\end{array}$$ [2]

Obuchowski and Rockette [9] proposed the following test statistic, which approximately follows a central F-distribution under the null hypothesis for the factorial design:

$${\text{F}}^{\ast }=\text{MS}(\text{T})/\{\text{MS}(\text{T}\times \text{R})+\mathit{max}[\text{J}\times \widehat{\phi },0]\}.$$ [3]

MS is shorthand for mean square. Details of the calculation of the MS terms are given in the Appendix.

The last term of Equation 3 can be written as max[J × (côv₂−côv₃),0], where côv₂ and côv₃ are estimates of cov₂ and cov₃. This term is a correction factor proposed by Bhat [22] for the situation where the data are correlated. The estimates côv₂ and côv₃ are typically computed by averaging corresponding pairwise covariance estimates, which can be estimated by various methods such as the nonparametric method of DeLong et al [23], the jackknife, the bootstrap, or parametric methods.

For the factorial design Obuchowski and Rockette proposed that F* be compared to a central F distribution with (I−1) and (I−1)(J−1) degrees of freedom (dfs). (Note that dfs are values associated with the test statistic and used in hypothesis testing.) Hillis [14] showed that the denominator df for F* should be:

$$\text{ddf}={\{\text{MS}(\text{T}\times \text{R})+\mathit{max}[\text{J}\times ({\text{c}\widehat{\text{o}}\text{v}}_2-{\text{c}\widehat{\text{o}}\text{v}}_3),0]\}}^2/\{\text{MS}{(\text{T}\times \text{R})}^2/((\text{I}-1)(\text{J}-1))\}.$$ [4]

An MRMC study using data collected in a split-plot design can be analyzed using the fully-crossed study design formulae with computation of the error covariances modified to account for zero covariances between AUCs from different blocks. Thus the factorial notation, factorial model mean square definitions, test statistic, and degrees of freedom for the OR method for the split-plot design are identical in appearance to those of the fully-crossed design. In the split-plot design, however, there are some between-reader covariances that are non-zero because the readers are in the same block and other between-reader covariances that are zero because the readers are in different blocks. For the split-plot design, φ̂ is computed just like côv₂ − côv₃ for the factorial design, but with between-block pairwise covariance estimates set to zero.

Marginal-mean ANOVA Test Statistic for Split-plot Design

The rationale for the marginal-mean ANOVA approach is summarized in the Appendix. Briefly, the method use a split-plot notation; i.e., Y_ijg denotes the AUC corresponding to the jth reader in block g reading the cases in block g under modality i. (In terms of the model in Equation 1 we have Y₁₁₁ = θ̂₁₁,Y₁₂₁ = θ̂₁₂,Y₁₁₂ = θ̂₁₃, etc., if there are 2 readers in each block.) Let r = J/G denote the number of readers in each block. Cov₂ and cov₃ are again defined as for the factorial model, but with the restriction that these covariances are only for pairs of outcomes from the same block. In work presently under review, Hillis [21] has proposed the following test statistic for testing the hypotheses in Equation [2] with the split-plot MRMC design:

$$F=\frac{\text{MS}(T)}{\text{MS}(T\times R(G))+max\left[r({\text{c}\widehat{\text{o}}\text{v}}_2-{\text{c}\widehat{\text{o}}\text{v}}_3),0\right]}$$ [5]

where

$$\text{MS}(\text{T}\times \text{R}(\text{G}))=\sum _{g=1}^G\sum _{i=1}^I\sum _{j=1}^r{({\text{Y}}_{\text{ijg}}-{\text{Y}}_{\text{i}.\text{g}}-{\text{Y}}_{·\text{jg}}+{\text{Y}}_{··\text{g}})}^2/[\text{G}(\text{I}-1)(\text{r}-1)],$$ [6]

and côv₂ and côv₃ are computed as the averages of the corresponding estimated covariances within reader blocks; these covariances can be estimated using the same methods discussed previously for the OR statistic.

It is easy to show that the treatment mean square MS(T) in Equation 5 is equal to the treatment mean square in Equation A1. In contrast, MS(T*R(G)) in Equation 6 is the treatment-by-reader-nested-within-block mean square, which differs from the treatment-by-reader mean square in Equation A1 because each squared term in MS(T×R(G)) is a function only of AUCs from a particular block, whereas a squared term in MS(T×R) can be a function of AUCs from several blocks. Finally, it is straightforward to show that (côv₂ − côv₃) =(J −1)φ̂/(r −1), when the same covariance estimation method is used to compute côv₂ − côv₃ and φ̂. Thus Equation 5 can be written as

$$F=\frac{\text{MS}(T)}{\text{MS}(T\ast R(G))+max\left[\frac{J-1}{J-G}J\widehat{\phi },0\right]}$$

The above expression shows the close relationship of F and F*: the numerators are the same, the first term in the denominators differ according to the treatment of blocks (nested or not), and the second term in the denominators differ by the factor (J−1)/(J−G).

The denominator degrees of freedom, derived in a manner similar to the degrees of freedom proposed by Hillis [14] for the factorial OR model, is

$$\text{ddf}=\frac{{\{\text{MS}(T\ast R(G))+max[r({\text{c}\widehat{\text{o}}\text{v}}_2-{\text{c}\widehat{\text{o}}\text{v}}_3),0]\}}^2}{\frac{{[\text{MS}(T\ast R(G))]}^2}{G(I-1)(r-1)}}$$ [7]

F is compared to a central F distribution with degrees of freedom (I−1) and ddf.

Three-Sample U-Statistic Test for Split-plot Design

Gallas [15] derived the variance of the reader-averaged non-parametric (trapezoidal) AUC and showed that it was equivalent to a three-sample U-statistics result; the three samples correspond to readers, non-diseased cases, and diseased cases [24]. Given that work, the covariance between θ̂_i. and θ̂_i′., the non-parametric reader-averaged AUCs from modalities i and i′, can be written as

$$\text{Cov}\left({\widehat{\theta }}_{i·},{\widehat{\theta }}_{i^{\prime }·}\right)=\left(\frac{{\alpha }_{1i{i}^{\prime }}}{N_0}+\frac{{\alpha }_{2{ii}^{\prime }}}{N_1}+\frac{{\alpha }_{3{ii}^{\prime }}}{N_0{N}_1}\right)+\left(\frac{{\alpha }_{4{ii}^{\prime }}}{J}\right)+\left(\frac{{\alpha }_{4{ii}^{\prime }}}{N_{0}J}+\frac{{\alpha }_{5{ii}^{\prime }}}{N_{1}J}+\frac{{\alpha }_{6{ii}^{\prime }}}{N_0{N}_{1}J}\right),$$ [8]

where J is the number of readers, N₀ is the number of non-diseased cases, N₁ is the number of diseased cases, and each α_ii′ is a variance when i=i′ and a covariance when i≠i′ [25, 26]. Gallas and Brown [20] generalized the variance derivation and estimation in Equation 8 to treat study designs that are not fully crossed by using scaling factors for the α’s. This generalization is exactly what is used for the split-plot study designs examined here. Further details of Gallas’ prior work are summarized in the Appendix.

The test statistic for the split-plot design is

$$T=\frac{{\widehat{\theta }}_1-{\widehat{\theta }}_2}{\sqrt{{\widehat{V}}_{UA}}}$$ [9]

where V̂_UΔ is the generalization of the three-sample U-statistic estimate of the variance of the difference in the reader-averaged empirical AUCs as described by Gallas and Brown [20]. When the sample size is large, we can assume that this test statistic is normal. For smaller sample sizes, we assume that T follows a Student’s t-distribution. Here we consider an estimate of the degrees of freedom motivated by the approximate degrees of freedom derived by Hillis [14] and a general 4-way ANOVA with one fixed factor (modality) and three random factors (readers, non-diseased cases, and diseased cases). Specifically, we estimate the degrees of freedom with

$$d.f.=\frac{{\left({\widehat{V}}_{U\mathrm{\Delta }}\right)}^2}{{\left(s_{BR}^2\right)}^2/{\left(N_R-1\right)}^3+{\left(s_{B0}^2\right)}^2/{(N_0-1)}^3+{\left(s_{B1}^2\right)}^2/{(N_1-1)}^3}$$ [10]

where

$$\begin{array}{l}{s}_{BR}^2={\widehat{\alpha }}_{B4ii}+{\widehat{\alpha }}_{B4i^{\prime }{i}^{\prime }}-2{\widehat{\alpha }}_{B4{ii}^{\prime }},\\ s_{B0}^2={\widehat{\alpha }}_{B1ii}+{\widehat{\alpha }}_{B1i^{\prime }{i}^{\prime }}-2{\widehat{\alpha }}_{B1{ii}^{\prime }},\\ s_{B1}^2={\widehat{\alpha }}_{B2ii}+{\widehat{\alpha }}_{B2i^{\prime }{i}^{\prime }}-2{\widehat{\alpha }}_{B2{ii}^{\prime }}\end{array}$$

are ideal bootstrap (method of moments) estimates of the components of variance for the three random effects: readers, non-diseased cases, and diseased cases. We can also refer to these as the non-parametric ML (maximum likelihood) estimates, and relate them to the mean squares of a 4-way ANOVA.

Note that if readers, non-diseased cases, or diseased cases are not paired across the modalities, the corresponding covariance term (α_4ii′, α_1ii′, or α_2ii′) is zero by definition.

Simulation Study

Roe and Metz [27] and Dorfman et al [28] described a method for simulating data for the MRMC fully-crossed study design. We have summarized their model in the Appendix. We utilized their general approach, modifying the model in Equation A2 for the split-plot study design under investigation here to reflect the nesting of reader and case within block. We examined designs where the study readers were divided evenly into 2 blocks. We considered reader sample sizes per block of 3, 5, or 7, and patient sample sizes per block of 60 (30 with disease and 30 without) and 120 (60 with disease and 60 without). We utilized an intermediate value for the mean ROC area under the null hypothesis around 0.90. We investigated scenarios where the readers’ average ROC area with the two modalities was the same (null hypothesis), and scenarios where the readers’ average ROC area with the two modalities increased by a small amount (0.030–0.032) (alternative hypothesis).

The values for the variance components were selected from values used by Roe and Metz [27] and Dorfman et al [28]. We generated test scores from an equal-variance binormal distribution (i.e., binormal parameter b = 1); the same variance components were used for diseased and non-diseased patients. There were a total of 36 different scenarios tested: 3 (reader set sizes) x 2 (case set sizes) x 3 (simulation configurations) x 2 (null & alternate hypothesis experiments). For each scenario, we simulated 2000 datasets, so that we would have at least 80% power to detect a type one error that differed by 0.015 or more from the nominal level of 0.05. The values of the variance components and fixed effects for the simulated data are summarized in Table 4.

Table 4.

Parameter Values for Simulated Test Scores

Parameter	Test Values
Intercept	For non-diseased patients, μ0=0. For diseased patients, μ1=1.53.
Fixed modality effect	Under the null hypothesis, τit=0 for i=1 and 2 and t=0 and 1. Under the alternative hypothesis, τi0=0 for i=1 and 2, and τ11=0 and τ21=0.25.
Random effect due to reader j	Two values of ${\sigma }_r^2$ were tested: 0.011 and 0.056 to represent small and large inter-reader variability.
Random effect due to case k	${\sigma }_C^2$ was set to 0.1.
Random effect due to modality × reader	Two values of ${\sigma }_{\tau R}^2$ were tested: 0.03 and 0.06.
Random effect due to modality × case	${\sigma }_{\tau C}^2$ was set to 0.1.
Random effect due to reader × case	${\sigma }_{RC}^2$ was set to 0.2.
Random effect due to pure error	${\sigma }_{\tau RC}^2$ was set to 0.2.

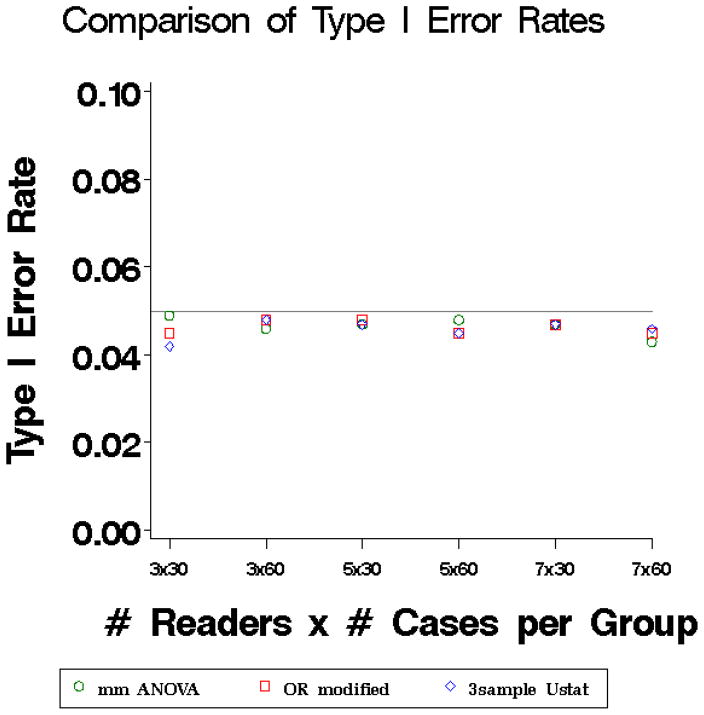
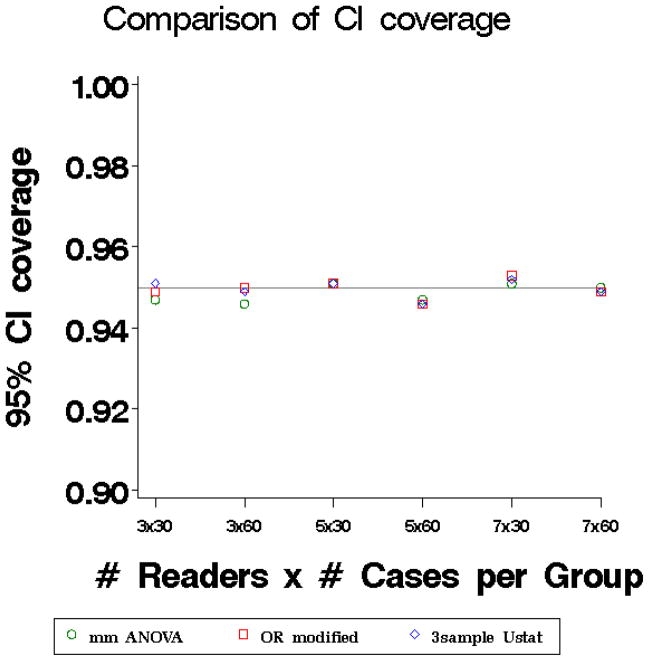
The results of the simulation study (averaged over the 3 simulation configurations) are illustrated in Figures 1 and 2. The nonparametric estimate of the AUC was calculated for each reader and modality [23]. Both the OR and marginal-mean test statistics were based on covariances estimated using the DeLong et al [23] method.

Figure 1.

Type I error rates of three methods: marginal mean ANOVA test statistic (mm ANOVA) (Equation 6) plotted with circles, modified OR test statistic (Equation 3) plotted with squares, and three-sample U-statistic (equation 10) plotted with diamonds. The nominal type I error rate was 0.05.

Figure 2.

Coverage of 95% Confidence Intervals of three methods: marginal mean ANOVA test statistic (circles), modified OR test statistic (squares), and three-sample U-statistic (diamonds).

The type I error rates (Figure 1) for all three methods are close to the nominal level but tend to be slightly conservative (i.e. run very slightly below the nominal level) even for larger numbers of patients and readers. The power is nearly identical for the three methods (results not shown). The coverage of 95% CIs (Figure 2) fall close to the nominal coverage for small and large sample sizes.

Example: Computer-Aided Detection of Breast Cancer

In this split-plot study 36 board-certified mammographers were randomized to the four blocks, such that there were 9 readers in each block. Similarly, 100 patients with breast cancer (biopsy-confirmed) and 100 patients without breast cancer (confirmed by biopsy or one year follow-up) were randomized to the four blocks, such that there were 25 cancer patients and 25 non-cancer patients in each block.

Each reader first interpreted a patient’s mammogram without computer-aided detection (CAD) and reported his or her result. Specifically, the reader was asked to mark the location of any and all suspicious findings and assign a confidence score (1–100) to each finding, where 1=the lowest probability of malignancy, and 100=the highest probability of malignancy. The compilation of findings by the reader constitutes the reader’s unaided findings and could not be altered by the reader.

Next, the reader was shown the CAD marks. The CAD system scans the image for abnormal features associated with malignancy and places a circle around each suspicious area. Readers were asked to consider each CAD mark, choosing either to dismiss the mark as a false hit or add the finding to their previous unaided findings. Readers were also allowed to increase or decrease the confidence scores of their previous findings. The compilation of findings by the reader after being shown the CAD marks constitutes the reader’s aided findings. Thus, in this four-block design, each reader provided 100 interpretations (i.e. 50 images interpreted both with and without CAD). With 36 total readers, there were 3600 total interpretations.

If a patient had cancer, and the reader correctly located it, then the reader’s confidence score for that lesion became the reader’s score for the patient. If a patient had a cancer, and the reader did not locate it, then a confidence score of zero was assigned to the patient for that reader’s interpretation. For a patient without cancer, the highest confidence score assigned by the reader to any false lesions was used as the reader’s interpretation for that patient. If no false lesions were reported for a patient without cancer, then a confidence score of zero was assigned to that patient.

The nonparametric area under the ROC area was calculated for each reader without CAD and with CAD [23]. The method of DeLong et al. [23] was used to compute covariances for the OR and marginal-mean methods. Fourteen readers showed improvement in accuracy with CAD, 16 showed no change, and 6 showed reductions in accuracy with CAD. The mean ROC area over the 36 readers was 0.7735 without CAD and 0.7812 with CAD.

Table 5 summarizes the results of the three statistical methods. The SE of the difference is smallest for the three-sample U-statistic method and largest for the marginal mean ANOVA method. All three methods yield a non-significant result with 95% CIs containing zero. The lower and upper bounds on the CIs are quite similar, with the three-sample U-statistic method giving a slightly more narrow interval. Further results from the analysis are given in the Appendix.

Table 5.

Summary of Results of Three Methods for Breast Cancer Example

Method	Test statistic, p-value	Estimated difference (SE)	95% CI for difference
Marginal mean ANOVA	F=3.12, p=0.0786	0.0076 (0.00431)	[−0.0009, 0.0161]
Modified OR	F=3.37, p=0.0678	0.0076 (0.00415)	[−0.0005, 0.0159]
3-sample U-stats	F=3.55, p=0.0644	0.0076 (0.00404)	[−0.0005, 0.0157]

Conclusions

For typical multi-reader imaging studies, readers and verified cases are of limited quantity; the fully-crossed design has been used in order to achieve maximum power with these limited resources. Split-plot designs, however, have a number of advantages over the traditional fully-crossed design. First, there is considerable savings in the number of interpretations required of each reader. This can be a useful recruiting tool for MRMC studies, especially when each interpretation is cumbered by lengthy CRFs, multi-levels of imaging to review, and/or complicated diagnoses. The results in Table 3 suggest that a study design with more splits of readers and cases can increase efficiency with respect to total number of readings, as long as more readers can be recruited. We note, however, that investigators should be warned not to split the cases into too small-sized blocks because there will be fewer empirical operating points sampling the ROC space. There are even fewer operating points if there are ties in the data, which is common for studies with human readers. In general we recommend at least 20 diseased and 20 non-diseased cases per block.

A second advantage of the split-plot design is that it can be used to efficiently study multiple imaging tests. For example, in the breast CAD study illustrated here, we presented results for the comparison of readers’ unaided accuracy versus a CAD system, but, in fact, the study compared four CAD systems against readers’ unaided accuracy. Table 6 illustrates the full study design. Each reader interpreted all 200 cases: 50 with and without CAD 1, 50 cases with and without CAD 2, 50 cases with and without CAD 3, and 50 cases with and without CAD 4. Each image was interpreted by all 36 readers unaided and with one of the four CAD systems. Thus, the study took advantage of the increased power offered by the split-plot design with respect to total readings, compared with the fully-crossed design, to simultaneously evaluate four CAD systems.

Table 6.

Lay-out of 4-Block Split-Plot Design simultaneously evaluating 4 CAD systems

	Reader Block 1	Reader Block 2	Reader Block 3	Reader Block 4
Patient Block 1	Unaided vs. CAD 1	Unaided vs. CAD 2	Unaided vs. CAD 3	Unaided vs. CAD 4
Patient Block 2	Unaided vs. CAD 4	Unaided vs. CAD 1	Unaided vs. CAD 2	Unaided vs. CAD 3
Patient Block 3	Unaided vs. CAD 3	Unaided vs. CAD 4	Unaided vs. CAD 1	Unaided vs. CAD 2
Patient Block 4	Unaided vs. CAD 2	Unaided vs. CAD 3	Unaided vs. CAD 4	Unaided vs. CAD 1

^•Each reader block contained 9 readers. Each patient block contained 25 patients with cancer and 25 patients without cancer.

In this paper we presented three test statistics for the split-plot MRMC study design and compared their performance. These three methods have important differences. First, the variance estimators that the different methods use are not equivalent: the marginal-mean ANOVA method uses a correlated-error, three-way split-plot ANOVA with three covariances, the modified OR method uses a correlated error two-way factorial ANOVA with three covariances, and Gallas uses U-statistics. Second, the full three-sample U-statistic result differs from the OR and Hillis variance models in its level of detail. The full U-statistic result has 21 terms, 7 for the variance of modality 1, 7 for modality 2, and 7 for the covariance. The OR and Hillis models each have 7 variance-component parameters total (Note that without replications, only 6 of these parameters are estimable). The OR and Hillis variance models pool information across modalities. In contrast, the U-statistic variance includes all of the variance components related to the reader, case, modality, and disease status interactions, which can be particularly important for sizing future studies, though there is a cost. The U-statistic variance does not immediately generalize for measures of test accuracy that are not U-statistics, while the OR and Hillis methods can be applied to these other measures of test accuracy. Lastly, the marginal-mean ANOVA and OR methods require complete data, and the marginal-mean ANOVA model requires a balanced design (i.e. the same number of readers and cases in each block). In contrast, the U-statistic method can be used for incomplete and/or unbalanced designs.

Despite these differences, the three test statistics performed quite similarly. The type I error rates of the three methods tended to run slightly below the nominal level, the power of the three methods was nearly identical, and the confidence interval coverage was at the nominal level. Thus, all three test statistics performed well and similarly for the datasets in our simulation study.

For comparison, we also investigated a standard normal distribution for the pivotal statistic in Equation 9 (results not shown). As expected, the type one errors were inflated but tended to the nominal rate as the number of readers increased: 0.06–0.09 for J/G=3 and 5 and 0.05–0.065 for J/G=7.

Our simulation study does have several limitations. First, our study was limited to normally distributed decision scores. In many imaging trials, an ordinal scale (e.g. 1–5) is used to measure reader confidence. All three proposed methods can be applied to studies using an ordinal scale, although we did not evaluate the performance of the methods for ordinal data. Similarly, decision scores expressed on a semi-continuous scale (e.g. 0–100) often do not follow a normal distribution. For example, in the breast CAD study the distribution of confidence scores for non-cancer patients was skewed to the right with 65% of cases assigned a score of zero. The distribution of confidence scores for the cancer patients was skewed very slightly to the left, but the mode occurred at a confidence score of zero (27% of cancer cases had a confidence score of zero). We evaluated the type I error rate of the three test statistics when low scores are binned at a confidence score of zero similar to the data in the breast CAD study, and found that the type I error rates of all three methods remain close to the nominal level: 0.053 for all three methods. Second, we only considered two-block designs; future work should include an expanded range of study designs. Lastly, we only considered the simple case where the variance and the number of patients in the experiment are the same for diseased and non-diseased patients and the same for both modalities. More research is needed under other conditions to determine if any of the methods has clear advantages.

Appendix

Calculation of Mean Square Terms for OR method

In equation 3, MS(T) is the mean square of the modality effect and MS(T×R) is the mean square of the interaction of reader and modality:

$$\begin{array}{l}\text{MS}(\text{T})=\text{J}{\mathrm{\sum }}_{\text{i}}{({\widehat{\theta }}_{i.}-{\widehat{\theta }}_{\mathrm{..}})}^2/(\text{I}-1),\text{and}\\ \text{MS}(\text{T}\times \text{R})=\{1/(\text{J}-1)(\text{I}-1)\}{\mathrm{\sum }}_{\text{i}}{\mathrm{\sum }}_{\text{j}}{({\widehat{\theta }}_{ij}-{\widehat{\theta }}_{i.}-{\widehat{\theta }}_{.j}+{\widehat{\theta }}_{\mathrm{..}})}^2.\end{array}$$ [A1]

Note that, in the expressions above, θ̂_i. is the estimate of the ROC area for modality i, averaged over all J readers, θ̂._j is the estimate of the ROC area for reader j, averaged over all I modalities, and θ̂.. is the estimate of the ROC area, averaged over all readers and modalities:

$$\begin{array}{l}{\widehat{\theta }}_{i.}={\mathrm{\sum }}_{\text{j}}{\widehat{\theta }}_{ij}/\text{J}\\ {\widehat{\theta }}_{.j}={\mathrm{\sum }}_{\text{i}}{\widehat{\theta }}_{ij}/\text{I}\\ {\widehat{\theta }}_{\mathrm{..}}={\mathrm{\sum }}_{\text{i}}{\mathrm{\sum }}_{\text{j}}{\widehat{\theta }}_{ij}/\text{I}\times \text{J}\end{array}$$

where i=1, … I, and j=1,…J.

Rationale for Marginal-Mean Model Approach

The OR model for the usual fully-crossed modality-by-reader-by-case design can be shown to be the same as the model for the marginal means, across cases, of a conventional modality-by-reader-by-case ANOVA with reader and case as random factors and all possible interactions included. The OR F statistic can be derived by modifying the conventional F statistic by replacing mean squares involving case by error-covariance estimates for the marginal-means model. This produces a valid ANOVA F statistic for the marginal-means ANOVA model, and hence also for the OR model.

This general approach can easily be extended to the split-plot design as follows. For the conventional ANOVA model corresponding to the split-plot design with reader and case as random factors, with block and test as fixed factors and all possible interactions included, the resulting model for the marginal means across cases is given by

$$Y_{\mathit{ijg}}=\mu +{\tau }_i+{\gamma }_g+R_{j(g)}+{(\tau \gamma )}_{ig}+{(\tau R)}_{ij(g)}+{\epsilon }_{\mathit{ijg}}$$

where g = 1,…,G, i = 1,…, t, j = 1,…, r, where G is the number of blocks, t is the number of tests, r is the number of readers in each block, τ_i denotes the fixed effect of test, γ_g denotes the fixed effect of block, and (τγ)_ig denotes the fixed test-by-block interaction. The R_j(g) and (τR)_ij(g) are random reader and test-by-reader effects, nested within block; they are mutually independent and normally distributed with zero means and respective variances ${\sigma }_{R(G)}^2$ and ${\sigma }_{\tau R(G)}^2$, where the subscript R(G) is read “reader nested within group,” etc. The ε_ijg are normally distributed with zero mean and variance ${\sigma }_{\epsilon }^2$. The ε_ijg are independent of the R_j(g) and (τR)_ij(g). The covariances are defined by Cov₁ ≡ Cov (ε_ijg, ε_i′jg), Cov₂ ≡ Cov (ε_ijg, ε_ij′g), and Cov₃ ≡ (Cov (ε_ijg, ε_ijg) where i ≠ i′, j ≠ j′, and are subject to these constraints: Cov₁ ≥ Cov₃, Cov₂ ≥ Cov₃, Cov₃ ≥ 0. Thus this is a 3-way split-plot ANOVA with correlated errors, with test and block crossed and reader nested within block. Thus readers are the whole plots, test is the split-plot factor, and block is the whole-plot factor.

The F statistic given by Equation 5 resulted from modifying the F statistic for the conventional split-plot ANOVA model by replacing mean squares involving case by error-covariance estimates for the corresponding marginal-means model.

Background Work for the Three-Sample U-sample approach

Gallas [15] derived the variance of the reader-averaged non-parametric (trapezoidal) AUC from a fully-crossed study design and expressed it as a linear combination of success moments, second-order moments of the AUC kernel. Gallas also provided unbiased estimates of the moments, which, consequently, yield unbiased estimates of the variance of the reader-averaged AUC itself. This estimate was referred to as the one-shot estimate, as it did not rely on any resampling (the jackknife or bootstrap). Gallas et al. [24] later recognized that the variance derived was equivalent to a three-sample U-statistics result; the three samples correspond to readers, non-diseased cases, and diseased cases, resulting in the estimate of the covariance between θ̂_i. and θ̂_i′. given in equation 8. This decomposition was introduced by Barrett, Clarkson, and Krupinski (BCK) [25, 26]. The first component α_1ii′ is that due to the non-diseased population, α_2ii′ is that due to the diseased population, α_4ii′ is that due to the readers, and the remaining α’s are due to interactions of these three populations.

Gallas and Brown [20] generalized the variance derivation and estimation in Equation 8 to treat study designs that are not fully crossed. The only difference between the variance given in Equation 8 and that of a split-plot study design are the scaling factors for the α’s. The estimation of the scaling factors and the α’s is controlled by a design matrix that indicates whether or not a reader×case observation is included in the dataset. This generalization is used for the split-plot study designs.

Simulation Model

Roe and Metz [27] and Dorfman et al [28] described a method for simulating data for the MRMC fully-crossed study design. They assumed a linear effects model for the decision variables (i.e. test scores), X_ijkt,

$${\text{X}}_{\text{ijkt}}={\mu }_{\text{t}}+{\tau }_{\text{it}}+{\text{R}}_{\text{jt}}+{\text{C}}_{\text{kt}}+{(\tau \text{R})}_{\text{ijt}}+{(\tau \text{C})}_{\text{ikt}}+{(\text{RC})}_{\text{jkt}}+{(\tau \text{RC})}_{\text{ijkt}}+{\text{E}}_{\text{ijkt}},$$ [A2]

where X_ijkt is the test score assigned by the j-th reader to the k-th case with truth state t (t=0 for non-diseased patients and t=1 for diseased patients) imaged with modality i. Every effect on the right-hand side depends on the truth state t: μ_t is an intercept term, τ_it is the fixed effect due to the i-th modality, R_jt is the random effect due to the j-th reader, C_kt is the random effect due to the k-th case, (τR)_ijt is the random effect due to the interaction between modality and reader, (τC)_ikt is the random effect due to the interaction between modality and case, (RC)_jkt is the random effect due to the interaction between reader and case, (τRC)_ijkt is the random effect due to the three-way interaction between modality, reader, and patient, and E_ijkt is the pure random error term.

Parameter Estimates from Breast Cancer CAD study

The estimated variances and covariances from the CAD breast cancer example are presented in Tables A1 (from the three-sample U statistic method) and A2 (from the OR and marginal mean ANOVA methods). These estimates are often useful for planning the sample size of future MRMC studies [29]. Note that the average between-reader correlations were 0.463 (between readers interpreting the same cases with the same modality) and 0.457 (between readers interpreting the same cases with different modalities); it is the difference between these two correlations, 0.006, that affects the efficiency of the split-plot design. Although this difference is quite small, the 4-group-split-plot used in the breast CAD study is 5 times more efficient than the fully-crossed design for the same total number of reader interpretations, though the better efficiency does take four times as many cases.