Influence of buoyancy-driven flow on mass transfer in a two-stream microfluidic channel: Introduction of cryoprotective agents into cell suspensions

Abstract

A variety of methods have been used to introduce chemicals into a stream or to mix two or more streams of different compositions using microfluidic devices. In the following paper, the introduction of cryoprotective agents (CPAs) used during cryopreservation of cells in order to protect them from freezing injuries and increase viability post thaw is described. Dimethylsulphoxide (DMSO) is the most commonly used CPA. We aim to optimize the operating conditions of a two-stream microfluidic device to introduce a 10% vol/vol solution of DMSO into a cell suspension. Transport behavior of DMSO between two streams in the device has been experimentally characterized for a spectrum of flow conditions (0.7 < Re < 10), varying initial donor stream concentrations, (1% vol/vol < C_o < 15% vol/vol) and different flow rate fractions (0.23 < f_q < 0.77). The outlet cell stream concentration is analyzed for two different flow configurations: one with the cell stream flowing on top of the DMSO-rich donor stream, and the other with the cell stream flowing beneath the heavy DMSO-laden stream. We establish a transition from a diffusive mode of mass transfer to gravity-influenced convective currents for Atwood numbers (A_t) in the range of (1.7 × 10⁻³ < A_t < 3.1 × 10⁻³) for the latter configuration. Flow visualization with cells further our understanding of the effect of A_t on the nature of mass transport. Cell motion studies performed with Jurkat cells confirm a high cell recovery from the device while underscoring the need to collect both the streams at the outlet of the device and suggesting flow conditions that will help us achieve the target DMSO outlet concentration for clinical scale flow rates of the cell suspension.

INTRODUCTION

Biological cells are used for fundamental studies of physiological and pathological functions and for diagnostic, therapeutic, and epidemiologic purposes. Effective methods of preserving cells typically require the use of cryoprotective agents (CPAs), molecules that act to protect cells from the stresses of freezing and thawing. The most commonly used is dimethylsulphoxide (DMSO). The addition of CPAs increases the osmolarity of the preservation solution. Cells respond to this change in environment with rapid changes in cell volume as water leaves the cell followed by penetration of the CPA. These volumetric excursions, if significant enough, can result in cell lysis,³ and protocols typically specify a method of introducing a cryoprotectant solution, which results in minimal cell losses.

Conventional protocols for addition of CPAs into cell suspensions typically involve the use of step-wise introduction or syringe pumps^{6, 8} designed to gradually increase the extracellular concentration and thereby minimize volumetric excursions and cell losses. Cell losses due to osmotic stresses can be observed both during introduction and removal of cryopreservation solution. Recently, we affirmed the ability to use microfluidic channels for the extraction of DMSO from a cell stream.^{4, 13, 7} These studies demonstrated our ability to model theoretically and validate experimentally the transport of CPAs in the microfluidic stream. Song and colleagues in Ref. 18 have shown that microfluidic devices can be used to introduce and remove cryopreservation solutions for small flow rates ranging from 2 to 20 μl/min. Furthermore, the study suggests that the use of microfluidic devices reduces osmotic stress and improves cell recovery and viability post thaw.

Excellent reviews of the main issues associated with mixing at the microscale and diverse methods to cause mixing are provided by Ottino and Wiggins¹⁰ and Ye et al.¹¹ Most of the applications^{17, 15, 9} studied to date have used either dilute systems (e.g., the concentration of solute to be mixed is low) or streams of different compositions with similar density. Yamaguchi et al.¹⁴ have studied the effects of gravity in a micro channel using numerical simulations and confocal microscopy of blood serum with a phosphate buffer solution, assuming negligible diffusion and viscous effects. Song et al.¹⁸ models a microfluidic device with three flow channels placed side-by-side in a horizontal set up where in density disparities in the various streams have not been taken into consideration. In the case of large physical systems (oceans: salt and fresh water mixing; earth and atmosphere: heat transfer from the ground), buoyancy effects on mixing of fluids is well investigated. Debacq et al. draw important inferences on the influence of density gradients, suggesting gravity induced mixing of the miscible fluids in a vertical tube.² Such correlations and inferences cannot be directly incorporated in microfluidic systems owing to heightened surface effects in small scale systems¹ and hence warrants independent investigation. Therefore, prior work in the realm of microfluidic systems have not addressed the effect of density gradients between the different streams that flow through the device and how that can influence the chemical concentration profiles, in the presence of diffusive and viscous forces. In addition, most of the existing designs for devices that can introduce and remove CPAs¹⁸ operate on much smaller flow rates (<0.1 ml/min) as compared to clinical scale flow rates (2–3 ml/min).

Cryoprotective agents are typically used at high concentration (∼2 M) and are added to solutions of considerably lower concentration (<0.154 M). These two streams have been found to have considerably different densities and the objective of this investigation is to characterize the behavior (mass transfer and cell motion) in a two-stream microfluidic device for this situation. This study will permit us to elucidate the influence of buoyancy driven flow in a microfluidic channel and use this knowledge to optimize the introduction of solutions with minimal cell losses. Such a device is aimed to be a closed, continuously operating system with a great potential to be automated for operation. This type of device will have applications in a variety of contexts beyond cell preservation, including screening of drugs for personalized medicine applications and development of microfluidic culture environments.

METHODS

Flow device

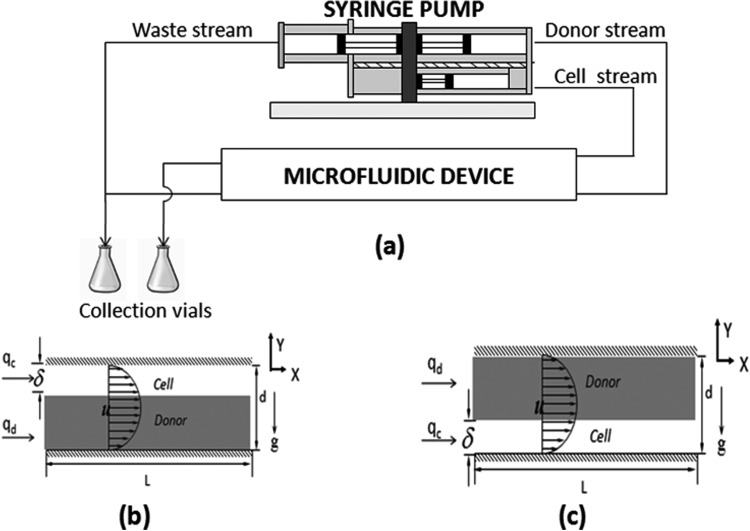
The objective of this investigation is to use a microfluidic channel to introduce DMSO into a cell stream. To that end, a microfluidic device was developed consisting of two streams flowing in parallel within a rectangular channel of constant cross sectional area as shown in Fig. 1a. The structure and geometry of the device have been previously described in more detail by Mata.^{12, 13} Briefly, two streams enter the device through adjacent inlets and are separated by a splitter plate, which acts to redirect flow so that the two streams flow in parallel. The flows are separated at the outlet of the device. The volumetric flow rates through the channel are controlled using a single syringe pump (Harvard Apparatus, Inc. Model 22). Samples of both the streams are collected at the outlet for further concentration analysis.

Figure 1.

(a) General experimental schematic; (b) flow configuration A consisting of the cell stream over the donor stream; (c) flow configuration B consisting of the donor stream over the cell stream.

Flow configurations and control

Two streams flow through the device: a cell stream that consists of phosphate buffered saline (PBS) solution (Fischer Scientific, Walkersville, MD) with or without Jurkat cells (ATCC TIB-1522, Manassas, VA), and the donor stream consisting of PBS with DMSO (Sigma, St. Louis, MO). DMSO will diffuse from the donor stream to the cell stream. The volumetric flow rate of the solutions is determined by the speed of the syringe pump. The flow rate fraction ($f_q$) is defined to be the ratio of the volume of the cell suspension (q_c) to that of the total volume flow (q_t) in the channel and is given by

$$\begin{array}{c}{f}_q=q_c/q_t,\\ q_t=q_c+q_d.\end{array}$$ (1)

Flow rate fractions that were used in the study included 0.23, 0.5, and 0.77. Volume flow rates for the cell stream ranged between 0.2 ml/min and 9.2 ml/min. Two flow configurations were used in the studies. The first configuration (configuration A) consists of the donor stream on the bottom and the cell stream on the top (Fig. 1b). Configuration B consists of the donor stream on the top and the cell stream on the bottom (Fig. 1c). For both of the configurations, the flow rate fraction is defined as given in Eq. 1. This flow rate fraction is a function of the relative depths (δ/d) of the cell stream and the donor streams in the channel.

DMSO concentration

The concentration of DMSO in each stream was quantified using spectrophotometry. The absorbance of a solution was measured using a spectrophotometer (SpectraMax Plus, Molecular Devices) at a wavelength of 209 nm. Solutions of interest were diluted until the concentration was between 1 × 10⁻⁴ M and 2 × 10⁻⁴ M, the range of linear variation of concentration with the absorbance. Optical densities were quantified and concentration determined based on a linear regression. Additional calibration was performed to determine dilution and formulation errors. More details on the method of calibration and analysis of data can be found in Ref. 13.

Solution density

The addition of DMSO to PBS increases the density of the solution, which may influence the concentration of DMSO at the outlet cell stream. DMSO solutions of various compositions were made (0%–15% vol/vol). The solution was transferred to a volumetric flask and the mass of solution measured. Density measurements were repeated 6 times. Fitting a linear equation to the data results in ρ(c) = 0.999 + 0.139 c, where c—vol/vol of DMSO in PBS; ρ—density of DMSO in g cm⁻³ (R² = 0.9952). Density measurements were recorded in a similar fashion for the cell stream containing the Jurkat cells. For all the cellular experiments in this work, we choose a 1.5% cell volume fraction (CVF) as the operating condition where CVF can be defined as

$$CVF=V_i/V_t,$$ (2)

where V_i is the intracellular volume and V_t is the total solution volume. Based on Mata's findings in Ref. 13, a 2% CVF at the inlet of the device exhibits high recovery of the cells at the exit of the device. The density of 1.5% CVF was estimated to be 1000.09 ± 0.004 kg m⁻³ in the same fashion as explained above and is hence only marginally heavier than plain PBS solution.

Flow visualization

We obtained still images of the distribution of Jurkat cells in the channel at proximal and distal locations through the length of the channel in order to quantify the influence of stream density differences on cell motion. A transparent version of the microfluidic channel was constructed for this purpose. A CCD camera (Diagnostic Instruments Inc., 11.2 Color) attached to a Leitz^® Laborlux D microscope and illuminated using bright field microscopy was used to obtain images of the cells.

RESULTS

Introduction of DMSO: Configuration A

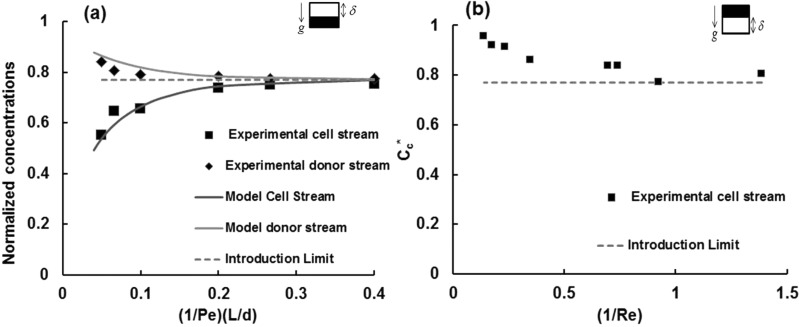
In configuration A, the heavier DMSO-rich donor stream is in the bottom and the cell stream is on the top. Based on our previous experiences with removal of DMSO,^{2, 3} we would expect DMSO to diffuse out of the donor stream and into the cell stream to gradually increase the concentration of the cell stream. The normalized cell stream concentration, $C_c^{*}$($C_c^{*}=C_c/C_o$) as a function of $\left(1/Pe\right)\left(L/d\right)$ for a single f_q (0.23) and C_o (15% vol/vol DMSO) is shown in Fig. 2. $\mathit{Pe}$ is the Peclet number, $Pe=d{U}_{\mathit{avg}}/D$, a ratio of diffusion to advection time scales based on the channel depth, d. The data were parameterized in this fashion because we have shown previously³ that for a constant value of $\mathit{Pe}$ the concentration data at different locations down the channel x/d collapse to a single curve. $C_c^{*}$ increases with $\left(1/Pe\right)\left(L/d\right)$ for a constant $f_q$ and $C_o$. The faster the average flow, the less time there is for molecules of DMSO to diffuse from the donor stream to the cell stream. The concentration of the outlet waste stream (what enters as the DMSO rich donor stream), $C_d^{*}$, was also determined as a function of $\left(1/Pe\right)\left(L/d\right)$ at a given $f_q$ and $C_o$. As would be expected, $C_d^{*}$ decreases (Fig. 2) with increase in $\left(1/Pe\right)\left(L/d\right)$. The value of the introduction limit (IL) is given in Fig. 2 which is defined as equilibrium non-dimensional DMSO concentration at the outlet of the channel. This is a function of $f_q$ and is given as, $IL=1-f_q$.

Figure 2.

(a) Flow configuration A: Normalized cell-stream concentration ($C_c^{*}$) vs (1/Pe)*(L/d) for Co = 15% vol/vol, f_q = 0.23; standard error = 3.1% and normalized donor stream concentration ($C_d^{*}$); standard error = 2.3%. (b) Flow configuration B: Normalized cell stream concentration ($C_c^{*}$) vs (1/Re) for C_o = 15% vol/vol and f_q = 0.23.

The normalized stream concentrations for both the cell stream ($C_c^{*}$) and the waste stream ($C_d^{*}$) can be compared to model predictions given in Refs. ^{2, 3}. The experimental values for C_c^* and C_d^* and model predictions for the same operating conditions (U and f_q) and channel geometry (L, d, w) match well.

Introduction of DMSO: Configuration B

Another flow configuration involves flow of the cell stream on the bottom and a donor stream containing higher concentrations of DMSO on the top. If this configuration is used for the same sample donor stream concentration and flow rate fraction as that described previously ($C_o$-15% vol/vol, $f_q$ = 0.23), a distinctly different behavior of the outlet concentration of the streams is noted. Specifically, the cell stream DMSO concentration, which is zero at the inlet of the device, should exhibit a slowly rising concentration with residence time in the channel ($L/U_{\mathit{avg}}$) if transport mechanism between the streams is dominated by diffusion, but instead the cell stream exhibits a very high concentration for short residence times in the device. Fig. 3 plots $C_c^{*}$ as a function of (1/Re), which directly relates to residence time. As (1/Re) increases, the residence time for the fluids within the channel also increases and $C_c^{*}$ approaches the introduction limit. This outcome suggests that for larger concentration differences, due to density gradient, the heavier DMSO molecules from the upper stream falls down into the lower stream and then, with time, diffuses back into the upper stream. This trend, of decreasing DMSO concentration in the cell stream with increasing residence time in the channel is plotted in Fig. 2b.

Figure 3.

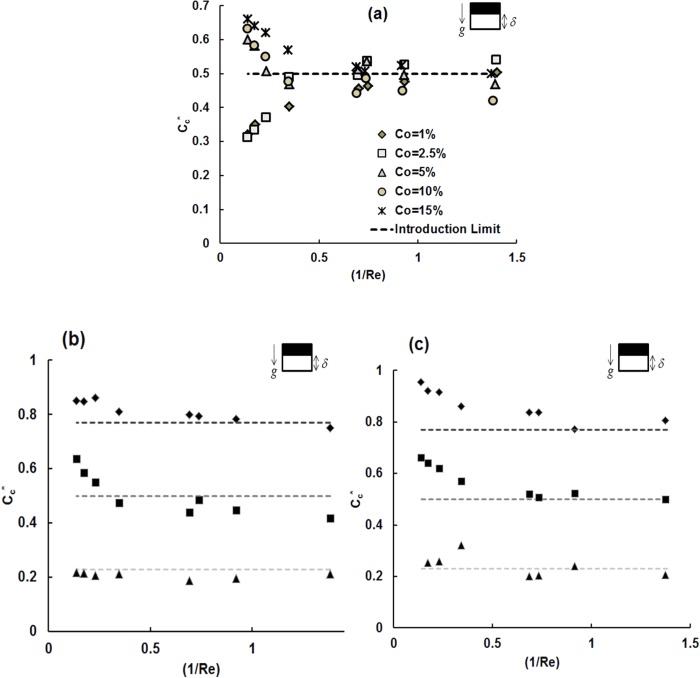
Configuration B (a) C_c* as a function of (1/Re) for different donor stream concentrations (% vol/vol) using f_q = 0.5; C_c* vs (1/Re) for different flow rate fraction values of f_q = 0.23 (rhombus), 0.5 (squares), 0.77 (triangles) in configuration B of the channel for a set of flow speeds for (b) C_o = 15% vol/vol, (c) C_o = 10% vol/vol.

The variation in outlet concentration of DMSO for different initial donor stream concentrations (C_o = 1%, 2.5%, 5%, 10%, 15% vol/vol) and various flow rate fractions (f_q = 0.23, 0.5, 0.77) in this configuration over a range of mean flow rates (1.6 –16 mm/s) in the channel has been determined.

Initial donor stream concentration

The initial donor stream concentration (C_o) was found to strongly influence the normalized cell stream outlet concentration, especially for lower residence times in the channel (1/Re). C_c* was determined for a range of initial donor stream concentrations and graphed as a function of (1/Re) and a specified flow rate fraction of f_q = 0.5. For low donor stream concentrations (1 and 2.5% vol/vol), concentration of DMSO in the cell stream at the device outlet increased gradually with increasing residence time in the channel (1/Re) suggesting that DMSO diffuses from the donor stream on top to the cell stream on the bottom. For donor stream concentrations ≥5% vol/vol, the concentration of the cell stream at the device outlet is very high for small residence times (1/Re) and decreases with increasing residence time, in contrast to what is observed for the lower initial donor stream concentrations.

Effect of flow rate fraction

As with our previous studies,^{4, 13}f_q plays an important role in the outlet concentration of streams leaving the device. The normalized cell stream concentration at the outlet as a function of 1/Re for different f_q (0.23, 0.5, 0.77) and C_o (10, 15% vol/vol) are given in Figs. 3b, 3c.

It is evident that the normalized concentration as a function of 1/Re exhibits a strong dependence on f_q. Slow flow rates (1/Re > 0.6) in the channel achieve equilibrium concentration between the two streams, as there is ample time for diffusion to smoothen the concentration gradients. For configuration B of the channel, it is interesting to note that for a flow rate fraction of 0.77, the outlet cell stream concentration attains the introduction limit for almost all flow rates of the streams in the channel. These results also suggest that the deviation from the introduction limit is the highest for a flow rate fraction of 0.5 when compared to the other flow rate fractions that were tested. This observation in particular led us to define a dimensionless deviation parameter ε^* (refer to Sec. 4A).

Cell motion experiments

All of the experiments described in the earlier sections were performed without cells in the device. Recovery of cells from the device is an important design parameter. We performed experiments with a CVF ∼ 1.5% and a flow rate fraction of f_q = 0.5 with initial donor stream concentration, C_o = 15% vol/vol DMSO. Two different flow rates for the cell stream of q_c = 1.2 ml/min and q_c = 2.4 ml/min were used. Cell counts at the outlet of the channel were performed using a hemocytometer and DMSO outlet concentration analysis was performed. Previous studies performed in our laboratory¹² have demonstrated that there is an initial startup period in which cells flowing into the device populate the device.

As a result, cell counts have been performed after steady state operation of the device has been achieved. Experiments were repeated twice for each of the Peclet numbers (flow rates), and the cell counts were obtained at the inlet and outlet of the device. This results in a total of eight trials for two different flow rates in two different configurations of the device. The number of cells at the outlet (cell and the waste streams) was obtained. The ratio of the cells present in the cell stream to the total number of cells flowing through the outlet is defined as f_c and is given by

$$f_c=\frac{CV{F}_{\mathit{out}}^{\mathit{cellstream}}}{CV{F}_{\mathit{out}}},$$ (3)

where $CV{F}_{\mathit{out}}^{\mathit{cellstream}}$ is the cell volume fraction at the cell stream outlet, $CV{F}_{\mathit{out}}$ is the total cell volume fraction at the outlet of the device. The ratio f_c was obtained for each of these trials and the average for each trial has been recorded in Table TABLE I.. The ratio $\frac{CV{F}_{\mathit{out}}}{CV{F}_{\mathit{in}}}$ is taken as an indicator of cell recovery of intact cells in the device.

TABLE I.

Cell recovery ($CV{F}_{\mathit{out}}/CV{F}_{\mathit{in}}$) and fraction of cells (f_c) present in the cell stream at the outlet of the channel, for f_q = 0.5, C_o = 15% vol/vol for configurations A and B.

Flow conditions		Configuration A			Configuration B
qc (ml/min)	Re	Cell recovery	fc	Cc vol/vol (%)	Cell recovery	fc	Cc vol/vol (%)
1.2	1.45	0.85 ± 0.08	0.52 ± 0.01	7.35	1.18 ± 0.01	0.48 ± 0.02	7.54
2.4	2.91	1.04 ± 0.01	0.75 ± 0.03	5.35	0.85 ± 0.03	0.26 ± 0.05	7.45

Cell motion and visualization

Images of cell position in the channel were recorded at two different spatial locations (a) a region close to entrance (8 cm from the entrance port), and (b) a region close to exit (18 cm from the entrance port of the channel) for configuration B with C_o = 15% vol/vol and C_o = 1% vol/vol and for a cell stream flow rate of 2.4 ml/min. The distribution of cells across the depth of the channel for two different initial donor stream DMSO concentrations is given in Fig. 4.

Figure 4.

Images for flow configuration B with DMSO stream on the top and cell stream with Jurkat cells flowing in the bottom (a) C_o = 15% vol/vol, entrance region (b) C_o = 15% vol/vol, exit region (c) C_o = 1% vol/vol, entrance region, (d) C_o = 1% vol/vol, exit region. The boxed region in each of these figures is sketched to highlight the region of cells along the depth of the channel.

DISCUSSION

Characterizing mass transfer

This investigation demonstrates that initial donor stream concentration directly affects the outlet concentration of the cell stream. For configuration A, in which the donor stream is at the bottom of the channel, transport of DMSO from the donor to the cell stream exhibits a behavior similar to that observed in Refs. ^{13, 5}. In this configuration, with the cells being present initially in the top stream, redistribution occurs between the two streams depending on the residence time in the channel. From Table TABLE I., it can be seen that for a faster flow rate of 2.4 ml/min, the fraction of cells in the cell stream, or the upper stream, at the exit is 0.75, implying that most of the cells remain in the upper stream with a few cells dropping down due to gravity. But for a slower flow rate, both the streams have an equal distribution of the cells at the outlet of the device. For configuration B, in which the donor stream is above the cell stream, for low values of C_o (1%, 2.5% vol/vol) diffusion-based transport of DMSO is seen. With increasing density contrasts due to higher C_o (10%, 15% vol/vol), DMSO molecules drop to the bottom of the channel and then diffuse upward depending on residence time.

When looking at flows that may be driven by density differences, it is helpful to define the Atwood number (A_t) for the experimental conditions studied in this investigation where A_t is given as

$$A_t=\frac{{\rho }_2-{\rho }_1}{{\rho }_2+{\rho }_1},$$ (4)

where ρ₁ and ρ₂ are the density of the two streams. Atwood number is a non-dimensional measure of the density differences between the two streams and is used in describing the growth rate of Rayleigh-Taylor instabilities.¹⁶A_t varies with initial donor stream concentration from 6.8 × 10⁻⁴ to 1.02 × 10⁻², respectively, for C_o varying from 1% to 15% vol/vol DMSO (Table TABLE II.). The trends in Fig. 3a suggest that for the smaller values of C_o, (1% vol/vol and 2.5% vol/vol), i.e., A_t≤ 1.71 × 10⁻³, transport of DMSO from top stream to the bottom stream is dominated by diffusion, which is why the concentration profile for these C_o values resemble the trend obtained for configuration A of the channel. As the density of the top stream increases, for A_t > 1.71 × 10⁻³, gravity causes the heavier stream to drop down and displace the fluid in the bottom stream. In this case, with increasing residence time, DMSO that has fallen into the bottom stream diffuses back into the top stream.

TABLE II.

Atwood (A_t) numbers for various initial donor stream concentration C_o.

Co vol/vol (%)	At
15	0.010173
10	0.006805
5	0.003414
2.5	0.00171
1	0.0006805

Whereas we do not directly visualize buoyancy-driven flow, cell visualization studies can help us indirectly visualize fluid flow patterns in the channel, as shown in Fig. 4. For an initial donor stream concentration of 15% vol/vol, A_t = 0.010173, cells are found to be concentrated in the top region of the channel suggesting that the DMSO-laden stream has dropped down to the bottom stream pushing up the cells that were originally in the cell stream at the bottom of the channel. For C_o = 1% vol/vol, we observe a more uniform distribution of the cells across the depth of the channel which is consistent with our argument of diffusion being the dominating mode of transport in the channel.

As with our previous studies,¹³f_q strongly influences the outlet concentrations measured. It is interesting to note that the introduction limit is attained even for the low residence times in the channel for a flow rate fraction of f_q = 0.77, as shown in Figs. 3b, 3c. In order to quantify the extent of mixing or the lack thereof for various flow conditions in configuration B, we introduce a variance parameter ε. There is a limit for the maximum attainable equilibrium concentration (C_eq) for a given donor stream concentration (C_o) and a flow rate fraction (f_q), which is given by

$$C_{\mathit{eq}}=C_o(1-f_q).$$ (5)

Ideally, we would like to reach this introduction limit for the cell stream at the outlet of the channel. The deviation of the cell stream concentration from the equilibrium concentration is given by ε, which is

$$\epsilon ={\left(C_c-C_{\mathit{eq}}\right)}^2.$$ (6)

A normalized dimensionless mixing coefficient, ε*, is developed based on ε, in the following fashion:

$$\begin{array}{c}{\epsilon }^{*}=1-\frac{\epsilon }{{\epsilon }_{\max }},\\ {\epsilon }_{\max }={C_{\mathrm{o**}}}^2{\left(1-f_q\right)}^2,\end{array}$$ (7)

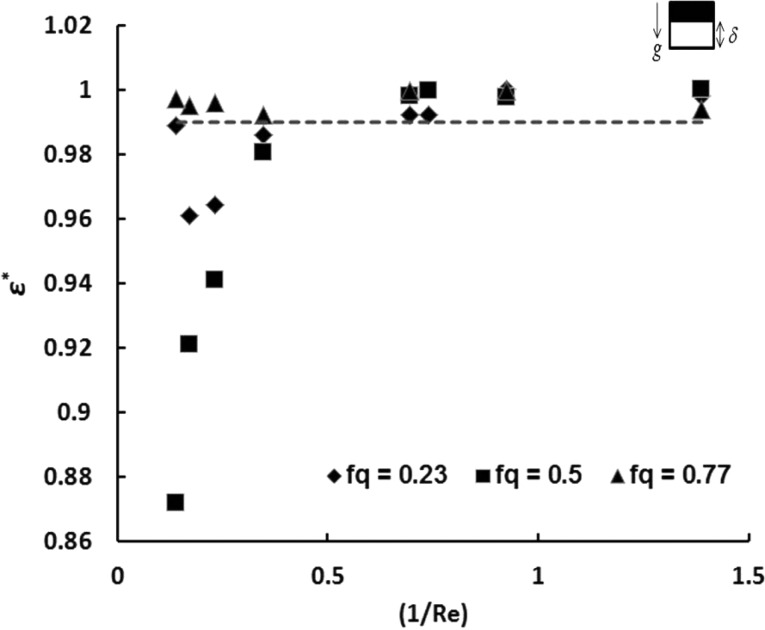
${\epsilon }_{\max }$ is the maximum possible value of deviation which will occur when C_c = 0. For higher values of ${\epsilon }^{*}$, there is less deviation from the introduction limit at a given flow rate fraction. We can now define a threshold mixing coefficient ${\epsilon }_{\mathit{th}}$, as the lower limit in order to assume homogenous DMSO concentration distribution at the outlet. When the outlet cell stream concentration is within 10% of the introduction limit, i.e., when $C_c^{*}\ge 0.9C_{\mathit{eq}}^{*}$, we consider the concentration distribution of DMSO to be uniform. This results in the threshold value of the mixing coefficient to be 0.99. Fig. 5 shows how ${\epsilon }^{*}$ varies with residence time in the channel for different flow rate fractions for C_o = 15% vol/vol wherein the dashed line represents the threshold value of the mixing coefficient, ${\epsilon }_{\mathit{th}}$). It is noteworthy to observe that for all of the experimental conditions in which f_q = 0.77 the streams are well mixed. For the low Re values (high residence times in the channel), uniform mixing of the streams is observed for all three flow rate fractions evaluated. For low residence times in the channel, the values of ${\epsilon }^{*}$ is the lowest for a flow rate fraction of 0.5 and highest for 0.77. The uniformity of concentration for the flow rate fraction of 0.77 can be attributed to (a) reduced mass fraction of the heavy donor stream resulting in lesser force due to density differences that causes the upturning of the heavier fluid (b) increase of average distance that the DMSO molecules need to travel to reach the cell stream affecting time taken for diffusion.

Figure 5.

ɛ* v/s (1/Re) for different flow rate fraction values of f_q = 0.23, 0.5, and 0.77 for configuration B.

Characterizing cell motion

Cell motion experiments were conducted with Jurkat cells for operating conditions described in Sec. 3C. We were particularly interested in understanding the manner in which cells moved or remained in the cell stream. As presented in Table TABLE II., the cell recovery ($CV{F}_{\mathit{out}}/CV{F}_{\mathit{in}}$) is very high (>85%) for all the trials.

For a flow rate of 1.2 ml/min (Pe = 2000), both configurations A and B have the cells equally distributed between the upper and the lower streams (given by f_c) at the outlet of the channel, and at the same time achieve a final outlet DMSO concentration in the range of 7%–8% vol/vol. For a faster flow rate of 2.4 ml/min (Pe = 4000), the final outlet DMSO concentration attains the introduction limit (∼8% vol/vol) for configuration B in contrast to a 5.4% vol/vol at the outlet cell stream in configuration A. For this flow rate, it can be noted from the f_c values in Table TABLE I. that for configuration A only one third of the cells remain intact in the cell (upper) stream (as f_c = 0.75). The fraction of the cells that do fall down to the bottom stream do so because of sedimentation effects due to gravity. For configuration B, however, most of the cells are displaced to the upper stream (f_c = 0.26) from their original location. This observation leads us to infer the following: First, the effect of density differences between the streams due to the initial donor stream concentration of 15% vol/vol DMSO results in the displacement of the cells from the bottom of the channel to the upper stream for configuration B. Second, the extent of lift-off of the cells in this configuration is directly related to the magnitude of buoyant force that acts on the cells (proportional to the difference between the cell density, ${\rho }_{\mathit{cell}}$ and the density of DMSO laden PBS stream, ρ). This explains why for the situation of smaller initial donor stream concentration (such as 1% vol/vol), which would result in relatively lower buoyant force, the cells are imaged to be almost uniformly distributed within the channel as shown in Figs. 4c, 4d.

The above results indicate that for a target outlet DMSO concentration of about 8% vol/vol with f_q = 0.5 in our microfluidic device, irrespective of the flow rates chosen for operation, both the streams will have to be collected at the outlet to recover all the cells that flow into the device. For a flow rate 1.2 ml/min, it essentially does not make a difference which configuration we use for the device as the introduction limit is attained and the cells redistribute themselves equally between the streams for both these cases. However, for a faster flow rate, configuration B is preferable for use to configuration A, as the introduction limit for concentration of DMSO is attained and the cells will be suspended in a uniform outlet DMSO concentration of about 7.5% vol/vol, even if distributed unevenly between the two streams.

The performed study helps us to understand that the effects of density gradients between the streams cannot be ignored, especially for the flow configuration with a heavy DMSO-laden stream on top of the cell suspension. But then, it is limited in its scope of proving the viability of the cells post processing since only cell recovery fraction has been determined in this study. It is anticipated from earlier work by Mata¹² and Song¹⁸ that cell viabilities, in general, are much higher when a microfluidic-based approach is used over typical cryopreservation protocols. In addition, the cells are not modeled individually for thorough calculations of particle level forces acting on the cells. Therefore, any cell density changes that might occur in the cell during loading and unloading of the CPA is not explicitly measured or taken into account in the model. The cells in our experiments are only marginally denser than PBS and the density changes due to CPA loading have been found to be insignificant to measure. Based on the impact of cell density changes due to CPA loading, one can expect to see different trends for cell motion within the channel.

CONCLUSIONS

The experiments demonstrated in this paper lead us into drawing the following conclusions about using the two-stream microfluidic channel for introduction of DMSO into a cell suspension.

First, the numerical diffusion transport model correlates very well with the experimental results for configuration A. Contrasting trends are observed (depending on the initial donor stream concentration), especially for low residence times, in the alternate flow configuration since the buoyant forces dominate over diffusion forces. Molecular diffusion prevails for all flow conditions when there is enough residence time which is directly related to average flow rate of the fluids into the device.

Second, we have asserted the significance of the Atwood number (A_t) to predict the relative importance of buoyancy and diffusion forces and on the extent of mixing of the fluids in configuration B. Somewhere in the range of 1.17 × 10⁻³ < A_t < 3.1 × 10⁻³, there lies a point where buoyancy becomes a more dominant mode of transport as compared to diffusion. This is why we see different trends for the concentration profiles for A_t = 1.17 × 10⁻³ as compared to A_t = 3.1 × 10⁻³. For A_t > 1.17 × 10⁻³, we observe that inertial forces dominate over molecular diffusion. Flow rate fraction, another critical dimensionless parameter also influences the extent of mixing. For f_q = 0.77, homogenous mixing (${\epsilon }^{*}\ge {\epsilon }_{\mathit{th}}$) was observed for all flow rate values of the fluids within the channel.

Finally, we have established that the target concentration of 7%–8% vol/vol DMSO can be obtained by operating this two-stream device by using a 15% vol/vol initial donor stream concentration (C_o) and a flow rate fraction of 0.5 (f_q) for either of the two flow configurations and by collecting the outlet streams together. The same result can be achieved for faster flow rates in the device for configuration B due to additional buoyancy forces acting on the system.

NOMENCLATURE

$A_t$

Atwood number

$C_c$

Outlet cell stream concentration (percentage volume fraction of DMSO) (ml ml⁻¹)

$C_c^{*}$

Normalized outlet cell stream concentration of DMSO

$C_d^{*}$

Normalized outlet waste stream concentration of DMSO

$C_{\mathit{eq}}$

Equilibrium concentration of DMSO (percentage volume fraction of DMSO) (ml ml⁻¹)

$C_o$

Initial donor stream concentration at inlet (percentage volume fraction of DMSO) (ml ml⁻¹)

$CV{F}_{\mathit{in}}$

Cell volume fraction of intact cells at the inlet

$CV{F}_{\mathit{out}}$

Cell volume fraction of intact cells at the outlet

$CV{F}_{\mathit{out}}^{\mathit{cellstream}}$

Cell volume fraction of intact cells at the cell stream outlet

D

Diffusivity of DMSO in water (m² s⁻¹)

d

Depth of microfluidic channel (cm)

DMSO

Dimethylsulphoxide

$f_c$

Cell fraction at the outlet of the channel

$f_q$

Flow rate fraction

$\mathit{IL}$

Introduction limit for the channel

L

Length of the channel (cm)

$\mathit{Pe}$

Peclet number

$q_c$

Volume flow rate of the cell stream (ml min⁻¹)

$q_d$

Volume flow rate in of the donor stream (ml min⁻¹)

Re

Reynolds number

$U_{\mathit{avg}}$

Average flow rate of fluids into the channel (m s⁻¹)

$V_i$

Intracellular volume of Jurkat cells (cm³)

$V_t$

Total local volume (cm³)

w

Width of the channel (cm)

δ

Depth of the cell stream in the channel (cm)

ε

Variance/deviation parameter

${\epsilon }_{\max }$

Maximum deviation for a given C_o and f_q

${\epsilon }_{\mathit{th}}$

Threshold value of mixing coefficient for uniform mixing

${\epsilon }^{*}$

Dimensionless mixing coefficient

ρ

Density (kg m⁻³)

${\rho }_{\mathit{cell}}$

Cell density (g cm⁻³)