Interpolation of tabulated proton Bragg peaks

Abstract

Treatment planning databases for pencil beam scanning PBS can be large, difficult to manage, and problematic for quality assurance when they contain tabulated Bragg peaks at small range resolution. Smaller range resolution, in the absence of an accurate interpolation method, improves the accuracy in dose calculations. In this work, we derive an approximate scaling function to interpolate between tabulated Bragg peaks, determine the accuracy of this interpolation technique, and determine the minimum number of tabulated peaks in a treatment planning database. With the new interpolation technique, three tabulated mono-energetic Bragg peaks (N =3) is a suitable lower limit for N to achieve interpolation accuracy better than ±1% of the maximum dose in pristine and spread out Bragg peaks for ranges between 6.8 and 32.1 cm of water.

1. Introduction

Dose calculations in pencil beam scanning PBS involve summations over depth-dose distributions of unmodified proton beams of various ranges. Bortfeld 1997 [1] gives an analytical expression for the unmodified proton depth-dose distribution, but the accuracy of the expression is not sufficient for treatment planning purposes [2].

Tabulated proton Bragg peak databases can be cumbersome when they contain every range deliverable by a machine. One method of interpolating between a subset of peaks is proposed by Kramer et al 2000 [3] for heavy ions. The method normalizes the depth by dividing by range and uses linear interpolation at each normalized depth to obtain a Bragg peak of intermediate range. Kramer’s Bragg peak database contains 45 simulated peaks between 50 and 500 MeV/u.

The data requirements for measured Bragg peaks for equipment and treatment planning commissioning are complicated [4] and may require many individual measurements [5]. An accurate interpolation technique can greatly facilitate these measurements. In this work, we use Bortfeld’s analytic expression to derive an approximate scaling function for mono-energetic proton Bragg peaks. We use this scaling function to interpolate between tabulated peaks generated by Monte Carlo in Clasie et al 2012 [4].

2. Methods

2.1. An approximate scaling function for Bragg peaks

We define: range, R, as the depth in water corresponding to 80% of the maximum dose; z as the geometric depth in water; and, t ≡ z/R as the normalized depth. Using the analytic Bragg peak formula in Bortfeld 1997 [1] and additional approximations described in Appendix A, Bragg peaks of mono-energetic proton beams have the functional form

$$D(t,R)\approx R^{n_1(t)}{Q}_1(t)$$ (1)

where D is the dose per unit proton fluence and n₁(t) and Q₁(t) are independent of R. In practice, the function Q₁(t) will depend weakly on R which ultimately affects the minimum number of tabulated Bragg peaks in the treatment planning database for a given level of accuracy.

2.2. Interpolation method

The interpolation of two Bragg peaks of range R₁ and R₂ to one of range R proceeds as follows. The depth ordinates of the two Bragg peaks are divided by by R₁ and R₂ resulting in dose as a function of normalized depth, D(t, R₁) and D(t, R₂), respectively. At a given t, Eq. 1 becomes a simple power law function of R which we use to interpolate between the values of R₁ and R₂ to R at the same normalized depth. After taking the natural logarithm of both sides of Eq. 1

$$ln(D(t,R))\approx ln(Q_1(t))+n_1(t)\times ln(R),$$ (2)

and the log of the dose depends linearly on the log of the range at the given t. Thus, the interpolation of the dose at arbitrary t and R is given by

$$ln(D(t,R))\approx ln(D(t,R_1))+\frac{ln(R)-ln(R_1)}{ln(R_2)-ln(R_1)}\times [ln(D(t,R_2))-ln(D(t,R_1))]$$ (3)

For this interpolation method, therefore, the functions n₁(t) and Q₁(t) can be arbitrary and we do not need knowledge of their shape. We do need Q₁(t, R) to be mostly independent of R.

3. Results

Fig. 1 shows that Q₁(t, R) is a slowly varying function of R and is, in fact, independent of R within ±4% over the entire 2-dimensional region 6.8 ≤ R ≤ 32.1 cm H₂0 and 0 ≤ t ≤ 1.01. The accuracy of the interpolation method is improved beyond the ±4% level by increasing the number of Bragg peaks in the database thus interpolating over a smaller R interval.

Figure 1.

Functions n₁(t) (left) and Q₁(t, R) (right) from Eq. 1 calculated using the database of Bragg peaks from Clasie et al 2012 [4] which has mono-energetic proton beams incident on a water phantom. Proton ranges, R [cm H₂0], are indicated within (b). These data show that Q₁(t, R) is a slowly varying function of R.

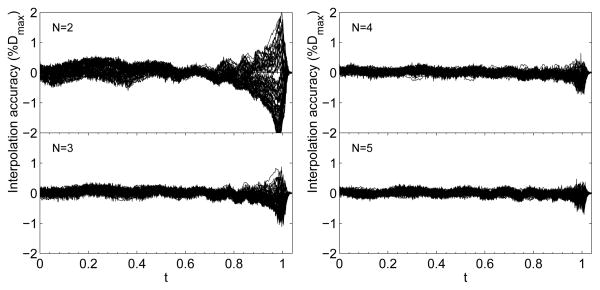
An extended database of mono-energetic Bragg peaks from Clasie et al 2012 [4], generated by Monte Carlo in steps of 0.5 cm H₂0 from 6.8 to 32.1 cm H₂0, are used to test the interpolation method. A subset of N peaks are selected, interpolated, and compared to the complete set of peaks and the interpolation accuracy is the dose difference between the interpolated peaks and peaks from the extended database. The interpolation accuracy improves with increasing N and converges within 1%D_max for N ≥ 3 (Fig. 2). For each N, the peaks are selected at ranges that optimize the interpolation accuracy (for N =3, R =7.9, 17.6 and 29.9 cm of water).

Figure 2.

The interpolation accuracy, defined in the text, as a percentage of D_max(R) (%D_max) for 2≤ N ≤5. The black band in each figure is composed of lines where each line is the accuracy of an interpolated Bragg peak for each R in the extended database between 6.8 and 32.1 cm of water. The accuracy converges within 1%D_max for N ≥ 3.

Measured pencil beams, especially those produced by a cyclotron, have a non-zero energy spread σ_E(R). These are modeled by convolving the interpolated mono-energetic peaks with σ_E(R), when known from the beam-optics or through measurement. If, however, one were to apply the interpolation method to non-zero energy spread pencil beams, then the interpolation accuracy depends on σ_E(R). For the energy spread function in Clasie et al 2012 [4], and if the interpolation method of Eq. 3 were used, then N =6 peaks in the treatment planning database would be the lower limit for N for an accuracy better than 1%D_max.

In treatment planning, we are not only concerned with the interpolation accuracy of pristine peaks but also with the accuracy of spread out Bragg peaks (SOBPs). Fig. 3a shows SOBPs generated from the extended, mono-energetic database with large, middle, and small range and modulations. Interpolated peaks using the N =3 mono-energetic database are multiplied by the same SOBP weights (number of protons in each pristine peak) as Fig. 3a and the resulting dose distributions are compared to the original SOBPs and the results are in Fig. 3b. The interpolation accuracy is better than 1%D_presc for these SOBPs. If, however, the interpolation method were applied to the non-zero energy spread beams and used to create SOBPs then we find that N =6 peaks are necessary for an interpolation accuracy better than 1%D_presc.

Figure 3.

(a) SOBP depth-dose distributions of various range and modulations generated from the extended mono-energetic Bragg peak database. (b) The difference between the dose distributions in (a) and distributions generated from the N =3 mono-energetic Bragg peak database as a percentage of the maximum dose in the SOBP (%Dpresc). The interpolation error of the N =3 database is better than l%Dpresc.

4. Conclusions

We derived an approximate scaling function for proton Bragg peaks using the analytical description in Bortfeld 1997 [1]. This results in a simple and accurate interpolation method (Eq. 3) for interpolating between tabulated Bragg peaks. With this method, a database consisting of three tabulated mono-energetic peaks (N = 3) is a suitable lower limit for N to achieve an interpolation accuracy better than ±1% D_max and ±1% D_presc for pristine Bragg peak and SOBP dose distributions, respectively, between 6.8 ≤ R ≤ 32.1 cm H₂0.

Appendix A. Derivation of the approximate Bragg peak scaling function

Bortfeld 1997 [1] gives the linear stopping power, S(t, R), of a monoenergetic proton beam as

$$S(t,R)=c_1{R}^{\frac{1}{p}-1}{(1-t)}^{\frac{1}{p}-1},$$ (A.1)

where c₁ and p are constants. Bortfeld incorporates range straggling by convolving the dose deposited in the absence of straggling with the Gaussian kernel

$$K(z,\overline{z})=\frac{1}{\sqrt{2\pi }\sigma }exp\left(-\frac{{(z-\overline{z})}^2}{2{\sigma }^2}\right),$$ (A.2)

where z̄ is the integration variable and σ =0.012 cm (R/1 cm)^0.935. We use a similar and simpler form of the Gaussian spread, instead, namely σ ≈ c₂R where c₂ is a constant, and the convolution with this Gaussian spread becomes

$$\begin{array}{l}S(t,R)=c_1{R}^{\frac{1}{p}-1}{\int }_{-\infty }^R{(1-\frac{\overline{z}}{R})}^{\frac{1}{p}-1}\frac{1}{\sqrt{2\pi }{c}_{2}R}exp\left(-\frac{{(z-\overline{z})}^2}{2c_2^2{R}^2}\right)\text{d}\overline{z}\\ =c_1{R}^{\frac{1}{p}-1}{\int }_{-\infty }^1{(1-\overline{t})}^{\frac{1}{p}-1}\frac{1}{\sqrt{2\pi }{c}_2}exp\left(\frac{-{(t-\overline{t})}^2}{2c_2^2}\right)\text{d}\overline{t}\\ =R^{n_2}{Q}_2(t),\end{array}$$ (A.3)

where t̄ = z̄/R, n₂ is a constant, and Q₂(t) is defined as c₁ multiplied by the integral. If we ignore the loss of fluence of protons due to nuclear interactions, then D(t, R) ∝ S(t, R) and we arrive at the same functional form as Eq. 1.

Eq. 1 has an exponent n₁(t) that depends on t, unlike the constant exponent n₂ in Eq. A.3. This additional degree of freedom in n₁(t) is used to partially compensate for the approximations. The new function Q₁(t) in Eq. 1 has the same shape as Q₂(t) in the limit that the accuracy of the approximations approaches zero.