Algorithms used in heterogeneous dose calculations show systematic differences as measured with the Radiological Physics Center’s anthropomorphic thorax phantom used for RTOG credentialing

Abstract

Purpose

To determine the impact of treatment planning algorithm on the accuracy of heterogeneous dose calculations in the Radiological Physics Center (RPC) thorax phantom.

Methods and Materials

We retrospectively analyzed the results of 304 irradiations of the RPC thorax phantom at 221 different institutions as part of credentialing for RTOG clinical trials; the irradiations were all done using 6-MV beams. Treatment plans included those for intensity-modulated radiation therapy (IMRT) as well as 3D conformal therapy (3D CRT). Heterogeneous plans were developed using Monte Carlo (MC), convolution/superposition (CS) and the anisotropic analytic algorithm (AAA), as well as pencil beam (PB) algorithms. For each plan and delivery, the absolute dose measured in the center of a lung target was compared to the calculated dose, as was the planar dose in 3 orthogonal planes. The difference between measured and calculated dose was examined as a function of planning algorithm as well as use of IMRT.

Results

PB algorithms overestimated the dose delivered to the center of the target by 4.9% on average. Surprisingly, CS algorithms and AAA also showed a systematic overestimation of the dose to the center of the target, by 3.7% on average. In contrast, the MC algorithm dose calculations agreed with measurement within 0.6% on average. There was no difference observed between IMRT and 3D CRT calculation accuracy.

Conclusion

Unexpectedly, advanced treatment planning systems (those using CS and AAA algorithms) overestimated the dose that was delivered to the lung target. This issue requires attention in terms of heterogeneity calculations and potentially in terms of clinical practice.

Introduction

Radiation therapy is a standard treatment for lung cancer. However, accurate determination of the dose distribution is particularly challenging due to the highly heterogeneous nature of the relevant patient anatomy within the thorax. Homogeneous dose calculation algorithms offer poor agreement with delivered dose to both the bulk and the periphery of the tumor (1–3).

To properly account for thoracic anatomy, heterogeneity corrected dose calculation algorithms are required. However, there is considerable variability in the nature of heterogeneous dose calculation algorithms, as has been well described (4,5). The simplest algorithms are pencil beam (PB) algorithms, employed with simple corrections such as Batho or Clarkson scatter integration. These heterogeneity correction algorithms have been shown to be dosimetrically inaccurate, by measurement in anthropomorphic phantoms (6–8) and recalculation in patient anatomy using Monte Carlo (MC) (1,5,9–10). Thoracic plans developed with PB algorithms overestimate the dose delivered to a target in the lung and do not properly account for the lateral loss of secondary electrons, resulting in inaccurate calculation of lung target coverage. Consequently, new National Cancer Institute (NCI)-sponsored clinical trials of thoracic radiation therapy do not allow the use of PB algorithms.

More advanced algorithms, including convolution/superposition (CS) and the anisotropic analytic algorithm (AAA) have been similarly evaluated in heterogeneous phantoms (relative to measurements) and patient anatomy (relative to MC calculations). Studies have generally found agreement within 3% of measured values (8,11) and within 2–3% of MC calculations (9,12,13). These observed differences are exacerbated in cases of low lung density (e.g., deep inspiration) and smaller target volumes (13,14). Although differences have been observed, the conclusions of such studies have consistently been that CS/AAA algorithms accurately describe the dose distribution in heterogeneous media.

The Radiological Physics Center (RPC) performs credentialing for institutions wishing to participate in NCI-sponsored clinical trials. One component of this credentialing process is an end-to-end phantom irradiation exercise, wherein the RPC provides an anthropomorphic phantom to an institution that must successfully develop and deliver a treatment plan meeting specific dose delivery objectives. One such phantom that has been irradiated for credentialing 304 times at 221 different institutions is the heterogeneous thorax phantom with a simulated lung tumor. A variety of treatment planning systems, beam models, and heterogeneous dose calculation algorithms have been used with this phantom. This paper presents a retrospective analysis of the results of these irradiations.

Methods and Materials

Phantom and Dosimeters

All planning and measurements were done using the RPC thorax phantom (Figure 1), which has been described previously in detail (15). Briefly, this mailable phantom is filled with water to represent soft tissue. It includes two lungs made of compressed cork (density: 0.33 g/cm³), a heart made of nylon (density: 1.15 g/cm³), and a spine made of polybutylene terephthalate-polyester (density: 1.31 g/cm³). A cylindrical target 3 cm in diameter and 5 cm long made of polystyrene (density: 1.04 g/cm³) is located in the center of the left lung. Densities and dimensions provide realistic conditions for the treatment planning and delivery process. This phantom has been in use since 2004, although >90% of irradiations have occurred since 2008.

Figure 1.

Radiological Physics Center thorax phantom and dosimetry insert (a), and corresponding computed tomography image set through the center of the target (b).

Absolute dose to the target center is measured with thermoluminescent dosimeters (TLD-100 powder; ThermoFisher Scientific, Waltham MA) following a previously detailed calibration and readout procedure with an uncertainty of ±2% (16). The TLD capsules are located at two locations in the center of the target (>1 cm from the target/lung interface). At each location, enough TLD powder is used to allow two readings that are averaged. Radiochromic film (EBT, EBT2; Ashland, Wayne NJ), placed orthogonally through the center of the target and extending out into the lung, is used to measure the dose distributions in the axial, coronal, and sagittal planes. The film dose is normalized to the absolute dose measured by the abutting TLD within the target.

Algorithms and Treatment Plans

Institutions irradiating the phantom as part of credentialing for RTOG clinical trials are instructed to treat the phantom as they would a patient. They are given specific instructions in terms of dose distribution requirements; however, the nature of the planning and delivery can vary between institutions based on their individual clinical practice. Treatment planning can be done using either intensity-modulated radiation therapy (IMRT) or 3-dimensional conformal radiotherapy (3D CRT). Additionally, the phantom can be used in conjunction with a motion table to simulate patient breathing. Motion can be accounted for with an internal target volume, by gating, or by using a breath-hold motion trajectory. All our analysis was based on irradiations performed at 6 MV.

For all irradiation scenarios, a treatment plan is generated by the participating institution to cover the cylindrical lung target (the clinical target volume [CTV]) expanded by 0.5 cm axially and 1 cm longitudinally to generate a planning target volume (PTV). Ninety-five percent of the PTV is required to be covered by the prescription isodose, with at least 99% of the PTV receiving 93% of the prescription dose. Dose constraints are also applied to the heart, cord, and lungs.

Broadly, three classes of algorithms were used to develop treatment plans for the phantom: MC algorithms, CS or AAA algorithms, and PB algorithms (Table 1). Because of documented problems with PB algorithms in heterogeneous media, PB algorithms have not been accepted for credentialing since 2009 (4–8). MC algorithms were primarily Cyberknife Multiplan (Accuray, Sunnyvale, CA), although three others were also used. CS/AAA algorithms included Eclipse AAA (Varian Medical Systems, Palo Alto, CA), Pinnacle CS (Phillips, Andover, MA), CMS Xio CS (Elekta, Stockholm, Sweden), and Hi-ART Tomotherapy (Accuray). PB algorithms were primarily Eclipse PBA (Varian Medical Systems), but six others were also used. All algorithms employed heterogeneity corrections.

Table 1.

Algorithms used for thorax phantom irradiation

Algorithm Class	Commercial Product	N
Monte Carlo		32
	MultiPlan	25
	BrainLab	3
	CMS Monaco	2
	In-house	1
CS/AAA*		236
	Eclipse AAA	98
	Pinnacle CS	90
	CMS Xio CS	23
	Tomotherapy CS	25
Pencil Beam		36
	Eclipse PBA	28
	Elekta PrecisePLAN	2
	BrainLab	2
	CMS Xio	1
	In-house	3

Abbreviations: CS/AAA, convolution/superposition and anisotropic analytic algorithms.

Analysis

For each TLD location, the measured dose was compared to the dose calculated by the treatment planning system, which was taken as the average dose over a contour corresponding to the TLD powder. The average agreement over the two TLD locations within the target was used for analysis.

Each algorithm was tested for how well the calculated dose compared to the TLD-measured dose in the target, and analysis of variance (ANOVA) was used to test for differences between the different algorithms. For plans developed with CS/AAA, further evaluation was conducted. First, those delivered with IMRT (n=136) were compared to those delivered as 3D conformal treatments (n=100). Second, those that used a motion table to deliver the treatment to a moving target (n=54) were compared to those that used a static phantom configuration (n=182). These results were compared with independent-samples t-tests. Finally, a regression analysis was conducted to determine if irradiation date was related to the results of the irradiations. All analysis was conducted in SPSS v.18 (IBM Corporation), using an alpha of 0.05.

Planar data were analyzed in one of two ways depending on date of irradiation (for 16 irradiations both analyses were conducted). For irradiations conducted prior to 2010 (n=188), distance-to-agreement was assessed between the measured and calculated doses in the dose fall-off region outside the PTV. This was the average agreement between measurement and calculation of the 25%, 50%, and 75% isodose lines in each of the six orthogonal directions defined by the film planes. For irradiations done as of 2010 (n=132), gamma analysis was conducted on the three films (over a region of the PTV + 2 cm), using 5%/5 mm acceptance criteria. Results for both types of planar analysis were compared between treatment algorithms. Because these data were not normally distributed, differences between algorithms were evaluated using the non-parametric Kruskal-Wallis test.

The analyzed data included data from institutions whose delivered doses did not meet credentialing criteria. However, known miss-irradiations were excluded from all analyses.

Results

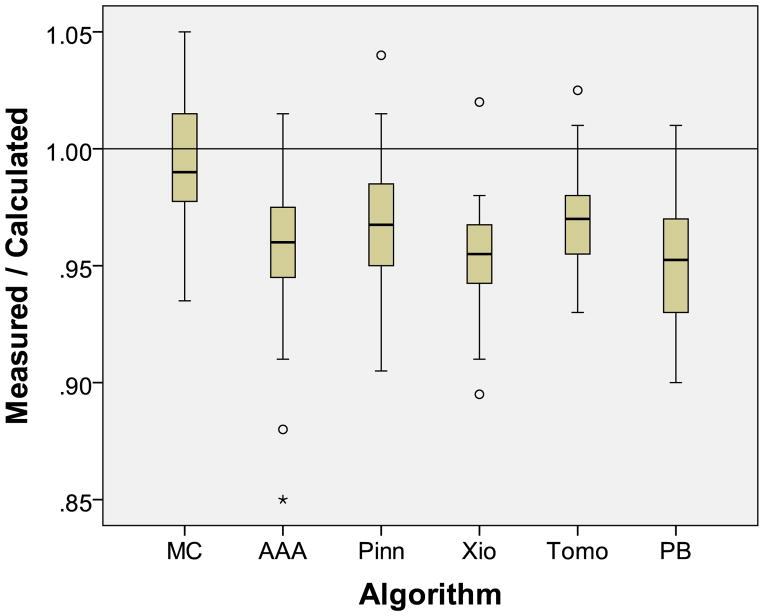
The ratios of TLD-measured to calculated dose to the target center are summarized for the six treatment planning algorithms in Table 2. The mean ratio for MC was 0.994 (not significantly different from unity, p=0.30). However, the mean ratios for the other algorithms were significantly different from unity (p<0.001). That is, all algorithms except MC algorithms overestimated the dose that was actually delivered to the tumor, by 3.9% on average (ranging between 2.9% and 4.9%). Even for the CS/AAA irradiations, the average overestimation of the dose to the center of the tumor was 3.7% (Figure 2).

Table 2.

Mean ratio and standard deviation (SD) of measured to planning system-calculated dose in the center of the lung target (Dose). Additionally, two-dimensional agreement between measured and planning system-calculated dose, including number of irradiations (N), and mean distance to agreement (DTA) or mean gamma value

Measure		Algorithm*
		MC	AAA	Pinn	Xio	Tomo	PB
Dose	Mean	0.994	0.959	0.968	0.955	0.971	0.951
	SD	0.030	0.027	0.024	0.025	0.024	0.027
DTA	N	11	54	56	18	13	36
	Mean	1.7	1.8	2.1	2.2	1.9	2.6
Gamma	N	19	56	39	6	12	0
	Mean	97.6	96.3	96.9	92.2	98.2	-

^*Algorithms are Monte Carlo (MC), Eclipse AAA (AAA), Pinnacle CS (Pinn), CMS Xio CS (Xio), Hi-ART Tomotherapy CS (Tomo), and pencil beam (PB).

Figure 2.

Ratio of the in-phantom-measured dose to the planning system-calculated dose to the center of the lung target by treatment planning algorithm. Algorithms are Monte Carlo (MC), Eclipse AAA (AAA), Pinnacle CS (Pinn), CMS Xio CS (Xio), Hi-ART Tomotherapy CS (Tomo), and pencil beam (PB).

Consistent with this, the mean ratio for MC (0.994, standard deviation [SD]=0.030) was significantly different from the mean ratio of the other five algorithms (p<0.01; Tukey HSD test). There was no significant difference in agreement between any of the CS/AAA algorithms (p=0.10). The PB algorithm results agreed worst with measurements; they were significantly worse than those obtained using Pinnacle (p=0.016) or Tomotherapy (p=0.039), although not significantly different from those obtained using Eclipse AAA (p=0.65) or CMS Xio (p=0.99) (Figure 2).

For the CS/AAA algorithms, further analysis indicated that there was no significant difference in how well the calculation matched the measured TLD dose for IMRT (mean=0.963, SD=0.026) versus 3D-CRT irradiations (mean=0.964, SD=0.025; t(233)=0.31, p=0.74], or for irradiations using the motion platform (mean=0.961, SD=0.025) versus static conditions (mean=0.964, SD=0.026; t(235)=0.68, p=0.53]. There was also no significant difference in agreement related to the irradiation date [β=−4.9×10⁻⁶, p=0.21].

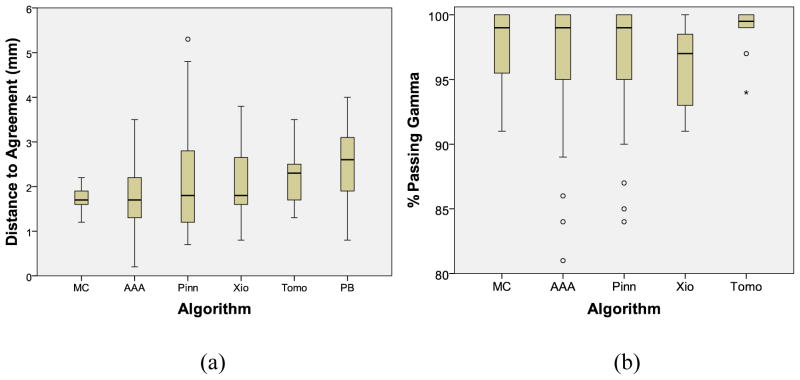
Planar agreement between treatment planning system calculations and film measurements (Table 2) showed small differences in the average distance to agreement between MC (1.7 mm), CS/AAA (2.0 mm), and PB (2.6 mm) algorithms. Considering all 6 algorithms separately, no significant difference existed between any of the MC or CS/AAA algorithms, although the PB algorithms showed significantly poorer agreement than Eclipse AAA [h=3.7, p=0.003] (Figure 3). Follow-up analysis, considering all CS/AAA algorithms as a single group found that the MC and CS/AAA algorithms remained equivalent, but both offered significantly better agreement than the PB algorithm [h>2.6, p<0.03]. For the more recent irradiations (since 2010), the average percentage of pixels passing the gamma analysis criterion ranged from 92.2% to 98.2% for each algorithm (Table 2). No PB data is in this series as this algorithm has not been accepted for credentialing since before implementation of gamma analysis. Comparing the CS/AAA and MC algorithms revealed no significant differences in terms of percentage of pixels passing gamma [h(4)=4.1, p=0.40] (Figure 3). Follow-up analysis also found no difference between MC and CS/AAA if all CS/AAA algorithms were considered as a single group.

Figure 3.

Two-dimensional agreement between the in-phantom-measured dose and the planning system-calculated dose, based on distance-to-agreement criteria (a) or the percentage of pixels passing the gamma criterion (b). Algorithms are Monte Carlo (MC), Eclipse AAA (AAA), Pinnacle CS (Pinn), CMS Xio CS (Xio), Hi-ART Tomotherapy CS (Tomo), and pencil beam (PB).

Discussion

The current work found sizeable differences in how well different heterogeneous calculation algorithms predicted the dose to a target inside the lung. It should be emphasized that this disagreement was observed in the center of the tumor, not at the periphery. The TLD locations were at least 1 cm from the lung/target interface, and for the low-energy beams employed in this study, the measurement would not be affected by buildup. Despite this, most of the algorithms overestimated the dose that was actually delivered. PB algorithms overestimated the dose to the target by 4.9% on average. Notably, the most common, and generally considered accurate CS and AAA algorithms also overestimated the dose to the tumor, by 3.7% on average (there was no difference between any of the CS/AAA algorithms). In contrast, MC algorithms, on average, agreed with measurements.

The RPC’s long history of TLD use and phantom credentialing for clinical trials adds credibility to the results of this work. Agreement between measured and calculated doses for 185 irradiations of the RPC’s nearly homogeneous anthropomorphic head and neck and prostate phantoms were within 1% on average using a variety of modern treatment planning algorithms (17). This indicates accuracy in both the dosimetry method, and common planning algorithms for homogeneous anthropomorphic phantoms.

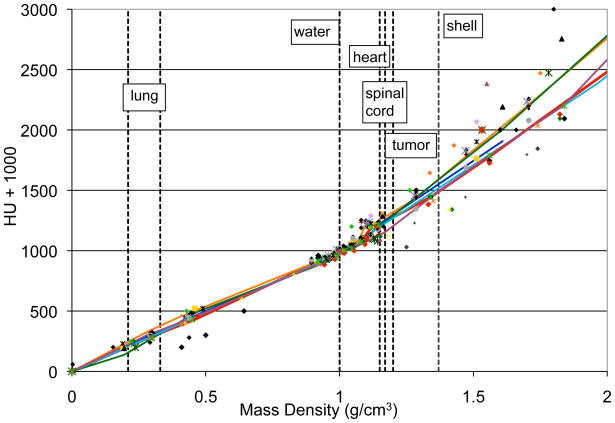
For the heterogeneous lung phantom, the most common planning systems agreed with measurement much less well. Previous studies have found specific treatment plans with differences of up to 3% between CS/AAA and MC algorithms or measurements (8–13), but average differences have typically been smaller. While this study showed a larger difference than the literature, it also did not require a normalization of treatment plans between algorithms, which can adjust plans by several percent (9) and could thereby mask differences between algorithms. Conceptually, there are several reasons why dosimetric discrepancies may exist between CS/AAA and MC algorithms, including radiation transport, dose reporting, and commissioning differences (10). While MC performs comprehensive radiation transport, CS/AAA algorithms make several computational approximations: scatter kernels are invariant with beam angle and medium, and scattered radiation is reduced to simple rays. Additionally, CS/AAA scatter kernels in heterogeneous media are typically scaled by physical density to account for the path length of scattered radiation. However, scaling by physical density has been shown to introduce errors of up to several percent as compared to more accurate radiation transport (18). Another difference is that MC algorithms typically report dose to the local medium, rather than dose to water (as reported by traditional algorithms), although this difference, in terms of calculated dose, is generally small (10). Finally, generation of the CT calibration curves also warrants attention. Hounsfield Units (HU) are converted to physical or electron density, typically based on calibration using a series of plastic inserts. A plastic-based calibration has been shown to introduce errors as compared to a stoichiometric calibration, although typically only by ~1% for dose in lung (19). While this could be a contributing factor to the dose discrepancies, this does not appear to be the case. Most MC calculations were done with Accuray Multiplan, which recommends its users perform an HU-to-physical density calibration based on plastic inserts (Accuray, personal communiqué). This is supported by the calibration curves used by institutions irradiating the lung phantom - Figure 4 shows the HU-physical density calibration curve for 33 institutions, including 6 using MC. Although there is spread in the data (particularly for large HUs), MC curves are very consistent with non-MC. Therefore, differences in calibration curves contribute to variations in the dose agreement, but not the systematic difference between MC and non-MC algorithms. Overall, it is possible that the dosimetric difference observed between algorithms resulted from a combination of the above factors.

Figure 4.

Hounsfield Unit to physical density calibration curves for 33 institutions that irradiated the phantom. Solid lines are MC-based systems while symbols are non-MC systems. Vertical dashed lines illustrate materials used in the phantom.

The reported absolute dose agreements (Table 2) are averages and all algorithms were associated with some large discrepancies with measurements (Figure 2): the standard deviation of these distributions ranged between 2.4 and 3.0%. However, due to the large number of samples, the standard deviation in the mean was less than 0.5% for each. Several sources of uncertainty contributed to the spread in the observed data, including uncertainty in the daily linear accelerator output during irradiation, HU-to-density calibration (Fig. 4), phantom setup, and TLD readout. However, in this study, these uncertainties are independent of the treatment planning system. For each algorithm, the distribution of agreement (Figure 2) was consistent with a normal distribution (based on a Kolmogorov-Smirnov test). This indicated that disagreement was not attributed to half the institutions disagreeing substantially and other half agreeing (producing a bimodal distribution). Rather, each algorithm performed consistently across the study.

The results of the planar analysis in this study found that PB algorithms performed poorest. No differences were seen in distance-to-agreement or gamma assessment between any of the MC or CS/AAA algorithms (Figures 3a and 3b), although the power of these analyses were substantially reduced because of reduced numbers (e.g., there were only 11 MC irradiations for distance-to-agreement analysis). Interestingly, the agreement for Tomotherapy was more consistent (tighter distribution) than for other algorithms (per Levene’s test; p=0.003). This may be due to the coordinated design of the Tomotherapy planning algorithm and accelerator, the consistent commissioning process for this planning system, or a combination of these factors.

The 5%/5mm criterion used for planar assessment appears larger than is commonly employed for clinical assessments. However, the film normalization is based on TLD dose measurements, which have a ±2% uncertainty, so this criterion is actually not dissimilar. The largest differences in planar agreement between different algorithms would be expected in the buildup region at the lung/tumor interface (7,9). However, the sensitivity of both the distance-to-agreement and the gamma analysis are somewhat limited in this study because the RPC phantom was designed for credentialing purposes, not for assessment of the dose in this particular region. Even still, as might be expected, better (non-PB) algorithms did show better agreement with measurements.

The potential overestimation of dose to the target in a thorax phantom warrants further study. If these phantom differences correspond to clinical under-dosing of lung tumors when non-MC algorithms are used in planning, then different dose prescriptions and/or reporting may be needed. Lower doses during radiotherapy of the lung have been associated with poorer local control, even with large ablative doses used in stereotactic body radiotherapy (20). Additional follow-up is also warranted in the context of the American Association of Physicists in Medicine Task Group 65 objectives (4), which state that heterogeneous dose calculation accuracy should be within 1–2%. Clearly, the vast majority of treatment plans studied did not meet this criterion.

Conclusions

More than 300 irradiations of the RPC’s heterogeneous thorax phantom revealed differences in the ability of different treatment planning heterogeneity-corrected dose calculation algorithms to determine dose to the center of a lung target. While MC algorithms, on average, agreed with measurement, Convolution Superposition and Anisotropic Analytic Algorithms significantly overestimated the dose to the center of the target, by 3.7% on average.

Further study is required to determine how these findings correspond to actual tumor under-doses in clinical care, which could substantially impact dose prescription and/or reporting. Further study is also required to determine the cause of this discrepancy between algorithms, as this level of accuracy is not consistent with heterogeneous algorithm objectives (4).

Summary.

We compared the accuracy of different heterogeneous dose calculation algorithms against measured doses in the center of a target in the Radiological Physics Center’s thorax phantom. While Monte Carlo algorithms accurately predicted the delivered dose, convolution superposition and anisotropic analytic algorithms overestimated the delivered dose by 3.7% on average. This dose difference requires attention in terms of heterogeneity calculations and potentially in terms of clinical practice.