An Analytic Expression for the Binormal Partial Area under the ROC Curve

1. INTRODUCTION

In diagnostic radiology receiver-operating-characteristic (ROC) curves are commonly used to quantify the accuracy with which a reader (typically a radiologist) can discriminate between images from nondiseased (or normal) and diseased (or abnormal) cases. Although the ROC curve concisely describes the trade-offs between sensitivity and specficity, typically accuracy is summarized by a summary index that is a function of the ROC curve. Commonly used summary indices include the area under the ROC curve (AUC), the partial area under the ROC curve (pAUC), sensitivity for a given specificity, and specificity for a given sensitivity. See Zou et al [1] for a concise introduction to ROC analysis.

A common method for estimating the ROC curve is likelihood estimation under the assumption of a latent binormal model [2–5]; alternatively, a generalized linear model approach can also be used [6, 7] based on the binormal model assumption. Under the latent binormal model assumption the ROC curve can be described by two parameters. Except for the pAUC, analytic expressions have been routinely employed for expressing the indices previously mentioned as a function of the binormal ROC curve parameters. Presently it is generally believed that the pAUC, assuming a latent binormal model, cannot be expressed as an analytic expression. For example, Pepe [8, p 84] states: “Unfortunately, a simple analytic expression does not exist for the pAUC summary measure. It must be calculated using numerical integration or a rational polynomial approximation.” Similarly, Zhou et al [9, p 128] state: “This partial area as it is known, is evaluated by numerical integration (McClish, 1989).” Although these methods can be programmed, having a simple expression for the pAUC would be much more convenient.

It is generally not known that Pan and Metz [10] provided analytic expressions for the two forms of pAUC. However, the expressions they provided were incorrect and they did not provide proofs for their results. More importantly, it is generally not known that Thompson and Zucchini [11] provided a correct analytic expression for one form of pAUC, as well as the proof. In fact, we only became aware of this latter result during the final stage of submitting this paper. The purpose of this paper is to bring to the attention of the reader the result provided by Thompson and Zucchini, extend their result to the second form of pAUC, and illustrate use of both pAUC expressions with a real data set that compares the relative performance of single spin-echo magnetic resonance imaging (SE MRI) to cinematic presentation of MRI (CINE MRI) for the detection of thoracic aortic dissection. In addition, we provide proofs for both results which are more accessible to radiology researchers and clinicians than the proof given by Thomas and Zucchini.

2. MATERIALS AND METHODS

2.1. Two different pAUCs

Let FPF and TPF denote false and true positive fractions for a given classification threshold such that an image with a test result equal or greater than the threshold is classified as diseased, and otherwise nondiseased. That is, FPF is the probability that a test result for a non-diseased subject exceeds the threshold and TPF is the probability that a test result for a diseased subject exceeds the threshold. The ROC curve is a plot of TPF versus FPF for all possible thresholds. FPF and TPF are the same as 1–specificity and sensitivity, respectively.

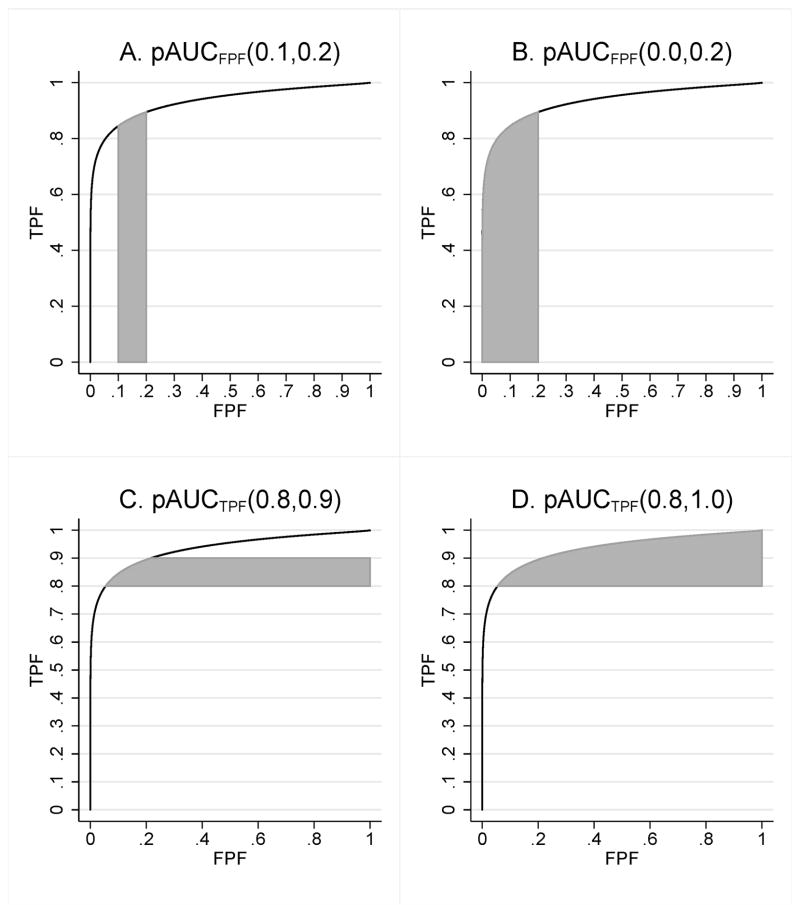
Two fundamentally different partial areas have been proposed [11–13]. One partial area corresponds to the area under an ROC curve over an interval (FPF₁ < FPF₂), which we denote by pAUC_FPF (FPF₁, FPF₂). This pAUC is illustrated in Figures 1A and 1B. Often this pAUC is normalized by dividing by FPF₂ – FPF₁, which allows it to be interpreted as the average value of TPF over all values of FPF between FPF₁ and FPF₂. This partial area is typically useful when a clinical task demands high specificity; for this situation FPF₁ = 0, FPF₂ is small (e.g., .10 or .20), and thus it is pAUC_FPF (0, FPF₂) that we are interested in computing. Because pAUC_FPF (FPF₁, FPF₂) = pAUC_FPF (0, FPF₂) – pAUC_FPF (0, FPF₁) for FPF₁ < FPF₂, it suffices to provide a a general formula only for pAUC_FPF (0, FPF₀). Walter [14] has discussed using this pAUC with summary ROC curves.

Figure 1.

Partial areas under the ROC curve

The other pAUC corresponds to the area to the right of the ROC curve in the interval (TPF₁ < TPF₂), which we denote by pAUC_TPF(TPF₁, TPF₂). This pAUC is illustrated in Figures 1C and 1D. Often this pAUC is normalized by dividing by TPF₂ – TPF₁, which allows it to be interpreted as the average value of 1–FPF (i.e., specificity) over all values of TPF between TPF₁ and TPF₂. This pAUC is typically useful when a clinical ask demands high sensitivity: TPF₁ is large, TPF₂ = 1, and thus it is pAUC_TPF (TPF₁, 1) that we are interested in computing. Because pAUC_TPF(TPF₁, TPF₂) = pAUC_TPF (TPF₁, 1) –pAUC_TPF (TPF₂, 1) for TPF₁ < TPF₂, it suffices to provide a a general formula only for pAUC_TPF (TPF₀, 1).

2.2. Analytic expressions for the pAUCs

In this section we present analytic expressions for the two forms of pAUC under the assumption of a latent binormal model. These expressions are the primary contribution of this paper. Corresponding proofs are presented in the Appendix.

2.2.1. Binormal model assumptions

Throughout we assume that the ROC curve is based on a latent binormal model. The latent binormal model assumes that the latent decision variable used to classify cases (or some unknown strictly increasing transformation of it) arises from a pair of normal densities corresponding to the nondiseased and diseased case populations, having generally different means and standard deviations. Because ROC curves are invariant under strictly increasing transformations of the decision variable, we can assume without loss of generality that the normal distribution for nondiseased cases has zero mean and unit standard deviation, whereas that for diseased cases has mean μ and standard deviation σ, where μ > 0 and σ > 0. Thus letting X and Y denote independent decision variables having the same distributions as the decision variable distributions for nondiseased and diseased cases, respectively, we are assuming that X ~ N (0, 1) and Y ~ N (μ, σ²).

2.2.2. Results for pAUC_FPF (0, FPF₀)

Let Φ (u) denote the standardized normal distribution function; i.e., Φ(u) = Pr (U < u) where U has a normal distribution with zero mean and unit variance. Let F_BVN (z, u; ρ) denote the standardized bivariate normal distribution function with correlation ρ; i.e., F_BVN (z, u; ρ) = Pr(Z < z and U < u), where Z and W jointly have a standardized bivariate normal distribution and ρ = corr(Z, U). This function is available in many statistical software programs, such as SAS, Stata, SPSS, and the freely available R program.

Assuming the binormal model described in Section 2.2.1, pAUC_FPF (0, FPF₀) is given by

$${\text{pAUC}}_{\text{FPF}}(0,{\text{FPF}}_0)=F_{\text{BVN}}\left(\frac{\mu }{\sqrt{1+{\sigma }^2}},{\mathrm{\Phi }}^{-1}({\text{FPF}}_0);-1/\sqrt{1+{\sigma }^2}\right)$$ (1)

In terms of the binormal parameters a = μ/σ and b = 1/σ, we can write Eq. 1 in the form

$${\text{pAUC}}_{\text{FPF}}(0,{\text{FPF}}_0)=F\left(\frac{a}{\sqrt{1+b^2}},{\mathrm{\Phi }}^{-1}({\text{FPF}}_0);-b/\sqrt{1+b^2}\right)$$ (2)

Equation 2 is also given by Thompson and Zucchini [11].

2.2.3. Results for pAUC_TPF (TPF₀, 1)

Assuming the binormal model described in Section 2.2.1, pAUC_TPF (TPF₀, 1) is given by

$${\text{pAUC}}_{\text{TPF}}({\text{TPF}}_0,1)=F_{\text{BVN}}\left(\frac{\mu }{\sqrt{1+{\sigma }^2}},{\mathrm{\Phi }}^{-1}(1-{\text{TPF}}_0);-\sigma /\sqrt{1+{\sigma }^2}\right)$$ (3)

In terms of the binormal parameters a = μ/σ and b = 1/σ, we can write Eq. (3) in the form

$${\text{pAUC}}_{\text{FPF}}({\text{TPF}}_0,1)=F_{\text{BVN}}\left(\frac{a}{\sqrt{1+b^2}},{\mathrm{\Phi }}^{-1}(1-{\text{TPF}}_0);-1/\sqrt{1+b^2}\right)$$ (4)

2.3. Estimation and inference for pAUC

Because pAUC is a function of the binormal ROC curve parameters, estimation of pAUC involves estimating the parameters for an ROC curve under the assumption of a latent bi-normal model and then using Eqs. 1–4 with the ROC curve parameters replaced by estimates. A likelihood or generalized linear model approach can be used to estimate the parameters, as mentioned in the Introduction. The variance of the pAUC estimate for one test or for the difference of two tests can be estimated using a first-order Taylor series approximation (the “delta method”) [12, 13, 15], or by resampling methods such as the bootstrap and jackknife [16, 17]. For multireader studies, the methods proposed by Dorfman, Berbaum, and Metz (DBM) [18] and by Obuchowski and Rockette (OR) [19] can be used for variance estimation and inference. Confidence intervals, assuming approximate normality for the pAUC estimates, can be based on the variance estimates in the usual way.

2.4. Example data set

To illustrate use of pAUCs, we consider an example from Carolyn Van Dyke, MD, that we have analyzed in previous papers. The study [20] compared the relative performance of single spin-echo magnetic resonance imaging (SE MRI) to cinematic presentation of MRI (CINE MRI) for the detection of thoracic aortic dissection. There were 45 patients with an aortic dissection and 69 patients without a dissection imaged with both SE MRI and CINE MRI. Five radiologists independently interpreted all of the images using a five-point ordinal scale: 1 = definitely no aortic dissection, 2 = probably no aortic dissection, 3 = unsure about aortic dissection, 4 = probably aortic dissection, and 5 = definitely aortic dissection. We estimate the ROC curves using likelihood estimation based on a latent binormal model [2–4]. From the binormal ROC curve parameters we estimate pAUCs corresponding to two different FPF and two different TPF intervals and compute corresponding standard deviations using the jackknife.

We also analyze the pAUC outcomes from the example data set using the multireader data analysis method proposed by Dorfman et al (DBM) [18, 21] and updated as described by Hillis et al [22]. This analysis tests if the means of the AUCs differ between the modalities. It has been shown that the method proposed by Obuchowski and Rockette (OR) [19], updated by the degrees of freedom estimate proposed by Hillis [23], yields results identical to those of DBM when the jackknife is used to estimate the error covariances. Thus our analysis results can be considered to have been produced by either method.

Data analyses were performed using SAS [24]. The binormal AUC was computed in SAS using a dynamic link library (DLL), written in Fortran 90 by Don Dorfman and Kevin Schartz, which was accessed from within the IML procedure in SAS; this DLL can be downloaded from http://perception.radiology.uiowa.edu. The SAS program for implementing this analysis [25], as well as a user-friendly stand-alone program [26] for implementing it, can also be downloaded from http://perception.radiology.uiowa.edu.

3. RESULTS

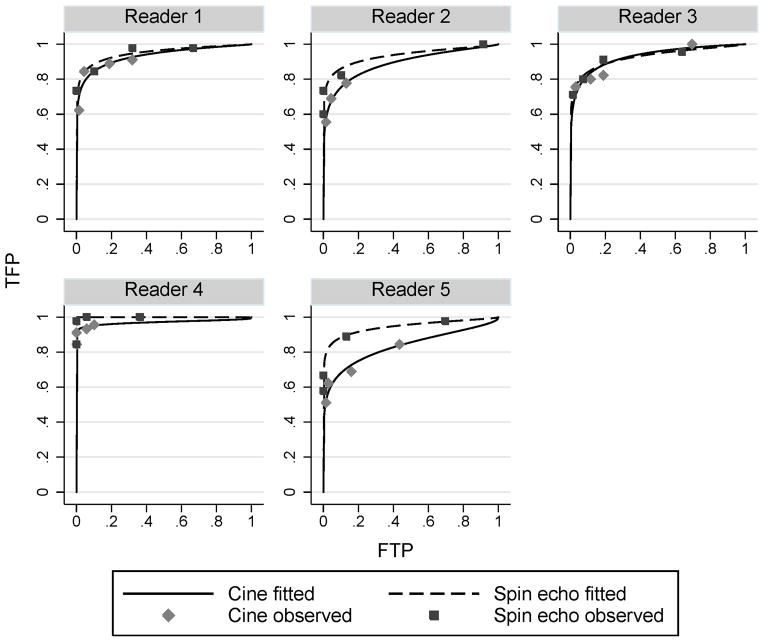
The ROC curves computed for the example data set are presented in Figure 2. Table 1 presents the corresponding binormal parameter estimates for a and b and estimates and standard errors for AUC, pAUC_FPF for FPF intervals (0.0, 0.2) and (0.0, 0.1), and pAUC_TPF for TPF intervals (0.8, 1.0) and (0.9, 1.0). The pAUCs have been normalized by dividing by the length of the defining interval; thus the pAUC values represent average sensitivity or specificity over the corresponding defining FPF or TPF interval. Having an analytic expression for the partial areas makes a table like Table 1 easy to construct, since the pAUCs can be computed directly from a and b. However, we note that the standard errors could not be directly computed from the ROC parameters, but rather they had to be computed separately using the jackknife.

Figure 2.

Binormal ROC curves for Van Dyke et al [20] data by reader.

Table 1.

VanDyke et al [13] binormal parameter estimates and corresponding summary indices. Notes: pAUC_FPF(interval below) is the area under the ROC curve with the given FPF interval; sens(spec below) is sensitivity for the stated specificity; pAUC_TPF(interval below) is the area to the right of the ROC curve within the stated TPF interval. pAUCs have been normalized by dividing by the length of the defining interval. Standard errors, computed using the jackknife, are shown in parentheses.

modality	reader	a	b	AUC		pAUCFPF(interval below)				pAUCTPF(interval below)
						(0,0.2)		(0,0.1)		(0.8,1)		(0.9,1)
Cine	1	1.7022	0.5368	0.93	(0.03)	0.82	(0.07)	0.77	(0.10)	0.69	(0.17)	0.49	(0.30)
	2	1.4033	0.5607	0.89	(0.06)	0.73	(0.07)	0.66	(0.09)	0.52	(0.27)	0.31	(0.34)
	3	1.7408	0.6346	0.93	(0.02)	0.79	(0.07)	0.73	(0.09)	0.68	(0.08)	0.51	(0.10)
	4	1.9255	0.2015	0.97	(0.02)	0.95	(0.03)	0.94	(0.03)	0.85	(0.12)	0.70	(0.24)
	5	1.0630	0.4635	0.83	(0.05)	0.66	(0.08)	0.60	(0.09)	0.32	(0.17)	0.12	(0.14)
Spin echo	1	1.8501	0.5030	0.95	(0.02)	0.87	(0.04)	0.83	(0.05)	0.76	(0.12)	0.58	(0.21)
	2	1.6552	0.4473	0.93	(0.02)	0.84	(0.05)	0.80	(0.06)	0.68	(0.10)	0.46	(0.14)
	3	1.6220	0.4878	0.93	(0.03)	0.82	(0.06)	0.77	(0.07)	0.66	(0.15)	0.44	(0.23)
	4	7.1233	0.8806	1.00	(0.00)	1.00	(0.00)	1.00	(0.00)	1.00	(0.00)	1.00	(0.00)
	5	1.7329	0.4221	0.94	(0.03)	0.87	(0.05)	0.84	(0.06)	0.73	(0.13)	0.52	(0.22)

Table 2 presents the results of the DBM/OR analyses. For our discussion we assume alpha = .05. AUC did not show a significance difference (p = 0.14). In contrast, pAUC_FPF(0.0, 0.2) almost reached significance (p = .06) and tests based on pAUC_FPF (0.0, 0.1) and pAUC_FPF (0.0, 0.05) were both significant (p = .0399 and 0.0278, respectively). These results suggest that partial AUC provides a more powerful test than AUC for these data. Sensitivity for a fixed specificity also resulted in more significant results than AUC. Results for the horizontal-band pAUCs was similar to that of AUC for two intervals (p = .14 and .15 for TPF > .8 and .9, respectively), but somewhat less for the third interval, defined by TPF > 0.95.

Table 2.

ROC summary measure estimates for Van Dyke et al [20] data assuming a latent binormal model. P -value is for H₀: the pAUC means are equal for cine and spin-echo MRI.

Type of estimator	Specific estimator	Estimates		P-value
		Cine	Spin-echo
AUC	AUC	0.911	0.952	0.1413
pAUCFPF	pAUCFPF (0.0, 0.2)	0.790	0.880	0.0600
	pAUCFPF (0.0, 0.1)	0.740	0.848	0.0399
	pAUCFPF (0.0, 0.05)	0.691	0.817	0.0278
Sensitivity at fixed specificity	Sens (spec = 0.80)	0.863	0.925	0.1265
	Sens (spec = 0.90)	0.811	0.894	0.0778
	Sens (spec = 0.95)	0.760	0.862	0.0491
pAUCTPF	pAUCTPF (0.8, 1.0)	0.613	0.765	0.1426
	pAUCTPF (0.9, 1.0)	0.427	0.599	0.1534
	pAUCTPF (0.95, 1.0)	0.251	0.430	0.2277

4. DISCUSSION

For the two types of pAUCs we derived analytic expressions under the assumption of a latent binormal model. Previously it was believed that analytic expressions did not exist, even though Thompson and Zucchini [11] had stated and proved Eq. 2, and thus numerical methods have been used to solve for pAUC values. The formulas presented in this paper greatly simplify computation of pAUCs.

We illustrated use of these expressions with a real data set where, using a multireader analysis, we found that pAUC_FPF gave more significant results than did AUC. This example illustrates the ease with which pAUC measures can be computed using the expressions provided in this paper. It also suggests that partial areas can be more powerful for comparing modalities than AUCs under certain circumstances. While we recognize that it is generally thought that AUC provides a more powerful test than a partial area [15, 27], this example suggests that there may be situations where pAUCs will be more powerful and provides motivation for a closer examination of the relationship between pAUC and AUC with respect to power.

Although Thompson and Zucchini [11] provided a proof for Eq. 2, their proof requires a solid understanding of calculus and familiarity with the bivariate normal density function. In contrast, the proofs that we provide for the expressions for both pAUCs requires only basic knowledge of statistics and algebra. Thus we believe that our proofs will be more accessible to radiological researchers and clinicians.

Appendix A. Appendix: Derivation of Eqs. 1–4 in Section 2.2.2

In this section we derive Eqs. 1–4 in Section 2.2.2. We assume an underlying binormal distribution, as discussed in Section 2.2.1. In particular, we assume that X and Y denote independent decision variables having the same distributions as the decision variable distributions for nondiseased and diseased cases, respectively, with X ~ N (0, 1) and Y ~ N (μ, σ²).

Appendix A.1. Derivation of pAUC_FPF (0, FPF₀) results (Eqs. 1–2)

It has been shown [8, 28] that

$$\text{pAUC}(0,{\text{FPF}}_0)=Pr[Y>X,X>S_X^{-1}({\text{FPF}}_0)]$$ (A.1)

where S_X, defined by S_X (x) = Pr (X > x), is the complement of the cumulative distribution distribution function of X. This is a general result that holds even if the conditional distributions are not normal. Noting that $S_X^{-1}({\text{FPF}}_0)={\xi }_0$, where FPF₀ = Pr(X > ξ₀), it follows from Eq. A.1 that

$${\text{pAUC}}_{\text{FPF}}(0,{\text{FPF}}_0)=Pr[Y-X>0,X>{\xi }_0]$$ (A.2)

We will use Eq. (A.2) to derive pAUC_FPF (0, FPF₀) below in terms of the latent binormal decision-variable distribution parameters.

From Eq. A.2 we have

$$\begin{array}{l}{\text{pAUC}}_{\text{FPF}}(0,{\text{FPF}}_0)=Pr[Y-X>0,X>{\xi }_0]\\ =Pr\left[\frac{Y-X-\mu }{\sqrt{1+{\sigma }^2}}>\frac{-\mu }{\sqrt{1+{\sigma }^2}},X>{\xi }_0\right]\\ =Pr\left[Z>\frac{-\mu }{\sqrt{1+{\sigma }^2}},X>{\xi }_0\right]\end{array}$$ (A.3)

where $Z=(Y-X-\mu )/\sqrt{1+{\sigma }^2}$. It is easy to show that Z ~N (0, 1) and $\text{corr}(Z,X)=-1/\sqrt{1+{\sigma }^2}$. To show the correlation result, note X and that Y are independent and corr (Z, X) = cov (Z, X) because both Z and X have unit standard deviation. Thus $\text{corr}(Z,W)=cov(Z,W)={(\sqrt{1+{\sigma }^2})}^{-1}cov(Y-X,X)={(\sqrt{1+{\sigma }^2})}^{-1}cov(-X,X)=-{(\sqrt{1+{\sigma }^2})}^{-1}var(X)=-{(\sqrt{1+{\sigma }^2})}^{-1}$. It follows that (Z, X) has a standardized bivariate normal distribution with correlation $-1/\sqrt{1+{\sigma }^2}$. Thus

$$\begin{array}{l}{\text{pAUC}}_{\text{FPF}}(0,{\text{FPF}}_0)=Pr\left[Z>\frac{-\mu }{\sqrt{1+{\sigma }^2}},X>{\xi }_0\right]\\ =1-F_{\text{BVN}}\left(\frac{-\mu }{\sqrt{1+{\sigma }^2}},{\xi }_0;-1/\sqrt{1+{\sigma }^2}\right)\end{array}$$ (A.4)

where F_BVN (z, x; ρ) is the standardized bivariate normal distribution function with correlation ρ as discussed in Section 2.2.2. Because F_BVN (z, x; ρ) = 1 − F_BVN (−z, −x; ρ), it follows from Eq. A.4 that

$${\text{pAUC}}_{\text{FPF}}(0,{\text{FPF}}_0)=F_{\text{BVN}}\left(\frac{\mu }{\sqrt{1+{\sigma }^2}},-{\xi }_0;-1/\sqrt{1+{\sigma }^2}\right)$$

Using the relationship −ξ₀ = Φ⁻¹(FPF₀) we have

$${\text{pAUC}}_{\text{FPF}}(0,{\text{FPF}}_0)=F_{\text{BVN}}\left(\frac{\mu }{\sqrt{1+{\sigma }^2}},{\mathrm{\Phi }}^{-1}({\text{FPF}}_0);-1/\sqrt{1+{\sigma }^2}\right)$$ (A.5)

In terms of the binormal parameters a = μ/σ and b = 1/σ, we can write Eq. A.5 in the form

$${\text{pAUC}}_{\text{FPF}}(0,{\text{FPF}}_0)=F\left(\frac{a}{\sqrt{1+b^2}},{\mathrm{\Phi }}^{-1}({\text{FPF}}_0);-b/\sqrt{1+b^2}\right)$$ (A.6)

Note that Eqs. A.5 and A.6 are identical to Eqs. 1 and 2.

Appendix A.2. Derivation of pAUC_TPF (TPF₀, 0) results (Eqs. 3–4) in Section 2.2.2

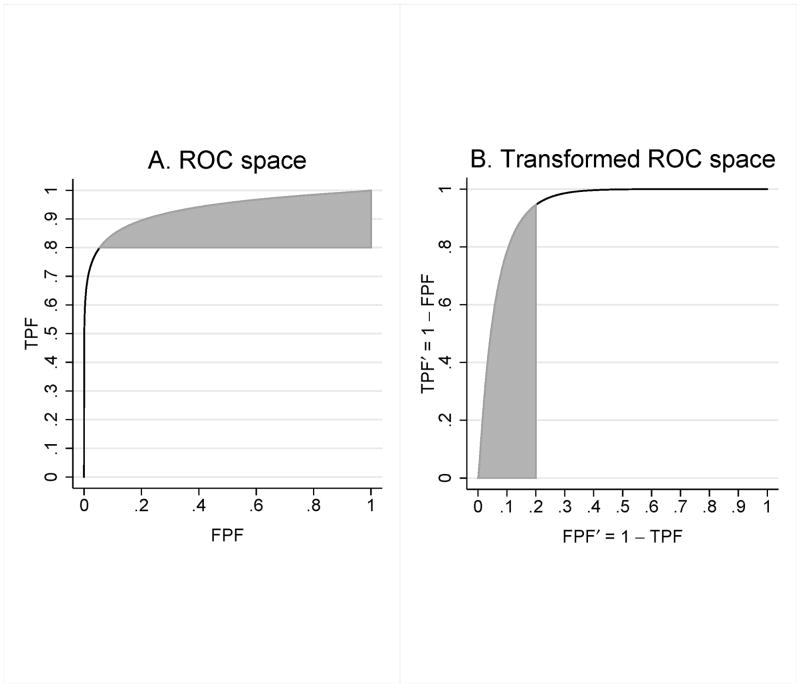
Our strategy for finding pAUC_TPF (TPF₀, 1) is to express pAUC_TPF (TPF₀, 1) in the form pAUC_FPF (0, FPF₀) for an appropriate binormal distribution and FPF₀ value. Consider part A of Figure A1, which shows the ROC curve and the shaded region corresponding to pAUC_TPF (TPF₀, 1), with TPF₀ = .8. Define

$$\text{FP}{\text{F}}^{\prime }=1-\text{TPF}\text{and}\text{TP}{\text{F}}^{\prime }=1-\text{FPF}$$

Part B shows the ROC curve and shaded portion after transformation to the coordinate system with FPF′ on the x-axis and TPF′ on the y-axis. We see that the resulting plot looks like an ROC plot with FPF′ and TPF′ as false and true positive fractions; below we prove this to be the case. Moreover, it is easy to show that area of the shaded region remains constant under the transformation.

Let ξ denote a threshold value. Corresponding values for FPF′ and TPF′ are given by

$$\begin{array}{l}\text{FP}{\text{F}}^{\prime }(\xi )=1-\text{TPF}(\xi )=1-Pr(Y\ge \xi )=Pr(Y\le -\xi )=Pr(-Y\ge \xi )\\ \text{TP}{\text{F}}^{\prime }(\xi )=1-\text{FPF}(\xi )=1-Pr(X\ge \xi )=Pr(X\le -\xi )=Pr(-X\ge \xi )\end{array}$$

Defining

$$X^{\prime }=-Y\text{and}{Y}^{\prime }=-X$$

we have

$$\text{FP}{\text{F}}^{\prime }(\xi )=Pr(X^{\prime }\ge \xi )\text{and}\text{TP}{\text{F}}^{\prime }(\xi )=Pr(Y^{\prime }\ge \xi )$$

Furthermore, it follows that X′ ~ N (−μ, σ²) and Y ′ ~ N (0, 1). Thus the plot shown in Figure 3 is the ROC curve corresponding to the binormal distribution defined by nondiseased and diseased decision variables X′ and Y′. Noting that TPF= 1 is mapped to FPF′ = 0 and TPF= TPF₀ is mapped to FPF′ = 1 − TPF₀ for TPF₀ < 1, it follows that pAUC_TPF (TPF₀, 1) for the binormal distribution with nondiseased and diseased distributions X and Y is equal to pAUC_FPF (0, 1 − TPF₀) for the binormal distribution for nondiseased and diseased distributions X′ and Y ′.

In order to use Eqs. 1–2, we rescale X′ and Y ′ so that rescaled X′, denoted by X̃, has zero mean and unit standard deviation:

$$\stackrel{\sim }{X}=\frac{X^{\prime }+\mu }{\sigma }\text{and}\stackrel{\sim }{Y}=\frac{Y^{\prime }+\mu }{\sigma }$$

Since the same transformation is applied to both X̃ and Ỹ, the ROC curve remains unchanged. It follows that

$$\stackrel{\sim }{X}~N(0,1),\stackrel{\sim }{Y}~N\left(\frac{\mu }{\sigma },\frac{1}{{\sigma }^2}\right)$$

and the standard binormal parameters for the (X̃, Ỹ) binormal distribution are

$$a=\mu \text{and}b=\sigma$$ (A.7)

From Eq. 1 it follows that, for the binormal distribution defined by X̃ and Ỹ, pAUC_FPF (1 − TPF₀, 0) is given by

$${\text{pAUC}}_{\text{FPF}}(1-{\text{TPF}}_0,0)=F_{\text{BVN}}\left(\frac{\mu }{\sqrt{1+{\sigma }^2}},{\mathrm{\Phi }}^{-1}(1-{\text{TPF}}_0);-\sigma /\sqrt{1+{\sigma }^2}\right)$$ (A.8)

Note that in Eq. A.5 that FPF₀, μ, and σ were replaced by 1 − TPF₀, μ/σ, and 1/σ, respectively, to yield Eq. A.8. Equivalently, in terms of a and b it follows from Eqs. A.7 and A.8 that

$${\text{pAUC}}_{\text{FPF}}({\text{TPF}}_0,0)=F_{\text{BVN}}\left(\frac{a}{\sqrt{1+b^2}},{\mathrm{\Phi }}^{-1}(1-{\text{TPF}}_0);-1/\sqrt{1+b^2}\right)$$ (A.9)

Note that Eqs. A.8 and A.9 are the same as Eqs. 3 and 4 in Section 2.2.2.

Appendix B

Figure A1.

ROC curve and pAUC_TPF (.8, 1) shaded area in ROC space (A) and after transformation (B) to the coordinate system defined by FPF′ = 1 − TPF on the x-axis and TPF′ = 1 − FPF on the y-axis. In the original ROC space (A) the nondiseased and diseased decision variables X and Y define the ROC curve; in the transformed ROC space (B) the ROC curve is defined by nondiseased and diseased decision variables X′ = −Y and Y ′ = −X, with the shaded area equal to pAUC_FPF (0, .2).