Prospective Head Movement Correction for High Resolution MRI using an In-bore Optical Tracking System

Abstract

In MRI of the human brain, subject motion is a major cause of magnetic resonance image quality degradation. To compensate for the effects of head motion during data acquisition, an in-bore optical motion tracking system is proposed. The system comprises two MR compatible infrared cameras that are fixed on a holder right above and in front of the head coil. The resulting close proximity of the cameras to the object allows precise tracking of its movement. During image acquisition, the MRI scanner uses this tracking information to prospectively compensate for head motion by adjusting gradient field direction and RF phase and frequency. Experiments performed on subjects demonstrate robust system performance with translation and rotation accuracies of 0.1 mm and 0.15° respectively.

Introduction

Magnetic resonance imaging (MRI) has been widely used as a noninvasive clinical and research modality for the study of human anatomy. However, subject motion during scanning remains a severe problem and may degrade image quality below levels acceptable for clinical diagnosis. Recent improvements that yield high spatial resolution MRI of the brain (~ 0.2 mm) make this problem more acute, since for this application the tolerance to motion is reduced, and scan time is increased. The latter makes it more difficult for the subject to maintain the same position throughout the scan, which is especially problematic for children and patients.

Several methods have been proposed to solve the head movement problem in MRI. All model head movement as rigid body motion with six degrees of freedom (DOF), namely three rotations and three translations along the MRI coordinate system. These parameters are then used to either retrospectively or prospectively compensate for the effects of motion on the image data.

Retrospective motion correction addresses motion artifacts after the acquisition of a complete set of raw image data. While this might work well for in-plane motion, it is generally inadequate for through-plane motion, primarily because it cannot correct for the effects of this motion on the local magnetization history (i.e. changes in saturation level of longitudinal magnetization due to motion-induced changes in the image-slice location). To avoid this problem prospective motion correction techniques have been proposed recently (1–5). They track the head motion and rectify the acquisition planes correspondingly, by adjusting gradient direction and RF phases and frequencies. This avoids problems related to the effects of motion on spin history.

The object motion parameters used by prospective and retrospective correction methods can be derived from MRI data using image or navigator based methods. Image based methods use image registration algorithms to detect the motion parameters (3,6–8). These techniques, while straightforward, can only calculate motion after acquiring a volume and are therefore always lagging the motion. Also, any ghosting and blurring artifacts that motion may cause may affect the accuracy of the registration algorithms.

Navigator based motion correction methods acquire a motion-sensitive reference signal with the image (1,2,4,9,10). The earliest navigator method was capable of detecting only one-dimensional (1D) translation (9) by employing a frequency encoding gradient but no phase encoding gradient before image acquisition. Soon after, orbital navigators (5,10), spherical navigators (11) and cloverleaf navigators (4) were proposed to allow full tracking of 3D motion. However, the extra time required for measuring the navigator echoes led to an increased scan time.

Self-navigating methods can also be used to retrospectively correct motion when combined with particular image acquisition techniques including projection acquisition (12,13), spiral acquisition (14–16), and PROPELLER (17,18). These all involve the collection of redundant MRI data, usually including the central region of the k-space. The over-sampled central region of k-space provides intrinsic averaging of image features that reduces motion artifacts, and can be further used to correct spatial inconsistencies in position, rotation, and phase between acquisitions. One drawback of these methods is the increased scan time related to redundant k-space sampling.

Alternatively, external motion tracking systems can be used for MRI motion correction. These tracking systems rely on additional hardware, such as miniature coils (19,20), fiducial samples (21), optical reflectors (22) or stereo cameras (23–25). Among them, stereo optical systems have been shown to give good motion correction results with reasonable accuracy retrospectively (24) as well as prospectively (23,25). The stereo tracking system works parallel with the scanner thus needs no extra scan time for motion detection in the imaging sequence. However, there are limitations to the current tracking systems, the most important being that the tracking target required for monitoring object position is either uncomfortable for the subjects (e.g., a mouthpiece used in (25)), or hard to combine with close-fitting receiver arrays (e.g., a cap used in (24)).

To overcome these limitations, we developed and evaluated an in-bore video tracking system for prospective motion correction that monitors the position of a target on the subject’s forehead. In the current implementation, this target consisted of visual feature points drawn on a small sticker. The system was designed to allow high resolution (~ 0.2 mm) MRI at 7T in the presence of substantial head motion.

Methods

System Setup

MRI experiments were performed on a GE (Milwaukee, WI, USA) 7T MRI system running with EPIC14 software, equipped with a detunable volume transmit coil (Nova Medical, Wilmington, MA, USA), a 32-channel receive-only head coil (Nova Medical, Wilmington, MA, USA), and a TRM gradient coil running in ‘zoom’ mode providing 40mT/m gradient with 150 mT/m/s slew rate. The optical tracking system included two MR compatible infrared cameras (MRC Systems GmbH, Germany) as part of a stereo-vision system to measure the subject’s head motion in 3D. The size of the cameras was 28 × 18 × 30 mm³. They were fixed on a custom made holder right above and in front of the head coil (Fig. 1b). The distance and the angle between them were 12 cm and 28° respectively. Surrounding each camera lens, six infrared light emitting diodes were used to illuminate the field of view (Fig. 1c). The distance from the cameras to the face was around 8cm. The high spatial resolution of this setup (640 × 480 pixels, about 13 × 10 cm² field of view) allowed detection of very small movements.

Figure 1.

Experimental setup. (a) is an illustration of the position of the cameras and head coil in the MRI scanner bore. O_m is origin of MRI physical coordinate system defined at gradient isocenter. O_c is the origin of the stereo coordinate system, which is defined at the camera centre of one of the cameras. (b) shows the real instruments. Cameras are highlighted with the red ellipse. They are fixed tightly on a custom-made holder on top of the head coil. (c) is a closer look of the two cameras. A ring with 6 LEDs surrounding each camera was used for illumination.

The two cameras were connected to a filter box (MRC Systems GmbH, Germany) via the camera connector cable. This low pass filter, which has the cutoff frequency of 1 MHz, was used to prevent damage and interferences caused by the high frequency signals of the MR scanner, as well as possible infiltration of MR-frequency noise into the magnet room. The video output signals were then captured by a Matrox Morphis frame grabber (Matrox Electronic Systems Ltd. Quebec, Canada), using a standard BNC cable connection, by a tracking computer running a Linux operating system. Real-time tracking and motion estimation software was developed using C++. The tracking speed was 10 Hz. The tracking computer communicated with the MRI scanner through a TCP/IP connection (26) to provide the console (scan computer) with the real-time motion parameters. This allowed the image acquisition pulse sequence to alter gradient direction and RF offset phases and frequencies to compensate for the changes in object position.

System Calibration

The optical tracking system measured the motion parameters in the camera coordinate frame. They needed to be converted to the MRI coordinate frame to be used by the imaging sequence. Therefore, an accurate calibration was necessary to estimate the rotation (a 3×3 orthonormal matrix R_mc) and translation (a 3×1 vector T_mc) between the camera and MRI coordinates.

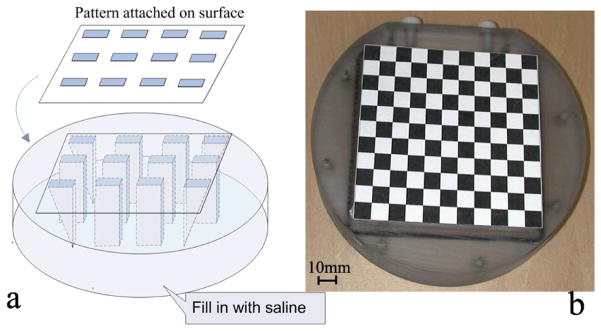
A calibration phantom was designed for this purpose, the internal of which consisted of a grid of rectangular prisms (Fig. 2a) carved out of a polycarbonate former with a high precision computer-controlled milling machine (TM Series Mill, HAAS Automation Inc. USA). The prisms were all of equal size, 10 × 10 × 18 mm³ (length × width × height), and were 10 × 10 mm² apart, except those on the four corners, which were cut into triangular prisms to provide differentiation in the height direction. The open spaces in the phantom were filled in with saline to make them visible to MRI. The cover of the phantom was 2.4 mm thick. On the surface of the phantom, a 0.5 mm thick square was carved out which matched exactly the internal contour of the phantom (shown as a big square on the phantom surface in Fig. 2a). A piece of paper (0.5 mm thick) with a black-and-white checkerboard representation of the internal grid (10 × 10 mm² squares) was attached into the carved-out square to make sure the checkerboard was fixed precisely over the prisms (Fig. 2b). This design provided many corners for calibration, and the clear sharp corners improved calibration accuracy.

Figure 2.

Calibration model. (a) Schematics of the phantom; (b) View of the actual phantom surface; (c) Registration between the 3D MR image and the ideal simulated phantom model and the estimated surface points.

The phantom was put in the target field (approximately the position of a subject’s face) within the field of view of the scanner and video cameras. A 3D gradient echo image of the phantom was acquired by the MRI scanner (resolution 0.4 × 0.4 × 0.7 mm³, TR=55 ms, TE=6 ms, FA=10°) and the cameras measured the 3D position of the calibration corners on the surface pattern based on stereo triangulation including lens distortion correction for the cameras (27).

To estimate the surface corner positions in MRI coordinate frame, the 3D MR image was registered to a simulated model of the phantom. After alignment, the calibration corner positions (on the camera-visible checkerboard grid, 2.4 mm from the liquid surface) of the simulated phantom were transformed into the MRI coordinates. Therefore, the rotation (R_mc) and translation (T_mc) between the cameras and the MRI scanner could be calculated based on the simultaneous measurements of the same points in both the MRI scanner (X_m, a 3×N matrix, where N is the number of calibration corners) and camera coordinates (X_c, a 3×N matrix):

$$X_m=R_{mc}{X}_c+T_{mc}$$ [1]

A closed-form solution for Eq. 1 is determined from the correlation matrix

$$C=\left[X_c-{\overline{X}}_c\right]{\left[X_m-{\overline{X}}_m\right]}^T$$ [2]

where X̄_c and X̄_m are the mean vector of the N points.

After decomposing C with singular value decomposition (SVD) into C = UDV^T, rotation R_mc is (28–30):

$$R_{mc}=V\left(\begin{array}{lll}1\hfill & \hfill & \hfill \\ \hfill & 1\hfill & \hfill \\ \hfill & \hfill & det({VU}^T)\hfill \end{array}\right)U^T$$ [3]

Translation T_mc is:

$$T_{mc}={\overline{X}}_m-R_{mc}{\overline{X}}_c$$ [4]

Motion Calculation in the MRI Coordinate Frame

During the actual experiment, M feature points on the object (or face) were automatically selected in the left camera image after which the corresponding points were identified in the right camera image. The changes in position of these feature points in the camera images were tracked over time by analyzing the camera image intensity I(x,t), at position x and time t.

In the limit of small motion per image acquisition frame (i.e. high image acquisition frequency or limited motion), one can model two successive images as:

$$I(x+d,t+\tau )=I(x,t)+n(x)$$ [5]

where τ is the time difference between sampling of the two frames; d is the displacement vector [d_x,d_y]^T; and n represents noise.

The displacement vector d follows from minimizing the residual error:

$${\epsilon }^2(x)=\sum _W{\left[I(x_i+d,t+\tau )-I(x_i,t)\right]}^2$$ [6]

where x_i represents a point in the Gaussian window W centered on x.

At small displacements, the intensity function can be approximated by Taylor series expansion truncated to the linear term. The displacement is therefore determined from (31,32):

$$\sum _{W}g(x_i)g{(x_i)}^{T}d=\sum _{W}h(x_i)g(x_i)$$ [7]

where $g(x_i)=\frac{\partial I}{\partial x}(x_i,t+\tau )$ is the Jacobian matrix, and h(x_i) = I(x_i,t+τ) − I(x_i,t) is the intensity difference between two successive images. Because of the linearization of Eq. 6, the solution of d needs to be iteratively refined by resampling h(x_i) as I(x_i+ d,t+τ) − I(x_i,t). The iteration is stopped when the change in d falls below a pre-defined threshold. We found this typically occurred within 5 iterations.

The positions of the feature points were calculated in 3D using triangulation (27) after correction for the image distortion of the camera lenses. The translation and rotation parameters were then estimated from this collection of 3D points. Denoting the points at time t₀ and t_i as X_c(t₀) and X_c(t_i) respectively, the motion parameters R_c and T_c were estimated similarly using Eq. 1–4,

$$X_c(t_i)=R_c{X}_c(t_0)+T_c$$ [8]

However, these parameters were in the camera coordinate frame and needed to be transformed into MRI coordinate frame. At time t₀, the relationship between the points MRI coordinates (X_m) and camera coordinates (X_c) was described based on calibration data (Eq. 1), rewritten here as:

$$X_m(t_0)=R_{mc}{X}_c(t_0)+T_{mc}$$ [9]

From the above two equations, we calculated the movement (rotation R_m and translation T_m) in MRI coordinates,

$$\begin{array}{l}{X}_m(t_i)=R_{mc}{R}_c{R}_{mc}^{-1}{X}_m(t_0)-R_{mc}{R}_c{R}_{mc}^{-1}{T}_{mc}+R_{mc}{T}_c+T_{mc}=R_m{X}_m(t_0)+T_m\\ \Rightarrow R_m=R_{mc}{R}_c{R}_{mc}^{-1}\\ T_m=-R_{mc}{R}_c{R}_{mc}^{-1}{T}_{mc}+R_{mc}{T}_c+T_{mc}\end{array}$$ [10]

Pulse Sequence Motion Correction

A 2D Cartesian trajectory gradient-echo (GRE) pulse sequence was modified to incorporate the motion correction. Before each RF excitation, the scan computer read the current values of the continuously updated motion parameters to adjust the gradient rotation matrix and RF offset phases and frequencies in the sequence to compensate for the changes in position.

Since the pulse sequence uses MRI logical coordinate system instead of physical coordinate frame, the motion parameters calculated from Eq. 10 needed to be transformed to the logical coordinate frame. The logical coordinate frame uses frequency-encoding, phase-encoding, and slice-selection gradient direction to define its x, y, and z axes. This coordinate frame varies depending on the scan prescription. In contrast, the MRI physical coordinate frame is fixed to the magnet. Its origin is at gradient isocenter; z axis is in the direction of the main magnetic field; y axis is up-down and x axis is left-right direction (shown in Fig. 1a).

The rotation and translation (R_pl and T_pl) between these two coordinate systems was read out from the pulse sequence after the scan-plane was prescribed:

$$X_m(t_0)=R_{pl}(X_l(t_0)+T_{pl})$$ [11]

Therefore, the final motion parameters to be used by the pulse sequence should be:

$$R_{\mathit{corr}}=R_m{R}_{pl}$$ [12]

$$T_{\mathit{corr}}=R_{\mathit{corr}}^{-1}{T}_m$$ [13]

The motion parameters (R_corr and T_corr) were sent from the tracking system to the MRI scanner over a TCP/IP connection (26). The pulse sequence updated the scan parameters before each RF excitation. Correction for rotation was performed by adjusting the gradient rotation matrix; correction for translation in the slice selection and read out direction was performed by adjusting the RF transmit and receive frequencies respectively; and correction for translation in the phase encoding direction was performed by adjusting the receiver phase with a linear phase ramp, which was a function of the translation and the phase encode step.

An additional feature of the pulse sequence was that it allowed for a re-acquisition of motion corrupted k-space lines. This feature was added to reduce the effect of motion that was too fast to be compensated by gradient and RF adjustment. Re-acquisition was performed when the motion that occurred during the acquisition of a given k-space line exceeded a preset threshold.

Evaluations of Stereo Accuracy

The checkerboard pattern (Fig. 2b) was attached to a highly sensitive, 6-axis-positioning system (M-824 compact 6-axis-positioning system, Physik Instruments, GmbH & Co. KG, Germany) to test the stereo’s accuracy. The hexapod was driven by six high-resolution actuators with sub-micron precision. Experiments were done outside of the scanner since the positioning system was not MR-compatible. The cameras were fixed firmly on top of the moving platform at a distance of about 8cm to simulate the position of the stereo with respect to the human face. The platform was controlled by a computer to move in the x, y, and z direction over known distances and rotate around the three axes with known angles, where the x, y and z were defined as the two orthogonal axes of the platform, and the z axis was defined as pointing out of it. Camera images were acquired at each position to measure these movements. The discrepancy between the real and measured positions was evaluated to determine the stereo’s accuracy.

Evaluation of Coordinate System Calibration Accuracy

The phantom (Fig. 2b) was used to test the calibration accuracy between the camera system and MRI. First, the phantom was put at an arbitrary position. The stereo camera system measured the corner positions in 3D, which were then transformed into MRI coordinates based on the calibration results. 3D MR images were acquired, from which the 3D MRI coordinates of the corners were determined. Accuracy was determined by measuring the discrepancy between the estimated position (obtained by using the camera model and calibration parameters) and real ones (measured from MR images). This procedure was repeated at different arbitrary phantom positions.

Evaluation of the Tracker Noise

Since the motion correction was performed for each acquired k-space line, the tracking noise was an important factor. Our real-time tracking was based on feature points (31,32), which provided a sub-pixel accuracy but was also sensitive to noise in the video images. The tracking noise was evaluated by monitoring a stationary object for several minutes and the number of feature points needed for controlling noise below 0.2 mm and 0.2° was to be determined.

Evaluation of the Motion Correction System

After all the individual parts of the prospective motion correction system validated, the performance of the system as a whole was tested.

The high-resolution calibration phantom was connected to two long rods sticking outside of the magnet, which allowed it to be moved manually during the scan. A “tracking pattern” (Fig. 3b) was fixed on top of the phantom for real-time motion computation. A GRE sequence with spatial resolution 0.2 mm², matrix size 1024×512, slice thickness 3 mm, TR 100 ms, TE 13.7 ms, flip angle 10°, was used to scan an axial slice. The phase encoding gradient was set to zero and a hybrid image was reconstructed.

Figure 3.

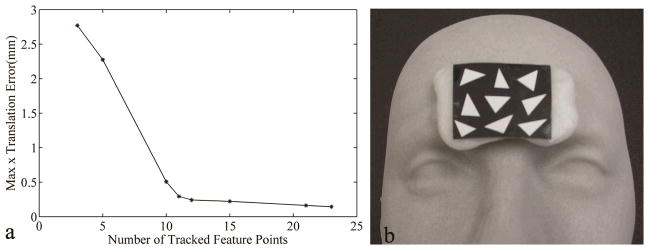
(a) Noise of the tracker. The maximum x translation error as a function of the number of tracked feature points. (b) The sticker with white triangles on black background was attached on a thermoplastic shaped to fit a volunteer’s forehead.

In absence of motion, all lines in the phase encoding direction of the hybrid image should be perfectly aligned. In the case of motion, however, misalignment would appear between lines. If motion correction was applied, any misalignment would indicate imperfect motion compensation as well as errors related to tracker noise. From one scan, we got 512 lines to assess the motion correction system, making the evaluation very efficient. Furthermore, since each line was independent from each other, the specific motion that caused imperfect compensation could be easily detected from the hybrid image, which was impossible from a 2D structure image because residual error originated from the combination of motion during the entire acquisition.

Volunteer Study

Using this pulse sequence, the efficacy of the tracking system was studied on a normal volunteer with written informed consent under an institutional review board-approved protocol. A nominal in-plane spatial resolution of 0.2 × 0.2 mm², a slice thickness of 3 mm, TR 300 ms, TE 25 ms and flip angle 30° were used. The effect of various forms of head motion on image quality was investigated, namely breathing-related, minimal, large step-wise and slow motion. The displacement threshold for the reacquisition of a k-space line was set to 0.2 mm. A rotation threshold was not used because head rotation was always perceived as a displacement as well. This was because rotation was defined relative to the center of the image, whereas the head actually pivoted around the back of the head, where it was supported by the receive coil array, opposite of the part of the head viewed by the cameras.

Results

Evaluations of Stereo Accuracy

Stereo accuracy testing using the micrometer driven positioning system showed that errors of translation in x, y and z were 0.04 ± 0.03 mm, 0.03 ± 0.02 mm and 0.02 ± 0.01 mm (mean ± standard deviation) respectively, and errors of rotation around x, y and z axes were 0.03 ± 0.13°, −0.02 ± 0.05° and 0.01 ± 0.03° respectively.

Evaluation of Coordinate System Calibration Accuracy

The phantom was placed in 8 arbitrary positions and therefore provided 800 points for accuracy evaluation. The accuracy in the x, y, and z coordinates of the MRI coordinate frame was found to be 0.06 ± 0.05 mm, 0.10 ± 0.08 mm and 0.15 ± 0.13 mm respectively.

Evaluation of the Tracker Noise

When the actual tracker setup was used outside of the scanner, the noise was very small even by tracking only 3 feature points, as shown in Table 1. However, when the tracker was put inside the MRI, a significant increase of the error was observed, even when not scanning. This was attributed to camera noise introduced by the static magnetic field as well as of the switching gradients and/or RF. The maximum translation error exceeded 2 mm, which was unacceptable for the high-resolution MRI motion correction.

Table 1.

Accuracy and noise of the tracker when it was put outside or inside of the scanner

	Tracker Outside			Tracker Inside (no scan)			Tracker Inside (during scan)
	Mean	σ	Max	Mean	σ	Max	Mean	σ	Max
x (mm)	−0.065	0.047	0.215	0.002	0.315	1.057	−0.702	0.609	2.772
y (mm)	0.027	0.014	0.068	0.076	0.034	0.179	0.052	0.057	0.314
z (mm)	0.029	0.025	0.107	0.158	0.221	0.918	0.111	0.288	1.138
rx (°)	−0.021	0.014	0.061	−0.146	0.169	0.740	−0.047	0.226	0.881
ry (°)	0.016	0.024	0.081	0.068	0.080	0.338	0.034	0.143	0.588
rz (°)	−0.038	0.028	0.132	0.019	0.249	0.864	−0.545	0.485	2.166

To remediate this problem and reduce tracker noise, multiple feature points were used. Fig. 3a shows the maximum x-translation error as a function of the number of feature points. It shows that tracker noise decreases with increasing number of feature points. For our application, we opted to select around 20 points to keep the maximum error below 0.2 mm and 0.2°. However, the number of feature points on the human face detectable with both video cameras was often below 20, in part because of the cameras’ limited field of view of about 13 × 10 cm². To overcome this we decided to place a sticker on the subject’s forehead that displayed a number of white triangles on a black background as shown in Fig. 3b. The base of the sticker was a reshapable thermoplastic which was shaped to a volunteer’s forehead curvature to improve contact between the sticker and skin, therefore minimizing the relative motion between them.

Evaluation of the Motion Correction System

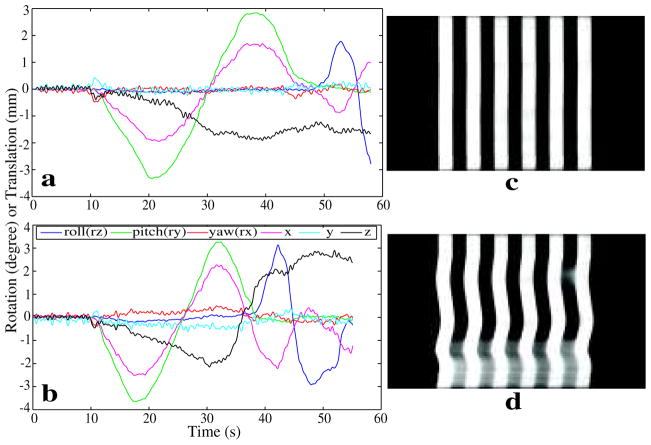
The phantom was manually moved during two separate experiments, of which only the latter incorporated prospective motion correction. Motion parameters reported by the tracker are shown in Fig. 4a and b, and resultant hybrid images in Fig. 4c and d respectively. Frequency-encoding was performed in the left-right direction. Each frequency-encoding line represented the profile of the phantom at one acquisition time point. Since the prescribed axial slice was across one row of prisms, the hybrid images showed striping patterns as in b and d. Lines were not aligned in Fig. 4d because of motion during the scan, Close to the end of the scan, a 2mm displacement in z moved the scan plane out of the prisms of the phantom, which resulted in the high intensity signal between stripes. In a scan with similar motion, but with motion correction, good alignment and no apparent through-plane motion were observed (d). These results suggest that the tracker’s accuracy is within the image resolution of 0.2 mm.

Figure 4.

Prospective motion correction for phantom motion. The phantom was moved manually during the acquisition. The triangle pattern shown in Fig. 3b was attached to the phantom for real-time motion tracking. Images (a, b) showed the motion parameters reported by the tracker. (c, d) showed the hybrid image with and without motion correction respectively.

Volunteer Study

a. Breathing related motion

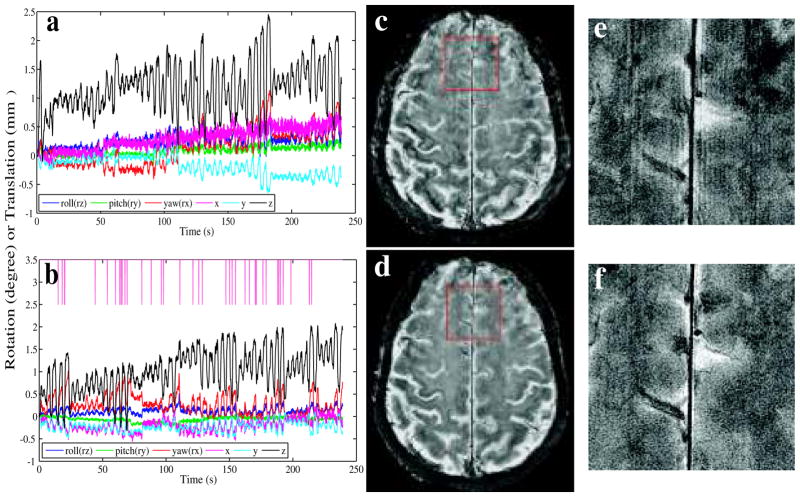
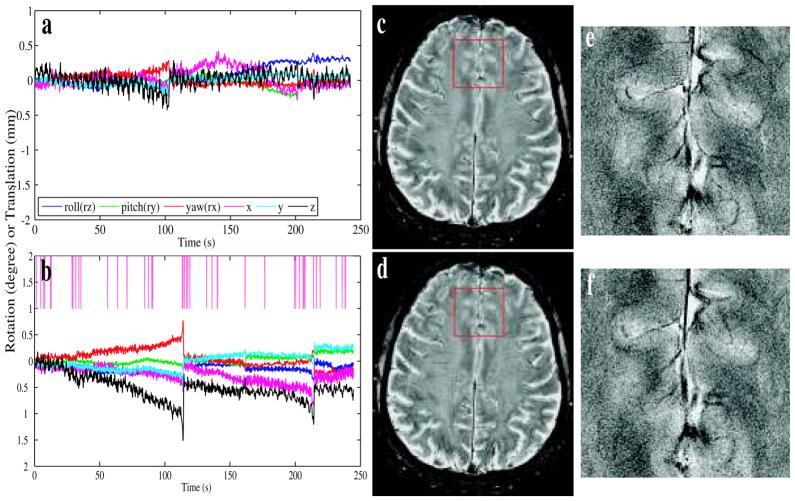
During this experiment, the volunteer was instructed to not pay any effort to laying still. Motion parameters reported by the tracker (Fig. 5a, b) showed cyclic head motion with a period consistent with the respiratory cycle. The observed rotation was mainly around the x-axis and the translation along the z-axis (in the MRI physical coordinate system), which suggested a nodding like motion. The scan was performed twice, once without motion correction and once by using the prospective motion correction technique proposed here. Fig. 5c, e showed that even though the motion was only about 2 mm and 1°, ghosting and blurring artifacts were clearly observed in the high-resolution images (0.23 × 0.23 mm² in-plane resolution). The prospective line-by-line motion corrected image using our real-time compensation system showed much improved image quality and a virtual elimination of ghosting artifact (Fig. 5d, f) as compared to the uncorrected images (Fig. 5c, e). The reacquisition rate was 2.3%.

Figure 5.

Prospective breathing induced motion correction for the 2D gradient echo acquisition. Images (a, b) showed the evolution of motion parameters reported by the tracker during the acquisition of images (c) and (d) respectively. The pink tick marks at the top of (b) mark the tine points of discarded k-space lines. Image (c) was scanned without motion correction, and (d) was with motion correction; (e) and (f) were zoomed in on an area in the frontal brain indicated by the red square in images (c) and (d) respectively.

b. Minimal motion

During this experiment, the volunteer was instructed to stay as still as possible. Despite the efforts of the volunteer, the motion parameters reported by the tracker (Fig. 6a, b) showed a small gradual and jittering motion. This scan was also repeated twice, once without (a, c, e) and once with (b, d, f) motion correction. Both uncorrected (c, e) and corrected (d, f) images have similar quality and show little evidence of ghosting. The reacquisition rate of Fig. 6d was 4.6%.

Figure 6.

Prospective motion correction data obtained for a volunteer that attempted to minimize head motion. Images (a, b) showed the motion parameters reported by the tracker during the acquisition of images (c) and (d) respectively. The pink tick marks at the top of (b) mark the time points of discarded k-space lines. Image (c) was scanned without motion correction, and (d) was with motion correction; (e) and (f) magnify an area in the front of the brain (the area marked by the red square in (c) and (d) respectively).

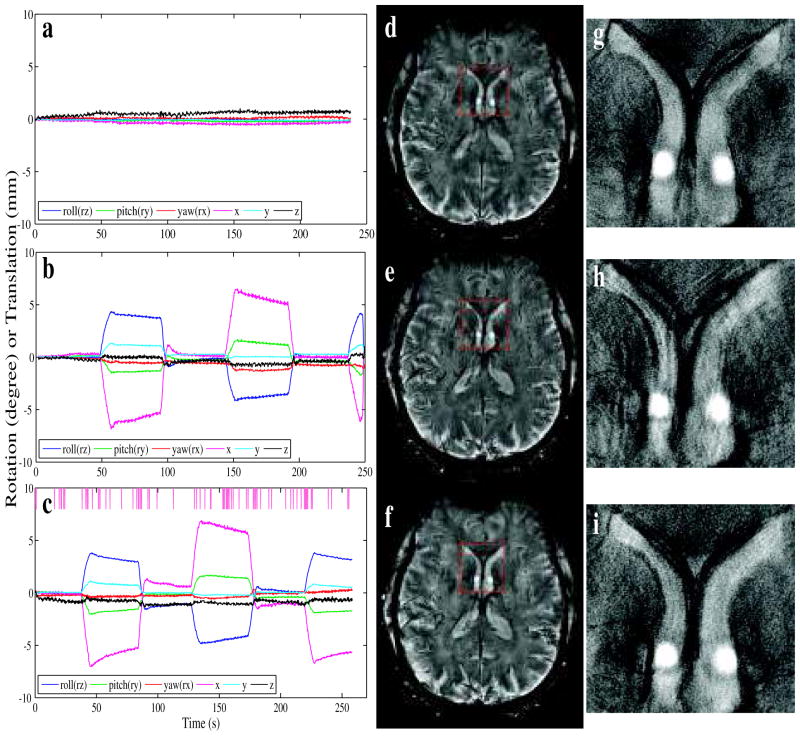
c. Large stepwise motion

Experiments in the presence of strong intentional motion demonstrated the robustness of the prospective motion correction technique (Fig. 7). The motion parameters reported by the tracker indicated a range of motion of close to 10 mm translation and 10° rotation. The severe ghosting and blurring artifacts observed without correction (e, h) were almost entirely avoided with prospective motion correction (f, i), and the image quality of (f, i) was very similar to (d, g), which were acquired in the absence of intentional motion and with motion correction on (motion parameters in a). The reacquisition rate for (f, i) was 10%.

Figure 7.

Example of the performance of the prospective motion correction method in the presence of large stepwise motion during the acquisition of multi-shot 2D gradient echo images on a normal volunteer. Images (a–c) showed the motion parameters reported by the tracker during the acquisition of images (d–f) respectively. The pink tick marks at the top of (f) mark the time points of discarded k-space lines. Image (d) was scanned without intentional motion during the scan, whereas (e, f) were scanned in the presence of motion; (e) was acquired without correction but (f) was acquired using the proposed method. (g–i) show additional detail in an area in the front of the brain that was indicated by the red square in images (d–f).

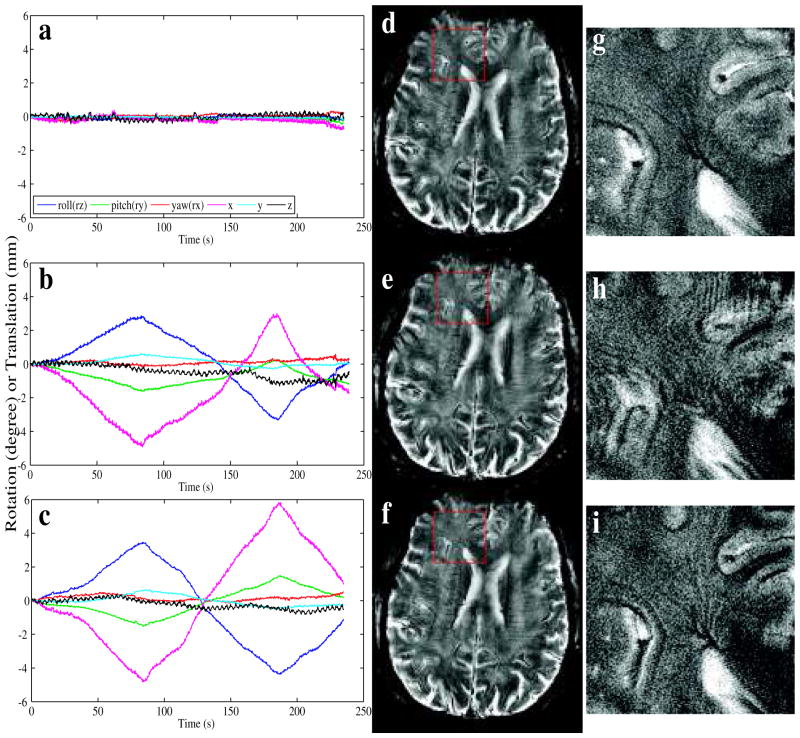
d. Slow motion

The final motion type that was investigated was slow motion resulting in large displacements and/or substantial rotation angles. Even without any reacquisition this type of motion was handled well by the prospective motion correction system. The motion parameters reported by the tracker (Fig. 8b, c) showed a the range of the motion of close to 10 mm of translation and 10° of rotation. The reacquisition rate for (f, i) was 0% since the reacquisition mode was turned off. Image quality of (f, i), when motion correction was used, was notably better than (e, h), acquired in the absence of motion correction. Furthermore, image quality of (f, i) was similar to (d, g), acquired in the absence of intentional motion (motion parameters in a).

Figure 8.

Prospective motion correction in the presence of slow motion. The motion parameters reported by the tracker during the scan of images (d–f) are displayed in (a–c), respectively. Image (d) was acquired in the absence of intentional head motion, (e, f) during slow head motion, where, unlike (e), (f) was acquired with the proposed correction method. A magnification of the area in the red box in (d–f) is shown in (g–i).

Discussion

In this study, a method for the prospective correction of 3D motion for high-resolution MRI was developed and evaluated. Preliminary data obtained on a human volunteer show substantial image quality improvement for high resolution gradient echo imaging at 7 T, in particular under conditions of periodic head motion related to breathing and intentional head rotation.

To obtain adequate tracking accuracy, the cameras were put right above the MRI receiver coil, monitoring the human face from a very small distance. Since the error from stereo estimation is a function of the true distance (33), a translation accuracy much better than 0.1 mm and rotation better than 0.15° were achieved with our setup. Motion towards and away from the cameras can be detected with high accuracy, which is seemingly counterintuitive. However, due to the close proximity of the cameras to the object such motion will lead to a significant perceived size change of the object in the camera images, which enhances detection accuracy. The stereo 3D reconstruction accuracy depends on the relative angle and distance between the two cameras, the best setup of the two cameras should be explored further for better accuracy.

The accuracy of the calibration between the tracker and the MRI scanner is also essential for system performance. Since all the motion parameters were estimated in the camera coordinate frame, they had to be transformed precisely to the MRI coordinate frame to be used in the sequence. However, calibration was difficult in this system because the tracker can only see the surface of the calibration object, whereas the MRI can only see its internal structure. A previous publication (25) dealt with this issue in an iterative way. They used three gel-filled reflective spheres for estimating the initial coordinate transformation, and then iteratively refined this transformation based on the internal structures of the phantom. This method, though accurate, took more than 30 minutes to accomplish. This limitation was addressed in our project by designing a phantom with high resolution, well ordered structures. Since every parameter of the phantom was known, the relationship between the external appearance (black-and-white checkerboard) and internal MR-visible structure was easily established, which simplified the calibration and shorten the calibration time to several minutes.

The use of phantom calibration data for head motion correction assumed that the patient table could be reproducibly moved to the magnet isocenter. However, this was not the case for our long non-standard table, which showed a misalignment error of 1~2 mm in the z direction when the bed was returned to the isocenter position after being moved out of the scanner. From Eq. 10, it can be seen that this uncertainty in T_mc does not affect the calculated rotations but only translations. The introduced translation error was $\left(I-R_{mc}{R}_c{R}_{mc}^{-1}\right)T_{mc}$, which was small when rotational motion was small (i.e. when R_c was close to an identity matrix). For larger rotations however, e.g. a 10° rotation around z axis, a z-alignment error of 2mm, would lead to translations of 0.25 mm, 0.09 mm, and 0.02 mm in x, y, and z directions respectively. This could partly explain the uncorrected residual in Fig. 7f and 8f compared to Fig. 7d and 8d, but needed to be explored further. A solution to this is simply to fix the cameras to the magnet bore.

Apart from the table uncertainty, calibration accuracy test showed a 0.15 ± 0.13 mm error in the z direction. But the contribution of this error to motion computation was much smaller than 0.1 mm, and could be neglected for our purposes. This suggests that even though calibration between the cameras and MRI scanner should be as accurate as possible, the motion calculation is rather tolerant for small imperfections in this calibration.

A different situation is encountered with regards to accuracy of feature point localization. Accuracy of motion estimation is highly dependent on tracker noise. Under the conditions described above, at least 20 feature points needed to be tracked for adequate precision. Because of the setup of our cameras, which imaged only part of a subject’s face, only a limited number of feature points could be identified with the cameras. This was remediated by using a sticker fixed to the forehead. However, facial twitching or frowning could introduce potential problem of relative motion between the sticker and the brain. Fast facial movements could be filtered out in our method by discarding and reacquiring k-space lines, but slow facial changes could compromise the effectiveness of the proposed methods. A potential improvement is to replace the rigid sticker used in the current implementation, with a number of separate stickers or facial markings, and detect facial twitching from changes in relative position of the stickers. This would allow a rescan of corresponding k-space lines. An alternative solution is to increase the camera field of view to allow the incorporation of facial feature points that are less sensitive to skin movements caused by effects such as frowning and twitching.

Due to the tracker’s limited (10 Hz) frame rate some fast motion could not be adequately corrected. For this reason, a reacquisition function was added to the sequence in this project. The number of re-acquired lines (reacquisition rate) was dependent on the type of head motion and quite variable, e.g. 2.3% for the conditions presented in Fig. 6d and 10% for those in Fig. 7f. Considering the resulting improvement in image quality and the small increase in total imaging time, this sacrifice appears worthwhile. Nevertheless, improved tracking speed might reduce or eliminate the need for re-acquisition. This was confirmed in the “slow motion” experiment, during which the re-acquisition was turned off. Under this condition, the tracking speed exceeded the head motion speed, resulting in excellent image quality without any reacquisition, as was seen in Fig. 8(f, i). With the continuing increase of computational power, and improved motion tracking algorithms, it is therefore expected that the need for re-acquisition will be reduced. One possible area for improved tracking is the use of predicative estimates for object motion, for example by using Kalman filtering.

Although the motion correction scheme presented here was effective in reducing the effects of motion on image quality (e.g. compare Figs. 5d and 7f with correction versus the not corrected versions in Figs. 5c and 7e), there remain possibilities for improvement. For example, the motion-corrected images in Figs. 7f and 8f are slightly inferior to the corresponding images acquired during the minimal head motion (Figs 7d and 8d). This apparently imperfect motion compensation could be due to not only the table uncertainty mentioned above, but also a number of other factors, for example phase changes due to small changes in local B₀ amplitude, or subtle changes in B₁ amplitude and phase. The contribution of these effects and their potential mitigation remains to be investigated.

Conclusion

We developed an optical motion correction system to prospectively correct motion for high-resolution MRI. The system is highly accurate and allows the acquisition of high quality brain images in the presence of substantial head motion. The system is anticipated to greatly facilitate brain MRI on subjects that have difficulty remaining still during scanning.