Abstract
Friction characteristics with respect to surface topographic orientation were investigated using surfaces of different materials and fabricated with grooves of different scales. Scratching friction tests were conducted using a nano-indentation-scratching system with the tip motion parallel or perpendicular to the groove orientation. Similar friction anisotropy trends were observed for all the surfaces studied, which are (1) under a light load and for surfaces with narrow grooves, the tip motion parallel to the grooves offers higher friction coefficients than does that perpendicular to them, (2) otherwise, equal or lower friction coefficients are found under this motion. The influences of groove size relative to the diameter of the mating tip (as a representative asperity), surface contact stiffness, contact area, and the characteristic stiction length are discussed. The appearance of this friction anisotropy is independent of material; however, the boundary and the point of trend transition depend on material properties.
Anisotropic surfaces are reported on the skins of wild animals, sandfish1 and snake2,3 for example, and are results of many fabrication and manufacturing processes, such as turning, grinding, honing, and shaping, etc. Friction anisotropy probed in different motion direction is widely observed in interactions of various surfaces, such as single crystal surfaces4,5,6, quasicrystal surfaces7,8, organic molecular monolayers9,10,11, monolayer graphene12, and textured surfaces13,14. It even exists in the presence of lubrication15,16,17. Differences in surface potential corrugations and bulk plasticity with respect to lattice structures4,5,18, distinct excitations of electron and phonon in quasicrystals7,8,19,20,21, surface stiffness differences caused by molecular chain alignments10,11 or graphene puckering12, and micro-hydrodynamic lifting and fluid side flows15,17,22 have been analyzed in the course of understanding the nature of friction anisotropy.
Friction anisotropy may involve complicated physical phenomena, but in many cases, surface topography plays a crucial rule and results in friction anisotropy with respect to topographic orientation. This type of friction anisotropy is gaining increasingly strong attention due to its importance to innovative designs of frictional interfaces; however, no systematic research has been committed so far to reveal the scientific nature of related friction variation.
A grooved texture surface mating with a tip of a known size, as illustrated in Fig. 1a, leads to a contact interface formed by single or multiple surface grooves with a relatively smooth spherical asperity (the tip), depending on the scale of the surface textures (Figs. 1b and 1c). The relative motion of the tip parallel and perpendicular to the grooves should reveal the sensitivity of friction to surface pattern orientation. The current study is committed with this setup, as a systematic comparative study, to investigate the friction anisotropy phenomena with respect to surface topographic characteristics and to understand the roles of pattern size, applied load, and materials. This study involves four materials, three scales of interactions, and a range of loads. Several key questions are addressed for the first time, such as whether friction anisotropy is a material related issue, would it change with topographic parameters, and is there a critical transition point of the friction anisotropy at which the effects of topographic orientations switch? The answers to these questions should shed light on friction control by means of surface patterning and texturing, similar to modifying the “landscape” of surface interaction to modulate friction at the atomic scale23.
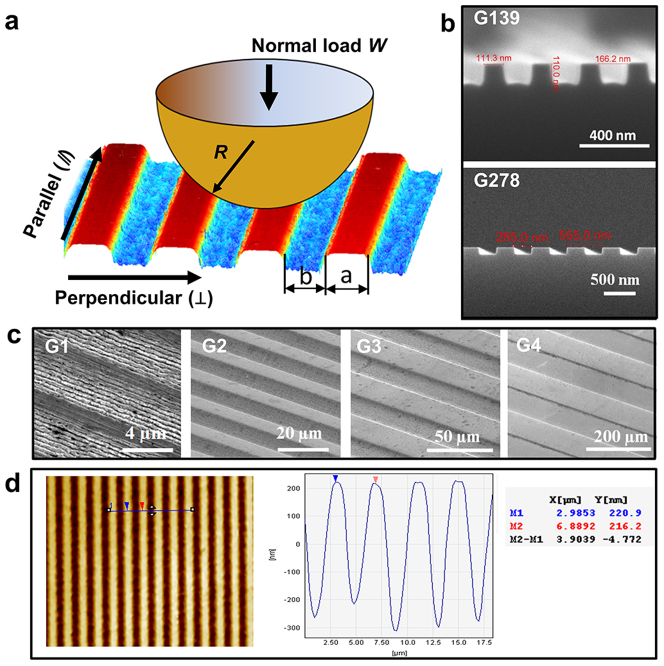
Figure 1. Surface orientations and groove patterns.
(a) Schematic of two characteristic surface orientations with respect to the relative motion directions (the drawing is not to scale). The bank width a and groove width b are shown. (b) SEM images of the G139 and G278 grooves in silicon surfaces (courtesy of LightSmyth Technologies, Inc.). (c) SEM images of the G1–G4 textures in 52100 steel surfaces. (d) Optical measurement results of the G1 52100 steel surface with topography (left) and cross section profile (right). The pitch, defined as a+b, of the G1 texture is confirmed to be about 4 μm.
Results
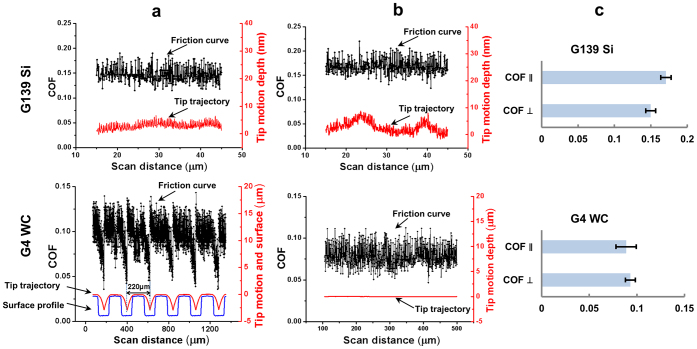
Friction coefficients of all samples were obtained with the same methods. Figure 2 shows the results for G139 Si surfaces (bank width 139 nm, pitch 278 nm) and G4 WC surfaces (bank width 110 μm, pitch 220 μm). In the perpendicular direction, both the friction coefficient history and the real-time tip trajectory fluctuate simultaneously following the texture profile. Although the period of the curves for the nano-scale pattern of G139 Si samples are not distinguishable considering the small tip motion (4.0E-03 nm as listed in Table S1 of the Supplementary material) in the depth direction and large friction variation, that for the G4 WC samples is clearly the same as the groove pitch (Fig. 2a) of about 220 μm, and the shapes of both curves in the parallel direction (Fig. 2b) are nearly flat. The tip motion trajectories in the two characteristic directions of the G139 Si surfaces are shown in nm to emphasize the details. In contrast to the G4 WC surfaces, the tip fluctuation on the G139 Si surface in the parallel direction is larger than that in the perpendicular direction. When the WC tip (root mean square (RMS) roughness = 66.0±5.6 nm) travels in the parallel direction, stick-slip happened on the nearly atomic smooth continuous Si banks (RMS roughness = 2.3±0.2 nm). The tip jump due to the release from stiction leads to the peaks in the tip trajectory. The discontinuous patterns in the perpendicular direction prohibit the tip from sticking to the grooved surface. However, no obvious stick and slip were observed on the G4 WC surface in the parallel direction due to the higher surface roughness (RMS roughness values are 151.0±2.0 nm for the 304 stainless steel tip and 10.3±2.1 nm for the non-grooved WC surface). It is worth mentioning that the low-speed friction responses of the G4 surface in the perpendicular direction is similar to a stick-slip behavior; however, the energy barrier imposed by the texture ridges, instead of stiction, is the source of friction variation.
Figure 2. Friction coefficient histories and real-time tip trajectories.
(a) Friction coefficient history curves and real-time tip trajectories in the perpendicular direction. The groove surface profile of G4 WC is plotted for reference. (b) Friction coefficient history curves and real-time tip trajectories in the parallel direction. Note that the tip trajectory fluctuations are around 5 to 10 nano meters in the G139 Si surfaces, much smaller than the groove size. (c) Average friction coefficients in the parallel (//) and perpendicular (⊥) directions of a G139 Si and a G4 WC surface. The experiment details are following: applied load: 5 mN, tip speed: 1 μm/s. The G139 Si sample (bank width 139 nm, pitch 278 nm) was mated with a WC ball (R = 803±12 μm, RMS roughness = 66±5.6 nm); the G4 WC sample (band width 110 μm, pitch of 220 μm) was mated with a 304 stainless steel ball (R = 800±3 μm, RMS roughness = 151±2 nm).
The friction coefficients were obtained by averaging data over a 220 μm traverse distance for at least 3 repeats. Figure 2c shows that the average friction coefficients are direction dependent, with higher values in the parallel direction for samples with narrower grooves, such as G139, and equal or higher values in the perpendicular direction for samples of wider grooves of G4. The large friction error bar in the parallel direction of the G4 samples is due to the location that the tip contact was made, e.g. on the bank or at the corner edges of a groove, and higher friction is associated with the contact on the bank as if there were no textures.
Friction coefficients of all samples are given in Fig. 3. The average friction coefficients for three types of surfaces, i.e., copper alloy (Cu), 52100 steel and tungsten carbide (WC), with G1 to G4 textures in two directions are plotted against the relative pattern size, b/R, groove width b mating over tip radius R, in Fig. 3a. This figure reveals that the comparison of the average friction coefficients from the parallel and perpendicular directions of motion depends greatly on the groove size with respect to the tip size. The average friction coefficients for the G1 surfaces plotted at the left end of Fig. 3a show higher values in the parallel direction; while those for the G4 surfaces, at the right end, are higher in the perpendicular direction. Variation of the average friction coefficient points out a relative size, b/R = (b/R)c, for the transition of the friction trend; assuming a perfect rectangle profile without deformation, the friction coefficient and topographic parameters, such as groove width b and tip radius R, are related as 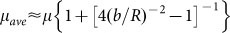 , where μave is the average friction coefficient, and μ is the friction coefficient related to a flat surface. It obviously indicates that the average friction coefficient increases with b/R, which explains the geometric meaning of the transition. This observation is in agreement with the higher friction reported at the edges of atomic-scale surface steps due to deeper potential barriers24,25. Moreover, the value of (b/R)c changes with material effective modulus, suggesting that surface deformation, or issues related to surface stiffness, might have played a role in the transition.
, where μave is the average friction coefficient, and μ is the friction coefficient related to a flat surface. It obviously indicates that the average friction coefficient increases with b/R, which explains the geometric meaning of the transition. This observation is in agreement with the higher friction reported at the edges of atomic-scale surface steps due to deeper potential barriers24,25. Moreover, the value of (b/R)c changes with material effective modulus, suggesting that surface deformation, or issues related to surface stiffness, might have played a role in the transition.
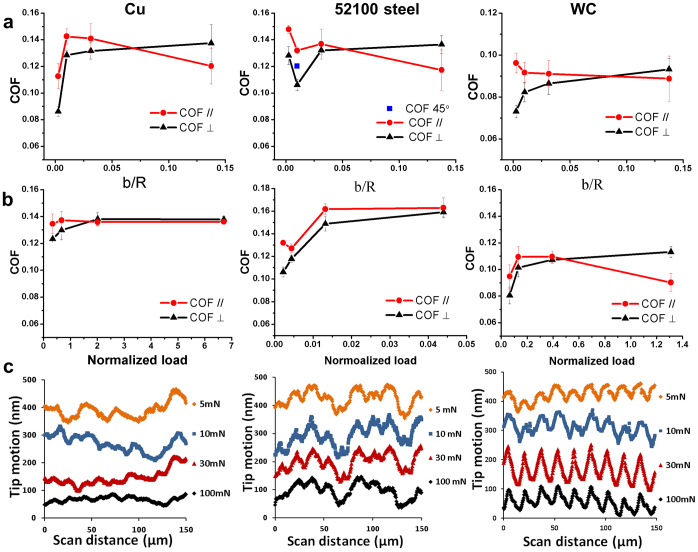
Figure 3. Friction characteristics from size-dependent and load-dependent tests.
(a) Friction anisotropy under the constant load of 5 mN with respect to the relative pattern size, b/R, corresponding to the groove bank sizes of 2, 8, 25 and 110 μm. (b) Friction anisotropy of the same grooves (8 μm) with respect to normalized load, defined as applied load over the critical load of yielding or failure, corresponding to the applied loads of 5, 10, 30 and 100 mN. (c) Real-time tip trajectories from the load-dependent tests. Note that the curves are separated with certain distance for clarity. The mating tips are 304 stainless steel balls (R = 800±3 μm, RMS roughness = 151±2 nm), and the scan speed was 1 μm/s for all of the above experiments.
Figure 3b plots the average friction coefficients with respect to normalized applied load defined as load over the critical load at yield, or a failure threshold of the corresponding smooth surface. The friction anisotropy phenomenon is revealed for each material pair under various loads. Note that the difference of friction coefficients reduces and the anisotropy vanishes, or the trend even reverses at a certain point, as load increases, which suggests boundaries of such friction anisotropy. The dependence of the position of an anisotropy boundary on load implies the effect of surface deformation, and hence the influence of modulus and hardness. The smoother tip trajectory on the G2 Cu sample under the 100 mN load reveals that the texture was smoothened (Fig. 3c) as a result of significant deformation. The textures in the 52100 steel surfaces were still in a good shape even after experiencing the maximum applied load of the test range, and for this reason the friction anisotropy remains. A higher load is needed to explicitly capture the boundaries of the friction anisotropy of this material. The decreasing amplitudes of the tip trajectories of the 52100 steel surfaces explain the reduction of the friction anisotropy. The average friction coefficients associated with the G2 WC surfaces in two directions merge at the normalized load of about 0.5; then they deviate again but in the opposite direction. This is attributed to the deformation occurred in the relatively more compliant stainless steel tip. Rubbing while deforming should increase the energy barrier for the motion along the perpendicular direction, as shown by the sharpened tip trajectories.
Macroscopic friction tests was conducted to confirm the above mentioned findings using a universal material tester (CETR, UMT-2) with a 6.35 mm diameter Cr ball indenting and sliding on the G2 WC surfaces under 196 mN load with sliding speed of 50 μm/s. The friction coefficient curve in the perpendicular direction has a period of about 16 μm, consistent with the groove size. The average friction coefficients in the parallel and perpendicular directions were 0.0422±0.0007 and 0.0331±0.0022, respectively. The result are in agreement with the data at the left-hand sides of the WC plots in Fig. 3a and 3b before the transition. Thus, friction anisotropy with respect to topographic orientation is confirmed by these macroscopic friction tests, with higher friction in the parallel direction for b/R < (b/R)c and a normalized load (0.16) lower than the critical load ratio for the friction transition to occur (0.5).
Discussion
The friction enhancement in the perpendicular directions for surfaces with wider groove patterns as a result of higher energy barriers is believed to lead to the transition of friction anisotropy. The reason why the friction coefficients in the parallel direction cases are higher than those in the perpendicular direction cases for surfaces with narrower patterns deserves an attention. In this work, moisture lubrication is not likely due to low humidity. The contact materials are dissimilar materials, so that commensurability and mismatch of the crystalline directions are not applicable. Plastic deformation and plowing are not involved under light loads. The surfaces were well cleaned and the tracks were not re-used, consequently no obvious third body or wear debris problems should be considered.
The strong orientation of grooves should lead to anisotropic surface stiffness. Finite element simulations were conducted using SIMULIA Abaqus FEA, and the results show that the surface contact stiffness, inversely proportional to surface deformation, is larger when the tip motion is parallel to the grooves than that when the tip motion is perpendicular to the grooves. Among the microscale G1–G4 52100 steel samples, for example, the maximum ratio of the surface stiffness (// over ⊥) is about 1.13 for the G1 textured surfaces, while the ratios for other 52100 samples decrease with increased bank widths, which should finally reach unit for very wide grooves. The surface stiffness ratios are normalized by their maximum value among all textured surfaces and shown as circles in Fig. 4. The same trend is observed for other samples although that for the nanoscale textured Si surfaces follows a different line. Trend discontinuity is observed in between the G1 and G278 samples as a result of pattern sizes in two different scales, which causes distinct number of banks in contact for these surfaces. When several texture banks are in contact, the load supported by each of them is quite different; therefore, the stiffness of each texture is different, and the overall surface stiffness is the combined action of all individual texture. However, the texture bank right underneath the tip takes the majority of the load. As a result, this bank has the maximum surface contact stiffness ratio (see Supplementary Fig. S2). Even with the surface stiffness impact examined, the direct correlation between surface stiffness and friction for the material group in this study is not as clear as that for compliant materials, graphene for example.
Figure 4. Relative friction anisotropy (COF change over COF ⊥) related to surface stiffness ratio (// over ⊥) and stiction length ratio (// over ⊥) in regard to surface orientations and energy-barrier induced COF change in the perpendicular direction.
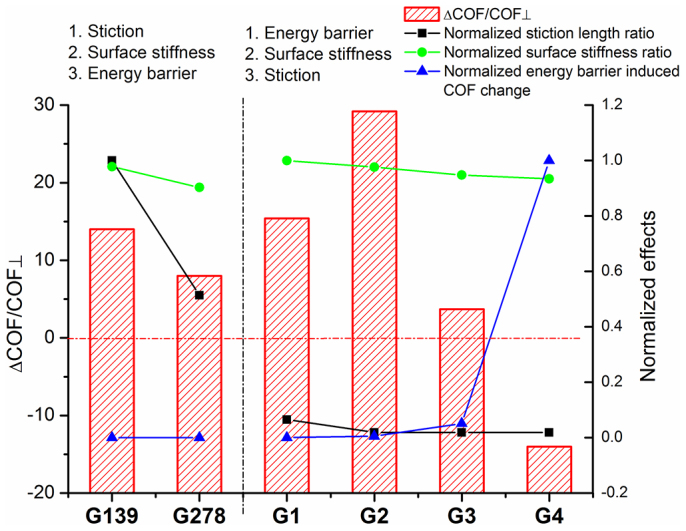
The results of each effect are normalized by its maximum value. The domain is classified as two groups: surfaces with nanoscale textures, G139 and G278, and other surfaces with microscale textures, G1–G4. In each region, the possible mechanisms of friction anisotropy are listed in the order of impact.
The evolution of contact areas follows the same manner as friction variations, i.e., continuously smooth in the parallel direction but fluctuating in the perpendicular direction. The degree of fluctuation depends on relative groove size b/R; slight change is associated with the case of a small b/R, while a larger fluctuation with the case of a larger b/R (see Fig. S3 in Supplementary Information). Since friction anisotropy holds even on surfaces with b/R as small as 1.7×10−4 (G139), the effect of this contact area difference in the two directions may be trivial.
The critical stiction lengths in the two orthogonal directions obtained from the micro-slip analysis at the local contacts are also believed to be responsible for friction anisotropy14. Compared with the discontinuous shorter contacts in the perpendicular motion cases, a longer stiction length is associated with the parallel cases prior to macro-slip initiation. At low-speed scratching, this means continuous adhesion in the contact junction when motion starts, and thus more energy has to be dissipated26 and a high friction is expected in the cases of low topography-induced barrier. From the peeling of a flexible plate bonded to a rigid substrate with an incision-patterned thin adhesive, Chung27 reported that longitudinal incisions demanded higher loads to propagate the cracks than lateral incisions did, which demonstrates the same trend as the friction anisotropy of surface with narrower grooves. Different crack propagation speeds and fracture contours from elliptical contacts in the shear mode along two directions were reported by Das et al.28, which are analogous to friction anisotropy with respect to topography.
A static friction model developed by Chen and Wang29 for solving the contact between a sphere and a rough surface was employed to analyze the maximum stiction length, which is the longest continuous length in the stick area measured along the direction of the tendency of motion (see Fig. S4 in the Supplementary Information). If the shear traction is less than the local shear strength, the local contact area is in stick, otherwise, in slip. The ratios of the maximum stiction length (// over ⊥) are normalized by their maximum value among all textured surfaces and shown as squares in Fig. 4. Among the microscale textured 52100 steel samples (G1–G4), the largest ratio before normalization is 3.41 for the G1 textured surface, while that of the rests are all unit because the contact widths are less than the bank widths for these cases. On the other hand, the stiction length of the nanoscale textured surfaces, G139, is dramatically reduced by the discontinuous patterns in the perpendicular orientation.
The variations of friction, surface stiffness, and stiction length with respect to surface orientations and the COF enhancement due to energy barrier in the perpendicular direction were shown altogether in the Fig. 4. The friction anisotropy is presented as the relative change of COF over the COF in the perpendicular direction; the stiction length and surface stiffness results are also displayed as ratios (// over ⊥); the energy barrier induced COF enhancement is estimated by 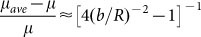 where μ and μave are the friction coefficient associated with a smooth surface and that with a textured surface in perpendicular direction, respectively, and b/R is the relative grove size. The impacts of the surface stiffness, stiction, and engery barrier are normalized by their maximum values in Fig. 4. The result domain can be clearly divided into two regions, one for the nanoscale grooves (left) and the other for the microscale textures (right). It seems that the stiction length difference dominates the COF variations in the former for G139 and G278, while the effect of surface stiffness plays a secondary role and the groove-induced energy barrier in perpendicular direction is negligible because their patterns are the smallest. In the region of microscale textured surfaces, G1–G4, the energy barrier effect is the strongest. The larger the relative pattern, the steeper the barrier; and this observation is supported by the friction trend reverse for the G4 samples. The effects of stiction length and surface stiffness are both active at this range, but they become less important as the surface patterns become larger. The effect of surface stiffness seems have larger influence zone compared with that of stiction length because the surface stiffness ratios are still distinguishable among G2–G4 samples.
where μ and μave are the friction coefficient associated with a smooth surface and that with a textured surface in perpendicular direction, respectively, and b/R is the relative grove size. The impacts of the surface stiffness, stiction, and engery barrier are normalized by their maximum values in Fig. 4. The result domain can be clearly divided into two regions, one for the nanoscale grooves (left) and the other for the microscale textures (right). It seems that the stiction length difference dominates the COF variations in the former for G139 and G278, while the effect of surface stiffness plays a secondary role and the groove-induced energy barrier in perpendicular direction is negligible because their patterns are the smallest. In the region of microscale textured surfaces, G1–G4, the energy barrier effect is the strongest. The larger the relative pattern, the steeper the barrier; and this observation is supported by the friction trend reverse for the G4 samples. The effects of stiction length and surface stiffness are both active at this range, but they become less important as the surface patterns become larger. The effect of surface stiffness seems have larger influence zone compared with that of stiction length because the surface stiffness ratios are still distinguishable among G2–G4 samples.
To summarize, the exploration of this work covers a wide range of materials; similar friction anisotropy was observed for all the surfaces of the materials studied, and the same trend of transition of friction anisotropy with respect to topography was observed. The analyses reveal that the surface contact stiffness, the energy barrier in the perpendicular direction and the stiction length in the direction of motion have notable impacts on the friction anisotropy phenomenon, and the contribution from each is closely related to the relative pattern size.
Methods
Groove fabrication and characterization
A series of groove-shape textures with bank width a of about 2 μm, 8 μm, 25 μm, and 110 μm, named as G1 to G4 respectively, were fabricated on polished copper alloys (Cu), 52100 steel, and tungsten carbide (WC) surfaces by laser ablation with a pico-second laser system (RAPID Lumera Laser). Silicon stamps (from LightSmyth Technologies, Inc.) with nano grooves of 139 nm and 278 nm, labeled as G139 and G278, were also available for study. Each sample is named based on its material and groove size, such as G1 WC for tungsten carbide surfaces with 2 μm grooves, G139 Si for silicon surfaces with 139 nm grooves. Figure 1b and 1c show the sample groove designs and measurements.
The grooved surfaces were examined by using a white-light interferometer (zygo, NewView 7300) and a scanning electron microscopy (SEM) (Hitachi, S-4500) prior to the friction tests. The coverage ratio, defined as bank width a over pitch a+b, where b is the groove size, is about 50% for all samples. The aspect ratio, which is defined as bank width a over groove height h, ranges from 1 to 22 (shallow features). Geometric parameters of WC samples can be found in Supplementary Table S1 online. The geometries of the other two materials are largely the same with very small variations due to the fact that laser ablation is material-dependent. The laser ablation method is capable of creating complicated patterns on various materials; however, the minimal feature size is constrained by the lens in use and tiny paths are generated on the bombarded surface, as shown in the SEM image of the G1 surface. The G1 profile measured with a white-light interferometer shows a sinusoidal-like cross section instead of the targeted perfectly rectangles. Therefore its real bank width at the top is less than the targeted value of 2 μm. However, the pitches were precisely controlled to be 4 μm for the G1 texture, and so were the others to be 16 μm, 50 μm and 220 μm for G2–G4 textures, respectively. The amplitude of tip trajectory A shows the tip motion in the height/depth directions and can be calculated from the geometric relationship between a spherical tip and a groove, assuming perfect rectangle profile without deformation. The depths of all the grooves are deep enough to prevent the tip from contacting the groove bottom land.
Mating tips
The mating tips were made by rigidly gluing WC balls (to mate with Si surface) and 304 stainless steel balls (for the rests) onto precisely machined tip holders fitting to the test equipment to be described later. The white-light interferometry measurements reveal that the true radius and the surface root mean square (RMS) roughness are 800±3 μm and 151±2 nm for the 304 stainless steel balls, and 803±12 μm and 66±5.6 nm for the WC balls, respectively.
Friction measurements
A nano-indentation-scratching system (NanoTest, Micro Materials Ltd, UK) was used to measure friction by slowly sliding a spherical indentor tip on a grooved sample surface in a controlled environment (about 26°C and 30% humidity). Each specimen was carefully aligned with the grooves either parallel or perpendicular to the indentor motion direction, as illustrated in Fig. 1a, with the assistance of the attached microscope. In the tests, normal loads of 5, 10, 30 and 100 mN were used to investigate the load effect, and 5 mN was used for all other tests. The scanning speed was 1 μm/s. The indenter penetration depth, scan distance, and the normal and lateral forces were recorded during each test after reaching the steady state. Friction coefficient (or COF) is obtained as the ratio of the recorded lateral force over the applied normal load. At least three measurements (scratches) were taken at different locations under each operating condition, and the results were averaged. For the surfaces with large textures, such as G4, the tests in the parallel direction were conducted on the banks and over the grooves for 3 times each. A pin-on-disk tester was also used to measure macroscopic friction at the same environment.
Author Contributions
C.Y. conducted the experiments, performed the numerical simulation and analyzed the data. Q.W. provided guidance on theoretical considerations and experiments. Both authors discussed the results and contributed equally to the manuscript.
Supplementary Material
Friction Anisotropy with Respect to Topographic Orientation
Acknowledgments
We would like to express our sincere gratitude to support from US National Science Foundation and Chinese Scholarship Council. We would like to thank Dr. Tom Lai for supplying the tungsten carbide material, Dr. Bo He on his assistance in testing and Dr. Wei Chen on his suggestions for stiction length analysis. We would also like to thank Mr. Zhe Li, Mr. Fan Zhou and Mr. Zhen Zhang for their help on SEM imaging, and Mr. Hualong Yu, Dr. Xiaoqing Jin, and Professor Jiadao Wang for valuable discussions.
References
- Maladen R. D. et al. Undulatory Swimming in Sand: Subsurface Locomotion of the Sandfish Lizard. Science 325, 314–318 (2009). [DOI] [PubMed] [Google Scholar]
- Hazel J. et al. Nanoscale design of snake skin for reptation locomotions via friction anisotropy. J. Biomech. 32, 477–484 (1999). [DOI] [PubMed] [Google Scholar]
- Klein M.-C. G. & Gorb S. N. Epidermis architecture and material properties of the skin of four snake species. J. R. Soc. Interface 9, 3140–3155 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowden F. P., Brookes C. A. & Hanwell A. E. Anisotropy of friction in crystals. Nature 203, 27–& (1964). [Google Scholar]
- Ko J. S. & Gellman A. J. Friction anisotropy at ni(100)/ni(100) interfaces. Langmuir 16, 8343–8351 (2000). [Google Scholar]
- Mancinelli C. M. & Gellman A. J. Friction anisotropy at pd(100)/pd(100) interfaces. Langmuir 20, 1680–1687 (2004). [Google Scholar]
- Park J. Y. et al. High frictional anisotropy of periodic and aperiodic directions on a quasicrystal surface. Science 309, 1354–1356 (2005). [DOI] [PubMed] [Google Scholar]
- Young Park J. et al. Tribological properties of quasicrystals: Effect of aperiodic versus periodic surface order. Phys. Rev. B 74 (2006). [Google Scholar]
- Liley M. Friction anisotropy and asymmetry of a compliant monolayer induced by a small molecular tilt. Science 280, 273–275 (1998). [DOI] [PubMed] [Google Scholar]
- Carpick R. W., Sasaki D. Y. & Burns A. R. Large friction anisotropy of a polydiacetylene monolayer. Tribol. Lett. 7, 79–85 (1999). [Google Scholar]
- Chen J. et al. Friction-anisotropy dependence in organic self-assembled monolayers. Surf. Sci. 600, 4008–4012 (2006). [Google Scholar]
- Choi J. S. et al. Friction anisotropy-driven domain imaging on exfoliated monolayer graphene. Science 333, 607–610 (2011). [DOI] [PubMed] [Google Scholar]
- Zhang H. & Komvopoulos K. Scale-dependent nanomechanical behavior and anisotropic friction of nanotextured silicon surfaces. J. Mater. Res. 24, 3038–3043 (2011). [Google Scholar]
- He B., Chen W. & Jane Wang Q. Surface texture effect on friction of a microtextured poly(dimethylsiloxane) (pdms). Tribol. Lett. 31, 187–197 (2008). [Google Scholar]
- Ajayi O. O., Erck R. A., Lorenzo-Martin C. & Fenske G. R. Frictional anisotropy under boundary lubrication: Effect of surface texture. Wear 267, 1214–1219 (2009). [Google Scholar]
- Pettersson U. Influence of surface texture on boundary lubricated sliding contacts. Tribol. Int. 36, 857–864 (2003). [Google Scholar]
- Ren N., Nanbu T., Yasuda Y., Zhu D. & Wang Q. Micro textures in concentrated-conformal-contact lubrication: Effect of distribution patterns. Tribol. Lett. 28, 275–285 (2007). [Google Scholar]
- Hirano M., Shinjo K., Kaneko R. & Murata Y. Anisotropy of frictional forces in muscovite mica. Phys. Rev. Lett. 67, 2642–2645 (1991). [DOI] [PubMed] [Google Scholar]
- Park J. Y. et al. Adhesion properties of decagonal quasicrystals in ultrahigh vacuum. Phil. Mag. 86, 945–950 (2006). [Google Scholar]
- Park J. Y., Ogletree D. F., Salmeron M., Jenks C. J. & Thiel P. A. Friction and adhesion properties of clean and oxidized al-ni-co decagonal quasicrystals: A uhv atomic force microscopy/scanning tunneling microscopy study. Tribol. Lett. 17, 629–636 (2004). [Google Scholar]
- Park J. Y. et al. Friction anisotropy: A unique and intrinsic property of decagonal quasicrystals. J. Mater. Res. 23, 1488–1493 (2008). [Google Scholar]
- Wang Q. J., Zhu D., Zhou R. & Hashimoto F. Investigating the effect of surface finish on mixed ehl in rolling and rolling-sliding contacts. Tribol. T. 51, 748–761 (2008). [Google Scholar]
- Carpick R. W. Physics - controlling friction. Science 313, 184–185 (2006). [DOI] [PubMed] [Google Scholar]
- Hölscher H., Ebeling D. & Schwarz U. Friction at atomic-scale surface steps: Experiment and theory. Phys. Rev. Lett. 101 (2008). [DOI] [PubMed] [Google Scholar]
- Muller T. et al. Frictional force between a sharp asperity and a surface step. Phys. Rev. Lett. 79, 5066–5069 (1997). [Google Scholar]
- Olofsson U. & Hagman L. A model for micro-slip between flat surfaces based on deformation of ellipsoidal elastic bodies. Tribol. Int. 30, 599–603 (1997). [Google Scholar]
- Chung J. Y. & Chaudhury M. K. Roles of discontinuities in bio-inspired adhesive pads. J. R. Soc. Interface 2, 55–61 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das S. & Kostrov B. V. An elliptical asperity in shear - fracture process and seismic radiation. Geophys. J. Roy. Astron. Soc. 80, 725–742 (1985). [Google Scholar]
- Chen W. W. & Wang Q. J. A Numerical Static Friction Model for Spherical Contacts of Rough Surfaces, Influence of Load, Material, and Roughness. J. Tribol. 131, 021402–1–8 (2009). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Friction Anisotropy with Respect to Topographic Orientation