Multiple applicator hepatic ablation with interstitial ultrasound devices: Theoretical and experimental investigation

Abstract

Purpose: To evaluate multiple applicator implant configurations of interstitial ultrasound devices for large volume ablation of liver tumors.

Methods: A 3D bioacoustic-thermal model using the finite element method was implemented to assess multiple applicator implant configurations for thermal ablation with interstitial ultrasound energy. Interstitial applicators consist of linear arrays of up to four 10 mm-long tubular ultrasound transducers, each under separate and dynamic power control, enclosed within a water-cooled delivery catheter (2.4 mm OD). The authors considered parallel implants with two and three applicators (clustered configuration), spaced 2–3 cm apart, to simulate open surgical placement. In addition, the authors considered two applicator implants with applicators converging and diverging at angles of ∼20°, 30°, and 45° to simulate percutaneous placement. Heating experiments (10–15 min) were performed and compared against simulations employing the same experimental parameters. To estimate the performance of parallel, multiple applicator configurations in an in vivo setting, simulations were performed taking into account a range of blood perfusion levels (0, 5, 12, and 15 kg m⁻³ s⁻¹) that may occur in tumors of varying vascularity. The impact of tailoring the power supplied to individual transducer elements along the length of applicators is explored for applicators inserted in non-parallel (converging and diverging) configurations. Thermal dose (t₄₃ > 240 min) and temperature thresholds (T > 52 °C) were used to define the ablation zones, with dynamic changes to tissue acoustic and thermal properties incorporated within the model.

Results: Experiments in ex vivo bovine liver yielded ablation zones ranging between 4.0–5.6 cm × 3.2–4.9 cm, in cross section. Ablation zone dimensions predicted by simulations with similar parameters to the experiments were in close agreement (within 5 mm). Simulations of in vivo heating showed that 15 min heating and interapplicator spacing less than 3 cm are required to obtain contiguous, complete ablation zones. The ability to create complete ablation zone profiles for nonparallel implants was illustrated by tailoring applied power levels along the length of applicators.

Conclusions: Parallel implants consisting of three interstitial ultrasound applicators in a triangular configuration yield complete ablation zones measuring up to 6.2 cm × 5.7 cm after 15 min heating. At larger interapplicator spacing, the level of blood perfusion in the tumor may yield indentations along the periphery of the ablation zone. Tailoring applied power along the length of the applicator can accommodate for nonparallel implants, without compromising safety.

INTRODUCTION

Thermal ablation is a well established therapy for the treatment of unresectable hepatocellular carcinoma and select secondary hepatic tumors.^{1, 2, 3} Ablation is also used for treatment of cancer and benign disease in bone, kidney, lung, prostate and uterine fibroids. Radio frequency (RF) currents, cryoablation, microwaves (MW), and interstitial laser fibers are the most commonly used energy modalities for minimally invasive thermal ablation of liver tumors, and high intensity focused ultrasound has emerged as a noninvasive technique for tissue ablation.^{4, 5, 6, 7} Thermochemical ablation and irreversible electroporation have recently emerged as other modalities for tissue ablation.^{8, 9, 10, 11} Irrespective of energy modality, the goal of thermal ablation treatment of liver tumors is to raise target (tumor and a 5–10 mm margin encompassing the tumor) temperatures to lethal levels, while ensuring thermal protection of surrounding critical structures. If a single ablation does not adequately cover the target, sequential overlapping ablations must be performed until the entire target is treated adequately.¹²

Catheter-based ultrasound devices are under development for thermal therapy of cancer and benign tissue in the prostate, uterine fibroids, liver, bone, and other organs. These devices consist of independently powered tubular, planar, or curvilinear transducers arranged in a linear array. Devices suitable for percutaneous ablation (13–14 g) have been developed and successfully evaluated in vivo for application in highly perfused organs such as the liver,^{13, 14, 15} prostate,^{16, 17} brain¹⁸ and uterine fibroids.¹⁹ Compared to other needle-based ablation devices, minimally invasive catheter based ultrasound devices have the unique ability to control the spatial energy deposition profile along the length of the applicator,^{14, 20} as well as across the angular expanse.^{16, 17} Ultrasound applicators for thermal therapy also offer the potential to be used as an imaging device to determine proper applicator placement as well as to monitor treatment progression.^{13, 21}

A randomized clinical trial comparing percutaneous thermal ablation to surgical resection for tumors < 5 cm in diameter, reported no differences in overall and disease-free survival between the two treatments.¹ However, for larger tumors >5 cm in diameter, studies have reported lower complete ablation rates, 24% and 62% in tumors measuring 5–9.5 cm and 5–7 cm.⁸ Similar results have been reported with early MW ablations systems. Suggested reasons for recurrence due to inadequate ablation include limitations of the heat-sink effect associated with large blood vessels, imprecise placement of applicators during sequential ablations resulting in nonoverlapping ablation zones, limitations of the heating technology, and poor visualization of the treatment zone on preoperative and postoperative imaging.²² It is also noted that the overall and disease free survival rates for patients with large tumors (>5 cm), are significantly lower than those with smaller tumors (<5 cm), possibly due to the more aggressive tumor biology.²³

Several strategies for increasing ablation zone sizes with RF and MW ablation systems have been explored, including: modification of tissue physical properties (e.g. saline infusion),²⁴ modification of blood flow,^{25, 26} power delivery strategies incorporating feedback control,²⁷ and simultaneous multiple-applicator ablation.^{28, 29, 30} Compared to sequential ablations, simultaneous multiple applicator ablations offer the potential for synergistic heating between applicators, leading to faster ablation of targets, however, there is a small risk of skin burns as has been observed in some clinical studies.^{31, 32, 33} A recent study by Sindram et al., reported that the occurrence of skin burns is a function of the array insertion depth and the minimum interapplicator spacing, in the case of nonparallel implants,³⁴ and could be avoided by placing constraints on insertion depth and applicator spacing.

Investigators have explored applicator designs and power delivery strategies for increasing sizes of ablation zones created by catheter-based ultrasound devices. Some of the techniques that have been considered are: applicator cooling (catheter cooled vs. internally cooled),^{15, 17, 35} transducer sizes and shapes,^{36, 37, 38} multifrequency transducers³⁹ and power modulation schemes.⁴⁰ While some studies have explored the feasibility of multiple applicator ablation with catheter-based ultrasound devices, there have been few systematic studies of multiple applicator configurations for treatment of large volume targets in the liver. Diederich et al.⁴¹ explored the possibility of creating conformal ablation zones in the prostate using interstitial ultrasound applicators in conjunction with a transurethral heating applicator. Nau et al.^{17, 42} demonstrated the feasibility of creating conformal ablation zones in muscle and prostate targets in vivo, using directional interstitial applicators. This work builds upon a preliminary investigation⁴³ to extensively analyze the performance of parallel and nonparallel configurations of interstitial ultrasound applicators used for liver ablation.

The objective of this study was to use a previously validated theoretical model and ex vivo experiments to define performance of interstitial ultrasound devices in multiple applicator configurations suitable for creating large volume ablation zones in the liver. We used finite element method (FEM) computer models of liver ablation with multiapplicator implants in parallel, diverging, and converging configurations which bracket common surgical approaches. Specific tests included the feasibility of creating conformal ablation zones with nonparallel implants by tailoring applied power levels along the length of the applicator. Heating experiments were performed in ex vivo bovine liver using a subset of configurations as informed by computational models. Critical temperature and thermal dose thresholds, and visible coagulation were used to assess the ablation volumes under different configurations, and to compare experiments to theoretical models.

METHODS

Minimally invasive ultrasound applicators for liver ablation

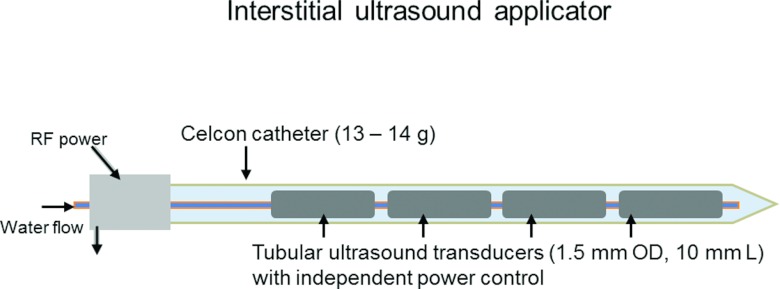
Minimally invasive, catheter-based ultrasound devices for thermal ablation have been described in detail elsewhere,^{17, 44, 46} and are only described briefly in this section. Catheter-based ultrasound applicators considered in this study consist of linear arrays of 1.5 mm (OD) ultrasound transducers, each 10 mm long (Fig. 1). Transducers are mounted on a polyimide tube, and enclosed in a Celon catheter (13 g, 2.4 mm OD). Cooling water is circulated through and over the transducers to protect them from thermal effects, couple the ultrasound energy, and to increase thermal penetration in to the target volume. Transducers are independently powered, enabling tailored heating along the length of the applicator.

Figure 1.

Interstitial ultrasound applicator consisting of a linear array of independently powered ultrasound applicators enclosed in a Celcon catheter (13–14 g). Energy deposition along length of the applicator can be controlled by tailoring power applied to each individual transducer.

Applicator configurations

We considered two types of configurations: (1) Configurations with interstitial applicators inserted parallel to each other and (2) configurations with interstitial applicators inserted in a nonparallel fashion. Parallel implants consisted of two and three applicators spaced 2 or 3 cm apart (see Fig. 2). Nonparallel implants consisted of two applicators in converging or diverging configurations inserted at angles of 20°, 30°, and 45° to a target volume within the liver (see Fig. 3). For converging implants, the spacing between applicator tips was set to 1 cm at a depth of 5 cm, while considering insertion angles of 20°, 30°(nominal), and 45° to the liver surface. For diverging implants, we considered interapplicator tip spacing of 2 cm, 3 cm (nominal), and 4 cm at a depth of 5 cm. Table 1 lists all the applicator configurations considered in this study. We performed heating experiments in ex vivo liver tissue with applicators in configurations 1-5 (only 30° case for configurations 4 and 5). Computer simulations of ex vivo heating (nonperfused liver) were performed and compared against experiments. Computer simulations of in vivo heating were then performed for promising implant configurations.

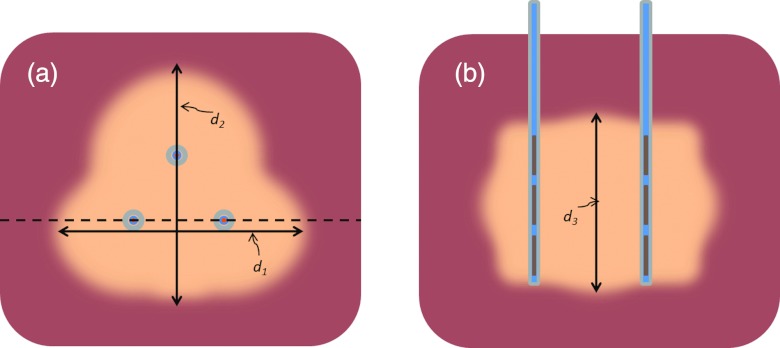
Figure 2.

Illustration of measurements of ablation zones from theoretical models and ex vivo experiments. (a) Top view of slice in a plane perpendicular to applicator insertion showing diameters of ablation zone, d₁ and d₂. Dashed line indicates slice along length of applicator (b), used to measured length of the ablation zone, d₃.

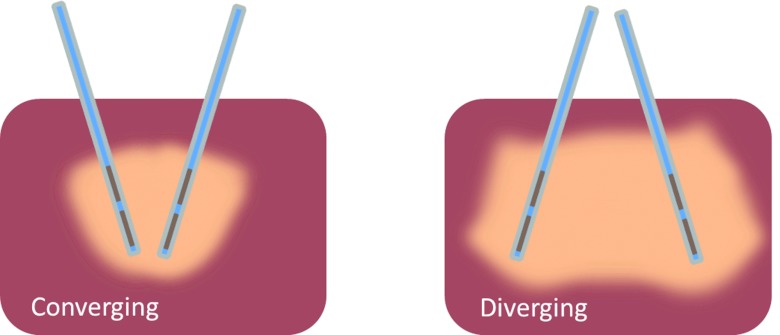
Figure 3.

Sketch of applicators inserted into liver in nonparallel (converging and diverging) configuration.

Table 1.

Multiple applicator configurations for liver ablation considered in this study.

Configuration number	Number of applicators	Applicator spacing (cm)	Notes
1	2	2	Parallel
2	3	2	Parallel
3	3	3	Parallel
4	2	3	Converging (20°, 30°, 45°)
5	2	3	Diverging (20°,30°, 45°)

Ex vivo experiments

While experiments in appropriate in vivo large animal models offer the most comprehensive evaluation, heating experiments in ex vivo liver tissue are a commonly used developmental step for benchmarking ablation technology. We performed ablations in ex vivo liver tissue using applicators in configurations 1–5. Fresh bovine livers were obtained from a local abattoir and transported to our laboratory immediately after excision. Bovine livers were sliced into blocks approximately 8 cm × 8 cm × 6 cm in size and placed in an isotonic saline solution maintained at 37 °C. Ablations were performed on liver samples within 24 h of being brought into the laboratory. Those samples not used immediately were placed in sealed containers containing isotonic saline and preserved on ice. Custom acrylic templates were built to insert applicators into liver at appropriate distances/angles for the various configurations considered in this study. Initial estimates of optimal transducer operating frequencies were obtained by determining the frequency of maximum real impedance using a network analyzer. Acoustic force-balance measurements were performed to determine the electro-acoustic efficiency, or acoustic output energy relative to applied electrical power. Applicators were inserted into the liver tissue up to a minimum depth of 3.5 cm. Independent four-channel RF amplifiers (Advanced Surgical Systems, Tucson, AZ, USA) were used to power individual transducers at their optimal frequencies. All ex vivo ablations were performed with ∼15 W/cm² applied to each transducer for 10 min. This power level was selected based on previous experience with interstitial ultrasound devices. After each application of power, the sample under test was left in the isotonic saline bath for a minimum of five minutes to allow for thermal dose accrual. Samples were then sliced orthogonally across the applicator implant within the central heating plane to take measurements and photographs of the ablation zone (as indicated by the extents of visible tissue discoloration). Figure 2 illustrates the dimensions of the ablation zone reported in this study.

Bioacoustic-thermal model

A 3D bioacoustic-thermal model using the FEM was implemented to determine the transient temperature profile during heating with interstitial ultrasound applicators. Heat transfer in liver tissue was modeled using the Pennes bioheat equation [Eq. 1].

$$\rho c\frac{\partial T}{\partial t}=\nabla ·k\nabla T+Q_s-{\dot{m}}_{bl}{c}_{bl}\left(T-T_{bl}\right),$$ (1)

where ρ [kg m⁻³] is density, c [J kg⁻¹ K⁻¹] is specific heat capacity, k [W m⁻¹ K⁻¹] is thermal conductivity, Q_s [W m⁻³] is the acoustic power deposition term, ${\dot{m}}_{bl}$ [kg m⁻³ s⁻¹]is blood mass perfusion rate, c_bl [J kg⁻¹ K⁻¹] is specific heat capacity of blood, and T_bl [°C] is the temperature of inflowing arterial blood. The acoustic power deposition due to each individual transducer was calculated using Eq. 2.

$$Q_s=2\alpha I_s\frac{r_0}{r}\exp \left(-\int 2\mu r^{\prime }d{r}^{\prime }\right),$$ (2)

where α [Np m⁻¹ MHz⁻¹] is acoustic absorption coefficient, I_s [W m⁻²] is acoustic intensity on the transducer surface, r [m] is the radial distance from the transducer center to a point in the computational domain, r₀ [m] is radius of the transducer, μ is acoustic attenuation coefficient, r^′ [m] is the radial distance from the transducer surface (r^′ = r − r₀). The cumulative power deposition at each point in the computational domain is the sum of acoustic energy due to individual ultrasound transducers. While the Pennes equation has limitations, particularly in accounting for heat transfer due to large blood vessels, it remains a reasonable approximation for modeling heat transfer in tissue and is widely used for evaluating performance of ablation technology.^{47, 48, 49} Recent studies have validated the temperature and thermal damage profile computed using Pennes model with experiments in perfused ex vivo liver, as well as in vivo animal models.^{49, 50, 51} The tissue acoustic and thermal properties used in the model for Eqs. 1, 2 are listed in Table 2.⁴⁴

Table 2.

Tissue physical properties used in computational models of hepatic thermal ablation.

Symbol	Tissue property	Value
ρ	Density	1050 kg m−3
c	Specific heat capacity	3639 J kg−1 K−1
k	Thermal conductivity	0.51 W m−1 K−1
${\dot{m}}_{bl}$	Blood perfusion rate	{5,12,15} → 0 kg m−3 s−11
cbl	Specific heat capacity of blood	3720 kg m−3 s−1
L	Latent heat of tissue water vaporization	1.53 × 106 J kg−1 K−1
Tbl	Temperature of inflowing arterial blood	37 °C
α	Ultrasound absorption coefficient	4.5 → 9 Np m−1 MHz−12
μ	Ultrasound attenuation coefficient	4.5 → 9 Np m−1 MHz−12

¹We considered nominal blood perfusion rates of 5 kg m⁻³ s⁻¹, 12 kg m⁻³ s⁻¹, and 15 kg m⁻³s⁻¹. Blood perfusion was reduced from a nominal value to 0 after a thermal dose of t₄₃ = 300 min was accrued.

²Ultrasound absorption and attenuation coefficients were adjusted linearly with the logarithm of thermal dose up to a value double the nominal value.⁴⁴, ⁷³

The FEM model was implemented in COMSOL Multiphysics v3.5a (COMSOL Inc., Burlington, MA) and all postprocessing was performed in MATLAB (The Mathworks, Inc., Natick, MA). Initial tissue temperature was set to 37 °C. A Dirichlet boundary condition on the edge of the modeled tissue (14 cm × 14 cm × 10 cm) was employed setting the boundary to a fixed temperature of 37 °C. A convective heat transfer boundary condition was applied on the inner catheter wall of each applicator to simulate water cooling, given by Eq. 3.

$$\vec{n}.k\nabla T=h(T_{\infty }-T),$$ (3)

where h = 1000 W m⁻¹ K⁻¹ is the convective heat transfer coefficient and T_∞ = 25 °C is temperature of the cooling water.⁵² An irregular FEM mesh consisting of Lagrangian elements was used to discretize the solution space. A submillimeter mesh resolution (maximum edge length ∼0.5 mm) was employed at each applicator surface, with progressively increasing mesh element size away from the applicator. Maximum element edge length was restricted to 3 mm within the entire computational domain. A nonlinear implicit solver with variable time steps was used to solve Eq. 1 for 10–15 min ablations.

Tissue damage due to thermal injury was determined using the Sapareto-Dewey thermal dose of equivalent minutes at 43 °C model, as specified in Eq. 4.

$$t_{43}={\int }_0^t{R}^{\left({43}^{\circ }\mathrm{C}-T\left(\tau \right)\right)}d\tau ,\left\{\begin{array}{c}\hfill R=0.25,T<{43}^{\circ }\mathrm{C}\\ \hfill R=0.5,T\ge {43}^{\circ }\mathrm{C}\end{array}\right..$$ (4)

Thermal dose calculations were performed at each time step and used to update values of tissue physical properties. The transient FEM solver was allowed to run for a period of 3 min after power to all transducers was turned off, in order to account for accumulated thermal dose due to elevated temperatures. Previous studies indicate a threshold of t₄₃ ≥ 240 min corresponds to coagulative necrosis in soft tissues, and is used as an indicator of treatment endpoint for in vivo simulations and clinical treatments.^{53, 54, 55, 56} Due to the sharp thermal dose gradients at the edge of the ablation zone, a conservative threshold of t₄₃ ≥ 600 min was used as an indicator of visible thermal coagulation for ex vivo experiments and simulations, similar to a previously validated model of catheter-based ultrasound ablation.⁴³

Tissue acoustic and thermal properties were dynamically adjusted during the course of ablations as a function of accrued thermal dose and tissue temperature exposure.⁵⁷ In particular, the acoustic attenuation and absorption coefficients of liver were adjusted linearly with the logarithm of accrued thermal dose, until they attained a value twice that of the nominal value.⁴² For simulations of in vivo heating, microvascular blood perfusion was held constant at its nominal value for tissue with accrued thermal dose t₄₃ ≥ 300 min, and set to zero for all tissue with accrued thermal dose t₄₃ > 300 min and T > 50 °C, an approximation to simulate the effect of microvascular stasis after sustained heating.⁴⁴ Theoretical models employing these changes in acoustic and thermal properties of liver tissue have been previously shown to closely predict experimentally measured temperature profiles and ablation zone boundaries.^{44, 58, 59}

When modeling heating of ex vivo liver tissue, we applied the same power/time settings as used in experiments (15 W/cm² applied power per transducer for 10–15 min, 0 kg m⁻³ s⁻¹ blood perfusion). For in vivo simulations, we considered a range of microvascular blood perfusion levels ranging from 5 kg m⁻³ s⁻¹ to 15 kg m⁻³ s⁻¹. While normal liver tissue has a relatively high blood perfusion rate (∼15 kg m⁻³ s⁻¹), solid tumors may have lower blood perfusion.^{60, 61} In the in vivo setting, where there is a substantial heat sink associated with blood flow, larger applied power levels were specified for heating durations of 10–15 min. The selected power levels were chosen to be the highest power levels which yielded a maximal tissue temperature below 100 °C for 15 min ablations. This yielded power levels up to 25 W/cm². It is noted that such power levels have been applied to similar applicators in prior in vivo studies.¹⁷ Above 100 °C, tissue water vaporizes and subsequent bubble formation may lead to increased ultrasound attenuation (reduced penetration) and unpredictable heating.⁶² Furthermore, in the in vivo setting we considered applicators consisting of 3 and 4 tubular ultrasound transducers in a linear array, similar in configurations as applied for hyperthermia with HDR brachytherapy.⁶³ We also included some simulations to approximate application of elevated power levels, where tissue temperatures in excess of 100 °C are expected. In these simulations, tissue specific heat capacity was modified to account for the substantial heat sink associated with tissue water vaporization.^{54, 64} This is achieved by incorporating the latent heat of water vaporization as shown in Eq. 5:

$$C\left(T\right)=C\left({37}^{\circ }\mathrm{C}\right)+L\frac{\exp \left(-{(T-{100}^{\circ }\mathrm{C})}^2/\Delta T^2\right)}{\sqrt{\Delta T^2\pi }},$$ (5)

where C(T) [J kg⁻¹ K⁻¹] is the tissue specific heat capacity at 37 °C, L [J kg⁻¹ K⁻¹] is the latent heat of tissue water vaporization, and ΔT is the temperature interval over which water vaporization occurs (taken to be 1 °C in this work).

RESULTS

Parallel implants: Ex vivo simulations and heating experiments

Table 3 lists dimensions (mean and standard deviation) of the extents of the observed ablation zone (as indicated by visibly discolored tissue) measured in orthogonal cross sections after 10 min ablations in ex vivo bovine liver for implant configurations 1–3. Table 3 also lists extents of the ablation zone as predicted by the t₄₃ ≥ 600 min isodose margin, computed using theoretical models of heating in ex vivo tissue, employing the same parameters used in the experiments. Maximal diameters (in the plane perpendicular to applicator insertion) of the ablation zone ranged between 4.0 cm (configuration 1) and 5.6 cm (configuration 2). Experimental measurements were repeatable, with standard deviations ranging between 2 and 5 mm. Dimensions of ablated tissue obtained from the presented ex vivo experimental study and the theoretical models developed here listed in Table 3, were quantitatively compared using a one-sampled student's t-test. Based on a 5% significance, statistical equivalence could be established for measured and simulated values of metrics d₂ and d₃ for implant configurations 1, 2, and 3, and metric d₁ for configuration 2. When compared to experimental measurements, theoretical models overestimated d₁ by 16% for configuration 1, and underestimated d₁ by 10% for configuration 3, at a statistical significance of 5%. Figure 4 shows images of ex vivo bovine liver samples ablated with a single applicator and multiple applicators in configurations 1–3. Both the experimental and computational results show that, in the absence of blood perfusion, contiguous ablation zones can be achieved using all the parallel applicator configurations considered in this study. We note that the ablated tissue in Fig. 4c (configuration 3) appears to be more desiccated and tightly coagulated than the other configurations, suggesting probable explosive tissue disruption in the central region between the clustered array. This may be expected since this configuration has the greatest potential for synergistic heating (greater temperatures and thermal dose exposure) applicators with three applicators spaced 2 cm apart (compared to two applicators in configuration 1, and three applicators spaced 3 cm apart in configuration 2).

Table 3.

Dimensions of ablation zone in ex vivo liver for parallel implants (configurations 1–3). Experimental data are the mean ± standard deviation of n experiments. Simulation data correspond to the t₄₃ ≥ 600 min isodose boundary calculated by the bioacoustics-thermal model, which did not include the effects of perfusion.

		Experiment			Simulation
Configuration	n	d1 (cm)	d2 (cm)	d3 (cm)	d1 (cm)	d2 (cm)	d3 (cm)
1	6	4.0 ± 0.3	3.2 ± 0.4	2.9 ± 0.2	4.5	3.0	2.9
2	9	4.6 ± 0.5	4.2 ± 0.5	3.3 ± 0.5	4.7	4.6	3.2
3	8	5.6 ± 0.5	4.9 ± 0.5	2.8 ± 0.3	5.2	4.9	2.8

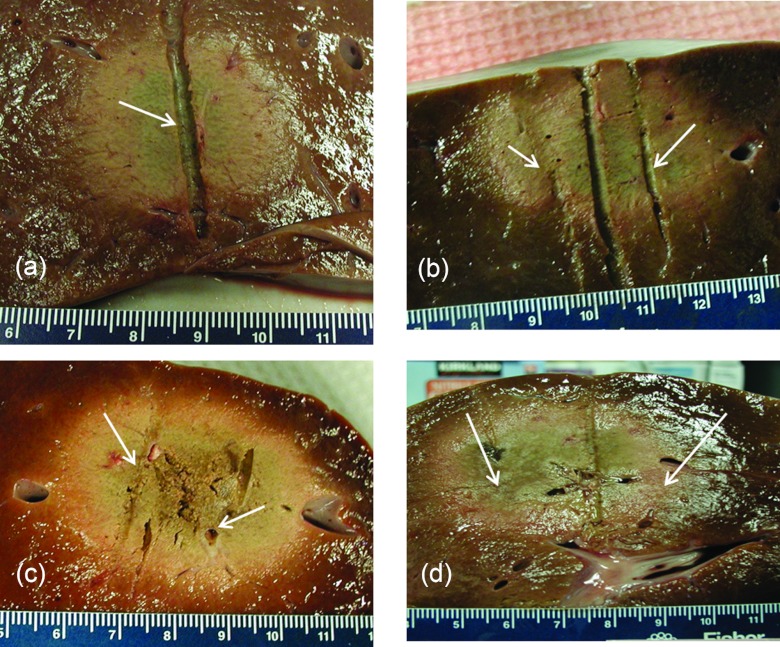
Figure 4.

Ablation zones in ex vivo liver tissue after 10 min ablations with (a) a single applicator, (b) two applicators spaced 2 cm apart (configuration 1), (c) three applicators spaced 2 cm apart (configuration 2) and (d) three applicators spaced 3 cm apart (configuration 3). Arrows indicate the position of ultrasound applicators. The indentation through the center of figures B and D correspond to place holders used to mark the midpoint between applicators.

Parallel implants: In vivo simulations

Table 4 lists dimensions of the extents of the ablation zone, as assessed by the t₄₃ > 240 min isodose boundary, after 10 and 15 min ablations using configurations 1–3. For each configuration, results are listed for applicators consisting of linear arrays of 3 and 4 transducers. Furthermore, we modeled heating with unrestricted applied power levels for configurations 1–3, with dimensions of the ablation zone for these simulations listed in Table 5. Figure 5 shows sample temperature profiles in orthogonal planes for the parallel implant configurations under evaluation.

Table 4.

Dimensions and volumes of the in vivo ablation zones, estimated from t₄₃≥ 240 min isodose boundary calculated by computer models (T restricted to ∼ 100 °C), after 10 and 15 min ablations with applicators in configurations 1–3. (NC = noncontiguous).

		mbl = 5 kg m−3 s−1				mbl = 12 kg m−3 s−1				mbl = 15 kg m−3 s−1
Time	Configuration	d1 (cm)	d2 (cm)	d3 (cm)	V (cm3)	d1 (cm)	d2 (cm)	d3 (cm)	V (cm3)	d1 (cm)	d2 (cm)	d3 (cm)	V (cm3)
Three transducers (each 1.2 mm OD × 10 mm L) per catheter
10 min
	1	4.5	2.8	4.0	33.8	3.7	1.6	3.4	16.3	NC	NC	NC	6.1
	2	4.0	3.8	3.7	34.7	4.1	3.9	3.9	37.6	3.6	3.3	3.6	24.8
	3	5.6	4.8	4.0	62.2	5.6	4.6	4.1	57.3	NC	NC	4.0	42.5
15 min
	1	5.0	3.5	4.4	47.3	4.2	2.5	3.8	27.4	3.7	1.5	3.4	15.1
	2	4.5	4.4	4.3	50.4	4.6	4.5	4.4	53.1	4.2	4.0	4.1	40.6
	3	6.1	5.6	4.5	87.6	6.0	5.4	4.4	80.7	5.7	4.9	4.1	65.3
Four transducers (each 1.2 mm OD × 10 mm L) per catheter
10 min
	1	4.5	2.9	5.2	46.7	4.2	2.3	5.0	35.6	3.8	1.6	4.8	23.8
	2	4.0	3.9	4.9	48.0	4.1	3.9	5.1	51.3	3.6	3.3	4.7	34.4
	3	5.7	4.9	5.2	85.8	5.6	4.6	5.3	79.0	NC	NC	5.1	58.9
15 min
	1	5.0	3.6	5.6	65.2	4.6	3.1	5.3	51.2	4.3	2.6	5.1	39.2
	2	4.6	4.5	5.5	68.9	4.6	4.5	5.6	71.8	4.2	4.1	5.2	55.3
	3	6.2	5.7	5.5	118.4	6.1	5.5	5.5	110.0	5.8	5.0	5.4	90.0

Table 5.

Dimensions and volumes of the in vivo ablation zones, estimated from t₄₃ ≥ 240 min isodose boundary calculated by computer models with no restriction on power levels (i.e., T > 100 °C), after 10 and 15 min ablations with applicators (three 10 mm long transducers each) in configurations 1–3.

		mbl = 5 kg m−3 s−1				mbl = 12 kg m−3 s−1				mbl = 15 kg m−3 s−1
Time	Configuration	d1 (cm)	d2 (cm)	d3 (cm)	V (cm3)	d1 (cm)	d2 (cm)	d3 (cm)	V (cm3)	d1 (cm)	d2 (cm)	d3 (cm)	V (cm3)
10 min
	1	5.6	4.1	4.9	68.9	5.0	3.3	4.5	48.6	4.8	3.1	4.3	43.0
	2	5.8	5.6	5.2	97.9	5.2	5.0	4.7	72.5	5.0	4.8	4.6	65.5
	3	6.6	6.1	4.8	110.1	6.0	5.2	4.4	75.7	5.7	4.8	4.3	64.5
15 min
	1	6.0	4.6	5.2	87.1	5.3	3.8	4.7	59.9	5.1	3.6	4.6	53.1
	2	6.2	6.2	5.5	121.0	5.5	5.4	5.0	87.2	5.3	5.2	4.9	78.4
	3	7.1	6.7	5.1	141.0	6.3	5.8	4.6	97.2	6.1	5.4	4.5	84.6

Figure 5.

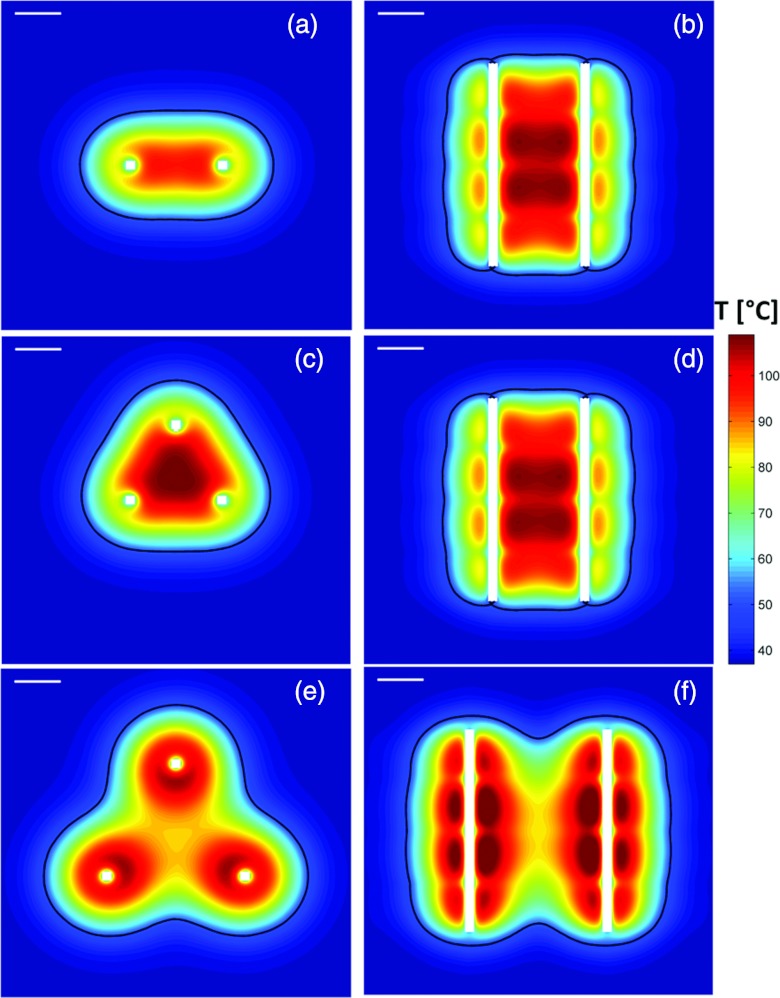
Temperature profiles in axial (left column) and sagittal (right) planes after 15 min ablations with applicators in configurations 1 (a,b), 2 (c,d) and 3 (e,f). The contours indicating extents of the ablation zone correspond to the t₄₃ ≥ 240 min isodose boundary. Temperature profiles shown here are calculated with a nominal perfusion rate of 15 kg m⁻³ s⁻¹. The white line in the top left corner of each panel indicates a scale of 1 cm.

Our simulations indicate that ablation zone volumes ranging between 6.1 cm³ and 90 cm³ can be created with applicators in parallel implant configurations (for m_bl = 15 kg m⁻³ s⁻¹) after 10–15 min heating, while limiting peak tissue temperatures to ∼100 °C. At elevated blood perfusion rates (m_bl = 15 kg m⁻³ s⁻¹), contiguous ablation zones cannot be obtained using only two applicators (configuration 1). Using three applicators spaced 2 cm apart (configuration 2), maximal ablation zone diameters of 4.0 and 4.6 cm could be obtained after 10 and 15 min heating. When inter applicator spacing was increased to 3 cm, maximal ablation zone diameters of 6.0–6.2 cm were obtained for perfusion rates up to 12.5 kg m^–3 s^–1. Our simulations indicate that, contiguous ablation zones can be created with configuration 2 within 10 min for all the blood perfusion levels considered in this study. At a nominal perfusion rate of 15 kg m⁻³ s⁻¹, 15 min ablations are required to create contiguous ablation zones using configurations 1 and 3. Figure 6 illustrates (a) the impact of blood perfusion and (b) treatment times on the extents of the ablation zone in a plane perpendicular to applicator insertion.

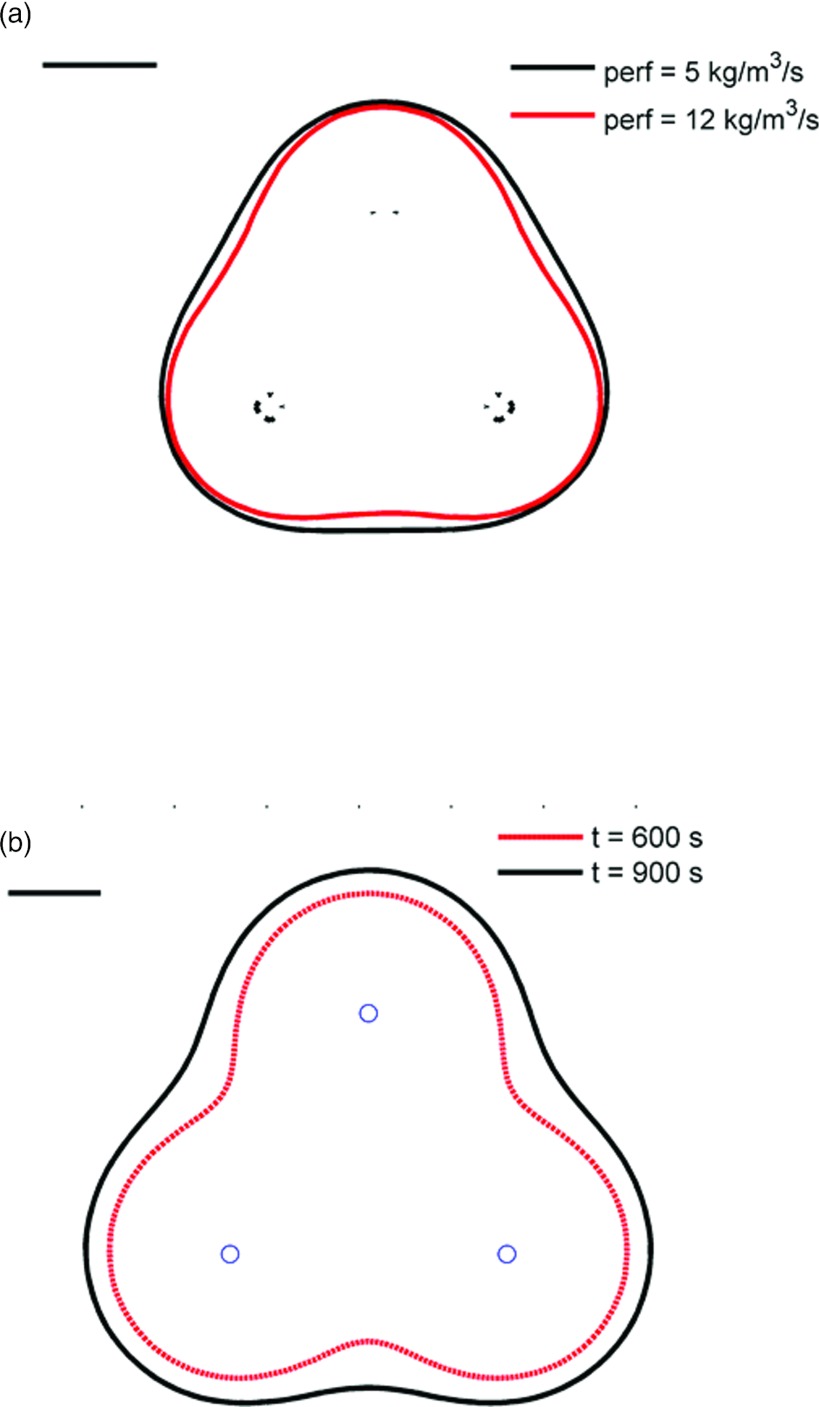
Figure 6.

(a) Extents of the ablation zone after 10 min ablation with applicators in configuration 2, computed using two different nominal blood perfusion rates. At higher blood perfusion rates, there are indentations along the periphery of the ablation zone. (b) Extents of the ablation zone after 10 and 15 min ablation with applicators in configuration 3 at a nominal perfusion rate of 5 kg m⁻³ s⁻¹. The ablation zone profile after 10 min exhibits scalloping/clefting along the boundary. After 15 min of heating, a contiguous ablation zone is formed. The black line in the top left corner indicates a scale of 1 cm.

Nonparallel implants

We performed ex vivo ablations with two applicators in converging and diverging configurations (see Fig. 5). In a converging configuration, applied power levels were 12.5 W/cm² to proximal transducers, and 8.5 W/cm² to distal transducers. Dimensions of the ablation zone were measured to be 3.2 ± 0.2 cm × 2.4 ± 0.2 cm (n = 3 experiments). In a diverging configuration, applied power levels were 12.5 W/cm² to proximal transducers and 15 W/cm² to distal transducers. Dimensions of the ablation zone were measured to be 4.8 ± 0.5 cm × 3.0 ± 0.1 cm (n = 4) experiments. Figure 7 shows sample ablation zones created in ex vivo liver tissue with two applicators inserted diverging and converging configurations.

Figure 7.

Sample ablation zone in ex vivo bovine liver after 10 min ablation with two applicators inserted in (a) diverging configuration and (b) converging configuration. Increased power levels were applied to the tip transducers, and lower power levels were applied to the proximal transducers. Complete, contiguous ablation zones were obtained with minimal clefts or indentations along the periphery.

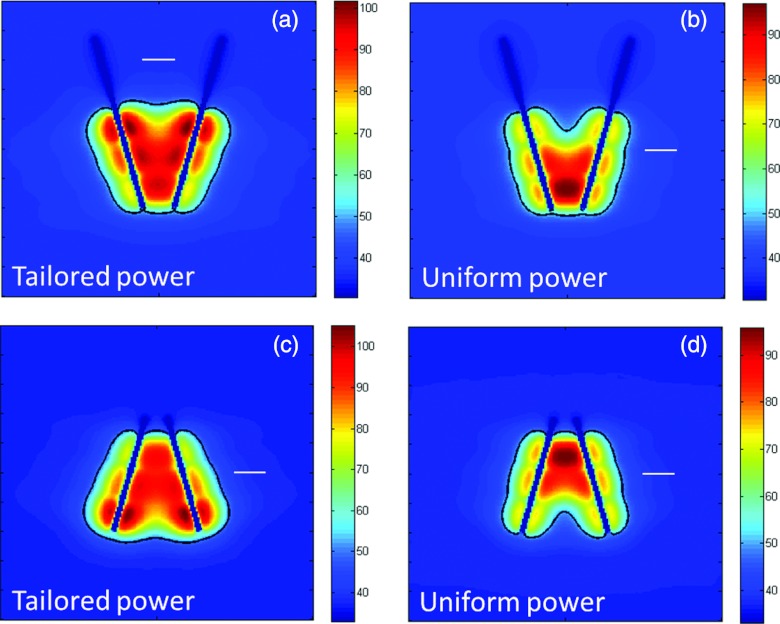
We simulated in vivo ablations with two applicators each containing three independently powered transducers. For converging applicators, power levels applied to transducers decreased from the proximal transducer (17 W/cm²) towards the tip (25 W/cm²), whereas the reverse power delivery scheme was applied for diverging applications. We also included simulations of ablations with uniform power (20 W/cm²) applied to transducers along the length of the applicator. Figure 8 shows the temperature profiles and lethal thermal dose profiles after 10 min ablations with applicators in nonparallel configurations using tailored and uniform power delivery profiles. In a converging configuration, implants with uniform power profiles create a hotspot where applicators are closest to each other. Conversely, in diverging implants, uniform power profiles result in noncontiguous ablation zones (clefts) where the applicators are furthest apart. These undesired heating profiles (clefts and hotspots) are avoided when tailored power profiles can be applied

Figure 8.

Temperature maps and extents of the ablation zone after 10 min ablations with two applicators inserted in converging (a and b) and diverging (c and d) implants. When power supplied to individual transducers is tailored along the length of the applicators (a and c), there are no clefts or indentations in the ablation zone. However, applying uniform powers to all transducers results in hotspots where applicators are closest to each other, and clefts or indentations in the ablation zone where applicators are furthest apart. The white line in each panel corresponds to a 1 cm scale.

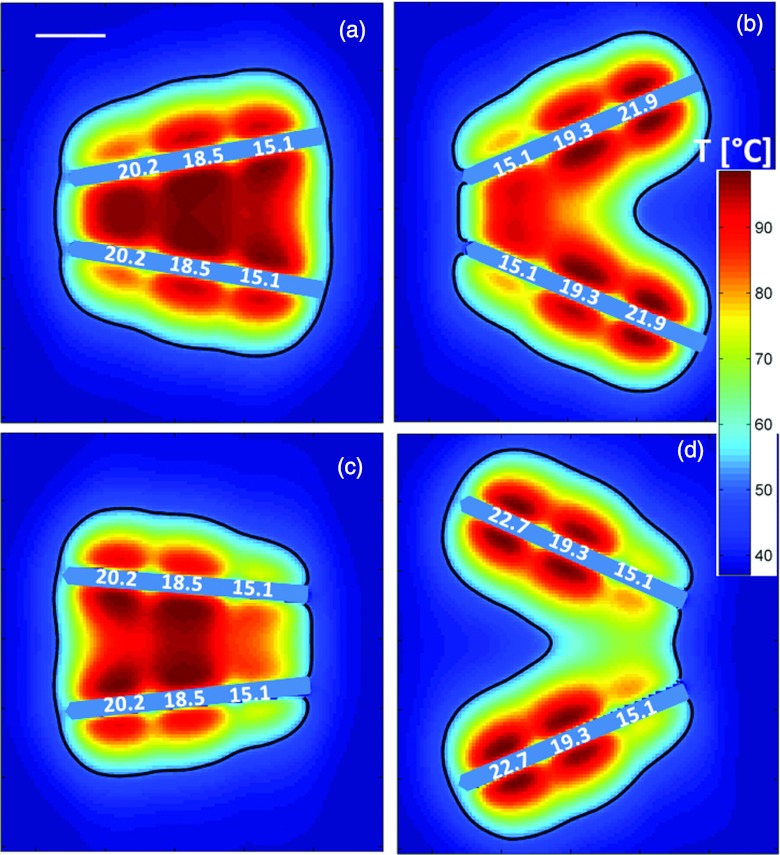
Figures 9a, 9b show temperature profiles and estimated extents of the ablation zone for applicators in converging configurations at angles of 20° and 45°. At 20°, a contiguous coagulation zone can be achieved by increasing applied power levels from the tip (15.1 W/cm²) to the proximal transducer (20.2 W/cm²). At an angle of 45°, however, a contiguous ablation zone cannot be obtained even with application of increased power levels (22.7 W/cm²) to the proximal transducers. Figures 9c, 9d shows temperature profiles and estimated extents of the ablation zone for applicators in a diverging configuration with interapplicator tip spacings of 2 cm and 4 cm. The model predicts a contiguous ablation zone cannot be obtained within 10 min of heating while limiting peak tissue temperatures to 100 °C.

Figure 9.

Temperature maps and extents of the ablation zone after 10 min ablations with two applicators inserted in converging (a and b) and diverging (c and d) implants at varying angles. For converging implants, applicator tips are spaced 1 cm apart, with applicators inserted at angles (a) 30° and (b) 45° to the normal. For diverging implants, applicator tips are spaced (c) 3 cm and (d) 4 cm apart. Applied intensity levels [W/cm²] for each transducer are indicated along the length of the applicators.

DISCUSSION

This study was performed to evaluate interstitial ultrasound in implant configurations suitable for multiple-applicator liver ablation with parallel and nonparallel implants, and explore the feasibility of tailoring ablation zones with longitudinal power control. Heating experiments in ex vivo bovine tissue demonstrated the ability to create contiguous ablation zones with applicators consisting of two transducers. The axial and cross section dimensions of the ablation zone predicted by computer models were in very good agreement with those observed experimentally. The computer model was used to determine the performance of these configurations in an in vivo setting at various blood perfusion rates.

Blood perfusion in highly perfused organs such as the liver poses a substantial heat sink during thermal ablation procedures. Using multiple applicators spaced up to 3 cm apart results in synergistic heating, leading to larger ablation zones. Ex vivo experiments and simulations indicated that complete, contiguous ablation zones could be created within 10 min with interstitial ultrasound applicators in configurations 1–3. When limiting peak tissue temperatures to 100 °C, our simulations indicated that blood perfusion rates were a major limiting factor for the size of ablation zones in vivo. At low and moderate blood perfusion rates (5 and 12 kg m⁻³ s⁻¹), contiguous ablation zones could be obtained using two applicators (2 cm spacing) or three applicators (spaced up to 3 cm apart) within 10 min of heating. At a blood perfusion rate of 15 kg m⁻³ s⁻¹, however, 15 min of heating were required to create a contiguous ablation zone using configurations 1 and 3, while restricting maximum tissue temperatures to 100 °C.

Of the three implant configurations considered in this study, configuration 2 created contiguous ablation zones with axial cross section closest to a circle. For all perfusion ranges, the difference between d₂ and d₁ remained under 2 mm using configuration 2 (an ideal circle would have d₂ = d₁). On the other hand, differences between d₂ and d₁ range between 5 and 10 mm for configuration 3, with larger differences for 10 min ablations and higher blood perfusion rates. Larger differences between d₂ and d₁ indicate scalloping along the periphery of the ablation zone (Fig. 6). These results suggest that interapplicator spacing should be restricted to 2 cm if near-spherical ablation zones are desired.

At a given perfusion level, increasing heating duration from 10 to 15 min results in increase of the maximum ablation zone diameter by up to 4–6 mm. Furthermore, for configurations 1 and 3, 10 min of heating were not sufficient for creating contiguous ablation zones at high blood perfusion rates. Both the experimental and simulation studies indicate that the length of the ablation zone (d₃) is restricted to the segment of the applicator containing the tubular ultrasound transducers. At all blood perfusion rates and heating durations, the ablation zones did not extend more than 5 mm beyond the edges of the proximal/distal transducers, consistent with other studies. For configurations 2 and 3, adding an additional transducer along the length of the applicator had little impact on d₁ and d₂. However, for configuration 1, adding a fourth transducer at higher perfusion rates results in up to 4 mm increases in d₁ and d₂. This is due to the increased power deposition and resultant increase in growth of the ablation zone by thermal conduction. These results demonstrate ability to control the length of the ablation zone with minimal impact on cross sectional dimensions of the ablation zone using interstitial ultrasound technology.

When power levels were restricted to maintain tissue temperature below 100 °C, simulations of in vivo heating showed that 10–15 min ablations were required to create complete, contiguous ablation zones for three applicators, spaced 2 cm apart, ranging from 4.5 × 4.4 cm to 3.3 × 3.6 cm for blood perfusion rates between 5 and 15 kg m⁻³ s⁻¹. When higher power levels were used, ablation zones ranged from 5.6 cm × 4.1 cm to 5.1 cm × 3.6 cm for blood perfusion rates between 5 and 15 kg m⁻³ s⁻¹. Applicators in configuration 3, a clustered array spaced 3 cm apart, yielded noncontiguous ablation zones after 10 min heating. The synergistic heating from three applicators after 10 min was unable to overcome the large heat sink due to blood perfusion. Contiguous ablation zones extending 6.1 cm × 5.6 cm were formed after 15 min of heating for low perfusion cases (m_bl = 5 kg m⁻³ s⁻¹), however, at high perfusion rates (m_bl = 15 kg m⁻³ s⁻¹) the outer boundary of the ablation zone is scalloped in between applicators reducing effective treatment diameter to 5.7 × 4.9 cm. We note that in these simulations, fairly high tissue perfusion values were utilized, however, necrotic tumors may have severely reduced blood perfusion rates. Furthermore, the type of the tumor, location in the liver, and extent of liver cirrhosis may have a dramatic impact on nominal perfusion values within the target.⁶⁵

Multiple applicator ablation with other energy modalities (RF and MW) are in clinical use for treatment of large tumors, and are briefly compared here to interstitial ultrasound technology. The commercially available Covidien 915 MHz Evident system creates ablation zones up to 4.6 cm × 4.6 cm × 5.1 cm in ex vivo bovine liver after 10 min ablations with three water cooled antennas spaced 2 cm apart.⁶⁶ The BSD Microtherm-X creates ablation zones 5.2 cm × 5.5 cm × 6 cm, operating synchronously with 45 W applied power for 10 min.⁶⁷ Similarly, clustered RF applicators have been demonstrated to produce ablation zones of 4.7 cm diameter in ex vivo liver after 15 min, and 4.5–7 cm for treatment of intrahepatic colorectal metastases in humans.⁶⁸ In a similar setting, the multiapplicator interstitial ultrasound implants were shown to produce comparable ablation zones of 4.9–5.6 cm diameter in the ex vivo experiments, and length of the ablation zone ranging from 3.8 to 5.6 cm depending on the number of ultrasound transducers in each catheter. These data indicate that multiple-applicator interstitial ultrasound devices can create ablation zones which may be slightly smaller than MW systems, and comparable to RF ablation systems, within similar heating times.

One advantage of interstitial ultrasound compared to other ablation modalities is the ability to tailor heating along the length of the applicators, through the use of linear arrays of independently powered ultrasound elements. While parallel insertion can be readily achieved in experimental studies using well-defined templates, this may not always be possible in practice due to anatomical considerations. The inability to tailor the heating pattern along the length of the applicator, may lead to hot spots where applicators are closest to each other, and cold spots (inadequate ablation) where applicators are furthest away (Fig. 8). While tailoring the applied power levels may enable the physician to adjust for nonparallel implants, we note that the ability to obtain contiguous ablation zones is dependent on the maximum spacing between applicators. When spacing between transducers exceeds 3 cm [Figs. 9b, 9d], contiguous ablation zones cannot be obtained within 10 min of heating while maintaining tissue temperatures below 100 °C. This is consistent with the limitations of interstitial ultrasound heating technology as analyzed in the parallel implant portion of this study. Knowledge of the applicator positions obtained from preprocedural and periprocedural imaging, placement of invasive temperature sensors, and predictive computer models may enable tailoring of heating profiles along the length of interstitial ultrasound applicators in nonparallel configurations to conform to patient-specific targets. Based on the positions of implanted applicators as determined by imaging, forward and/or inverse treatment planning tools may be used to determine appropriate power levels for adequate thermal coverage of the target, as has been implemented for interstitial ultrasound hyperthermia procedures.⁶⁹ CT and ultrasound are the most commonly used imaging modalities for guiding percutaneous tumor ablation.⁷⁰ For parallel implants, the use of surface templates (as used for currently available RF and MW ablation systems) can augment imaging data to assess applicator positioning. Recent developments in precise placement and electromagnetic tracking of applicators and multimodality image fusion provide the promise of improved applicator localization relative to the tumor, and may enable tailored heating with the use of catheter-based ultrasound technology.⁷¹ A detailed study of the feasibility of tailoring heating profiles—from nonparallel, multiple interstitial ultrasound applicators—to patient-specific targets is a subject of ongoing research in our laboratory.

Another advantage of interstitial ultrasound applicators is the relative independence of their energy deposition patterns from applicator insertion depth or proximity of adjacent devices. The wavelengths of ultrasound energy in the 6–8 MHz range are small in soft tissue, thus the energy emitted from each transducer segment is collimated and well-defined by the dimensions of the respective element.¹⁴ This is in contrast to the wavelength of MW energy in the 915 MHz–2.45 GHz range, which varies from 4.5 to 2 cm, thereby making it difficult to control or vary heating length of individual devices. Currently available MW antennas, typically have a minimal insertion depth below which the antenna efficiencies and radiation pattern diverge from prescribed values.⁷² A recent study by Sindram et al.,³⁴ noted the occurrence of skin burns when a cluster of MW applicators was inserted at a moderate angle (10°) and at insertion depths < 5 cm. Since ultrasound energy from interstitial applicators is tightly collimated to the individual transducers along the length of the applicator,¹⁶ it offers the potential to avoid skin burns and unpredictable energy deposition patterns, especially when heating tumors closer to the surface of the liver. It should be noted that this collimation and high operating frequency (6–8 MHz) precludes the possibility of using phasing strategies between applicators for focusing energy, which is possible with MW applicators.⁷²

SUMMARY

We evaluated configurations of multiple, interstitial ultrasound applicators for large volume liver ablation using bioacoustic-thermal models and experiments in ex vivo bovine liver.

Simulations of these implant configurations within moderate to highly perfused liver tissue (m_bl = 5–15 kg m⁻³ s⁻¹), indicated that lesion dimensions with 2–3 cm clustered arrays vary from 3.8 × 1.6 cm (15 kg m⁻³ s⁻¹) to 6.2 × 5.7 cm (5 kg m⁻³ s⁻¹), with scalloping and variation of diameter more apparent at the higher perfusion and shorter times. When unrestricted power is applied to transducers without consideration of maximum tissue temperatures, ablation zone up to 6.1 × 5.4 cm can be attained in 15 min, even at high perfusion rates (15 kg m⁻³ s⁻¹). Ex vivo ablations with 2–3 parallel applicators spaced 2–3 cm apart yielded ablation zones of 4.0–5.6 cm × 3.2–4.9 cm in cross section. Simulations of ex vivo heating using the same parameters as the experiments yielded ablation zone dimensions in close agreement to experiment. These are comparable to current values obtained for clustered arrays of RF and MW ablation systems. Further, the ability to tailor heating along the length of interstitial ultrasound applicators allows the possibility to adjust heating profiles for converging or diverging implants as anticipated for percutaneous insertion under image guidance, independent of insertion depth and alignment with adjacent applicators, and may enable conformal heating of patient-specific targets.